Proceedings of International Conference on Applied Mathematics (ICAM 2017), Taza, Morocco

Editorial

Proceedings of International Conference on Applied Mathematics (ICAM’ 2017), Taza, Morocco
October 19-20, 2017 (Editorial)

Youssef Akdim, Soumia Lalaoui Rhali, Abdelhakim Chillali, Mounir Mekkour, Abdelhai El Azzouzi, Chihab Yazough.

Adv. Sci. Technol. Eng. Syst. J. 2(5), 193-194 (2017); DOI: 10.25046/aj020527

Articles

Comparison of K-Means and Fuzzy C-Means Algorithms on Simplification of 3D Point Cloud Based on Entropy Estimation

Abdelaaziz Mahdaoui, Aziz Bouazi, Abdallah Marhraoui Hsaini, El Hassan Sbai

Adv. Sci. Technol. Eng. Syst. J. 2(5), 38-44 (2017);

View Description

In this article we will present a method simplifying 3D point clouds. This method is based on the Shannon entropy. This technique of simplification is a hybrid technique where we use the notion of clustering and iterative computation. In this paper, our main objective is to apply our method on different clouds of 3D points. In the clustering phase we will use two different algorithms; K-means and Fuzzy C-means. Then we will make a comparison between the results obtained.

Degenerate 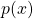$p(x)$ -elliptic equation with second membre in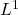 $L^1$

Adil Abbassi, Elhoussine Azroul, Abdelkrim Barbara

Adv. Sci. Technol. Eng. Syst. J. 2(5), 45-54 (2017);

View Description

In this paper, we prove the existence of a solution of the strongly nonlinear degenerate $p(x)$ -elliptic equation of type:
$\mathcal{(P)}\left\{\begin{array}{rl} - div\; a(x,u,\nabla u) +g(x,u,\nabla u)& = f \quad in \;\Omega, \\ u = 0 \quad on \quad \partial\Omega, \end{array}\right.$
where $\Omega$ is a bounded open subset of $I\!\!R^{N}, N\geq 2, a$ is a Caratheodory function from $\Omega\times I\!\!R\times I\!\!R^{N}$ into $I\!\!R^{N}$ , who satisfies assumptions of growth, ellipticity and strict monotonicity. The nonlinear term $g: \Omega\times I\!\!R\times I\!\!R^{N}\longrightarrow I\!\!R$ checks assumptions of growth, sign condition and coercivity condition, while the right hand side $f$ belongs to $L^{1}(\Omega)$ .

Steel heat treating: mathematical modelling and numerical simulation of a problem arising in the automotive industry

Jose Manuel Diaz Moreno, Concepcion Garcia Vazquez, Maria Teresa Gonzalez Montesinos, Francisco Ortegon Gallego, Giuseppe Viglialoro

Adv. Sci. Technol. Eng. Syst. J. 2(5), 55-62 (2017);

View Description

We describe a mathematical model for the industrial heating and cooling processes of a steel workpiece representing the steering rack of an automobile. The goal of steel heat treating is to provide a hardened surface on critical parts of the workpiece while keeping the rest soft and ductile in order to reduce fatigue. The high hardness is due to the phase transformation of steel accompanying the rapid cooling. This work takes into account both heating-cooling stage and viscoplastic model. Once the general mathematical formulation is derived, we can perform some numerical simulations.

Petrov-Galerkin formulation for compressible Euler and Navier-Stokes equations

Nacer E. El Kadri E, Abdelhakim Chillali

Adv. Sci. Technol. Eng. Syst. J. 2(5), 63-69 (2017);

View Description

The resolution of the Navier-Stokes and Euler equations by the finite element method is the focus of this paper. These equations are solved in conservative form using, as unknown variables, the so-called conservative variables (density, momentum per unit volume and total energy per unit volume). The variational formulation developed is a variant of the Petrov-Galerkin method. The nonlinear system is solved by the iterative GMRES algorithm with diagonal pre-conditioning. Several simulations were carried out, in order to validate the proposed methods and the software developed.

Simulation of flows in heterogeneous porous media of variable saturation

Nacer E. El Kadri E, Abdelhakim Chillali

Adv. Sci. Technol. Eng. Syst. J. 2(5), 70-77 (2017);

View Description

We develop a resolution of the Richards equation for the porous media of variable saturation by a finite element method. A formulation of interstitial pressure head and volumetric water content is used. A good conservation of the global and local mass is obtained. Some applications in the case of heterogeneous media are presented. These are examples which make it possible to demonstrate the capillary barrier effect.

Models accounting for the thermal degradation of combustible materials under controlled temperature ramps

Alain Brillard, Patrick Gilot, Jean-Francois Brilhac

Adv. Sci. Technol. Eng. Syst. J. 2(5), 78-87 (2017);

View Description

The purpose of this conference is to present and analyze di_erent models accounting for the thermal degradation of combustible materials (biomass, coals, mixtures…), when submitted to a controlled temperature ramp and under non-oxidative or oxidative atmospheres. Because of the possible rarefaction of fossil fuels, the analysis of di_erent combustible materials which could be used as (renewable) energy sources is important. In industrial conditions, the use of such materials in energy production is performed under very high temperature ramps (up to 105 K/min in industrial pulverized boilers). But the analysis of the thermal degradation of these materials usually _rst starts under much lower temperature ramps (less than 100 K/min), in order to avoid di_usional limitations which modify the thermal degradation.

Threshold Multi Split-Row algorithm for decoding irregular LDPC codes

Chakir Aqil, Rachid El Alami, Ismail Akharraz, Abdelaziz Ahaitouf

Adv. Sci. Technol. Eng. Syst. J. 2(5), 88-93 (2017);

View Description

In this work, we propose a new threshold multi split-row algorithm in order to improve the multi split-row algorithm for LDPC irregular codes decoding. We give a complete description of our algorithm as well as its advantages for the LDPC codes. The simulation results over an additive white gaussian channel show that an improvement in code error performance between 0.4 dB and 0.6 dB compared to the multi split-row algorithm.

A new color image encryption algorithm based on iterative mixing of color channels and chaos

Mohamed Essaid, Ismail Akharraz, Abderrahim Saaidi and Ali Mouhib

Adv. Sci. Technol. Eng. Syst. J. 2(5), 94-99 (2017);

View Description

In this paper, we present a novel secure cryptosystem for direct encryption of color images, based on an iterative mixing spread over three rounds of the R, G and B color channels and three enhanced chaotic maps. Each round includes an affine transformation that uses three invertible matrices of order 2 _ 2; whose parameters are chosen randomly from a chaotic map. The proposed algorithm has a large secret key space and strong secret key sensitivity, which protects our approach from a brutal attack. The simulation results show that our algorithm is better for color images in terms of Peak Signal to Noise Ratio (PSNR), entropy, Unified Average Changing Intensity (UACI) and Number of Pixels Change Rate (NPCR).

Cyclical contractive conditions in probabilistic metric spaces

Abderrahim Mbarki, Rachid Oubrahim

Adv. Sci. Technol. Eng. Syst. J. 2(5), 100-103 (2017);

View Description

The purpose of this paper is to prove a fixed point theorem for a probabilistic k-contraction restricted to two nonempty closed sets of a probabilistic metric spaces, then we prove that these results can be extended to a collection of finite closed sets.

Group law and the Security of elliptic curves on $F_p[e_1,...,e_n]$

Abdelalim Seddik, Chaichaa Abdelhak, Souhail Mohamed

Adv. Sci. Technol. Eng. Syst. J. 2(5), 104-108 (2017);

View Description

In this paper, we study the elliptic curve $E_{a,b}(A_P)$ , with $A_P$ the localization of the ring $A=F _p[e_1,...,e_n]$ where $e_ie_i=e_i$ and $e_ie_j=0$ if $i\neq j$ , in the maximal ideal $P=(e_1,...,e_n)$ . Finally we show that $Card(E_{a,b}(A_P))\geqslant (Card(E_{a,b}(F_p))-3)^n+Card(E_{a,b}(F_p))$ and the execution time to solve the problem of discrete logarithm in $E_{a,b}(A_P)$ is $\Omega(N)$ , such that the execution time to solve the problem of discrete logarithm in $E_{a,b}(F_p)$ is $O(\sqrt{N})$ . The motivation for this work came from search for new groups with intractable (DLP) discrete logarithm problem is there great importance.

Nonlinear parabolic problem with lower order terms in Musielak-Orlicz spaces

Mhamed Elmassoudi, Ahmed Aberqi, Jaouad Bennouna

Adv. Sci. Technol. Eng. Syst. J. 2(5), 109-123 (2017);

View Description

We prove an existence result of entropy solutions for the nonlinear parabolic problems: $\frac{\partial b(x,u)}{\partial t} + A(u) - div(\Phi(x,t,u))+H(x,t,u,\nabla u) =f,$ and $A(u)=-div(a(x,t,u,\nabla u))$ is a Leary-Lions operator defined on the inhomogeneous Musielak-Orlicz space, the term $\Phi(x,t,u)$ is a Cratheodory function assumed to be continuous on u and satisfy only the growth condition $\Phi(x,t,u)\leq c(x,t)\overline{M}^{-1}M(x,\alpha_{0}u)$ , prescribed by Musielak-Orlicz functions $M$ and $\overline{M}$ which inhomogeneous and not satisfy $\Delta_2$ -condition, $H(x,t,u,\nabla u)$ is a Cratheodory function not satisfies neither the sign condition or coercivity and $f\in L^{1}(Q_T)$ .

S-asymptotically w-periodic solutions in the p-th mean for a Stochastic Evolution Equation driven by Q-Brownian motion

Solym Mawaki Manou-Abi, William Dimbour

Adv. Sci. Technol. Eng. Syst. J. 2(5), 124-133 (2017);

View Description

In this paper, we study the existence (uniqueness) and asymptotic stability of the p-th mean S-asymptotically !-periodic solutions for some nonautonomous Stochastic Evolution Equations driven by a Q-Brownian motion. This is done using the Banach fixed point Theorem and a Gronwall inequality.

On the Spectrum of problems involving both p(x)-Laplacian and P(x)-Biharmonic

Abdelouahed El Khalil, My Driss Morchid Alaoui, Abdelfattah Touzani

Adv. Sci. Technol. Eng. Syst. J. 2(5), 134-140 (2017);

View Description

We prove the existence of at least one non-decreasing sequence of positive eigenvalues for the problem,
$\begin{gathered}\left\{ \begin{array}{ll} \Delta_{p(x)}^{2}u-\triangle_{p(x)}u= \lambda |u|^{p(x)-2}u, \ \ \quad in \ \Omega \\ u\in W^{2,p(x)}(\Omega)\cap W_{0}^{1,p(x)}(\Omega),\end{array}\right. \end{gathered}$
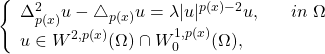
Our analysis mainly relies on variational arguments involving Ljusternik-Schnirelmann theory.

Existence and Boundedness of Solutions for Elliptic Equations in General Domains

Elhoussine Azroul, Moussa Khouakhi, Chihab Yazough

Adv. Sci. Technol. Eng. Syst. J. 2(5), 141-151 (2017);

View Description

This article is devoted to study the existence of solutions for the strongly nonlinear $p(x)$ -elliptic problem:
$- \Delta_{p(x)} (u) + \alpha_0 |u|^{p(x)-2}u = d(x)\frac{|\nabla u|^{p(x)}}{|u|^{p(x)}+1} + f- div g(x) \quad \text{in } \Omega,$

$u \in W_0^{1,p(x)}(\Omega),$
Where $\Omega$ is an open set of $\mathbb{R}^N$ , possibly of infinite measure, also we will give some regularity results for these solutions.

Nonresonance between the first two Eigencurves of Laplacian for a Nonautonomous Neumann Problem

Ahmed Sanhaji, Ahmed Dakkak

Adv. Sci. Technol. Eng. Syst. J. 2(5), 152-159 (2017);

View Description

We consider the following Neumann elliptic problem
$\left\{ \begin{array}{rl} -\Delta u =\alpha\,m_{1}(x)\,u+m_{2}(x)\,g(u)+h(x)\quad & in \: \Omega,\\ \quad\\ \frac{\partial u}{\partial\nu} = 0\qquad\qquad\qquad\qquad\qquad\qquad\quad& on\: \partial\Omega. \end{array} \right.$
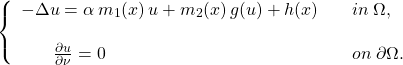
By means of Leray-Schauder degree and under some assumptions on the asymptotic behavior of the potential of the nonlinearity g, we prove an existence result for our equation for every given $h\in L^{\infty}(\Omega)$ .

Existence Results for Nonlinear Anisotropic Elliptic Equation

Youssef Akdim, Mostafa El moumni, Abdelhafid Salmani

Adv. Sci. Technol. Eng. Syst. J. 2(5), 160-166 (2017);

View Description

In this work, we shall be concerned with the existence of weak solutions of anisotropic elliptic operators $Au +\sum_{i=1}^{N}g_{i}(x, u, \nabla u)+\sum_{i=1}^{N}H_{i}(x, \nabla u)=f-\sum_{i=1}^{N} \frac{\partial }{\partial x_{i}}k_{i}$ where the right hand side $f$ belongs to $L^{p^{'}_{\infty}}(\Omega)$ and $k_{i}$ belongs to $L^{p_{i}^{'}}(\Omega)$ for $i=1,...,N$ and $A$ is a Leray-Lions operator. The critical growth condition on $g_{i}$ is the respect to $\nabla u$ and no growth condition with respect to u, while the function $H_{i}$ grows as $|\nabla u|^{p_{i}-1}$ .

Boundary gradient exact enlarged controllability of semilinear parabolic problems

Touria Karite, Ali Boutoulout

Adv. Sci. Technol. Eng. Syst. J. 2(5), 167-172 (2017);

View Description

The aim of this paper is to study the boundary enlarged gradient controllability problem governed by parabolic evolution equations. The purpose is to find and compute the control $u$ which steers the gradient state from an initial gradient one $\nabla y_{_{0}}$ to a gradient vector supposed to be unknown between two defined bounds $b_1$ and $b_2$ , only on a subregion $\Gamma$ of the boundary $\partial\Omega$ of the system evolution domain $\Omega$ . The obtained results have been proved via two approaches, The sub-differential and Lagrangian multiplier approach.

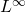$L^\infty$ -Estimates for Nonlinear Degenerate Elliptic Problems with p-growth in the Gradient

Youssef Akdim, Mohammed Belayachi

Adv. Sci. Technol. Eng. Syst. J. 2(5), 173-179 (2017);

View Description

In this work, we will prove the existence of bounded solutions for the nonlinear elliptic equations

$- div(a(x,u,\nabla u)) = g(x,u,\nabla u) -divf,$

in the setting of the weighted Sobolev space $W^{1,p}(\Omega,w)$ where $a$ , $g$ are Caratheodory functions which satisfy some conditions and $f$ satisfies suitable summability assumption.

Doubly Nonlinear Parabolic Systems In Inhomogeneous Musielak- Orlicz-Sobolev Spcaes

Ahmed Aberqi, Mhamed Elmassoudi, Jaouad Bennouna, Mohamed Hammoumi

Adv. Sci. Technol. Eng. Syst. J. 2(5), 180-192 (2017);

View Description

In this paper, we discuss the solvability of the nonlinear parabolic systems associated to the nonlinear parabolic equation: $\frac{\partial b_{i}(x,u_{i})}{\partial t} -div(a(x,t,u_{i},\nabla u_{i}))- \phi_{i}(x,t,u_{i})) +f_{i}(x,u_{1},u_{2})=0$ where the function $b_{i}(x,u_{i})$ verifies some regularity conditions, the term $\Big(a(x,t,u_{i},\nabla u_{i})\Big)$ is a generalized Leray-Lions operator and $\phi_{i}$ is a Caratheodory function assumed to be Continuous on $u_i$ and satisfy only a growth condition. The source term $f_{i}(t,u_{1},u_{2})$ belongs to $L^{1}(\Omega\times(0,T))$ .