An Adaptive Heterogeneous Ensemble Learning Model for Credit Card Fraud Detection
Volume 9, Issue 3, Page No 01-11, 2024
Author’s Name: Tinofirei Museba1,a), Koenraad Vanhoof2
View Affiliations
1 Department of Information Systems, College of Business and Economics, University of Johannesburg, Johannesburg, 2006, South Africa
2 Department of Quantitative Methods, Universiteit Hasselt, Campus Diepenbeek, Diepenbeek, Kantoor B10, Belgium
a)whom correspondence should be addressed. E-mail: tmuseba@uj.ac.za
Adv. Sci. Technol. Eng. Syst. J. 9(3), 1-11(2024); ![]() DOI: 10.25046/aj090301
DOI: 10.25046/aj090301
Keywords: Credit Card Fraud, Machine learning, Concept drift, Ensemble selection, Class imbalance
Export Citations
The proliferation of internet economies has given the corporate world manifold advantages to businesses, as they can now incorporate the latest innovations into their operations, thereby enhancing ease of doing business. For instance, financial institutions have leveraged credit card usage on the aforesaid proliferation. However, this exposes clients to cybercrime, as fraudsters always find ways to breach security measures and access customers’ confidential information, which they then use to make fraudulent credit card transactions. As a result, financial institutions incur huge losses amounting to billions of United States dollars. To avert such losses, it is important to design efficient credit card fraud detection algorithms capable of generating accurate alerts. Recently, machine learning algorithms such as ensemble classifiers have emerged as the most effective and efficient algorithms in an effort to assist fraud investigators. There are many factors that hinder the financial sector from designing machine learning algorithms that can efficiently and effectively detect credit card fraud. Such factors include the non-stationarity of data related to concept drift. In addition, class distributions are extremely imbalanced, while there is scant information on transactions that would have been flagged by fraud investigators. This can be attributed to the fact that, owing to confidentiality regulations, it is difficult to access public data. In this article, the author designs and assesses a credit card fraud detection system that can adapt to the changes in data distribution and generate accurate alerts.
Received: 15 December 2023, Revised: 22 February 2024, Accepted: 23 February 2024, Published Online: 16 May, 2024
1. Introduction
The internet offers a great deal of convenience to people’s daily routines. However, in the financial sector, which has been progressively adopting e-commerce, web-based technologies can also be a curse. The internet and related applications grow continually because they enable individuals and organisations to digitise and innovate their operations, thus, enabling them to perform more efficiently. With regard to commerce, the advent of the internet saw the birth of cashless transactions through the use of credit and debit cards, in addition to net banking and Unified Payments Interface (UPI) options [1, 2]. In [3], the author explains that fraudulent incidences have invariably risen in proportion with the rising volume of cashless commerce, thus, causing financial institutions to incur enormous losses.
In [4] the author defines credit card fraud as the use of stolen identity details to purchase goods and services or effect electronic cash transfers. Such fraud is not limited to online transactions as stolen or lost physical credit cards can also be used to transact [5]. The last ten years have seen a growing trend in credit card fraud, thus, prompting financial institutions globally to seek for techniques that can accurately and efficiently detect such crime. In this case, machine learning approaches are the most preferred techniques for detecting credit card fraud [6,7,8,9,10]. However, in [11] the author notes that machine learning has some inherent limitations, notably class imbalance, concept drift and verification latency. In [12] the author contends that these challenges are further compounded by lack of reliable up-to-date datasets, wherein hardly 1% of the samples that are labelled fraudulent are classified as such. The author in [13] refers to this phenomenon as class imbalance and, according to the author in [9], it inhibits standard classifiers from optimally detecting credit card fraud.
Apart from class imbalance, credit card transactions are dynamic in nature, which then introduces the concept drift problem. This implies that there are no clear demarcations between normal and fraudulent transactions, given that there may be no variance between the fraudsters’ and the legitimate cardholders’ behaviour spending patterns. In any case, spending habits are dynamic, so non-fraudulent and fraudulent transactions have more or less equal chances of being flagged as suspicious. In attempting to solve the class imbalance problem, researchers have applied both oversampling and under sampling techniques, or combined these with the SMOTE technique [13]. Notwithstanding the aforementioned efforts, concept drift continues to be a hindrance in the detection of fraudulent card transactions using ensemble classifiers.
1.1 Credit Card Fraud
Credit card fraud is a criminal case and occurs when a person uses someone else’s personal credentials together with their credit standing to borrow money or use credit cards to transact with no intention of refunding the debt. Credit card is considered to be a form of identity that is most prevalent. When a credit is misappropriated, the victim typically accrues unpaid debts in their names. The process of identifying and detecting credit card flaws can be solved but the implementation process demands more effort and time and may lead to a temporary setback of credit scores temporarily and affect a person’s credit score to get new credit for a time. To detect credit card transactional flaws and minimize identity theft, the implementation of machine learning in the design of models capable of addressing such problems has gained momentum due to the results obtained. This research article proposes a machine learning ensemble architecture capable of detecting credit card transaction flaws. For credit card fraud detection, machine learning algorithms can classify whether a credit card transaction is authentic or fraudulent. Machine learning algorithms can make a prediction to determine whether it is the cardholder or the fraudsters using the credit card through credit card profiling. In addition, machine learning algorithms can use outlier detection techniques to identify vast amounts of transactions for outliers from regular credit cards transactions to detect credit card fraud. When compared to other conventional fraud detection techniques, machine learning algorithms offer faster detection and adaptation to drifting concepts. A machine learning model has the capacity to quickly identify any drifts from regular transactions and user behaviour in real time. By detecting anomalies such as a sudden increase in transactional amount or location change, machine learning algorithms are capable of minimising the risk of fraud and ensure more secure transactions.
1.2 Ensemble Learning
Machine Learning algorithms are capable of learning from data, find complex and noise patterns, and predict credit card theft. Ensemble Learning is a machine learning approach capable of optimising generalization performance and resilience in prediction tasks through the process of combining multiple models. Combining multiple prediction models enables the mitigation of errors or biases prevalent in classifier models by leveraging the combined outputs of the ensemble. Ensemble learning combines the output of diverse models to generate an accurate prediction. Ensemble methods leverage the diversity and complementarity of their predictions to improve their generalization performance. As the underlying concept, ensemble learning considers multiple perspectives and utilizes the capacity of diverse models in an effort to optimize the overall generalization performance of the learning model. Ensemble learning optimises the accuracy of the learning model and also provides resilience against uncertainties in the data such as noise, skewed distributions and missing values. Effectively combining predictions from multiple diverse models has proven to be a powerful technique in various domains, providing more robust, accurate and reliable generalization performance for classification, clustering, regression tasks and anomaly detection by combining different types of base models and aggregation methods. For credit card transaction flaws, ensemble learning techniques are capable of detecting whether a transaction is a fraud or not given the historical spending patterns of a client. Ensemble learning techniques are capable of adapting to spending habits of clients and detect anomalies and alert the bank.
This study proposes a credit card fraud detection system that can be capable of accurately handling class imbalance and concept drift, and detecting credit card fraud. In addition to the foregoing section, there are six ensuing section that make up this paper. Section 2 provides a preview of precious work conducted on credit card transaction fraud. Section 3 describes the data processing process techniques, a description of the base learners, parameter optimisation techniques and feature selection strategy. Section 4 provides a description of the Dynamic Classifier Selection algorithm, performance metrics and the datasets used. Section 5 provides an outline of the experiments conducted and the performance comparisons with other state of the art algorithms. Section 6 provides the conclusion of the study.
2. Literature Review
Scenarios associated with credit card fraud are not uncommon. Consequently, there are various contemporary approaches for detecting and generating accurate alerts that have been proposed. All these approaches are based on machine learning. To improve the detection performance of an ensemble classifier, in [14], the author suggests a machine learning approach-based credit card fraud detection engine that implements a genetic algorithm for feature selection. The prediction performance of the proposed credit card engine is validated with a dataset generated from European cardholders. The proposed engine disregards the relevance of class imbalance and concept drift on the performance of the engine. In order to optimise the efficiency and accuracy of machine learning algorithms for detecting credit card fraud, the author in [15] proposes that blockchain techniques and machine learning algorithms can be combined. Subsequent experiments showed that the approach outperformed all the other proposed algorithms of machine learning. The proposed approach does not consider the prevalence of class imbalance and the presence of concept drift. The author in [16] suggests the application of the Just-Add-Data (JAD) to automate the selection of machine learning algorithms, tune hyperparameter values and estimate prediction performance in the detection of illicit transactions. The proposed version of JAD fails to detect data distribution drift and generate false alarms automatically. The authors in [17] propose a novel approach for detecting credit card fraud by analysing customers’ past transactions details and extracting their behavioral patterns, before clustering them into different groups.
It is difficult to detect credit card fraud with accuracy, because there is need to process enormous streaming data. However, the learning models are not entirely capable of quickly adapting or responding to the fraud. This problem is exacerbated by concept drift, which introduces changes to the target concept. Optimum model performance is further inhibited by class imbalance, overlapping data, the dynamic nature of transactions, the scarcity of datasets and verification latency. These feedback mechanisms may cause delays in signaling fraudulent transactions, thus, not all of them are either caught or reported. Fraudsters design their own adaptive techniques against the existing detection models. This paper formulates a credit card fraud detection system, which incorporates class imbalance and concept drift. The proposed system is also robust against false alarms.
The authors in [18] proposed a machine learning model that implements random forest algorithm to predict and detect daily credit card fraud. The model lacks diversity thereby compromising its accuracy. In [19], the authors proposed a machine learning method with Hybrid feature selection technique consisting of filter and wrapper feature selection steps to ensure that only the most relevant features are used. For feature selection the approach uses Genetic Algorithm which can converge prematurely, and the problem of class imbalance was not addressed. To enhance the accuracy of machine learning algorithms in detecting credit fraud, the authors in [20] proposed a soft voting ensemble learning approach for detecting credit card fraud on imbalanced data. The impact of ensemble diversity and data standardization was not discussed. To address challenges such as class imbalance, concept drift, false positives/negatives, limited generalizability and challenges in real time processing, the authors in [21] proposed a novel ensemble model that integrates a Support Vector Machine, K-Nearest Neighbour, Random Forest, Bagging and Boosting classifiers. The approach is computationally inefficient. In credit card fraud detection, there is little time to perform any resampling of the data when training models, generally precluding the use of bagging, boosting or related methods that resample training data.
3. Data Preprocessing
This study uses standardized datasets, which are scaled within the 0-1 interval and all the missing values are approximated. The study focuses on the problem of class imbalance of credit card fraud datasets. The mean is removed and scaled to unit variance in an effort to standardize numeric features. The data are scaled using the 0-1 normalization method. If 𝑥 is a given feature, then the normalized feature can be computed as follows:
= , where expresses the standardised value.
Feature normalization can significantly improve classifier accuracy. This especially applies to those classifiers that are based on distance or edge calculations and it results in the model being more assertive and accurate. All data related to credit card fraud are subject to class imbalance and their distribution is highly skewed. This can be attributed to the fact that the proportion of fraudulent transactions (minority class) is significantly lower than that of legitimate transactions (majority class). As a result, credit card fraud detection becomes an extremely challenging task. The level of difficulty is compounded by the prevalence of missing values in the relevant datasets. However, this gap can be closed by using XGBoost, which incorporates an algorithm for sparsity segmentation. The algorithm can approximate the missing values with significant accuracy. In addition, the use of standardization helps to subdue the influence of outliers. At the same time, the centralization process is used to curb extreme values. To solve the class imbalance problem, a resampling technique called Synthetic Minority Oversampling Technique (SMOTE) [22] is made use of to enhance the performance of the minority class classifiers recognition. The SMOTE technique generates artificial cases close to observed ones. In the process, it oversamples the minority class. In order to handle class imbalance with overlap, the imbalance ratio and the structure of the dataset are considered in an overlapping metric, which is known as degOver [23]. To handle different types of drifting concepts accurately, the Dynamic Ensemble Selection (DES) is applied, while verification latency is handled by employing the integrated Fraud Detection (FD) [24]. The FD is further integrated with Smooth Clustering based Boosting (SCBoost), which is a noise-robust boosting method and the k-Shortest Distance Ratio (k-SDR). The latter enables the full use of the labelled dataset and prevents interferences from the class imbalance therein. The key function of the k-SDR is to classify an instance by the ratio of its mean distance to k nearest instances in the positive class.
3.1. Base Learners
From an intuitive point of view, the success of an ensemble of classifiers is dependent on the diverse performance of base classifiers [25]. To achieve this, the approach that was adopted in this study used two base learners namely: XGBoost and Support Vector Machines. In the process, these two can also effectively yield both accuracy and efficiency. In addition, Support Vector Machines have proved to be tremendously capable of handling regression and classification challenges in both static and dynamic domains. These machines are widely used to redress dimensionality, which is prevalent in classification problems. In such cases, SVMs find hyperplanes that can separate two classes of linear data in such ways that there can be large distances between the training instances. If the data are non-linear, the SVM kernel function can map them into high dimensional spaces.
For purposes of solving authentic classification problems, particularly the mitigation of model variances, the authors in [26] developed the eXtreme Gradient Boosting (XGBoost). It can also optimise the loss function by including regularisation in handling sparse data and a weighted quantile sketch for tree learning. In terms of speed and accuracy, XGBoost is arguably the best machine learning algorithm, due to the superiority of its mechanisms and weights, such as Taylor’s expansion, which approximates the loss function with remarkable promptness.
3.2. Parameter Optimization
The study employed SVMs and XGBoost as base learners, which are associated with a number of parameters. With regard to predicting how the credit card fraud detection system will perform, the parameters are significantly impactful. For the fraud detection system to perform optimally, the parameters have to be optimised using a number of existing optimisation algorithms, most of which are prone to dimensionality. Moreover, the resultant cost of computation tends to increase dramatically, in proportion to the number of hyperparameters or extended search space. Hyperparameter tuning for most applications is subjective and it relies on empirical judgement and trial and error approaches. To counter the limitations that are associated with existing optimisation algorithms, this study employed an adaptive heterogeneous Particle Swarm Optimiser (PSO), in order to optimise and generate an appropriately optimal subset of accurate parameters. This was also meant to improve the efficacy of XGBoost and SVMs for the classification problem. PSO is a heuristic algorithm and evolutionary computational method that is used extensively. The authors in [27] developed the algorithm and it can also be described as a heuristic population based iterative, global and stochastic optimisation system, which is inspired by the flocking and schooling social behaviours of birds and fish, respectively, for conducting intelligent searches for the optimal solutions [28]. Since it is derivative free, PSO does not require the optimisation problem to be differentiable, therefore, it does not require gradients. These characteristics enable PSO to be applicable to a variety of problems, including those that are discontinuous or non-convex and multimodal. In this study, the instantiation of the particles in the swarm was performed at individual level, thereby introducing heterogeneity. The individual instantiation of particles enables different search behaviours of particles in the swarm to be assumed, as they can randomly select the velocity and position update rules from the behaviour pool. The process also allows for the creation of a swarm composed of particles that are both explorative and exploitative in nature. This enables the optimisation algorithm to explore and exploit for the duration of the search process, thus, preventing premature convergence.
3.3. Feature Selection
XGBoost was employed for the purpose of performing feature selection. As a base learner, XGBoost is used to generate feature importance scores, which are used for measuring the average objective reduction. This is performed as soon as the specific variables have been selected for splitting. In the tree building process, a variable that is associated with a score that is high has a higher importance. This study used XGBoost as a joint base learner with SVM. The researcher followed propositions by the author in [29] when implementing the scores that were derived from feature importance. These propositions provided a guideline in terms of the sequential forward search (SFS) feature selection algorithm. SFS places all related features into a subset, after which it iteratively adds the remaining features until the highest score is attained. This results in the generation of a series of candidate feature subsets. In this case, the feature subset that maximises the cross-validated accuracy is selected as the optimal feature set that is appropriate for the process of training the model in the subsequent steps.
4. Dynamic Classifier Selection
For ensembles of machine learning, there are two key features namely: diversity and accuracy. For the purpose of this study, the researcher selected classifiers based on their accuracy on the validation set, as well as diversity to accommodate both batch and incremental learning, given that transaction data vary with time. To select classifiers based on accuracy and diversity, the Selection by Accuracy and Diversity (SAD) algorithm in [30], which works as shown below, was used:
- Train a set of heterogeneous classifiers from XGBoost and SVM
- Determine the accuracy of each classifier on validation set
- Select the most accurate classifiers
- Measure the diversity between the most accurate classifiers
- Select classifiers with strong diversity into the ensemble and repeat the process until the predetermined size of the ensemble is attained.
- Use majority voting to combine classifiers into an ensemble
- Evaluate the generalisation of the ensemble.
The Q static diversity measure in [31] was adopted in this study. The training dataset was used for generating and learning a pool of classifiers. Given a training dataset D_train = {𝑥,𝑦}, where 𝑥 is an 𝑀x𝑁 dimensional feature matrix and 𝑦 ∈ {0,1}N denote the label. If 𝑦 yields a value of 1, that would indicate a fraudulent transaction, while a value of 0 would imply a legitimate transaction. Here, the aforementioned two base learners, SVM and XGBoost, were used to create a heterogeneous ensemble architecture. SVM and XGBoost are highly renowned in credit card fraud detection, as they can generate highly efficient models. This can be attributed to the fact that the two base learners are frequently updated, in keeping with the behavior change of fraudsters.
4.1. Performance metrics
This paper presents a study that was modelled as a machine learning binary classification task, using five performance evaluation metrics. The main performance metric was the accuracy of the test data. Furthermore, for each model, the Precision, Recall, F1_Score and the Area Under the Curve (AUC) were computed. The AUC provides a proper assessment of the quality of classification of each given model. The AUC metric measures the effectiveness of each classifier for a specific task. The value of AUC is within the interval 0 to 1 and an efficient classifier is identified with an AUC value that is almost close to 1. Accuracy is calculated by dividing the number of correct predictions by the sum of forecasts. Precision is the proportion of correct forecasts to the sum of correct guesses. On the other hand, recall is the ratio of position predictions to the total of positive class values in the test data. The F1 score represents the balance between accuracy and recall. The performance metrics can be expressed mathematically, as shown below:

4.2. Datasets
To conduct the research, two credit card fraud transaction datasets were used. The first dataset was from the Machine Learning group, ULB, which is obtained from Kaggle. The transactions were labelled as either legitimate or fraudulent and they were all made over two days in September 2013 by European cardholders. The dataset consisted of 284 807 transactions instances, of which 492 (0.172%) were fraudulent, thus, making it highly imbalanced. The dataset consisted of 30 features, which ranged from V1 to V28; Time and Amount.
The dataset comprised numerical attributes and its last column indicated the class type (type of transaction) and the value 1 represented a fraudulent transaction, while the value 0 denoted a legitimate transaction. The features V1 to V28 were not named for data security and integrity reasons [32]. The dataset was highly imbalanced and, to solve the class imbalance problem, the Synthetic Minority Oversampling Technique (SMOTE) was applied. A scikit_learn library, called imbleam oversampling, was used to import SMOTE, whose function is to pick samples that are close to each other within the feature space, thereby drawing a line of separation between the data points in the feature space and creating a new instance of the minority at a point along the line. The Time column indicated the number of seconds that transpired between the initial and subsequent transactions. The Amount column featured the amount that was transacted, while the Class column had a values of 1 and 0, which denoted fraudulent and legitimate transactions, respectively.
The second dataset contained credit card transaction data that were sourced by an unnamed institute and were made available on Kaggle. The dataset featured five columns, the first of which was distance from home. As the labelling suggests, the first column showed the distance between the cardholders’ registered home addresses and transactions locations.
The second column, ratio_to_median_purchase, represented the ratio of the transaction to the median of the purchase price, while the third, repeat_retailer, featured checks on whether the last two transactions were made at the same retailer. Used_chip was the penultimate column, which contained verifications on whether or not a physical card was used to make the transaction.
Finally, the used_pin_number column featured verifications pertaining to weather online transactions were fraudulent or not. This dataset consisted of 912 597 legitimate and 87 403 fraudulent transactions, respectively, thereby rendering it exceedingly imbalanced.
The two datasets were loaded from the local host of the researcher’s laptop and imported onto an online Python text editor, Google Colaboratory, in separate notebooks, as follows:
Df = pd.read_csv(‘/content/creditcard.csv’)
Df = pd.read_csv(‘/content/card_trasdata.csv’)
A scikit-learn module known as train_test_split was used to train and split the two datasets and the test size for each was set to 30 percent, while the random state was set to 42. These values are widely used for data training and splitting.
The creation process entails combining existing items by randomly selecting a point from the minority class and computing the k-nearest neighbours (default=5) for that point. Subsequently, each synthetic point is inserted between the chosen point and its neighbours by multiplying the distance by a value between 0 and 1.
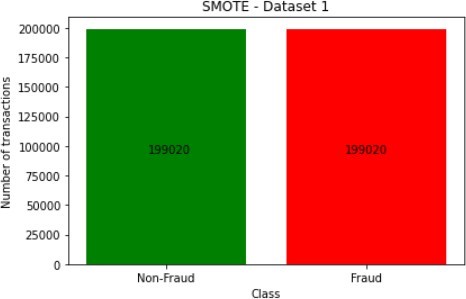
The figures below illustrates the class imbalances of the two datasets. The figures show the differences between legitimate and fraudulent transactions.
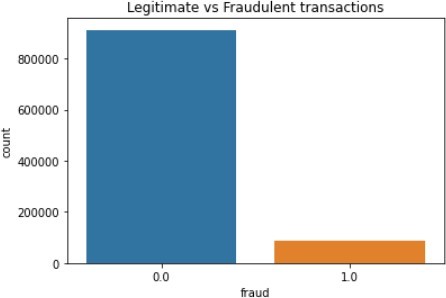

The figures above show the class imbalances in the datasets. It is easy to deduce how the datasets would look like after the application of the SMOTE technique, which is used to create items for the minority class.
For most applications, the difference between oversampling and SMOTE is insignificant, unlike in the data distribution, as illustrated in the figures below for dataset 1.

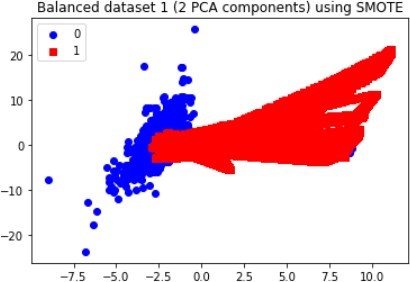
The above graphs clearly show that new observations, which are labelled 1 (fraudulent transaction), are found in numerous locations, thus, demonstrating how the SMOTE and Oversampling algorithms can generate instances. Moreover, PCA can be used to display the data in a two-dimensional view, thereby vividlyshowing the unique differences between legitimate and fraudulent transactions, as each class has a specified pattern and cluster.
5. Experiments
The experiments on the two datasets were conducted on Google Colab [33]. The specifications of the computer were as follows:
Intel Xeon Phi 7290 CPU with 72 cores at 1.5 GHz and 125 GB RAM on Ubuntu 18.04. The experiments were conducted on the Python 3.6.8 and the machine learning framework that was used was the Scikit-Learn [34]. The base learners XGBoost and SVM were implemented through Scikit-Learn. For each feature vector in the dataset, the following algorithms were trained and tested: Decision Tree, Random Forest, Neural XGBoost and an Ensemble of XGBoost and SVM. The results of the experiments, which were conducted without the application of DES on the first dataset are depicted in Table 1.
Table 1: Performance evaluation of the algorithms on dataset 1
| Models | Accuracy | Precision | Recall | F1_Score | ROU AUC |
| Decision Tree | 95.85% | 3.45% | 85.14% | 6.63% | 94.47% |
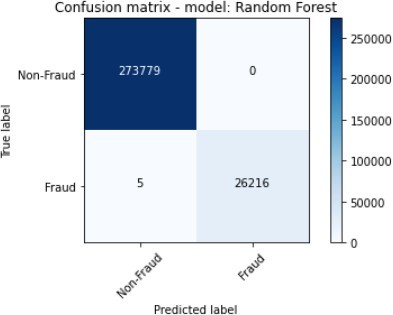
| Random Forest | 99.95% | 88.15% | 80.41% | 84.10% | 94.93% |
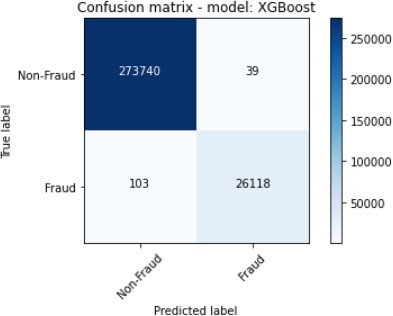
| XGBoost | 99.44% | 21.7% | 85.81% | 34.07% | 96.92% |
| Ensemble | 99.94% | 89.06% | 77.03% | 82.61% | 95.9% |
The Ensemble were composed of the XGBoost and SVM, while the Random Forest classifiers were the best performing algorithms with regard to Accuracy and F1_Score, and these were followed.
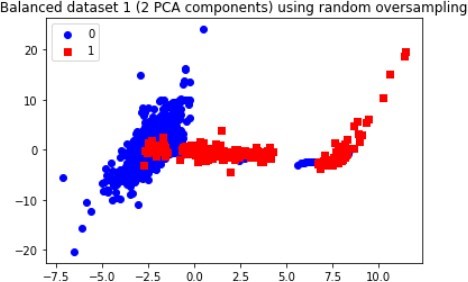
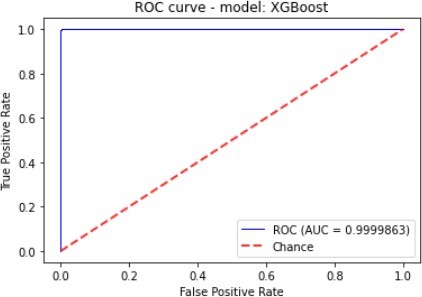
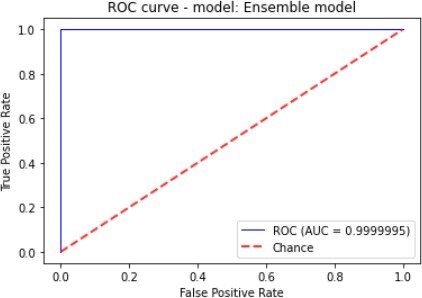
Figure 7 to figure 10 shows the ROC Curve of each learning algorithm for dataset 1.
by the Decision Tree. The ensemble also scored highly on Precision. The Decision Tree classifier and XGBoost showed the worst performance given that they score a Precision of 3.45% and 21.75% as well as F1_Score of 6.63% and 34.07% respectively.
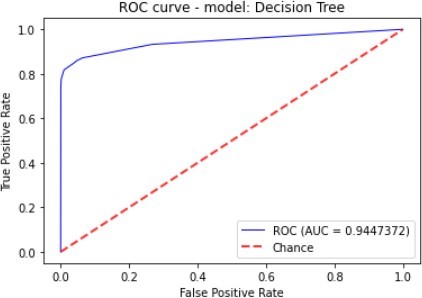
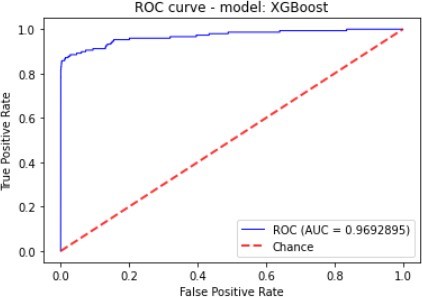
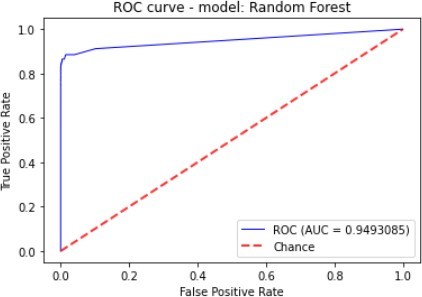
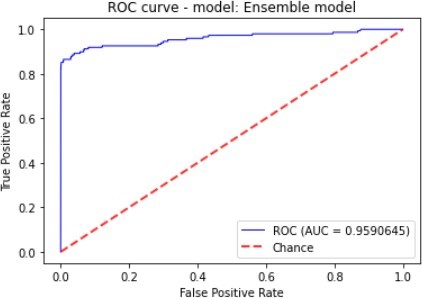

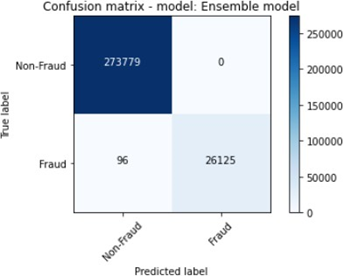
The figures 11 to figure 14 show the ROC curves and confusion matrix for dataset 1.
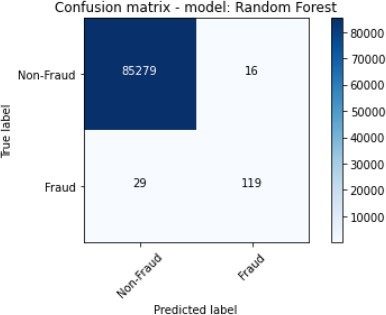

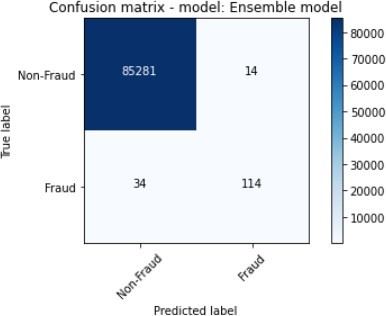
We conducted further experiments using a second dataset to validate the efficiency and effectiveness of our proposed approach. The dataset consists of the following features: ratio_to mean purchase, repeat_retailer, Used_chip, Used_pin_Number and fraud. The feature fraud denotes the target variable. Table 2 shows the details of the results that were obtained after the experiments were conducted.
The Ensemble were composed of the XGBoost and SVM, while the Random Forest classifiers were the best performing algorithms with regard to Accuracy and F1_Score, and these wer e followed by the Decision Tree. The Ensemble also scored highly in Precision. The Decision Tree classifier and XGBoost showed the worst performance, given that they scored a Precision of 3.45% and 21.75%, as well as an F1_Score of 6.63% and 34.07%, respectively
Table 2: Performance evaluation of the algorithms on dataset 2
| Models | Accuracy | Precision | Recall | F1_Score | ROC AUC |
| Decision Tree | 97.60% | 79.77% | 97.15% | 87.61% | 99.59% |
| Random Forest | 99.75% | 99.65% | 99.98% | 99.98% | 99.89% |
| Neural Networks | 99.95% | 99.85% | 99.73% | 99.73% | 99.96% |
| Ensemble | 99.97% | 99.76% | 99.82% | 99.83% | 99.94% |
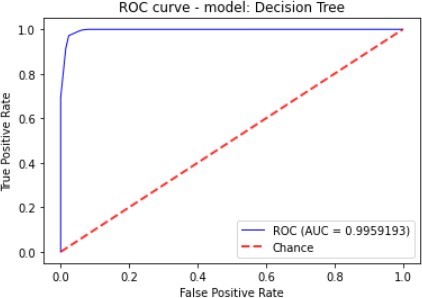
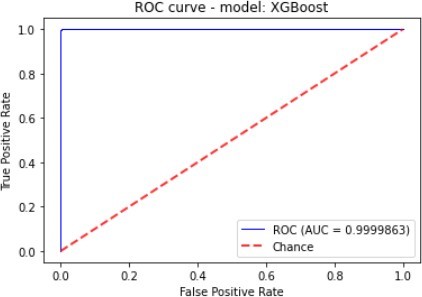

I am text block. Click edit button to change this text. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
5.1. Comparison with state-of-the-art algorithms
The European dataset, which is found on Kaggle, has been implemented in several researchers’ proposed models. The comparisons that were made in this section were based on the results obtained from this very dataset, which is also the first dataset of this study. The proposed model was compared to the ensemble of models that were implemented on the European dataset, which the author found to have outperformed some state of the art models. Table 3 shows the comparative performances of the proposed ensemble. The comparison used five metrics against other state of the art algorithms.
Table 3: Performance evaluation of the DESP algorithms against state-of-the-art algorithms
| Models | Accuracy | Precision | Recall | F1_Score | ROU AUC |
| DESP-ENSEMBLE | 98.76% | 72.65% | 97.26% | 61.49% | 99.97% |
| KNORA-U | 83.46% | 61.24% | 96.65% | 70.25% | 99.88% |
| KNORA-E | 86.34% | 84.87% | 98.45% | 80.76% | 99.87% |
| GRU | 81.63% | 86.26% | 72.08% | 77.92% | 86.02% |
| ℓ | 79.85% | 95.69% | 66.74% | 78.13% | 83.37% |
| LSTM | 80.54% | 85.75% | 74.08% | 76.87% | 87.02% |
The proposed model achieved the best results in terms of Accuracy, Precision, F1_Score, Recall, and AUC ROC. The proposed model used Dynamic Ensemble Selection Performance (DESP), K_Nearest Neighbour Oracle Eliminate (KNORA-E), K_Nearest Neighbor Union (KNORA-U). The results shown in the tables shows that this model has an overall better performance. The DESP technique picks all base classifiers that produce better classification performance than the random classifier in their domain of competence. The random classifier’s performance is defined as RC=1/L, where L is the number of classes in the task.
If no base classifier is chosen, and the pool as a whole is utilized for classification.
If the KNORA-E technique looks for a local Oracle, which is a base classifier that properly classifies all samples in the test samples’ zone of competence. All classifiers with faultless performance in their domain of expertise are chosen (local oracles). If no classifiers achieves complete accuracy, the size of the competence zone is lowered (by eliminating the farthest neighbor) and the classifier’s performance is re-evaluated. The majority voting system is used to integrate the outputs of the selected ensemble of classifiers. If no base classifier is chosen, the pool as a whole is utilized for classification. In the KNORA-U technique, all classifiers are picked that accurately categorized at least one sample from the query sample’s zone of competence. Each chosen classifier receives the same number of votes as the number of samples in the zone of competence for which it predicts the correct label. The votes from all base classifiers are combined to get the final ensemble.
As shown in Table 3, GRU, LSTM and ensemble model ℓ have the best precision performance with ensemble model ℓ being number one. However, the DESP model proposed in this paper has the best overall performance, with KNORA-E. Together with ensemble ℓ, GRU had the worst Recall performance. DESP and KNORA-U outperform LSTM in Recall and AUC ROC performance with KNORA-E is superior performing model.
With regard to Accuracy, Precision, F1_Score, Recall, and AUC ROC, the proposed model produced the best results. The model employed Dynamic Ensemble Selection Performance (DESP), K_Nearest Neighbour Oracle Eliminate (KNORA-E), and K_Nearest Neighbour Union (KNORA-U). In terms of the competence domain, the DESP technique is better than the random classifier. This is because the former has a more superior capability to pick pick base classifiers that can yield more superior classification performance. The performance of the random classifier is defined as RC=1/L, where L is the number of classes in the task. If no base classifier were chosen and the pool as a whole were utilised for classification, the execution process would require more memory.
6. Conclusion
This study proposed and evaluated the performance of the Dynamic Ensemble Selection Performance (DESP) for credit card fraud detection. The study made use of two datasets, which were sourced from Kaggle, and both were found to be extremely imbalanced and associated with different types of concept drift. To address these challenges, the study used the SMOTE technique, which is broadly used for handling imbalance in the detection of credit card fraud. The technique yielded impressive results. To handle drifting concepts, the researcher employed an accuracy and diversity oriented algorithm. The aim of the research was to compare the performance of homogeneous ensembles with heterogeneous ensemble learning before performing a comparative study of the proposed approach against existing state of the art heterogeneous algorithms. The paper also sought to demonstrate how DESP handled class imbalance and concept drift in credit card fraud detection. The paper introduced diversity by combing two learning base algorithms namely: XGBoost and SVM and the Q Statistic diversity measure was used. Combining algorithms of different classifications, particularly in adaptive models, enables fraud detection models to be more efficient in picking the best classifiers for particular data in fraud transactions. Ensemble classifiers make it possible to build models that are capable of overcoming challenges like class imbalance, verification latency and concept drift, which are inherent in credit card fraud detection. The proposed DESP model outperformed existing state of the art techniques.
Several limitations were encountered in the process of conducting this research. The major challenge was unavailability of authentic contemporary datasets because of the attendant privacy and security issues. For future work, there is need fo strike the balance between accuracy and computational efficiency. Machine learning algorithms exhibit distinct trade-offs between training and testing times as the prediction performance is evaluated using training and testing time and memory usage. In future, the efficiency of the learning model can further be improved by refining the training and testing durations. Streamlining computational overheads has the potential to develop fraud detections systems capable of real time operation ensuring swift responses to evolving fraud trends. For future work, the integration of deep learning can be explored in conjunction with traditional machine learning approaches with the potential of yielding more accurate and adaptable fraud detection solutions.
Conflict of Interest
The authors declare no conflict of interest.
- N. S. Alfaiz, S. M. Fati, “Enhanced credit card fraud detection model using machine learning,” Electronics, 11(4): 662, 2022, DOI: 10.3390/electronics.11040662.
- M. Z. Khan, A. Indian A., K. K. Mohbay K. K., “Credit card fraud prediction using XGBoost- An-Ensemble-Learning-Approach,” International Journal of Information Retrieval Research (IJIRR), 12(2): 1-17, 2022, DOI: 10.4018/IJIRR.299940.
- E. Kim, J. Lee, H. Shin, H. Yang, S. Cho, S. Nam, Y. Song, J. Yoon, J. Kim, “Champion-Challenger analysis for credit card fraud detection: Hybrid ensemble and deep learning,” Expert Systems with Applications, 128: 214-224, 2019, doi: https://doi.org/10.1016/j.eswa.2019.03.042.
- Ross D. E. (2016). Credit card fraud. Retrieved from https://www.britannica/topic/credit-card-fraud.
- P. Tomar, S. Shrivastara, U. Thakar, “Ensemble learning based credit card fraud detection system,” 2021 5th Conference on Information and Communication Technology, CICT2021, 10-12 December 2021, Kurnool India, doi: 10.1109/CICT53865.2020.9672426.
- F. Carcillo, A. Dal Pozzolo, Y.-A. Le Borgne, O. Caelen, Y. Mazzer Y., G. Bontampi G., “SCARFF: A scalable framework for streaming credit card fraud detection with spark,” Information Fusion, 41: 182-194, May 2018, DOI: 10.1016/j.Inffus.2017.09.005.
- J. Femila Roseline, GBSR Naidu, V. S. Pandi, S. A. Rajasree, D. N. Mageswari, “Autonomous credit card fraud detection using machine learning approach,” Computers and Electrical Engineering, 102: 108132, September2022, https://doi.org/10.1016/j.compeleceng.2022.108132.
- W. Liu, C. Wu, S. Ruan S, “CUS-RF-Based credit card fraud detection with imbalanced data,” Journal of Risk Analysis and Crisis Response, 12(3), https://doi.org/10.54560/jracr.v12i3.332.
- L. Gao, A. Li, Z. Liu, Y. Xie Y, “A heterogeneous ensemble learning model based on data distribution for credit card fraud detection,” Wireless Communications and Mobile Computing, Volume 2021, Article ID: 2531210, https://doi.org/10.1155/2021/2531210.
- J. Forough, S. Momtazi, “Ensemble of deep sequential models for credit card fraud detection,” Applied Soft Computing, 99: 106883, February 2021, https://doi.org/10.1016/j.asoc.2020.106883.
- C. Alippi, G. Bontempi, O. Caelen, G. Boracchi, A. Dal Pozzolo A, “Credit card fraud detection: A Realistic Modeling and a Novel Learning Strategy,” IEEE Transactions on Neural Networks and Learning Systems, 29(8): 3784-3797, https://doi.org/10.1109/tnnls.2017.2736643.
T.Museba et al. / Advances in Science, Technology and Engineering Systems Journal Vol. 9, No. 3, 01-11 (2024)
www.astesj.com 11 - S. Bagga, A. Goyal, N. Gupta, “Credit card fraud detection using pipelining and ensemble learning,” Procedia Computer Science, 173: 104-112, 2020, https://doi.org/10.1016/j.procs.2020.06.01
- U. Nambiar, R. Pratap, I. Sohony I, “Ensemble learning for credit card fraud detection,” ACM International Conference Proceeding Series, pages 289-294, 2018, https://doi.org/10.1145/3152494.3156815.
- E. IIeberi, Y. Sun, Z. Wang, “A machine learning based credit card fraud detection for feature selection,” Journal of Big Data, 9: 24, 2022, https://doi.org/10.1186/s40537-022-00573-8.
- A. Maurya, A. Kumar A, “Credit card fraud detection system using machine learning technique,” 2022 IEEE International Conference on Cybernetics and Computational Intelligence (CyberneticsCom), 16-18 June 2022, Malang, Indonesia, doi: 10.1109/cyberneticsCom55287.2022.9865466.
- V. Plakandaras, P. Gogas, T. Papadimitriou, I. Tsamardinos I, “Credit card fraud detection with automated machine learning systems,” Applied Artificial Intelligence International Journal, 36(1), 2022, https://doi.org/10.1080/08839514.2022.
- V. N. Dornadula, S. Geetha S, “Credit card fraud detection using machine learning algorithms,” Procedia Computer Science, 165: 631-641, 2019, https://doi.org/10.1016/j.procs.2020..01.057.
- J. K. Afrivie, K. Tawiah, W. A. Pels, S. Addai-Henne, H. A. Dwamena, E. O. Owiredu, S. A. Ayeh S, J. Eshun, “A supervised machine learning algorithm for detecting and predicting fraud in credit card transactions,” Decision Analytics Journal, Volume 6, March 2023, http://doi.org/10.1016/j.dajour.2023.100163.
- M. Ienye, Y. Sun, “A machine learning method with hybrid feature selection for improved credit card fraud detection,” MDPI Applied Sciences, 2023, https://doi.org/10.3390/app13127254.
- M. A. Mim, N. Majadi N, P. Mazumder, “A soft voting ensemble learning approach for credit card fraud detection,” Heliyon, 10(3): ee25466, 2024, PMD:38333818, https://doi.org/10.1016/j.heliyon.2024.e25466.
- A. R. Khalid, N. Owoh, M. A. Ashawah, J. Osmor J, J. Adejoh, “Enhancing credit card fraud detection: An Ensemble Machine Learning Approach,” Big Data and Cognitive Computing, 8(1): 6, 2024, https://doi.org/10.3390/bdcc8010006.
- Y. Xia, C. Li, N. Liu, “A boosted decision tree approach using Bayesian hyperparameter optimization for credit scoring,” Expert Systems with Applications, 78: 225-241, 2017, https://doi.org/10.1016/j.eswa.2017.02.017.
- M. Mercier, M. Santos, P. Henriques Abreu, C. Soares, J. Soares, J. Santos, “Analyzing the Footprint of classifiers in overlapped and imbalanced contexts,” 17th International Symposium, IDA 2018, Hertogenbosch, The Netherlands, October 24-26, 2018, pages 200-212, https://doi.org/10.1007/978-3030-01768-2_17.
- R. Eberhart, J. Kennedy J, “Particle Swarm Optimization,” In Proceedings of the IEEE International Conference on Neural Networks, pages 1942-1948, Perth, Australia, November 27-December 1, 1995, https://doi.org/10.1109./ICNN.1995.488968.
- L. L. Minku, X. Yao X, “DDD: A New Ensemble Approach for Dealing with Concept Drift,” IEEE Transactions on Knowledge and Data Engineering, 24(4), April 2012, doi: 10.1109/TKDE.2011.58.
- T. Chen, C. Guestrin C, “XGBoost: A scalable tree boosting system,” In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, pages 785-794, 2016, https://doi.org/10.1145/2939072.2939785.
- W. Rui, L. Guanjun, “Ensemble Method for credit card fraud detection,” 2021 4th International Conference on Intelligent Autonomous Systems, 14-16 May 2021, Wuhan, China, doi: 10.1109/ico/AS53694.2021.00051.
- Google Colab [Online] Available on:https://colab.research.google.com/
- N. V. Chawla, K. W. Bowyer, L. O. Hall, W. Kegelmeyer, “SMOTE: Synthetic Minority Over-Sampling Technique,” Journal of Artificial Intelligence Intelligence Research, 16(2002): 321-357, doi: 10.1613/jair.953.
- L. Yang L, “Classifier selection for ensemble learning based on accuracy and diversity,” Procedia Engineering, 15:4266-4277,2011,
DOI: https://doi.org./10.1016/j.poeng.2011.08.800. - G. Yule, “On the association of attribute in statistics,” Philosophical Transaction. Royal Society of London. Series A, Volume 194, pages 257-319, 1900, https://doi.org/10.1098/rspi.1899.0067.
- The credit card fraud [Online], https://www.kaggle.com/mlg-ulb/creditcardfraud.
- A. P. Engelbrecht, “Computational Intelligence: An Introduction,” John Wiley and Sons, Chichester, December 2002.
- Scikit learn: machine learning in Python [Online]: https://scikit-learn.org/stable.
Citations by Dimensions
Citations by PlumX
Crossref Citations
- Tinofirei Museba Museba, Koenraad Vanhoof Vanhoof, "An Adaptive Heterogeneous Ensemble Learning Model for Credit Card Fraud Detection." Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 1, 2024.
No. of Downloads Per Month
