1. Introduction

Social media has received widespread attention due to its rise as one of the most essential tools for societal interaction and communication. Social media platforms have significantly contributed to the rapid dispersion of news and information and the facilitation of communication between different groups worldwide. Nevertheless, in the past few years, there has been a notable surge in the spread of misinformation, a trend propelled and magnified by the influence of social media platforms such as Facebook and Twitter. Due to this, it has become increasingly vital to understand opinion dynamics in social networks to minimize the detrimental effects of malicious agents, fake news, and other polarizing factors. This work builds on the work presented in [1], where we discussed how updating dynamics on social media and competition for influence affect the overall opinion and how intelligent agents decrease polarization and disagreement in social media networks.

Extensive research has been conducted to examine and understand this issue of misinformation in social media networks [2]–[4]. The prevailing trends to combat this issue are automated tools for detecting fake news and misleading posts [5]. However, this presents multiple challenges, such as defining what is fake and true. For example, simply defining what is true and false can generate a lot of discussion and controversy. This is compounded by the availability of artificial intelligence tools that can mimic a human’s voice or generate fake video recordings. Additionally, misinformation in social media can result in polarization, economic impacts, time and resource wastage, and cybersecurity concerns.

Furthermore, understanding the effect of RL on influencing opinions in a social media environment is vital for several avenues such as public opinion management [6], policy implementation [7], commercial interests [8], platform design [9], and Ethical Considerations [10].

This paper proposes an RL-based method for influencing and controlling opinions in a social media environment. Unlike what is presented in the literature, where the model or algorithm is static and does not react to changes in the social network, our method proposes that each control agent can react and take action using Deep Q-Networks (DQN) to influence and persuade the other agents in the network to adopt a similar opinion. This paper expands the work in [1] with the following contributions:

1. The control agents can change their expressed opinions to influence the social media network.
2. The environment is a two-state expressed and private opinion dynamics model with asynchronous and synchronous updating dynamics that emulate the interactions of individuals in social media networks.
3. The agents work to influence the opinions of others in the network to a set goal.
4. Simulation results that demonstrate our approach for multiple social media networks.

The rest of the paper is organized as follows. Related works and preliminaries are provided in Section 2. We introduce the Markov decision process (MDP), partially hidden MDPS, and RL in Section 3. In Section 4, we formulate the problem and present the paper’s main results. The experimental results are given in Section

5. Concluding remarks are given in Section 6.

2. Related Work

Social media networks have become an integral part of our society. This resulted in widespread attention to opinion dynamics and social network analysis. Opinion dynamics studies how opinions, beliefs, and attitudes form, evolve, and interact within social networks and communities. Opinion dynamics encompasses a variety of disciplines, such as sociology, political science, complex systems analysis, psychology, and multi-agent systems. One of the essential assumptions in opinion dynamics is that opinions in social networks are mainly influenced by others.

Many opinion dynamics have been proposed to study the evolution of opinions in social networks [11]–[13]. One of the most popular opinion dynamics models is agent-based models [14]. In agent-based models, individuals are depicted as agents, and their opinions on a specific topic are captured as evolving real values over time. The underlying communication network in agent-based models is represented by a graph, where a node represents an agent, and an edge represents communication between two individuals.

One of the earliest agent-based models is the French-DeGroot model, commonly referred to as the DeGroot model [15]. The model assumes that the opinion of each individual evolves as a result of integrating the opinions of their connected neighbors with agents’ own opinions using weighted averaging (modeled using a differential or a difference equation). The DeGroot model was experimentally validated in [16, 17]. An extension of the DeGroot model is the Friedkin-Johnsen model, which simulates strong diversity due to stubborn agents by introducing a variable that measures the agent’s susceptibility to social influence [18]. This model has been experimentally verified for small and medium-sized networks [19]–[21]. A model that encodes the effects of social pressure on the agents in the network, termed the expressed and private opinion (EPO) dynamics model, was introduced in [22]. The EPO model is based on Asch’s conformity experiments and Prentice and Miller’s field experiments on pluralistic ignorance [23, 24]. An extension of the EPO model is the asynchronous and synchronous expressed and private opinion dynamics model (EPOAS) [25]. This model introduces different updating dynamics for the agent’s expressed and private opinions, which emulates the interaction of individuals in social media networks.

These models tend to reach a consensus if all the agents in the network agree on one opinion on a specific topic. However, it can be observed that in most social networks, the presence of stubborn (who insist on their own opinion) or controlling agents has a significant impact on the opinions of the other agents in the network [26]. This trend is evident in social media marketing, economics, and political campaigns [27]. Moreover, numerous political and economic entities utilize data mining techniques and social science principles to strategically engage specific individuals within social networks, aiming to enhance profit margins [28].

There have been many attempts to study and simulate opinion control in social networks. The control of the DeGroot model under the influence of a leader was investigated in [29]–[31]. In [32], the authors study the optimal placement of control agents in a social network to influence other individuals to reach a consensus where the control agents have a fixed common state. Another control approach using noise to affect the opinions of individuals in the network was investigated in [33]. A control strategy based on the degree of connection each agent has shown that it is possible to drive the overall opinion toward a desired state even if we control only a suitable fraction of the nodes was presented in [34].

In [35], the control of public opinion using social bots was investigated. In this approach, an agent’s opinion is modeled as a static value, based on the approach described by Sohn and Geidner [36]. The study demonstrates that, depending on the density and position within the network, a mere 2% − 4% of bots are sufficient to influence all the opinions in the network.

3.  Markov Decision Process

An MDP is a mathematical framework designed to model decisionmaking where sequential actions are involved, and the outcomes of each action are partially random and partially under the control of the decision-making agent [37]. An MDP was developed to model decision-making problems where the outputs are probabilistic and are affected by the agent’s actions. An MDP is modeled by a tuple (S, A, P_a,R_a) where:

1. States (S) encapsulate all potential scenarios the agent could encounter at any given time step.
2. Actions (A) embody all the options or decisions accessible to the agent in any given state. Agents select an action to transition from one state to another.
3. Transition probabilities (P_a) specify the likelihood of transitioning to a new state. These probabilities represent the dynamics of the environment and determine how the agent’s actions influence the next state.
4. Rewards (R_a) quantify the desirability of taking a specific action in the current state. The agent’s goal is to maximize the rewards it receives to reach its desired goal efficiently.

The goal of an MDP is to have the agent learn a good policy for decision-making. A policy π(S) can be defined as a strategy that maps states to actions, indicating the action the agent should choose in each state to maximize the agent’s reward and help the agent reach their goal.

3.1        Partially Observable MDP

Partially Observable Markov Decision Processes (POMDPs), Figure 1, provide a robust framework for effectively modeling and resolving decision-making challenges in contexts marked by uncertainty and partial observability. A POMDP represents a decision-making scenario for an agent. In this scenario, it is assumed that the system’s behavior is governed by a MDP. However, the agent is unable to perceive the inherent state of the system directly.

Decision-making in real-world environments often involves inherent uncertainty and partial observability, where agents lack complete information about the underlying states and face uncertain outcomes from their actions. The framework of POMDPs is sufficiently versatile to represent a wide array of sequential decision-making scenarios encountered in the real world.

In POMDPs, an agent makes decisions based on a belief state (a probability distribution over all possible states) rather than the actual state. The agent’s belief state is updated based on the actions it takes and the observations it receives. The agent’s goal is to choose actions over time to maximize its expected cumulative reward.

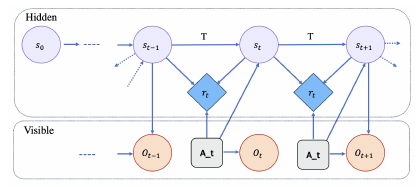
Figure 1: Partially Observable Markov Decision Processes (POMDPs).

3.2        Reinforcement Learning (RL)

One of the most powerful and widely used machine learning tools in data science is RL. The ability of RL algorithms to learn about the environment and generate a suitable policy, which can be improved through trial and error, has made them a popular choice for tasks such as game playing, autonomous driving, robotics, and resource management, among others. One of the most essential RL algorithms is the Q-learning algorithm. This can be attributed to the algorithm’s versatility, simplicity, and robustness.

Q-learning is a model-free RL algorithm, meaning it does not require knowledge of the environment’s dynamics to generate an efficient policy for solving the problem. This characteristic makes the algorithm particularly suitable for problems where a model of the environment is challenging to obtain or the environment is non-deterministic.

The essence of Q-learning is learning the action-value function

(Q-function). The Q-function evaluates the value of taking a specific action in a given state

where s represents the agent’s present state, s^′ represents the agent’s next state, and a is the action taken by the agent in the current time step. The Q-value of the action a for the current state s is denoted by Q(s,a), which is the state-action value. The reward the agent receives at each time step is represented by r, and γ is the discount factor that reduces the value of future rewards over time.

The value Q(s,a), for the current state s, is updated at every time step based on a blend of the existing value and the equation that identifies the optimal action in the current state. Initially, the Q-value table is randomly populated for each state and potential action. The Q-learning process continues by updating the Q-value for each state using (1). The policy is then updated using the highest Q-values for each state-action pair. After the agent performs an action a in state s, it transitions to the next state s^′. This procedure is repeated multiple times until the overall Q-values reach a point of convergence [38]. The algorithm for Q-learning is described below.

Algorithm 1: Q-learning for estimating π ≈ π^∗

Algorithm parameters: step size l_r ∈ (0,1] ε, γ; Initialization: Q(s,a) for all s ∈ S,a ∈ A for episode ← episodes do

The learning rate l_r needs to be fine-tuned over time to solidify the learned policy. Discount factor γ is a numerical value between 0 and 1 that determines the importance of future rewards compared to immediate ones. If γ is close to 0, then the agent will prioritize immediate rewards and largely ignore future rewards. However, if γ is close to 1, then the agent will consider future rewards almost as important as immediate ones.

4. Problem formulation

Consider a group of n agents interacting in a social media environment, where agents form and evolve their opinions at each time step by interacting and exchanging information with other connected agents.

An independent agent or a group of agents is arbitrarily selected to control and influence the network to a desired outcome. The agents can have the same goal and work together to achieve that goal or they can have different goals and compete for influence in the network.

4.1        Modeling the Agents

We model n agents as nodes interacting in a multi-agent opinion dynamics environment. The agents are interconnected via an underlying graph G[W], which maps out the relationships between these agents. The underlying graph G[W] is a directed graph that encodes the flow of information from one agent to another. Each individual i in the network has two states: one state represents the individual’s expressed opinion yˆ_i(t), and the second state is the individual’s private opinion y_i(t). Each agent within the network starts with an initial private opinion, denoted as y_i(0), and an initially expressed opinion, represented as yˆ_i(0) (for the remainder of this paper, the terms ’state’ and ’opinion’ will be used interchangeably). The initial private and expressed opinions of each agent can either coincide (y_i(0) = yˆ_i(0)) or differ (y_i(0) , yˆ_i(0)). This mirrors real-world scenarios where individuals may choose to voice their genuine opinions or, due to external influences, conceal their private views by expressing differing opinions. At every time step t, each individual i in the network has two choices encoded by the variable α. The individual can express his/her opinion (α_i = 1) or hide the opinion (α_i = 0). If an individual decides to hide his/her opinion, then the last expressed opinion made by that individual will appear as his/her current expressed opinion to his/her neighbors. Note that for control agents α(t) = 1∀t. At every time step, all individuals in the network, except control agents, update their private opinions using the following dynamics

where λ_i ∈ [0,1] represents the coefficient of susceptibility of agent i, w_ij ≥ 0 represent the weights assigned by agent i to agent j, w_ii ≥ 0 represents the weight assigned by agent i to his/her opinion.

The expressed opinion is updated asynchronously, utilizing the information in the vector α(t) ∈ [0, N]. This vector encodes the decisions made by each agent at the time step t. If agent i opts to express their opinion, then the update of their expressed opinion adheres to the subsequent dynamics

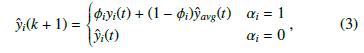
where ϕ represents the resilience of the agent to social pressure and yˆ_avg(t) represents social pressure or the prevailing opinion (public opinion) throughout the network. The average opinion, as observed by agent i, is given by the following dynamic

where m_ij ≥ 0 satisfy ^Pn_j=1 m_ij = 1. In many instances, w_ij and m_ij are not identical. This occurs as an individual’s viewpoint can be shaped and influenced by a certain group of individuals, all while concurrently feeling the urge to align with the expectations of the overall network.

Note that control agents do not follow the same updating dynamics and do not have a private opinion. The expressed opinions of the control agents are controlled by the Q-learning dynamics based on the optimal policy learned by the agent.

4.2        Communication Topology

The communication topology for n individuals (agents) can be represented as a directed graph G = (V,E[W],W), where V = {v₁,…,v_n} is the set of nodes (which represent agents or individuals in the network), and E ⊆ V × V is the set of ordered edges, E = {e₁,…,e_n}. Each edge in the network is denoted as e_ij = (v_i,v_j) ∈ E. With N_i we denote the neighbor set for the agent i (set of agents connected to the agent i).

The relative influence matrix of the network is modeled by W. The influence matrix W encodes how much trust or weight each agent has in the opinions of his/her connected neighbors. It is assumed that the influence matrix is static and connected. However, the communication network changes at each time step based on the updating dynamics of the agents in the network.

Each agent can only observe the expressed opinions of other connected agents. This means that the Q-table depends on the number of individuals connected to the control agents rather than the size of the network. The agent can have an idea of the overall opinion of the network based on the M weight matrix in (4). However, in this work, we assume that M = W. The observation space depends on the connections (neighbors) of the control agents. For example, if the control agent has three connections, the agent will have an observation space of three expressed opinions, as shown in Figure2.

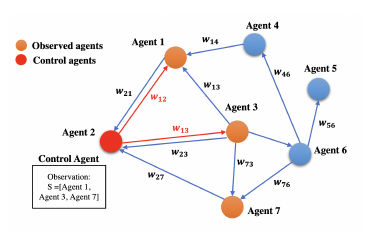
Figure 2: Observation of a control agent.

Some key information about the agent can be summed up in the following table.

Table 1: Agent information.

Action Space	Discrete(5)
Observation Shape	(number of neighbors,)
Observation High	1.0
Observation Low	0.0

4.3        The Environment Dynamics

The environment is based on the asynchronous and synchronous expressed and private opinion dynamics model. Consider a connected network of n agents. Let y(t) = [y₁,y₂,…,y_n]^T ∈ Rⁿ, and yˆ(t) = [yˆ₁,yˆ₂,…,yˆ_n]^T ∈ Rⁿ be a vector representing the private, and expressed opinions (states) of all the agents in the network, respectively. Next, we define Y(t) = [y(t)^T,yˆ(t)^T]^T, as the vector of all opinions (states) among the individuals at time step t. The vector of initial private opinions (prejudices) is defined as u = [u₁,u₂,…,u_n]^T ∈ Rⁿ. We define M as a matrix that encodes the weights for calculating social pressure. This matrix can be similar to the influence matrix M = W (which is followed in this work) or it can be different depending on the source of the social pressure (prevailing opinion in the network).

We use W = [w_ij] as the influence matrix of the network which is a stochastic matrix. We define W˜ = diag(w_ii) as the diagonal

matrix containing the diagonal values of W which represents the self-confidence of each agent in the network, and Wˆ as the exact matrix as W with 0 in its diagonal (wˆ _ij = w_ij for all j , i). The influence matrix can be rewritten as W = W˜ + Wˆ .

Additionally, we define λ = [λ₁,λ₂,…,λ_n] as a vector that encodes the agent’s susceptibility to social influence, while ϕ = [ϕ₁,ϕ₂,…,ϕ_n] is a vector that encodes the agent’s resilience to social pressure. The matrix Λ = diag(λ) is a susceptibility matrix that encodes the susceptibility of the agents in its diagonal, and the matrix Φ = diag(ϕ) is a resilience matrix encoding the resilience of the agents in its diagonal.

We designate α(t) = [α₁(t),α₂(t),…,α_n(t)] as a choice vector of zeros and ones that encode the actions agents have chosen by the agents at time t, where a zero value indicates that a particular agent has chosen not to express their opinion at the time step t, and a value of one signifies the agent’s choice to share their opinion with their neighbors. Let E = diag(α(t)) be a zero matrix with the choices of the agents encoded in its diagonal, and T = I_n − E be an identity matrix where the value of the activated agents are set to zero.

To demonstrate the dynamics of the system we define P_α(t) and

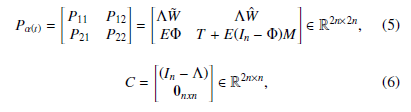
0nxn

where 0_nxn is a square zero matrix, and I_n is the identity matrix. The dynamics of the environment are updated using the following equation

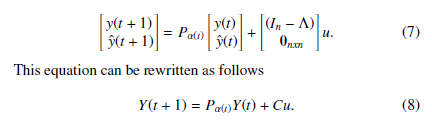
The matrix P_α(t) changes with each time step t based on the changes that occur in the choice vector α(t). Each control agent in the environment has the following available actions.

Table 2: Action space

Action	Opinion value	Meaning
0	0.1	Strong disagreement
1	0.3	Slight disagreement
2	0.5	Neutral
3	0.7	Slight agreement
5	0.9	Strong agreement

The following algorithm is used to update the dynamics of the system at each time step.

Algorithm 2: Step function in system dynamics time step = time step +1

Agents Activation = random(size=number of agents) E = diag(Agents Activation)

for i in range(length(control agents) do E[control agents[i]] = 1

4.4        Reward Function

Every control agent in the network aims to influence the individuals’ opinions to a specific value (opinion). The opinions of the agents in the network range from 0, which represents strong disagreement, to 1, which represents strong agreement. Let ref_i be the opinion goal or reference of the control agent i.

We define the disagreement d(i, j) between two individuals i, j as the squared difference between their opinions at equilibrium: d(i, j) = w_ij(y^∗_i − y^∗_j)², and the total disagreement is defined as

DG = P(i,j)∈V d(i, j), [39].

The overall goal of the control agents is to influence the network to a predetermined opinion. To encourage the agents to reach their goal within the desired number of steps, we define O_i(t) as the vector containing the expressed opinions of the agents connected to agent i at time step t. The reward function for each control agent is given by

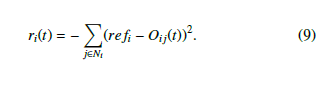
The control agent is given an increasingly negative reward for each connected agent that does conform to the goal opinion to encourage it to influence as many individuals as possible.

5. Experimental Results

We tested the effectiveness of the RL agent in influencing and controlling the opinions of individuals in social media networks. A graph was randomly generated using the Erdos-Renyi random graphs model, preferential attachment model, or the stochastic block model. The weights agents assigned to themselves and their neighbors were generated randomly.

The susceptibility and resilience values were randomly generated to ensure the agent learned under different conditions. Then one or more control agents were randomly selected to influence the rest of the network to one specific opinion. At each time step, the agent observed the expressed state of their connected neighbors and took action to influence their opinion. The reward was calculated at each time step to motivate the agent to complete the task in a timely manner. Note that the agents start with no knowledge of the underlying network. In addition, the agents do not have any prior knowledge about other agents in the network.

The agents started with a very high exploration factor ε that decayed gradually until the value reached 0.01, which means that the agents reverted to an almost purely greedy algorithm when choosing their action. The factor ε is decayed by a factor of 0.0001 every episode. The discount factor for the agents was selected as 0.99, which means that the agents developed long-term planning to achieve their goal rather than focus on immediate rewards.

The agent was trained for 500,000 episodes, and the reward was logged for every 1,000-th episode. Additionally, for every 1,000-th episode, we log the episode’s length to measure how fast the agent completes the assigned task. Figure 3 shows the evolution of an agent’s learning process, starting with a randomly defined knowledge base and no experience over 250,000 iterations. The rewards (orange line) show the 500 rolling average of the rewards for a more clear illustration.

Figure 3 shows an agent’s learning in a random network. The agent starts to receive high rewards after 150,000 iterations. However, there are still episodes where the control agents struggle to efficiently control the network due to the difference in agent personality (susceptibility and resilience) or opinions.

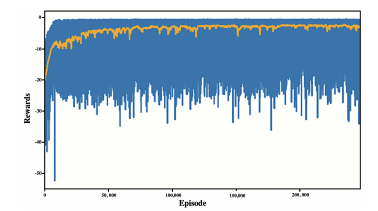
Figure 3: Training reward of a control agent over 250,000 training episodes with data collected every 1,000 episodes.

Figure 4 shows the reward over 250,000 training episodes with the reward logged every 1,000-th training episode and a 500 rolling average. The agent starts with a large negative reward when they are exploring ways to influence the network, then the agent starts getting consistent rewards close to 0, which is the optimal reward, after 150,000 training iterations. The figure shows that the agent is able to influence the system where the reward of the network reaches 0 meaning that the opinions of the agents in the network converge to the opinion desired by the control agent. However, increasing the training time after 250,000 iterations does not have much effect on the reward received by the agent.

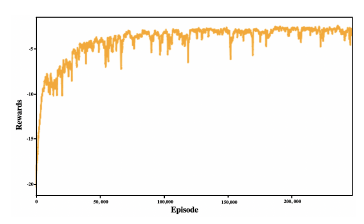
Figure 4: Training reward of a control agent over 250,000 training episodes (with 500 rolling average).

Figure 5 shows the length of every episode and how long the agent takes to reach an efficient policy. It can be seen that with more training, the agent can influence the individual’s opinion in a much smaller period of time. It can also be observed that for the first 90 training episodes, the agent cannot influence the network in less than 30 time steps. However, this improves as the agent learns more techniques to gather influence and control the network more efficiently. Any training over 150,000 episodes did not generate drastically different results.

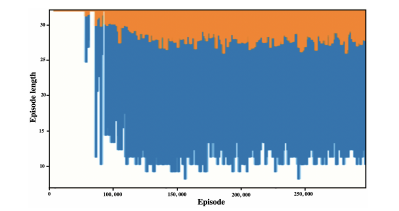
Figure 5: Episode length of a control agent over 250,000 training episodes.

Figure 6 shows a random group of 4 connected agents interacting in a social media environment with one control agent (Agent 1). The control agent can observe the expressed opinion of the other three individuals in the network. However, the agent can only influence two of these individuals (the size of the nodes indicates the level of influence each individual has). The network shows that all other agents have more influence than the control agent. The agents in the network randomly expressed their opinions at each time step.

The evolution of opinions of the agents in Figure 6 is observed in Figure 7. The control agent aims to have all others in the network reach an opinion value of 0.9 (strong agreement) on the discussed topic. The control agent changes their opinion to influence the rest of the group. At the end of the discussion, the other agents in the network adopt an opinion similar to the goal of the control agent. Additionally, we can see that occasionally the control agent changes their opinion to match those of his/her neighbors in order to increase their overall reward.

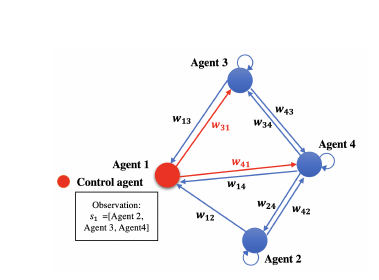
Figure 6: A network of 4 agents with one control agent (red) (size of the agent indicates their connections).

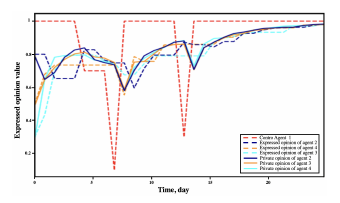
Figure 7: The evolution of private and expressed opinions of a network of 4 agents with one control agent (red).

6. Conclusion and Future Work

In this paper, we proposed an approach based on RL to solve the problem of disagreement between agents in multi-agent systems as well as social network control. To do so we used the expressed and private opinion dynamics model with asynchronous and synchronous updating dynamics to create an environment that closely resembles a social media network. Additionally, we used independent RL control agents to influence and control the network to a desired output. The method was validated using a random social media environment where agents interact and update their opinions randomly at every time step.

For future work, we are planning to investigate the interaction of control agents that are working cooperatively in very large networks. Additionally, we will explore the performance of controlling agents on evolving networks, and on networks with stubborn agents.

1. M. N. Zareer, R. R. Selmic, “Modeling Competing Agents in Social Media Networks,” in 2022 17th International Conference on Control, Automation, Robotics and Vision (ICARCV), 474–480, 2022, doi:10.1109/ICARCV57592. 2022.10004247.
2. H. Allcott, M. Gentzkow, “Social media and fake news in the 2016 election,” Journal of economic perspectives, 31(2), 211–236, 2017.
3. A. Fourney, M. Z. Racz, G. Ranade, M. Mobius, E. Horvitz, “Geographic and Temporal Trends in Fake News Consumption During the 2016 US Presidential Election.” in CIKM, volume 17, 6–10, 2017, doi:10.1145/3132847.3133147.
4. A. Guess, B. Nyhan, J. Reifler, “Selective exposure to misinformation: Ev- idence from the consumption of fake news during the 2016 US presidential campaign,” 2018.
5. E. Tacchini, G. Ballarin, M. L. Della Vedova, S. Moret, L. De Alfaro, “Some like it hoax: Automated fake news detection in social networks,” arXiv preprint arXiv:1704.07506, 2017, doi:10.48550/arXiv.1704.07506.
6. D. M. Lazer, M. A. Baum, Y. Benkler, A. J. Berinsky, K. M. Greenhill, F. Menczer, M. J. Metzger, B. Nyhan, G. Pennycook, D. Rothschild, et al., “The science of fake news,” Science, 359(6380), 1094–1096, 2018.
7. M. Howlett, Designing public policies: Principles and instruments, Routledge, 2019.
8. P. Kotler, H. Kartajaya, I. Setiawan, Marketing 4.0: moving from Traditional to Digital, John Wiley & Sons, 2016.
9. J. Van Dijck, T. Poell, M. De Waal, The platform society: Public values in a
   connective world, Oxford University Press, 2018.
10. L. Floridi, J. Cowls, “A unified framework of five principles for AI in society,” Machine learning and the city: Applications in architecture and urban design, 535–545, 2022, doi:10.1002/9781119815075.ch45.
11. M. Saburov, “Reaching a consensus in multi-agent systems: a time invariant nonlinear rule,” Journal of Education and Vocational Research, 4(5), 130–133, 2013, doi:10.22610/jevr.v4i5.110.
12. Y. Dong, W. Liu, F. Chiclana, G. Kou, E. Herrera-Viedma, “Are incomplete and self-confident preference relations better in multicriteria decision making? A simulation-based investigation,” Information Sciences, 492, 40–57, 2019, doi:10.1016/j.ins.2019.04.015.
13. S. E. Parsegov, A. V. Proskurnikov, R. Tempo, N. E. Friedkin, “Novel multi- dimensional models of opinion dynamics in social networks,” IEEE Transac- tions on Automatic Control, 62(5), 2270–2285, 2016, doi:10.1109/TAC.2016. 2613905.
14. B. D. Anderson, M. Ye, “Recent advances in the modelling and analysis of opinion dynamics on influence networks,” International Journal of Automation and Computing, 16(2), 129–149, 2019, doi:10.1007/s11633-019-1169-8.
15. M. H. DeGroot, “Reaching a consensus,” Journal of the American Statistical association, 69(345), 118–121, 1974.
16. J. Becker, D. Brackbill, D. Centola, “Network dynamics of social influence in the wisdom of crowds,” Proceedings of the national academy of sciences, 114(26), E5070–E5076, 2017, doi:10.1073/pnas.1615978114.
17. A. G. Chandrasekhar, H. Larreguy, J. P. Xandri, “Testing models of social learning on networks: Evidence from two experiments,” Econometrica, 88(1), 1–32, 2020, doi:10.3982/ECTA14407.
18. E. Johnsen, “Social influence and opinions,” J. Math. Sociology, 15(3-4), 193– 205, 1990.
19. N. E. Friedkin, E. C. Johnsen, Social influence network theory: A sociological examination of small group dynamics, volume 33, Cambridge University Press, 2011.
20. H. Kreft, W. Jetz, “Global patterns and determinants of vascular plant diversity,” Proceedings of the National Academy of Sciences, 104(14), 5925–5930, 2007.
21. C. C. Childress, N. E. Friedkin, “Cultural reception and production: The social construction of meaning in book clubs,” American Sociological Review, 77(1), 45–68, 2012, doi:10.1177/0003122411428153.
22. M. Ye, Y. Qin, A. Govaert, B. D. Anderson, M. Cao, “An influence network model to study discrepancies in expressed and private opinions,” Automatica, 107, 371–381, 2019, doi:10.1016/j.automatica.2019.05.059.
23. S. E. Asch, “Effects of group pressure upon the modification and distortion of judgments,” Groups, leadership, and men, 177–190, 1951.
24. D. A. Prentice, D. T. Miller, “Pluralistic ignorance and alcohol use on campus: some consequences of misperceiving the social norm.” Journal of personality and social psychology, 64(2), 243, 1993.
25. M. N. Zareer, R. R. Selmic, “Expressed and private opinions model with asynchronous and synchronous updating,” in 2021 IEEE International Con- ference on Systems, Man, and Cybernetics (SMC), 2840–2846, IEEE, 2021,
    doi:10.1109/SMC52423.2021.9659269.
26. S. Moscovici, M. Zavalloni, “The group as a polarizer of attitudes.” Journal of
    personality and social psychology, 12(2), 125, 1969.
27. R. Felix, P. A. Rauschnabel, C. Hinsch, “Elements of strategic social media marketing: A holistic framework,” Journal of business research, 70, 118–126, 2017, doi:10.1016/j.jbusres.2016.05.001.
28. S. Issenberg, “Cruz-connected data miner aims to get inside US voters’ heads,” Bloomberg, https://www. bloomberg. com/news/features/2015-11-12/is-the- republicanparty-s-killer-data-app-for-real, 2015.
29. J. Shao, J. Qin, A. N. Bishop, T.-Z. Huang, W. X. Zheng, “A novel analysis on the efficiency of hierarchy among leader-following systems,” Automatica, 73, 215–222, 2016, doi:10.1016/j.automatica.2016.07.007.
30. F. Dietrich, S. Martin, M. Jungers, “Control via leadership of opinion dynamics with state and time-dependent interactions,” IEEE Transactions on Automatic Control, 63(4), 1200–1207, 2017, doi:10.1109/TAC.2017.2742139.
31. J. Shao, W. X. Zheng, T.-Z. Huang, A. N. Bishop, “On leader–follower con- sensus with switching topologies: An analysis inspired by pigeon hierarchies,” IEEE Transactions on Automatic Control, 63(10), 3588–3593, 2018, doi: 10.1109/TAC.2018.2797205.
32. A. Clark, B. Alomair, L. Bushnell, R. Poovendran, “Leader selection in multi- agent systems for smooth convergence via fast mixing,” in 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), 818–824, IEEE, 2012, doi:10.1109/CDC.2012.6426323.
33. W. Su, X. Chen, Y. Yu, G. Chen, “Noise-Based Control of Opinion Dynam- ics,” IEEE Transactions on Automatic Control, 67(6), 3134–3140, 2022, doi: 10.1109/TAC.2021.3095455.
34. G. Albi, L. Pareschi, M. Zanella, “On the optimal control of opinion dy- namics on evolving networks,” in System Modeling and Optimization: 27th IFIP TC 7 Conference, CSMO 2015, Sophia Antipolis, France, June 29- July 3, 2015, Revised Selected Papers 27, 58–67, Springer, 2016, doi: 10.1007/978-3-319-55795-3 4.
35. B. Ross, L. Pilz, B. Cabrera, F. Brachten, G. Neubaum, S. Stieglitz, “Are social bots a real threat? An agent-based model of the spiral of silence to analyse the impact of manipulative actors in social networks,” European Journal of Infor- mation Systems, 28(4), 394–412, 2019, doi:10.1080/0960085X.2018.1560920.
36. D. Sohn, N. Geidner, “Collective dynamics of the spiral of silence: The role of ego-network size,” International Journal of Public Opinion Research, 28(1), 25–45, 2016, doi:10.1093/ijpor/edv005.
37. R. S. Sutton, A. G. Barto, Reinforcement learning: An introduction, MIT press, 2018.
38. M. Langlois, R. H. Sloan, “Reinforcement learning via approximation of the Q-function,” Journal of Experimental & Theoretical Artificial Intelligence, 22(3), 219–235, 2010, doi:10.1080/09528130903157377.
39. C. Musco, C. Musco, C. E. Tsourakakis, “Minimizing polarization and dis- agreement in social networks,” in Proceedings of the 2018 world wide web
    conference, 369–378, 2018, doi:10.1145/3178876.3186103.

(Click Here)