1. Introduction

Oil is one of the most important raw materials in the world. It has been the primary energy source since the mid-1950s. The oil and gas industry plays a vital role as the engine of the global economy. The products produced by this industry support many other vital industries like automotive industry and manufacturing industry.

Changing technologies, markets and customer needs affect the competitiveness of companies, which requires a continuous restructuring of the strategy and positioning tactics of the oil industry. Currently, the main problem facing the oil industry is to minimize transportation costs and production costs. Effective supply chain management can increase overall efficiency, competitiveness, and good sourcing.

The economic importance of the transport sector explains the interest of researchers in the problems of vehicle routing Laporte [1-3]. Much attention has been paid to the development of route definition techniques as they have the potential for major cost savings.

The gas station supply problem consists in determining how to optimally distribute several products (mainly gasoline and diesel fuel) to customers (gas stations) from a depot (refinery or regional depot) according to a planning horizon chosen. It is therefore necessary to determine for each period of the planning horizon, the stations to be visited, the routes and the trucks to be used, the quantity to be delivered of each product and their assignment to the trucks, and this, in ensuring that no client station is out of stock.

The Vehicle Routing Problem with Time Windows (VRPTW) is a major operational research problem. It consists of determining a set of routes to collect or deliver goods to customers within time windows and capacity constraints. Customers are usually visited once and only once by a vehicle; their request must be satisfied by this single visit.

The article is divided into four sections. After the introduction, section 2 presents a review of the literature on vehicle routing problems especially VRPTW. Section 3 offers a presentation of our case study. And Section 4 presents our conclusions and directions for future research.

conformity of style throughout a conference proceedings. Margins, column widths, line spacing, and type styles are built-in; examples of the type styles are provided throughout this document and are identified in italic type, within parentheses, following the example. Some components, such as multi-leveled equations, graphics, and tables are not prescribed, although the various table text styles are provided. The formatter will need to create these components, incorporating the applicable criteria that follow.

2. Literature review

Vehicle routing problems are much studied because of the growing importance of passenger and freight transportation today. The simplest and best-known problem of this type is the Traveling Salesman Problem (TSP). It consists of determining a route routed by a vehicle, so as to serve a set of customers distributed in a network at minimal cost. This basic model can be enriched by various constraints relating to the number of vehicles, to their loads, or to constraints relating to the nodes, to their time windows, or to dependencies between them.

Several researches are mainly oriented towards solving the vehicle routing problem VRP (Vehicle Routing Problem). The latter is a problem of optimizing vehicle routes to satisfy transport demands. These vehicle routing problems are generally subject to several types of constraints.

The general vehicle routing problem is known as the Vehicle Routing Problem (VRP) and represents a multi-objective combinatorial optimization problem that has been the subject of many works and many variants in the literature. It belongs to the NP-hard category [4-6].

The VRPTW constitutes a generalization of the VRP insofar as we also introduce a temporal constraint on the requested service. Each customer has a window of time within which he wishes to be served. The central depot also has a time window which we commonly refer to as the service horizon or open time of the day. Its role is to set a time slot during which vehicles can make their rounds.

These time constraints will make it necessary to use several vehicles to satisfy all customers over the service horizon. We may want to limit the number of vehicles to be used and in this case customers may not be served [7].

Each customer must be served within a defined time interval, known in advance by the delivery person and any violation of this constraint may result in a penalty. When the time window constraint is not satisfied, either we reject the solution if we consider the rigid case or we construct a penalty function which will be added or combined with the objective function for the case released. In fact, this is a very common problem. Distribution of perishable products (milk, meat, etc.), newspapers, outpatient services, . . . are practical examples of the VRPTW. Within this class of problems, there are two subclasses:

• The rigid PTVFT where the service must imperatively be performed within the time window.
• The released PTVFT or the delay or the advance only generates a penalty [7].

A time window (TW – Time Window) imposes that one or more problem requests be processed respecting an interval for the start of vehicle processing (delivery, collection). This interval is defined by an earliest date and a latest date.

This constraint can apply to pickup or delivery requests [8]. This type of constraint most often involves allowing the vehicle to arrive early, in which case it waits on the vertex in order to start its operations at the start of the time window. This waiting can be authorized on all the vertices of the graph or, only on a part of the vertices. However, the vehicle is not allowed to arrive after the end of the time window. In the classical version of the constraint, if one of the time windows is not respected then the solution is not valid. There are variants in the literature, for example the Soft Time Window (STW) introduced for the first time on a TSP problem [9], then on a VRP problem [10], which allows violation of the time window but penalizes the objective function [8].

The vehicle routing problem (with time windows) is one of the routing problems. Lenstra and Rinnooy Kan proved that VRP is an NP-DUR problem. Its resolution by an exact method turns out to be inappropriate for large instances. It is therefore inevitable to proceed to its resolution by heuristic approaches, which provide feasible and appreciable solutions in a reasonable time [11]. Recently, researchers treat VRPTW by different ways [12-18].

3. Case study

This part evaluates the effectiveness of the solutions proposed at the level of our previous work [19], and this is done by adding more constraints on the model which will make it more real and better solve the problem of distribution of petroleum products of the company.

This work makes a contribution in two ways. First, we deal with an actual case that differs slightly from the scenario that was previously addressed. Trucks, for instance, operate in shifts with predetermined loading and distribution window times. In contrast to earlier language, shift start and finish times varied from truck to truck.

The ultimate goal in this situation is to maximize customer order fulfillment while adhering to a specific priority and using a small, heterogeneous fleet. Additionally, because each journey has a distinct duration and cost, the charges are unaffected by the amount of time that passes between the start of the first trip and its conclusion.

By forcing the execution of the orders, the priority of the consumers may have been managed; however, because the orders can only be concentrated for a limited period of time, the issue is insoluble.

Our second contribution consists of a heuristic suggestion for this particular instance, the major goal of which is to quickly arrive at a workable operational solution so that people in charge of supply chain management can assist it.

This heuristic is an adaptation of Solomon’s insertion heuristic for problems involving vehicle scheduling or routing with time windows.

Since each customer has value that is not always reflected in the net benefit of a transaction, looking at it from the perspective of customer compliance offers a more comprehensive perspective than merely cost reduction. In the case of fuels, this is crucial because the profit per transaction is generally low and the gain is based on the volume sold. As a result, it could be crucial to prioritize a customer who makes a lot of orders.

In this section, we’ll explicitly characterize the issue at hand and provide some premises and traits that will affect how we approach finding a solution.

3.1.  Problem definition

The VRPTW used in this real case can be defined as follows:

Let ? = ({0, ? + 1} ? ?, ?) be a directed graph where:

{0, ? + 1} is the deposit,

? = {1, . . . , ?} is the set of customers,

? = {(?, ?) ∶ ?, ? ∈ {0, ? + 1} ? ?, ? ≠ ?} is the set of arcs. Each arc (?, ?) is associated with a travel time ??,?. Similarly, the service time ?? at depot or station ?, where ? ∈ {0, ? + 1} ? ?, is known. The set of trucks associated with the depot is denoted ?.

Customer ? orders are made up of order lines, where each line specifies a different product type, bucket type to use, and ideal time window. Trucks must arrive at customer ? within the proposed time window. Also, each truck must respect their team’s time window.

It is crucial to strike a balance between the aspects of reality that we will model and those that we will simplify through assumptions because of the true nature of the problem, which frequently results in instances where theory and reality diverge.

The model’s route generating step contains one of its most significant simplifications. Travel time is directly related to the zone a customer is in because customers are organized by zones. Generally speaking, trucks that visit multiple stations should only go to those that are nearby. Orders may be clubbed together for the purpose of assigning them to one and only one feasible route due to this and other limitations. In relation to capacity, the resulting routes will only have one type of vehicle, allowing us to solve the problem for each type of truck separately. Orders that do not comply with these rules are left out of this issue, as the compliance decision is in the hands of the planners.

• It’s interesting to see that less than 1% of all orders are frequently refused. Following that, more crucial presumptions for this specific issue are noted:
• Orders are made up of order lines, which each client can create until a truck is full. More than one product type may be present in these orders, but only one may be present in each compartment.
• Customers are permitted to create multiple orders. Each of these is handled independently because it has its own specifications and due dates.
• All deliveries must be made in a single trip.
• More than one consumer may accompany a journey, but no more than two.
• Trucks may operate many shifts throughout the day. They are viewed differently because they are independent.
• There is a relevance associated with the priority of a command, this will be represented by the constant ρ.

3.2.  Resolution process

We divided the problem into two phases in order to solve it in a reasonable amount of computation time:

– Phase I: Creation of requests on a monthly basis (in our example, the month of July).

– Phase II: Scheduling and truck assignments based on the VRPTW mathematical model. The following notations will be used in addition to the parameters that have already been defined:

•  Hints:

?, ?: Road index

?: Truck index

? : Trip position index

•  Sets:

? : Road set

?? : Set of routes associated with truck ?

? : Set of possible path indices. ? = {1,2, . . . , ?}

?? ∶ Set of possible route clues for truck ?

•  Parameters:

?? : D????? of ??????? ?

? : Number of ????????

??? : D???????

? : Truck ??????ty

??: Residual demand < 33, which can be delivered in a second time

?? = {?, ?} / ? ∈ [1: ?] : cluster of station i and j that we will deliver them in one truck

(the clusters must group together a maximum of 2 stations) and n is the total number of clusters

?_?: Total demand of day ?

?_?/?: Customer i should be delivered the day s

? _??: Number of full trucks to deliver for a customer i which will define the frequency / duration in which I can deliver a single truck to a station. Example: If nij =2 truck then the frequency is 1 month, nij = 4 , frequency ) 1 truck per week. nij> 4, frequency every 2 days..)

?_? = ??/? : Number of trucks to be loaded at a time

? ∶ Maximum number of possible trips during a shift

?_? ∶ Value associated with the priority of path t

?_? ∶ Start time of route time window t

?_? ∶ End time of route time window t

?_? ∶ Route duration t

?_? ∶ Start date of truck time window k

?_? ∶ End date of truck time window k

Next, we describe the two phases of this problem and how we deal with them.

Phase I : Generation of requests according to a monthly schedule (the month of July in our case)

This first phase is considered an initialization process.

It consists of generating the delivery schedule for monthly requests (the month of July in our case) for all the service stations, as well as the total number of trips during this month and subsequently the number of trucks to rent. The aggregation of orders in the trucks must follow certain rules of the company. This allows us to group commands so that they are assigned to one and only one possible route.

• Depot: working hours (from 5 a.m. to 1 p.m. // 2 p.m. to 4 p.m.) 26 days a month:

It is a common depot between 5 companies located in Mohammadia, it contains 17 truck loading stations (full load). The number of trucks to be loaded at a time varies from one company to another with a loading time of 1 hour.

Shell 17 trucks at a time;

OLA ENERGY 10 trucks simultaneously with Winxo 7 Trucks;

Total 12 simultaneous with Petruom 5 Trucks.

The order of passage is done in turn each week, which then defines the maximum number of possible loadings. Let I be the maximum number of trips to be made in one day for our company:

Week 1: Ola is the first: 4 trips *10 = 40 trucks

Week 2: Ola is second: (I = 3 trips) *10 = 30 trucks

Week 3: Ola is third: (I = 3 trips) *10 = 30 trucks

Week 4: Ola is the first: (I = 4 trips) *10 = 40 trucks.

• Customer storage capacity:

Each customer has a monthly demand and storage capacity. If the capacity is less than 33T, we cannot deliver a full truck so we split the complete order into 2 orders or more. Otherwise, we deliver a complete truck.

• Algorithm :

1- ?? /? = ??

2- ?? – ?(??) = ??, 26 / ?(??) = ??? and ? ∈ {1, … . , 26}

3- ??????? ????????  : {?? + ?? = 1(1 ?????? ) and ??? ≤ 30?? à ??

?=1

4-   ??  =  ∑^?         ??/? for ? = 1 : 26

??/? = 1 ?? ? ?????? ??? = 0 & ??/? = 0 ????

?? (??/? ≠ 0 & ??/? ≠ 0) ???? ?, ? ∈ ??; ? ∈ [1: ?]

?? = ?? + 1 (We add the trucks that will deliver the residual of the cluster ) & [1: ?] = [1: ?] −1 (We subtract the cluster that we will deliver on the day s)

?????

5- ?? = ?? / ?

?? ?? > 10 so  ?? = ? ∗ 10

?? = ?? – ??

( ?? it’s the deliveries that I have to deliver but I don’t have the right for the day s, so I will memorize these deliveries and satisfy them the day I have more trucks)

6-   ?? = ???−1 + ??

??? ? = 1 : ??

?? ?? < 10

?? = ?? + 1

?? = ?? – 1

?? = ??? ?? ??? {? =1, … . , 26}

Phase II : Truck assignment and scheduling from the VRPTW mathematical model

The company’s primary goal is to maximize the trucks and trips that stop at the most service stations while adhering to their time restrictions, each station’s priority weighted accordingly.

The assignment problem’s goal function can be stated as follows: Maximize:

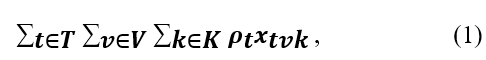
The binary variable xtvk has a value of 1 if route t corresponds to the v-th trip of truck k and a value of 0 otherwise. We employed a sequential insertion heuristic, which distributes roads to one truck at a time until the truck can no longer accept another one, because addressing this problem using exact approaches proved challenging with a huge number of trucks and roads.

For each route of the truck, the starting position and time must be defined, which leads to the scheduling problem. The following model deals with route scheduling for each truck ?:

• Variables :

?_??: binary variable which takes the value 1 if the route t corresponds to the v-th trip of truck k; 0 otherwise.

?_?: departure date of the truck’s v-th trip ?

Minimize :

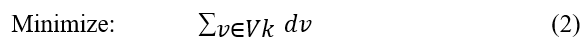
Under constraints of:

The goal function (2), which relates to a supplementary optimization criterion, seeks to decrease departure times while prioritizing the shortest routes before the longest ones. Truck k will only make one of the trips given to it, thanks to constraint (3). Each travel position will only be able to handle one route, according to constraint (4). Each route must adhere to its time frame if it corresponds to the v-th trip, according to constraint (5). The start time of the v-th trip will begin after the previous trip has ended, according to constraint (6). The first journey is required to adhere to the truck’s departure time per constraint (7). The last trip must finish before the truck’s end time k, according to constraint (8). Lastly, limitations (9) and (10) show the nature of the variables.

The sequential insertion heuristic we propose can be expressed as follows:

For each truck:

1. Populate a list with all unassigned routes.
2. Sort routes in descending order of priority.
3. Filter routes based on truck time window compatibility.
4. Assign the truck a route from the list that meets a certain departure criteria.
5. For each item in the list:

(A) Verify compatibility with the allocated routes as of right now. If the (a) check is positive, solve the scheduling problem including the current route.

If not, proceed to the next thing on the list.

(b) If the scheduling issue has been correctly resolved, assign the current route to the truck, remove it from the list, and determine if any other possible routes are still available. If not, proceed to the next thing on the list. (c) Go to the next item on the list if there are any suitable paths. If not, proceed to the next truck.

Once all vehicles have been moved or all routes have been assigned, the process is complete.

On real data from the month of July, we tested our heuristic.

Each day’s orders and truck involvement varied, allowing a wide range of potential scenarios to be covered.

The Python code for our heuristic was created using Jupyter Anaconda Navigator on a Windows 10 PC with an Intel Core i5-4200U processor clocked at 1.6 to 2.3 GHz and 4GB of RAM.

Table 1 and Figure 1 present the findings.

Our heuristic therefore allowed us to plan the path or the circuit of truck 1 for example in an optimized way.

Table 1: Planning extract for Truck 1

	Truck 1
	ID	Day	Arrival Time	Departure Time	Delivery Volume	Distance traveled
Deposit	LOMA0662668	Thursday		07:00		0
Station-service 6	LOMA0672999	Thursday	08:00	09:30:00	33	18
Deposit	LOMA0793001	Thursday	10:53	12:00		104
Station-service 11	LOMA0662997	Thursday	12:59	13:29	16	124
Station-service 28	LOMA0662974	Thursday	13:36	14:06	17	127
Deposit	LOMA0662668	Thursday	15:16		0	304

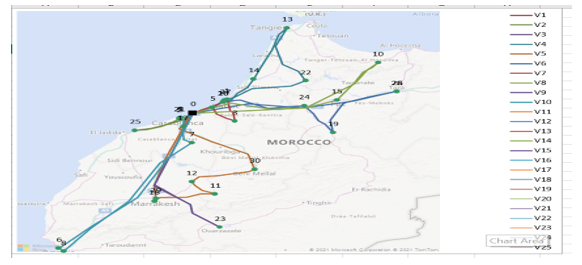
Figure 1: Truck route for the first day of July

4. Conclusion

Our heuristic produces a suggestion that planners typically ask for in the morning or throughout the day, particularly when significant alterations to the current schedule are required. As a result, they must be able to quickly deliver a solid initial plan. The greatest cases of this problem can be handled by the heuristic in a maximum of 10 minutes, which is a respectable amount of time given the compliance attained.

According to the data, it is possible to achieve at least the same level of compliance as the company, thus it is possible to include the truck teams’ time slots in the scheduling issue the company confronts.

Future research will concentrate on the impact of more real-world factors in the two phases mentioned, testing the heuristic’s various aspects to see if it can solve them, including: the environmental factor, worker safety, road quality, and the efficiency of using secondary optimization criteria on the solution. Finally, testing various route departure criteria may help the heuristic perform better.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

I am grateful to all of those with whom I have had the pleasure to work during this and other related projects.

1. “The vehicle routing problem: An overview of exact and approximate algorithms”, European Journal of Operational Research, 59, 345-358, 1992, doi.org/10.1016/0377-2217(92)90192-C.
2. G. Laporte, “The traveling salesman problem: An overview of exact and approximate algorithms”, European Journal of Operational Research, 59, 231-247, 1992, doi.org/10.1016/0377-2217(92)90138-Y.
3. G. Laporte, I. H. Osman, “Routing problems: A Bibliography”, Annals of Operations Research, 61, 227-262, 1995, doi.org/10.1007/BF02098290.
4. N. Christofides, A. Mingozzi, P. Toth, “The vehicle routing problem”, 315-338. Wiley, Chichester, 1979, doi.org/10.1007/978-1-4615-5755-5_1.
5. M. Desrochers, J.K. Lenstraa et M.W.P. Savelsbergh, “A classication scheme for vehicle routing and scheduling problems”, European Journal of Operational Research, 46(3), 322-332, 1990, doi.org/10.1016/0377-2217(90)90007-X.
6. M. Sol et M. Savelsbergh, “A branch-and-price algorithm for the pickup and delivery problem with time windows”, Memorandum COSOR 94-22, Dept. Of Mathematics and Computin, 1994.
7. H. Housroum, “Une approche génétique pour la résolution du problème VRPTW dynamique”, Thèse Doctorat en informatique, Université d’Artois, 2005.
8. M. Chassaing, “Problèmes de transport à la demande avec prise en compte de la qualité de service”, Thèse Doctorat en informatique, Université Blaise Pascal-Clermont Ferrand II, 2015.
9. T.R. Sexton, Y.M. Choi, “Pickup and delivery of partial loads with “soft” time windows”, American Journal of Mathematical and Management Sciences, 6(3-4), 369-398, 1986, doi.org/10.1080/01966324.1999.10737484
10. S.P. Greaves, M.A. Figliozzi, “Collecting commercial vehicle tour data with passive global positioning system technology: Issues and potential applications”, Transportation Research Record, 2049(1), 158-166, 2008, doi.org/10.3141/2049-19.
11. M. Akil, “Problème de tournées de véhicules avec contraintes et fenêtre de temps”, Mémoire Magister en informatique, UMMTO, 2013.
12. W. Dong, K. Zhou, H. Qi, C. He, J. Zhang, “A tissue P system based evolutionary algorithm for multi-objective VRPTW”, Swarm and evolutionary computation, 39, 310-322, 2018, doi.org/10.1016/j.swevo.2017.11.001.
13. W. Zhang, D. Yang, G. Zhang, M. Gen, “Hybrid multi-objective evolutionary algorithm with fast sampling strategy-based global search and route sequence difference-based local search for VRPTW”, Expert Systems with Applications, 145, 113-151, 2020, doi.org/10.1016/j.eswa.2019.113151.
14. M. Saint-Guillain, Y. Deville, C. Solnon, “A multistage stochastic programming approach to the dynamic and stochastic VRPTW”, In International Conference on Integration of Constraint Programming, Artificial Intelligence, and Operations Research, 357-374, Springer, Cham, 2015, doi.org/10.1007/978-3-319-18008-3_25.
15. T. Gocken, M. Yaktubay, “Comparison of different clustering algorithms via genetic algorithm for VRPTW”, 2019, doi.org/10.2507/IJSIMM18(4)485.
16. V. Pureza, R. Morabito, M. Reimann, “Vehicle routing with multiple deliverymen: Modeling and heuristic approaches for the VRPTW”, European Journal of Operational Research, 218(3), 636-647, 2012, doi.org/10.1016/j.ejor.2011.12.005.
17. H.B. Ticha, N. Absi, D. Feillet, A. Quilliot, “Empirical analysis for the VRPTW with a multigraph representation for the road network”, Computers & Operations Research, 88, 103-116, 2017, doi.org/10.1016/j.cor.2017.06.024.
18. W. Xu, X. Wang, Q. Guo, X. Song, R. Zhao, G. Zhao, D. He, “Gathering Strength, Gathering Storms: Knowledge Transfer via Selection for VRPTW”, Mathematics, 10(16), 28-88, 2022, doi.org/10.3390/math10162888.
19. Y.F. El Bahi, L. Ezzine, Z. Aman., H. El Moussami, “Distribution management problem: case of vehicle routing problem with capacity constraints “CVRP” in the Moroccan petroleum sector”, In 8th International Conference on Control, Decision and Information Technologies (CoDIT) (1), 1149-1154, IEEE, 2022, doi.org/10.1109/CoDIT55151.2022.9803955.

(Click Here)