1. Introduction

This paper is an extension of work originally presented in the eighth (8^th) edition in the series of the International Conference on Control, Decision and Information Technologies, CoDIT’22 [1], in order to clarify how orientation and quantity of magnetic moments affect the in-fluid swimming potential of the soft robots.

Our body inside is a fantastic and complex system consisting of the circulation of diverse biological fluids and unstructured environments. Untethered miniature robots with millimeter scale or less have been promising to access the hard-to-reach biomedical regions for minimally invasive treatments (e.g., targeted drug delivery, biopsy) [2]. Due to the small size of the robot, the battery and motion mechanism were unable to set up inside the robot’s structure. In order to function locomotion of the robots, active elements to respond with the external power sources were embedded in their body instead, during the fabrication process. Some types of the robots received the light emission pulse to transform its structure for mobility. Another type of robots employed the chemical reaction with the surrounding environment for propulsion. Other types of robots holding magnetic property were active after experiencing the actuating magnetic field. Each of robots has own mechanism functioned by particular active elements to create locomotion in environments.

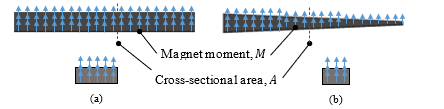
Figure 1: The different magnetic property of magnetic-soft structure between previous works and this work (a) uniform distribution of magnetic moments, (b) non-uniform distribution of magnetic moments

The use of magnetic field was proved no harm to human tissue, especially affording the clinical imaging (e.g., MRI). It was one of the most selective sources to remotely manipulate robots. In order to generate magnetic energy to manipulate the robots, magnetic actuation systems were specifically designed in diverse configurations with a variety of control techniques (e.g. magnetic navigation in a large workspace) [3]. Once the actuation system generated magnetic field, the magnetic property of the robots as called magnetization responded with such that actuation through magnetic alignment. This concept allowed the robot to have effective locomotion via motor-less mechanism [4].

Table 1: Raw materials and tools Material Property Function Liquid silicone rubber: LSR (SIMTEC) Density: 1.13 g/cm3, Young modulus: 300 kPa, temperature resistance: -50 to 250 ºC, tensile strength: 1.5 MPa, elongation at break: 700% Base material to form a soft structure NdFeB (Neodymium) magnetic microparticles Particle size: 4 µm to 40 µm, density: 7.57 g/cm3, Remanence: 720-760 mT, coercivity: 360-480 A/m, magnetic energy: 80 to 98 kJ/m3 Active elements; base material to respond to magnetic actuation A stainless-iron plate 30 mm x 100 mm with 80 µm 10 µm cavity A mold doe the mixture to fabricate a magnetic-soft sheet A shape guider PLA (Polylactic Acid) 3D-printed parts with sinusoidal profile* ( )) at the inner surface To constraint a magnetic-soft sheet before applying a magnetizing magnetic field to specific magnetic orientation of magnetic moments * Profile to specify orientation of magnetic moments can be adjusted to any form.

In life, environments are mostly viscous, which is hard for matters to perform motion, but microorganism-inspired robots adopt the asymmetric body movement with solid components as a key of success in fluidic maneuverability to swim effectively (e.g. beating or waving of flagella or cilia, helical propulsion) [5, 6], but having a solid structure limits safe interaction. The transition from a hard structure to a soft structure is wide-opening to fabricate swimming tiny robots by using materials embedded with functional elements. The integration of magnetic particles into the deformable structure enables controllability, leading to continuous and controllable movement under magnetic actuation due to magnetic alignment of magnetic moments within specimens of the structure. This aspect allows medical tools and medical robots to become more deformable and dexterous in various types of biomedical application (e.g. compliant-soft medical tools, flexible wearable devices) [7]-[10]. Moreover, having a deformable structure benefits a soft interface to greatly deal with uneven terrains and unstructured geometry without harmfulness [11, 12]. Such that soft structure with additional matters (e.g., drug molecule, chemical nanoparticles) still fulfil the remote applications in medicine, such as drug delivery, biopsy, detoxification [13]-[16].

In previous research, there were soft robots employing only anisotropic magnetization or non-uniform magnetic orientation to generate the body movement based on the continuous alignment of magnetic moments with the dynamic magnetic field. The deformation degree of each specimen of the robot’s structure is equal and uniform because the distribution of magnetic moments is uniform across the whole soft structure, resulting in uniform magnetic strength. However, property of magnetic moments embedded in the soft structure still remains a challenge in the core detail. Magnetic moment typically comprises of orientation and strength, and what if they are not uniform across the whole deformable structure. In this paper, effect of orientation and strength of magnetic moments in the deformable structure of the soft robot is investigated in term of swimming behavior and performance based on lateral undulation. Three types of soft milli-robots are fabricated; the I robot: uniform magnetic strength and non-uniform magnetic orientation, II: non-uniform magnetic strength and uniform magnetic orientation, and III: non-uniform magnetic strength and orientation.

Those robots having the magnetically deformable structure utilizes high-degree of freedom provided by magnetic compliance as if motor-less mechanism set up inside, and they become more dexterous, especially in the applications of biomedicines (e.g. compliant robotics, flexible medical tools). In particular, in order to operate the robot for treatment and therapy, potential of the robot to swim in fluidic and wet environments is a critical requirement.

Methods and materials are detailed in the next section. Next, experiments are conducted to test performance in swimming of the robots in fluid under the change in controlled parameters. Finally, the conclusion is issued.

2. Material and Method

2.1.  Conceptual design

In the case that the size of a matter moving in media is millimeter or less, inertia term is dominated over viscous term, resulting in low Reynold number condition ( ). Purcell stated that one of feasible motion patterns for small objects to effectively move in fluid was the use of the asymmetric body deformation under time-reversal [17]. Consequently, liquid silicone rubber (LSR) as a base material is used to obtain a deformable property, and magnetic particles is filled in order to respond with magnetic actuation. The combination of them leads to a controllable-deformable structure under magnetic field. This aspect results a motor-less mechanism in a soft small-scaled robot remotely controlled by the dynamic magnetic field to serve as a medical device.

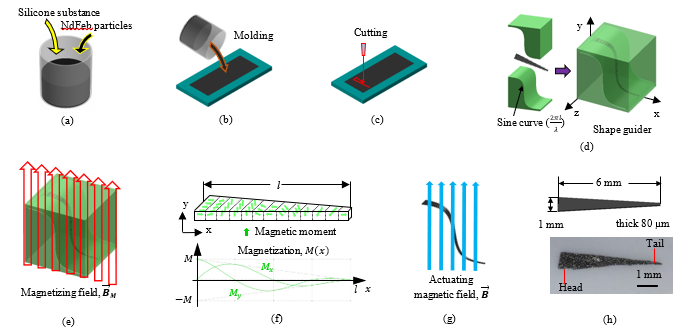
Figure 2: Example of fabricating the III robot. (a) Liquid silicone substances and NdFeb particles with 1:1 of mixing ratio. (b) molding on the stainless-steel plate, then subjects it to heat curing. (c) cutting into a triangular shape. (d) inserting into the sinusoidal-surface shape guider. (e) 700 mT of uniform magnetizing magnetic field. (f) magnetization profile of the film robot: (upper) magnetic orientation. (lower) magnetic strength decreases by increasing the body length. (g) the robot responding to the actuating magnetic field. (h) the triangular body: 1 mm  6 mm  80 µm.

Theoretically, magnetic moment or magnetic dipole is a vector that consists of magnitude and direction. It can be played in the detailed to define a specifically magnetic property. The soft milli-robot is designed to have three types of distinguish magnetic property; the I robot is with uniform magnetic strength and non-uniform magnetic orientation, the II robot is with non-uniform magnetic strength and uniform magnetic orientation, and the III robot is with non-uniform magnetic strength and orientation. Based on the modeling of magnetism [18], magnetic moment in a structure can be expressed by

where , ,  are respectively the cross-sectional area, length of the structure, and magnetization which is a quantity of magnetized magnetic moment in a concerned volume, . Thus, the existence of magnetic moment, according to Figure 1a and the definition of the eq. (1), can expressed that each specimen of the soft rectangular structure has the uniform magnetic orientation which points upward, and the uniform magnetic strength due to having equal number of the moments.

Otherwise, in Figure 1b, the existence of magnetic moment expresses that each specimen of the soft triangular structure has the uniform magnetic orientation which directs upward, but magnetic strength is non-uniform due to unequal number of magnetic moments along the length of the structure. The specimen where is the biggest cross-sectional area contains the strongest magnetic strength, but at the smallest area, magnetic strength is the weakest. Thus, the eq. (1) is rewritten to

Eq. (2) expresses that at a position, x, on the length, l, if cross-sectional area across the length of the structure is unequal, magnetic moments at each position is different along the length, resulting in non-uniform magnetic strength.

2.2.  Fabrication process

In this work, three-type property of the soft robot is modified with the existence of magnetic moments in the soft structure. List

Table 2: Three types of soft swimming milli-robots Type Width (w) Length (l) Thick (h) Shape Profile of magnetic direction* Magnetic strength** Magnetic response*** I 1 mm 6 mm 80 µm   Triangular     Sine       Uniform       II 1 mm 6 mm 80 µm   Rectangular     Transverse       Non-uniform   III 1 mm 6 mm 80 µm   Triangular     Sine       Non-uniform   *  A set of arrows depicts the direction of magnetic moments, and its quantity refers to magnetic strength in the robot’s structure. ** A graph shows the relation of magnetic strength and magnetic orientation of magnetic moments as a function of body length. *** Blue hidden line represents the original shape of teach robot before magnetic deformation due to alignment of magnetic moments with respect to the direction of the actuating magnetic field.

of the main materials is reported on Table 1. In Figure 2, the robot fabrication starts from the mixing of liquid silicone rubber and NdFeB magnetic microparticles with the 1:1 mass ratio. Later, pouring the mixture into a stainless-steel mold with 80 µm cavity to form a magnetic soft sheet with 80 µm thickness, and putting the mold to cure at 250 ºC about 8-10 minutes. Finally, getting a magnetic soft sheet to prepare for making a magnetic-soft robot.

Figure 3: Magnetic actuation system. (a) It generates uniform-based field across the large bore. (b) a silicone-filled container as a workspace inserted into the bore.

At this step, the finishing is the sheet embedded with magnetic elements across the whole volume, but its magnetic property is still not defined. In order to specify the direction of all magnetic moments, the sheet must be subjected to the 700-mT magnetizing magnetic field, . For example, if the direction of magnetic moments is similar to a wave, the sheet must be confined into the wave pattern, and then placing it into the    for permanent direction. Once removing it from the , the direction of magnetic moments follows as the wave across the whole volume permanently.

According to the eq. (2), uniform or non-uniform magnetic strength across the whole volume can be defined by the shape of the structure. For example, if the structure is symmetric as a rectangle, quantity of magnetic moments at each specimen will be equal across the whole length, resulting in uniform magnetic strength of magnetic moments. Otherwise, if being triangular, the cross-sectional area is not equal across the length, resulting in non-uniform magnetic strength of magnetic moments. As depicted in Figure 1, at the same position on the length, quantity of magnetic moments is different between two shapes. In Figure 3, after getting a desire shape, the sheet is cut into a triangular shape. Then, it is placed into a shape guider to form a sine-based

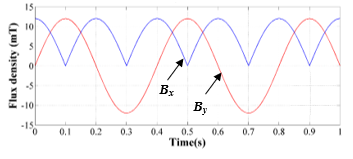
Figure 4: Signal sample of the x- and y-magnetic field, B_x and B_y, generates oscillating magnetic field with 2.5 Hz.

curve, and subjected into the  to profile the magnetic orientation of magnetic moments embedded in the triangular sheet. In this case, if it is actuated by magnetic field, the triangular sheet self transforms into a wave shape or a body wave deformation. Finally, the magnetic-soft sheet becomes a magnetic-soft robot. In this work, the robot is fabricated into three types to have different property of magnetic moments according to the Table 2.

2.3.  Actuation and control procedure

The magnetic actuation system shown in Figure 3 consists of seven electromagnetic coils to achieve 3D-magnetic field in order to cover 6-DOF motion of the soft robot. It provides three directions of homogeneous magnetic field across a cylindrical workspace (radius: 7.5 cm and length: 18 cm). This aspect guarantees a pure magnetic torque exerted to actuate the soft robots without any drifting caused by the wrench of magnetic force. Each coil is individually operated by seven current drivers (Dimension engineering; 25 kHz, 30V/10A), and electrically supplied by SIEMENS GR60 (40A/48V). A custom controller with 8-bit-packeted-serial communication commands the drivers to pass electrical current into the coils to generate magnetic field. A stationary CMOS camera with zoom lens (working distance: 6-120 mm and 1.6-mm depth-of-field) is mounted to observe locomotion of the robot, and localize the robot’s position to feedback the coordinate into the control algorithm in order to adjust a proper magnetic field. Maximum magnetic field is 25 mT and 100 T/m at 15 A input electrical current, measured by a gaussmeter GM-08 Hirst.

The magnetic-soft robot responds to magnetic actuation due to having magnetic moments, , as active elements embedded in the soft structure. It acts as a motor-less mechanism to make the robot swim in fluid. Depicted in Figure 3, the electromagnetic actuation system [3] is specifically designed to power the robot by using three-dimensional magnetic field, , which is

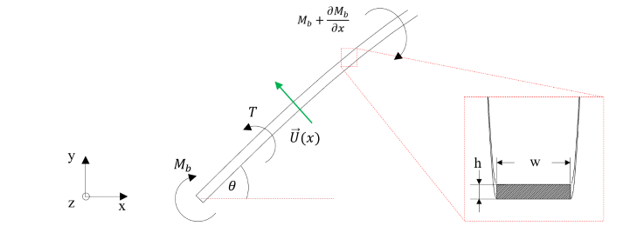
Figure 5: Physical interpretation of a deformable structure. When magnetic torque is exerted to deform a soft robot long, l, its local body segment, x, with thickness, h, and width, w, is bent with angle, , resulting in the moving of each local segment with velocity, .

Once the robot is under magnetic field, its soft body is deformed toward the direction of the magnetic field due to an alignment of magnetic moments across the volume. Magnetic torque, , and force, , are exerted to the robot, expressed by

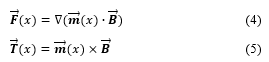
Magnitude and direction of magnetic field is adjustable by using the superposition technique resulting from sources of magnetic field. In this work, the oscillating magnetic field is applied to manipulate the deformable structure of the robot continuously, leading to the body wave propagation or undulation as if swimming. The oscillating magnetic field is a product of the superposition of the magnetic field in the x- and y-direction, B_x and B_y, which oscillates with frequency,  (Hz: cycle number in a second). As shown in Figure 4 of the signal sample, the eq. (3) is rewritten by

Frequency and magnitude of the oscillating magnetic field in the eq. (6) are adjustable by varying magnitude and direction of the electric input current supplied into each electromagnetic coil.

2.4.  Modeling of deformation

Regarding the soft property of robots, Euler-Bernoulli beam theory is adopted to determine the local body deformation caused by magnetic field, depicted in Figure 5. Once magnetic torque, , as bending moment, , is exerted to the robot, expressed by

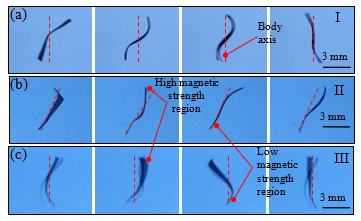
Figure 6: Swimming behavior of three robots holding different magnetic property. (a) The I robot symmetrically deforms as a wave. (b) The II robot sweeps at a specimen of high magnetic strength. (c) The III robot propagates a body wave along the body length.

where  is Young modulus of the robot (Pa),  is bending angle defined by deformation degree over length estimated by , and  is area moment of inertia ( ) which is a function of the thickness, h, and width, w. When the body of robot is long, l, the area moment of inertial at each local body becomes a function of the unit length, x, of the full length, l, expressed by

where  is cross-sectional area at the x position on the body length l. Substituting the eq. (5) and the eq. (8) in the eq. (7), so

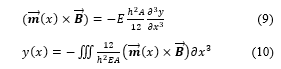
As mentioned, considering that the whole body of the robot consists of many magnetic domains. Magnetic moment, , at a specimen or a local is a function of magnetization and cross- sectional area. The eq. (10) expresses that deformation of a specimen at the position x, on the body length depends on magnitude and direction of magnetic moment significantly. Differentiating the eq. (10) over time to obtain swimming velocity, , at that local, is expressed by

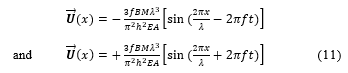
where , , , , E, t is the oscillating frequency, magnetic field, magnetization, body wavelength, Young modulus of material, oscillating time respectively. Positive and negative sign express the deformation direction of a specimen of the body. From the eq. (11), in short, the swimming velocity, , is proportional to magnitude and direction of magnetic moment which is a function of magnetization, M, at that specimen.

3. Experiments and Results

As mentioned, a key to have an effective swimming in fluid for a small-scaled robot is the use of an asymmetric body deformation, and the robots in this work follow such that concept utilizing a deformable structure triggered by magnetic field. The magnetic-soft robots are fabricated into three types, according to Table 2, and they are experimentally investigated in the term of swimming behavior and performance.

Experiments are all set up under the same parameters and conditions. Three types of the robots are all fabricated under the same process, but different in the post-fabrication, which is the cutting process to define quantity of magnetic moments via the final shape, and the magnetizing process to program the orientation of magnetic moments. A tank contains silicone oil to simulate viscosity of biological fluid, and it is inserted into the bore of the magnetic actuation system, depicted in Figure 3b. The system generates the oscillating magnetic field with three numbers of magnitude (5, 10, 15 mT) and fifteen numbers of frequency (1 to 15 Hz) to manipulate three types of the soft milli-robot.

3.1.  The I robot

The I robot has a property of uniform magnetic strength and non-uniform magnetic orientation due to having a rectangular film shape (1 mm  6 mm  80 µm) and being magnetized with the sine profile, detailed in Table 2. Thus, its magnetic property is modeled by

The eq. (12) clearly details that magnetic orientation of the robot follows the sine profile depicted by the direction of arrows varying as a wave, and magnetic strength is uniform, depicted by number of arrows which is symmetric at each column along the body length.

Depicted in Figure 6a, once the I robot is actuated by the oscillating magnetic field, the magnetic moments embedded in the soft structure aligns with respect to the direction of the magnetic field, leading to the body deformation, and the deforming shape of the robot turns to be a sinusoidal curve. Next, when the direction of magnetic field oscillates with a frequency, the body of the robot is continuously deformed with respect to the oscillation of magnetic field under the same frequency, resulting in a lateral undulation, leading to swimming in fluid. It is noticed that the deformation of the robot is symmetric, and all of magnetic specimen in the structure simultaneous responds to the magnetic field at the same time because magnetic strength in each specimen is uniform.

3.2.  The II robot

The II robot holds a property of non-uniform magnetic strength and uniform magnetic orientation, due to having a triangular shape (1 mm  6 mm  80 µm), detailed in Table 2. Number of magnetic moments in the triangular shape decreases along the body length, according to the eq. (2), resulting in non-uniform strength across the whole structure. The larger the volume, the stronger the magnetic strength. It is magnetized to have the direction of magnetic moments aligned in the same direction, resulting in uniform magnetic orientation. Its magnetic property is expressed by

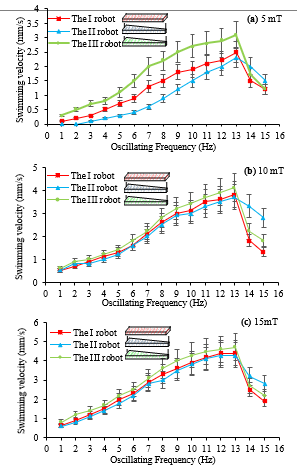
Figure 7: Under (a) 5 mT, (b) 10 mT, (c) 15 mT of magnetic field, the plot of swimming velocity against the different numbers of the oscillating frequency (ranged from 1 to 15 Hz). Three robots are powered by those input parameters to swim in fluid. The robots all swim faster with the increase of the actuating frequency, and drops after reaching the step-out point at 13 Hz.

The eq. (13) expresses that magnetic strength of the II robot is a function of a position along length l, and the magnetic moments all point to the y direction. Under this condition, once the robot is magnetically actuated, a specimen has a stronger magnetic strength firstly respond, and when the magnetic field is stronger, a specimen has a lower magnetic strength orderly follows. Thus, under the oscillating magnetic field with constant magnitude, the robot sweeps its body with respect to the oscillation of the magnetic field, making the robot propel as shown in Figure 6b.

3.3.  The III robot

The III robot has a property of both non-uniform magnetic strength and orientation. Same to the II robot, number of magnetic moments varies along the body length due to having a triangular shape. It is maximum at the largest cross-sectional area, but minimum at the smallest area, resulting in non-uniform magnetic strength. The direction of magnetic moments aligned with respect to a sine curve, same to the I robot, resulting in non-uniform magnetic orientation. Its magnetic property can be expressed by

The eq. (14) explicitly expresses that both magnetic orientation and strength are varying along the body length. Once the III robot is actuated by magnetic field, its body deforms as a curve, but the magnetic response of specimen where contains a higher magnetic strength is prior to another specimen where contains a lower magnetic strength. Under the oscillating magnetic field, it propagates the body as if a body waving for swimming interestingly and smoothly, depicted in Figure 6c.

3.4.  Comparison in swimming behavior and performance

Under the actuation of oscillating magnetic field, each of robots (I, II, III) shows its own specific mechanism to swim in fluid. Magnetic alignment of magnetic moments embedded in the soft structure of each robot draws the deformable pattern differently due to being magnetized with the different profile. Sine profile magnetization causes a body wave propagation for the robot, resulting in more effective swimming, as appeared in the I and III robot. However, in experiments, one more interestingly magnetic aspect in the soft structure is figured out that quantity of magnetic moments has an influence to define the response degree to external magnetic actuation. If higher, magnetic strength is stronger, resulting in a fast response. If lower, magnetic strength is weaker, resulting in a slow response. When both high and low magnetic strength are together in one soft structure, leading to unequal magnetic strength of each specimen. Magnetic response of the entire body is different, and active orderly from the high to low magnetic strength. As apparent in the magnetic response of the I and III robot, both is profiled by sine pattern, but magnetic strength is different. The I robot transforms the entire soft body to a curve pattern immediately, but of the III robot, a specimen containing a higher magnetic strength is firstly attractive to magnetic field, but another with a lower strength follows orderly. Moreover, the III robot is better in manipulation because it allows another control of dynamic magnetic field. The rotating magnetic field can drive the robot to swim curvilinearly along clockwise or counter-clockwise direction. (Supplementary video 01)

In order to compare performance of three robots embedded with the distinguish magnetic property, swimming velocity is plotted against actuating input parameters; three numbers of magnetic field (5 mT, 10 mT and 15 mT) with fifteen numbers of the oscillating frequency (from 1 to 15 Hz), shown in Figure 7. The results report that velocity tends to continuously increase by an increase of the gaining frequency. The plot still expresses that the III robot can swim fastest at any magnitude of magnetic field, including the oscillating frequency. All of the robots have the step-out point of the oscillating frequency about 13 Hz at all ranges of magnetic field. At this point, the robot lost in synchronization to the actuating magnetic field, resulting in lack of control and dramatical decrease in velocity. However, swimming velocity of the II robot does not drop fast interestingly if comparing with the others because its body deformation caused by magnetic alignment is the simplest, pointing toward only one direction. Compared with the I and III robot profiled with the sine-curve manner, the II robot’s deformation has least lost in synchronization to the magnetic field. After the step out point at 13 Hz, it turns to be a better swimmer than others. Interestingly, at the lowest magnetic field; 5 mT, the III robot still shows a better control and performance than others at all ranges of the actuating frequency, including having the fastest response and performance even at the low oscillating frequency whereas the others cannot swim out due to lost in the magnetic synchronization.

4. Conclusion

In the research of biomimetic robots, fish-like swimming relies on a flexible body to achieve the higher performance, but this mechanism aspect is limited with the size of the robot down to millimeter or less. The use of magnetic field can be a solution to such that problem promisingly. Remotely magnetic manipulation of tiny robots is an effective and non-harmful technique to deal with biomedical applications in which the small-scaled swimming robots can contribute tremendous results as medical devices. In this works, the combination of both magnetic actuation and flexible structure is presented with the purpose of medical application. It enables the wireless power of the external magnetic field generated by the magnetic actuation system. This concept is beneficially applicable to the small-scale robot to employ motor less-mechanism. Three types of soft swimming robots are fabricated with distinguish magnetic property. Their swimming behavior and performance is investigated under the actuation of the oscillating magnetic field. The magnetic alignment of magnetic moments embedded in the deformable structure of the robot leads to maneuverability in fluid under the minimal control of the oscillating magnetic field. The experimental results report that the swimming performance of the robot mainly relies on two parameters; firstly, the strength of magnetic field to adjust the amplitude of the body deformation, and secondly, the frequency to gain the rate of the body deformation. Finally, we found out that quantity and orientation of magnetic moments in the soft structure function in swimming behavior and performance differently. Either of them can be employed solely to create a motion mechanism of the small-scaled robots. The contribution of this study is wide-opening and promising for a soft small-scaled robot to serve multi-purposes towards biomedical applications.

5. Discussion

There are several concerns to avoid error of the data collection, and prepare the robot to be ready for the application. During the experiments, the swimming velocity data of each robot at all input parameters is critical and needs a precise measurement in order to compare the swimming performance between those robots properly. Object tracking is applied to the camera mounted on the top of the magnetic actuation system, and the center of robot is captured to obtain the coordinate. Another issue of the work would be about the future work. According to the fabrication process, the robot allows us to add more functions to make the robot greater in performance. We definitely plan to extend this study to an advance experiment such as in-vitro and in-vivo experiment. Even though the results of the study are reliable, the robot still needs to improve biocompatibility. Typically, the magnetic active element used as a main component to fabricate the soft robot is not biocompatible. Consequently, the robot is partially biocompatibility. However, the use of biocompatible polymer (e.g., PEG, hydrogel) to wrap the robot is possible, and it does still not constraint the deformation degree actuated by magnetic field. Another would be about how to image the robot inside the blind area. There are two possible methods; Ultrasound imaging using a probe to detect the robot and PA (Photoacoustic) imaging visualizing the robot via the excited signal from additional components. Both imaging techniques can track the robot accurately. If these issues are managed properly, the robots will be ready for the medical applications.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This work is supported by the Research Fund of Faculty of Engineering, Thammasat School of Engineering, Thammasat University, the Thammasat University Research Fund No. TUFT 49/2566, the Thammasat Postdoctoral Fellowship No. TUPD 19/2565, and the Thailand Science Research and Innovation Fundamental Fund fiscal year 2023.

1. X. Tang, L. Manamanchaiyaporn, “Magnetic-Powered Swimming Soft-Milli Robot Towards Non-Invasive Applications,” The eighth (8th) edition in the series of the International Conference on Control, Decision and Information Technologies (CoDIT’22), 1562-1566, 2022, doi: 10.1109/CoDIT55151.2022.9804108.
2. B.J. Nelson, I.K. Kaliakatsos, J.J. Abbott, “Microrobots for Minimally Invasive Medicine,” Annual Review of Biomedical Engineering, 12, 55–85, 2010, doi: 10.1146/annurev-bioeng-010510-103409.
3. L. Manamanchaiyaporn, T. Xu, X. Wu, “An Optimal Design of an Electromagnetic Actuation System towards a Large Homogeneous Magnetic Field and Accessible Workspace for Magnetic Manipulation,” Energies, 13 (4), 911, 2020, doi: 10.3390/en13040911.
4. L. Manamanchaiyaporn, T. Xu, X. Wu, “Magnetic soft robot with the triangular head-tail morphology inspired by lateral undulation,” IEEE/ASME Transactions on Mechatronics, 25 (6), 2688-2699, 2020, doi: 10.1109/TMECH.2020.2988718.
5. S. Palagi, P. Fischer, “Bioinspired microrobots,” Nature Review Materials, 3, 113-124, 2018, doi: 10.1038/s41578-018-0016-9.
6. L. Zhang, J.J. Abbott, L.X. Dong, B.E. Kratochvil, D.J. Bell, B.J. Nelson, “Artificial bacterial flagella: fabrication and magnetic control,” Applied Physics Letters, 94, 2009, doi: 10.1063/1.3079655.
7. H. Huang, M.S. Sakar, A.J. Petruska, S. Pane, B.J. Nelson, “Soft micromachines with programmable motility and morphology,” Nature Communication, 7, 12263, 2016, doi: 10.1038/ncomms12263.
8. E. Diller, J. Zhuang, G.Z. Lum, M.R. Edwards, M. Sitti, “Continuously distributed magnetization profile for millimeter-scale elastomeric undulatory swimming,” Applied Physics Letters, 104, 2014, doi: 10.1063/1.4874306.
9. G.Z. Lum, Y. Zhou, X. Dong, H. Marvi, O. Erin, W. Hua, M. Sitti, “Shape-programmable magnetic soft matter,” PNAS, 113(41), 6007–6015, 2016, doi: 10.1073/pnas.1608193113.
10. W. Hu, G.Z. Lum, M. Mastrangeli, M. Sitti, “Small-scale soft-bodied robot with multimodal locomotion,” Nature, 554, 81-85, 2018, doi: 10.1038/nature25443.
11. M. Cianchetti, C. Laschi, A. Menciassi, P. Dario, “Biomedical applications of soft robotics,” Nature Review Materials, 3, pp.143-153, 2018, doi: 10.1038/s41578-018-0022-y.
12. M. Sitti, “Miniature soft robots – road to the clinic,” Nature Review Materials, 3, 74–75, 2018, doi: 10.1038/s41578-018-0001-3.
13. L. Manamanchaiyaporn, X. Tang, X. Yan, Y. Zheng. “Molecular Transport of a Magnetic Nanoparticle Swarm Towards Thrombolytic Therapy,” IEEE Robotics and Automation Letters, 6(3), 5605-5612, 2021, doi: 10.1109/LRA.2021.3068978.
14. E. Gultepe, J.S. Randhawa, S. Kadam, et. al, “Biopsy with Thermally-Responsive Untethered Microtools”, Advanced Materials, 25, 514–519, 2013, doi: 10.1002/adma.201203348.
15. W. Zhu, J. Li, Y. J. Leong, et. al, “3D-Printed Artificial Microfish”, Advanced Materials, 27, 4411–4417, 2015, doi: 10.1002/adma.201501372.
16. C.W. de Silva, S. Xiao, M. Li, C.N. de Silva, “Telemedicine-Remote Sensory Interaction with Patients for Medical Evaluation and Diagnosis,” Mechatronic System and Controls, 41, 2013, doi: 10.2316/Journal.201.2013.4.201-2536.
17. E.M. Purcell, “Life at low Reynolds number,” American Journal of Physics, 45, 3-11, 1977, doi: 10.1119/1.10903.
18. N. A. Spaldin, “Magnetic Materials Fundamentals and Applications,” 2nd ed. Cambridge University Press, USA, 2010.

(Click Here)