1. Introduction

In recent years, the use of blockchain technology in many fields has gained increasing interest and popularity [1]. As a distributed and decentralized ledger, blockchain technology allows for the protection of transactions and data while maintaining the data sharing and reliability of a peer-to-peer network [2]. Peers maintain “chains” of blocks consisting of various types of data stored as transactions. Each block contains the hash value of the previous block in the chain, so any attempt to modify one block has a ripple effect on all subsequent blocks in the blockchain. These altered hash values can be easily identified because peers in the network maintain copies of the chain and can independently verify transactions and blocks. Permissioned blockchains allow peers in the network with the required permissions to access recorded transactions, while the key benefits of security, immutability, integrity, and transparency are preserved for transaction records [3]. The reliability and ease of securing and accessing data may explain the growing prevalence of blockchain technology worldwide. Bitcoin, a digital currency that utilizes public blockchain technology, had over 100 million users in 2022. The Bitcoin blockchain grew by more than 400 gigabytes from January 2012 to July 2022, and has even doubled since February 2019. In the face of this incredible growth, the cost of becoming a full-fledged node in a blockchain network is daunting and could become completely impractical. Similar to public networks like Bitcoin and Ethereum, consortium networks also run into storage problems [4]. In general, applications that require big data storage pose such problems, even if these networks do not consist of many peers or transactions. A wide range of domains, such as healthcare, real estate, insurance, and the Internet of Things (IoT), have adopted blockchain technology, resulting in a variety of data types and applications. While these applications typically use consortium blockchain networks, data-rich applications inevitably face storage issues, which raise significant concern about blockchain scalability.

The concern for blockchain scalability is the main reason for many studies on consortium blockchain storage management [5], [6]. However, most of the proposed solutions employ various off-chain storage strategies such as InterPlanetary File System (IPFS) and cloud storage, where IPFS is a decentralized, secure, verifiable, distributed storage system that can be integrated with blockchain networks [7]. Although off-chain approaches can alleviate the scalability issues of blockchain storage, the benefits of using blockchain technology are lost as the data is moved off the chain and new issues regarding the security and maintainability of off-chain data can be introduced. In this paper, we propose an on-chain approach, called HistoChain, to reduce the storage burden on most peers in a blockchain network by splitting the current blockchain (CB) and transferring the old data to a historical blockchain (HB), thereby reducing the size of the CB by half. In the HistoChain approach, HBs are immutable blockchains containing historical data separate from the CB, while the CB contains only the most recent years of blockchain data. After a set period of time, the CB will have grown further, and it will then be split again, generating another HB. In our approach, the nodes in the network are set up as either super peers or regular peers, with a smaller but substantial number of nodes forming a group of super peers, each of which maintains a copy of the CB and all HBs. Regular peers, which comprise most of the nodes in the network, need only retain the CB. This greatly reduces the storage burden on regular peers, which can then access data from the historical blockchains by making queries to the super peer group. In our approach, we use a time-based partitioning method to split the CB when it reaches a certain age. For example, if this age is 10 years, an HB will be created containing the first 5 years of data, leaving only the most recent 5 years of data in the CB. This splitting process can continue over time, resulting in the creation of multiple HBs.

Since regular peers are not required to store HBs, making query requests to the super peer group is their means of accessing historical data from the blockchain. When a super peer receives a request to search for historical data, it retrieves the requested data from the historical blockchains, and sends a summary report containing all retrieved information back to the requesting regular peer. In our approach, we introduce a meta-block, a mutable block attached to the beginning of the CB or each of the HBs, which contains index information for all transactions stored in the corresponding blockchain. This index information can facilitate fast and efficient data retrieval from a large blockchain that contains many years of data; therefore, the search time for historical data can be significantly reduced.

This work significantly extends the scalable storage scheme we previously proposed for on-chain big data using historical blockchains, originally presented at the IEEE International Workshop on Blockchain and Smart Contracts in 2022 (IEEE BSC 2022). In our previous work [8], we defined a primary super peer, called PSP, as an elected super peer who plays a role in efficiently facilitating access to data in HBs by regular peers. However, this approach introduces centralization and requires the necessary trust in a particular super peer (i.e., the PSP), which shall be best avoided in a blockchain architecture. In this paper, we allow a query to be sent to any super peer, which is responsible for collecting retrieved historical data and returning a summary report. To ensure temporal efficiency in query execution, query delegation will be performed within the super peer group. We design a dynamic load balancing algorithm to support fulfilling a request in a timely and concurrent manner. Each request for historical data sent to the super peer group is divided into subqueries with a search time of no more than 5 years, which are assigned to super peers based on their current workload. For this purpose, each super peer maintains a Shared Assignment Table (SAT) that keeps a record of assignments for all super peers and their completion times. Once an assignment is accepted by a super peer, an update to the SAT is broadcast within the super peer group to ensure that the super peers are aware of the latest status of the blockchain network.

The rest of the paper is organized as follows. Section 2 discusses related work. Section 3 presents the HistoChain framework for scalable storage using historical blockchains and describes the procedure for generating historical blockchains. Section 4 describes in detail the dynamic load balancing algorithm and the retrieval process of historical blockchain data. Section 5 presents the case studies and their analysis results. Section 6 concludes the paper and mentions future work.

2. Related Work

Scalability challenges in blockchain technology, especially in public blockchain systems, remain a persistent issue. In [9], the authors introduced the Bitcoin Lightning Network (BLN), a decentralized system where transactions can be sent off-chain for value transfer through channels. The BLN, through its ability to make micro-payments, has positively impacted the scalability of the global Bitcoin blockchain network by reducing the need to broadcast many transactions. Danksharding is a newer type of sharding architecture proposed to scale the Ethereum network [10]. In the Danksharding proposal, nodes can validate larger data volumes through distributed data sampling across blob; therefore, nodes can avoid processing all data and larger data volumes can be handled by the Ethereum network. Scalability challenges also arise in consortium blockchain networks when large amounts of data need to be stored. In the context of consortium, off-chain strategies to improve the scalability of blockchain applications are the main focus of further research. To reduce the high cost of computation and storage for blockchain-based applications, in [11], the authors investigated a series of off-chain computation and storage approaches. They proposed five off-chain models that move computation and data off the blockchain without violating the trustless property. In [12], the authors proposed an off-chain scalability solution, called ChainSplitter, for Industrial Internet of Things (IIoT) blockchain applications. The proposed approach features a hierarchical storage structure where the recent blocks are stored in an overlay network and the majority of blockchain data is stored in the cloud. Despite being structured as a decentralized cloud storage system, the blockchain data in the cloud is not maintained by peers and thus acts as an off-chain repository for blockchain data. IPFS also offers a scalable off-chain solution for blockchains. In [13], the authors presented a blockchain-based application using IPFS specifically for healthcare systems. They focused on storage of electronic health records (EHRs) and used the IPFS service to transfer data off-chain while retaining hashes of the data on the blockchain. In [14], the authors attempted to reduce the transaction size and increase the transaction throughput of an experimental consortium blockchain network by storing the hash values of encrypted data on-chain and using IPFS to store the encrypted data itself off-chain. They integrated Hyperledger Fabric [15], which is a modular blockchain framework typically using off-chain storage for big data, with IPFS services and provided a solution for secure storage and efficient access to a task-scheduling scheme. While the off-chain approach provides a viable way to mitigate the scalability problem of blockchains, as noted in [11], the fundamental properties of blockchains can be compromised to varying degrees when using the off-chain approach. In contrast, our HistoChain approach stores big data in historical blockchains and does not rely on off-chain storage; therefore, all essential properties of the blockchain data can be strictly maintained using our on-chain storage mechanism.

There are very few on-chain based approaches that address the scalability issues in blockchain networks. In [16], the authors proposed to use Hyperledger Fabric to implement a consortium blockchain for patient access and management of personal health records (PHRs). Although scalability issues remain a major challenge, they concluded that Hyperledger Fabric for on-chain data storage could offer a more practical solution to ensure the privacy of PHRs than the Ethereum public blockchain. In [17], the author introduced the concept of section-blockchain, an on-chain approach for reducing the storage cost of blockchain networks with under-stored devices. In their approach, all nodes store a portion of the complete blockchain and provide incentives for upgrading their local storage. Furthermore, they proposed segmented blockchains to enable nodes to store a blockchain segment [18]. They showed that their approach can help reduce the storage cost of a blockchain without compromising the security requirement of the blockchain. In [19], the authors proposed a framework for cloud-based blockchains to store medical multimedia files on-chain securely and reliably. They used a cloud-based blockchain to store all blockchain data to support data accessibility, redundancy, and security, while a lite blockchain allows local storage of text-based information and metadata for multimedia files. Although the above methods allow for big data storage, data retrieval can be slow because portions of transactions are stored in different blockchains. Conversely, our HistoChain approach divides a complete blockchain into a current blockchain and multiple historical blockchains, each of which are full-fledged blockchains containing complete transaction information. Regular peers can then access their local current blockchain and request historical blockchain data from super peers concurrently, making the data retrieval process much more efficient.

One of the main advantages of the HistoChain approach is that it supports dynamic load balancing, so requests for historical blockchain data can be retrieved in a timely and concurrent manner. There is a great deal of research efforts in developing dynamic load balancing algorithms in the context of cloud computing and P2P systems. In [20], the authors proposed a load balancing scheduling algorithm for virtual server clusters applied to storage systems to ensure uniform load distribution of virtual server clusters. Their approach is based on the state of the server clusters and periodically sends collected feedback to the load balancer to bring the internal load performance of the system to a more balanced state. In [21], the authors introduced a strategy to use a dynamic hashing scheme to locate data keys based on a structured P2P architecture and maintain the load balance among the peers. They showed that the load balancing of P2P systems can be significantly improved using their proposed method. In [22], the authors proposed a dynamic load management algorithm for cloud computing based on the current state of virtual machines (VM). In their approach, the allocation table is parsed to find each idle and available VM, from which the active load of all VMs under consideration is calculated. Similarly, in our HistoChain approach, we utilize a shared assignment table to achieve dynamic load balancing within the super peer group, where the assignment is determined on the basis of the lowest total workload of the super peers. In this sense, our approach complements existing dynamic load balancing mechanisms in cloud computing and P2P systems and provides a simple yet efficient solution to support concurrent processing of complex query requests for current and historical blockchain data.

3. Scalable Storage Using Historical Blockchains

3.1.  A Framework for Scalable Blockchain Networks

Data storage technologies such as physical storage and cloud storage each have their inherent advantages, but this meteoric rise in blockchain-enabled applications has led to a great deal of research focused on decentralized storage for managing large amounts of data while maintaining its viability for nodes and networks. To demonstrate this storage requirement, we examine an example of blockchain applications in healthcare. A patient visiting a hospital may generate a certain amount of data, especially in the case of multimedia files such as X-rays or CT scans. If a hospital is to consider adopting blockchain technology for data storage, it must remain scalable because a large number of patients will generate large amounts of data over a long period of time. This issue is further complicated for an entire network of hospitals that utilize a consortium blockchain as a means of sharing medical data. While viable techniques do exist to store off-chain medical data, the benefits offered by using blockchain storage are compromised in this use. In this paper, we propose the HistoChain approach that supports the maintenance and sharing of medical data on the chain, with the burden being borne by a smaller group of well-equipped super peers representing large and resourceful hospitals in a local area. Such large hospitals will be able to dedicate more resources to the network to maintain older on-chain data stored in historical blockchains. This makes it feasible for regular peers to participate in the network to maintain the benefits and convenience offered by blockchain technology while having a much lower storage burden without moving their data off-chain. Figure 1 shows the HistoChain framework for a scalable consortium blockchain network.

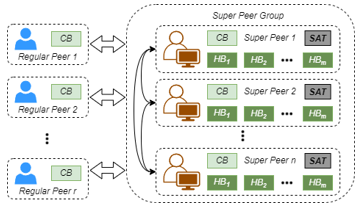
Figure 1: A Framework for a Scalable Consortium Blockchain Network

As shown in Figure 1, a consortium blockchain network consists of n super peers and r regular peers. The super peers are tasked with maintaining the current blockchain CB and all historical blockchains HBs, as well as creating and verifying new blocks and transactions using a consensus process. Shifting the burden of historical data storage and freeing regular peers from participating in the consensus process allows the introduction of highly lightweight regular peers. Regular peers maintain only the CB, but can access historical data stored in HBs through queries to the super peer group. Upon receiving a query, a super peer splits it into subqueries and assign them to super peers based on the shared assignment table SAT as a means of dynamic load balancing to ensure that access to the data remains timely. More importantly, as described in Section 3.4, when the current blockchain reaches a certain age, a super peer can split it into a chain of historical blocks and a reduced chain of current blocks.

3.2.  The Block Structure

A block, as a building block of a blockchain, can be defined by three parts: the block header, the list of transactions, and the verification section. Figure 2 shows the structure of a block with a list of m transactions.

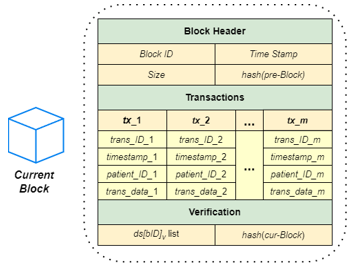
Figure 2: The Structure of a Block with a List of Transactions

As shown in Figure 2, the block header is defined as a 4-tuple (B, T, S, H), where B is the block ID, T is the timestamp when the block is created, S is the size of the list of transactions recorded in the block, and H is the hash value of the previous block. In the context of healthcare, each transaction in the transaction list is defined as a 4-tuple (TI, TS, PI, TD), where TI is the transaction ID, TS is the timestamp when the transaction is created, PI is the patient ID, and TD is the transaction data, including text-based messages and images files. The verification section is essential for the integrity of the blockchain storage, which includes a list of digital signatures, ds[bID]v, for a block with ID bID, where v is a super peer that approves it as a new block in the consensus process. Any pending block must be approved by the majority of the super peers before it can be added to the blockchain, at which point the hash of the block is computed by applying a hash function to the block file containing all the above components excluding the verification section, and the hash value hash(cur-Block) is attached to the end of the block file. Note that in order to limit the block size, each block contains no more than 500 transactions and only contains transactions created during the same day. Therefore, the last block created at the end of a day may contain less than 500 transactions.

3.3.  The Structure of a Meta-Block

To support efficient data retrieval in a blockchain, we define a meta-block as a special block that stores metadata for the current blockchain or each of the historical blockchains. A meta-block is the only mutable block in a blockchain and is attached at the beginning of the blockchain. Figure 3 shows the structure of a meta-block. As shown in the figure, a meta-block consists of two parts: the block header and a HashMap HM. The block header is defined as a 4-tuple (SD, ED, SB, EB), where SD is the timestamp of the first transaction in the first block of the blockchain; ED is the timestamp of the last transaction in the last block of the blockchain; SB and EB are the block IDs of the first block and the last block of the blockchain, respectively. In the second part, the HashMap HM contains a list of <key, value> pairs, where the key is a patient ID and the value is a list of locations where the patient transactions are stored. Each location is defined as a triple (B, A, O), where B is the block ID, A is the address of the transaction in the block, and O is the offset of the transaction size.

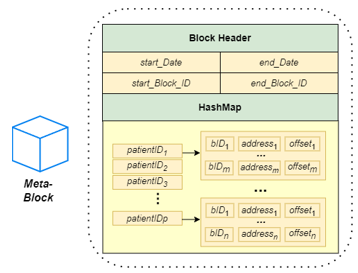
Figure 3: The Structure of a Meta-Block

The use of meta-blocks in a blockchain network provides an additional layer of organization and structure. By placing metadata in a separate block attached to the beginning of a blockchain, searching for information in the blockchain becomes much easier. This metadata allows peers to determine the exact location of transactions in the blockchain that need to be extracted to complete queries on current and historical blockchain data. Thus, the search space is much reduced and the time it takes to execute a query can be minimized. Note that to ensure the integrity of the blockchain metadata, a meta-block can be reviewed, validated and refreshed at any point in time by reading data from the relevant part of the blockchain.

3.4.  Generation of a Historical Blockchain

At its inception, the current blockchain is the only blockchain in the network. When the current blockchain reaches a certain age, say 10 years, a split occurs. The oldest 5 years of data are transferred to a new blockchain, called a historical blockchain, while the most recent 5 years of data remain in the current blockchain. When a new historical blockchain is generated, a new meta-block containing its metadata is appended to the beginning of the historical blockchain, and the current blockchain’s meta-block is refreshed to reflect the movement of that data. This process is repeated 5 years later when the current blockchain again contains 10 years of data. Figure 4 shows how the current blockchain CB is split into a historical blockchain and a new current blockchain. Let the block IDs of the first and last block in CB be m and n, respectively. Note that m = 1 if the current blockchain has never been split before. Let block k be the most recent block in CB that is at least 6 years old. We establish blocks m through k as a historical blockchain HB and generate a new meta-block MBHB for it. Blocks k+1 through n persist as the updated current blockchain, while blocks m through k are removed. The meta-block MBCB associated with the current blockchain is refreshed by scanning the data in the new current blockchain (i.e., blocks k+1 through n). We now have an updated current blockchain and a historical blockchain, each containing 5 years of data.

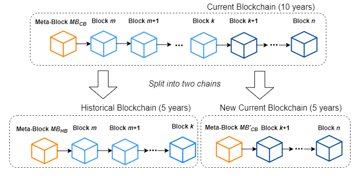
Figure 4: A Blockchain Split into a Historical and a Current Blockchain

A super peer is responsible for splitting a current blockchain with a certain age into a reduced current blockchain and a historical blockchain. When a super peer completes this task, it broadcast the updated current blockchain to all peers and the new historical blockchain to all super peers for updating. Algorithm 1 shows the process of splitting the current blockchain CB with 10 years of data into a historical blockchain HB and an updated current blockchain CB.

Algorithm 1: Splitting of a Current Blockchain

Input: A current blockchain CB containing 10 years of data Output: Historical blockchain HB with 5 years of old data and an updated CB with the most recent 5 years of data

1.   Let m and n be the IDs of the first and the last block in CB 2.   Let k be the most recent block at least 6 years old, where n > k 3.   Extract blocks m through k from CB and create a new historical blockchain HB with the k–m+1 blocks 4.   Create an empty meta-block MBHB associated with HB 5.   Set SD in MBHB as the date of the first transaction in block m 6.   Set ED in MBHB as the date of the last transaction in block k 7.   Set SB and EB in MBHB to m and k, respectively 8.   for each block β in HB 9.       Scan block β and add each triple (B, A, O) associated with            patientID α to a list LSα 10. Create a HashMap in MBHB and add all pairs of <α, LSα> to it 11. Attach MBHB to the beginning of HB 12. Remove blocks m through k from CB 13. Update CB’s meta-block MBCB accordingly, as with MBHB 14. return HB and CB

As shown in Algorithm 1, the meta-block of HB, MB_HB, contains the date of the first transaction in the first block of HB, the date of the last transaction in the last block of HB, and the block IDs of the first and last block of HB. To create a HashMap that contains all <key, value> pairs, each block in HB is scanned, and each triple (B, A, O) associated with the patient ID α is added to a list LT_α. Once the scanning process is complete, all pairs of <α, LT_α> are added to the HashMap in MB_HB. Now in CB, all blocks that have been recorded in HB are deleted, and the meta-block of the updated CB must be refreshed by removing all triples that reference transactions that have been transferred to HB. Finally, the new HB and the updated CB are returned for broadcasting.

4. Retrieval of Historical Blockchain Data

4.1.  Load Balancing Data Retrieval Requests

In the context of blockchain applications in the healthcare domain, suppose a regular peer (e.g., a doctor) queries patient information from blockchains for multiples of 5 years. When the data to be searched is for the most recent 5 years, the regular peer can search directly from its local current blockchain. When the data to be searched is for the past sLen years, where sLen Î {5n | n ≥ 2}, the regular peer can search for patient information for the most recent c years directly from its local blockchain, where c is the age of the current blockchain; while the remaining (sLen – c) years of data must be retrieved from the historical blockchains by making a query to any of the super peers. The request for such a query involves a patient ID (for which data is collected) and the number of years of data being search, called the search length. Figure 5 shows the querying process for accessing historical blockchain data.

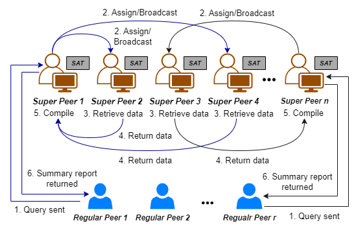
Figure 5: Querying Process for Accessing Historical Blockchain Data

From Figure 5, we can see that when a super peer receives a query from a regular peer, it acts as a director, dividing the query into subqueries and distributing them evenly based on the weights of queries to be completed by the super peers. Each query receives a weight based on the search length. For example, for a blockchain with a current blockchain of 7 years, a query with a search length of 20 years can be split into three subqueries, a 3-year search and two 5-year searches with weights of 3/5 and 1, respectively. Data retrieved from all subqueries are returned to the assigning super peer (if not completed by the assigning super peer) and compiled into a single summary report that is returned to the requesting regular peer. Note that the search for the most recent 7 years of blockchain data must be performed locally by the requesting regular peer, who is responsible for combining its local report with the summary report received from the assigning super peer into a single summary report.

A new subquery with a 5-year search length is always assigned first to the super peer with the lowest total weight. Subqueries sent to super peers are stored in their query queues, and the total weight of the queries assigned to each super peer must be approximately equal. A super peer processes subqueries in its query queue on a first-come, first-served basis. When a super peer retrieves relevant historical data for a subquery, it compiles the results and returns a response to the assigning super peer, including a summary report of the relevant transactions with links to associated files that a regular peer can download. Note that each super peer maintains its own copy of the historical blockchains; therefore, searches assigned to multiple super peers can be performed by them simultaneously.

4.2.  The Structure of Shared Assignment Table

In our proposed HistoChain approach, the lightweight nature of regular peers allows for a scalable architecture with the super peers facilitating access to historical data. To this end, queries for patient data are sent from regular peers to the super peers and the summary reports are returned upon completion. To ensure efficient execution of this approach, dynamic load balancing is employed, where each super peer retains a copy of SAT and broadcasts an updated SAT with any assignment changes made by the super peer to the super peer group. These broadcasts contain the current workload and assignment of each super peer as well as estimated time when the subquery must be completed. In case no response is received by the end of the estimated completion time, the task must be completed at the highest priority by the assigning super peer to avoid further delay. Figure 6 illustrates the structure of an SAT shared by a group of n super peers.

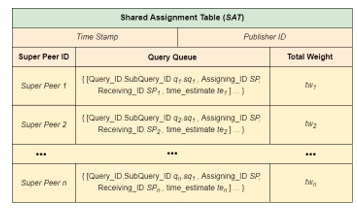
Figure 6: The Structure of a Shared Assignment Table (SAT)

When a query is received by an assigning super peer Ψ, it will be split into multiple subqueries, each of which can be assigned to a super peer based on the lowest total weight. This ensures the uniform distribution of weights among the super peers and the timely completion of the subqueries. Each subquery consists of a query ID, a patient ID, a requested start date (SD), and an end date (ED), defined as a 4-tuple (qID, pID, SD, ED). Once the assignment is recorded into SAT, the updated SAT is broadcast within the super peer group. To prevent conflicts, a super peer always uses the latest version of SAT for the assignment by checking the publishing timestamp. A super peer may reject a subquery request due to various reasons. When this happens, Ψ must update SAT and broadcast it again. Algorithm 2 shows the query assignment process done by Ψ. Let the blockchain be of age 5 or more. Since the age of the current blockchain ranges from 5 to 10 years, the search length of subquery sq₁ can be less than 5 years. To avoid adding network time to the data retrieval time of short subqueries with a search length less than 5 years, the assigning super peer always completes such a subquery by itself rather than assigning it to another super peer.

Algorithm 2:  Query Assignment by Assigning Super Peer Ψ

Input: Query q with a search length sLen in 5x years, x Î [1, 10], current blockchain age c, shared assignment table SAT Output: Updated shared assignment table SAT

1.   if sLen ≤ c return SAT // only local search is needed 2.   Split q into subqueries sq1…sqm, where m = (sLen – c)/5, search length |sq1| = 10 – c, and |sqi | = 5, 2 ≤ i ≤ m. 3.   if |sq1| < 5 4.         Assign sq1 to Ψ  //self-assign sq1 for less than 5-year search 5.   else // when |sq1| == 5 6.         Assign sq1 to the super peer with the lowest total weight in SAT 7.   for each subquery ρ­ in sq2…sqm 8.         Assign ρ­ to the super peer with the lowest total weight in SAT 9.   Broadcast updated SAT to all super peers 10. return updated SAT

4.3.  Retrieval of Historical Blockchain Data

We now define the procedure for the retrieval of historical data by a super peer SP. Let subquery ρ, defined as a 4-tuple (qID, pID, SD, ED), be a subquery assigned to SP by an assigning super peer Ψ, then the search length of the subquery |ρ| must be no more than 5 years that is covered by one of the historical blockchains. To identify the historical blockchain to be searched, SP needs to compare the start date SD and end date ED of the subquery with those of the historical blockchains by examining their meta-blocks. Once the historical blockchain is identified, the search is facilitated by investigating again its meta-block, which contains indices specifying the exact location of transactions in the identified historical blockchain. Algorithm 3 shows how historical data can be retrieved from historical blockchains by super peer SP.

Algorithm 3:  Historical Blockchain Data Retrieval (Subquery)

Input: Subquery ρ as a 4-tuple (qID, pID, SD, ED) Output: A summary report with retrieved historical data for ρ

1.   Create an empty summary report SR_ρ.qID 2.   for each historical blockchain Π 3.      Read MBΠ.SD and MBΠ.ED from meta-block MBΠ 4.      if MBΠ.SD > ρ.ED || MBΠ.ED < ρ.SD 5.         continue // outside of the search period, search next Π 6.      Get a list of triples LTX from MBΠ.HM with pID as the key 7.      for each triple (B, A, O) in LTX 8.         Read transaction tx from block B at address [A, A + O] 9.         if tx.TS ≥ ρ.SD && ts.TS  ρ.ED 10.          Add retrieved tx and links to relevant files to SR_ρ.qID 11.     break // only one Π needs to be searched for subquery ρ 12. return summary report SR_ρ.qID

As shown in Algorithm 3, the patient ID in the subquery ρ is used as the key in the meta-block’s HashMap to access the exact locations of relevant transactions in the associated historical blockchain. Super peer SP then reads the relevant transactions and record them in a summary report SR_ρ.qID. The summary report may contain links to multimedia files, which are hosted by SP. Finally, the summary report SR_ρ.qID is returned to the assigning super peer Ψ.

Based on Algorithm 2 and Algorithm 3, we now define the entire process by which the assigning super peer Ψ completes a summary report for a query q with a search length sLen, made by a requesting regular peer. This query completion process done by Ψ is described in Algorithm 4.

Algorithm 4:  Query Completion by Assigning Super Peer Ψ

Input: Query q with a search length sLen, shared assignment table SAT Output: A completed summary report SR_Ψ

1.   Invoke Algorithm 2 on q to create and assign subqueries 2.   if any assigned subquery sq is rejected by a super peer 3.      Assign sq to Ψ itself 4.      Broadcast the updated SAT 5.   for each super peer SP with an assigned subquery ρ 6.      Wait summary report SR_ρ.qID to be received from SP after SP invokes Algorithm 3 7.      if time estimate of ρ is exceeded and SR_ρ.qID is not received 8.         Assign ρ to Ψ itself and invoke Algorithm 3 9.      Remove subquery assignment for SP from SAT 10.    Broadcast updated SAT 11. Compile each summary report into a complete report SR Ψ 12. return summary report SR_Ψ

As shown in Algorithm 4, upon receiving query q, the assigning super peer Ψ splits it into subqueries and assigns them to super peers by invoking Algorithm 2. If any assigned subquery ρ is rejected by an assigned super peer SP, ρ is reassigned to Ψ itself and an updated SAT is broadcast. Each super peer SP receiving an assignment then retrieves the historical data requested in the assignment by invoking Algorithm 3. The assigning super peer Ψ then awaits the summary report from each SP. When a summary report for a subquery ρ is returned, Ψ removes the corresponding assignment in its SAT and broadcasts this update. If any subquery is not completed by the time estimate, Ψ assigns the subquery to itself, broadcasts an updated SAT, and completes the subquery. When all summary reports for the subqueries become available, Ψ compiles them into a complete final summary report (in chronological order of the subquery start date) and returns it to the requesting regular peer.

Note that a regular peer can perform a local search for a query whose search length is equal to the age of the current blockchain in a similar manner. Remote searches of historical blockchain data by super peers are conducted concurrently with the local search of the current blockchain by a regular peer. The historical data returned from a remote search is then merged with the local search data by the requesting regular peer.

5. Case Study

In this section, we present a series of simulations in the context of healthcare to demonstrate the feasibility and effectiveness of the HistoChain approach. In our experiments, we assume that there are 10 large local hospitals participating in a consortium blockchain network. There are also 30 small and medium medical facilities in the network. A consortium blockchain may have a 50-year lifespan, which is enough time to aggregate a substantial amount of data to be useful for experiments. We limit the total number of transactions in each block to 500, where each transaction may contain medical data in the form of image and text files. For simulation purposes, the number of visits per day is between [200, 500] and [50, 200] for large hospitals and small/medium sized medical facilities, respectively.

5.1.  Estimation of Blockchain Size

To estimate the blockchain sizes along years, we use a time-based partitioning method to generate historical blockchains. A time-based partitioning occurs in the 10th year of the current blockchain; the earliest 5 years of data make up an historical blockchain, while the most recent 5 years of data are retained by the current blockchain. Using this method, super peers representing large local hospitals retain all historical blockchains as well as the current blockchain, while regular peers representing small/medium sized medical facilities store only the current blockchain. Table 1 lists the parameters used in our experiments.

Table 1: Parameters Used for Blockchain Size Estimate

Image occurrence (%)	Image size	Image count	Text occurrence (%)	Text size	File size growth rate (%)	Time to split (year)
5%	1 ~ 3 MB*	1 ~ 5	100%	0.003 ~ 0.007 MB*	0, 1, 3, 5	10

* File sizes are subject to increase by a 5-year file size growth rate.

As shown in Table 1, for a hospital visit, we assume that there is a 5% probability of including images, such as x-rays, in the doctor’s notes. The size of the images is typically between [1MB, 3MB] and the number of images attached is limited to 5. The sizes of text-based medical records are also listed in Table 1. Note that in our experiments, we consider 5-year file size growth rates of 0%, 1%, 3% and 5%, with the file size bound increasing uniformly each year over the 5-year period. For example, when the 5-year growth rate is 3%, the image size increases by 0.6% per year and the maximum image size can reach 4.89 MB in 50 years, which is usually large enough for medical image files.

We now simulate the creation of a 50-year blockchain to estimate the storage burden of regular and super peers in the network. On each day, a large hospital or a small/medium sized medical facility in the network generates a random number of visits within the given range [200, 500] or [50, 200], respectively. A transaction is generated for each visit and stored in a block that can hold up to 500 transactions, independent of the transaction size. Each transaction has a 5% chance of including at least one image file. If a transaction does include image files, the number of image files is chosen randomly within the given range [1, 5]. In addition, the size of each image file or text file is also randomly generated within the certain ranges, as defined in Table 1.

To address the possible growth of image and text file sizes along years, we consider 5-year file size growth rates of 0%, 1%, 3% and 5% in our experiments. For each growth rate, we collected data from a sample of 10 simulations to establish the mean of the evaluation. The 0% growth rate is included as a baseline; while not a realistic assumption, this establishes the minimum size of the blockchain against which the other growth rates can be considered. Figure 7 shows the change of blockchain storage along the years for the entire blockchain (including both current and all historical blockchains). The experimental results show that the effectiveness of using a historical blockchain structure is evident. After 50 years, the storage volume of the entire blockchain exceeds 33 TB at 0% growth rate, 35 TB at 1%, 38 TB at 3%, and 43 TB at 5%. Due to the storage burden, this would not be a viable solution for regular peers to store the entire blockchain.

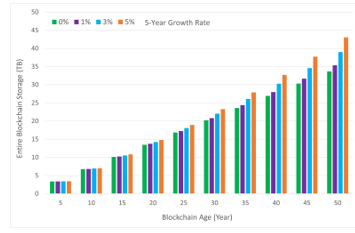
Figure 7: Total Blockchain Size by Year with 5-Year Growth Rates

Now, with the introduction of the historical blockchain structure, the storage load for regular peers can be greatly reduced, as regular peers no longer need to store the entire blockchain. Figure 8 shows the change of blockchain storage along the years for the current blockchain. The experiment records the size of the current blockchain in the year before the current blockchain split (e.g., year 4, year 9, year 14, etc.) to show the approximate maximum size of the current blockchain along the way.

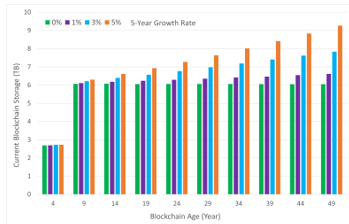
Figure 8: Current Blockchain Size by Year with 5-Year Growth Rates

From Figure 8, we can see that the size of the current blockchain is much smaller than the size of the entire blockchain. At 0% growth rate, the current blockchain size is at most 6.05 TB; at 1%, 6.62 TB; at 3%, 7.83 TB; and at 5%, 9.26 TB. The results show that for a growth rate of 0%, the size of the current blockchain is consistent regardless of the age of the blockchain. At a growth rate of 5%, the size of the current blockchain increases with the year but remains manageable for regular peers. Note that the size of the current blockchain doubled from year 4 to year 9 because the current blockchain did not need to split during those 9 years.

5.2.  Data Retrieval Time for a Single Request

In this experiment, we measure the data retrieval time for a single query request for blockchain historical data by a regular peer. The data retrieval request is a search for a patient’s medical records within a specified number of years. For any search within the current blockchain age, the data can be readily retrieved from the current blockchain; however, when the search length is greater than the current blockchain age, a query needs to be sent to a super peer to identify the relevant data and retrieve them from the historical blockchain(s). In this experiment, we let the age of the entire blockchain be 50 years old; therefore, up to 50 years of data can be retrieved from the blockchain. Table 2 lists additional parameters used for data retrieval in the simulations.

Table 2: Parameters for Data Retrieval Used in the Simulations

Search length (year)	Annual patient visits	File size growth rate (%)	Network latency time	Data extraction time	Data export time	Average meta-block size
5, 10, 15, …, 50	1 ~ 7	3	0.5 seconds	0.02s /MB	0.017s /MB	100MB

Since one of the important factors affecting the search time is in reading meta-blocks of the historical blockchains that contain 5-years of data, we consider search lengths in 5-year intervals up to 50 years. A 50-year blockchain also means that the current blockchain has just been split, so the current blockchain contains only the most recent 5 years of data. This setting helps to show the data retrieval time for the maximum amount of historical data. For a 5-year search, it will only be processed by a regular peer. For any search length of 10 years or more, the most recent years of data will be retrieved by a regular peer and the rest of data must be retrieved by super peers.

We assume a maximum of 7 hospital visits per patient per year and set a file size growth rate of 3% for 5 years, which allows for a reasonable increase in the size of medical image files and text files. Parameters such as image size bounds, image count bounds, text size bounds, and probability of occurrence of images in medical records can be found in Table 1. For search length of 10 years or more, measuring data retrieval time requires consideration of the network latency time for searching data in the historical blockchain(s), data extraction time for extracting index information from the relevant meta-blocks and the data from relevant blocks, and data export time for writing the extracted historical transaction data to a summary file. While the exact location of a transaction in a historical blockchain can be determined in constant time from the index information stored in a meta-block, opening a meta block file and reading the data from the file takes nontrivial time. Based on the average size of the meta-blocks, retrieving the index information from a meta-block can take up to several seconds. Since in our experiments, transactions are generated randomly, the extraction time is dependent upon the size of the transactions. For historical blockchain data, a super peer needs to write the extracted transaction data to a summary file. If a request is split by an assigning super peer and completed by multiple assigned super peers in parallel, the summary reports returned must be compiled by the assigning super peer and returned to the requesting regular peer. This amount of time is included in the data export time, where a longer query adds more compilation time as it can be split into more subtasks and more reports need to be compiled.

We call our approach decentralized, fine-grained because there is no single trusted peer for load balancing; instead, dynamic load balancing is utilized by each super peer in the group based on the SAT. We now compare our decentralized, fine-grained approach to a centralized, coarse-grained approach [8], where a search query is processed by a single super peer, regardless of the search length. Figure 9 shows the results of 30 simulations for the centralized and decentralized approaches for each given search length up to 50 years.

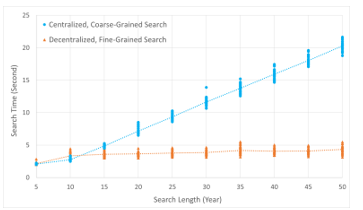
Figure 9: Retrieval Time for Individual Request with Varying Search Length

From Figure 9, we can see that for 5-year search, the average search time for both approaches is about 2 to 3 seconds. This is because the 5-year search can be processed locally by a regular peer and does not require remote data retrieval by super peers. The average 10-year search time with the decentralized approach is slightly larger, which can be attributed mainly to the increase in network time; the assigning super peer may need to delegate a remote 5-year search to another super peer and await its response. Otherwise, the search time would be the same, since the remote search for 5-year data is handled by one super peer in both methods. As the search length increases, the data retrieval time increases accordingly, with a maximum of about 20 seconds in the centralized approach for a 50-year search length. We see this growth is approximately linear, which is expected because the searches in multiple historical blockchains are performed sequentially by a single super peer, rather than in parallel by multiple super peers. In contrast, in the decentralized approach, there is a slight initial increase in search time for a 10-year search, but this increase is flat for longer searches. We see that a 50-year parallel search takes just over 4 seconds on average. The very small increase in time from a 10-year search to a 50-year search can be explained by the time it takes to compile summary reports received from multiple super peers.

Note that the 10-year search time does not increase significantly over the 5-year search time in both approaches because the 10-year search consists of a local search by a regular peer in the current blockchain and a remote search of the remaining data by a super peer, both of which are performed concurrently. The insignificant increase in the average data retrieval time in the 10-year search in both approaches is due to the additional network time and export time caused by the remote search of the historical data.

5.3.  Data Retrieval Time for Concurrent Requests

Our approach supports simultaneous processing of multiple query requests. In this experiment, we compute the distribution of weights across a group of 10 super peers for 10, 25, and 50 concurrent requests. Since requests are expected to be received at 5-minute intervals and up to 50 concurrent requests can be processed in this interval (at times of high workload), there is no overflow. Weights are assigned in proportion to the number of years involved in the search. We again consider searches involving up to 50 years of data at 5-year intervals. A 5-year search is not considered, as it can be retrieved locally from the current blockchain by a regular peer. We assume the probability of each search length occurring is equal, forming a uniform distribution. Figure 10 shows the variance of the weights assigned to each super peer in this strategy, where a number of simulations are generated for each number of concurrent query requests.

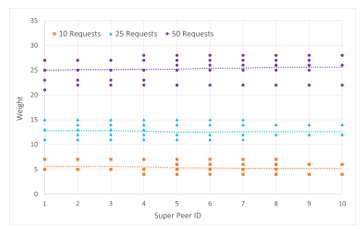
Figure 10: Distribution of Weights for Varying Numbers of Concurrent Requests

In a group of 10 super peers, queries are randomly sent to super peers who split the queries and assign subqueries to others to ensure even load balancing among the super peers. In this way, simultaneous historical blockchain data retrieval requests can be processed concurrently by the super peers. To examine the search time of concurrent data retrieval requests, the requests of regular peers for 10 to 50 years of data are measured. From Figure 10, we can see that the distribution of weights among the super peers is approximately uniform. For 10 concurrent queries, the average weight of the super peers is 5.37; for 25 queries, it is 12.65; and for 50 queries, it is 25.32. This demonstrates the effectiveness of the dynamic load balancing algorithm, which allows for even workload distribution in the super peer group and leads to efficient concurrent data retrieval by the super peers.

We further compare the centralized and decentralized approaches to demonstrate the efficiency of the decentralized, fine-grained approach. Load balancing can also be incorporated in the centralized approach, so weights are assigned to each request according to the length of the request [8]. We assume search lengths of up to 50 years and simulate 10, 20, 30, 40, and 50 concurrent searches at 5-minute intervals to calculate the total data retrieval time. Note that 50 concurrent requests represent a very high volume of requests in a 5-minute interval, this may occur at certain times of the year, such as a flu season. We calculate the average data retrieval time for completion of all concurrent requests in a 50-year blockchain, which we refer to as the completion time. Figure 11 shows the average and individual completion time for the specified numbers of concurrent requests by running 30 simulations of each approach.

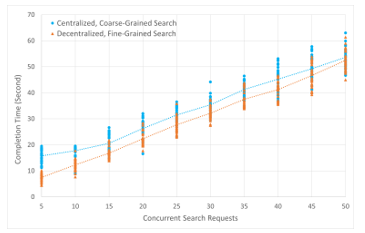
Figure 11: Completion Time for Varying Number of Concurrent Requests

From Figure 11, we can see that employing a decentralized, fine-grained approach is superior to a centralized, coarse-grained load balancing mechanism. Since in the decentralized approach, long queries are split into 5-year subqueries, the dynamic load balancing would result in more even workload distribution among super peers than in the centralized approach. On the other hand, although the average completion time of the centralized approach is higher than that of the decentralized approach for each number of concurrent requests, we note that as the number of concurrent requests increases, the queue completion times of the centralized and decentralized approaches start to converge and are almost equal at 50 concurrent requests. This is because when there are more concurrent requests, the weight distribution of the centralized approach can become more uniform and may approach the performance of the decentralized approach. This finding suggests that the decentralized, fine-grained dynamic load-balancing algorithm could be more effective in the off-season or normal season than in the peak season, although it performs better than the centralized, coarse-grained load-balancing mechanism in general.

6. Conclusions and Future Work

To address the scalability issues of consortium blockchains, recent solutions have focused on transferring data off-chain by using IPFS and cloud-based storage structures. In this paper, we propose a novel approach, called HistoChain, to improve consortium blockchain scalability using historical blockchains and dynamic load balancing. We introduce a time-based partitioning strategy to generate a historical blockchain, where older sections of the current blockchain are transferred to the historical blockchain after a specified time interval (e.g., 5 years). This approach allows the current blockchain to contain a useful amount of the up-to-date data, while freeing regular peers with limited resources or storage from maintaining the entire data-intensive blockchain. The historical blockchains are maintained by a group of super peers with greater resources and computing power. In addition, we introduce a meta-block, attached to a historical or the current blockchain, which serves as an index file for facilitating efficient data retrieval. To support concurrent processing of queries, we split a query into subqueries and employ a dynamic load balancing algorithm to assign the subqueries to a group of super peers. This assignment is based on a shared assignment table that records the current workload of each super peer. Once the relevant data for the query has been collected, the assigning super peer sends a summary report of the retrieved data to the requesting regular peer. Finally, we provide a case study of healthcare data storage using a consortium blockchain. The experimental results show that our HistoChain approach can effectively reduce the storage burden of data-intensive blockchain applications on regular peers while providing efficient access to historical data through a group of super peers.

In future work, we will implement HistoChain and conduct more experiments to illustrate the effectiveness of using historical blockchains to efficiently retrieve historical blockchain data in real scenarios. We will further investigate effective methods to improve the performance of concurrent data retrieval by super peers. One such method to be developed is to analyze the efficiency of parallel searches by a super peer across multiple historical blockchains. This parallelization should allow a super peer to reduce and optimize the search time if the historical blockchains are stored on different hard drives. Furthermore, a hierarchical architecture can be considered to orchestrate multiple consortium blockchains to support blockchain data sharing across cities and states. Finally, to ensure strong data privacy, it is necessary to design access control policies so that users with different roles can access blockchain data with the required permissions [23]. This is especially necessary in applications with multilevel security requirements [24], such as healthcare blockchain applications.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

We thank the editors and all anonymous referees for the careful review of this paper and the many suggestions for improvements they provided. We also thank the University of Massachusetts Dartmouth for their financial support to the first author in completing this work.

1. H. Guo and X. Yu, “A survey on blockchain technology and its security,” Blockchain: Research and Applications, 3(2), February 2022, doi: 10.1016/ j.bcra.2022.100067
2. S. Nakamoto, “Bitcoin: a peer-to-peer electronic cash system,” October 2008. Retrieved on January 15, 2022 from https://bitcoin.org/bitcoin.pdf.
3. M. J. Amiri, D. Agrawal, and A. El Abbadi, “Permissioned blockchains: properties, techniques and applications,” In Proceedings of the 2021 International Conference on Management of Data (SIGMOD’21), 2813-2820, Virtual Event China, June 2021, doi: 10.1145/3448016.3457539
4. O. Dib, K.-L. Brousmiche, A. Durand, E. Thea, and E. B. Hamida, “Consortium blockchains: overview, applications and challenges,” International Journal on Advances in Telecommunications, 11(1&2), 51-64, 2018.
5. S. Liu and H. Tang, “A consortium medical blockchain data storage and sharing model based on IPFS,” In Proceedings of the 4th International Conference on Computers in Management and Business (ICCMB 2021), 147-153, Singapore, January 30 – February 1, 2021, doi: 10.1145/3450588. 3450944
6. X. Chen, K. Zhang, X. Liang, W. Qiu, Z. Zhang, and D. Tu, “HyperBSA: A high-performance consortium blockchain storage architecture for massive data,” IEEE Access, 8, 178402-178413, September 2020, doi: 10.1109/ ACCESS.2020.3027610.
7. D. P. Bauer, “InterPlanetary File System,” In Getting Started with Ethereum: A Step-by-Step Guide to Becoming a Blockchain Developer, 83-96, Apress, Berkeley, CA, July 2022, doi: 10.1007/978-1-4842-8045-4_7.
8. M. Felipe and H. Xu, “A scalable storage scheme for on-chain big data using historical blockchains,” In 2022 IEEE 22nd International Conference on Software Quality, Reliability and Security Companion (QRS-C), 54-61, IEEE BSC 2022, Guangzhou, China, December 5-9, 2022, doi: 10.1109/ QRS-C57518.2022.00017.
9. J. Poon and T. Dryja, “The Bitcoin lightning network: scalable off-chain instant payments,” White Paper, 2016. Retrived on September 1, 2022 from https://lightning.network/lightning-network-paper.pdf
10. Ethereum Foundation, “DankSharding,” White Paper, 2023. Retrieved on May 12, 2023 from https://ethereum.org/en/roadmap/danksharding/
11. J. Eberhardt and S. Tai, “On or off the blockchain? insights on off-chaining computation and data,” In: De Paoli, F., Schulte, S., Broch Johnsen, E. (eds) Service-Oriented and Cloud Computing, ESOCC 2017, Lecture Notes in Computer Science (LNCS), 10465, 3-15, Springer, Cham, 2017, doi: 10.1007/978-3-319-67262-5_1.
12. G. Wang, Z. Shi, M. Nixon, and S. Han, “ChainSplitter: towards blockchain-based industrial IoT architecture for supporting hierarchical storage,” In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain), 166-175, Atlanta, GA, USA, July 14-17, 2019, doi: 10.1109/ Blockchain.2019.00030.
13. J. Jayabalan and N.Jeyanthi, “Scalable blockchain model using off-chain IPFS storage for healthcare data security and privacy,” Journal of Parallel and Distributed Computing, 164, 152-167, June 2022, doi: 10.1016/ j.jpdc.2022.03.009.
14. D. Li, W. E. Wong, M. Zhao, and Q. Hou, “Secure storage and access for task-scheduling schemes on consortium blockchain and interplanetary file system,” IEEE 20th International Conference on Software Quality, Reliability and Security Companion (QRS-C), 153-159, IEEE BSC 2020, Macau, China, December 2020, doi: 10.1109/QRS-C51114.2020.00035.
15. E. Androulaki, A. Barger, V. Bortnikov, C. Cachin, K. Christidis, A. De Caro, D. Enyeart, C. Ferris, G. Laventman, Y. Manevich, S. Muralidharan, C. Murthy, B. Nguyen, M. Sethi, G. Singh, K. Smith, A. Sorniotti, C. Stathakopoulou, M. Vukolic, S. Cocco, and J. Yellick, “Hyperledger Fabric: a distributed operating system for permissioned blockchains,” In Proceedings of the Thirteenth EuroSys Conference (EuroSys’18), Article No. 30, 1-15, Porto Portugal, April 23-26, 2018, doi: 10.1145/3190508.3190538.
16. H. Im, K. H. Kim, and J. H. Kim, “Privacy and ledger size analysis for healthcare blockchain,” In Proceedings of the 2020 International Conference on Information Networking (ICOIN), 825-829, Barcelona, Spain, 2020, doi: 10.1109/ICOIN48656.2020.9016624.
17. Y. Xu, “Section-Blockchain: A storage reduced blockchain protocol, the foundation of an autotrophic decentralized storage architecture,” In Proceddings of the 23rd International Conference on Engineering of Complex Computer Systems (ICECCS), 115-125, Melbourne, VIC, Australia, December 12-14, 2018, doi: 10.1109/ICECCS2018.2018.00020.
18. Y. Xu and Y. Huang, “Segment blockchain: a size reduced storage mechanism for blockchain,” IEEE Access, 8, 17434-17441, 2020, doi: 10.1109/ACCESS.2020.2966464.
19. A. Thamrin and H. Xu, “Cloud-based blockchains for secure and reliable big data storage service in healthcare systems,” In Proceedings of the 15th IEEE International Conference on Service-Oriented System Engineering (IEEE SOSE 2021), 81-89, Oxford Brookes University, UK, August 23-26, 2021, doi: 10.1109/SOSE52839.2021.00015.
20. X. Yang, H. Shi, S. Yang and Z. Lin, “Load balancing scheduling algorithm for storage system based on state acquisition and dynamic feedback,” In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), 1737-1742, Ningbo, China, 2016, doi: 10.1109/ ICInfA.2016.7832098.
21. Y. Chang, H. Chen, S. Li and H. Liu, “A dynamic hashing approach to supporting load balance in P2P Systems,” The 28th International Conference on Distributed Computing Systems Workshops, 429-434, Beijing, China, June 17-20, 2008, doi: 10.1109/ICDCS.Workshops.2008.109.
22. R. Panwar and B. Mallick, “Load balancing in cloud computing using dynamic load management algorithm,” 2015 International Conference on Green Computing and Internet of Things (ICGCIoT), 773-778, Greater Noida, India, 2015, doi: 10.1109/ICGCIoT.2015.7380567.
23. H. Guo, W. Li, M. Nejad, and C. Shen, “Access control for electronic health records with hybrid blockchain-edge architecture,” In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain-2019), 44-51, Atlanta, GA, USA, July 14-17, 2019, doi: 10.1109/Blockchain. 2019.00015.
24. R. Anderson, Security engineering: a guide to building dependable distributed systems, 3rd Edition, John Wiley & Sons, Indianapolis, Indiana, USA, December 2020.

(Click Here)