1. The Introduction

The case presented in this paper is the first application of the new multistage one-shot decision-making approach (MOSDMA) in reevaluating a former decision problem. The paper is an extension of work originally presented at the 2021 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM)[1]. In decision-making, decisions are typically made with a certain level of uncertainty. Uncertainty is principally deemed inherent in decision-making and significantly influences the decision alternatives. Uncertainty can be generally defined as the lack of knowledge about the probabilities of the future state of events that cannot be entirely eliminated [2]. Numerous theories have been suggested to cope with decision-making under uncertainty (e.g.,  [3–14]). Most existing theories adhere to the Bernoullian framework of the weighted average. Nevertheless, some decisions under uncertainty are irreversible and can be made only once, where the probability distribution is partial or insufficient. These types of decision problems are known as one-shot decision problems that could lead to significant gains or losses. In such problems, a decision-maker has only one chance to make a decision under uncertainty. Typical examples are private real-estate investments, new technology innovations, product developments, and emergency management for abnormal events. The accelerated industry clock speed environment makes one-shot decision problems extremely applicable in the technology project management fields.

Psychological experimentations studies have demonstrated that individuals systematically disregard the axioms for the expected utility and for the subjective expected utility (e.g.,[15,16]) and do not perform a  summing process and weighting process (e.g.,[17–19]). Empirical studies have revealed that salience (attention-grabbing) information is crucial in human decision-making (e.g.,[20,21]). Accordingly, in [22,23] the author discusses that a decision-maker assesses alternatives based on some associated event or scenario called (the focus of a decision), which is most salient to the decision-maker because of its consequent payoff and probability, thus offering a one-shot decision theory (OSDT)  [22]. In place of conventional (lottery-based) methods, the  author reasons that the OSDT is needed to solve one-shot decision problems because it is scenario-based, appealing to common phenomena and intuition. When making such a one-shot decision with little or partial information, it is most common to take on one scenario, which is crucial to the decision-maker and the decision-maker’s basis for reaching the desired conclusion. The OSDT presents twelve focus points that describe the decision-maker’s attitude towards the possibility, satisfaction, and optimality criteria. The OSDT is generalized to the focus theory of choice (FTC) in [24–26], employing (positive and negative) evaluation systems and relative likelihood. Relative likelihood is used to measure probabilities by the highest probability event in a subset of events. Hence, as the FTC is event-based, it offers a model for practical rationality.

Detailed comparisons are offered in [23,27], to explain the advantages of OSDT and to address the differences between other decision theories based on optimistic and pessimistic utilities such as SEU. In SEU, for example, if the optimal alternative reappears many times, the total payoff gained almost confidently attains the maximum. In contrast, OSDT provides a clear answer to why an alternative is optimal when only one decision chance is left to a decision-maker. In brief, as OSDT is close to the human way of thinking, the OSDT appeals to intuition, ease of application, and explicability. A decision with OSDT results directly from human-centric decision-making, involving the decision-maker rather than just the decision analyst. This is because the decision analyst usually develops decision models based on non-human-centric methods such as the SEU. The OSDT has been successfully applied to production planning problems [28], auction problems [29], newsvendor problems for innovative products [30–32], duopoly markets of innovative products [27,33], and private real estate investment [34].

Founded on the OSDT success, the multistage one-shot decision-making approach (MOSDMA) is proposed in [35] as an extension of OSDT to cope with multistage decision-making under uncertainty problems, where decision-making can be performed only once for each stage. Extending the advantages of OSDT, MOSDMA  is an essential option for multistage decision-making under uncertainty because it is scenario-based and different from other lottery-based approaches. In multistage problems, decisions are made only once at each stage to reach a final result in a series of interdependent decisions.   In [36], the authors have proposed a decision model for individual multi-period consumption–investment problems utilizing the MOSDMA.   In MOSDMA, according to the decision-maker’s attitude towards satisfaction and likelihood, one state (focus point) is chosen at each stage. The indicated backward induction determines the sequence of optimal decisions. In such problems, the obtained sequence of optimal decisions is suitable for making a final decision. However, studies on MOSDMA are still at an early stage, particularly from the applied aspects.

          Uncertainty oversight and risk management fields have evolved as essential to decision-making and project management science [37–39]. Nonetheless, studies need to gain a mutual comprehension of the portrayal of risk and uncertainty in various fields and sufficient ways to handle it [40]. For example, managerial decision-making research discussed the significance of practical and applicable models to assist decision-making under uncertainty [41], as decision-makers will be compelled to make critical decisions based on appropriate assessments. Correspondingly, recent research [41–43] established difficulties in employing mathematical models and scientific approaches in practice. For example, some challenges include limited evidence on the approaches’ efficiencies, not reflecting past experiences, practicality, and lack of capabilities to apply them.

In this paper, the MOSDMA is applied to reevaluate a former information technology (IT) project decision problem. This is the first time utilizing the MOSDMA to solve a decision-making problem in actual practice. The aim is to verify the explicability and effectiveness of the proposed approach to solving decision-making under uncertainty problems in actual practice. The MOSDMA is relatively newer than OSDT; the research can contribute to closing the gap between the theory and application aspects. In the theoretical contribution, this paper extends MOSDMA for a multiple-criteria evaluation problem concerning qualitative and quantitative data [44]. Consequently, research can offer real-life applications for further improvement in the approach, alternatives evaluation stage, and decision-making process in similar fields such as IT project decision-making, decision governance, and activities related to former decision evaluation. For example, evaluations of the former decisions can be relevant to lesson-learned activities, assurance, consulting, and governance-related activities.

          The remainder of the research is arranged in the following structure. Section 2 presents the case study decision problem. Then, in section 3, the problem is solved by applying the approach. Finally, sections 4 and 5 present the discussion and conclusion of this research.

2. The case study

The case study is a former Information Technology (IT) project which went through a sequence of decisions in an IT system lifecycle within a  financial institution in Oman. The institution is developing and incorporating best practices in corporate governance and decision-making. The non-routine decision problems related to such projects are normally raised to a dedicated project committee for group consensus. The institution is committed to employing and improving decision-making governance practices.

An assurance function (AF) decided to implement a Department Management System (DMS) to improve and automate the department workflow, which could have been inspired by the department’s needs and the country’s encouragement to enhance efficiency through technology in all sectors around 2008. The DMS is a technology solution  that streamline and automates the department’s operations and assignments, such as planning, reporting, monitoring, and follow-up . Consequently, a vendor was chosen to deliver one of the best systems in the international market.

Although the first implementation of DMS was concluded, users could only partially utilize the system because of flows in the implementation, such as process compatibility, system reliability, and user adoption. In addition, users found that the implemented version could have been more user-friendly and sufficiently aligned with the practiced workflow. Various efforts were made to solve the identified challenges through a series of patches and customization—still, some issues needed to be fixed satisfactorily. After an extensive debate with the solution provider, the DMS was decided to be upgraded to a newer version. Considerable person-hours were spent in revising and implementing the new version from both sides.

A time came to review the entire project as a part of the department review and the system lifecycle. Though the system may have introduced new benefits, the absence of DMS was not causing a significant hindrance to their workflow and not yielding the best-desired outcome. Therefore, a view was to present this experience and information before the decision-makers and seek a decision to abandon the project. However, the previous decision-makers felt abandoning the system would be a waste after spending a considerable amount of the contract, the experience gained with this competitive product, and the remaining retention fees. Given this rationale, the directives were to evaluate other alternatives or make an additional effort to utilize the DMS for fair use of investment.

In reconsidering the circumstances, the most recent version from the existing DMS provider could be more reliable and user-friendly. Nevertheless, the latest version will add an additional cost to the contract. In a separate endeavor for other alternatives, it was determined by an organization functioning in a similar sector that they had developed a customized in-house system for their Department. The expense was less than the current DMS, and the experience with their vendor was satisfactory. However, their locally customized system has limited features and scope compared to the international DMS product upgrade in the discussion. Moreover, details about implementation feasibility, additional costs, and future capacity are not accessible yet at the time of making the decision.

Until this point of  system lifecycle, the decision-making process was mainly based on similar discussions and intuitions with limited use of scientific decision analysis tools and related mathematical decision-making approaches in the alternatives evaluation stage. However, not using these approaches may not hinder making an informed decision but can provide more context and improvements to the decision-making process for better judgment and justification. Next, the above-introduced case will be defined and reevaluated using the MOSDMA.

3. The solution

3.1.  Problem description

The study employed a decision-making simulation with a focus group of mainly three participants involved in the project and aware of the decision made. The participants assist in supplying, designing, and harvesting qualitative and quantitative data sources, including interviews, discussions, documents, and workshops.

The data-gathering methodology is arranged in three main steps, as summarized in Figure 1. In step 1, an initial case review was performed to understand the case and collect foundational information for the subsequent steps. The foundational information is collected through a short questionnaire, discussions, and examination of relevant project documents. The goal is to construct the case decision story by determining the system’s objective, the decision-making process, the previous alternatives, risk appetite, the type of decision-makers, and the satisfaction of the decisions made in the case. Step 1 main result is manifested in the summarized case study in section 2. Building on step 1, the research can proceed by tailoring a decision-making tool kit to harvest data related to solving this case study in step 2. The decision-making tool kit consists of a decision tree, a probability scale card, and a weighted sum scorecard. Through collaboration, three inputs of the participants are captured using the consented decision-making tool kit. The probabilities and the weight of each considered objective are donated following the decision tree in Figure 2. After the final values are placed  in the finalized decision tree, the described problem can be solved. All data are detailed in the following sections.

      The alternatives, in this case, are evaluated by considering three objectives: payoff as cost and benefit (CB), social impact (SI), and user satisfaction (US). First, to find the payoff (CB), the savings are obtained, as shown in Table 1. Then the CB of the three potential options is computed, as displayed in Table 2. Next,  a tailored weighted sum scorecard and probability scale card are developed, as shown in Tables 3 and 4. The main weight assigned for CB, SI, and US objectives are 0.4,0.3, and 0.3, respectively. The objectives and weight are subjective to the participants’ experience and agreement. Then using this kit, appropriate values are selected for each scenario. Therefore, the decision tree and the final values are visualized in Figure 2.

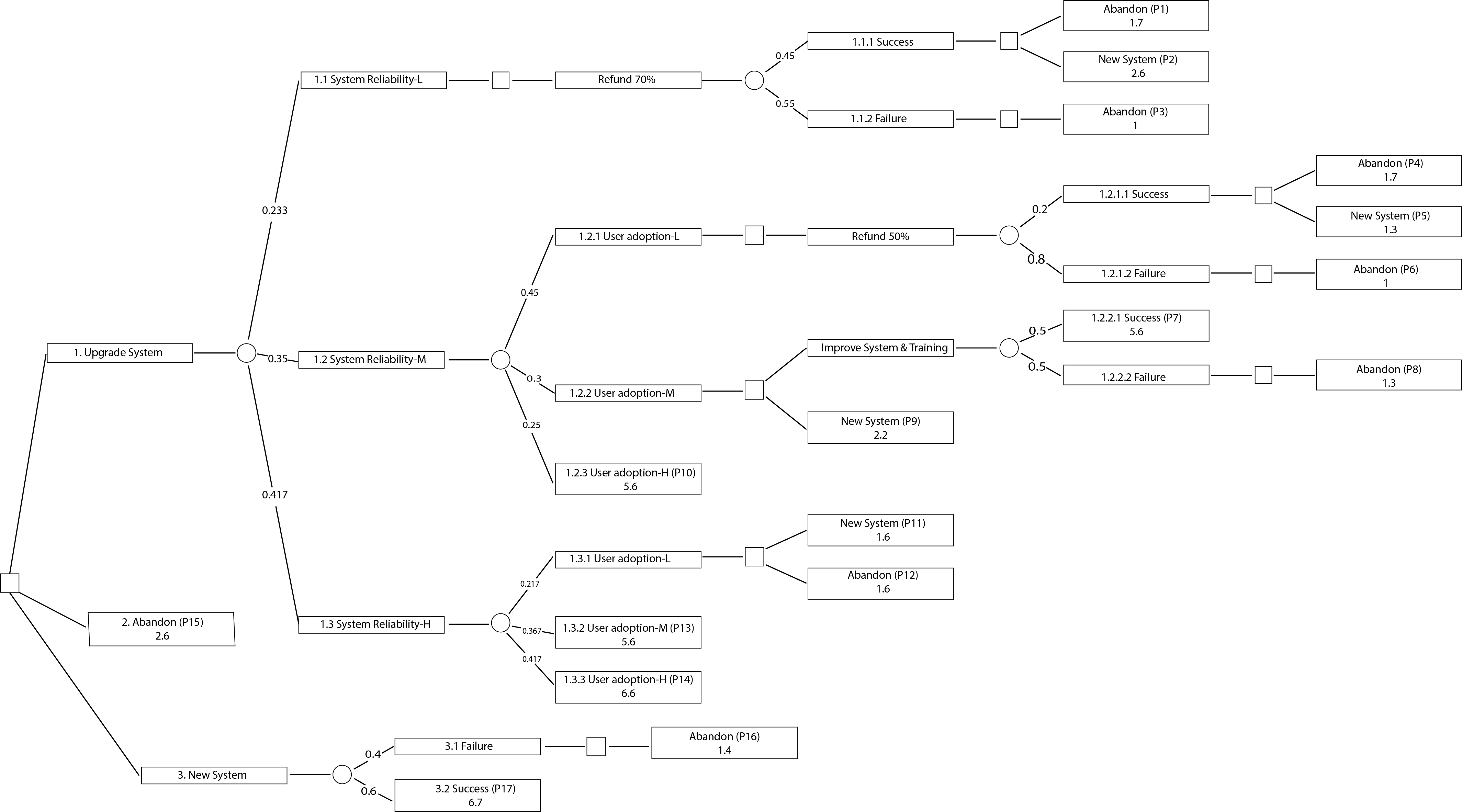
Figure 1:The data-gathering methodology steps

Figure 2: The decision tree showing final values.

Table 1. Estimated savings
Hours Before Automation (HBA)	Hours After Automation (HAA)	Hours Savings per assignments a (HS)	Total Hours Saved per year b (THS)	Total saved cost per year c	Total saved cost in 5 years
200 Hours	113 Hours	87 Hours	4350 Hours	121,800 USDd	609,000 USD
The above data is based on the solution forecasted benefit analysis provided by the vendor and applied to AF’s annual average functions. a ( HS = HBA – HAA) b ( Average 50 assignments per year ) ´ HS c ( Average hour costs 28 USD ) ´ THS d USD (United States dollars).

Table 2: Cost and Benefits (CB) estimations

Alternatives	Annual total savings cost a	5 years of total savings cost a	Previous payments (PP)	1st Year Cost (YC)	Total Setup Cost 1st Year (TYC)	4 years total annual maintenance cost (TAMC)	5 years Cumulative Cost (CC)	5 Years Net Benefits (NB)
Upgrade Current System	121,800	609,000	PP1	YC1	TYC1	TAMC1	CC1	NB1 (Highest Value)
New System	121,800	609,000	PP2	YC2	TYC2	TAMC2	CC2	NB2
Abandon	0	0	PP3	0	0	0	0	0 (Lowest Value)
a Values are estimated in table 1. Values are shown in  USD (United States dollars).

Table 3: The weighted sum method

Objectives	Aim	1	2	3	4	5	6	7
Cost/Benefits (CB) in USD	Max.	-300,000 or less	-299, 000 to -200,000	-199, 000 to -1	0 to 49,000	50,000 to 149,000	150,000 to 249,000	250, 000 or more
User satisfaction (US)	Max.	VL	L		M		H	VH
Social impact (SI)	Min.	VH	H		M		L	VL
(1) indicates the least favorite outcome, while (7) indicates the most favorable outcome.
VL = (Very High) , L= (Low), M = (Medium), H = (High) , VH = (Very High)
USD = United States dollars

Table 4: Probability scale card tool.

Levels	Impossible	Nearly Impossible	Very Low	Low	Moderate Low	Moderate	Moderate high	High	Very High	Extremely High	Certain
Probabilities	0	10%	20%	30%	40%	50%	60%	70%	80%	90%	100%

      The CB objective is achieved for all the outcomes based on a simple premise: Payoff is equal to potential benefits after subtracting applicable costs or losses. After finalizing the payoff details, the team decides on the values for each path’s objective. Then, the values are normalized based on the weighted sum scorecard described in Table 3. Finally, the values are normalized by multiplying them by the corresponding main weight of the objective. For example, in path 1, the CB, SI, and US values are normalized to the scores 2, 2, and 1 and then to the scores multiplied by the weights of the objectives 0.4, 0.3, and 0.3, which yield a final outcome of 1.7. This process of collecting and normalizing the outcome with weight scores is detailed in Table A2  in the appendix.

      Based on the case study review and previous undesired outcomes, two major uncertainties were identified: system reliability and user adoption. Subsequently, the event branches low (L), medium (M), and high (H) are assigned to the parent uncertainties. The alternative (Upgrade System)  has 14 possible scenario paths (numbered from P1 to P14), and the alternative (New system) has two. While the alternative (Abandon)  has one certain value (P15), as expressed in the decision tree in Figure 1 and Table A2 in the appendix.

To find the probability of each scenario, the average of the three responses is taken using a customized probability scale card with 11 scales corresponding to a level and a probability, as shown in Table 4. The lowest level, “impossible,” denotes a probability of 0 for the event. Comparably, the highest level, “Certain,” denotes a probability of 1. Subsequently, the final outcomes and the final probabilities are positioned in the decision tree presented in Figure 2 to solve the decision problem using the MOSDMA.

3.2.  Applying the approach

The multistage one-shot decision-making approach (MOSDMA) offers in which twelve types of focus points to harmonize with different types of decision-makers  [36]. Out of twelve focus points, four examples of focus points characteristics are described in Table 5  by considering combinations of likelihood and satisfaction. In type (I), both likelihood and satisfaction are higher, which appears appropriate for an active decision-maker. In contrast, in type (III), it appears appropriate for an apprehensive decision-maker as although some scenario has a lower likelihood, it is still considered can induce more significant losses (as shown by the lower satisfaction level). Purchasing insurance can exemplify a type (III) focus point behavior. Type (II) looks appropriate for passive decision-makers with lower satisfaction levels and higher likelihood. Whereas in type (IV), the focus point appears proper for daring personalities. Because though the likelihood of some scenarios is lower, higher gains (higher satisfaction level) could tempt individuals to contemplate such a scenario (for example, purchasing a lottery).

Based on the focus point characteristics, the types (I), (II), (III), and (IV) are named active focus point, passive focus point, apprehensive focus point, and daring focus point, respectively.

Table 5: Characteristics of four focus points (types I-IV)

Four types of focus points	Satisfaction	Likelihood
(I) Active Focus Point (AFP)	higher	higher
(II) Passive Focus Point (PFP)	lower	higher
(III) Apprehensive Focus Point (APFP)	lower	lower
IV. Daring Focus Point (DFP)	higher	lower

Taking into account the stakeholders in this study case, only the Passive Focus Point (PFP) is considered to incorporate the overall intuition and feelings at this point of the project. First, consider a decision  on a decision node A at the initial stage (stage 1). Then, the outcomes and probabilities are normalized using the satisfaction function  and the relative likelihood function  , as per (1) and  (2) below.

which means that for      is a state that can obtain a relatively low outcome with a relatively high probability (an unfavorite scenario of ). This state mirrors the pessimistic mentality of decision-makers. Following computing all the PFPs of , the final optimal alternative on the decision node A denoted as  is chosen by

indicates that decision-makers select the alternative with the highest outcome among the unfavorite scenarios.

In MOSDMA, the PFP of each alternative is found from the last stage (stage 4 in Figure 2), compared by their outcomes fitting to the focus point, and rolled back until the initial stage (stage 1) is reached to make the final selection. Rather than computing the expected utility of each alternative, comparing each other on a decision node and then rolling back in stochastic dynamic programming.  Figure 3 has been designed to resemble the decision tree in Figure 2 to translate the results computed by applying (1), (2), (3), and (4). In this case, there are four stages: stage 4 is the last, and stage 1 is the initial stage. Stages 4, 3, and 2 are condensed to the chance nodes, and stage 1 is the primary decision node. First,  (1) and (2) are employed to normalize the outcomes and probabilities to find satisfaction and likelihood values. Then, (3) is used to get PFP between siblings’ branches in each stage, starting from the last stage (stage 4) to stage 2. The PFPs are highlighted in gray in Figure 3. Finally, following the migration of the outcome values corresponding to the highlighted PFPs in stage 2 to stage 1, the final decision can be selected using (4) in stage 1.

For example, starting from stage 4, to acquire the PFP between the sibling branches 1.2.2.1 and 1.2.2.2, first by applying (3), the minimum value of {π(x) , 1-u(x,a) } at each branch is found. The minimums for branches 1.2.2.1 and 1.2.2.2 are 0 and 0.768, respectively. From these two minimums, the maximum value is 0.768, which indicates that the focus point between these two siblings is branch 1.2.2.2. Subsequently,  the outcome and probability values of branch 1.2.2.2 are migrated to parent branch 1.2.2. The outcome r(x, a) migrates with the same value 1.3; however, probability p(x) is multiplied by the parent’s branch 1.2.2 probability (0.5´0.30 = 0.15). The same rolling-back process employed in stage 4  is replicated in stage 3. Similarly, by applying (3), the minimum values for the branches 1.2.1, 1.2.2, and 1.2.3 are  0.821, 0.424, and 0, respectively. As a result, branch 1.2.1 is the focus point with the maximum value among its sibling. Likewise, the rest of the PFPs in stage 3 are found, and their outcomes and probabilities are migrated to the parent’s branches in stage 2 as in the previous stage. The outcome and probability values for parent 1.2 after migration from the child branch 1.2.1 are 1 and 0.126 (0.35 ´ 0.36), respectively. Duplicating the same process in previous stages, the PFP in stage 2 are the branches 1.1 and 3.1. For the initial stage (stage 1), only the outcomes of branches 1.1 and 3.1 are migrated to stage 1. In stage 1, as shown in Figure 3, the final outcomes 1, 2.6,  and 1.4 are compared using (4) to make the final decision. Accordingly,  alternative number 2 (Abandon the system) is the highest outcome among the unfavorite scenarios, which resembles a pessimistic mentality as per the PFP type.

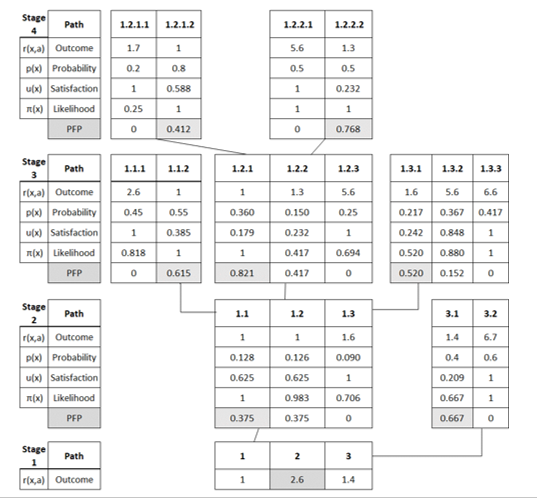
Figure 3: Applying the Passive Focus Point (PFP).

4. Discussion

In this paper, the pessimistic mentality was considered to apply the passive focus point (PFP) following the MOSDMA. The PFP brings a relatively low outcome with a relatively high probability. In the PFP type of the MOSDMA approach, the decision-maker chooses one decision that can get the highest outcome amongst the unfavorite scenarios from the decision alternatives in the initial decision stage (stage 1 in Figure 3). This paper considered the pessimistic mentality to apply the passive focus point (PFP), one of the twelve focus points introduced by the MOSDMA. The PFP obtains a moderately low outcome with a relatively high probability. The decision-makers select one conclusion to obtain the highest outcome among the unfavorite scenarios proposed in the initial decision stage, as represented by stage 1 findings in Figure 3. The endorsed alternative is the alternative (Abandon the system) with the outcome of 2.6. This decision-making mirrors the pessimistic mental set in using the PFP. The acquired empirical reevaluation of alternatives is intuitively acceptable and comparable to the actual feelings of the individuals concerned. No major difficulties were noticed in applying and understanding the approach. Participants found it uncomplicated and valuable for future use.

Eventually, despite the pessimistic feelings when deciding back around 2014, the chosen alternative was “upgrade the system,” while other alternatives were discounted. The motivation was founded on the discussion of not demolishing the consumed resources; the experience gained, and the time devoured in this solution and the initiative implementation. More in-depth evaluations could give more systematic explanations and justification for the decisions made. In this case, the decision-makers did not include comparable decision analysis approaches in the alternative evaluation stage and leaned mainly on deliberating the available information and intuition. They may have believed that other alternatives may bring the lowest outcomes and satisfaction levels if unsuccessful, which could be supported using such a scenario-based method. This reveals opportunities for improvements in the alternatives evaluation stage and fills the gaps in acknowledging the value of such decision-making approaches in actual practice.

If the case is solved assuming the decision-maker is optimistic using the same approach but with an active focus point (AFP) type, the result would be “3. New System”. Later, it was found that the project did not produce the best-desired outcomes. The new management is reviewing alternative 3, “discard the current product and implement a new system.” However, there is a high degree of attention to reviewing the problem and improving the decision-making process. The new direction could be based on the undesired project outcomes and immaculate corporate governance improvements.

5. Conclusion

This study employs the multistage one-shot decision-making approach (MOSDMA) to revisit an actual decision problem for the first time. More studies are required from both theoretical and applied aspects, as MOSDMA is considered a new approach at an early stage. Nevertheless, this research is the first contribution involving the passive focus point (PFP) suggested by MOSDMA to reexamine a real multistage decision-making-under-uncertainty problem.

 The obtained empirical reevaluation of alternatives is intuitively acceptable to the contributors. The study showed that MOSDMA could assist in reevaluating previous decisions and its capability to make an informed one with proper analysis and justifications aligned to stakeholders’ satisfaction levels and intuition. This establishes the effectiveness of the MOSDMA and the promising capability of the introduced workflow to reevaluate such decision problems in similar environments. Furthermore, the approach was found reasonably explicable, practical, and systematically considering the decision-makers’ intuitions.

 The quality of the assessed scenarios and the gathered data is restricted to the experience and commitment of the participants in this decision-making analysis exercise. The knowledge of the future outcome and collaborating in a group setup or open disclosed style may have influenced the participant’s inputs since this is a reevaluation of a past problem with currently known outcomes compared to the pressure confronted in real-time decision-making or undisclosed inputs of each participant. Since 2014, considerable restructuring has occurred in the financial institution. Accordingly, a number of applicable people involved in this case were unreachable to participate and to add more inputs to this study. Nevertheless, this limitation could be mediated since this is a decision review of a recently known outcome and a well-documented project.

Further future research is needed to improve MOSDMA theoretically and for more practical applications. For instance, forthcoming approach applications may consider more contemporary decision problems, complex stages, more data and comparisons with other approaches,   other focus groups and organizations, and various details in capturing the participant inputs and reactions. Nevertheless, this study demonstrates that the approach could be employed to reexamine a former decision problem which can contribute to analyzing lessons learned and areas for improvement. Likewise, MOSDMA has the prospect of being utilized in the areas of crucial new unresolved problems, auditing, governance practices,  and consulting assignments.

Conflict of Interest

The author declares no conflict of interest.

Acknowledgment

Appreciation is extended to the immense support of the participants. The views and opinions expressed in this paper do not necessarily reflect the official policy or position of the Omani institutions.

1. M. Aishanfari, P. Guo, “Application of the Multistage One-shot Decision-making Approach to an IT Project in the Central Bank of Oman,” in 2021 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), 552–557, 2021, doi:10.1109/IEEM50564.2021.9672939.
2. F.H. Knight, Risk, uncertainty and profit, Houghton Mifflin, 1921.
3. S. Cerreia-Vioglio, D. Dillenberger, P. Ortoleva, “Cautious Expected Utility and the Certainty Effect,” Econometrica, 83(2), 693–728, 2015, doi:https://doi.org/10.3982/ECTA11733.
4. D. Dubois, H. Prade, R. Sabbadin, “Decision-theoretic foundations of qualitative possibility theory,” European Journal of Operational Research, 128(3), 459–478, 2001, doi:10.1016/S0377-2217(99)00473-7.
5. T. Galaabaatar, E. Karni, “Subjective Expected Utility With Incomplete Preferences,” Econometrica, 81(1), 255–284, 2013, doi:https://doi.org/10.3982/ECTA9621.
6. I. Gilboa, “Expected utility with purely subjective non-additive probabilities,” Journal of Mathematical Economics, 16(1), 65–88, 1987, doi:10.1016/0304-4068(87)90022-X.
7. P. Guo, Y. Wang, “Eliciting dual interval probabilities from interval comparison matrices,” Information Sciences, 190, 17–26, 2012, doi:10.1016/j.ins.2011.12.014.
8. D. Kahneman, A. Tversky, “Prospect Theory: An Analysis of Decision under Risk,” Econometrica, 47(2), 263–291, 1979, doi:10.2307/1914185.
9. J. von Neumann, O. Morgenstern, A. Rubinstein, Theory of Games and Economic Behavior (60th Anniversary Commemorative Edition), Princeton University Press, 1944.
10. J. Quiggin, “A theory of anticipated utility,” Journal of Economic Behavior & Organization, 3(4), 323–343, 1982, doi:10.1016/0167-2681(82)90008-7.
11. L.J. Savage, “The foundations of statistics.,” Naval Research Logistics Quarterly, 1(3), 236–236, 1954, doi:https://doi.org/10.1002/nav.3800010316.
12. D. Schmeidler, “Subjective Probability and Expected Utility without Additivity,” Econometrica, 57(3), 571–587, 1989, doi:10.2307/1911053.
13. F. Gul, W. Pesendorfer, “Expected Uncertain Utility Theory,” Econometrica, 82(1), 1–39, 2014, doi:https://doi.org/10.3982/ECTA9188.
14. P. Guo, H. Tanaka, “Decision making with interval probabilities,” European Journal of Operational Research, 203(2), 444–454, 2010, doi:10.1016/j.ejor.2009.07.020.
15. M. Allais, “Le comportement de l’homme rationnel devant le risque: critique des postulats et axiomes de l’école américaine,” Econometrica: Journal of the Econometric Society, 503–546, 1953.
16. D. Ellsberg, “Risk, ambiguity, and the Savage axioms,” The Quarterly Journal of Economics, 643–669, 1961.
17. Z. Zhou, W. Zhao, X. Chen, H. Zeng, “MFCA extension from a circular economy perspective: Model modifications and case study,” Journal of Cleaner Production, 149, 110–125, 2017, doi:10.1016/j.jclepro.2017.02.049.
18. N. Stewart, F. Hermens, W.J. Matthews, “Eye Movements in Risky Choice,” Journal of Behavioral Decision Making, 29(2–3), 116–136, 2016, doi:https://doi.org/10.1002/bdm.1854.
19. L. Zhou, Y.-Y. Zhang, Z.-J. Wang, L.-L. Rao, W. Wang, S. Li, X. Li, Z.-Y. Liang, “A Scanpath Analysis of the Risky Decision-Making Process,” Journal of Behavioral Decision Making, 29(2–3), 169–182, 2016, doi:https://doi.org/10.1002/bdm.1943.
20. N. Lacetera, D.G. Pope, J.R. Sydnor, “Heuristic Thinking and Limited Attention in the Car Market,” American Economic Review, 102(5), 2206–2236, 2012, doi:10.1257/aer.102.5.2206.
21. M.R. Busse, N. Lacetera, D.G. Pope, J. Silva-Risso, J.R. Sydnor, “Estimating the Effect of Salience in Wholesale and Retail Car Markets,” American Economic Review, 103(3), 575–579, 2013, doi:10.1257/aer.103.3.575.
22. P. Guo, “One-Shot Decision Theory,” IEEE Transactions on Systems, Man, and Cybernetics – Part A: Systems and Humans, 41(5), 917–926, 2011, doi:10.1109/TSMCA.2010.2093891.
23. P. Guo, One-Shot Decision Theory: A Fundamental Alternative for Decision Under Uncertainty, Springer, Berlin, Heidelberg: 33–55, 2014, doi:10.1007/978-3-642-39307-5_2.
24. X. Zhu, K.W. Li, P. Guo, “A bilevel optimization model for the newsvendor problem with the focus theory of choice,” 4OR, 2022, doi:10.1007/s10288-022-00520-6.
25. P. Guo, “Focus theory of choice and its application to resolving the St. Petersburg, Allais, and Ellsberg paradoxes and other anomalies,” European Journal of Operational Research, 276(3), 1034–1043, 2019, doi:10.1016/j.ejor.2019.01.019.
26. P. Guo, “Dynamic focus programming: A new approach to sequential decision problems under uncertainty,” European Journal of Operational Research, 2022, doi:10.1016/j.ejor.2022.02.044.
27. P. Guo, “One-shot decision approach and its application to duopoly market,” International Journal of Information and Decision Sciences, 2(3), 213, 2010, doi:10.1504/IJIDS.2010.033449.
28. X. Zhu, P. Guo, “Bilevel programming approaches to production planning for multiple products with short life cycles,” 4OR, 18(2), 151–175, 2020, doi:10.1007/s10288-019-00407-z.
29. C. Wang, P. Guo, “Behavioral models for first-price sealed-bid auctions with the one-shot decision theory,” European Journal of Operational Research, 261(3), 994–1000, 2017, doi:10.1016/j.ejor.2017.03.024.
30. P. Guo, X. Ma, “Newsvendor models for innovative products with one-shot decision theory,” European Journal of Operational Research, 239(2), 523–536, 2014, doi:10.1016/j.ejor.2014.05.028.
31. X. Zhu, P. Guo, “Single-level reformulations of a specific non-smooth bilevel programming problem and their applications,” Optimization Letters, 14(6), 1393–1406, 2020, doi:10.1007/s11590-019-01444-7.
32. X. Zhu, P. Guo, “Approaches to four types of bilevel programming problems with nonconvex nonsmooth lower level programs and their applications to newsvendor problems,” Mathematical Methods of Operations Research, 86(2), 255–275, 2017, doi:10.1007/s00186-017-0592-2.
33. P. Guo, R. Yan, J. Wang, “Duopoly Market Analysis within One-Shot Decision Framework with Asymmetric Possibilistic Information,” International Journal of Computational Intelligence Systems, 3(6), 786–796, 2010, doi:10.2991/ijcis.2010.3.6.9.
34. P. Guo, “Private Real Estate Investment Analysis within a One-Shot Decision Framework,” International Real Estate Review, 13(3), 238-260., 2010.
35. Y. Li, P. Guo, “Possibilistic individual multi-period consumption–investment models,” Fuzzy Sets and Systems, 274, 47–61, 2015, doi:10.1016/j.fss.2015.01.005.
36. P. Guo, Y. Li, “Approaches to multistage one-shot decision making,” European Journal of Operational Research, 236(2), 612–623, 2014, doi:10.1016/j.ejor.2013.12.038.
37. S. Ward, C. Chapman, “Transforming project risk management into project uncertainty management,” International Journal of Project Management, 21(2), 97–105, 2003, doi:10.1016/S0263-7863(01)00080-1.
38. A. Jaafari, “Management of risks, uncertainties and opportunities on projects: time for a fundamental shift,” International Journal of Project Management, 19(2), 89–101, 2001, doi:10.1016/S0263-7863(99)00047-2.
39. S.D. Green, “Towards an integrated script for risk and value management,” Project Management, 7(1), 52–58, 2001.
40. O. Perminova, M. Gustafsson, K. Wikström, “Defining uncertainty in projects – a new perspective,” International Journal of Project Management, 26(1), 73–79, 2008, doi:10.1016/j.ijproman.2007.08.005.
41. B.J. Galli, “The Future of Economic Decision Making in Project Management,” IEEE Transactions on Engineering Management, 67(2), 396–413, 2020, doi:10.1109/TEM.2018.2875931.
42. W.G. Meyer, “The Effect of Optimism Bias on the Decision to Terminate Failing Projects,” Project Management Journal, 45(4), 7–20, 2014, doi:10.1002/pmj.21435.
43. B.J. Galli, “Effective Decision-Making in Project Based Environments: A Reflection of Best Practices,” International Journal of Applied Industrial Engineering (IJAIE), 5(1), 50–62, 2018, doi:10.4018/IJAIE.2018010103.
44. M. Aruldoss, T.M. Lakshmi, V.P. Venkatesan, “A Survey on Multi Criteria Decision Making Methods and Its Applications,” American Journal of Information Systems, 1(1), 31–43, 2013, doi:10.12691/ajis-1-1-5.

(Click Here)