1. Introduction

As is well-known, modern society sets complex tasks for citizens that require non-standard decisions and the manifestation of critical and creative thinking in the constantly changing and non-predictable environment of our world. Accordingly, in a modern school, the discovery-based method as an effective aid for working with gifted children and its optimal organization, combining various formats of such work, is increasingly coming to the fore [1-3].

Despite many studies of the theory and practice of working with gifted children, this issue has not been sufficiently discussed in the methodological and mathematical studies known to us, which indicates the relevance and importance of the present study.

The response to this challenge should consider the specifics of the subject. The process of teaching mathematics to gifted students at school seems to be quite laborious, since here it is necessary, firstly, to ensure the development of the main curriculum, and, secondly, to effectively develop their “non-standard potential”. These two goals in existing educational practice are not always coordinated. Elective and basic mathematics courses are taught by different teachers under time pressure. Moreover, this often do not take into account the individual characteristics of students.

As a rule, in the real educational process, the work of a mathematics teacher, both in ordinary and specialized classes, focuses primarily on the development of students’ basic competencies, which are taken into account during the current and final certification. The second component of this process – the actual mathematical development – is decided on elective courses and consultations of various kinds by completely different people – “invited lecturers’ within their areas of expertise. These two groups of teachers do not always have the opportunity and desire to closely contact each other professionally. As a result, gifted students study, as it were, two different subjects: “basic mathematics” and “Olympiad mathematics’, which does not always allow them to effectively realize the developing potential of the studied mathematical content. This was confirmed by our survey of mathematics teachers, most of whom indicated that the spontaneous interaction of the various formats of such training, as occurs in the existing system of training gifted children, does not fully ensure its effectiveness. From the foregoing, it is evident that there is a need for theoretical development and practical implementation of a special model for the rational combination of basic and elective courses in the process of teaching mathematics to gifted students. Summarizing, we can conclude that as a rule, the traditional strategy for teaching mathematics to gifted children is one-sided, being limited to an emphasis on elective courses, or individual consultations. At the same time, the learning process itself is spontaneous in nature, not providing for the educational needs of all such students. An analysis of the pedagogical studies known to us revealed that the issue of a rational combination of various formats for mathematical training of gifted schoolchildren was not specifically addressed in these studies.

 Thus, the relevance of this study stems from the need for theoretical development and practical implementation of a holistic strategy for working with gifted children in the field of mathematics, which includes the possibility of a rational combination of various learning formats for each gifted student.

2. Mathematically Gifted Students

Many psychological and pedagogical studies have been devoted to the mathematical development of gifted children [4-10]. According to most authors, mathematical giftedness is understood as a kind of intellectual giftedness, which is associated with and develops in special mathematical activity. Its basic characteristics are integrity, multicomponent nature, hierarchy and dynamism [11, 12]. Mathematically gifted schoolchildren are characterized by the ability to think logically, the ability to operate with mathematical symbols, quickly and correctly solve mathematical problems, successfully moving from simple to more complex mathematical constructions.

Such students have a flexible mind, that is, they are able to find a way out of a non-standard mathematical situation and they have a well-developed abstract memory [13]. Approaches to the study of mathematical giftedness, reflected in the literature, are very diverse: they are based on the psychology of individual differences in students, on the special abilities of mathematically gifted students.

The scientists Joy Gilford, Ellis Torrance, Frank Barron and Charles Taylor carried out a number of major studies in the psychology of giftedness and contributed to the unification of theoretical studies on the psychology of individual differences and practical work on the construction of new curricula in the field of differentiated learning [14-18]. They found that giftedness was manifested in the fact that, unlike for ordinary, traditional experiments, students built their own tasks. Scientists have observed the behavior of creatively gifted people in natural situations of communication, work and leisure. They tried to determine the specific manifestations of talent in various activities, as well as the characteristic features of the personality of gifted people, which emerged in behavior, thinking, inclinations and attitudes. The tasks were set to change the idea of giftedness as “a symptom of hereditary degeneration of the epileptoid type” [19]. This process of change took place over a period of more than 30 years from the beginning of the 20th century. The results of their research have shown that by the end of school, many gifted children sometimes experience severe depression. They are forced to hide their giftedness from their peers and adults. Gifted children experience “discrimination” in school due to the lack of differentiated teaching, due to the school’s focus on the average student, due to excessive reduction to a uniform system of curricula [20].

Psychologists Sergei Rubinstein and Boris Teplov developed a classification of the concepts of “ability”, “giftedness” and “talent”. The classification was carried out according to the success of the activity [16]. Abilities are considered as individual psychological characteristics that distinguish one person from another, on which the possibility of success in activity depends, and giftedness is considered as a qualitatively unique combination of abilities (individual psychological characteristics), on which the possibility of success in activity also depends.

In various definitions of the concept of giftedness (source), a number of basic features of giftedness can be traced. A person has:

(1) outstanding (high level) abilities,

(2) developed intelligence,

(3) an increased level of mental development,

(4) creative approach,

(5) the possibility of achieving high results in various activities.

Intellectual giftedness is a developing systemic quality of the personality psyche in the structure of general abilities. The development of this quality requires a holistic didactic approach to working with gifted adolescents [6]. The personal growth of intellectually gifted adolescents depends on the type of educational environment. The environment should contribute to the disclosure and optimal manifestation of the creative nature of the psyche of gifted adolescents. By minimizing the difficulties of a gifted child in contact with his environment, the educational environment contributes to the adequate personal development of gifted adolescents [21].

Professor Gennadiy Sarantsev in his works talks about methods for developing the ability of gifted children to solve non-standard tasks. He considered various heuristic approaches to solving problems and building new curricula in the field of differentiated learning.

Scientists Vadim Krutetsky, Viсtoria Yurkevich, Irina Levochkina, Elena Kryukova examined in detail the special abilities that characterize mathematically gifted students, as well as ways to recognize them in a child and adolescent.

They emphasize that schoolchildren who are especially gifted in mathematics are characterized by a peculiar mathematical orientation of the mind (the tendency to perceive many phenomena through the prism of mathematical relations, to realize them in terms of logical and mathematical categories).

They single out several components of mathematical talent: the ability to arrive at mathematical generalization;  rationality of the decision (the ability to find the shortest way to solve, cut off the excess, not directly related to the achievement of the goal, the task); a sense of “mathematical aesthetics” (the ability to see beauty and elegance in a simple and at the same time witty, concise and economical way of solving a problem); reversibility of thinking; mathematical intuition.

The results of studies of mathematically gifted adolescents show that adolescents gifted in mathematics develop such features of their mental activity as the ability to generalize mathematical material (the ability to see the general in what is outwardly different, singular), the flexibility of thought processes and the desire to find simpler but more effective ways to solve problems [22].

The issue of teaching methods for mathematically gifted schoolchildren is presented in the works of many psychologists and teachers [11, 23]. They consider various methods of working with mathematically gifted students, describe a system of special tasks for gifted students, and describe the necessary conditions for creating a support system for talented students. They discuss the technologies that the teacher should rely on when developing the unique abilities of each child, describe the construction of a program for mathematically gifted students, where they propose to integrate Olympiad tasks into sections of the basic mathematics course (resources). A number of authors describe the development of creative potential in the process of participating in competitions, in the process of solving non-standard problems [24, 25]. They view work with gifted children in the context of differentiated and individualized learning. Such training, as is well known, is implemented on the basis of a full account of the individual and typological characteristics of a person in the form of grouping or ungrouping students and differentiated construction of the learning process in educated groups or individually; learning technology, the purpose of which is to create conditions for the identification of existing inclinations, the effective development of the interests and abilities of students [26].

However, the authors known to us do not specifically consider the correlation and connections of various approaches to differentiated work with gifted students, the conditions for their effective integration within the framework of such work, the difficulties that arise in this, and ways to overcome them. The foregoing determines the relevance and significance of building and creating a model for training gifted students in mathematics, based on a rational combination of various approaches for working with them and, in particular, in both basic and elective mathematical courses.

In the context of our study, the “Working Concept of Giftedness” developed by Diana Bogoyavlenskaya and Vladimir Shadrikov is of great interest [7]. This concept involves the disclosure of giftedness on the basis of the theoretical provisions of psychology and the definition of basic principles in solving the problems of identifying, training and developing gifted children. ‘Giftedness’ is interpreted as a systemic quality that characterizes the child’s psyche as a whole. At the same time, it is the personality, its orientation and the system of values that lead to the development of abilities and determine how its potential will be realized.

Giftedness entails a humanistic approach to the education and development of gifted students, that is, special attention is paid to caring for a gifted child, which implies an understanding of not only the advantages, but also the difficulties that his giftedness brings with it.

3. Methodological framework

As a basis for building the authors’ model of work with gifted schoolchildren in mathematics, they used differentiated and individual approaches to learning and the above-mentioned “Working concept of giftedness” [15, 27]. Differentiation of learning is a process involving the division of students into groups according to their mathematical abilities. Individualization of learning – learning aimed at developing the individual abilities of each student – is an integral element of student-centered learning. Such work may include, for example, external studies, elective courses, individual consultations, implementation of project activities. At the same time, it should not lead to the need to separate gifted students from their peers, but should involve the integration of various collective, group and individual learning activities.

As you know, today, work with gifted children is carried out in schools, gymnasiums, and lyceums. In particular, differentiated education is carried out by dividing classes into profiles: physical and mathematical, humanitarian, chemical and biological, and others. At the same time, work with gifted children is carried out both within the framework of school lessons and within the framework of additional courses (elective courses, courses for preparing for Olympiads, individual lessons). A rational combination of these formats makes it possible to implement regular and systematic work to maximize the full disclosure of the creative potential of schoolchildren [26, 28].

To organize such work, the following factors are necessary:

(1) a strategy for teaching gifted students heuristic methods for solving problems,

(2) continuity of basic and elective mathematical courses of a developing orientation,

(3) a system of students-centered methods of working with gifted students.

4.  A strategy for teaching gifted students’ heuristic methods for solving non-standard problems

The main forming factor in organizing such work is the strategy of teaching gifted schoolchildren heuristic methods for solving non-standard problems. Non-standard problems are understood as problems that cannot be solved by standard algorithms known from the basic mathematical course. When solving them, it is necessary to use one or another heuristic procedure.

The essence of heuristic methods for solving problems lies in the fact that the student is naturally involved in the process of rediscovering a non-standard condition of the problem and finding a way to solve it, without having a direct opportunity to apply the basic algorithm for solving. The selection of such tasks and the development of an individual learning plan is a serious challenge for a mathematics teacher. This plan should include the possibility of targeted implementation of several individual learning approaches that correspond to different strategies for working with a particular gifted student.

Scholars define an educational plan as a set of learning stages, forms of learning, and combinations of individual topics from mathematics curricula. In other words, the educational plan is a differentiated educational program that provides the student with a choice of the type and amount of pedagogical support he needs for his self-determination and self-realization [28].

An individual educational plan is built based on the educational needs, individual abilities and capabilities of the student (level of readiness to master the program), as well as existing regulatory documents. The purpose of such training is to purposefully ensure the differentiation and individualization of the education of gifted children, giving it a personality-oriented character.

An individual educational plan consists of a number of “sections” corresponding to various formats of work (basic course, elective course, individual work, group projects, competitions, Olympiads, etc.). All these approaches should be closely related and organically combined with each other.

5. Ensuring the continuity of the basic and elective components of the mathematical teaching of gifted children

In the combination of various formats of work with gifted children in mathematics mentioned above, a special role is played by the continuity of basic and elective mathematical courses of a developing orientation. This factor, as the analysis of the literature and our own pedagogical experience show, has not yet become one of the imperatives of the educational process for the considered contingent of schoolchildren.

In particular, often different mathematical courses in the same group are taught by teachers of different qualifications (school and university), while the material studied in parallel within these courses is often characterized by “diversity”, “patchwork” both in content and in developmental aspects. Overcoming such diversity, obviously, involves providing an organic combination of basic (profile) and elective courses. To illustrate the latter point, we present Figure 1, in which the first and third columns present some topics that are quite important in terms of preparing schoolchildren for mathematical Olympiads. In the central part of the diagram, sections are presented that are the result of the “interaction” of the corresponding basic and additional mathematical courses (Figure 1).

Commenting on the structure and content of the above diagram, it is necessary, first of all, to note that work with gifted students is a holistic, systematic process that emerges from the basic course.

Here, when solving developmental problems, students mainly apply the heuristic method at the stage when they discover some general algorithms that are practiced with all students in a collective form. On the elective course, in a differentiated or individual form, the studied material is deepened by varying and combining the mastered algorithms when solving problems of a search nature. Such work, in turn, creates the basis for mastering various heuristic procedures by gifted students, which, in particular, further contributes to their successful participation in Olympiads at various levels.

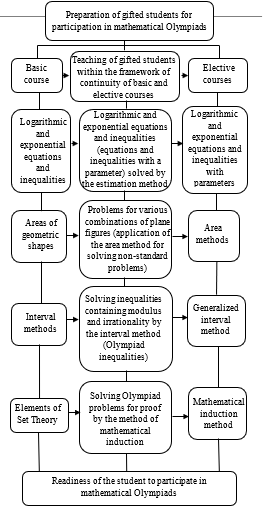
Figure 1: Continuity of Basic and Elective Courses in the Preparation of Students in Grades 4-5 for Olympiads in Mathematics

For example, within the framework of the basic course, the traditional topic “Method of intervals” is studied. Here we touch upon square inequalities, cubic inequalities, inequalities of higher degrees, fractional rational inequalities solved by the interval method based on the sign placement rule. Within the framework of the elective course “Selected Issues of Mathematics”, it is advisable to consider the generalized method of intervals, which is used, in particular, in solving irrational and trigonometric inequalities, as well as inequalities containing unknowns under the module sign, unknowns in the exponent, inequalities containing logarithms of the type:

The consideration of such inequalities is directly based on the material of the basic course, while providing for the variable application of the known algorithm.

At the same time, tasks of a search (Olympiad) nature are beginning to be involved, which are an example of tasks of an even more generalized nature.

Problem: For what values of the parameter ? among the solutions of the inequality , will there be two solutions, the difference between which is equal to 4?

When solving this problem, obviously, the generalized method of intervals is used and the analysis of all possible cases of the state of the considered mathematical construction is carried out, depending on the value of the parameter a. Accordingly, when analyzing a possible solution path, it is advisable for the teacher, if necessary, to rely on the material of the basic mathematics course, projecting it onto a higher level of generalization of the content.

Irrational and trigonometric inequalities are included in the curriculum for mathematics in high school. Here they are considered to be inequalities, the solution of which, depending on their complexity, is carried out by the method of intervals both at the basic and advanced levels (in the elective course), as well as in preparation for the Olympiads. The method of intervals in various modifications is used at all stages of the study of inequalities, providing a connection, in the context under consideration, between the relevant substantive sections of the basic and elective courses.

The interval method can be used in solving irrational inequalities of a certain type, subject to the appropriate restrictions arising from the properties of the arithmetic root of the nth degree. The algorithm for using this universal method is well known.

6. Model of preparation of gifted children in mathematics

Based on the idea of purposefully ensuring the continuity of basic and elective courses, we have built and implemented a methodological model for working with gifted students in mathematics (Table 1).

Table 1: Model of Preparation of Gifted Children in Mathematics

Purpose: Creation of conditions for the development of mathematical abilities of gifted students, their self-development, the harmonious development of the personality of a unique child; ability to independently acquire and apply knowledge
Tasks:	1.       Identification of gifted students in the field of mathematics 2.       Development of methodological support for the effective development of the mathematical abilities of gifted students, providing for the continuity of various forms of their preparation 3.       Implementation of mathematical training of schoolchildren, aimed at achieving socially and personally significant results 4.       Approbation and monitoring of the proposed methodological solutions
Principles of building the educational process of gifted students
The principle of rational combination of various forms of work with gifted children, the principle of differentiation and individualization of the learning process, the principle of student-centered learning, the principle of advanced learning, the principle of openness, the principle of adequate control, the principle of democracy, the principle of reflection
The content of work with gifted children in mathematics		Profile course When teaching gifted children in mathematics, the existing programs of specialized courses and relevant textbooks are involved
		Elective course When teaching children gifted in mathematics, topics are considered that deepen the relevant topics of the profile course, and topics that go beyond its scope (for example, the method of mathematical induction, graph theory, etc.)
		Project work When working on an individual project, attention is paid to topics that go beyond the core and basic courses, topics that affect the relationship of mathematics with other areas of knowledge, non-standard solutions to standard tasks are considered (for example, the project “Ten ways to solve one quadratic equation”)
		Preparation for the Olympics When preparing schoolchildren for participation in the Olympiads, first of all, various sets of tasks are considered, which include non-standard tasks (e.g. coloring problems, double counting problems)
Forms and methods of organizing work with gifted children in mathematics
Forms of work organization 1.Standard school lesson as part of the basic course 2.Standard school lesson within the profile course 3.Elective courses in mathematics 4. Math events 5. Work on an individual project 6. Individual preparation for the Olympiads 7. As a result of work on all previous formats – participation in subject Olympiad			Dominant methods of organizing work 1.Discovery-based method 2.Partial discovery-based method 3. Problem-Based learning 4. Project-Based Learning
Expected learning outcomes for gifted students
1.      Successful participation of students in Olympiads and conferences 2.      Readiness to pass exams 3.      The formed ability of students to independently acquire and apply knowledge in the framework of project-based learning 4.      Increasing motivation to work on solving problem of a discovery-based method and partial discovery-based method nature
Criteria for success in working with gifted students
It is necessary to understand how much the student’s giftedness was enhanced, which is manifested in the following indicators of the student’s preparation: 1) can work with mathematical text, solve text problems of increased difficulty 2) can solve non-standard problems using heuristic methods 3) can solve problems of an increased level of complexity by various methods, choosing from them the more rational one 4) can effectively solve problems of an Olympiad nature 5) has high-level thinking according to Bloom’s taxonomy, has high levels of cognitive ability: a) identifies hidden (implicit) assumptions in the problem, evaluates the significance of the data (analysis) b) uses knowledge from various fields to make a plan for solving a non-standard problem (synthesis) c) has the ability to evaluate particular mathematical material, that is, he can select and study in-depth material based on different criteria (evaluation)

As can be seen from this table, the formulation of this model is guided by the principles of a rational combination of various forms of work with gifted children, differentiation and individualization of the learning process, student-centered learning, advanced learning, openness, democracy, reflection and adequate control.

Let us briefly explain the content of the last three principles in our understanding (the content of the rest is obvious).

The principle of openness implies an approach to the subject of study as potentially open, allowing constant expansion and generalization by connecting initially non-obvious meaningful relationships.

The principle of democracy presupposes the right of the student to voluntarily choose the level and the corresponding form of education that he considers most acceptable.

The principle of reflection implies the need for the teacher to constantly monitor the nature of the interaction of a gifted student with peers, his behavior in situations of success and failure. In the course of devising a problem, it is necessary to carry out an ongoing adjustment of the individual plan for the training and education of a gifted student.

Finally, the principle of adequate control presupposes a variety of diagnostic tools for assessing the mathematical training and development of gifted schoolchildren, which are not limited to existing regulatory documents (control and independent work, exam materials, competitions and Olympiads of various levels).

This diagram shows the dominant methods of working with gifted students, their relationship. We will reveal the essence of each of them. All these methods are based on the active discovery-based and creative activity of students.

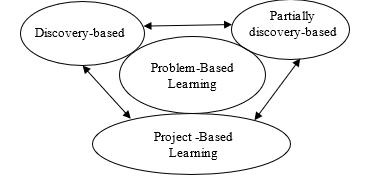
Figure 2: The relationship of various methods of working with gifted students

6.1. Partially discovery-based teaching method

In order to gradually bring students closer to independent problem solving, including non-standard tasks, it is necessary to first teach how to perform individual steps of solving a problem, individual stages of search [1, 2, 6, 29]. In this case, the partial discovery-based method of teaching should be used. It is necessary to offer students independent work with a mathematical text, to provide them with the opportunity to independently derive and formulate the basic mathematical concepts by means of a plan devised using heuristic conversation, well-known sources and their own search work. Another variant of this method is to break down a complex problem into a series of available subproblems, each of which makes it easier to approach the solution of the main problem. To complete a separate part of the task, a gifted student has to draw on knowledge from various branches of mathematics, which he could meet both when studying the basic program, and in elective classes. Thus, within the framework of this method, the teacher constructs a task, divides it into auxiliary ones, outlines the steps to find a solution to the problem. Students, on the other hand, perceive the task, comprehend its condition and solve part of the problem, actualizing the available knowledge and discovering the necessary information, exercising self-control in the process of arriving at a solution and self-motivating. But at the same time, the student’s activity does not involve planning the research stages and correlating the stages with each other. The partial discovery-based method is used within the framework of the basic course and elective classes.

6.2. Discovery-based teaching method

The next method that should be introduced into the process of teaching gifted students is the discovery-based method of teaching. Within the framework of this method, the activities of students target the independent resolution of practical problems that require creative solutions–hypotheses [1, 13, 30]. The teacher gradually moves away from drawing up a plan for solving problems, dividing them into subtasks, and invites gifted students to put forward their own hypotheses to find a solution. This method can be used both during the development of a profile course when solving problems of an increased level of complexity (for example, problems with parameters), and in the process of working on a student research project. This method is actively used in solving Olympiad problems. Initially, the student expresses a hypothesis for solving such a problem, and then builds his own small study to prove or disprove it. Also, this method will be appropriate when mastering new knowledge. An important role is played by independent experiments on the derivation of basic mathematical concepts and statements.

6.3. Problem-based Learning

Within the framework of the data of the problem-based method of teaching, a gifted student always faces a problem that requires a creative, heuristic approach to its solution [25, 31-33]. First, in the basic course, at the very beginning of the elective courses, the teacher himself puts forward small problem situations to the students, dividing the more complex ones. Further, the students themselves meet and recognize them, organizing their research activities to find solutions to these problem situations. With the help of the problem-based method of teaching, the skill of independent search work is formed, which helps in preparing for the Olympiads, when working on an individual research project. The problem-based method is also implemented in the process of participation by schoolchildren in various mathematical festivals and mathematical Olympiads. In these formats, a gifted student is constantly faced with a new, partially or completely unknown mathematical situation that requires a heuristic solution.

6.4. Project-based Learning

One of the most difficult methods for organizing the activities of schoolchildren is the project method. The essence of the project method is the solution of a problem based on the independent activity of students using appropriate methods, means, knowledge, including interdisciplinary, intellectual and practical skills, as well as the realization of creative potential to obtain a specific result [27, 34-35, 39].

 In our opinion, the use of projects as applied to gifted students, first of all, helps to maintain constant motivation for an in-depth study of mathematics. Students can choose an interesting topic for themselves, for example, explore different ways to solve one problem and study the proof of a little-known theorem. Thus, the student is constantly developing independently and expanding his knowledge with interesting mathematical facts primarily for himself [36-38].

The project method can also be used as part of a school lesson, an elective course, or an extracurricular activity. It is possible to offer schoolchildren the opportunity to independently acquire knowledge in solving practical problems and problems that require the integration of knowledge from various subject areas. Similar problems are encountered in preparing for examinations in mathematics.

Revealing the structural elements of Figure 2 and their relationship, we can conclude that the proposed system of methods is aimed at developing the research abilities of gifted students and their creative potential in solving non-standard problems. Each method can be implemented or partially implemented in different learning formats. That is, this system of methods is the main integration factor for various formats of training gifted students. Using a system of methods, it is possible to construct a diagram of the relationship between various teaching formats in the preparation of mathematically gifted students (Figure 3).

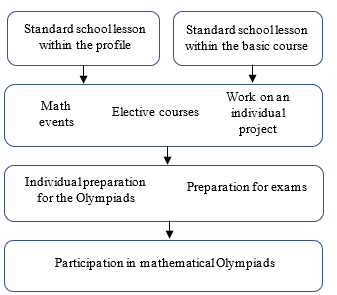
Figure 3: Relationship between different learning forms

7. Implementation of Model of Preparation of Gifted Children in Mathematics

The constructed model was used by us over a period of two years, working as mathematics teachers with gifted students at the Abulfazl Balami gymnasium for gifted children in the city of Vahdat, Republic of Tajikistan.

Let us briefly outline the strategy we employed.

First, during the lesson we observed how students solved partially algorithmic problems and identified which students were potentially capable of mathematics. These students were further involved in attending mathematical circles, where they tried their hand at school-level Olympiads.

If a student developed a sufficiently persistent interest in mathematics, and significant progress in the development of his abilities was evident, then he entered specialized classes. The persistent interest of students was seen in the process of students solving non-standard tasks [33]. The desire to solve such tasks, and, most importantly, the success in applying heuristic methods showed progress in the development of the abilities of the gifted students. Here they more purposefully, in parallel with the lessons of the profile course, continued their studies in the classroom of elective courses. For the most successful students, we developed a special learning plan that involved additional training activities and consultations in addition to elective classes.

In addition to the training of gifted schoolchildren immersed in subject mathematical activity, we made special efforts to ensure that all schoolchildren were constantly involved in joint communicative activities with classmates. In particular, in the classroom they could act as consultants on the subject, constantly participating in school competitions, concerts, sports events. This practice contributed to the development of the communicative abilities of schoolchildren, their emotional and volitional sphere, and reduced the risk of manifestation of possible difficulties in productive interaction with peers and adults around them.

Thanks to such an organization of the educational process, as our experience showed, non-standard abilities of schoolchildren developed and improved quite successfully, which was partially confirmed by the results of examinations and Olympiads.

In more detail, the methodological features of the implementation of this model are reflected in methodological materials we created and published in several articles.

Table 2 presents examples of some individual educational plans that we have built for gifted schoolchildren, as well as the first results of schoolchildren studying within the framework of the constructed model (Table 2).

Table 2: The Results of Work within the Framework of the Constructed Model

Student A – Grade 3 Works within the framework of the model for 1 year	Student B – Grade 4 Works within the framework of the model for 2 years
Forms of study: 1. standard school lesson within the framework of the basic course 2. elective courses 3. mathematical events Results: 1. shows interest in solving non-standard problems 2. Olympiads winner	Forms of study: 1. standard school lesson within the framework of the basic course 2. elective courses 3. individual preparation for the Olympiads 4. participation in mathematical Olympiads Results: 1. can solve problems of an increased level of complexity by various methods, choosing the most rational one 2. has high-level thinking according to Bloom’s taxonomy, that is has high levels of cognitive ability 4. has a strong interest in learning mathematics 5. Olympiads winner
Student C- Grade 5 Works within the model for 2 years	Student D- Grade 6 Works within the model for 2 years
Forms of study: 1. standard school lesson within the framework of the basic course – 2. elective courses 3. individual preparation for the Olympiads 4. participation in mathematical Olympiads Results: 1. can solve problems of an increased level of complexity by various methods, choosing the most rational one 2. has a strong interest in the study of mathematics 3. goes to the final rounds of level Olympiads 4. is the winner and prize-winner of the final rounds of level Olympiads	Forms of study: 1. standard school lesson within the framework of the basic course – 2. elective courses 3. individual preparation for the Olympiads Participation in mathematical Olympiads 4. preparation for the profile Results: 1. can solve problems of an increased level of complexity by various methods, choosing the most rational one 2.  has high-level thinking according to Bloom’s taxonomy, that is has high levels of cognitive ability 3. has a strong interest in advanced mathematics 4. goes to the final rounds of level Olympiads 5. is the winner and prize-winner of the final rounds of level Olympiads 6. claims for high scores in the profile

A pedagogical experiment to determine the possibilities of the proposed strategy for the training of gifted students, based on a rational combination of various formats of such training, was carried out over a two-year course of mathematical training of gifted schoolchildren in the Abulfazl Balami gymnasium for gifted children in the city of Vahdat, Republic of Tajikistan and a number of educational organizations in Dushanbe. In total, 41 students of the basic and senior levels of education were included in the experimental sample. The control groups in the study included two classes, in one of which (26 students) the dominant format for preparing gifted students was a series of elective courses devised by the authors. In the other the leading factor in training was individual consultations with specialists (15 students).

The data collection methodology included an analysis of the performance of current diagnostic work, including tasks of increased complexity, as well as taking into account the achievements of schoolchildren participating in the study in mathematical Olympiads of municipal, regional and republican status. In particular, the readiness of schoolchildren to solve non-standard tasks of increased difficulty using heuristic methods, their ability to find and compare different methods of performing the same task and to perform Olympiad tasks of a research nature were assessed. The evaluation of the results was carried out using the traditional five-point scale. The generalized result was considered as an average score for all diagnostic work. Students who received marks in the interval (2;3] were assigned to the first (low) level; in the interval (3;4] to the second (middle) level, and in the interval (4;5] – to the third (highest) level.

The received ordinal data at the pre- and post-implementation stages in the experimental and control groups were subjected to qualitative and quantitative analysis.

At the initial stage, the differences between the groups according to the selected levels proved to be unreliable. Statistical processing using the non-parametric fit method  – Pearson showed that the empirical values of the Pearson criterion when comparing the distributions of estimates in pairs in three samples proved to be lower than the corresponding critical values for given sample sizes. This fact indicates a relatively similar distribution of gifted schoolchildren by levels of success.

Experimental work within the framework of the ongoing study was carried out for two years. The experimental group studied according to the authors’ model described above. For one control group the teacher used elective courses only. For the second control group the teacher used individual consultation only. The educational material in different formats in the control groups did not specifically correlate in any way either, in the program or in the procedural aspect.

As a result of experimental training, control measures were again carried out. A comparison of the dynamics of changes in success in the selected groups of students showed that over the same time interval in the experimental classes, about 40% of schoolchildren moved to a higher level of success, while the number and composition of students at each level in the second and third groups changed less significantly (Table 3).

Table 3: Results of Pedagogical Experiment

Level	After the experiment
	Experimental group		Control group 1		Control group 2
	Quantity	%	Quantity	%	Quantity	%
Initial	8	19	10	42,3	8	66,7
Medium	15	35,7	10	38,4	2	6,7
High	19	45,2	6	19,2	5	26,7

Statistical processing using the non-parametric fit method — Pearson showed that the empirical values of Pearson’s criterion in a pairwise comparison of the distributions of estimates in three samples turned out to be higher than the corresponding critical values for given sample sizes. When comparing the experimental sample and the first control sample, the following empirical value of the –Pearson criterion was obtained =8.2. The corresponding critical value at ρ≤0.05 is significantly less than the empirical one (5.991). Similar results were obtained when comparing the experimental sample and the second control sample. Thus, after the use of the authors’ model in the experimental group, students showed significant improvement in comparison with students in the two control group which used other approaches.

Due to the largely individual nature of work with gifted children, the generalized results of this diagnosis, in our opinion, cannot be considered an absolutely reliable indicator of the effectiveness of the study. Therefore, we also carried out an expert assessment of the study materials as an additional diagnostic technique. It was attended by 18 experienced mathematics teachers working in specialized mathematics classes. Their survey showed that the vast majority of teachers confirmed the feasibility and prospects of the proposed methodological solutions.

8. Conclusion

The problem of training gifted students is now becoming particularly relevant. Purposeful provision of such training involves the development of a number of methodological solutions relating, in particular, to the rational correlation in the educational process of the relevant content, methods and teaching resources.

When considering this, we analyzed regulatory and policy documents, programs in mathematics of basic and elective courses for specialized mathematical classes, scientific and scientific-methodical works of leading domestic and foreign experts in the field of developmental psychology, didactics, theory and methodology of mathematical education, as well as existing textbooks, teaching aids, methodological recommendations and software for educational purposes. In addition, a longitudinal observation was made of mathematics courses for gifted schoolchildren in a number of educational institutions and a survey was conducted of mathematics teachers working in specialized classes. The survey revealed the difficulties that arise when studying in these classes. As a result of this work, it was discovered that the majority of the teachers surveyed indicated, for the most part, that there is insufficient interaction of various formats of mathematical training of gifted students, which does not ensure its integrity.

The following relatively new results were obtained.

1. The authors’ model of teaching gifted schoolchildren in mathematics has been developed and theoretically substantiated. The model includes components that reflect the content, forms and methods of working with gifted children in the framework of the main and optional courses.
2. The main methods of working with gifted children in mathematics classes which ensure their active search and research and creative activity are disclosed. The “mechanism of their interaction” in the educational process is also disclosed.
3. A holistic strategy for the work of a mathematics teacher with gifted children has been determined, encompassing classes within the framework of basic and elective mathematical courses, work on individual projects, participation in mathematical holidays and preparation for mathematical Olympiads. All of these formats are integrated into the individual educational routes of each of the students, ensuring the quality of their mathematical preparation and a high level of intellectual development.
4. Various options for constructing individual educational routes were identified and tested in the implementation of the developed strategy, depending on the stage of teaching mathematics. The implementation of these options formed the basis for the development of methodological materials and recommendations for the preparation of gifted students, taking into account the continuity of basic and optional mathematical courses.

A pedagogical experiment to determine the possibilities of the proposed strategy for the training of gifted students based on a rational combination of various formats of such training. was carried out in the course of a two-year subject mathematical training of gifted schoolchildren in the Abulfazl Balami gymnasium for gifted children in the city of Vahdat (Republic of Tajikistan) and a number of educational organizations in Dushanbe. During the experiment, the educational and developmental capabilities of three models of mathematical training of gifted children were compared: one experimental group and two control groups, in which the relationship of related formats of teaching mathematics was not specifically taken into account. As a result of experimental training, a pairwise comparison of the degree of change in success in the selected groups of students showed that for the same time interval in the experimental classes, 40 % of the students moved to a higher level of success, while the number and composition of students at each level in the control groups changed less significantly.

In general, it can be concluded that empirical learning based on the methodological determinants and recommendations outlined above proved to be feasible and quite effective within the framework of the current regulatory formats. This is evidenced, in particular, by a fairly large number of schoolchildren participating in Olympiads of various levels, and high scores in examinations. This result was also confirmed by the results of an expert evaluation of the proposed methodological solutions by mathematics teachers working in specialized mathematical classes.

As a further development of our work, we are considering the development of an adaptive pedagogical technology for working with gifted students, which will contribute to the development of their mathematical abilities, as well as provide for effective learning to solve Olympiad problems. For teachers, this technology will help build an individual learning plan for each gifted student, naturally updating his cognitive activity.

1. A. G. Balım, “The Effects of Discovery Learning on Students’ Success and Inquiry Learning Skills,” Eurasian Journal of Educational Research, Issue 35, 1-20 Spring 2009, 2009.
2. L. Alfieri, P.L. Brooks, N.J. Aldrich, H. R. Tenenbaum, “Does discovery-based instruction enhance learning?” Journal of Educational Psychology, 103(1), 1–18, 2011, doi.org/10.1037/a0021017.
3. J. Gallagher, Teaching the gifted child (2nd ed.). Boston: Allyn and Bacon. 1975.
4. S. Assouline, A. Lupkowski-Shoplik, Developing Math Talent. Texas: Prufrock Press, 2011.
5. F. Barron, Creativity and the gifted. In New directions for gifted education. Report on bicentennial mid-year Leadership Training Institute. Los Angeles: National/State Leadership Training Institute on the Gifted and Talented, 1976, doi.org/10.1177/001698628002400306
6. C.P. Benbow, L. L. Minor, “Cognitive profiles of verbally and mathematically precocious students: Implications for identification of the gifted,” Gifted Child Quarterly, 34(1), 21–26, 1990, doi.org/10.1177/001698629003400105.
7. D. Bogoyavlenskaya, V. Shadrikov Working concept of giftedness. (2nd ed). M., Progress, 2003.
8. G. Davis, S. Rimm, Education of the gifted and talented (5th ed.). Boston, MA: Allyn & Bacon, 2004.
9. F. Gagné, “Transforming gifts into talents: The DMGT as a developmental theory,” In N. Colangelo & G. A. Davis (Eds.), Handbook of gifted education (3rd ed., 60–74). Boston, MA: Allyn & Bacon, 2003.
10. L. Vygotsky, Imagination and creativity in childhood. St. Petersburg, SOYUZ, 1997.
11. M. Hoeflinger, “Developing mathematically promising students,” Roeper Review, 20(4), 244–247, 1998, doi.org/10.1080/02783199809553900.
12. E. P.Torrance, Guiding creative talent. Englewood Cliffs, N. J.: Prentice-Hall, 1962.
13. G. A. Goldin, “Mathematical creativity and giftedness: perspectives in response,” ZDM 49, 147–157, 2017 doi.org/10.1007/s11858-017-0837-9.
14. F. Barron, Creative Person and Creative Process, Holt, Rinehart & Winston, New York, 1969.
15. J. Gilford, Three sides of the intellect. Psychology of thinking. M., Progress, 1965.
16. C. W. Taylor, “Cultivating simultaneous student growth in both multiple creative talents and knowledge,” In J. S. Renzulli (Ed.), Systems and models for developing programs for the gifted and talented, 306–351, 1986.
17. E. P. Torrance, “Growing up creatively gifted: A22-year longitudinal study,” Creative Child and Adult Quarterly, 5(3), 148–158, 1980.
18. E. Torrance, J. Khatena, “Originality of imagery in identifying creative talent in music,” Gifted Child Quarterly, 13, 3-8, 1969, doi.org/10.1177/001698626901300101.
19. C. Lombroso, The Man of Genius. London: W. Scott, 1891.
20. J. Guilford, The nature of intelligence. New York: McGraw-Hill, 1967.
21. S. Rubinshtein, Fundamentals of general psychology. M, Uchpedgiz. 1940.
22. A. Karp, “Knowledge as a manifestation of talent: Creating opportunities for the gifted,” In B. Sriraman (Ed.), Creativity, giftedness, and talent development in mathematics (209–224). Charlotte, NC: Information Age Publishing, 2008, https://www.diva-portal.org/smash/get/diva2:1390686/FULLTEXT01.pdf.
23. T. Hirano, “Achieving mathematical excellence in Japan: Results and implications,” Journal of Educational Research, 25(6), 545-551, 1996, doi.org/10.1016/S0883-0355(97)86731-6.
24. K. Heller, A. Lengfelder, German Olympiad study on math, physics and chemistry. Paper presented at the American Educational Research Association, New Orleans, 2000, doi.org/10.1080/02783193.2011.530202.
25. C. E. Hmelo-Silver, H. S. Barrows, Goals and Strategies of a Problem-based Learning Facilitator. Interdisciplinary Journal of Problem-Based Learning, 1(1), 2006, doi.org/10.7771/1541-5015.1004.
26. R. Campbell, H. Walberg, “Olympiad Studies: Competitions Provide Alternatives to Developing Talents That Serve National Interests,” Roeper Review, 33(1), 8-17, 2011, doi.org/10.1080/13803610701785949
27. Y. Terada, Boosting student engagement through project-based learning. Edutopia, 2018.
28. K. Tirri, “Finland Olympiad Studies: What factors contribute to the development of academic talent in Finland,” Journal of NACE., 5(2), 56-66, 2001.
29. J. Boaler, “Promoting ‘relational equity’ and high mathematics achievement through an innovative mixed-ability approach,” Br. Educ. Res. J. 34, 167–194, 2008 doi.org/10.1080/01411920701532145.
30. D. P. Wolf, The art of questioning. Academic Connections, 1987.
31. A. Benson, D. Blackman, “Can research methods ever be interesting?”, Active Learning in Higher Education 4(1), 39-55, 2003, doi.org/10.1177/1469787403004001859.
32. C. H. Chen, Y. C. Yong, “Revisiting the effects of project-based learning on students’ academic achievement: A meta-analysis investigating moderators,” Educational Research Review, 26, 71–81, 2019, https://www.learntechlib.org/p/207141/.
33. S. Cho, H. Lee, “Korean gifted girls and boys: What influenced them to be Olympians and non Olympians,” Journal of Research in Education, 12(1), 106–111, 2002.
34. D. Kokotsaki, V. Menzies, A. Wiggins, “Project-based learning: a review of the literature,” Improving schools., 19(3). pp. 267-277, 2016, doi.org/10.1177/1365480216659733.
35. A. Mettas, C. Constantinou, “The Technology Fair: a project-based learning approach for enhancing problem solving skills and interest in design and technology education,” International Journal of Technology and Design Education, 18, 79-100, 2007, doi.org/10.1007/s10798-006-9011-3.
36. J. Brunstein, Achievement motivation (H. Heckhausen, Ed.). In J. Heckhausen & H. Heckhausen (Eds.), Motivation and action (137–183). Cambridge University Press, 2008, doi.org/10.1017/CBO9780511499821.007
37. A. Conley, “Patterns of motivation beliefs: combining achievement goal and expectancy-value perspectives,” Educ. Psychol. 104, 32–47, 2012, doi.org/10.1037/a0026042
38. C. S. Dweck, Self-theories: Their role in motivation, personality and development. Philadelphia, Psychology Press, 1999.
39. S. K.W. Chu, S. K. Tse, K. Chow, “Using collaborative teaching and inquiry project-based learning to help primary school students develop information literacy and information skills,” Library & Information Science Research, 33, 132-143, 2011, doi.org/10.1016/J.LISR.2010.07.017.

(Click Here)