1. Introduction

Based on previous contribution [1], this paper is an extension of the original work which aims to ensure a robust attitude stabilization of a quadrotor subject to stealthy actuator attacks. The modelling and control aspect were considered in this first contribution, where in the following the observer design for both state and stealthy attacks is added. Robust polytopic state feedback stabilizing controller based on PDC (Parallel Distributed Compensation) polytopic framework observer with disturbance attenuation (guaranted by the H_∞ norm) for the obtained uncertain system is also considered.

Design and implementing feedback control strategies that are robust against cyber-attacks is of critical importance nowadays. Assuming that the behavior of the system is driven via actuator commands, the actuator data deception attack corresponds to a manipulation of an attacker on the communication channels between the plant and the controller. The actuator commands are then corrupted and it becomes necessary to integrate this data in the control system design and make it as robust as possible to these stealthy attacks.

The objective is then the design of a resilient control for a system where an attacker corrupts control packets; and of course, to detect and reduce/attenuate the effect of these corrupted signals on the well-behaviour of the considered system.

In the following contribution, the novelty comparing the work originally presented in [1] is about the estimation and robust control part where both state and stealthy attacks are now estimated with an H_∞ disturbance attenuation property.

One solution in order to represent and implement heuristic knowledge to control nonlinear systems when remaining the study relatively simple consists in the use of the polytopic Takagi-Sugeno (T-S) structure. Indeed, this representation was initially proposed by [2] and [3], and proven its efficiency in various applications in the past decades [4].

Based on the polytopic T-S approach, a number of most important issues in control systems have been addressed in the past few years. These includes stability analysis [5], state and output feedback control [6], [7], performances and robustness [8], [4], as well as recently cyber-security [9]–[12].

Solving the considered problem (H_∞ control of stabilization), the nonlinear behavior of the quadrotor, including stealthy attacks, is represented in terms of an uncertain poly topic system subject to bounded external disturbances. The stabilization and robust H_∞ control, based on state estimation feedback is then deduced based on classical Lyapunov theory leading to a set of matrices inequalities (constraints) to solve. These constraints, solvable through convex optimization techniques allows to obtain poly topic controllers and observers that guarantee both stability and robustness of the closed loop system.

Indeed, this paper focuses on the problem of observer-based H_∞ control for polytopic T-S systems under actuator data deception attacks. Sufficient conditions for the simultaneous controller and observer design with a desired H_∞ disturbance attenuation level are derived in terms of linear matrix inequalities wich can be easily solved by using available software package (Matlab for example).

The present paper objective is to contribute to the cybersecurity and resilience design of Unmanned Aerial Vehicles (UAVs). It is known that the wireless control used to monitor drones makes them defenceless to a large variety of cyberattacks, which may have severe consequences on the system behaviour/security/integrity/performances.

In this contribution, stealthy attacks disturbing and destabilizing the control and navigation system of the UAV are studied. We aim to propose a robust control ensuring the safety and security of the UAv despite these assaults.

This contribution strategy was previously developed for cyberattacks estimation [1], [10] and is now adapted to the quadrotor robust control. The estimation of the system states and stealthy signals will be given.

Considering the estimable premise variables, the attacked system will be presented as an uncertain T-S model. Based the resulting system, a PDC observer based control will be designed.

The paper organized as follows: a brief state of the art is presented in section 1; the system modelling with the actuator data deception attack and the uncertain system representation are detailed respectively in section 2 and 3. Section 4 is about the robust output H_∞ observe-based T-S controller. Section 5 is about the approach illustration through an application to quadrotor attitude stabilization with simulation results. The final section, 6 is about conclusion and perspectives.

The applied methodology solving the considered problem is the following:

1. The modelling aspect: such that the nonlinear behaviour and threats attacks are both represented in a polytopic T-S form based on the sector nonlinearity transformation (SNT); it is important to note that in this representation, there is no approximation or any loose of information. The main advantage of this method consists into an exact rewriting of the original nonlinear equations.
2. In order to be able to implement the state feedback observer based PDC H_∞ control law, the main constraint in the obtained model (5) is about the immeasurable state and timevarying parameters present in the weighting functions h_i & µ_j, and the control law. In order to overcome this difficulty, it is imperative to standardize the system equations in order to have only measurable and/or estimable premise variables. For that, an uncertain representation of the system equations (5) is proposed in section 3 in order to obtain a more convenient model for the study; i.e. (19).
3. Based on the chosen structure for the observer and control law, a robust H_∞ T-S control of the nonlinear system is considered in section 4. The objective, in addition to the system stabilization, is to ensure an attenuation of the external perturbation, guaranteed thanks to the H_∞
4. The final step of our study would be the application of the developed approach to our case study; i.e. the attitude stabilization of the quadrotor.

2. System Modelling: a Polytopic representation

In the following section, based on the nonlinear state space model of a system, a polytopic representation will be deduced applying the sector nonlinearity approach (SNT).

Assuming that our system is subject to actuator data deception attacks (modeled as unknown, but bounded, multiplicative timevarying parameters); our nonlinear model under these attacks may be represented by the following state space system equations:

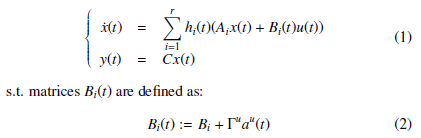
In this model, B_i is called the nominal input matrix (i.e. when none attack occurring); Γ^u is known as the binary incidence matrix, which indicates the data channels that can be accessed by the attacker; finally a^u(t) represents the actuator data corruption signal. The stealthy signals a^u(t) are unknown (in terms of value), but bounded (limits assumed to be known) a^u(t) ∈ [a₂^u,a₁^u]. Applying the SNT transformation, the following representation is proposed:

3. Uncertain System Representation

Based on contributions [11] and [12], where the data deception representation of cyber-attacks via a time-varying model and thanks to a polytopic form of an uncertain system representation, a state and actuator data deception attacks observer is proposed and given by the following equations:

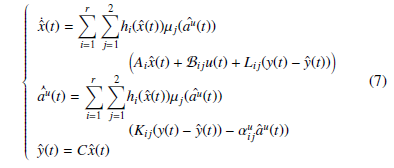
s.t. Lij ∈ R nx×m, Kiju ∈ R n×m and αuij ∈ R n×n are solution of a LMI–H∞₂ attenuation conditions ensuring both estimation errors for the states and malicious input parameters to converge to zero. Let us now define the estimation errors e_x(t) and e_au (t) (for the state and cyber-attacks) as:

Using the above definitions (12)-(17), system (11) is then written as an uncertain system given by:

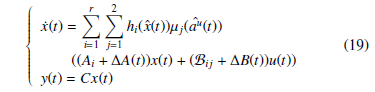
4. Robust Output H_∞ T-S Control

The objective in the following section is to determine polytopic T-S controller and observer gains ensuring that:

• The system given by (19) is asymptotically stable in the presence of data deception attacks.
• The attenuation of the external perturbations like (i.e. actuator attacks) is guaranteed by the H_∞ i.e. find for a given scalar γ > 0, an observer (7) and a PDC controller (20) such that the attenuation condition (26) is satisfied. The resulting conditions to be solved will be given in Lemma 2.

Considering the nonlinear system subject to data deception attacks given by the system equations (1), and the polytopic T-S observer to estimate the unmeasurable state variables and unknown time-varying parameter (actuator attack signal a^u(t)) given by system equations (7) with the following PDC (Parallel Distributed Compensation) controller defined by:

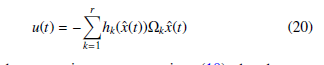
By combining the uncertain system equations (19), the observer equations (7), the polytopic PDC controller and the estimation errors definitions (8), the following uncertain system with bounded external disturbances is obtained:

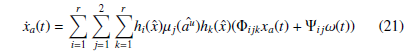
s.t. x_a(t) = x(t) e_x(t) e_au (t) represents the augmented (extended) state vector; ω(t) =  a^u(t) a˙^u(t) ^T represents the exogenous input (signal attack a^u(t) and its derivative), supposed unknown but bounded.

Before presenting the stabilization and control conditions, the following definition and lemma are remembered:

Definition 1 Given a positive scalar γ, the system equation (24) is said to be stable with H_∞ attenuation level γ if it is exponentially stable with:

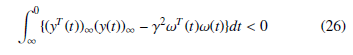
where γ is the desired level of disturbance attenuation.

Lemma 1 Based on Lyapunov theory, the continuous-time system

(24) is stable with an H_∞ disturbance attenuation γ if there exists a positive symmetric matrix P = P^T > 0 s.t.

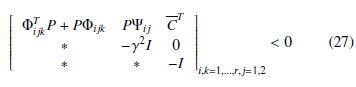
In order to relax the stability conditions given in Lemma 1, the following formulation is proposed [14], [4]:

Lemma 2 [15] For a given positive scalar γ, if there exist matrices

P, Z_ijk, where P = P^T > 0 and Z_iji are symmetrical, Z_kji = ^Z_ijk^T , i , k, i,k = 1,…,r, j = 1,2 satisfying the following matrix inequalities, then for the uncertain polytopic T-S system (19), the controller (20) makes the H_∞ norm of fuzzy system (24) less that γ

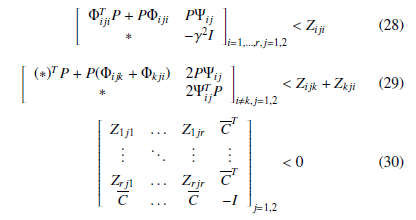
By replacing Φ_ijk and Ψ_ij by their expressions, with some change of variables and classical linearization procedure (Schur’s complement and bounded real lemma), the obtained constraints can be easily solved using convex optimization tools and/or the use of a dedicated resolution tool for bilinear constraints like the PenBMI Matlab toolbox (see [16], [17] and [18] for some examples). The proposed solution presents the advantage of a simultaneous design of both the controller and the observer gains using a single-step procedure rather that a classical two-steps procedure of resolution like the one presented in [19].

5. Numerical Example

In the following, let us consider the study case of a dynamic modeling and control for quadrotor. The objective of this work is to ensure the quadrotor safe behaviour and stabilization via an observer based control design. Indeed, stealthy actuator attacks aiming to disturb and destabilize the control and navigation system of the UAV are here considered. These attacks are modeled as unknown but bounded time-varying signals affecting the system matrix B(t).

The first step to this aim will be the quadrotor Polytopic modelling; then, considering the actuator stealthy attacks, the resulting system (attacked one) will be written as an uncertain one, as detailed in previous sections . The proposed control and observer design approach will be then applied to illustrate the its efficiency thanks to simulation results.

5.1. Polytopic Model of a UAV

In this section, we address the polytopic T-S modelling of a UAV. The considered representation is used in order to rewrite the nonlinear behaviour of the quadrotor into a polytopic-Multiple Model way, without any linearisarion, loss of information or approximation. The nonlinear dynamic of the quadrotor is given by the following model:

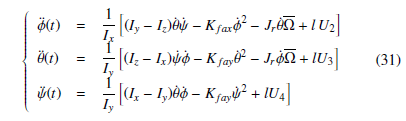
s.t. Ω is given by Ω = ω₁ − ω₂ + ω₃ − ω₄. The motors control inputs, denoted U_i,i = 1,2,3,4, are given as a function of the rotors angular velocities as follows:

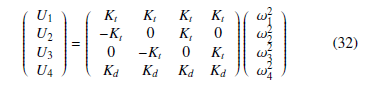
The angles (given in [rad]), ϕ, θ and ψ represent the Roll, Pitch, and Yaw angles respectively. We denote the moment of inertia among axes x, y and z as I_x, I_y andI_z respectively. J_r, K_t and K_d are the rotor inertia, propeller thrust and drag coefficients and K_fax, K_fay, K_faz the frictions’ aerodynamic coefficients. Interested readers can see [1] and [20] for more calculation details. From the SNT tranformation, the nonlinear system model (31) can be in a straightforward way written as a quasi-LPV model given by:

Presuming that the variation of angular velocities occurs between known minimum and maximum values, and applying the SNT approach [2], [5], [7], when choosing the following premise variables:

z₁(t) = ϕ,˙ z₂(t) = θ,˙ z₃(t) = ψ˙ the resulting polytopic model is then deduced:

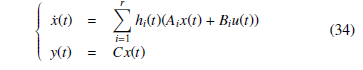
5.2. Uncertain System Modelling under Attacks

In the previous subsection, and for the nominal case (no attacks), the polytopic model of the quadrotor-UAV (34) was deduced from its nonlinear dynamics. In the following, the data deception signal will be included and, the global system under attacks will be represented as an uncertain system.

The quasi-LPV system (34) under actuator attacks may be represented as the following:

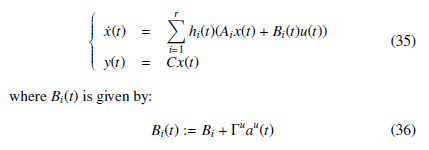
Based on the results presented in section 3, the system and attacks observer is given by the system equations (7), and the nonlinear system subject to actuator attacks is modeled thanks to system (19). The objective now is to apply the proposed approach in order to design the robust control law (20) and the observer gains.

5.3.  Simulation results

The designed observers and controller are implemented and tested through a numerical simulation of a quadrotor robust attitude stabilization despite stealthy actuator data deception attacks.

The design goals and the controller structure (20) based on the state feedback control law is applied to the the nonlinear system equations (33) and (35) subject to the actuator stealthy attacks (36). The control gains are obtained by applying the developed polytopic approach given in Lemma 2 and solving the LMI constraints (28), (29) and (30).

The resulting figures illustrate the stability, robustness and convergence of the system states regarding the attacks.

The state, their estimates and estimations error are illustrated in the following figures:

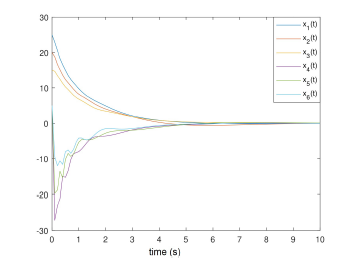
Figure 1: System states estimation errors

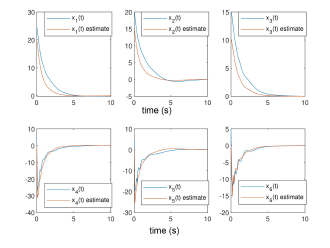
Figure 2: System states estimation errors

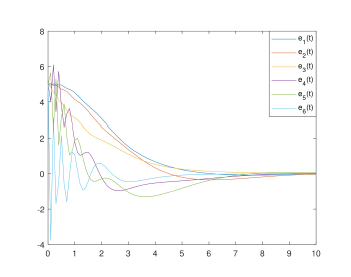
Figure 3: System states estimation errors

The stealthy attack signal a^u(t) and its estimate is represented in figure 4.

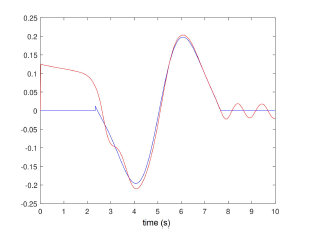
Figure 4: Stealthy attack signal From the obtained results, one can conclude to the effectiveness of the proposed approach.

Indeed, the system states (angles and velocities) are converging asymptotically despite the stealthy attacks (unknown behaviour), where the estimation errors for both states and data deception attacks tend to zero for the state and with an attenuation level γ for the stealthy signal.

6. Conclusion

This paper contribution aimed to propose a polytopic Takagi-Sugeno strategy for the modelling and H_∞ robust control of a quadrotor subject to stealthy actuator attacks. The attacked UAV system under attacks was modeled as an uncertain polytopic T-S fuzzy one; which allowed us to generalize existing results for the state feedback observer based control design.

The nonlinear system was represented under an uncertain shape (with observable premise variables) allowing the implementation of the observer and control design. The attenuation of the external like perturbation (attack) was guaranteed thanks to the H_∞ norm. Numerical simulations were given in order to illustrate the effectiveness of the proposed approach. As an extension of this work, a real application example is also under investigation.

Conflict of Interest

  The author declares no conflict of interest.

1. S. Bezzaoucha Rebai, ”Robust Attitude Stabilization of Quadrotor Subject to Stealthy Actuator Attacks”, in the 2022 International Conference on Control, Robotics and Informatics (ICCRI), Danang, Vietnam, April 2-4, 2022, doi: 10.1109/ICCRI55461.2022.00018.
2. T. Takagi, M. Sugeno, ”Fuzzy identification of systems and its applications to modeling and control”, IEEE Transactions on Systems, Man and Cybernetics 15(1), 116-132, 1985, doi 10.1109/TSMC.1985.6313399.
3. M. Sugeno, G. Kang, ”Structure identification of fuzzy model”, Fuzzy Sets and Systems, 28(1), 15-33, 1988, https://doi.org/10.1016/0165-0114(88)90113-3.
4. A. Benzaouia, A. El Hajjaji, ”Advanced Takagi-Sugeno Fuzzy systems, Delay and saturations”, Studies in Systems, Decision and Control 8, 2014, Springer books, https://doi.org/10.1007/978-3-319-05639-5.
5. K. Tanaka, H. Wang, ”Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach”, Ed Hardcover, John Wiley and Sons, Inc., New York, 2001, doi:10.1002/0471224596.
6. K. Tanaka, T. Ikeda, H. Wang, ”Fuzzy regulators and fuzzy observers: relaxed stability conditions and LMI based designs”, IEEE Transactions on Fuzzy Systems 6(2), 250-265, 1998, doi: 10.1109/91.669023.
7. K. Tanaka, T. Hori, H. Wang, ”A Multiple Lyapunov Function Approach to Stabilization of Fuzzy Control Systems”, IEEE Transactions on Fuzzy Systems 11(4), 582-589, 2003, doi: 10.1109/TFUZZ.2003.814861.
8. T. Guerra, A. Kruszewski, L. Vermeiren, H. Tirmant, ”Conditions of output sta- bilization for nonlinear models in the Takagi-Sugeno’s form”, Fuzzy Sets and Systems 157(9), 1248-1259, 2006, ttps://doi.org/10.1016/j.fss.2005.12.006.
9. S. Bezzaoucha, H. Voos, M. Darouach, ”A contribution to Cyber-Security of Networked Control Systems: an Event-based Control Approach”, in 3rd Interna- tional Conference on Event-Based Control, Communication and Signal Process- ing, Funchal, Madeira, Portugal, 2017, doi: 10.1109/EBCCSP.2017.8022805.
10. S. Bezzaoucha Reba¨ı, H. Voos, ”Stability Analysis of Power Networks under Cyber-Physical Attacks: an LPV Descriptor Approach”, in the 6th International Conference on Control, Decision and Information Technologies, Paris, France, 2019, doi: 10.1109/CoDIT.2019.8820425.
11. S. Bezzaoucha Reba¨ı, H. Voos, ”Simultaneous State and False-Data Injection Attacks Reconstruction for NonLinear Systems: an LPV Approach”, in the 3rd International Conference on Automation, Control and Robots, ICACR2019, Prague, Czech Republic, 2019, doi: 10.1145/3365265.3365280.
12. S. Bezzaoucha Rebai, ”A Cyber-Security Contribution to Estimation and Event- Based Control Scheduling Co-Design for Polytopic and T-S Fuzzy Models Using A Lyapunov Approach”, Springer Nature – International Journal of Fuzzy Systems, 2022, https://doi.org/10.1007/s40815-022-01282-3
13. S.Bezzaoucha, B. Marx, D. Maquin, J. Ragot, ”Nonlinear joint state and parameter estimation: Application to a wastewater treat- ment plant”, Control Engineering Practice, 21(10), 1377-1385, 2013, https://doi.org/10.1016/j.conengprac.2013.06.009.
14. L. Xiaodong, Z. Gingling, ”New approaches to H∞ controller design based on fuzzy observers for T-S fuzzy systems via LMI”, Automatica 39(9), 1571-1582, 2003, doi: 10.1016/S0005-1098(03)00172-9.
15. M. Oudghiri, M. Chadli, A. El Hajjaji, ”One step procedure for robust outpur fuzzy control”, in the 15th meditarranean conference of control automation, Athens, 1-6, 2007, doi: 10.1109/MED.2007.4433964.
16. M. Kocvara, M. Stingl, ”PENNON – a code for convex nonlinear and semidef- inite programming”, Opt. Methods and Software, 18(3), 3170-333, 2003, https://doi.org/10.1080/1055678031000098773.
17. M. Kocvara, M. Stingl, ”PENBMI, Version 2.0”, See www.penopt.com for a free developer version, 2004.
18. D. Henrion, J. Lofberg, M. Kocvara, M. Stingl, ”Solving polynomial static output feedback problems with PENBMI”, Proceedings of the 44th IEEE Conference on Decision and Control, 7581-7586, 2005, doi: 10.1109/CDC.2005.1583385.
19. J. Lo, M. Lin, ”Observer-based robust H∞ control for fuzzy systems using two-steps procedure”, IEEE Trans Fuzzy Systems, 12(3), 350-359, 2004, doi: 10.1109/TFUZZ.2004.825992.
20. F. Torres, A. Rahbi, D. Lara, G. Romero, C. Pe´gard, ”Fuzzy State Feedback for Attitude Stabilization of Quadrotor”, International Journal of Advanced
    Robotic Systems, InTech, 2016, https://doi.org/10.5772/61934.

(Click Here)