1. Introduction

The quality of a data digital transmission [1]-[3]. Largely depends on the number of errors introduced via the transmission channel. Error control by coding technique is important. Indeed, this technique called “channel coding”[4]-[6], permit both detection and correction of possible transmission errors by using error-correcting codes such as RS codes (Reed-Solomon.) [7], [8] BCH (Bose, Ray-Chaudhuri and Hocquenghem) [9], [10] and LDPC (Low-Density -Parity-Check) [11] .

However, the “channel coding” technique [12], [13] uses a very complex decoding mechanism requiring a very large number of logic gates, which influences the response time.

The main aim of this work is to develop, concept and simulate a new architecture for RS and BCH codes to reduce the number of iterations in the syndrome block using a new method based on the factorization technic (factorization method: we develop and factorize the equation corresponds to the syndrome block, the basic circuit is transformed into a new circuit which the inputs are parallel). Other points are noted like a summary of Reed Solomon codes is furnished in chapter 2. chapter 3 talks about the proposed algorithm that uses a new syndrome Block .Finally comparison of the basic and the proposed circuits for various RS codes is presented in chapter 4, ended with a conclusion

2. Reed Solomon Code

The RS (255,239) code [14] has length n = 2⁸-1= 255 so m = 8, which imply that the Galois field contains 256 symbols (m = 8), where the polynomial of an element in the Galois field can be represented as:

The symbols are 8 bits. It is thus constructed from the Galois Field GF (2⁸) [15]. The control symbols is N-K=16, t=N-K=2t=8 symbols correctable by N-bit words. The correction power therefore corresponds to a maximum of 64 bits since each symbol is on 8 bits.

The efficiency of this code is given by is:

The symbols used in RS codes are:

• t=corrected errors number.
• n= total number of symbols
• K= symbols of message.
• (n-k) = detected errors number
• t= detected errors number

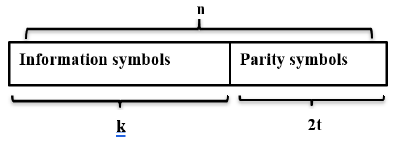
Figure 1: Reed Solomon code word structure

3. Galois Field Properties

The principal properties of a Galois field [16] are:

• Two operations characterize the Galois Field: addition and multiplication.
• The result of addition or multiplication of Galois field elements allows us an element in the same field.
• For each element m in the field, “zero” is the Identity of addition, such that m + 0 = m.
• For each element m in the field, “one” is the Identity of multiplication, such that m * 1 = m.
• For each element m in the Galois field, n is an inverse of addition element such that m+n = 0.
• For each element m ≠ 0 in the Galois field, n⁻¹ is an inverse of multiplication such that n*n⁻¹ =1.
• Addition and multiplication operations should verify the laws of commutative, associative and distributive. Galois Field GF (2m) Knowing that Galois field [17] can be considered a general case to Binary Field. We hypothesize that we want to generate a finite field GF (q) where q a prime number. For the Galois field GF (2⁸) = 256 symbols composed of 8 bits. GF (2⁸) = (0, α0, α₁, α₂, α₃, α₄ ……………. α₂₅₄)

The corresponding primitive polynomial is:

This allows us to construct the elements of Galois fields GF (255).

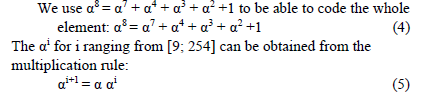
4. Proposed of a new architecture for Syndrome Block

The proposed algorithm [18][19] of the Reed-Solomon code RS (255, 239) used in DVB-T has 86 iterations, while 256 iterations using the existed method .This algorithm is based on the new syndrome block to reduce the number of iterations with a percentage which can reach 40% compared to the existing algorithm.

Basic syndrome computation block   a) Case  of the basic  circuit for RS (15,11)

The basic syndrome computation block for RS (15, 11) is expressed by the equation 6.

In the equation 6, the circuit corresponding shown in the figure2:

Figure 2: Basic syndrome block for RS (15, 11)

7. b) Case of the basic circuit for RS (63,53) The basic syndrome computation block for RS (63, 53) is expressed by the equation 7.

In the equation 7, the circuit corresponding shown in the figure 3:

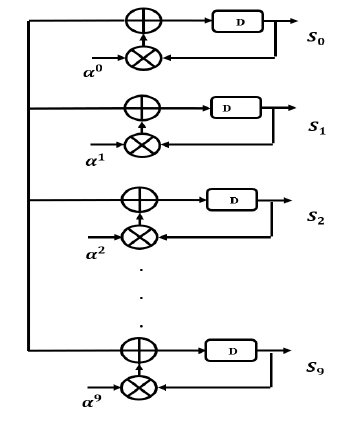
Figure 3: Basic Syndrome block for RS (63, 53)

The proposed Syndrome Computation Block

1. a) Case of the proposed circuit for RS (15,11) Using both equations 7 and 8, we can calculate all coefficients of syndrome block polynomial [20]:

Si  = R(αi) = r14 (αi)14 + r13(αi)13 + ⋯ r1(α1) + r0      (7)

Where i = 1, 2, 3. . . 2t.

The proposed Syndrome computation Block calculated by this equation:

Si  = R(αi) = ((… . (r14 (αi)2 + r13(αi)1 + r12(αi)3 + r11(αi)2

+ r10(αi)1 + r9(αi)3 + ⋯ r2(αi)2 + r1(αi)

+ r₀)                                                              (8)

The first clock, the mot received in parallel is (r₁₄, r₁₃, r₁₂).

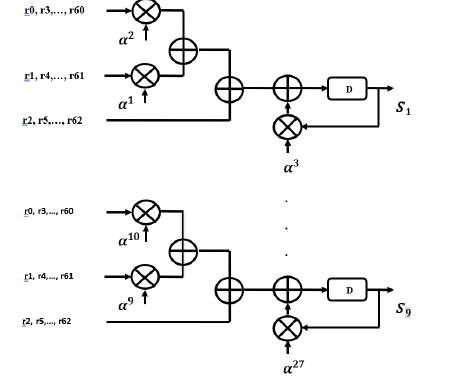
Figure 5: Proposed syndrome block for RS (63, 53)

1. c) Case of the Proposed circuit for RS (255,239) For the case of the RS (255,239) we have: n-k = 2t = 16 syndromes.

For calculate of the example the syndrome S₁ we have the circuit:

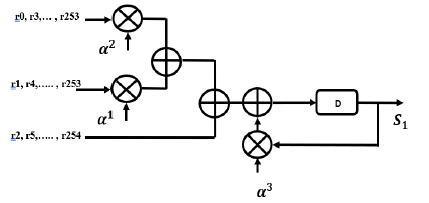
Figure 6: Proposed syndrome block for RS (255,239) We generally use the following circuit:

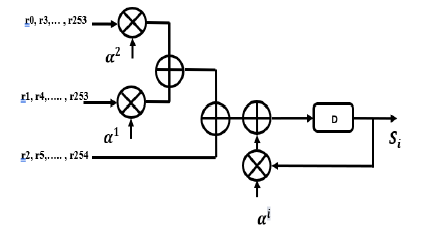
Figure 7:  Proposed syndrome block for RS (255,239)

5. Comparison of circuits and performance analysis Comparison of Circuits

For the table 1.Shows the number for the basic, the proposed and the gained iterations for different Reed Solomon codes:

Table 1. Comparison of the basic and proposed circuit for different Reed

Solomon codes

Code N°	Code Name	Number of iterations for the basic circuit (Nb)	Number of iterations for the proposed  circuit (Nm)	Number of gained iterations
1	RS (15, 11)	16	6	10
2	RS (63, 55)	64	22	42
3	RS (255, 239)	256	86	170
4	RS (1023, 1019)	1024	342	682
5	RS (3240, 3070)	3241	1081	2159
6	RS (4095, 4091)	4096	1366	2730
…	…..	….	…..	……
n	RS (n, k)	Nb+1	(Nm/3) + 1	Nb – Nm

In the table 1 the Reed Solomon RS (255, 239) code used 256 iterations for the basic syndrome block, while just 86 iterations for the modified method .This algorithm use the new syndromes blocks to reduce the number of iterations. This method also reduces energy consumption with apercentage that can reach 33% compared to the existing algorithm.

Performance analysis

Proving the performance of the proposed algorithm, we fulfill an important number of checks in context of syndrome block for different RS code; different parallel syndrome block is tested.

The figure 8 represents the different RS codes of the parallel syndrome block.

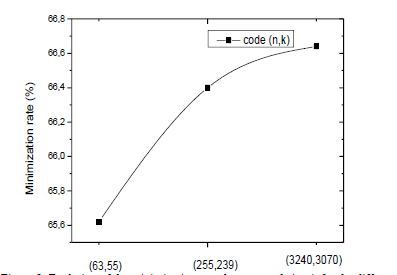
Figure 8: Evolution of the minimization rate the proposed circuit for the different RS codes.

6. Simulation results

The simulation of the basic and proposed syndrome block using the hardware description language VHDL [21] for the RS and BCH decoders are presented in this party.

Simulation the basic circuit of RS (15, 11)

The simulation of the developed and basic syndrome bloc is presented in this part for the RS and BCH decoders. Thus, simulation results on the tested scenario show that the proposed system is very effective and achieves high performance in the minimization rate. The Simulation result of RS (15, 11) is shown in the figure 9. The Simulation result of the modified RS (15, 11) is shown in the figure 10.

7. FPGA implementation

Implementation of decoder algorithms for Reed-Solomon codes [22], [23] can be considered as a problematic cases on account of  the very large amount of used electronic elements in order to implement the new  algorithm on FPGA card to discuss how to save the hardware resources [24], [25] .In this paper a new hardware model of the Syndrome Block has been concepted and developed using the programming Language (VHDL) and implemented using Xilinx Synthesis Tool. The circuit scheme of the implemented program is shown in Figure11.

Figure 9: Simulation result of the basic decoder (15, 11).

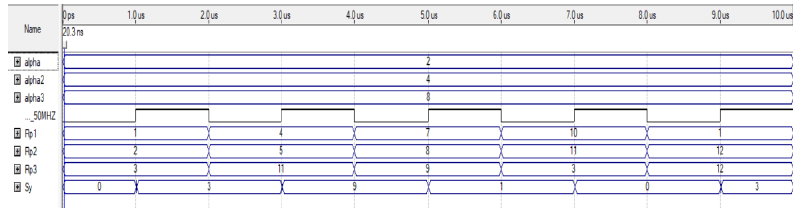
Figure 10: Simulation result of the modified decoder RS (15, 11)

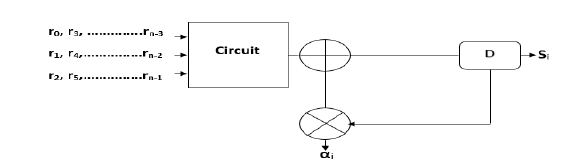
Figure11: Block diagram of Syndrome Block

The proposed Syndrome Block consists of a global ‘Clk’ and Three Parallel Inputs initiate the calculating Syndrome Block process, the ‘result’ can be obtained immediately after entering inputs.

Syndrome Block

The calculation of the syndrome block furnishes us two results: 1- all syndrome polynomial coefficients are equal to zero, in this case we stop the rest of the decoder process because the received code word is correct, 2- if one of polynomial coefficients is different to zero, the code word is erroneous, so we continue the process of the decoder. We need 2t basic scheme as defined in Fig.12.Where 1≤i≤2t, or for each Syndrome Si, n iterations are needed to calculate the polynomial coefficients.

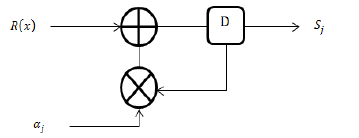
Figure12: Basic syndrome calculator cell

Test procedure for RS (15, 11)

The proposed algorithm has been implemented on a FPGA Card using Xilinx Spartan 3E-500 to verify the test setup which presented in figure13. For the case of RS (15, 11), we have four coefficients of syndrome Block (S₀, S₁, S₂, S₃). In Fig.13, the value is equal to 15 (S₀ =15) in decimal, (1111) in binary, so we can get the same result with only 5 iterations in comparison with the basic circuit.

The code specified for DVB-T

The Digital Video Broadcasting-T standard defines RS (255, 239, 8) code, a main version is proposed to generate (204, 188, 8) code, this code contain 204 symbols, where 188 represent the symbols of message [8]. The Galois field of RS (255, 239) code has 256 symbols (m=8) so we can represent the polynomial of a field element as: a7 x7 + a6 x6 + a5 x5 + a4 x4 + a3 x3 + a2 x2 + a1 x1 + a0      (9)

Where the polynomial generator for t = 8, can be presented as:

 P(x) = x⁸ + x⁴ + x³ + x² + 1                                                              (10)

For the case of RS (255, 239) used in Digital Video Broadcasting-T standard, the decoder detects 2t=16 errors and corrects t=8 errors.  Test procedure for RS (255, 239) The proposed algorithm has been implemented on a FPGA Card using Xilinx Spartan 3E-500 to verify the test setup which presented in figure14.

Figure 14: Value of Syndrome block for RS (255, 239) codes

For the case of RS (255, 239), we have four coefficients of syndrome Block (S0, S1, S2, S3). In Figure 14 the value is equal to 186 (S0 = 186) in decimal, (10111010) in binary, so we can get the same result with only 5 iterations in comparison with the basic circuit.

8. Conclusion

A recent algorithm of syndrome block for Reed-Solomon RS and BCH codes has been presented in this paper. This algorithm presents a new syndrome computation block with a view to minimize the number of iterations. The proposed algorithm has been generated, simulated, implemented on the FPGA card and compared to the existed one to demonstrate the difference between the two circuits and the number of reduced iterations, the comparison between circuits in table 1 proves that the RS code (255, 239) has 256 iterations using the modified method while, 86 iterations using the basic method.

Conflict of Interest 

The authors declare no conflict of interest.

Acknowledgments

This work was supported by the Laboratory of Electrical System, Transmission of Information, Mechanics and Energetics, Faculty of Sciences, Ibn Tofail University Kenitra, Morocco.

1. R. Huynh, N. Ge, H. Yang, “ A Low Power Error Detection in the Syndrome Calculator Block for Reed-Solomon Codes: RS(204,188) ”, Tsinghua Science and Technology, 14(4), 474‑477, 2009, doi:10.1016/S10070214(09)70105-1.
2. Y.J. Tang, X. Zhang, “ Fast En/Decoding of Reed-Solomon Codes for Failure Recovery ”, IEEE Transactions on Computers, 71(3), 724‑735, 2022, doi:10.1109/TC.2021.3060701.
3. V. Torres, J. Valls, M.J. Canet, F. García-Herrero, “ Soft-decision lowcomplexity chase decoders for the RS(255,239) code ”, Electronics (Switzerland), 8(1), 1‑13, 2019, doi:10.3390/electronics8010010.
4. R.T. Chien, “Cyclic Decoding Procedures for Codes », IEEE Transactions on Information Theory, 10(4), 357‑362, 1965.
5. P.D. Surkar, S.D. Ninawe, “ VLSI Design of Syndrome Computation Block for RS ( 255 , 239 ) Code ”, 5248‑5254, 2016, doi:10.15680/IJIRSET.2016.0504130.
6. D.S. Reay, T.C. Green, B.W. Williams, “ Field programmable gate array implementation of a neural network accelerator ”, IEE Colloquium (Digest), (61), 1994.
7. R. Martinek, J. Zidek, “ The implementation of channel coding into the digital transmission chain consisting of VSG PXI-5670 – VSA PXI-5661 ”, Przeglad Elektrotechniczny, 89(7), 64‑68, 2013.
8. W. Ji, W. Zhang, X. Peng, Y. Liu, “ High-efficient Reed-Solomon decoder design using recursive Berlekamp-Massey architecture ”, IET Communications, 10(4), 381‑386, 2016, doi:10.1049/iet-com.2015.0500.
9. Y.H. U, M.R. Hiremath, “ Implementation of BCH Code (n, k) Encoder and Decoder for Multiple Error Correction Control ”, International Journal of Computer Science and Mobile Applications, 2(5), 45‑54, 2014.
10. S.S. Sonawane Vaishali Baste, “ Implementation of RS-CC Encoder & Decoder using MATLAB”, IJSTE-International Journal of Science Technology & Engineering |, 5(7), 22‑30, 2019.
11. C. Sahana, V. Anandi, “ INTERNATIONAL JOURNAL OF ENGINEERING SCIENCES & RESEARCH TECHNOLOGY ERROR DETECTION USING BINARY BCH (255, 215, 5) CODES Sahana C*, V Anandi ”, 4(6), 1113‑1118, 2015.
12. P. Trifonov, V. Miloslavskaya, C. Chen, Y. Wang, “Fast encoding of polar codes with reed-solomon kernel”, IEEE Transactions on Communications, 64(7), 2746‑2753, 2016, doi:10.1109/TCOMM.2016.2576448.
13. M. Elghayyaty, O. Mouhib, A. Wahbi, A.A. Barakate, A.E.H. El Idrissi, L. Hlou, A. Hadjoudja, “ Performance comparison of new designs of chien search and syndrome blocks for BCH and Reed Solomon codes ”, International Journal of Communication Networks and Information Security, 12(2), 235‑241, 2020, doi:10.17762/ijcnis.v12i2.4562.
14. M. Elghayyaty, A. Wahbi, A. El Habti El Idrissi, O. Mouhib, L. Hlou, A. Hadjoudja, “ Conception and Hardware Minimization of a New Chien
    Search Block for Reed Solomon Codes With Implementation on Fpga Card ”, ARPN Journal of Engineering and Applied Sciences, 15(11), 1248‑1254, 2020.
15. D. Gunduz, “ Source and Channel Coding for Wireless Networks ”, (September), 2007.
16. J.L. Massey, “ Step-by-step decoding of BCH codes ”, IEEE Transactions on Information Theory, 11(3), 3‑8, 1965.
17. G.A. Hussain, L. Audah, “ BCH codes in UFMC: A new contender candidate for 5G communication systems ”, Bulletin of Electrical Engineering and Informatics, 10(2), 904‑910, 2021, doi:10.11591/eei.v10i2.2080.
18. E. Costa, S.V. Fedorenko, P.V. Trifonov, “ On computing the syndrome polynomial in Reed-Solomon decoder ”, in European Transactions on Telecommunications, 2004, doi:10.1002/ett.982.
19. Z.Y. Lam, W.L. Pang, C.P. Ooi, S.K. Wong, K.Y. Chan, “ VHDL modelling of Reed Solomon decoder ”, Research Journal of Applied Sciences, Engineering and Technology, 4(23), 5193‑5200, 2012.
20. M. Prashanthi, P. Samundiswary, “An Area Efficient (31, 16) BCH Decoder for Three Errors ”, International Journal of Engineering Trends and Technology, 10(13), 616‑620, 2014, doi:10.14445/22315381/ijett-v10p323.
21. Z. Gao, L. Zhang, Y. Cheng, K. Guo, A. Ullah, P. Reviriego, “ Design of FPGA-Implemented Reed-Solomon Erasure Code (RS-EC) Decoders with Fault Detection and Location on User Memory ”, IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 29(6), 1073‑1082, 2021, doi:10.1109/TVLSI.2021.3066804.
22. J. Samanta, J. Bhaumik, S. Barman, “ FPGA based area efficient RS(23, 17) codec ”, Microsystem Technologies, 23(3), 639‑650, 2017, doi:10.1007/s00542-016-3058-1.
23. C. Engineering, M. Prashanthi, P. Samundiswary, M. Tech, “ An Enhanced (15, 5) BCH Decoder Using VHDL ”, International Journal of Advanced Research in Electrical, Electronics and Instrumentation Energy, 2014(11), 2014.
24. K.M.M. Chennaiah, K. Prasadbabu, S. Ahmedbasha, “ IMPLEMENTATION OF BCH LFSR ENCODER DECODER ”, 5(1), 21‑30, 2017.
25. P. Mathew, L. Augustine, S. G, T. Devis, “ Hardware Implementation of (63, 51) Bch Encoder and Decoder for Wban Using LFSR and BMA ”, International Journal on Information Theory, 3(3), 1‑11, 2014, doi:10.5121/ijit.2014.3301.

(Click Here)