1. Introduction

This paper is an extension of a work initially presented at the In- ternational Conference on Recent Advances in Mathematics and Informatics (ICRAMI) [1]. The main objective is to contribute to attracting attention to the importance of the quantum computer in the future for those who now use classical computers in all their dif- ferent fields or who work in the development of technology and the computer industry and anyone related to this advanced technology. To be convincing, an example of a spy hunter simulation will be presented and discussed. The relevance of using quantum computers in image processing security will also be presented and discussed. The impact of using multilevel or ternary quantum systems com- pared to binary quantum systems will be presented to argue their advantage in minimizing the memory size in image processing.

The technological evolution of the processors has considerably improved their efficiency, namely the calculation time and the energy consumption. However, the processor’s physical core is changing qubit instead of the bit, by studying quantum physics.

Studying quantum physics and aiming to make it representative of the information will help us conceive the quantum computer and use it efficiently. Following that idea, several laboratories invest budgets in research to have the first quantum computer and benefit from quantum physics.

Quantum physics history goes back to the 1940s and plays a central role in manufacturing computers’ electronic components. In 1982 [2], the author was the first to propose the concept of the quantum computer, and in 1986 by another paper [3], he confirmed his thought. However, quantum computing got its big break in the 1990s. The most important being that idea [4, 5], where the author used a quantum algorithm for the factorization of prime numbers of size n in a time O((n)3) and space O((log n)).

Another idea of a quantum algorithm in 1992 was developed [6], which did not have significant importance. But in 1996, another one [7], developed a quantum algorithm which consists in searching one√or more elements out of N elements within a time proportional as well as the nature of the data which will be represented by N, with a storage space which is proportional to logN.

Security requirements are essential for a secure transaction on a transmission canal using an asymmetric encryption algorithm. In- formation systems exchange data over the transmission canal using the RSA (Rivest-Shamir-Adleman) algorithm; since the encryption key is different from the decryption key, it is difficult to break the RSA keys.

So far, no one has been able to break RSA keys. Once we are in the era of quantum computers, it will be possible to factorize large numbers in a fast time and, consequently, RSA keys may be broken and the security of the information systems would be at risk. There- fore it will be necessary to think of a post-quantum cryptography [8].

Quantum Image Processing (QIP) using Quantum image-based data security techniques are more efficient and provide higher se- curity than conventional image processing. The processing speed and the amount of data processed in image processing are the most advantages guaranteed by QIP. The strength of this approach is subject to quantum physics rules which we do not have in classical image processing.

The rest of this paper is organized as follows. In 2, Literature review is presented. In 3, Basics of quantum computer are presented. In 4, Computation using Quantum computer will be described. In 5, The quantum computer and data security are presented. And finally, in 6 The conclusion.

2        Literature review

It is noteworthy that after a rising technological revolution, it has been quite a while since a scientific work on information processing using quantum physics was published [2, 3, 9].

In [10], the authors presented in their survey on quantum com- puting the basic components that are required to build a real quantum computer. They also have pointed out the basics of each capability to be translated from a classical environment to a quantum environ- ment and vice versa.

In [11], the authors proposed initial ideas and several schemes for quantum computing architectures that satisfy the physical con- straints; the architectures restrict the way to map the logical qubits used to describe the algorithm to the physical qubits to realize the corresponding functionality.

In a paper [12], the authors presented the difference between classical and quantum cryptography and have pointed out the im- plications of quantum computing in current cryptography and intro- duced the basic post-quantum algorithm and said that it deals with different quantum keys distribution methods and mathematically based solutions.

In [13], the authors discussed the connection between the strong by the quantum computer during computation, which decreases its efficiency. To minimize these errors, they suggested the deployment of quantum error-correcting code, and to achieve fault-tolerance, it will be important to make advancement in engineering.

In their work [16], the authors compared different methods of im- age storage, image representations and image retrievals in a quantum system. They have also presented and discussed the advancement in quantum image processing.

Another review article[17], the authors reported an outline of the QIMP as well as a diagnostic analysis of the enhancement of existing models of quantum image representations, the design of quantum algorithms to solve sophisticated operations, and the fur- ther development of physical hardware and software architecture to both capture and manipulate quantum images.

In a recent paper [18], the authors highlighted that a prominent example is secure communication and presented the cryptographic requirement of transmitting confidential messages from one location to another.

In [19], the authors presented in their work the possibilities that quantum mechanics can add to strengthen the cypher code to be unbreakable.

In [20], the authors discussed details in their work towards ap- plying quantum computation to image processing which can be improved through the application of Quantum Computing.

In a recent work [21], the authors presented in their paper the role of quantum mechanics on image and data processing, they presented three quantum algorithms for comparing the similarity between two quantum images and declared that their proposed algo- rithms achieve exponential acceleration than the existing quantum and classical methods in all three cases.

Table 1 represents a summary of the different works of the selected articles in literature in relation to our present paper.

3        Basics of a quantum computer

The item bit is the basic element for data representation in conven- tional computer science, which can only have one value among two values 0 or 1. In quantum physics, a third situation is possible, the qubit (quantum bit), which represents the new item for the basic element of data representation, can be in a superposition of two states |0⟩ and |1⟩ that can be represented by (1):

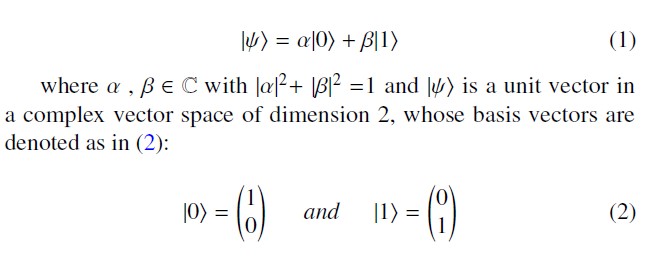
In [14], the authors reported on the relevance of using quantum computing in the biological sciences and how the problems posed by quantum algorithms in this area could provide increased computational efficiency, which was much lacking.

In [15], the authors mentioned that the major challenges faced in designing a quantum computer are related to the errors generated

A geometric representation in a three-dimensional sphere called Bloch Sphere [22] (see Figure 1), is used to describe many opera- tions of a single qubit, for multiple qubits, there is no generalization known of the Bloch sphere. In such a situation, in the whole sphere, we can have an infinity of information represented by an infinity of states.

Table 1: A Review Summary

——–Focused study Releted work        ——-	Quantum computer architecture	Quantum cryptogra- phy	Quantum       Image processing	Other Quantum in- terests
Paper [10]	✓
Paper [11]	✓
Paper[12]		✓
Paper [13]		✓
Paper [14]				✓
Paper [15]	✓
Paper [16]			✓
Paper [17]		✓
Paper [18]		✓
Paper[19]		✓
Paper [20]		✓
Paper [21]		✓
Present paper	✓	✓	✓

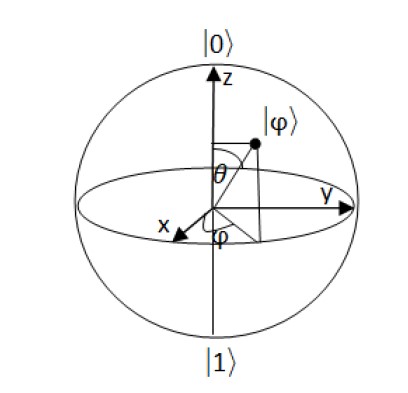
Figure 1: Qubit representation by Bloch Sphere

In computer science, all useful information is represented using a succession of bits of 0’s and 1’s in low-level codes that can be decoded using low-level to high-level transcription programs for different purposes, such as displaying, reading and writing or even other useful purposes, each bit has to be 0 or 1 but not both.

By using a superposition of two states |0⟩ and |1⟩, the qubit have

the qubit interaction with its environment. In [24], was mentioned five requirements, one of them being to minimize the interaction of the qubit with its environment, otherwise, the computation will collapse and then the complete system will collapse.

If we need a numerical analysis of the possible coherence time of a qubit, in an experiment [25], where the authors made atoms interact with photons one by one, measured the time it takes to observe progressive decoherence, and they obtained a time of about 100 µ seconds for only ten atoms, and this was considered too small to be measured which means that when we increase the number of atoms, the time will decrease exponentially and this will affect the coherence of the qubit.

For a given computation time and considering the microproces- sor’s technological evolution; with 100 µ seconds we can perform a lot of computations, but considering the gate’s latency, we will have to increase this time so that it is appropriate to a given computation. We can have a comparison with the frequency of a conven- tional processor to see how many quantum processes it can manage, for that purpose, we can convert the qubit coherence time into a frequency that we can obtain a ratio S _C/Q that we can calculate using (4); a number which represents the number of cycles that a

conventional processor can handle.

the potential to represent both values 0 and 1 at the same time in a state |ψ⟩ that can be noted in (3).

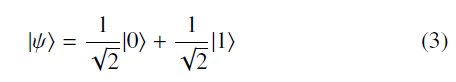
where:

• F_CP is the coventional Processor frequency,

In Equation (3), at the moment of measurement, the state |ψ⟩ will be |0⟩ with a probability equal to ( √1  )2  or |1⟩ with a probability

• F_DQub is the qubit decoherence rate,
• S _C represents the speed ratio between the conventional

equal to ( √2 ) , and this is known in quantum physics as decoherence [23], which has to be exactly the same bit case of coventional computer.

To make calculations using qubits, we must have to leave the measurement at the end to avoid losing the state superposition due to qubit decoherence, which means we must maintain the qubit coherence as long as possible, for this reason, we should eliminate the constraints that help the qubit decoherence and especially minimize /Q processor frequency and the qubit decoherence rate.

If we consider a conventional processor frequency of 3.2 GHz, and if we transform the qubit coherence time into a frequency, we will have 10 KHz. By using (4), we can calculate the ratio between the conventional processor frequency and the coherence frequency that gives us 320000 times faster, which means that the conventional processor can manage 320000 qubit’s cadencies (see Figure 2).

Figure 2: Illustration of cadency of S _C/Q qubits by a conventional processor rate time

To increase the number S _C/Q it is only sufficient to increase the frequency of the conventional processor, or to reduce the decoher- ence rate (i.e. to extend the decoherence time), and for that purpose Chapter 10 of the book [26] discusses various approaches to extend the decoherence time effectively.

The conventional computer’s technological evolution makes it possible to have the classical processor’s frequency increased. But it is a difficult mission to reduce qubit decoherence rate because it is not easy to isolate the qubit from its environment.

3.1    Concepts and Physical realization of the qubit and the quantum computer

To have a quantitative evaluation and to see the measurable size  of a qubit, in [27],The authors succeeded in fabricating a 60 µm qubit in a 6 GHz resonant system. The realized qubit is considered giant compared with the size of an atom, which means that with this qubit size, we have the horizon opened to the fabrication of quantum electronic chips that are also considerably larger than the size of an atom.

A qubit is a fundamental unit of data representation and a basic element of the quantum computer’s hardware architecture. This architecture, quite particular compared to the classical one, needs to meet certain engineering requirements to be able to engineer    a quantum computer. These requirements are linked to quantum physics specificities, which cannot be found in the classical one.

One of the relevant concepts in quantum physics is energy,  which forms discontinuous scales known as a quantum leap. In their experiment [28], by using Barium, the authors measured the quantum leap, which confirms that, by the quantum physics nature, an electron can occupy two energy levels at the same time; that is known as a states superposition.

For the concept of entanglement, where two electrons or two photons will be linked to each other; namely, if we act on one auto- matically we act on the other instantaneously, and if one chooses its state whether it is  0  or  1  the other one automatically is in   the opposite state. This phenomenon was described as strange and mentioned in a scientific paper [29] known as the EPR paradox, since no velocity, until today, is higher than the velocity of the light.

In a recent experiment [30], Chinese researchers, have proven and demonstrated that even at large distances (1203 km), photons were entangled.

For example, taking two superposed electrons where we have four possibilities  11  10  01   00  . The most relevant case is  10 01 called the entangled states, where the two electrons are irre- mediably linked to each other, when measuring one of them we necessarily interact with the other one, i.e. the entangled systems are linked each to other, and this is proved by experiments [30, 31].

4        Computation using Quantum computer

Computing with a quantum computer is quite different from com- puting with a classical computer. The entanglement and the super- position of the states of a qubit are very fragile that we can only make measurements at the end of the calculation for fear that the entanglement and the superposition of the states will collapse. To overcome this problem, we can use an ingenious solution which consists in duplicating thousands of copies of the qubit and making the calculation, two scenarios are to be considered; we check the calculation and it is good so we go ahead, otherwise, we stop it and start again.

When doing computations, we cannot escape from the compu- tational errors which are so far in the range of 1 , and by taking into account the number of qubits to be handled, we can expect to have one million of qubits to carry out an appropriate computation. If we assume having a decoherence time four times the time observed in the experiment [25], i.e. a decoherence time of 400

µ seconds, which represents a frequency of 2.5 kHz and let’s take (4) to calculate the quotient S _C/Q for a conventional processor fre- quency of 3.2 GHz, we obtain 1280000 cadences. If we duplicate copies of the qubits and we verify at a given moment if the calcu- lation is good or not, and let’s say that everything is good and that the calculation we are doing is correct without collapsing as shown in Figure 3, in this case, the total time T is equal to the time at the end of the computation, i.e. equal to the qubit decoherence, but if we were in the second case (see Figure 4), where the computation is not correct and therefore we stop it and start again, in this case, the total time is T1 and is different from T, it will be equal to m Conventional Processor instruction time, where m represents the number of repetitions.

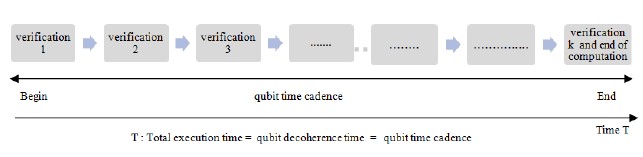
Figure 3: Time computation T: Computation verification without errors

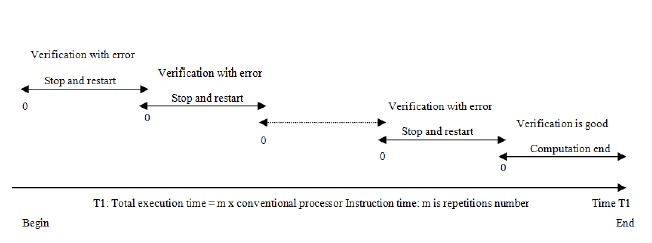
Figure 4: Time computation T1: Computation verification error with stop and restart

We point out that even though the calculation is correct, this does not mean that there are no errors; this is due to the probabilis- tic measurements and the superposed states that occur each with a probability. Also, the quantum computer runs on a different clock separated from that of a conventional computer.

Quantum programming cannot replace conventional program- ming completely, it is estimated only for solving some complex

problems that are difficult to solve using a classical computer. In [32], a list of 50 sample problems was compiled that may be inter- esting to use as examples for writing quantum programs.

Quantum computer can be considered as a co-processor for the conventional computer, in which our programs are divided into two different parts; a conventional programming part for the conven- tional computer side, and another quantum programming part for the quantum computer as shown in Figure 5.

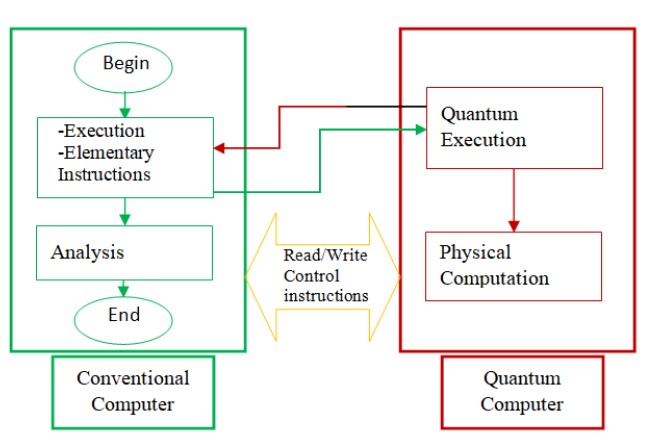
Figure 5: Illustration of two programming parts

5 The Quantum computer and data secu- rity

5.1          Internet Security and the RSA encryption method

Internet at high speed is difficult to define, as what constitutes ”high speed” changes over time as technology advances and applications develop. There are advantages and weaknesses in each technology. The final selection should attend to the specific requirements of the Internet application, mainly determined by the factors that affect Internet objectives: low power, low cost, high number of devices, and medium-long range [33]. The high-speed of the Internet has affected many areas, especially those that use it as a medium for communication and data exchange.

In the era of information technology, data exchange has rapidly progressed, especially with the availability of high-speed commu- nication such as the internet. However, data exchange is subject to hackers’ attacks to hack the information, which has led us to use technical solutions to protect our information systems as well as the data exchanged on the Internet.

The RSA encryption method [34, 35], is an asymmetric algo- rithm used to exchange data on the Internet. This algorithm depends on two keys: a public key and a private key. No one has been able to break these keys, but once we have the quantum computer, these keys may be compromised, and the information system will then be at risk.

To address this risk, we develop quantum cryptography methods to secure the information system and the data exchange algorithm. The technology used to design a qubit plays a huge role in the accuracy of computations performed with a quantum computer, but

the question arises seriously: is quantum computing accurate? In order to provide an answer, we need to look at one of the latest works done. In [36], the authors mentioned that quantum opera- tions are accurately characterized using gate set tomography (GST)

, resulting in average single-qubit gate fidelities of up to 99.95%, average two-qubit gate fidelities of 99.37%, and two-qubit prepa- ration/measurement fidelities of 98.95%. They precised that these three metrics are approaching the performance demanded in fault- tolerant quantum processors. which means that by the time the first generation of quantum computer appears, we will be able to achieve 100% accuracy.

To take advantage of quantum physics, we can benefit from the concepts of entanglement and superposition of qubit states, and since the measurement can only be performed at the end of the computation to avoid the system collapse. We have simulated an 8-qubits (i.e. a quByte) code, Based on the original sample code example [37], to illustrate how can we do to perform a secure data exchange.

The spy hunter continuously checks and tunes the transmission channel to get accurate information by hacking the data. They  use sophisticated tools and devices to get powerful that give them techniques to decrypt any data. With the quantum computer, spies can easily intercept and decipher data,  and it is of great interest  to understand quantum physics to know how to manage a secure transmission medium.

By capturing the data, they behave as if they had not caught   it and send it back to the receiver (Bob). When Bob receives the data, and before reading, Alice informs him that she had applied a quantum gate (and maybe a combination of quantum gates) to the data, and then Bob applies the inverse of the quantum gate to the received data and compares it with Alice’s data. If their data are identical, Bob and Alice conclude that the data has not been hacked, otherwise, they understand that it has been hacked.

In the case of applying quantum gates, and even if the hackers intercept the data, they will not be able to read it because they will never be able to guess the combination of quantum gates applied to the data before sending it.

Figure 6 represents the result of the simulation using QCEngine, and Figure 7 represents the result of the simulation using Qiskit.

For illustration presented on Algorithm 1, Alice wants to send some data to Bob (as example here data are an arbitrary information coded on 8 Qubits).

It is necessary to secure our information systems by thinking about post-quantum-cryptography solutions; i.e. working a lot in the technological field of quantum cryptography to prevent the RSA key from being broken because 1024-bit or even 2048-bit keys will be broken using quantum computers.

One day we will be in an era where the use of the quantum computer will be available to everyone, and then the spies of the computer will have the possibility to factorize long numbers, there- after, they will be able to break the RSA algorithm keys. However, we have seen from the presented example that it will be guaranteed to ensure the security of our information systems and the strength of the RSA keys, while based on the characteristics of quantum physics.

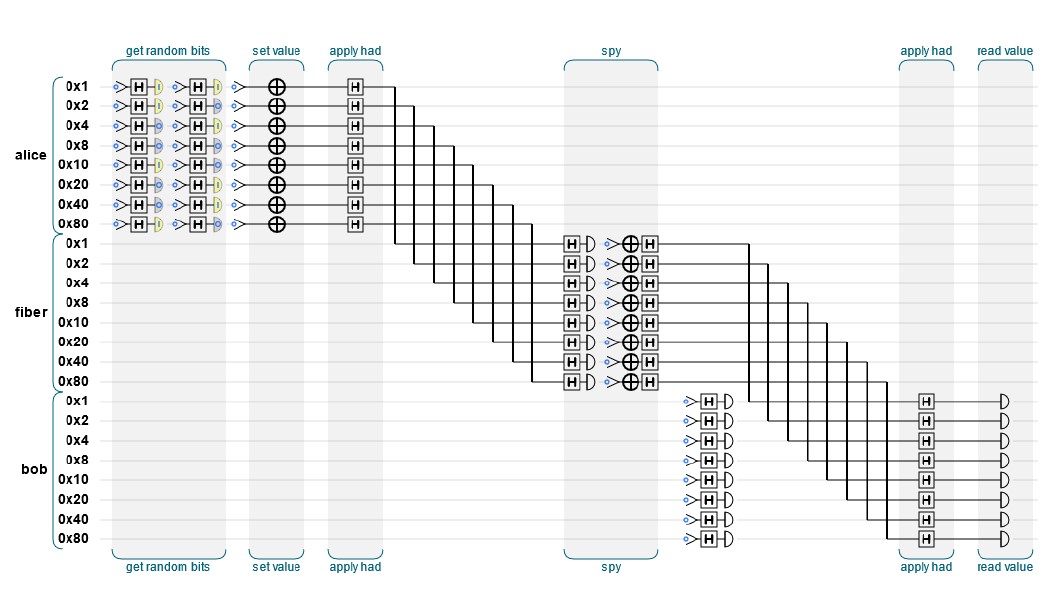
Figure 6: Illustration of spy hunter quantum program simulation using QCEngine

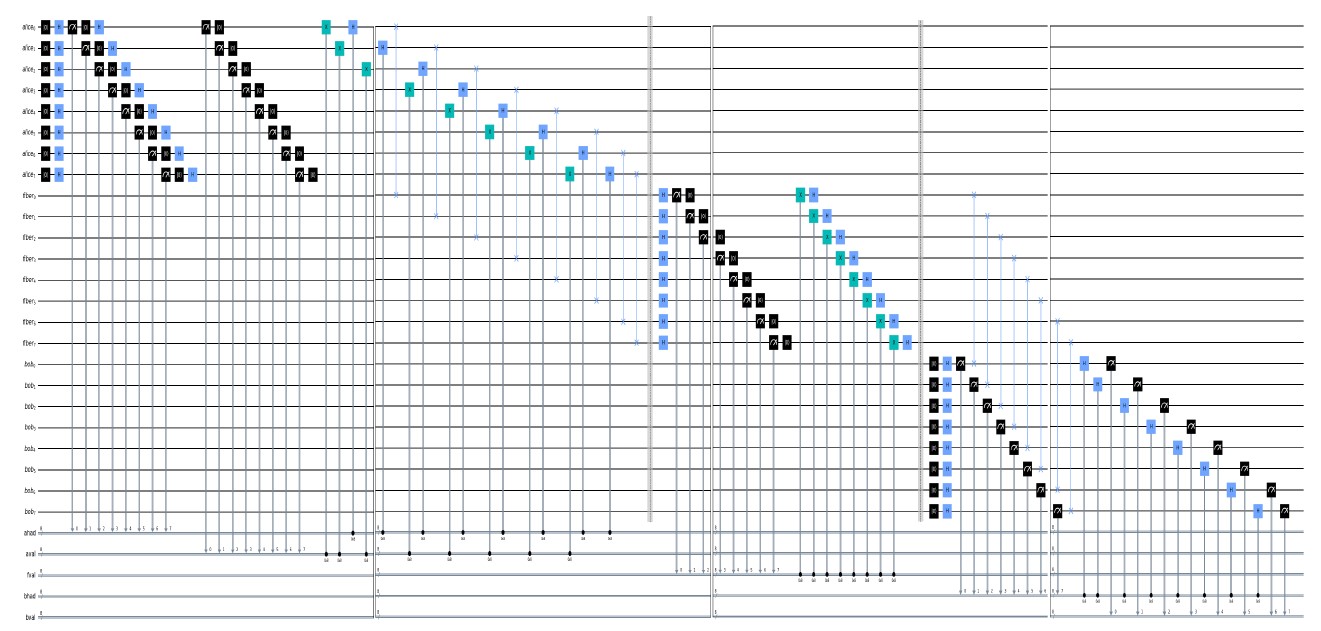
Figure 7: Illustration of spy hunter quantum program simulation using Qiskit

The field of quantum programming is expanding, and we look forward to the first real and commercialized quantum computer to apply everything we know as quantum algorithms, but we may state that this is only for certain applications that need fast solutions, and anything we use in a conventional computer, for example, Word or all our existing applications cannot be replaced by quantum programs.

5.2          Quantum Image Security

In cryptography, encryption is the process of hiding information to make it unreadable without special knowledge. In steganography or in watermarking, the technique used to hide information seems to be more secure because it is not easily detected by hackers. However, its major problem is a large amount of information that can be hidden inside an image without distortion of its visual imperceptibility.

In 2012, the authors of [38] have proposed the first quantum image security protocol, by a scheme of watermarking and authentication of quantum images (WaQI ), and was based on restricted geometric transformations on the images.

In 2013 [39], a novel watermarking scheme based on Quantum Wavelet Transform (QWT) was proposed , and in 2014 [40],another watermarking scheme based on Hadamard transform was proposed.

In [41], the authors have proposed an improvement of the water- marking protocol proposed in [39].

In the field of quantum image encryption, methods are classified into spatial domain-based strategies or frequency domain-based strategies, on which quantum image encryption algorithms focus [42].

5.3          Multilevel Quantum Systems

In many works in literature, various models of quantum image representation have been proposed, and many of the proposed models are based on a binary quantum system.

Instead of a binary quantum system, a ternary quantum system is a new tendency to represent and process the quantum image.

A ternary quantum system is a 3-level quantum system having three mutually orthogonal states 0 , 1 and 2 that form a basis in the Hilbert space H³ called qutrit.

As in a quantum binary system for a qubit, the superposition state of a qutrit can be formulated as:

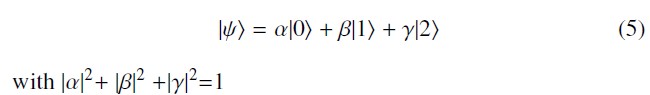
In [43], the authors have proposed an RGB color image repre- sented and stored on a ternary (3-levels) quantum system. They postulate that ”images on quantum computers can be represented in the form of a normalized state which captures information about colors ( c ) and their corresponding positions ( p ) in the images”. The image can be represented as:

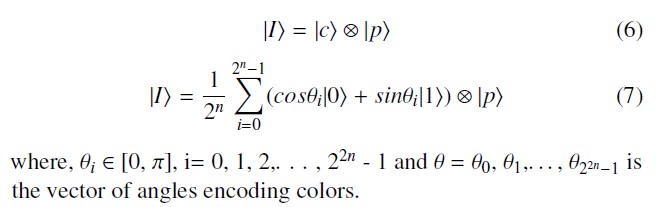
In the case of the qutrits-based quantum system, According to Klimov qutrit phase model [44] can be represented as:

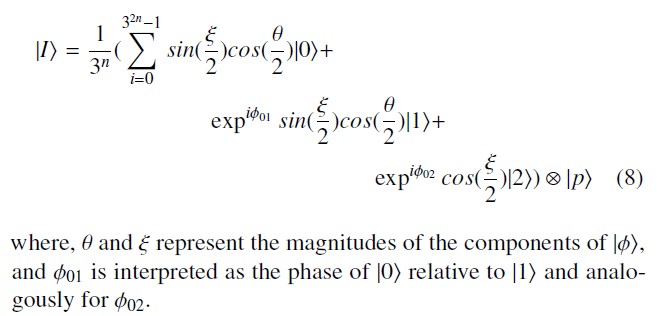
The multilevel quantum system was implemented and designed in various works for different image processing purposes. In their work [45], the authors designed a circuit-level implementation of the quantum multilevel threshold-based color image segmentation technique.

Using multilevel quantum system have more advantages compared to binary quantum system in the most cases that can be stated for example:

With the same amount of physical resources, the use of higher-dimensional quantum states increases exponentially the available Hilbert space.

An n-qutrit quantum system can be represented by a superposition of 3n basis states, thus a quantum register of size n can hold 3n values simultaneously, in the other side an n-qubits register can only hold 2n values.

More efficient ternary logical gates implementation are used in multilevel quantum system.

For representing, storing and processing the color im- ages, ternary quantum system is more beneficial than binary quantum system.

6        Conclusion

In this paper, we describe how we can profit from the quantum computer to strengthen the security of our data on the Internet using quantum physics, based on the principles of quantum physics that we do not have in classical computers.

The unequalled power of the quantum computer led us to think of using it to represent and process big-size images. We have presented the new tendency of using ternary quantum systems com- pared to binary ones.

In future work, we will use the idea of sending a scrambled im- age with a ternary quantum system, which will guarantee us better security and an exponential gain in processing time and memory.

Conflict of Interest  

The authors declare no conflict of interest.

Acknowledgment

The authors acknowledge the use of IBM Quantum services in this article. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team. They also acknowledge the support of the DGRSDT of the Ministry of Higher Education and Scientific Research of the Algerian Government.

1. T. Nouioua, A. H. Belbachir, “The Quantum Computer and the Security of Information Systems,” in 2021 International Conference on Recent Advances in Mathematics and Informatics (ICRAMI), 1–9, 2021, doi:10.1109/ ICRAMI52622.2021.9585929.
2. R. P. Feynman, “Simulating physics with computers,” Int. J. Theor. Phys., 21, 467–488, 1982.
3. R. P. Feynman, “Quantum mechanical computers,” Foundations of Physics, 16, 507–531, 1986.
4. P. W. Shor, “Algorithms for Quantum Computation: Discrete Logarithms and Factoring,” in in Proceedings of the 35th Annual Symposium on the Foundations of Computer Science, 124–133, 2021.
5. P. W. Shor, “Polynomial-time algorithms for prime factorization anddiscrete logarithms on a quantum computer,” SIAM review, 41, 303–332, 2020.
6. D. Deutsch, R. Jozsa, “Rapid solution of problems by quantum computation,” SIAM review, 439, 553–558, 2020.
7. L. K. Grover, “A fast quantum mechanical algorithm for database search,” in In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, 212–219, 1996.
8. J. A. Buchmann, D. Butin, F. Go¨ pfert, A. Petzoldt, “Post-Quantum Cryptog- raphy: State of the Art,” Lecture Notes in Computer Science, 9100, 2016, doi:10.13140/RG.2.2.29502.18243.
9. M. A. Nielsen, I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2011.
10. S. M. Pranav, M. Ritwik, “A Comprehensive but not Complicated Survey on Quantum Computing,” in In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, 144–152, 2014, doi:10.1016/j.ieri.2014. 09.069.
11. D. Arighna, D. Gerhard W, W. Robert, “Towards exploring the potential of alternative quantum computing architectures,” in Proceedings of the 23rd Con- ference on Design, Automation and Test in EuropeMarch, 682–685, 2020.
12. M. Vasileios, V. Kamer, M. D. Zych, A. Jøsang, “The Impact of Quantum Com- puting on Present Cryptography,” International Journal of Advanced Computer Science and Applications, 9, 2018.
13. Y. Dulek, F. Speelman, “Quantum Ciphertext Authentication and Key Recy- cling with the Trap Code,” Leibniz International Proceedings in Informatics, 1–17, 2020.
14. P. S. Emani, J. Warrell, A. Anticevic, “Quantum computing at the fron- tiers of biological sciences,” Nat Methods, 18, 701–709, 2021, doi:10.1038/ s41592-020-01004-3.
15. D. C. Doimari, “computing versus classical computing in the field of Bi- ological Sciences,” E-ZINE OF BIOLOGICAL SCIENCES, 2020, doi: 10.1038/s41592-020-01004-3.
16. S. Chakraborty, S. B. Mandal, S. H. Shaikh, “Quantum image processing: challenges and future research issues,” International Journal of Information Technology, 1–15, 2018.
17. F. Yan, S. E. Venegas-Andraca, K. Hirota, “Toward implementing efficient image processing algorithms on quantum computers,” Soft Computing, 1–13, 2022.
18. P. Christopher, R. Renato, “Renato,Security in quantum cryptography,” Rev.Mod. Phys, 2022, doi:10.1103/RevModPhys.94.025008.
19. Bennett, H. Charles, G. Brassard, A. K. Ekert, “Quantum Cryptography,” Sci- entific American 267, 4, 50–57, 1992.
20. G. Beach, C. Lomont, C. Cohen, “Quantum image processing (QuIP),” in 32nd Applied Imagery Pattern Recognition Workshop, Procedongs, 39–44, 2003, doi: 10.1109/AIPR.2003.1284246.
21. Y. Liu, Z. Qi, Q. Li, “Comparison of the similarity between two quantum images,” Sci Rep 12, 50–57, 2022, doi:10.1038/s41598-022-11863-9.
22. M. A. Nielsen, I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2010.
23. C. Kiefer, E. Joos, “Quantum Future From Volta and Como to the Present and Beyond,” Lecture Notes in Physics, 1999, doi:10.1007/BFb0105342.
24. D. P. DiVincenzo, “The Physical Implementation of Quantum Computa- tion,” Fortschr. Phys, 48, 771–783, 2000, doi:10.1002/1521-3978(200009)48: 9/11⟨771::AID-PROP771⟩3.0.CO;2-E.
25. M. Brune, . Hagley, J. Dreyer, X. Maˆıtre, A. Maali, C. Wunderlich, J. M. Raimond, S. Haroche, “Observing the Progressive Decoherence of the “Meter” in a Quantum Measurement,” Phys. Rev. Lett, 77, 301, 1996.
26. N. Mikio, O. Tetsuo, Quantum Computing – From Linear Algebra to Physical Realizations, CRC Press, 2010.
27. A. D. O’Connell, M. Hofheinz, M. Ansmann, B. Radoslaw, M. Lenander, L. Erik, M. Neeley, D. Sank, H. Wang, W. Martin, J. Wenner, M. John, A. Cle- land, “A. Quantum ground state and single-phonon control of a mechanical resonator,” Nature, 464, 697–703, 2010, doi:10.1038/nature08967.
28. T. Sauter, W. Neuhauser, R. Blatt, P. E. Toschekt, “Observation Of Quantum Jumps,” PHYSICAL REVIEW LETTERS, 57, 697–703, 1986.
29. A. Einstein, B. Podolsky, N. Rosen, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? ,” PHYSICAL REVIEW, 47, 1935.
30. J. Yin, Y. Cao, Y.-H. Li, S.-K. Liao, L. Zhang, J.-G. Ren, W.-Q. Cai, W.-Y. Liu, B. Li, H. Dai, G.-B. Li, Q.-M. Lu, Y.-H. Gong, Y. Xu, S.-L. Li, F.-Z. Li, Y.-Y. Yin, Z.-Q. Jiang, M. Li, J.-J. Jia, G. Ren, D. He, Y.-L. Zhou, X.-X. Zhang, N. Wang, X. Chang, Z.-C. Zhu, N.-L. Liu, Y.-A. Chen, C.-Y. Lu,R. Shu, C.-Z. Peng, J.-Y. Wang, J.-W. Pan, “Satellite-Based Entanglement Distribution Over 1200 kilometers ,” Science, 356, 1140–1144, 2017, doi: 10.48550/arXiv.1707.01339.
31. A. Aspect, J. Dalibard, G. Roger, “Experimenta lTest of Bell’s Inequalities Using Time-Varying Analyzers ,” Physical Review Letters, 49, 1982.
32. “quantum algorithm zoo,” 2020.
33. G. D. Campo, I. Gomez, G. Canada, L. Piovano, A. Santamaria, “Guidelines and criteria for selecting the optimal low-power wide-area network technol- ogy ,” LPWAN Technologies for IoT and M2M Applications, 281–305, 2020, doi:10.1016/b978-0-12-818880-4.00.
34. N. Shireen, F. Mohammed, “RSA Public Key Cryptography Algorithm. A Review ,” International Journal of Scientific and Technological Research, 6, 187–191, 2017.
35. X. Zhou, X. Tang, “Research and implementation of RSA algorithm for encryption and decryption,” 2011, doi:10.1109/IFOST.2011.6021216.
36. M. T. Madzik, S. Asaad, A. Youssry, B. Joecker, K. M. Rudinger, E. Nielsen, K. C. Young, T. J. Proctor, A. D. Baczewski, A. Laucht, V. Schmitt, F. E. Hudson, K. M. Itoh, A. M. Jakob, B. C. Johnson, D. N. Jamieson, A. S. Dzu- rak, C. Ferrie, R. Blume-Kohout, A. Morello, “Precision tomography of a three-qubit donor quantum processor in silicon ,” Nature, 601, 348, 2022, doi:10.1038/s41586-021-04292-7.
37. E. R. Johnston, N. Harrigan, M. Gimeno-Segovia, Programming Quantum Computers: Essential Algorithms and Code Samples, O’Reilly Media, 2019.
38. A. Iliyasu, P. Le, F. Dong, K. Hirota, “Watermarking and authentication of quantum images based on restricted geometric transformations,” Inf. Sci., 186, 126–149, 2012.
39. X. Song, S. Wang, S. Liu, A. A. El-latif, X. Niu, “A dynamic watermarking scheme for quantum images using quantum wavelet transform,” Quantum Information Processing, 12, 3689–3706, 2013.
40. X. Song, S. Wang, A. A. El-latif, X. Niu, “Dynamic watermarking scheme for quantum images based on Hadamard transform,” Multimedia Systems, 20, 379–388, 2014.
41. Y. Yang, P. Xu, J. Tian, H. Zhang, “Analysis and improvement of the dynamic watermarking scheme for quantum images using quantum wavelet transform,”
    Quantum Information Processing, 13, 1931–1936, 2014.
42. F. Yan, A. M. Iliyasu, P. Q. Le, “Quantum image processing: A review of advances in its security technologies,” International Journal of Quantum Information, 15, 1730001, 2017.
43. S. Chakraborty, S. B. Mandal, , S. H. Shaikh, L. Dey, “Ternary quantum circuit for color image representation,” In Advanced Computing and Systems for Security, 95–108, 2017.
44. A. B. Klimov, L. L. Sa´nchez-Soto, H. de Guise, G. Bjork, “Quantum phases of a qutrit,” Journal of Physics A, 37, 4097–4106, 2000.
45. S. Chakraborty, S. B. Mandal, S. H. Shaikh, “Design and implementation of a multivalued quantum circuit for threshold-based color image segmentation,” Intell. Decis. Technol., 12, 251–264, 2018.

(Click Here)