1. Introduction

Cloud service providers offer various services that attract users and encourage them to outsource their personal data to reduce maintenance costs and increase user satisfaction, convenience, and flexibility. Nevertheless, these services come at the cost of losing complete control over the outsourced data, which raises security and privacy concerns. Although encrypting data before uploading it into the cloud addresses privacy concerns, it suffers from low efficiency. Keyword search is an essential requirement in these systems which is not supported by traditional encryption schemes. A naive solution is to download and decrypt all the encrypted documents to search for a keyword. Obviously, this solution suffers from excessive communication overhead and is inefficient.

Hence, Searchable Symmetric Encryption (SSE) schemes [1]– [4] were introduced to tackle this challenge. In SSE schemes, a cloud can perform search queries on user’s outsourced data while the queries, results, and data are encrypted. In the other words, SSE schemes address both privacy challenges and the searchability requirement. However, the early approaches only work for static data which means that no additions, updates, and deletions are feasible in a low-cost and efficient manner after the setup phase (securing and storing data into the cloud). Later, researchers proposed Dynamic SSE (DSSE) approaches [5]–[8]. These schemes enable users to update\modify the outsourced corpus arbitrarily in addition to performing search queries.

Moreover, SSE schemes support Multi-keyword [4, 9] search or Boolean [7, 10, 11] . Boolean schemes search for a single keyword and returns all of the documents that contain the queried keyword. Alternately, Multi-keyword search supports multiple keywords search which prevents unacceptably coarse results and improves result accuracy. Moreover, some of the SSE schemes support ranked search [4, 9] which means the cloud returns most relevant files by ranking them based on their relevance to the query.

However, DSSE approaches leak sensitive information such as search and access pattern. These methods employ deterministic queries \search tokens, which allow a server to determine if multiple queries consist of the same keyword (search pattern). furthermore, the matching document identifiers (access pattern) will be leaked after each query. Many scholars have shown [12]–[14] that revealing such important meta-data can be used to obtain critical information and even to expose underlying plaintext data. Note that, in theory it is possible to design SSE scheme with no information leakage using several cryptographic primitives such as oblivious RAM, homomorphic encryption, and secure two-party computation[15]–[17]. However, these methodologies suffer from excessive computation power, low efficiency, and large storage costs.

Moreover, in Dynamic SSE approaches, it is still feasible to link previous search and update requests to a file that is recently added. For example, if we add a new document to the corpus, the server can determine whether the new document contains the keyword that we searched for in the past. Moreover, the cloud can execute the queries on deleted documents. To tackle these challenges, researchers introduced Backward and Forward privacy [5]. Backward privacy guarantees the privacy of deleted documents while forward privacy guarantees the privacy of newly added documents. No efficient approach currently provides full backward privacy.

Forward-private (FP) approaches employ one-time use search tokens to preserve the newly added documents’ privacy [7, 6]. This means the search token for a keyword changes after being used in a query. Moreover, server index entries are ephemeral, which means the user generates new encrypted index entries after each time of access. Hence, the server cannot track the queries. As a result, Scholars believe that privacy attacks on traditional SSE approaches do not apply to forward-private schemes. In particular, Zhang et al. [14] believes these features “highlights the importance of forward privacy”, and Song et al. [18] believes with forward privacy these attacks can be thwarted and prevented. Furthermore, applying these attacks will become a cumbersome task, considering that forward-private schemes are primarily dynamic and provide update functionalities (including add and delete). Therefore, monitoring and linking the queries turns significantly harder, if multiple update requests occur between two search queries.

Nevertheless, this paper extends work initially presented in the Eleventh ACM Conference on Data and Application Security and Privacy [10] and shows that it is still possible to reveal the documents and queries accurately. All DSSE approaches accept a certain level of leakage to achieve an acceptable level of performance\efficiency [2, 7, 13, 19]. Hence, the primary objective is to increase the performance as high as possible while decreasing the leakage. In particular, access pattern leakage is among the acceptable leakages [5]–[7] and, thus, one of the open challenges that has not been addressed among the forward-private and traditional approaches.

In this paper with introducing two attacks we show that it is possible to retrieve the search pattern with high accuracy that can be exploited by previous attacks to unveil the search tokens and consequently the documents in FP approaches. Our introduced attacks reverse-analyze (see Section 4) the access pattern to recover the search pattern. The first attack is applicable on the forward-private DSSE approaches that only provide “add” functionality such as [7]. We modified the the first attacked (based attack) and introduced the advanced attack which can invade the forward-private DSSE approaches that provides both “add” and “del” functionalities such as [18].

In this paper, a new forward-private DSSE approach is introduced to tackle this problem. In contrary with other scheme, our approach hides and obfuscates the access and search pattern and employs non-deterministic search tokens. All these features thwart and prevent the introduced attacks in this paper and also previous privacy and security attacks. Particularly, our contributions are:

1. Defining two concrete attacks and demonstrating its potential threats and privacy\ security risks.
2. Tackling the access pattern leakage challenge in DSSE approaches with forward privacy with a novel method.
3. Constructing an forward private DSSE scheme that support search and update (add and delete) operation. Furthermore, our efficient approach supports parallelism which is an important efficiency factor [7].
4. Providing a security proof against adaptive adversaries which verify the privacy and security of our method.
5. Demonstrating the efficiency of our approach in real-world by implementing it using real-world datasets.

The rest of this article is organized as follows. We present related work and the state-of-the-art work in Section 2. We then state the preliminaries in Section 3. In Section 4, we introduce two new attacks on current forward-private DSSE schemes, and in Section 5 we construct a new scheme that prevents the introduced attacks in Section 4. Experiments and evaluation are detailed in Section 6, and the security proof is provided in Section 7. Finally, we conclude our paper in Section 8.

2. Related Work

During the last decade, various privacy constructions and security definitions have been proposed for searchable encryption. Efficiency has always been a key requirement and a primary challenge in this research area. For example, Oblivious RAM [15] achieves full privacy and security without leaking any information to the server, but it is impractical for real-life applications because of its excessive computation costs. Hence, several approaches were designed [1, 2, 4, 9, 19] that selectively leak information (e.g., search and access pattern). This means, these schemes accept a low level of information leakage to gain a higher level of efficiency.

Searchable Symmetric Encryption (SSE) and Public-key Encryption with Keyword Search (PEKS) are the two main divisions of searchable encryption schemes. In [20], the author introduced the notion of the public key encryption with keyword search, which followed by several methods [21]–[23] to improve the system cost and efficiency of PEKS approaches. In particular, these methods use one key for encryption and another key for decryption. Hence, only data users who possess the private-key can search the encrypted outsourced data. In this paper we focus on the SSE schemes and our introduced construction is build on symmetric security primitives.

The first SSE scheme was introduced by [1]. They employed a two-layered encryption to encrypt each keyword. However, they suggest a sequential search which impacts the search time (makes it linear to the document size). Later, in [2] the author used a secure index structure called Bloom filters to address this issue. In [19], the author proposed a scheme which preserves the security of the outsourced data against an adaptive adversary. However, this comes at the cost of higher communication overhead and requires more memory space on the server side.

Nevertheless, traditional SSE approaches provide exact keyword search and cannot tolerate any imperfections or format inconsistency. In [24], the author addressed this issue and proposed a method in which resultant documents are selected based on the keyword similarity and closest possible matching documents. In [25], the author tackled the same challenge and proposes a scheme that decreases system cost and provides more efficiency.

Moreover, SSE schemes support Boolean [7, 10, 11] or Multikeyword [4, 9] search. Boolean schemes search for a single keyword and returns all of the files that contain the respective keyword. On the other hand, multi-keyword ranked search solutions [4, 8, 26, 27] enhance the result accuracy by supporting multiple keywords search. In [4], the author introduced the notion of “coordinate matching” which is a similarity measure that matches as many keywords as possible. They also constructed a multi-keyword search approach using coordinate matching. However, previous methods only support single data owner. In [26], the author designed a new scheme with a trusted proxy that supports multiple data owners. In [8], [27] the author considered a system model with semi-honest cloud server and proposed verifiable SSE approaches that can detect a malicious server. Moreover, in [9] the author propose a multi-keyword ranked search scheme that solve the problem of search pattern, and cooccurrence information leakage. They introduce a novel chaining encryption notation which prevent the aforementioned information leakages.

Dynamic Searchable Symmetric Encryption (DSSE) methods were introduced to support add, delete, and update operations in an efficient manner. In particular, the author in [28] introduced a DSSE approach that preserve users’ privacy and security against adaptive chosen keyword attacks. In [29], the author proposed a new DSSE method called “Blind Storage” that hinders leaking sensitive information such as the size and number of stored documents. DSSE approaches employ interactive protocols which results in leaking more information about the outsourced data in compare with traditional SSE approaches. In [5], the author introduced the notion of forward-privacy and designed a forward private DSSE construction to address this issue. However, their proposed method suffers from low efficiency. In [6], the author improved the system efficiency by using trapdoor permutations and designed a more efficient forward private DSSE scheme. However, these approaches use sequential scan to execute a query which makes palatalization impossible. In [7], the author addressed this issue with designing a new forward private DSSE method that provides parallelism by design.

3. Problem Formulation

3.1        Preliminaries

For a finite set X, we employ x ← X to represent that x is sampled uniformly from the set X. λ is the security parameter, and || shows concatenation. Function neg(k) : N → [0,1] is negligible if for all positive polynomial p, there exists a constant c such that: ∀ k > c, neg(k) < 1/p(k).

Definition 1 (Symmetric-key Encryption). A symmetric encryption scheme is a set of three probabilistic polynomial time (PPT) algorithms SE = (Gen, Enc, Dec) such that Gen takes an unary security parameter λ and generates a secret key k; Enc takes a key k and n-bit message m and returns a ciphertext c; Dec takes in a key k and a ciphertext c, and returns m if k was the key under which c was generated. The SE is required to be secure against chosen plaintext attack (CPA). We refer to [19] for formal definitions.

Definition 2 (Pseudorandom function). Let F : {0,1}^λ × {0,1}^l → {0,1}^l0 be a deterministic function which maps l-bit strings to l⁰-bit strings. We define F_s(x) = F(s, x) as a pseudorandom function (PRF) if: ∀ PPT distinguishers D : |Pr[D^Fs(.)(1^λ) = 1] − Pr[D^f(.)(1λ) = 1]| ≤ neg(λ), where f(.) is a truly random function, and λ is the security parameter.

In Definition 3, the notation (c_out, s_out) ← protocol(c_in, s_in) denotes an interaction between client and server where c_in and s_in are the client and server input, and the c_out and s_out are the output of client and server after performing a protocol.

Definition 3 (DSSE Scheme). Let D = {D₁,…, D_n} be a corpus of n documents, a Dynamic Searchable Symmetric Encryption consists of five PPT algorithms:

• (sk, ⊥) ← GenKey(1^λ,1^λ): In this algorithm, the data owner (client) generates a secret key sk using the security parameter λ.
• (I_c, I_s) ← BuildIndex((sk, D), ⊥): In this algorithm the client’s secret key sk and document collection D are used to produce a client-index I_c, and server outputs index I_s.
• (⊥,C) ← Encryption((sk, D), ⊥): The client inputs secret key sk, and document collection D, and outputs the encrypted corpus C = {C₁,…,C_n}.
• ((I⁰_c, D_w), I⁰_s) ← Search((sk, I_c,w),(I_s,C)): In this algorithm the client inputs the secret key sk, index I_c, and query w; and it outputs the updated index I_c, and resultant documents D_w. The server also, inputs the index I_s, and the encrypted document collection C and outputs the updated index I⁰_s.
• (I⁰_c,(I⁰_s,C⁰)) ← Update((sk, I_c, op,,in),(I_s,C)): In this algorithm the client inputs the secret key sk, index I_c, and an operation op = add or op = del, and an input “ in”, which is parsed as a set of keywords w_in and a document identifier id_in. It outputs the updated index I⁰_c. The server inputs the index I_s, and the encrypted document collection C; it outputs the updated index I⁰_s and updated encrypted document collection C⁰.

We call the first three protocols (GenKey, BuildIndex, Encryption) the Setup phase.

3.2        Our System Architecture

Our system architecture, as illustrated in Figure ??, consists of two parties: a cloud server and a client (data owner – user). The client is the actual owner of the data and intends to outsource its personal corpus into a cloud server for several reasons including maintenance costs. The client first creates an inverted index for each keyword.

Each entry in this index maps the respective keyword, w_i, to the documents IDs that contain w_i. The client then encrypts the documents and index entries and outsources them into the cloud server. Once the cloud receives a search request, it performs the query using the provided index and outputs the resultant files. Note that the documents and index entries are all encrypted, so the cloud server will not know the content of search tokens or the documents. Nevertheless, in see Section 3.5 we explain that like other related work [5]–[8], some meta-data may leak over time and after executing a number of queries.

3.3        Threat Model

In our approach, the server follows the prescribed protocol, however, it is keen to gather meta-data and information about the client. This type of cloude server is called honest-but-curious and is employed in many related work such as [5]–[7]. In addition, we suppose the server knows the encrypted index, documents, queries, and the employed encryption scheme, but it does not know the secret key.

3.4        A short overview of our approach

The client initiate the protocol by extracting keywords, ∆ ={w₁,w₂,…,w_m}, and creating the inverted plain-index. Each entry (id_i, L) in the index is a pair of an id_i and a list of L. Each keyword, w_i in the corpus corresponds to an id_i in the index, and L consists of all the files that contain w_i. To achieve our primary objectives which are hiding and obfuscating the access and search pattern, we inject random files IDs (noise) among the nodes in each list. The client is the only party who can distinguish the noise nodes. To monitor the lists, the user must keep a small index, I_c (see Section 5.2) on her side. Then, the index entries and files will be encrypted and transfered to the cloud server. Upon receiving the data, the server stores the encrypted index entries, I_s, and the encrypted corpus C and stands by for the first search or update request. Every query in our approach, q, consists of a limited number of sub-queries q = {q₁,…,q_k}. The fake\noise sub-queries are added to hide and obfuscate the search and access pattern. Once a query is received, q = {q₁,…,q_k}, the server performs the sub-queries one-by-one, or parallelly if we employ the parallel algorithm, and returns the results. The user can retrieve the real results and discard the noise. Lastly, using new keys and IDs, new encrypted index entries will be created and sent to the cloud server. Note that the user (I_c) and cloud (I_s) indexes will be updated respectively.

3.5        Security Definitions

To gain efficiency, most of the SSE schemes leak some meta-data such as number of keywords, file size, and file IDs [4, 5, 19]. In addition, more meta-data may leak after performing each query. Thus, we start this sections by defining the leakage functions that show the leaked meta-data to the cloud server after executing each step of the protocol.

Definition 4 (Search pattern). Let Q = (q₁,q₂,…,q_t) be the query list over t queries. The search pattern over a query list Q is a tuple, SP = (wˆ₁,wˆ₂,…,wˆ _t), where wˆ _i,1 < i < t is the encrypted keyword (or its hash) in the i-th query.

Definition 5 (Access pattern). The access pattern over a query list Q is a set, AP = (R(q₁),R(q₂),…,R(q_t)) over t queries, where R(q_i),1 < i < t is the i-th query’s resultant document identifiers

(result set).

To demonstrate the leakage to the server, we employ leakage function L^op which indicates the information revealed to the adversary after executing operation op. We first define the L^Setup and L^Search, and then demonstrate the information leakage of Update through Definition 6.

• L^Setup(D) = {N,n,(id(D_i), |D_i|,C_i)_1≤i≤n}, where N is the number of server index entries, I_s; n is the number of documents, id(D_i) is the document D_i’s identifier, |D_i| is the size of document D_i, and C_i is the encrypted corpus.
• L^Search(q_i) = {R(q_i), |R(q_i)|,C_qi } where q_i is a client’s query, and R(q_i) is the resultant document identifiers, and C_qi is the encrypted resultant documents.

Definition 6 (Forward privacy). A SSE scheme is forward private if the update leakage function L^Update is limited to:

L^Update(in, D_i, op) = {id_in(D_i), |w_in|, |D_i|, op}.

To define the security of the DSSE scheme we employ the standard simulation model which requires a real-ideal simulation [5, 7]:

Definition 7 (DSSE Security). Let DSSE = (GenKey, BuildIndex,

Encryption, Search, Update) be a DSSE scheme. Let A be an adversary (server), and the L^Setup, L^Search, and L^update be the leakage functions. The following describes the real and ideal world:

• Ideal^DSSE_{F ,S,Z}(λ): An environment Z sends the client a set of documents D to be outsourced. The client forwards them to the ideal functionality F . A simulator S is given L^Setup. Later, the environment Z asks the client to run an Update or a Search protocol by providing the required information. The search request is accompanied with a keyword w. For an update request, Z picks an operation from {add,del}. Add requests are accompanied with a new document and del requests contain a document identifier. The client prepares and sends the respective request to the ideal functionality F . Using L^Update and L^Search, F notifies S of leakages. S sends F either abort or continue. The ideal functionality F sends the client either abort or “success” for Update, or set of matching document identifiers for Search. Finally, the environment Z outputs a bit as the output of the experiment.
• Real^DSSE_ΠF_,A,Z(λ): An environment Z sends the client a set of documents D to be outsourced. Then, the client executes the GenKey(1^λ) to generate the key sk and starts the BuildIndex and Encryption protocols with the real world adversary A. Later, the environment Z provides the required information and asks the client to run a Search or an Update The search request contains a keyword w to search for. Z picks an operation from {add,del} for an update request. Add requests are accompanied with a new document and del requests contain a document identifier. The client then executes the real-world protocols with the server on the inputs that are selected by Z. The client outputs either abort or “success” for Update, or a set of matching document ids for Search. Z observes the output. Finally, outputs a bit b as the output of the experiment.

We say that a DSSE scheme (Π_F) emulates the ideal functionality F in a semi-honest model, if for all PPT real world adversaries A, there exists a PPT simulator S such that for all polynomial-time environments Z, there exists a negligible function negl(λ) on the security parameter λ such that [5]:

|Pr[RealDSSEΠF,A,Z(λ) = 1] − Pr[IdealDSSEF ,A,Z(λ) = 1]| ≤ negl(λ).

4. Attack methods

The first step of the attacker to launch an attack is to put the file IDs in a random order. For instance, (id(D₅),id(D₇),id(D₄)) is a valid order for a corpus with three documents {D₄, D₅, D₇}. Based on the chosen arbitrary order, the server creates a bit-string after executing each query. Each bit will be set to one if the corresponding file exists in the result set and to zero otherwise. For instance, suppose after executing a query, q_i, the results set is the R(q_i) = {D₄}. Thus, 001 is the corresponding bit-string that is generated based on result set of the current query. Moreover, to keep track of the frequency of each bit-string, the cloud server creates a Search Pattern Map (SPM) which is a hash map data structure. The attacker’s main challenge is to track the queries and since the search tokens are one-time use, storing them is pointless. However, the bit-strings that are created in our attacks can be employed as search token identifiers. Hence, the attacker stores them in the SPM along with the number of times that each token is searched.

In other words, the search tokens are ephemeral and change after each use, but the result set for each keyword remain the same and it becomes a major vulnerability for forward private schemes because of the access pattern leakage. For instance, (11, {001,7}) can be possible element in SPM that demonstrates the keyword with 001 bit-string has queried seven times. The “11” number is the hash map key that starts from zero and increments by one after adding a new element. The complexity (number of elements) of the SPM is O(m) where m is the number of keywords.

Like other related work [30], in our attacks it is assumed that the bit-strings are unique. To challenge this assumption, we extracted and studies 1927 keywords from the 50,000 files in Enron email dataset [31]. The results shows a scarce 0.2% conflict probability. In other words, there were only 2 conflicts among the investigated files. As a result, the search pattern can be recovered with 99.8% accuracy using our attack. In addition, remark that the keywords that had conflicts were among the very low frequency keywords, thereby, perhaps the cloud server is not interested in. Furthermore, the conflict probability significantly decreases as the number of files in the corpus increase. This is because the state space of bit-string’s , all possible bit strings set, expands and becomes larger. Nevertheless, we later address this attacker’s challenge and describe how keywords with unique bit-string can be distinguished. We emphasize that all assumption in related work [13, 14, 30, 32] and our work are consistent and we add no new assumption in this attack.

The basic attack is explained in Algorithm 1. Briefly, once each query is executed, the cloud server looks in the SPM to find a match for the resultant bit-string (r bitString). If there is a match, the server increments the respective frequency by one, otherwise, the new bit-string will be added to SPM with frequency of one (line

24).

Algorithm 1 Basic Attack
input: SPM, r bitString output: updated SPM 1: found = false 2: for each e ∈ SPM & until !found do 3:             etmp = e.bitString
4:	rtmp = r bitString
5:	flag = true
6:	while flag & etmp > 0 do
7:	erem = etmp mod 2
8:	rrem = rtmp mod 2
9:	if erem , rrem then
10:	flag = false
11:	end if
12:	etmp / = 2
13:	rtmp / = 2
14:	end while
15:	if flag then
16:	found = true
17:	match = e
18:	end if
19: end for 20: if found then 21:          match.bitString = r bitString 22:         match.frequency++ 23: else 24:           Add (r bitString,1) to SPM 25: end if		. new keyword found

Nevertheless, the length of the bit-string can be affected by

“add” operation. In other words, adding a new file increases the length of the bit-string. To tackle this issue, the new file ID will be added to the left of the arbitrary order by the cloud server. Recall the previous example and suppose the server has received a new request to add D₆ to the dataset. The updated arbitrary order will be (id(D₆),id(D₅),id(D₇),id(D₄)). Hereafter, SPM bit-strings are a bit shorter than queries’ bit-strings. However, this does not stop the server\attacker from recovering the search pattern, because, the attack algorithm compare the SPM and query bit-strings bit-wisely starting from left bit to the right. The algorithm halts (line 6) when it achieves the last bit of the respective SPM bit-string. For instance, suppose {D₄} and 001 are the result set and respective bit-string of query, q_i. If the user issues the same query q_i again, after adding D₆ and of course with a new search token, the resultant bit-string would be either 0001 or 1001. Remark that only one can happen at a time, because either the new file, in this case D₆, contains respective keyword in q_i or not. Hence, if the server detects a bit-string in SPM that matches the first three bits (from right-side) of the resultant bit-string, it can be confident that these two token IDs refer to same keyword. Remark that, the respective bit-string will be updated to n + 1 from n-bit string in line 21 of the algorithm where n is the number of files. This means, in our example the bit-string will be updated to a four-bit from a 3-bit string.

The traditional attacks are not effective on schemes that support forward privacy. The main reason is that forward-private approaches hide and obfuscate the search pattern to a certain extent. However, by applying our attack on schemes with forward privacy, we reveal the search pattern. Once the attacker possess the search pattern, forward-private approaches will become susceptible against previous attacks. The output of our attack can be exploited by frequencybased attacks such as [12]–[14], [32]. Moreover, after applying a small modification, our attack can be used by occurrence-based attacks such as [30]. To support the occurrence-based attacks the attacker creates a n × m matrix M instead of SPM. In this matrix each column represents a bit-string\keyword, and each row corresponds to a document. We set the value of an entry to zero if the respective keyword does not exist in the corresponding document, and to one otherwise. Once a query is executed, the cloud server updates the value of the respective entry, If it finds the same bit string, or it adds the bit-string as a new keyword otherwise. If a new file is added, the cloud server append a new row to the matrix M.

To address the problem of distinguishing the keywords with the same result set, the cloud server can inject a limited numbers of documents into the corpus (keywords with the same result set). For instance, suppose {k₁,k₂} and {k₃,k₄,k₅} are two groups of keywords that have the same result set. The attacker can distinguish k₁ from k₂ by injecting a file that contains either of the keywords. The same method can be used to make the other group keywords distinguishable. To maximize the efficiency, we should minimize the number of injected files. Hence, the attacker creates new files that contains only one keyword from each group. For instance, the attacker creates a file that contains k₁ and k₃ from the first and second group. It also generates a another file which only contains k₄. With injecting only two files these keywords will become distinguishable. Generally, suppose we have l groups of keywords that possess the same result set, {P₁, P₂,…, P_l}, the minimum number of required injected documents is max^l_j=1{|P_j|} − 1, in which |P_j| shows the cardinality of j-th group.

This techniques is also employed in many related work such as [13, 32, 14] in which the cloud server sends the documents of its choice to the user. The client then encrypts and transfers them back to the cloud [14]. For example, consider a company that uses an automatic email process. Remark that in both occurrence-based and occurrence-based attacks the attacker commonly benefits from public information and auxiliary knowledge that rectifies the indistinguishable keywords challenge in advance. For instance, Liu et al.’s attack [12] benefits from public web facility services such as Google Trends ^R .

Nevertheless, the basic attack is not applicable on DSSE approaches that provide “del” functionality. We modified the basic attack, see Algorithm 2, that can successfully attack DSSE schemes that provide both add and del functionality. In our advanced attack, a new bit-string, d bitString, will be generated by the cloud server to monitor the deleted documents. Each bit in the d bitString represents a document in the corpus (considering the same arbitrary order). Each bit will be set to zero if the respective file still exists in the corpus, and to one if it is deleted. After executing a delete request, the cloud updates this bit-string accordingly. Once a query is executed, the resultant bit-string will be bit-wisely compared to the data in SPM, but this time, we ignore the bits that their corresponding files are deleted. We demonstrate the changes with red lines in Algorithm 2.

Algorithm 2 Advanced Attack
input: SPM, r bitString, d bitString output: updated SPM 1: found = false 2: for each e ∈ SPM & until !found do 3:             etmp = e.bitString
4:	rtmp = r bitString
5:	dtmp = d bitString
6:	flag = true
7:	while flag & etmp > 0 do
8:	drem = dtmp mod 2
9:	if !drem then
10:	erem = etmp mod 2
11:	rrem = rtmp mod 2
12:	if erem , rrem then
13:	flag = false
14:	end if
15:	etmp / = 2
16:	rtmp / = 2
17:	end if
18:	dtmp / = 2
19:	end while
20:	if flag then
21:	found = true
22:	match = e
23:	end if
24: end for 25: if found then 26:          match.bitString = r bitString 27:         match.frequency++ 28: else 29:           Add (r bitString,1) to SPM 30: end if		. new keyword found

4.1        An example of our attack with “del” operation

Assume there are four documents, {D₁, D₂, D₃, D₄}, and four keywords, ∆ = {w₁,w₂,w₃,w₄}, in the user’s corpus. Moreover, (id(D₄),id(D₃),id(D₂),id(D₁)) is the arbitrary order that the attacker\cloud uses to create the bit-strings. Suppose D₁ contains

{w₁,w₂,w₃}, D₂ includes {w₂,w₃,w₄}, D₃ has {w₁,w₃}, and D₄ contains {w₂,w₄}. Furthermore, we assume the setup phase is successfully executed, and the encrypted index and documents are outsourced.

Case 1: Searching for a keyword for the first time. The user searches for all documents that contain w₁, so he generates an ephemeral search token (q₁) and send it to the server. Upon receiving the search token, the server finds the related index entries and the respective encrypted documents (R(q₁) = {D₁, D₃}). Since there is no bit-string in the SPM that matches the current bit-string, the server adds the respective bit-string (0101,1) to the SPM (1 is the frequency). The user then generates and sends an encrypted query (q₂) to the server to search for w₃. After returning the results (R(q₂) = {D₁, D₂, D₃}), the server adds (0111,1) to the SPM.

Case 2: Searching again for a keyword that exists in the SPM. Now imagine the user searches again for w₁ with a new ephemeral search token (q₃). Once the query executed, the server searches for the resultant bit-string (0101) in the SPM. Since the bit-string already exists in the SPM, the server only updates its frequency (0101,2).

Case 3: Adding a new document. The user then adds a new document (D₅) that contains (w₁,w₂,w₄). The server updates the arbitrary order to {id(D₅),id(D₄),id(D₃),id(D₂),id(D₁)} respectively. Now the user issues a new query (q₄) to search for w₄ for the first time. The resultant bit-string will be 11010. Hence, (11010,1) will be added to the SPM. Note that at this point the bit-strings in the SPM may have different length (4 and 5). The user may also searches again for a keyword after adding a new document. For example, suppose the user searches again for w₃. The new resultant bit-string is 00111. The server looks for a bit-string in the SPM that is either equal to our current bit-string or is equal to the first four bits (from right-side) of the resultant bit-string. In this case the sever will find the (0111,1) entry and will update it to (00111,2) respectively.

Case 4: Deleting a document. To monitor the deleted documents, the attacker creates a bit-string, d bitString, in which each bit represent a document and its value demonstrates whether the respective file is deleted (=1) or not. This vector will be updated after each delete request. Once a query is executed, the resultant bit-string will be bit-wisely compared to the data in SPM, but this time, we ignore the bits that their corresponding files are deleted.

Assume the user asks server to delete D₃. The server deletes the document and updates the d bitString to 00100. If the user searches for w₁ again, the resultant bit-string will be 10∗01 (“∗” means its value is not important and can be 0 or 1). Since D₃ is deleted (based on the d bitString), the server ignores the value of that position when it is searching for the current bit-string in the SPM.

5. Construction

To prevent the attacks that we introduced in the previous section, we build and construct a new dynamic SSE scheme that supports forward privacy. Our construction hides and obfuscates the access pattern to thwart the above privacy attacks. In our approach, the client first creates an inverted index for each keyword in the corpus. In an inverted index, every entry maps a keyword to the corresponding document IDs that contains the respective keyword. We add fake\noise document IDs among each keyword result-set to hide and obfuscate the access pattern. The fake IDs can only be distinguished by the client. In addition, in our approach each query q_i consists of a limited number of sub-queries q_i = {q_i1,q_i2,…,q_ik}. All sub-queries except one are noise which can only be recognized by the user and sub-query searches for a keyword. We propose two methodologies to inject the noise file IDs:

1. Random injection. We first determine a threshold , τ_d, that represents the lower and upper bound of noise injections in a specific result-set. Once τ_d is set, we arbitrarily inject file IDs into the result set of the every keyword.
2. Aforethought injection. Our main objective is to flatten the the number of times that each document accessed. With this strategy the number of times that each document is accessed will be in the same range as others. This makes it much harder for the attacker to gain information about the data, search tokens, and the files by using the access pattern meta-data. To achieve this objective, the client generates an Access Pattern Vector (APV) that stores the number of times that each file is accessed. For instance, < 1,0,4,2 > demonstrates D₁, D₃, and D₄ are accessed one, four, and two times since launching the system. This information is valuable in our approach and will help to choose the fake sub-queries wisely. For each query, the user monitor and analyze the APV vector and selects the keywords that are accessed less in compare with others. Considering our earlier example (< 1,0,4,2 >), the client can inject keywords that return D₁ and D₂ to straighten the access pattern vector.

Creating the noise sub-queries are a significant challenge in the aforethought injection. To query the less requested files in the corpus, the user must be able to identify the keywords that return a specific file ID in their resultant-set. The number of files in the corpus is myriad and increasing over time, thereby keeping this information on the users’ devices is not a realistic approach. In addition, to hide the clients’ foot tracks (activities), we intend to put each file ID into more than one keyword’s result-set. This makes the above solution more infeasible.

To tackle this problem, we first label all of the files with a number in a random order. Note that even storing these labels on the users’ machines are not practical. Hence, we then generate an arbitrary number called δ. Afterward, we begin with δ and label each document successively. remark the files are shuffled before being labeled with successive numbers, so, the labels will not leak additional meta-data about the files. To identify the keyword w that a specific file ID, D_i, is injected in, we employ the G_w(.) PRF. G_w(.) accepts a key k and a document label and returns a keyword number, m, where m ∈ [1..m]. For instance, in G_n(k,7654321) = 123 the user is searching for a keyword number (123) that holds a document that is labeled as 7654321. In other words, after calculating G_n(k,7654321) = 123, the user learns that the file with 7654321 label is injected in the w₁₂₃’ result set.

To inject each file ID a number of times, we define a new parameter called step, s_δ. Step (s_δ) shows the number of result-sets that each file ID is injected into. As a result, we increase the label number by s_δ instead of labeling them consecutively. By exploiting this technique we expedite the flattening process of the APV vector. Therefore, instead of possessing one label, each file will have s_δ labels that is reserved for the respective file. For instance, suppose s_δ = 3 and we want to search for keyword w_i that returns the document that is labeled as 7654321. Hence, the client executes G_n(k,7654321) = 123, G_n(k,7654322) = 77, and G_n(k,7654323) = 2105. This means, keywords w₁₂₃, w₇₇, and w₂₁₀₅ are having file 7654321 in their result-sets. Consider that, due to the definition of the pseudo random function the keyword numbers are not necessarily successive even if the the input labels are.

5.1        Our linked-list structure

In this section we explain a customized linked-list data structure that we employ in our scheme. Our linked-list consists of 4 tuples: (id,type,data,next). In particular, id refers to the ID of a node, type shows whether a node is real R fake\noise (F), data is a file identifier, and next refers to the ID of the next node in the respective linked-list. The red elements will be secured and encrypted using the user’s key, while an ephemeral key will be used to encrypt the orange elements. Hence, type will be encrypted using the user’s key and, we will be using an ephemeral key to encrypt data and next. Note that elements in black (i.e., id) is plaintext data. To prevent leaking any additional meta-data, we use a random even number for real and a random odd number for noise nodes. In addition we set the next to null if a node does not have a successive node. Consider that, the ephemeral key will be provided for the server if the respective keyword is being queried, but we never share the user’s secret key with server. Hence the server will never know which nodes are fake and which ones are real.

• AddNode(L,k₁,k₂,id,type,data): This function employs the input data to append a node to the beginning of the current linkedlist, L.
• RestoreList(k,id_h): This function looks for the node with the provided ID; it then retrieves type and decrypts next and data and looks for the next node in the linked-list. The process stops when the algorithm reaches the last node in the linked-list (e., next = null).

In our approach, all of the secure inverted index is constructed using the aforementioned linked-list data structure. To add more security, the client injects fake\noise nodes in each and every linked-list to hide and obfuscate the relevance between a keyword, w_i, and its corresponding linked-list, L. Note that the noise will not be injected if it already exists in the linked-list. for instance, assume that one of the inverted index entries is (w₇, {D₃, D₆, D₅}). The objective is to inject D₆ and D₉ in random positions in the respective linked-list. however, we only inject D₉ because D₆ is already in the linked-list. Now suppose after injecting the noise node(s) the index entries will be (w₇, {D₃, D₆, D₉, D₅}). Hence, the user generates four nodes (id₁,R,id(D₃),id₂), (id₂,R,id(D₆),id₃),(id₃, F,id(D₉),id₄) (id₄,R,id(D₅),null). Consider that, since the nodes are encrypted and will be sent in a random order to the server, the attacker is not able to link them.

5.2        Our scheme

In this section we demonstrate and describe how each algorithm in Definition 3 operates:

• GenKey: let SE = (Gen, Enc, Dec) be a CPA-secure symmetric encryption scheme. Let G_n(.), G_id(.) and G_w(.) be three PRFs and GenPK(1^λ) be a key generator function. The following describes (sk, ⊥) ← GenKey(1^λ,1^λ):

1: k_SE = SE.GEN(1^λ)

2: k_G ← GenPK(1^λ)

3: return sk = (k_SE,k_G)

We employ a secret key, sk, to fulfill the encryption objectives. sk is a tuple of two, k_SE and k_G. The former will be used to encrypt the documents and latter for G_w(.), G_n(.) and G_id(.) functions.

Algorithm 3 (I_c, I_s) ← BuildIndex((sk, D, s_δ), ⊥)

Client

1: ∆ = ExtractKeywords(D)

2: δ = Rand()

3: lbl_next = δ

4: D⁰ = {}

5: while D , empty do

6:             D_cur = randomly choose one doc and assign lbl_next to it

7: D0 ∪ Dcur 8: id_next + = sδ

9: end while

10: PI = BuildPlainIndex(∆, D⁰, s_δ)

11: Create I_c and APV and initialize all elements to zero

12: L = GenLinkedList(sk, PI)

13: Send L to server

Server

14: Generate I_s using L

• BuildIndex. In this algorithm (see Algorithm 3), after extracting the keywords, ∆ = {w₁,…,w_m}, we assign an label\id to each file according to the value of the δ (the starting point), and s_δ (step). Afterward, the client index I_c, and its corresponding linked-lists will be created. To enable the client to generate the search queries, the client must store a m × 2 look-up table (index), I_c. In particular, this table stores length of the list, len_i and the number of nodes, cnt_i, that is generated for each keyword. Moreover, the APV (access pattern vector) will be created and initialized to zero. Once the index entries are generated, they will be sent to the cloud server. Note that a random number will be assigned to δ which is generated by Rand().

We explain generating the plain-text inverted index PI in Algorithm 4. Using the aforethought injection method, we first generates the noise nodes (line 5-9), and then we append the real nodes to their corresponding list (line 11-15). Note that as we mentioned in Section 5.1, every entry in PI consists of two tuples which are a keyword and the receptive list (w_i, L). recall that beside the file label, each node in the list keeps a type (F\R). For instance, D₂ is fake, and D₄ and D₈ are real nodes in (w₂₃, {{D₈,R}, {D₂, F}, {D₄,R}}). In addition, to decide the lists that each file ID must be injected in, we employ G_w(k_G,doc_id) function. Consider that this is process happen in the setup phase and only for once. Next, a linked-list will be generated for each generated list in the previous step. The node IDs are one-time use and will be generated by the G_id function. In particular, the G_id function uses a counter, ctn, which shows the number of nodes that are created for the respective keyword, w_i. The client store this number in the client index (I_c[i][0]).

Algorithm 4 BuildPlainIndex

1: procedure BuildPlainIndex(∆, D⁰, s_δ)

2:             PI = {}

3:            for all w_i in ∆ creates an empty L_i

4:              for all D_j in D⁰ do

5:                   for k = 0 to s_δ-1 do

6:                            i = G_w(k_G,(lbl(D_j) + k))

7:                           if D_j < L_i then

8:                                  L_i ∪ {D_j, F}

9:                         end if

10:                end for

11:                  for all w_i in ∆ do

12:                         if w_i ∈ D_j then

13:                                 L_i ∪ {lbl(D_j),R}

14:                       end if

15:                end for

16:          end for

17:           Shuffle and Add all (w_i, L_i) to PI

18:           return PI

19: end procedure

Algorithm 5 GenLinkedList

1: procedure GenLinkedList(sk, Ic, PI) 2:             L = {}
3:	for all e ∈ PI do
4:	wi = e.wi
5:	L = e.Li
6:	len = 0
7:	cnt = Ic[i][0]
8:	for all lbldoc & type ∈ L do
9:	idn = Gid(kG,wi||cnt)
10:	if len == 0 then
11:	kh = Gn(kG,idn)
12:	Ls = {}
13:	end if
14:	AddNode(Ls,kSE,kG,idn,type)
15:	len + +
16:	cnt + +
17:	end for
18:	L ∪ Ls
19:	Ic[i][0] = cnt
20:	Ic[i][1] = len
21:	end for
22:          return L 23: end procedure

We employ an ephemeral key to encrypt the private data in each node. This key will be generated using the receptive function, k_h = G_n(k_G,id_n), which is shown in line 10-13 of Algorithm 5. All of the data in a linked-list will be encrypted using the same ephemeral key except the type data. We employ the secret key, k_SE, to encrypt the type field, because the client should be the only party who can decrypt this data. For instance, assume the client intends to create a secure linked-list for w₂₁’s list, {D₄, D₇}. Assuming cnt = 0, we generate the node IDs, id₁₀ = G_id(k_G,w₂₁||0), id₁₁ = G_id(k_G,w₂₁||1). Afterward, we create an ephemeral key k_h = G_n(k_G,id₁₀) to encrypt the nodes.

Remark that for the whole linked-list, we only generate one ephemeral key (see line 10). Lastly, using AddNode, we create and encrypt the required nodes and add them to the corresponding linked-list. We demonstrate how we create a linked-list from an inverted plain-index in Algorithm 5. Once all of the nodes and required linked-list are created, the user sends them to the cloud server to be stored on the server index, I_s. Remark that the index entries are encrypted and sent in an arbitrary order and the server cannot link them.

• Encryption. Using the secret key k_SE, the client encrypts the entire corpus (all of the files), transfers them to the cloud server including the file IDs.

Algorithm 6                                   ← Update((sk,I_c,add, in),(I_s,C))

1: ExtractKeywords(D_n+1)

2: L = {} 3: for all wi ∈ ∆D do
4:	cnt = Ic[i][0]
5:	len = Ic[i][1]
6:	idh = Gid(kG,wi||cnt)
7:	idn = Gid(kG,wi||cnt − len)
8:	kh = Gn(kG,idn)
9:	L ∪ (idh,kh)
10:	Ic[i][0] + +
11:	Ic[i][1] + +

12: end for

13: C_n+₁ = Enc(k_SE, D_n+₁) 14: Send L,C_n+1 to server

16: Update I_s using L

• Search. Obfuscating and hiding the access and search pattern is our primary goal. To achieve this objective, we append a bounded number of sub-queries, q_i = {q_i1,q_i2,…,q_ik}, to each query q_i. Every sub-query consists of two tuples, (k_h,id_h). k_h is an ephemeral key that decrypts a linked-list starting with id_h (linked-list’s header). Employing I_c and k_G enable the user to re-generate k_h and id_h which are required for generating the query. In addition, the noise sub-queries will be added to boost the security and privacy of the outsourced data and obfuscate the access and search pattern.

To flatten the APV and amplify the privacy of the outsourced files, we use a biased random generator function called GenRandom(). This function chooses high accessed documents with lower probability, so the less accessed files has more opportunity to be selected which impact directly the pace of flattening the APV. Note that we assign s_δ number of labels to each file. Hence, along with APV, GenRandom() inputs s_δ to randomly choose one of the available labels for the file of interest. ν holds the number of fake\noise queries that can be determined randomly. Before sending the query to the cloud server, we insert the sub-queries in arbitrary positions in query q_i.

The query generation process for a keyword w is demonstrated in Algorithm 7. Remark that the node ID (of the linked-list header) and its respective ephemeral key are regenerated in line 15. Since the users may possess various devices with different level of computation power and resources, a number of parameters including ν and s_δ can be set by the client.

Once a query, q_i, is received, the cloud server runs each sub-query q_ij = (id_h,k_h) by finding id_h (header of the requested linked-list) in I_s. Employing the k_h, the server then decrypts all of the nodes (except the type field) and discards all of the used index entries. All of the extracted document IDs and their respective type fields will be added to the result set. Note that the server can store the used index entries, however, it is pointless because they are already leaked and enclose no new meta-data. Lastly, the server returns a result set consists of (R(q_i1),…,R(q_ik),bag) where R(q_ij),1 < j ≤ k, is the q_ij’s resultant file IDs; and the bag is q_i’s resultant encrypted files.

Once the result set of q_i is received, the client who is aware of the location of the noise and real sub-queries, decrypts and separates the real results form the bag. Next, the GenLinkedList algorithm will be called to generate new entries for queried keywords in q_i.

The forward privacy of our approach is guaranteed by using nondeterministic search tokens and adding random noise sub-queries. The client then updates its index, I_c, and creates new node IDs and ephemeral keys for each linked-list. Note that, since the value of the cnt is updated, brand new keys and node IDs will be generated. To track the access frequency of each file, the client then updates the APV. lastly, the new index entries will be sent to the cloud server to be stored on the server index, I_s.

Albeit the cloud server is aware of the relation between the last query and new entries, it cannot determine the noise keywords from the real search keyword. In addition, the node IDs and their respective keys are one-time use and vary after each search. Furthermore, there exist fake\noise nodes among the actual nodes in every linked-list. As a result, it is impossible for the server to realize the actual search and access pattern. All of these specifications in our approach guarantee the forward privacy requirement and preserving the access and search pattern. The search process is described in detail in Algorithm 7.

• Update. The update algorithm consists of two functions, del and add, as follows:
• add. In add algorithm, we first extract the keywords from the new file. The algorithm then generates a node for each keyword and adds them to the respective linked-list. Next, we encrypt the the new file using the user’s secret key and transfer it to the cloud server. On the other side, the server updates the I_s, once the the Update request is received. The add function is described in detail in Algorithm 6.
• del. The user creates a Update request and sets the operation to del and includes the file ID in the request to delete a file, D_k. Upon receiving the del inquiry, the cloud server deletes the respective file form its storage. Nevertheless, the corresponding index entries cannot be removed because the server does not possess the keys.

Algorithm 7 ((I⁰_c, D_w),(I⁰_s)) ← Search((sk,I_c,w,ν, APV),(I_s,C))

Client

1: counter = 0;

2: ∆_q = {w}

3: while counter < ν do

4:              lbl = GenRandom(APV, s_δ)

5:              i = G_w(k_G,lbl)

6:             if w_i < ∆_q then

7: ∆_q ∪ w_i 8: counter + +

9:            end if

10: end while

11: q = {}

12: for all w_i in ∆_q do

13: cnt = I_c[i][0] 14: len = I_c[i][1]

15:           id_n = G_id(k_G,w_i||cnt − len)

16:           id_h = G_id(k_G,w_i||cnt)

17:            k_h = G_n(k_G,id_n)

18:           q ∪ (id_h,k_h)

19: end for

20: Shuffle(q)

21: Send q to server

Server

22: bag = {}

23: for all q_i in q do

24:          Find respective node with id_h

25:           while node , null do

26:                 Decrypt the node using k_h in q_i

27:                 Add lbl and type to R(q_i)

28:                Find next node

29:          end while

30:          Add files corresponds to R(q_i) to bag

31: end for

32: Send (R(q₁),…,R(q_k),bag) to client

Client

33: Decrypt results R

34: PI = {}

35: update APV based on the results

36: for all w_i in ∆_q do

37:            L = All doc-ids contain w_i in R

38:           PI ∪ (w_i, L)

39: end for

40: L= GenLinkedList(sk,I_c, PI)

41: Send L to server

42: Delete noise results

43: Consume real results

Server

44: Update I_s using L

However, the index entries will be removed over time and after receiving a number of queries. The server simply removes the nodes that are pointing to a deleted file. To incorporate this feature in Algorithm 7, the server first investigate the availability of the a file extracted from a node (line 28). The server removes them from the result set, if they do not exist.

6. Experimental results and complexity analysis

To assess the efficiency of our approach, we study and compare the complexity of the state-of-the-art methods (Etemad et al. [7], Bost et al. [6], Stefanov et al. [5]) with our approach. Lastly, we finish this section by demonstrating the experimental results that are obtained using real world datasets.

6.1        Analyzing the complexity of our proposed algorithm

Required storage space for client and server. We first show that the amount of data that the server and especially the client should store is reasonable and manageable. Recall that user must store a dictionary, I_c, on her side which holds the number of nodes (a counter) and the length of each linked-list for each keyword. Hence, the client index look likes a table with two column and m rows where m is the number of keywords. Hence, I_c is an O(m × 2) ≈ O(m) dictionary. Assume the user’s dataset consists of 1M keywords. Moreover, suppose each integer requires 4 bytes on the memory and each keyword has an average 10 bytes. In this scenario, the user needs to store a 18 MB dictionary on her side (1M ×(10 + 4 + 4) ≈ 18MB).

Considering resource-constrained devices such as cellphones which have limited memory space and constrained computations, 18 MB is rational, cost-efficient, and manageable. As an alternative, by using the method that Etemad et al.[7] also proposed, it is feasible to outsource the user index. In comparison to other work, Etemad_√

et al.[7] needs O(m + n), Stefanov et al.[5] requires O( N), and Sophos [6] occupies O(m), where n is the number of documents and N is the number of (keyword,doc id) tuples. Regarding the size of the server index, our method needs O(N + k) , in which k is the number of fake\noise nodes. All state-of-the-art methods that we mentioned above require a space with size of O(N) to store the server index.

Supporting parallelism by design. Beside our approach, this requirement is also fulfilled in Etemad et al. [7] among the Dynamic SSE schemes that support forward privacy. Since in our approach the node IDs are generated by a pseudo-random function and the server index entries are independent, it is possible to distribute the sub-queries among the processors to expedite the update and search process, and achieve parallelism. The complexity of our search method is O(d + k_d)/p and our update (add) system-cost is O(r/p), where p is the number of cores\CPUs, d holds the number of a files containing a keyword, k_d shows the number of fake nodes in a keyword list, and r holds the number of keywords in a file. The best-case scenario happens when the number of sub-queries are equal to the number of available cores\CPUs. As a result, all subqueries will be executed concurrently. The search cost in Etemad et al.’s [7] is O(d + n_d)/p and the add\update cost is O(r/p), where n_d shows the number of times that a keyword has been affected by file deletions since last search. Table 1 shows our complexity analysis.

Table 1: Complexity Analysis of Related Work and Our Approach

Approach	Ic √	Is	Parallelism	Search	Update
Stefanov[5]	O(         N)	O(N)	–	O(d)	O(r)
Bost[6]	O(m)	O(N)	–	O(d)	O(r)
Etemad[7]	O(m + n)	O(N)	X	O(d + nd)/p	O(r/p)
Ours	O(m)	O(N + k)	X	O(d + kd)/p	O(r/p)

6.2        Experimental results

We implemented a prototype and conducted a through and comprehensive evaluation to study our approach using real-life datasets. We employed Java (JDK 1.8) as the programming language and Crypto packages for the encryption process. The server and client connect and communicate through a TCP connection. Moreover, Windows machines were used for both server and client. Each machine came with 8GBs RAM and a Corei7 CPU at 3.6 GHz. To assess our scheme, we used the real-world Enron email dataset [31]. We ran each experiment ten times and the output is the average of all trials. The variance of the 10 trials were very low to be notable. We implemented the search\query algorithm twice, once using a parallel algorithm (four cores) and another time in a sequential manner. We call the former multi-threaded and the latter single-threaded. The results shows an admissible and reasonable overhead on the system that even a user with a resource-constrained device can benefit from our approach.

Table 2: # of server index entries

#Docs	#server entries
10000	829799
20000	1571676
30000	2568438
40000	3548027
50000	4404160
60000	5341524
70000	6194452

Setup time. We first started by studding the setup time per various number of files. As we discussed in Section 5.2, the setup phase includes several steps including the encryption process, creating the plain index, and the encrypted linked-lists. Our results indicate that a dataset with 20K files requires less than minute (≈ 59 sec), while the same experiment, setup process, for a corpus with 50K needs less than seven minutes to be finished (see Figure 2). Remark that, this process only happens at the beginning of our approach, so it is a one-time process. In addition, we investigated the number of server index entries. Our study shows that around 4.4 × 10⁶ entries were generated for 50K files, and 1.57 × 10⁶ for 20K documents (see Table 2).

Query generation process time. To search for a keyword, the user needs to create a query. Each query consists of numerable search tokens\sub-queries. Every search token includes the header ID of a linked-list and its receptive key. To study the impact of number of fake\noise sub-queries on the query generation process, we queried the same keyword several times but with various number of fake keywords. The results demonstrate that the system requires less than 1.5 milliseconds to generate a query which contains 50 fake keywords. Remark that we used 50000 files for this experiment.

Setup time

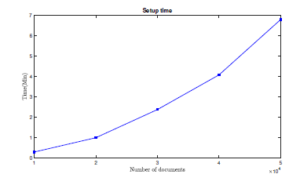
Figure 2: Client setup time

Search time. Once the server receives a search request, it will look for all files that match the search token. In this experiment we aimed to measure the amount of the time that each query requires. However, the size of the result-set (number of resultant files for a specific query) is a crucial factor in this experiment. Hence, we created ten keywords and injected them into our corpus with frequencies from 100 to 1000. These new injected keywords will enable us to investigate the effects of the number of resultant documents on the search time. Our results from the single threaded algorithm show that it takes around two seconds from the server to execute a query with 1000 resultant files. Moreover, multi-threaded algorithm requires considerably less time(around 45 percent) to answer the same query. Note that, the noise was set to three in both experiment settings.

Update (Add\Delete) requests. The user may request for an update on the corpus that can be a delete or an add request. Creating a delete query is a very low-cost operation, and takes less than 1ms in our approach. To remove a file, the user should sets the operation mode to del and embeds the file ID in the query. To add a new file, we first remove the stop words and extracts the main keywords. We then creates the index entries, plain index, encrypted linked-lists, and encrypt the file. Lastly, we transfer it to the cloud server. Once the cloud server receives the add query, it adds the encrypted file to the corpus and store the index entries. Note that because all of the index entries are encrypted with a new ephemeral key, the cloud server cannot determine the relation between current files in the corpus and the new file. To run our experiment, a file with 155 words and 68 keywords (excluding the stop words) from Enron dataset was selected. The operation lasts around 1.8 ms.

Obfuscating the Access Pattern. The most important goal in our approach is preserving the search and access pattern. To achieve this goal, we injected noise nodes among each linked-list’s nodes, and also added noise sub queries to the main query. With this strategy, the access pattern vector (APV) become flattened and obfuscated. To measure how flattened\uniform the APV become before and after applying our approach, we used the Shannon entropy. Due to not having access to the real-life search requests, we randomly selected the queries from the keyword-set. We set the noise to three and issued 1000 queries. To calculate the entropy improvement we employed ((e_our − e_org)/e_org) × 100, where e_org and e_our are the Shannon entropy of the calculated APV before and after applying our approach. Figure ?? demonstrates our results in detail. To illustrate, applying our approach on a corpus with 30K files flattens the APV more than two times. This means our approach has made the access pattern more secure and private more than twice.

For example, exploiting our approach on a corpus of 30K documents flattens the access pattern vector more than two times. That is, the access pattern is two times more private than before applying our scheme.

7. Security proof

We defined the DSSE Security in Definition 7 and designed our dynamic SSE scheme in Section 5.2. Here, we prove that our scheme is secure using the standard simulator model.

Theorem 1 Let SE = (Gen, Enc, Dec) be a CPA- secure symmetric encryption scheme, and G_n, G_id, and G_w be three pseudo-random functions, our DSSE scheme in Section 5.2 is secure under Definition 7.

Proof 1 We demonstrate how the ideal world is indistinguishable from the real world by any probabilistic polynomial time (PPT) distinguisher to prove that our dynamic and forward private SSE scheme is secure. We illustrate and explain a PPT simulator S that imitate the user actions using the provided leakage functions that are defined and provided in Section 3.5. In other words, we explain how a simulator, S, can adaptively mimic the user behavior including generating the encrypted indexes, queries, and documents:

Setup. In the first step, the simulator S generates the encrypted document set , C, simulates N index entries, and creates a secret key, k_SE. To generate the simulated data, S employs leakage function L^Setup(D) = {N,n,(id(D_i), |D_i|)_1≤i≤n}. Note that all data including the index entries, I_s, and generated files, C, are encrypted with the secret key that was generated earlier. This means, the simulator S does not require to have access to the contents of the files, and as a result, it encrypts strings of size |D_i| containing all zeros to create the encrypted files. Note that no probabilistic polynomial time distinguisher (attacker) can detect and discern this behavior due to the CPA security of the applied symmetric encryption scheme. Moreover, the simulator requires to generate and keep two dictionaries, keyDict and ∆_s, to answer the Update and Search queries. ∆_s simply keeps track of the simulated keywords. For each linkedlist, KeyDict dictionary stores a key, keyword, and the first node identifier of the respective linked-list. The simulator then generates the keywords and arbitrary values for linked-lists which are selected from a keyword distribution based on the range of the encryption scheme. To facilitate generating the search and update tokens, the simulator, S, updates the ∆_s and keyDict dictionaries adaptively.

We explained the setup phase in Algorithm 8.

Add. To add a new file, the simulator S uses the update leakage function, L^Update(in, D_i, op) = {id_in(D_i), |w_in|, |D_i|, op}, and employs the same keyword distribution and ∆_s. First, the simulator randomly selects |w_in| keywords to be assigned to the new document. It then generates an encrypted file C_i and the respective linked-lists. Lastly, S updates the dictionaries respectively for future references. This process, add simulation, is shown in Algorithm 9. Remark that to follow our scheme’s architecture, beside using a new key, every keyword is appended as a new linked-list to the cloud index. As a result, it is impossible for the server to link the newly added file to the previous search tokens even if the simulator generate a query that has the new file among the results.

Algorithm 8 Simulator’s setup phase

Simulator

1: k_SE ← SE.Gen(1^λ)

2: Simulate C as {C_i ← SE.Enc(k_SE, {0}^|Di|)_1≤i≤n} 3: Create keyDict dictionary.

4: Create keyword dictionary ∆_s

5: L = {}

6: node cnt = 0

7: word cnt = 0

8: while node cnt , N do

9:            word flag = 1

10:           ∆s ∪ wword cnt

11: while word flag & node cnt , N do . Randomly generates a linked-list

12:                  list flag = 1

13:                  L = {}

14:  k_G ← {0,1}^λ         . k_G is used to encrypt the current linked-list

15:                 idnode ← {0,1}l0

16:                   Add (w_{word cnt},id_node,k_G) into keyDict

17: while list flag & node cnt , N do . Adds new nodes to L until flag becomes false

18:                           id_doc ← {id(D_i)|id(D_i) < L,1 ≤ i ≤ n)}

19:           AddNode(k_G, L,id_node,id_doc) 20:            node cnt + +

21:                         list flag ← {0,1}

22:                        if list flag then

23:                               idnode ← {0,1}l0

24:                       end if

25:                 end while

26:                  L ∪ L

27:                 word flag ← {0,1}

28:          end while

29:           word cnt + +

30: end while

31: Send L to server

Server

32: Generate I_s using L

Search. L^Search is the leakage function that the simulator S uses to imitate the search function. This information provides enough data for the simulator to randomly selects a required number of keywords from ∆_s. In the next step, the sub-queries will be created using keyDict dictionary. This means, the simulator should look in the keyDict to find the key and node IDs for each keyword that is being searched. Once the simulator receives the results, it generates new index entries for the queried keywords and updated the respective dictionary. We explained every step in detail in Algorithm 10. Since the queries\search tokens are non-deterministic and ephemeral, it is not feasible to unfold the search pattern using the search tokens. Moreover, recall that each sub-query can be real or fake\noise (known only to the user\simulator) which makes more difficult for the attacker to ascertain the search pattern.

Simulator

1: Simulate new file as {C_i ← SE.Enc(k_SE, {0}^|Di|)}

2: L = {}

3: ∆_tmp = {}

4: for i = 1 to i < |w_in| do

5:             w ← {w|w ∈ ∆_s,w < ∆_tmp}

6:             ∆_tmp ∪ w

7:             L = {}

8:             k_G ← {0,1}^λ

9:             idnode ← {0,1}l0

10:            Add (w,id_node,k_G) into keyDict

11:            AddNode(k_G, L,id_node,id_doc)

12:           L ∪ L

13: end for

14: Send L to server

Server

15: Update I_s using L

Algorithm 10 Search simulation

Simulator

1: Generate a random value k which shows the number of keywords in the current search

2: ∆_tmp = {}

3: q = {}

4: for i = 1 to i ≤ k do

5:             w ← {w|w ∈ ∆_s,w < ∆_tmp}

6:             ∆_tmp ∪ w

7:           Find w entries in keyDict and add them to q

8: end for

9: Shuffle(q)

10: Send q to server

Server

11: Perform q and return the result R = (R(q₁),…,R(q_k),bag)

Simulator

12: Generate new I_s entries based resultant bag from the server

13: Update keyDict respectively

14: Send new entries to the server

Server

15: Update I_s according to the new entries

Hence, we programmed a simulator that mimics our approach’s operations with the defined leakage functions in consideration. Remark that all simulated operations in Algorithm 8, 9, 10 are executing in polynomial time where a polynomial number of queries exists. Thus, the cloud\attacker is unable to discern the output generated by a real user from a simulator’s output unless with a neg(λ) amount or it shatters the employed pseudo random functions or the encryption scheme.

8. Conclusions

In this paper, first, we demonstrated that DSSE schemes with forward privacy are vulnerable to leakage-abuse attacks. Moreover, we introduced two new attacks to demonstrate the vulnerability of the forward-private approaches. All SSE schemes, including approaches with forward privacy, allow a defined level of information leakage (e.g., access\search pattern) to acquire more efficiency. In our introduced attacks, we showed by reverse analyzing the access pattern, it is feasible to recover the search pattern accurately. The recovered data can be used by traditional attacks to reveal the queries, search tokens, and as a result the documents in approaches with forward privacy. Our research demonstrates that the former attacks on traditional SSE schemes are adequate to methods that follows forward privacy principals.

We then addressed this problem by constructing a new Dynamic SSE approach that support update, search, and parallelization. Our method also obfuscates the search and access pattern. In our approach, we first create an inverted-index that maps each keyword to the documents IDs containing the respective keyword. We inject fake documents’ IDs in the result-set of each keyword to hide the access pattern. Only the user can discern the fake IDS from real ones. Furthermore, each search request consists of a number of sub queries where all except one are noise which is only known to the user.

Last, using a standard simulation model, we provided the security proof of our approach. Moreover, we conducted a through performance analysis on the implemented prototype that demonstrates the efficiency and low system-cost of our proposed method. As a future work, we plan to upgrade our scheme to support semihonest cloud servers.

1. D. X. Song, D. Wagner, A. Perrig, “Practical techniques for searches on en- crypted data,” in Security and Privacy, 2000. S&P 2000. Proceedings. 2000 IEEE Symposium on, 44–55, IEEE, 2000.
2. E.-J. Goh, et al., “Secure indexes.” IACR Cryptology ePrint Archive, 2003, 216, 2003.
3. Y.-C. Chang, M. Mitzenmacher, “Privacy preserving keyword searches on remote encrypted data,” in International Conference on Applied Cryptography and Network Security, 442–455, Springer, 2005.
4. N. Cao, C. Wang, M. Li, K. Ren, W. Lou, “Privacy-preserving multi-keyword ranked search over encrypted cloud data,” IEEE Transactions on parallel and distributed systems, 25(1), 222–233, 2014, doi:10.1109/TPDS.2013.45.
5. E. Stefanov, C. Papamanthou, E. Shi, “Practical Dynamic Searchable Encryp- tion with Small Leakage.” in NDSS, volume 71, 72–75, 2014.
6. R. Bost, “Forward Secure Searchable Encryption,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 1143– 1154, ACM, 2016, doi:10.1145/2976749.2978303.
7. M. Etemad, A. Ku¨pc¸u¨, C. Papamanthou, D. Evans, “Efficient dynamic search- able encryption with forward privacy,” Proceedings on Privacy Enhancing Technologies, 2018(1), 5–20, 2018, doi:10.48550/ARXIV.1710.00208.
8. X. Liu, G. Yang, Y. Mu, R. Deng, “Multi-user verifiable searchable symmetric encryption for cloud storage,” IEEE Transactions on Dependable and Secure Computing, 2018, doi:10.1109/TDSC.2018.2876831.
9. K. Salmani, K. Barker, “Leakless privacy-preserving multi-keyword ranked search over encrypted cloud data,” Journal of Surveillance, Security and Safety, 2020, doi:10.20517/jsss.2020.16.
10. K. Salmani, K. Barker, “Don’t Fool Yourself with Forward Privacy, Your Queries STILL Belong to Us!” in Proceedings of the Eleventh ACM Confer- ence on Data and Application Security and Privacy, CODASPY ’21, 131–142, Association for Computing Machinery, New York, NY, USA, 2021, doi: 10.1145/3422337.3447838.
11. K. Salmani, K. Barker, “Dynamic Searchable Symmetric Encryption with Full Forward Privacy,” in 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), 985–995, 2020, doi:10.1109/ICSIP49896.2020. 9339338.
12. C. Liu, L. Zhu, M. Wang, Y.-A. Tan, “Search pattern leakage in searchable en- cryption: Attacks and new construction,” Information Sciences, 265, 176–188, 2014.
13. D. Cash, P. Grubbs, J. Perry, T. Ristenpart, “Leakage-abuse attacks against searchable encryption,” in Proceedings of the 22nd ACM SIGSAC confer- ence on computer and communications security, 668–679, ACM, 2015, doi: 10.1145/2810103.2813700.
14. Y. Zhang, J. Katz, C. Papamanthou, “All Your Queries Are Belong to Us: The Power of File-Injection Attacks on Searchable Encryption,” in 25th USENIX Security Symposium (USENIX Security 16), 707–720, USENIX Association, Austin, TX, 2016.
15. O. Goldreich, R. Ostrovsky, “Software protection and simulation on oblivious RAMs,” Journal of the ACM (JACM), 43(3), 431–473, 1996.
16. M. Naveed, “The Fallacy of Composition of Oblivious RAM and Searchable Encryption.” IACR Cryptology ePrint Archive, 2015, 668, 2015.
17. R. Canetti, U. Feige, O. Goldreich, M. Naor, “Adaptively Secure Multi-party Computation,” in Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing, STOC ’96, 639–648, ACM, New York, NY, USA, 1996, doi:10.1145/237814.238015.
18. X. Song, C. Dong, D. Yuan, Q. Xu, M. Zhao, “Forward private searchable symmetric encryption with optimized I/O efficiency,” IEEE Transactions on Dependable and Secure Computing, 2018, doi:10.1109/TDSC.2018.2822294.
19. R. Curtmola, J. Garay, S. Kamara, R. Ostrovsky, “Searchable symmetric encryp- tion: improved definitions and efficient constructions,” Journal of Computer Security, 19(5), 895–934, 2011.
20. D. Boneh, G. Di Crescenzo, R. Ostrovsky, G. Persiano, “Public key encryption with keyword search,” in International conference on the theory and applica- tions of cryptographic techniques, 506–522, Springer, 2004.
21.  M. Bellare, A. Boldyreva, A. O’Neill, “Deterministic and efficiently search- able encryption,” in Annual International Cryptology Conference, 535–552, Springer, 2007.
22.  N. Attrapadung, B. Libert, “Functional encryption for inner product: Achieving constant-size ciphertexts with adaptive security or support for negation,” in International Workshop on Public Key Cryptography, 384–402, Springer, 2010.
23. A. Boldyreva, N. Chenette, Y. Lee, A. O’neill, “Order-preserving symmetric en- cryption,” in Annual International Conference on the Theory and Applications of Cryptographic Techniques, 224–241, Springer, 2009.
24. J. Li, Q. Wang, C. Wang, N. Cao, K. Ren, W. Lou, “Fuzzy keyword search over encrypted data in cloud computing,” in INFOCOM, 2010 Proceedings IEEE, 1–5, IEEE, 2010.
25. M. Kuzu, M. S. Islam, M. Kantarcioglu, “Efficient similarity search over en- crypted data,” in Data Engineering (ICDE), 2012 IEEE 28th International Conference on, 1156–1167, IEEE, 2012, doi:10.1109/ICDE.2012.23.
26. Z. Guo, H. Zhang, C. Sun, Q. Wen, W. Li, “Secure multi-keyword ranked search over encrypted cloud data for multiple data owners,” Journal of Systems and Software, 137, 380–395, 2018, doi:https://doi.org/10.1016/j.jss.2017.12.008.
27. S. K. Kermanshahi, J. K. Liu, R. Steinfeld, S. Nepal, “Generic Multi-keyword Ranked Search on Encrypted Cloud Data,” in European Symposium on Re- search in Computer Security, 322–343, Springer, 2019.
28. S. Kamara, C. Papamanthou, T. Roeder, “Dynamic Searchable Symmetric Encryption,” in Proceedings of the 2012 ACM Conference on Computer and Communications Security, CCS ’12, 965–976, ACM, New York, NY, USA, 2012, doi:10.1145/2382196.2382298.
29. M. Naveed, M. Prabhakaran, C. A. Gunter, “Dynamic Searchable Encryption via Blind Storage,” in 2014 IEEE Symposium on Security and Privacy, 639–654, 2014, doi:10.1109/SP.2014.47.
30. J. Ning, J. Xu, K. Liang, F. Zhang, E.-C. Chang, “Passive attacks against search- able encryption,” IEEE Transactions on Information Forensics and Security, 14(3), 789–802, 2018, doi:10.1109/TIFS.2018.2866321.
31. “Gutenberg Publication,” https://www.cs.cmu.edu/˜enron/, accessed: 2019-11-08.
32. M. S. Islam, M. Kuzu, M. Kantarcioglu, “Access Pattern disclosure on Search- able Encryption: Ramification, Attack and Mitigation.” in Ndss, 20, 12, Citeseer, 2012.

(Click Here)