1. Introduction

In our article we have shown the possibilities and necessity of applying an interdisciplinary approach to solving the problem of flow and fracture of materials [1]. Kauzmann was one of the first scientists who applied the theory of reaction rates to the yielding of solids, examining creep as a process of directional diffusion under the effect of applied stresses [2]. Assuming that the applied stress reduces the energy barrier in one direction and increases the barrier to approximately the same extent in the opposite direction, he derived an equation for the excess number of transfer acts per unit time in the direction of applied stresses:

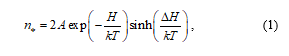
where H is the initial height of the energy barrier, DH is the variation of this height under the stress effect, k is the Boltzmann constant, T is the absolute temperature, and A is the reaction constant. At high values of ΔH, the reverse flow through the barrier is usually ignored, and Eq. (1) takes the form

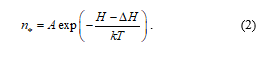
Kauzmann assumed that ΔH depends in a linear manner on stresses, and (2) was confirmed by some experiments.

If some process in the material is caused by thermal activation, the dependence of the process rate on the stress σ and temperature is described by the Arrhenius equation in which the pre-exponential factor depends in the general case on the stress and temperature. Specific types of the expressions V₀(σ, T) and activation energy U(σ) are determined by the range of temperature–force conditions of loading. Each such region is characterized by the dominance of some deformation mechanism or mass transfer mechanism. The physical interpretation of this equation is based on the theory of overcoming potential barriers. The exponent in (3) is interpreted as the probability of the transition through the barrier or as the fraction of atoms that are in the activated state at each time instant [3].

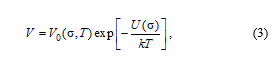
Based on this concept, the analysis of strength and deformation characteristics of any material should be started from the analysis of results of simple experiments on fracture at constant stress and temperature to identify the basic features of these processes corresponding, for example, to the form (2). Tests performed under monotonic loading provide additional data, which may ensure a more accurate description of the material behavior [4, 5]. In this case, the main research method is the thermally activation analysis.

With cyclic loading with small amplitudes leading to fatigue failure, thermal activation analysis cannot be performed. The process of failure is localized and distributed in the volume of the material according to the field of internal stresses. The problem can be solved only by mathematical modeling of local processes of fracture, based on the same patterns of fracture that were revealed during the study of the creep of the material.

There are objective reasons for the lack of reliable methods of durability calculations. Because of the large variety of operation conditions, investigations were separated into individual fields, and the bearing capacity of particular structural elements was studied only for particular conditions of their operation. Internal processes in the material under fracture are rather complicated and versatile; the lack of information about their relationship with macroscopic properties of solids gave rise to many approaches both to understanding the fracture phenomenon and to developing engineering methods of estimating the bearing capacity of various structures.

Despite comprehensive investigations, there is no unified concept, which would allow successful evaluation of strength and durability of structures under hostile conditions of their operation. There are many publications dealing with physical and metal science aspects of strength and durability. These studies assist in understanding what happens in the material and explain experimentally observed specific features of the material behavior. However, such studies are not directly related to calculations of strength and durability in practice. There are many approaches and methods for determining the bearing capacity of structures depending on the loading character and temperature, though each of these approaches and methods is applicable only in a limited range of operation conditions. If the range of operation conditions is extended, there arises a problem of matching these approaches. The problem is difficult because the basis of the problem solution, i.e., the material itself, is ignored. It is sufficient to say that even different units of durability measurement are different for different loading types: these may be the time, or the number of cycles, or even the sum of loads. It is necessary to revise the traditional methods used for estimating strength and durability of structures from the viewpoint of physics of material properties.

The solution of the problem of assessing the durability of materials in structures under arbitrary thermal-force loading is impossible without constructing new models of continuous media on the basis of physics and thermodynamics of internal processes that occur in loaded solids. It is only an adequate presentation of a solid as a physical medium that offers a possibility of considering the entire multitude of interrelated processes of deformation and fracture, structural transformations, and physical and chemical effects. The analysis of experimental data from this viewpoint leads to qualitatively new ideas of material properties and allows determining the optimal volume of the experiment and the sequence of obtaining the characteristics of new alloys, thus, reducing the cost and time of structural design.

2. Basic laws of failure and deformation of materials

Examination of the kinetics of fracture of polymers, pure metals, alloys, and other materials showed that the following dependence of durability as the inverse of the average rate of failure  on the temperature and stress is satisfied in many cases (for a mole of a substance by replacing the Boltzmann constant k with the universal gas constant R):

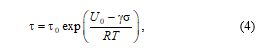
or in the general case when temperature, stress and parameter g depend on time t,

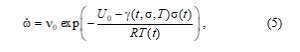
where U₀ is initial activation energy of fracture, g is the structure-sensitive coefficient (activation volume),  – characteristic Debye frequency [6, 7]. The expression for the plastic strain rate at a constant stress (steady creep stage) obtained in the same experiments has a similar form

indicating a close relationship of the fracture processes with the processes of plastic deformation. A comparison of the parameters of (4), (5) and (6) for many materials in fact shows the equality (within the limits of the error of experimental data processing) of U₀ and Q₀, γ and a, and the product  is equal to the residual strain  accumulated at the steady creep stage [6]. The residual strain changes only slightly (approximately by an order of magnitude) with a large change in the duration of fracture (9–10 orders) [7]. The values of the pre-exponential factors in (4) and (6) determined in processing of experimental data for different materials were in the range 10⁻¹¹–10⁻¹⁴ s for  and 10¹²–10¹³ s⁻¹ for .

In many cases, the activation characteristics of atomic rearrangement processes are reflected in the macroscopic characteristics of the solid under loading. Therefore, natural attempts have been made to examine the mechanism of these processes by means of the thermal activation analysis. For this purpose, in accordance with (2), (3), (4) or (5), we plot the logarithm of the process rate on the stress at different temperatures and on the reciprocal value of temperature and different stresses.

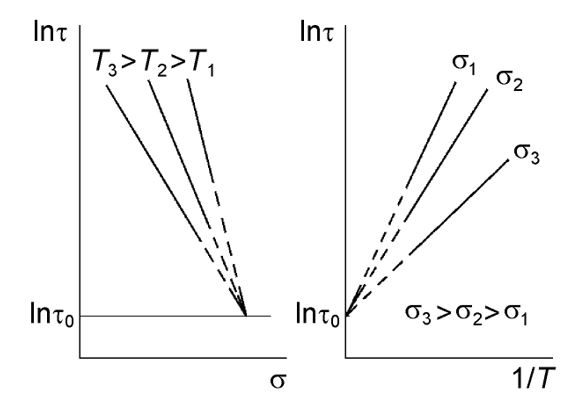
Figure 1: Temperature–force dependences of durability for determining the activation parameters of the fracture process

If, for example, (4) is valid and its parameters are constant, then we obtain a series of straight lines in the corresponding coordinates, with the lines converging in a band (Fig. 1 and 2). At the same time, it is evident that the process itself may lead to changes in the state of the medium in which it takes place. This results in changes of the parameters and in their dependence on both the external conditions (σ, T) and the stage of the process, i.e., internal conditions. For materials, these are structural changes, being the result of the combined effect of different atomic mechanisms in different configurations at each scale level.

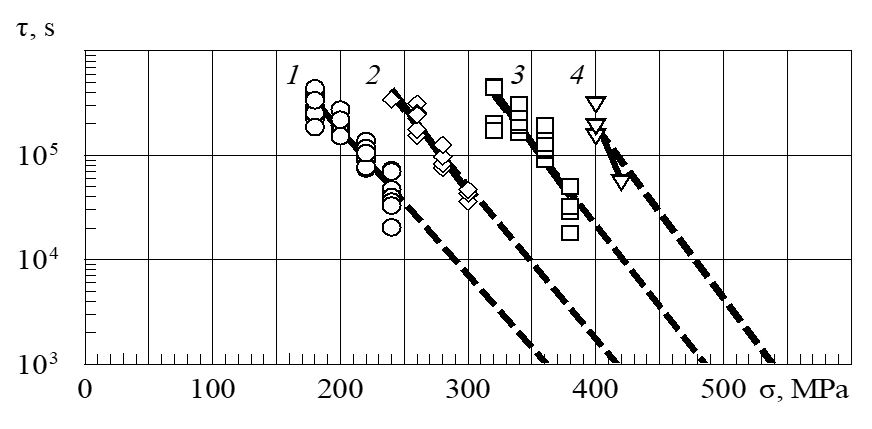
Figure 2: Temperature–force dependences of durability for determining the activation parameters of the fracture process

In the article [1], the force dependences of the activation energy of fracture and deformation for alloy 1201 T1 were shown in Figure 1 (Al-Cu-Mn system). The same refers to duralumin (the durability of its specimens is shown in Figure 2, Al-Cu-Mg system). The force dependence of the activation energy of fracture obtained in this experiment is shown in Figure 3. In the range of stresses and temperatures in which they were tested, the coefficient g also has a constant (minimum) value, and the specimens demonstrate structurally stable “long-term strength,” which can be recalculated from one temperature-force mode to another. Similar dependences were previously given earlier for this and other aluminum alloys, including quasi-stable states at g = g_max [1, 4, 5, 8, 9]. All this can be seen only through the thermal activation analysis, taking into account, among other things, the quantum effects of low-temperature fracture of materials [9].

For mechanical engineers who are used to terms “strength” or “long-term strength,” we can offer a more stringent strength characteristic – the strength parameter. Let us define it as P_b = 1/g. Then the above-mentioned specimens in a certain temperature-time interval, regardless of the loading speed and temperature, will have P_b = const, i.e., exactly the same “strength” determined only by the material structure (activation volume g). The dimension of P_b is MPa×mol/kJ, and it is also independent of the loading trajectory if the loading rate is variable. Thus, the comparison of the “strength” tests results is justified.

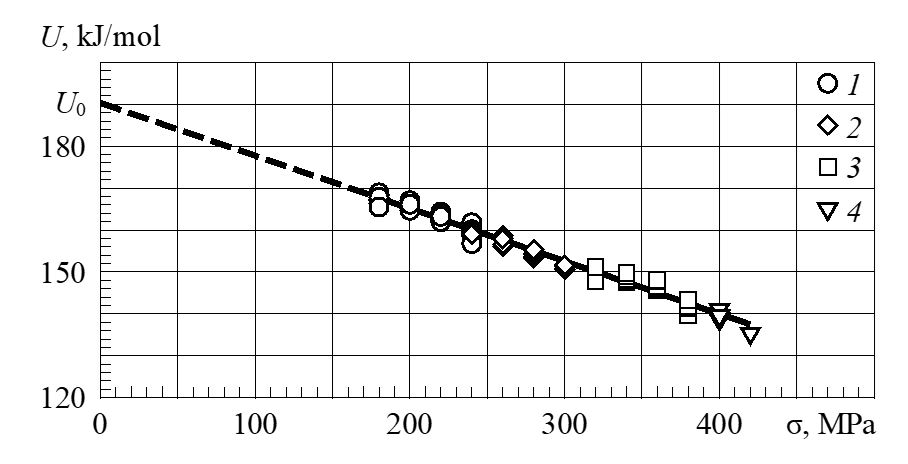
Figure 3: Force dependences of the activation energy of fracture of 80 duralumin specimens (Fig. 2) in the range of stresses of 180¸420 MPa and temperatures
of 398¸473 K; temperature, K: 1 – 473, 2 – 448, 3 – 423, 4 – 398

For mechanical engineers who are used to terms “strength” or “long-term strength,” we can offer a more stringent strength characteristic – the strength parameter. Let us define it as P_b = 1/g. Then the above-mentioned specimens in a certain temperature-time interval, regardless of the loading speed and temperature, will have P_b = const, i.e., exactly the same “strength” determined only by the material structure (activation volume g). The dimension of P_b is MPa×mol/kJ, and it is also independent of the loading trajectory if the loading rate is variable. Thus, the comparison of the “strength” tests results is justified.

An extensive experiment analyzed by the methods described here revealed the influence of creep of the binder on the strength properties of fiberglass plastic [10]. Figure 4 shows the force dependences of the activation energy of fiberglass plastic fracture under longitudinal bending (a) and tensile loading (b). For longitudinal bending, the mean values for 20 or 40 specimens tested in each mode are shown. The diamonds denote modes of monotonic loading with different rates, and the circles show loading by a constant bending moment. For tensile loading, the data for each specimen are provided. The stress scatter corresponds to monotonic loading, and the scatter of the activation energy corresponds to a constant load.

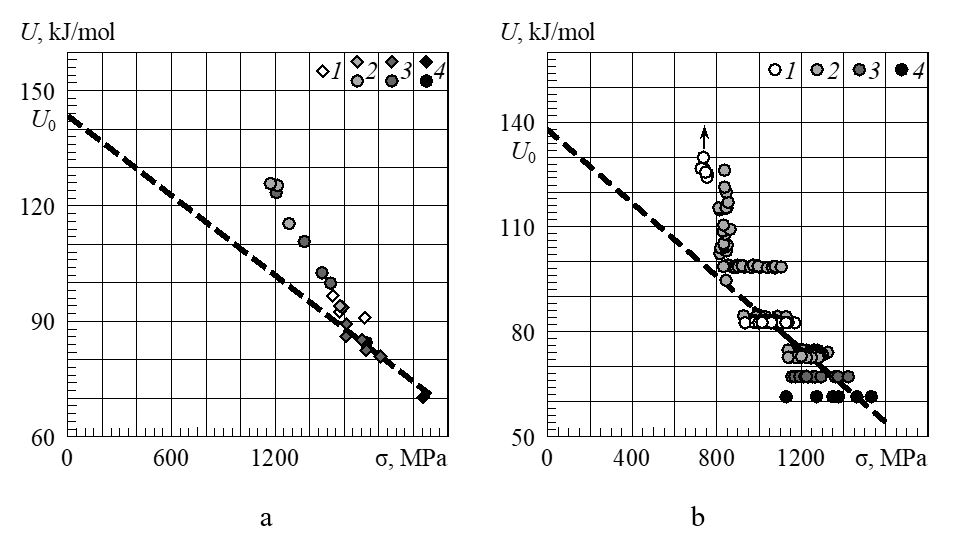
Figure 4: Force dependences of the activation energy of fiberglass fracture
(rods with a diameter of 5.5 mm) under longitudinal bending (a)
and tensile loading (b) [10]; temperature, T, °C:
a) 1 – +60, 2 – +50, 3 – +20, 4 – −30; b) 1 – +50, 2 – +9–20, 3 – −8, 4 – −30

The lines drawn through those values of U(s) that satisfy the equation of a straight line with the minimum slope showed approximately the same values of the initial activation energy U₀. The deviations from these lines illustrate the role of binder creep in the distribution of forces over the fibers in the composite, which is equivalent to changing the material structure. Thus, the straight lines correspond apparently to some stable state of the material structure, when the initial stage of creep has already ended. With a decrease in stresses and an increase in the duration of the failure process, the experimental values of U(s) deviate from these lines in the direction of increasing durability. Rapid loading or temperature reduction leads to more uneven loading of the fibers, and they begin to break down sequentially. The rod failure process is finalized even at lower loads [10] in contrast to metals in which the rupture stresses of the specimens increase in proportion to the growth of the logarithm of the loading rate (or to the decrease in the logarithm of the fracture time).

Under monotonous loading, the values of U(s) are calculated by the equivalent failure time t_eq in accordance with (5) reduction to maximum stresses, based on the same damage in accordance with the Bailey criterion [11], according to the formula

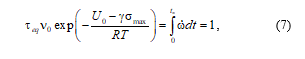
where  is the loading time along a particular trajectory to a stress , often less , at which specimen fracture occurs. The error in determining the activation volume g turns out to be small, since the entire process of failure is short-lived and concentrated in the range of action of high stresses.

The change in the activation volume g is associated with a change in the structure of the material and each material has its own reasons and characteristics. These can be, for example, relaxation processes of internal stresses, diffusion of alloying elements in the alloy matrix or creep of the binder in the composite material. And each of them requires separate study and modeling.

3. Mathematical modeling of the rheological properties of the material

In accordance with the patterns of fracture and deformation of materials (1) and (2) observed in the experiment, new bodies were introduced into rheology, called Zhurkov (Zh) and Kauzmann (Km) bodies [12]. Denoting  and  in (6), we obtain the rheological equations of the Zh and the Km solid:

The sequential and parallel connections of these bodies with the Hooke body (H) having an elastic modulus M form bodies similar to the Maxwell and Kelvin (Voigt) bodies, which describe the general and local plastic flow in materials. They are indicated by the symbols PM₁ and PM₂ (with Zh bodies) or PM₅ and PM₆ (with Km bodies) [1, 12]. A set of such elements is a structural model of the material that shows in Figure 5. The difference from the similar mechanical structural model of the material based on the Saint-Venant body [13] is the replacement of dry friction elements with elements that describe plastic flow kinetics (8). An element of the general plastic flow of the material has also been added.

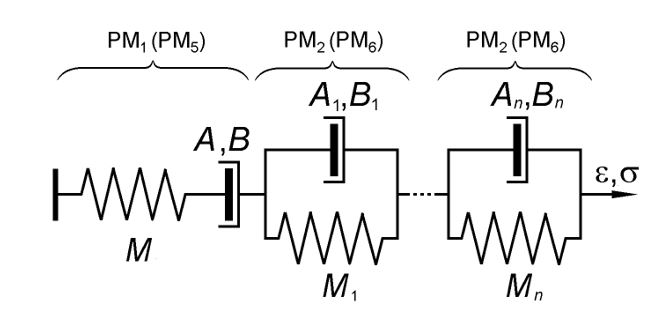
Figure 5: Structural model of a material describing the elasticity, creep, and hysteresis-type inelasticity by a set of elements with a parallel connection
of an elastic Hooke’s body and a plastic flow body
(Zhurkov’s or Kauzmann’s body) [1, 4]

The plastic flow and the process of material failure are both occurring and interrelated [14]. Therefore, describing the rheological properties of materials, it is possible to associate them with the accumulation of damage and to assess the durability of structural elements under arbitrary external effects [5].

The rheological equation, for example, of the PM₁ solid (Fig. 5) as the equality of the total strain rate to the sum of the elastic strain rate of the H solid and the plastic strain of the Zh solid (8) has the following form [1, 12]:

which depends on the strain rate and temperature;

• at loading with a constant rate, we obtain the dependence of strain on time

At , this dependence transforms to the steady creep equation

Here  and  are the stress and strain at the time instant .

Solutions of (9) for a constant strain rate C (11) or for a constant loading rate D (13) give two different relationships between stresses and strains. As a result, we get several “theories of plasticity” [5]. If the material structure changes during plastic flow, the parameters of (9) should be replaced with functions describing the transition of the material from one state to another. This can be done by analyzing the experimental deformation curves by time steps [1, 12]. No new “theories of plasticity” are required. And stress relaxation according to solution (10), in which the material also is also fractured, does not require any energy expenditure. Everything happens due to the internal energy of a solid, the measure of which is temperature.

For the PM₂ solid (Fig. 5), on the basis of solving the equilibrium and strain compatibility equations, we can write the following rheological equation:

Solutions (10), (16) and (17), (18) provide completely identical results in the range of high stresses. Therefore, when using the Km solid in the models, it is more efficient to use the solutions for models with the Zh solid in appropriate sections of the loading program, because this is a simpler procedure. This also refers to the algorithms of processing the experimental data for determining the parameters of the rheological models. Figure 6 shows the stresses in the PM₁ and PM₅ solids with their rapid deformation to the establishment of constant flow stresses and subsequent curing at a fixed strain. Calculations were carried out for duralumin: Q₀ = 192.6 kJ/mol, a = 0.142 kJ/(mol×MPa).

If the material is characterized by the same behaviour in tensile and compressive loading, it is only necessary to change the signs of the stresses, strains, and their rates to the opposite signs when passing to the compression region. Otherwise, the parameters A and B should also differ. The algorithm of calculations in the transition through zero should be also accurate. The time step in unloading should be selected in such a manner that the stresses in the flow elements should approach zero prior to “reversing” of the equations. Otherwise, the strains would be determined with errors.

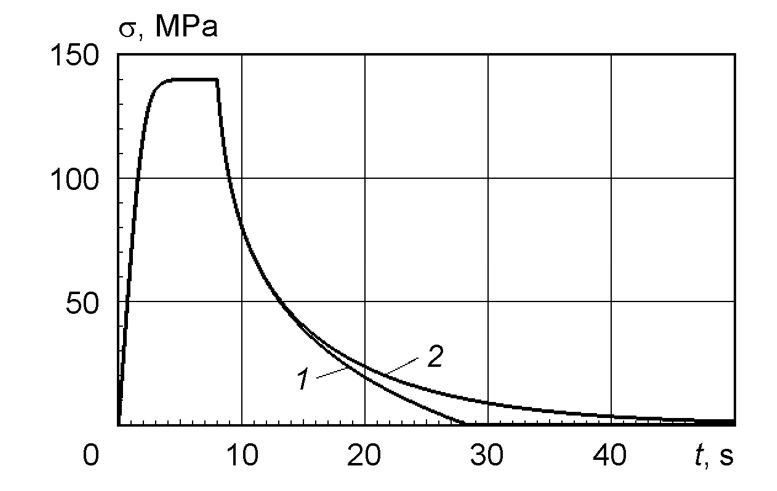
Figure 6: Deformation of the PM₁ (1) and PM₅ (2) solids with a constant strain rate to the “yield limit” and subsequent stress relaxation at a constant strain (the parameters of the rheological solids were taken for the D16 T material at 573 K)

When the stresses are greater than −ln(AM/D)/B in (15), there is something like a functional relationship between the stresses and strains in subsequent loading. In this case, we have “plasticity with hardening.” If loading is terminated, we obtain equations of the so-called logarithmic creep [16], which were interpreted analytically in (16). In processing experimental data for an actual material, it is necessary to separate the plastic flow with actual hardening accompanied by changes in the material structure and by a decrease in the activation volume a from the local flow. The latter takes place in a set of local volumes; in each volume, it is characterized by its own activation parameters.

As a test problem, we study with a stress jump. Experimental results of such tests have long been known [16]: in the unsteady stage of creep, the initial stress increased or decreased by a jump, and after some time it returned to the same level.

Figure 7 gives results of calculations of the deformation process in the D16 T alloy performed using its model. The flow characteristics of the material predicted by the model are exactly the same as those of the real flow. No additional conditions apart from specification of the loading program and the temperature are required [12].

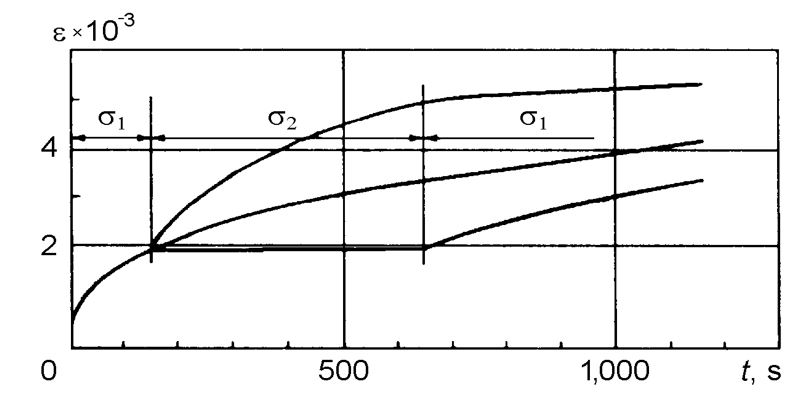
Figure 7: Creep with a stress jump: calculations using the model of the material D16 T (423 K); s₁ = 300 MPa, s₂ = 270 and 310 MPa

Other examples of the calculation of strains of specimens during loading and unloading are given in the article [5]. Experimental data, with which the results of calculations are compared, are contained in the article [17] or obtained by the author himself.

For such calculations based on the amplitude dependence of inelasticity, parametric identification of the structural model of the material (PM₂ or PM₆ bodies) is performed by dividing it into components that characterize each structural element. The typical amplitude dependence of the inelastic deformation of the material in the form of the width of the inelasticity loop is shown in Figure 8.

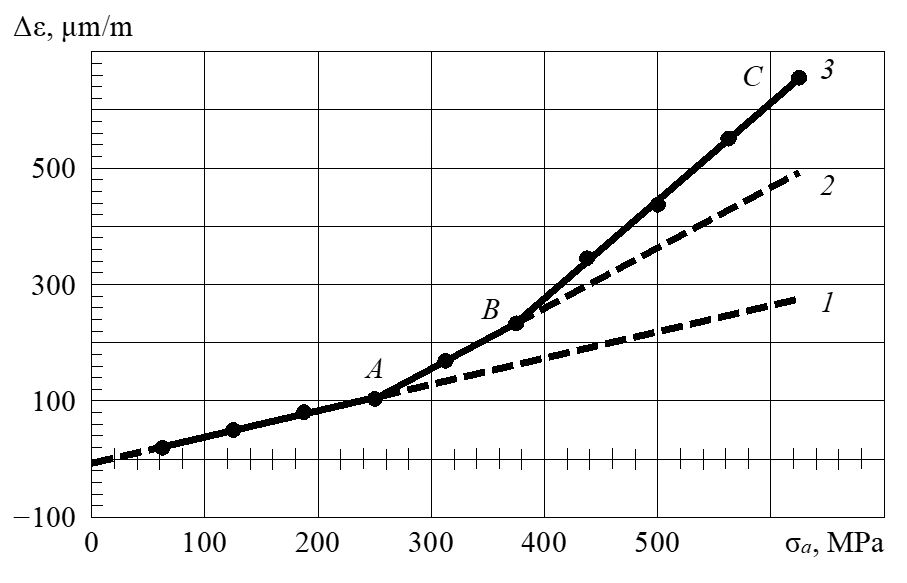
Figure 8: An example of a typical amplitude dependence of the inelasticity loop width of an eight-layer unidirectional carbon fiber reinforced plastic

The broken line 3 in the figure shows the value of the loop width: the maximum distance between the loading and unloading curve e = f(s), calculated at a constant mean value of the cycle stresses. The data are taken from an experiment performed on unidirectional carbon fiber reinforced plastic. Up to point A (line 1), there is always relaxation-type inelasticity in any material [18, 19]. As the loading amplitude increases, hysteresis-type inelasticity additionally appears (segment AB on line 2). This is followed by a new increase in inelasticity (segment BC). Each loop width increment is ascribed to one structural element of the material model, which will determine its durability in the corresponding range of amplitudes.

The dependence of durability on mean cyclic stresses is taken into account in the rheological model of the material by changing the loop width through the change of the parameter  in (6) for each structural element of the material model. For this purpose, in each amplitude range it is necessary to test with a different asymmetry index [4], and the endurance value N (the number of cycles passed during the specimen fracture) will be inversely proportional to the increment of the loop width in this range.

After parametric identification of the mathematical model carried out using experimental data for a specific frequency and temperature of tests, it is possible to proceed to calculations of the durability of the material under arbitrary changes in temperature and stress within the studied range of temperature-force dependences of the deformation activation energy and the fracture activation energy. When the material structure changes, the parameters A and B in (8) should be replaced by functions describing the accompanying thermally activated processes or the results of some other external effects leading to these changes.

An example of this is the fracture of duralumin at various combinations of temperature and stress. A precipitation aged alloy, which has reached the first maximum of hardness, undergoes an phase aging stage in the process of failure (intermetallic precipitation). Its hardness, having reached the second maximum, begins to decrease. This also happens in the absence of stresses, and the process accelerates under load, which affects the residual strain of the specimens. Figure 9 shows the dependence of the residual strain of duralumin specimens on the tensile test mode. The observed minimum of residual strain during the period of steady creep is associated with the achievement of the maximum hardness of the material.

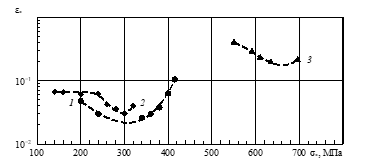
Figure 9: Dependence of the residual strain of duralumin specimens on the stresses and temperature of the tests (creep under constant and monotonically increasing loads); T, K: 1 – 423, 2 – 448, 3 – 293¸523; 1, 2 – average values for several specimens, 3 – true residual strains in the neck of specimens under monotonic loading;  – initial stress values at constant load (1, 2) and the highest stress values at specimen rupture (3).

The change in hardness over time of alloys similar in composition was studied in [20–23] and others. The time to reach a certain state of the alloy in the process of transformation, which occurs due to thermal activation, is determined by a typical expression of the theory of the rates of processes [24]

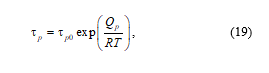
where Q_p is the activation energy of precipitate growth, the value of which is equal to the effective value of the activation energy of diffusion of alloying elements in the alloy matrix. The activation energy of diffusion, similar to what we observe during failure, depends approximately linearly on stresses, and the diffusion process is accelerated as a result of plastic deformation [18]. Then, taking into account the simultaneity of the process of precipitations in the centers, which additionally arise due to the accumulated plastic strain , expression (19) takes the form

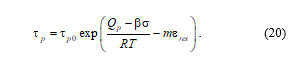
In the case of an additional increase in the number of precipitation centers due to a greater concentration of vacancies, the pre-exponential multiplier in (20) should include a multiplier expression that takes into account the temperature of the cooling medium during quenching [18]. At this temperature, the equilibrium concentration of vacancies has time to be established [20], and in this form this expression can participate in the calculations of the aging process at low temperatures and in the description of the recovery process. The characteristic maximum hardness of isolate-aged alloys and the corresponding minimum of plasticity make it possible to estimate the activation parameters in the expression (20).

By equating the failure time (4) and the time to reach the minimum of the residual creep strain (20) obtained under certain loading conditions (Fig. 9), it is possible to estimate the parameters included in (20). Having the parameters of (20), we obtain an expression for the conditional rate of the precipitation process , the integral of which in time will give one when the second hardness maximum is reached. The next task is to link the aging rate with the strength and deformation properties of the material. This can be done through the hardness of the alloy, since indentation of the indenter is the same process of failure associated with large plastic strains [18].

In the absence of a load for triple alloys (2.5% Cu, 1.14% Mg and 3.0% Cu, 1.36% Mg), similar in composition to D16 T and AK4-1 T1 alloys of the same system, Hardy obtained a Q_p value of 32 and 33 kcal/mol, respectively [22]. This is approximately equal to the value of the activation energy of diffusion of copper in aluminum (32.6 kcal/mol [25], 1.4 ± 0.1 eV or 31.8 ± 2.3 kcal/mol [26]). After processing the reference data on changes in the deformation characteristics of AK4-1 T1 alloy specimens under monotonous loading after different aging modes, we obtained an estimate of Q_p = 32.4 kcal/mol and  = 10^-10 s. That is, all estimates of the activation energy of the decay process of a solid solution turn out to be quite close.

After the introduction of the hardness function into the equation of the failure rate (5), with which the activation parameters of the fracture process are associated, and then calculations of the thermo-cyclic loading of structural elements were performed, taking into account the decay of a supersaturated metallic solid solution in these precipitation hardening alloys. Calculations of the fatigue failure process at low temperatures do not require taking into account such structural transformations, and it is quite acceptable to assume the structure of the material corresponding to the initial state of the alloy [18].

4. Examples of applying an interdisciplinary approach to practical tasks

Having the activation parameters U₀ and g (which correspond to parameters A and B in Figure 5), it is possible to perform calculations for those loading conditions when the material flows throughout the entire volume, regardless of how the stresses and temperature change. The internal stresses in the so-called “fracture centers” naturally change, and this requires special modeling. Figure 10 shows the comparison of experimental data with the calculation for different temperature-time and temperature-force loading conditions of structural specimens made of AK-1 T1 alloy. Vertical lines correspond to the actual scatter of durability in the experiment, horizontal lines to the range of calculated estimates made taking into account the basic errors of the test program by load and temperature.

The figure shows that the calculated estimates of durability fall within a twofold range of deviations from the experimental data, which is usually observed when testing the same material of different batches. The calculations are made taking into account the decay of supersaturated metallic solid solution in a given alloy, aged to the second maximum hardness (T1 state), representing the parameter  in (6) as the product of the residual strain by the frequency multiplier  and relating it to the change in the hardness of the alloy. In all cases, fracture occurs as a result of creep, regardless of how the stresses in material or the dangerous places of structural components change [4, 18].

 

Figure 10: Comparison of calculated (t_c) and experimental (t_e) values of the durability of specimens and structural components made of AK4-1 T1 alloy tested at various loads and temperatures: 1, 2 – strip with a central hole and a longitudinal stringer under thermo-cyclic loading [4]; 3 – rod: constant and variable stresses at 543 K at 10 Hz [18]; 4 – full-scale structure fracture, tested under the specified temperature-force program (with addition of crack propagation period)

The determination of the remaining parameters of the structural model of the material (Fig. 5) requires cyclic loading at a constant mean stress component of the cycle s_m. The values of temperature, frequency and shape of the loading cycle must be set. Stepwise increasing the amplitude of loading, we obtain the amplitude dependence of inelasticity (Fig. 8), which is used to select amplitude values for fatigue tests according to characteristic points. That is, for example, for the AB and BC ranges, two amplitude values must be selected each. Then, these modes must be tested with two mean load components. For each amplitude range, it is sufficient to know for any one mode the inelastic strain in the loading cycle. After parametric identification of the model, it is possible to perform calculations at a different temperature, frequency, cycle shape and generally at arbitrary changes in them, if one assumes that no changes in the structure occur in the material. Otherwise, this requires a separate study, and the material model parameters must be replaced by functions that represent these changes.

Using the relationship between inelastic strains and damage accumulation, the mathematical model makes it possible to calculate the durability for various spectra of external effects, be it stress or temperature, representing their implementation by piecewise linear approximation. Having solutions of differential equations, for example, (9) and for other structural elements of the model at constant stresses or strains and linearly varying, for example, (15) and (16), it is possible to calculate any arbitrary process of temperature-force loading [4].

In Figure 11 shows a comparison of the calculated estimates of durability of structural components with experimental data for various loading cases. All tests were carried out at a temperature of 293 ±2 K. Calculations were performed for a temperature of 293 K, assuming the structure of the material unchanged, corresponding to its initial state.

As in the previous example (Fig. 10), the calculated estimates of durability were made using a model of a design element that transforms in time the nominal stresses or loads into strains in the places of their concentration [4, 9]. For the specimens whose durability is marked by points 3, 4 and 6, the calculations were performed for two different quality batches of this material.

As in the previous example (Fig. 10), the calculated estimates of durability were made using a model of a design element that transforms in time the nominal stresses or loads into strains in the places of their concentration [4, 9]. For the specimens whose durability is marked by points 3, 4 and 6, the calculations were performed for two different quality batches of this material.

The time step of calculations at wide-band load spectrum is chosen minimum 0.25 or 0.5 period of the highest-frequency component of the spectrum. All load spectra were represented by equivalent polyharmonic pseudo-random processes (PRP) having the same spectral density, or by a real loading process recorded in operation [27]. The degree of discreteness of the spectrum depends on the material and type of the design element.

Figure 11: Comparison of calculated (t_c) and experimental (t_e) values of durability of structural specimens and structures made of 1201 T1 alloy tested under different loading programs (T = 293 ±2 K): 1 – plate-bar without notch, constant spectral density value in the interval 0.5÷10.5 Hz, 6 harmonics;
2 – plate-bar without notch, narrowband random noise in the interval 0÷5.5 Hz, 13 harmonics; 3 – plate-bar with notch, narrowband random noise in the interval 0÷5.5 Hz, 13 harmonics; 4 – plate-bar with notch, block 87-step program, triangular cycle shape at 10 Hz; 5 – acoustic tests of panels in the interval 0÷200 Hz; 6 – notched plate-bar, forced flight cycle 1200 s [23], compiled from records of bending moments on the wing of an airplane-laboratory; 7 – notched plate-bar, forced flight cycle GAG at 0.025 Hz; 8–30 mm wide plate-bar with a central hole 20 mm, cyclic tests in the frequency range 0.1÷40 Hz with different cycle shape of loading

As in the case of variable temperatures (Fig. 10), the calculated estimates of durability are located in the range of twofold deviations from their experimental values. The calculations were performed based on the average statistical data of the durability of one of the semi-finished products of this material. To do this, two values of the mean cycle stresses are taken for each amplitude which selected by the inelastic characteristics of the material.

In each case, the structures are loaded in a different way; therefore, obtaining estimates requires statistical data on the typical operation conditions. Calculations are performed with averaged statistical data on loading, i.e., the averaged spectral density of the processes, which is then transformed to a discrete spectrum by the method of summation of elementary random functions [18]. As a result, one obtains a PRP, which is statistically equivalent to a real random process.

Examples of calculations for various PRPs, compared with the experiment, are given in the article [5]. The same real loading spectrum was modeled by a different number of harmonics distributed in several ways by frequency. This shows the significant effect of changes in the dispersion of the process in the high-frequency part of the spectrum on the durability of structural components.

To distinguish creep from fatigue, the units of measurement of durability must be uniform. Any unit of measurement always has a physical justification and a reference value [28]. The unit of measurement “cycle” does not exist in any system of units of measurement and cannot exist, since in each case it has a different content. Therefore, it is possible to distinguish cyclic creep from fatigue only if the durability is expressed in units of time, that is, the way the failure process actually occurs. In Figure 12 shows the dependences of durability on tensile stresses at their constant value and at cyclic tension with different frequencies and constant s_min = 40 MPa. The abscissa shows the equivalent stresses s_eq corresponding to the constants at which the durability has the same value in accordance with expression similar to (7), –

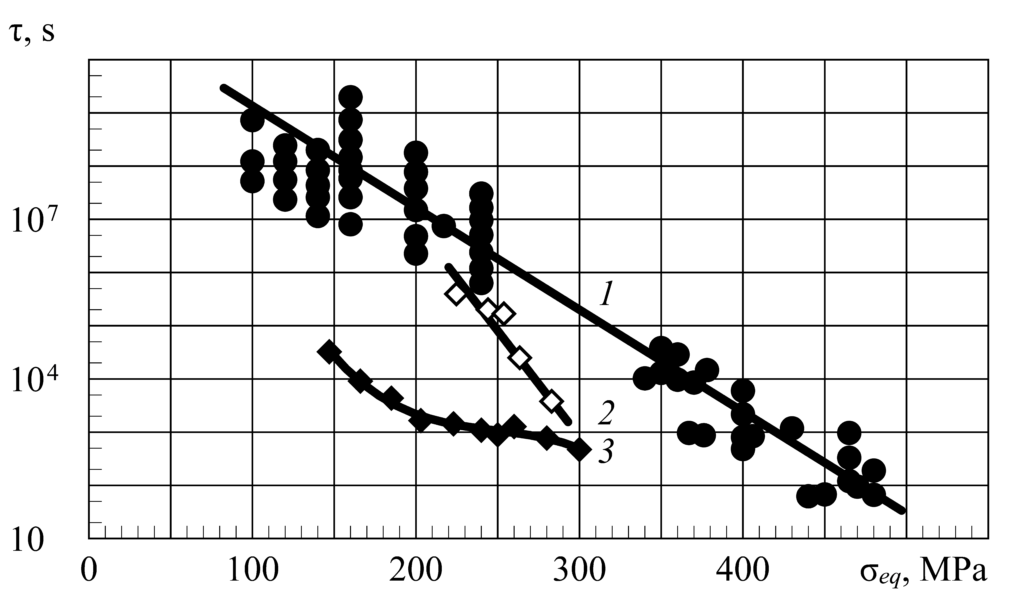
Figure 12: Durability of smooth specimens of AK4-1 T1 alloy tested at constant (1) and cyclically varying with a frequency of 0.05 (2) and 30 Hz (3) stresses (temperature 423 K)

The figure shows that at constant stresses, the logarithm of the durability linearly depends on the stresses, thereby illustrating the main regularity of fracture (line 1). With alternating stresses varying with a low frequency (straight line 2), a decrease in the stress swing brings the value of the cyclic durability closer to the static one. It is clear that here we are dealing with cyclic creep, in which a decrease in durability occurs as a result of a concomitant relaxation of internal stresses, which decrease with a decrease in the loading rate [4, 6]. If the frequency is high (curve 3), a decrease in the stress swing increases the discrepancy between the durability under static and cyclic loading, which first increases and then becomes smaller, approaching the static durability at s_a → 0. With an increase in the stress swing, fatigue failure will be replaced by fracture from cyclic creep, and curve 3 intersects with straight line 2.

If the use of expression (5) is quite justified for a frequency of 0.05 Hz, then for fatigue failure at a frequency of 30 Hz, the approximating curve should be considered conditional (the lines in both cases are drawn according to the average logarithmic values of the durability). The process of failure during fatigue occurs in local volumes, the stresses in which are not known. In polymers, they can be evaluated by indirect methods, for example, by infrared spectroscopy [29]. In metal alloys and composite materials-structures, this can be done by inelasticity using mathematical models based on thermodynamic laws of fracture [4, 5, and 18].

Studies have targeted an interdisciplinary approach to the problem of the fracture of solids, for example, [30]. They consider in detail various aspects of the processes, depending on certain loading conditions, the materials used and their structures, and the mechanisms of the processes. A number of areas of knowledge related to the fracture of materials are considered and which explain what happens in this case. This is the knowledge necessary to understand the essence of the events taking place. Our approach does not consider the numerous details of the phenomena observed during fracture. This is like a cross-section of the whole problem in a certain plane. It is based on the fundamentals of the thermodynamics, and all types of fracture are considered from the same positions. The formulas given above are used specifically for calculations. Although for particular cases the mechanics hikes give quite satisfactory results, but fundamentally this does not solve the problem. The progress in solving complex strength problems is possible by combining the knowledge and methods of mechanics, physics and physical materials science.

The above and in article [1] examples show how large a body of information is provided by analysis of the rheological properties of materials and how many possibilities arise in modeling these properties if the mechanical models are filled with physical content. The approach outlined here, unlike the others currently in use, relies on a single conceptual framework: the notions of what a solid is and why it failures. Any material is an atomic-molecular system in thermal motion, and fracture occurs as a result of anharmonicity and stochasticity of the process of thermal vibrations of atoms in a solid body [7]. This is confirmed by a numerical experiment performed by the molecular dynamics method [31]. It follows that fracture is due to the internal energy of the solid, the measure of which is temperature [5, 7]. External effects only change the failure rate of a solid if they change its internal energy (thermal energy, electromagnetic radiation, chemical reactions). The end of the process is the achievement of a certain concentration of damage (microcracks, pores, delamination in composites), leading to its transition to the next dimensional level [4, 5, 7, 9, and 14]. And the prediction of further fracture, such as crack propagation, is reduced to modeling the process of material failure at its tip by the same methods [7, 18, and 32].

5. Conclusion

The proposed methodology for predicting the durability of materials in structures shows that an interdisciplinary approach and reproduction in mathematical models of the processes of their failure and deformation as thermodynamic, allows us to solve those problems that have not yet been solved by methods of fracture mechanics. It is shown that it is based primarily on the study of the physical laws of fracture, which are revealed in experiments to determine durability at constant stresses and temperatures. Then these laws should be applied to other loading cases: variable loads and temperatures. And by involving the knowledge of materials science, it becomes possible to take into account in the calculation procedures other thermally activated processes accompanying the flow and failure of a solid, which changes its structure.

The above approach shows the practical sequence of actions required when investigating the strength properties of any new material. In order to study the strength, it is necessary, as a minimum, to test its specimens with different loading rates and at different temperatures, and then perform thermally activation analysis of the obtained data. To study the resource characteristics of a material, it is necessary to investigate their inelastic properties, comparing the results obtained with the endurance data, while taking into account the temporary nature of fatigue failure. This is followed by mathematical modeling of processes for solving problems of arbitrary temperature-force loading.

Conflict of Interest

The author did not have a conflict of interest with his colleagues using other approaches to the problem under consideration. The author experienced only a benevolent attitude, support and understanding.

Acknowledgment

The author is deeply grateful to H. D. Gringauz and N. A. Moshkin for a number of joint works that gave a lot of new, useful information and initiated the described approach, and with whose permission their results are presented here. He is also grateful to many other colleagues who, to one degree or another, helped him in numerous and laborious experiments.

1. M.G. Petrov, ”Interdisciplinary approach to solving problems on the flow and fracture of materials,” in XX International Conference on Methods of Aerophysical Research (ICMAR 2020), AIP Conference Proceedings 2351, doi: 10.1063/12.0004278.
2. W. Kauzmann, “Flow of solid metals from the standpoint of the chemical-rate theory,” Transactions of the AIME, 143, 57–83, 1941.
3. S. Glasstone, K.J. Laidler, H. Eyring, The theory of rate processes, McGraw-Hil, 1941.
4. M.G. Petrov, “Mathematical modeling of failure and deformation processes in metal alloys and composites,” American Journal of Physics and Applications, 8 (4), 46–55, 2020, doi: 10.11648/j.ajpa.20200804.11.
5. M.G. Petrov, “Investigation of the longevity of materials on the basis of the kinetic concept of fracture,” Journal of Applied Mechanics and Technical Physics, 62 (1), 145–156, 2021, doi: 10.1134/S0021894421010181.
6. V.A. Stepanov, N.N. Peschanskaya, V.V. Shpeizman, G.A. Nikonov, “Longevity of solids at complex loading,” International Journal of Fracture, 11, 851–867, 1975.
7. V.A. Petrov, A.Ya. Bashkarev, V.I. Vettegren, Fizicheskiye osnovy prognozirovaniya dolgovechnosti konstruktsionnykh materialov, Polytechnika, 1993.
8. M.G. Petrov, A.I. Ravikovich, “Deformation and failure of aluminum alloys from the standpoint of kinetic concept of strength,” Journal of Applied Mechanics and Technical Physics, 45 (1), 124–132, 2004.
9. M.G. Petrov, “Fundamental studies of strength physics – methodology of longevity prediction of materials under arbitrary thermally and forced effects,” International Journal of Environmental and Science Education, 11 (17), 10211–10227, 2016.
10. M.G. Petrov, “Rol’ protsessa polzuchesti svyazuyushchego v kinetike razrusheniya stekloplastika,” in XII Mezhdunarodnoy nauchnoy shkoly-konferentsii: Fundamental’noye i Prikladnoye Materialovedeniye, Izdatelstvo AltGTU, 50–66, 2015.
11. J. Bailey, “An attempt to correlate some tensile strength measurements on glass,” Glass Industry, 20. 21–25, 1939.
12. M.G. Petrov, “Rheological properties of materials from the point of view of physical kinetics,” Journal of Applied Mechanics and Technical Physics, 39 (1), 104–112, 1998.
13. A.R. Michetti, “Fatigue analysis of structural components through math-model simulation,” Experimental Mechanics, 2, 69–76, 1977.
14. S.N. Zhurkov, “Dilatonnyy mekhanizm prochnosti tvordykh tel,” Fizika Tverdogo Tela, 25 (11), 331983323, 1983.
15. H.B. Dwight, Tables of integrals and other mathematical data, Macmillan Company, 1961.
16. A.J. Kennedy, Processes creep and fatigue in metals, Oliver and Boyd, 1962.
17. T-S. Kê, “Experimental evidence of the behavior of grain boundaries in metals,” Physical Review, 71 (8), 533–546, 1947.
18. M.G. Petrov, Prochnost’ i dolgovechnost’ elementov konstruktsiy: podkhod na osnove modeley materiala kak fizicheskoy sredy, Lambert Academic Publishing, 2015.
19. A.S. Nowick, B.S. Berry, Anelastic relaxation in crystalline solids, Academic Press, 1972.
20. M.L.V. Gayler, P. Parkhouse, “The ageing of high-purity 4 percent copper-aluminium alloy,” Journal of Institute of Metals, 66, 67–84, 1940.
21.  M.L.V. Gayler, “The cold working of a high-purity aluminium alloy containing 4% of copper and its relation to age-hardening,” Journal of Institute of Metals, 72, 543–563, 1946.
22. H.K. Hardy, “The ageing characteristics of some ternary aluminium-copper-magnesium alloys with copper : magnesium weight ratios of 7 : 1 and 2.2 : 1,” Journal of Institute of Metals, 83, 17–33, 1954.
23. R. Graf, A. Guinier, “Influence de l’ecrouissage apres trempe sur les phenomenes de precipitation dans l’alliage aluminim-cuivre a 4% de cuivre,” Comptes rendus hebdomadaires des seances de l’academie des sciences, 238, 819–821, 1954.
24. J.W. Christian, The theory of transformations in metals and alloys. Part I. Equilibrium and general kinetic theory. 2nd ed., Pergamon Press, 1975.
25. L.H. Van Vlack, Materials science for engineers, Addison-Wesley, 1970.
26. A. Kelly, R.B. Nicholson, “Precipitation hardening,” Progress of Material Science, Pergamon Press, 10, 151–391, 1963.
27. M.G. Petrov, “On test programs of aircraft structures,” in XVI International Conference on the Methods of Aerophysical Research (ICMAR 2012): abstracts, Part I, Kasan Federal University, 2012.
28. D. Kamke, K. Krämer, Physikalische Grundlagen der Maßeinheiten, B. G. Teubner, 1977.
29. V.I. Vettegren, I.I. Novak, K.J. Friedland, “Overstressed interatomic bonds in stressed polymers,” International Journal of Fracture, 11, 789–801, 1975.
30. T. Yokobori, An interdisciplinary approach to fracture and strength of solids, Wolters–Noordhoff Scientific Publications Ltd, 1968.
31. V.S. Yuschenko, E.D. Schukin, “Molekulyarno-dinamicheskoye modelirovaniye pri issledovanii mekhanicheskikh svoystv,” Fiziko-khimicheskaya mekhanika materialov, 4, 46–59, 1981.
32. V.R. Regel, A.M. Leksovskii, S.N. Sakiev, “The kinetics of the thermofluctuation – Induced micro- and macrocrack growth in plastic metals,” International Journal of Fracture, 11, 841–850, 1975.

(Click Here)