1. Introduction

This paper is an extension of work originally presented at the IEEE 2020 International Conference on Computer Science and Computational Intelligence [1]. Extended content is mainly in the research background section, dealing with scaffolding in blended learning environments and the importance of the design of online teaching material. It includes discussion of the unsuitability for mathematics learning of existing instruments used to evaluate students’ approaches to studying. Results contain effect sizes. The discussion includes more detail, and a conclusion section has been added.

The reported project stems from a change in first year mathematics teaching in a large Australian university, which replaced one out of two face-to-face tutorials with on online tutorial consisting of a set of tasks designed to lead the student through the required material step by step from simpler to more complex tasks. The change was made in the core sequence of first year mathematics subjects, Mathematics 1A and Mathematics 1B, which is taken by science and engineering students. Before the change, teaching was entirely face-to-face, consisting of lectures to large groups, plus two tutorials given to problem solving and answering students’ questions, in much smaller groups.

The only change in the organization of teaching was the replacement of one face-to-face tutorial by an online tutorial. In the online tutorial, immediate feedback identified errors without giving solutions. Completing the tutorial tasks earned a small contribution to the student’s final mark.

The study was carried out before higher education was disrupted by the Covid19 epidemic, and apart from the change in one tutorial, there was no other change in the organization and material in the core sequence. That is, the syllabus and the written teaching material did not change, and the online tasks were very similar to those used in face-to-face tutorials. All students had access to help from staff and discussion with peers was still available in the face-to-face teaching groups. The study dealt with two cohorts of students in adjacent years, the last year before the change, and the first year of its introduction. Admission criteria had not changed, and the secondary school mathematics course taken by local students had not changed. It is therefore reasonable to conclude that the two cohorts were comparable in background and level of selection. In the year of the change, survey results indicated that students were satisfied with the teaching delivery.

It seems, therefore, that the natural quasi experiment afforded by the change offered good control for a study of any effect that the change might have on the quality of learning outcomes among students in the two cohorts. Making a comparison requires a valid method for evaluating outcomes, and validation requires the use of observable evidence. The course evaluation procedures advocated in improvement programs by the Accreditation Board for Engineering and Technology [2] emphasize the importance of direct assessments.

The present study uses observable evidence from students’ final examination scripts. The comparison is based on a method described below in Section 2. It is emphasized here that the method has potential importance because it is direct and criterion-based. Before giving detail about the method, one needs to examine existing research that suggests directional predictions that can be tested.

2. Background

2.1.  Students’ use of resources

The newly implemented program studied in the present work represents provision of an online learning resource, rather than online instruction, given that the majority of instruction was face-to-face, and the online segment involved students’ work rather than online instruction. This means that the program is not comparable with projects involve online instruction such as that reported in [3].

In [4] the authors make the important point that evaluation of any new learning resource can be invalidated if there is no evidence about whether students have used the resource. Findings in [5] were that mathematics students who were offered several optional leaning resources, they tended to use only one of the set of resources. It is worth clarifying that the present study deals with only one new resource, so that the problem of choice does not arise. There is also no uncertainty about whether the new resource was used because students’ work online leaves an audit trail.

2.2.  Student learning and the transition to university mathematics

There are three research strands that are important to the purpose of the present work.

First, in the review of research on student learning made in [6], it is noted continuing importance is found for an approach to learning that contains a continuing purpose of understanding material and attempting to link and compare different ideas. Understanding and high quality of learning are unlikely when students’ approach is atomistic, focused on the accumulation of unrelated detail. For mathematics students, understanding is achieved and tested by active problem-solving. The instruments used in the British and Australian research reviewed in [6] measure the search for understanding using items describing wide reading and venturing beyond the syllabus. Among undergraduate mathematics students, such items are irrelevant for all but the most highly gifted students, but at all levels of talent the intention and achievement of understanding relate to activity in doing mathematical tasks appropriate to the level of study.

Active problem solving requires effort and persistence, which relates to North American research underlying the National; Survey of Student Engagement (NSSE), [7]. This research strand found that self-regulation of study is very important to students’ learning, and this is an obvious requirement for activity in working on mathematical tasks.

Directly relevant Australian work on student engagement in mathematics learning is supported by the theoretical outline given in [8] The authors note that student engagement in mathematics is multidimensional, with fuzzy boundaries between categories. The principal components that have been identified as affecting student engagement are consistent with components of the student learning research. Expectancy-value theory is defined by the value given to a learning goal and the learner’s expectation of achieving it. This entails interest factors and confidence, as well as practical reasons for valuing achievement, and research has shown that it relates to quality of learning outcome. Similar importance is attached to the factor of self-regulated study identified in the North American research.

University students’ choice of mathematics requires some previous success, and the choice implies that they attach some value to the subject. But there is no lack of evidence that many students find the transition to university mathematics very difficult, and the evidence comes from a wide variety of settings. Examples are afforded by the work reported in [9], for Britain, in [10] for Sweden and in [11] for Australia. Beginning university students can find self-regulation difficult. For mathematics students, previous levels of motivation, goal setting and self-regulation will not be sustained at university level if successful mathematical activity is not sustained.

Experience of difficulty may lead to discouraged and anxious avoidance of attempted engagement with mathematical tasks. The work reported in [12], done in an Australian setting indicates, that beginning mathematics students can benefit from learning support that facilitates engagement with mathematical tasks. The next requirement is for evidence relevant to beneficial types of support.

2.3.  Scaffolding and transfer of responsibility

The material for the online tutorials was specially designed to lead the student through the week’s mathematical topic using a sequence of tasks that progressed from simple to more complex. Immediate feedback was given for each response, informing the student only whether the response was correct or not, without giving a solution. In addition, the sequences of tasks were designed so that solutions to earlier tasks could help with the later more difficult tasks. The online work could be done in multiple sessions within a specified time period, so the student could temporarily leave a task to look up material, ask for help, or discuss it with peers. Such a design has the potential to function as scaffolding for the extension of students’ understanding.

Scaffolding is defined as intervention by a teacher to support students in achieving a learning goal that they would be unlikely to achieve without support [13]. There has been considerable discussion of the method of intervention and the design of the teacher’s intervention, so that it extends the student’s own reasoning without imposing or supplying a solution. The original idea rests on Vygotsky’s thesis, described in [14], that the most valuable instruction is that which leads a learner into a development defined as being in the zone of proximal development. That is, the learner is already on the border of extended capability, and hence can reach extension with minimal appropriate help. The idea of scaffolding is defined by interaction between teacher and student. The authors in [15] found that interactive scaffolding led by the teacher in relatively small community college mathematics classes was very much more successful than previously used approaches. For large enrolment groups, limits of resourcing make the original form of scaffolding impossible. But it is argued here that the design of the online tutorials affords an approximation to scaffolding, because the gradient of task difficulty and the immediate feedback provide indirect assistance in the extension of understanding, with the limitation of the feedback also implying that assistance is not too intrusive.

Transfer of responsibility to the learner is also an important underlying goal of providing scaffolding [16]. It is pointed out in [17] that, for scaffolding to make its widest contribution, it needs a definition that empowers the learner, so that the student becomes independent of the presence of an insightful teacher as agent. In the context of mathematics, they propose problem solving as the means of creating self-scaffolding. In contrast to face-to-face tutorials, online tutorials give all responsibility for work on the given tasks to the student, with the minimal assistance designed to foster effort and persistence. Organizational responsibility in scheduling time is also required, but the important factor is the design of the tasks facilitating active engagement in the tasks, which serves to build the understanding, independence and self-regulated study found important in the studies described here and in Section 2B.

2.4.  Blended mathematics teaching and the importance of design

Evidence is available that well-designed online materials can function in this way. Studies of statistics programs [18], [19] indicate that achievement gains follow careful adjustment of materials, designed to integrate the learning environment consistently, and to foster understanding. The results of [18] are particularly important, because the material provided to students was revised from year to year, and benefits to students’ achievement appeared only in later years. These results are compatible with the established distinction between medium as a means of delivery and the designed study program as the goods delivered [20] Rapid and flexible delivery can give an advantage only if goods of value are delivered.

The study described in [21] is also highly relevant to the idea of scaffolding afforded by suitably designed material. It deals with a very large group of statistics students of variable academic and national background, who were offered an online tutorial system that proceeded from diagnostic testing to select tasks best adapted to each student’s stage of learning. The study found that the time spent using the online program was positively related to achievement, with the strongest effect among students whose scores on Vermunt’s Inventory of Learning Styles [22] indicated that they were less well adapted to university study.

2.5.  Assessing learning outcomes

In Australian work on learning outcomes, [23] the researchers developed a classification of the quality of learning outcomes based on actual responses to a variety of educational tasks. The classification used criteria defined by the complexity, adequacy of coverage, and consistency of observable responses to set tasks. They defined a system of levels of outcome called the Structure of Observed Learning Outcomes (SOLO) Taxonomy. The value of the reference to the observable is clear. The researchers claimed that the classification was invariant across disciplines and justified the claim by giving illustrations from the work done in the principal areas of school study, across the middle years of schooling, from upper primary level to junior secondary. The SOLO levels, as defined in [23] are listed in Table 1 below.

The SOLO split between the Multistructural and Relational levels is based on consistency in reasoning, and so reflects the dichotomy between understanding relationships and atomistic display of facts which is of obvious importance in mathematics, with achievement of the relational level providing evidence of understanding. The wide applicability of the SOLO taxonomy is not relevant to the present study, but the issue of consistent reasoning is central to it. The applicability of SOLO to mathematics was based on research that identified patterns of errors and misconceptions in students’ mathematics learning.

Table 1: The SOLO taxonomy

Level	Definition
Prestructural	No valid response
Unistructural	One aspect of the problem correctly identified, but no diversity of aspects presented, so that questions of consistency cannot arise.
Multistructural	Multiple relevant information presented and used, but without considering relationships between different parts, so that inconsistency appears.
Relational	Multiple relevant information presented and used in a way that recognizes relationships and achieves consistency within the given task.
Extended abstract	Multiplicity recognized and consistency achieved over a context beyond that of the given task.

The SOLO taxonomy has been used at tertiary level as a framework for defining intended learning outcomes for programs in mathematics and computer science [24] and its application in other science disciplines at tertiary level has been found to be a valuable diagnostic tool [25]. The SOLO levels were adapted for the work reported in [26] to define a method of evaluating levels of learning outcomes in tertiary students’ mathematics.

The focus was on examination performance in early undergraduate years, so the highest SOLO level was not considered relevant. The other four levels were used to construct a scoring system intended to provide a common scale usable across tasks involving the same mathematical material, examined at a similar level of difficulty.

The criteria used were, first, logical consistency, and second, adequate coverage of the task. A student’s response to an examination question was assigned to one of six levels, labelled from 0 to 5. Levels 4 and 5 required the logical consistency of the SOLO relational level, with 5 given for a completely correct solution, and 4 given if there was a small error that did not affect consistency, like a minor slip in arithmetic or a copying error. Levels 0 and 1 correspond to SOLO Prestructural and Unistructural levels: nothing right or only one relevant aspect of the problem identified. Solutions with an error of logic at the Multistructural SOLO level, with more than one good step presented, were classified as level 2 or 3, depending on how much of a satisfactory solution was present. Examination questions were split into self-contained tasks, and each was scored independently. A composite score was obtained by summing the task scores, weighted using the proportion of the examination marks assigned to each.

The method does not attempt the generality claimed for the SOLO taxonomy. Validity is claimed only for the close relationship between tasks, depending on the stability of syllabus, staffing, student intake, teaching materials and most of the implementation of teaching in the two adjacent year groups. The SOLO taxonomy is well adapted to mathematics because its criteria fit the requirements of mathematical tasks. But its most important characteristic is its being defined in terms of the observable. The North American Accreditation Board for Engineering and Technology [2]) argues that a teaching program cannot be adequately evaluated without a direct method for examining students’ learning outcomes, one which is closely fitted to the actual study program, both of which requirements apply to the method described. Applying the scoring method is similar to examination marking, and scores correlate at over 0.9 with examination marks, which implies similar ranking. What the method is intended to achieve is a common ranking for the two year-groups’ performance on similar tasks. It is worth noting also that a direct method of examining learning outcomes has advantages over the use of questionnaires to assess approaches to studying. Two reasons are important. The first is intrinsic: direct assessment avoids problems associated with the reliability of self-reported data about behaviour and attitudes. The second reason is the mismatch between the existing instruments used to assess approaches and the study of mathematics, at least at undergraduate level. This has already been mentioned in connection with the approach instruments described in [6]. But one should also note that similar remarks apply to the North American NSSE, and the Australian Survey of Student Engagement (AUSSE) derived from it [27] derived from it.

The point here is that the AUSSE measure higher level thinking by items dealing with extended essay- style writing and multiple revision of drafts. In the development work for the AUSSE, it was found [27] that science students had low scores of higher-level thinking, but it is probable that such results are contaminated by the inadequacy of the instrument.

3. Method

3.1.  Sample

The target population was the set of students enrolled for Mathematics 1A and 1B, in adjacent years, taking the groups from the first time in each year that the unit was offered. Simple random samples were drawn from those students who sat the final examination. This means that those who did not survive to the final examination could not be considered, but this restriction applies to all the groups being compared. Questions involving students’ gender were not part of the study, but gender information was available, and was recorded, because any gender-related patterns that might emerge would be of interest. Sample numbers are in Table 1. The proportions of females and males in the sample are very similar to proportions in the total groups.

Table 2 Sample

Cohort	Mathematics1A		Mathematics 1B
	Female	Male	Female	Male
1 (from the last year before the change)	53	152	38	142
2 (from the first year when the change was introduced)	49	154	44	153

3.2.  Analyses

The two cohorts were compared within each of the two mathematics subjects. In each subject, four groups defined by cohort and gender were compared using analysis of variance. In the case of a significant overall result, differences between groups were examined using least significant differences. For cases where there were significant results, effect sizes were calculated. Analyses were done using the open-source package Rstudio [28].

4. Results

4.1.  Mathematics 1A

Descriptive statistics are in Table 3, and the analysis of variance data are in Table 4.

Table 3 Mathematics 1A Descriptive statistics

Cohort		Female	Male
1 All teaching	Mean	10.66	10.07
face-to-face	St. dev.	3.58	3.62
	n	63	152
2 Blended	Mean	12.87	12.24
teaching	St. dev.	3.93	3.73
	n	49	154

Table 4 Mathematics 1A Analysis of variance

Analysis of variance
Source	Sums of squares	df	Mean squares	F
Between groups	521.29	3	173.76	12.74***
Residual	5510.47	404	13.64
Total	6031.44	407

*** p < 0.001

The means for Cohort 2 are higher than those for Cohort 1, and the analysis of variance gives a high level of significance to differences between groups. Results for comparisons between pairs of groups using least significant differences are in Table 5

Table 5: Least significant differences

Groups in order of means
Cohort	t	1 female	2 male	2 female
1 male		0.90	5.14***	4.62***
1female			2.79**	3.10**
2 male				1.04

** p < 0.01;  ***p < 0.001

The differences are significant for all comparisons of Cohort 1 groups with Cohort 2 groups, and no within-cohort comparisons between females and males were significant. The purpose of the study did not include gender comparisons but grouping by gender was in the analysis because it was possible that different delivery of teaching might have different effects for females and males.

Effect sizes for the four significant comparisons are in Table 6. The interpretations use the classification described in [29] and are high or very high in all cases.

Table 6 Effect sizes

Group	Cohort 2 male		Cohort 2 female
	Effect size		Effect size
Cohort 1 male	0.60	Very high		0.77	Very high
Cohort 1 female	0.46	High		0.46	High

4.2.  Mathematics 1B

Descriptive statistics are in Table 7 and the analysis of variance results are in Table 8. There were no significant differences between groups in Mathematics 1B.

Table 7 Mathematics 1B:  Descriptive statistics

Cohort		Female	Male
1 All teaching	Mean	11.48	11.46
face-to-face	St. dev.	3.77	3.74
	n	38	142
2 Blended	Mean	11.82	11.32
teaching	St. dev.	3.46	3.44
	n	44	154

Table 8 Mathematics 1B Analysis of variance

Analysis of variance
Source	Sums of squares	df	Mean squares	F
Between groups	8.52	3	2.84	0.82 ns
Residual	4819.82	373	12.92
Total	4828.34	378

5. Discussion

It is worth noting here again that no gender differences were found. Marginally higher mean scores for females probably only reflect the higher selection of the female groups, given that tertiary mathematics groups still contain considerably more males.

It is clear that the results for Mathematics 1A show advantages in the online component of delivery of teaching. The advantage is in the direction predicted from the research background, subject to the importance of the design of the online teaching material. The digital audit trail afforded by the technology gives assurance that the online learning resource was used by the students, which functions as an additional control factor. Because Mathematic 1A is the first core mathematics subject taken by engineering and science students, one can conclude that the online program facilitated students’ transition to university study.

The lack of significant differences between the two cohorts in Mathematics 1B can be explained by combining evidence from the literature with the conclusion given for Mathematics 1A. Mathematics 1B is the second subject in first-year core mathematics, its students are at least one semester further into university study than most students in Mathematics 1A and are more highly selected because they have already passed Mathematics 1A.  In [21] the findings indicated that online resources were most helpful to students who were initially less well adapted to university study. The mathematics 1B groups, therefore, are likely to have less need of help than students who are mostly new to university study.

But the finding for Mathematics 1B is still useful evidence because it indicates that the online program shows no disadvantage compared with fully face-to face teaching. This means that, if one regards the medium as a delivery vehicle, the results indicate delivery of adequate goods. The speed and flexibility of delivery therefore become relevant. The audit trail permitted by the technology also enables improvement of the online material through tracking areas where students have most difficulty. The method of comparison of outcomes used in the present study can be used to compare different sets of online material, serving as the direct Students’ written assessments can be scanned into digital records, which opens the way to a cyclic use of technology to provide research material for evaluation of what the technology delivers. Such material would also permit research on changes in students’ learning over some years.

In a review of research on fully online teaching of undergraduate mathematics, [30] it is reported that the results are mostly unfavorable to online teaching. It should be emphasized, however, that the present study represents a different field, because the blended learning environment involved retained easy contact with staff and peers. That is to say, the learning environment was not exclusively online and, indeed, assumed a degree of offline interpersonal engagement.

It should also be noted that the direct assessment of quality of learning outcomes in the present study has advantages over alternative methods. It clearly is unreasonable to judge online teaching using correlations between results of assessments of different teaching components, but the use of grades alone also does not provide a clear determination of efficacy. Hence, results of the study [31], which used grades, cannot be considered as corroboration for the present study.

It was noted In Section 2B that instruments used to assess students’ approaches to studying are not well adapted to mathematics learning. The underlying concept of the value of a search for understanding is clearly important in all fields, so that, even after some decades of stabilization of existing instruments, adaptation to mathematics would be useful. Records from online tutorial tasks and written examinations could be combined with initial qualitative investigation of students’ approaches to and experience of studying mathematics.

6 Conclusion

The results indicate that the use of an online component in the delivery of first year tertiary mathematics can be justified as producing enhanced learning outcomes among beginning students, and no disadvantage to those at a slightly later stage, provided that the online teaching material is carefully designed to lead the students from simpler to more complex tasks. Hence any recommendation for the extended use of online teaching material, and any future research of online mathematics teaching, must focus primarily on the quality of the design of that material.

The present study is limited to first-year mathematics. It follows that investigation in other contexts and later stages of university study would be a necessary supplement. The increasing use of online teaching delivery affords the opportunity for such work. In addition, one should note that the technology furnishes detailed records of students’ use of materials and performance on assessment tasks that provide valuable data for study.

The present study did not address students’ experience of studying. In the background section it was noted that existing self-report questionnaires on students’ approaches to studying are unsuitable for mathematics learning. The development of suitable instruments with a similar purpose, but targeting more appropriate approaches, is an open field. The development of such instruments would be facilitated by initial exploratory work using qualitative methods to elucidate salient aspects of students’ experience of studying mathematics.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors wish to acknowledge the support of the University of New South Wales and Le Cordon Bleu Australia.

Appendix: Examples of the scoring method

1. Algebra 1

Find conditions on  to ensure that the following system of equations has a solution.

1. Algebra 2
2. a) Find all roots in the complex numbers of

Conclusion

Solutions exist if and only if

Table 9 Scoring examples for Algebra 1

Score	Example
5	All correct
4	Step 1 correct. Step 2;   [Mistake in arithmetic.] Conclusion: solutions exist if and only if
3	Row operations correct to the end of Step 2. But conclusion given as:
2	Row operations correct to the end of Step2. No conclusion.
1	Step 1 correct. Then replace Row 2 by Row 2 + (1/2) Row 1, giving [This shows row operations are not understood.]

Factorise 1 over the complex numbers.

Factorise 1 over the real numbers.

Solution

Table 10 Scoring examples for Algebra 2

Score	Example
5	All correct
4	Correct (a), (b), then (c)
3	Correct (a), (b), then (c) .
2	Roots given as  then (b) corresponding to this, no (c)
1	and no more

1. Calculus 1
2. a) State the Mean Value Theorem
3. b) Use the theorem to prove sinhx> x for x> 0

Solution

1. a) If is continuous on and differentiable on , then there exists in  such that
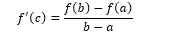
2. b) is continuous and differentiable everywhere and . So, there is c ε such that

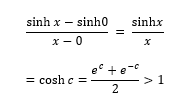
It follows that  for x > 0

Table 11 Scoring examples for Calculus 1

Score	Example
5	All correct
4	Correct up to  , then a sketch showing , but conclusion stated as ,  and hence
3	Correct up to  , then “  so  as required.”
2	Correct statement of the theorem, no more
1	Ratio formula for the theorem stated, no conditions, no more

1.  Calculus2

So, the original integral converges, by the comparison test.

Table 12 Scoring examples for Calculus 2

Score	Example
5	All correct
4	Chosen comparison right, but integral evaluated as -1/4x2, with consistent valid conclusion
3	Evaluation of  correct, but no comparison made.
2	Wrote  but no more
1	Stated  but no more

1. M.R. Freislich, A. Bowen-James, “Observable learning outcomes among tertiary mathematics students in a newly implemented blended learning environment”. In 2020 IEEE International Conference on Computer Science and Computational Intelligence (CSCI), 976-980, 2020, doi:10.1109/CSCI151800.2020.00181.
2. Accreditation Board for Engineering and Technology, 2020,ABET accreditation. https://www.abet.org.
3. S. Lambert, “Reluctant mathematicians: skills-based MOOC scaffolds a wide range of learners”, Journal of Interactive Media in Education, 2015(1), 1-11, 2015 doi.org/w5334/jime.bb.
4. P. Sharma, M.J. Hannafin2007, “Scaffolding in technology enhanced learning environments”,. Interactive Learning Environments, 15(1), 27-46, 2007, doi:101080/10494820600996972.
5. M. Inglis, A. Palipura, S. Trenholm, J. Ward, 2011, “Individual differences in students’ uses of optional learning resources’”, Journal of Computer Assisted Learning, 27(6), 490-502, doi:10.1111/j.1365-2729.2011.00417.x.
6. J.T.E.Richardson, ‘Student learning in higher education: A commentary’, Educational Psychology Review, vol. 29, pp. 353-362, 2017, doi: 1007/s10648-017-9410-x.
7. Indiana University School of Education, National Survey of Student Engagement, University of Indiana, 2017.
8. H.M. Watt, M. Goos, M, “Theoretical foundations of engagement in mathematics’” Mathematics Education Research Journal, 29(2), 133-142, 2017, doi:10.1007/s13394-017-0206-6.
9. M. McAlinden, A. Noyes, “Mathematics in the disciplines at the transition to university”, Teaching Mathematics and its Applications, 38(2), 61-73, .2019, doi.org10.1093/teamat/hry004.
10. S.H. Bengmark, H. Thunberg, T.M. Winberg, 2017, “Success-factors in transition to university mathematics”, International Journal of Mathematical Education in Science and Technology, 48(7), 988-1001, 2017,doi: 10.1080/0020739X.2017.1310311.
11. P.W. Hillock PW, R.N. Khan, 2019, “A support learning programme for first-year mathematics”, International Journal of Mathematical Education in Science and Technology, 50(7), 1073-1086, 2019, doi:10.1080/0020739X.2019.16569026.
12. L.J. Rylands, D. Shearman, “Mathematics learning support and engagement in first year engineering”, International Journal of Mathematical Education in Science and Technology., 49(8), 1133-1147, 2017, doi: 10.1080/0020739X.2018.1447699.
13. C. Quintana, 2021, ‘Scaffolding inquiry’, in R.G. Duncan, & C.A. Chinn, (Eds.), International handbook of inquiry and learning, Routledge, 176-188.
14. B.H. Johnsen, BH, 2020, ‘Vygotsky’s Legacy Regarding Teaching-Learning Interaction and Development’, In B.H. Johnsen (ed.), Theory and Methodology in International Comparative Classroom Studies, Cappelen Damm Akademisk, 82-98.
15. T. Gula, C. Hoesler, W. Majciejewski, W, “Seeking mathematics success for college students: A randomised field trial of an adapted approach”, International Journal of Mathematical Education in Science and Technology, 48(8),127-143, 2021, doi: 10.1080/0020739X2015.1029026.
16. B.R. Belland, A.E. Walker, M.W. Olsen H. Leary, H., “A pilot meta-analysis of computer-based scaffolding in STEM education”, Educational Technology and Society, 18(1), 183-197, 2015, https://www.jstor.org/stable/jedtechsoci.18.1.18.
17. D. Holton, D. Clarke, D., “Scaffolding and metacognition”; International Journal of Mathematical Education in Science and Technology, 37(2), 127-143, 2006, DOI:10.1080/0020730500285818.
18. L. Zetterqvist, “Applied problems and use of technology in an aligned way in basic courses in probability and statistics for engineering students: a way to enhance understanding and increase motivation,”, Teaching Mathematics and its Applications, 36(2), 108-122, 2017, doi.org/ 10.1093/teamat/ hrx004
19. A.H. Jonsdottir, A.A. Bjornsdottir, G. Stefansson, G., “Difference in learning among students doing pen-and-paper homework compared to web-based homework in an introductory statistics course”, Journal of Statistics Education, 25(1), 12-20, 2017, doi: 10.1080/10691898/2017.1291289.
20. R.E. Mayer, “Thirty years of research on online learning”, Applied Cognitive Psychology, 33(2), 152-159, 2019, doi: 10.1002/acp.3482.
21. D.J. Tempelaar, B. Rienties, B. Giesbers, “Who profits most from blended learning?’” Industry and Higher Education, 23(4), 285-292, 2009, doi.org/10.1145/3170358.3170385.
22. J.D. Vermunt, Y.J. Vermetten, YJ, 2004, ‘Patterns in student learning: relationships between learning strategies, conceptions of learning and learning outcomes’, Educational Psychology Review, 16(4), 359-384, 2004, doi:org/10.1007/s10648-004-0005-y.
23. J.B. Biggs, K.F. Collis, KF (2014). Evaluating the quality of learning: The SOLO taxonomy. Academic Press, 2014.
24. C. Braband, B. Dahl, B, “Using the Solo taxonomy to analyze competence progression in science curricula”, Higher Education, 58(4),.531-549, 2009, doi: 10.1007/s10734-009-9216-4.
25. L.C. Hodges, L. Harvey, “Evaluation of student learning in organic chemistry using the SOLO taxonomy”, Journal of Chemical Education, 80(7) 785-787, 2003, doi:org/10.1021/ed080 p785.
26. M.R. Freislich, A. Bowen-James, 2019 “Effects of a change to more formative assessment among tertiary mathematics students”, Anziam Journal Electronic Supplement, 61, C255-C271, doi:10.21914/anziamj.v6110.15166.
27. A. Radloff, H. Coates, 2009, Doing more for learning: Enhancing engagement and outcomes. Australian Council for Educational Research, 2009.
28. RStudio, Open source and professional software for data science, <https://rstudio.com>,, 2020
29. S. Higgins, M. Katsipataki, 2016, “Communicating comparative findings from meta-analysis in educational research: some examples and suggestions”, International journal of Research and Method in Education, 30(3), 237-254, doi: 10/1080/ 1743727X. 2016.1166486.
30. S. Trenholm, J. Peschke, “Teaching undergraduate mathematics fully online: a review from the perspective of communities of practice”, International Journal of Educational Technology in Higher Education, 17, Article 37, 2020, doi:org/10.1186/s41239-020-00215-0.
31. B. Loch, R. Borland, N. Sukhurovka, ‘Implementing blended learning in tertiary mathematics teaching’, The Australian Mathematical Society Gazette, 46(2), 90-102, 2019.

(Click Here)