1 Introduction

Cloud data storage has exploded over the last decade, for both business and personal purposes. The latter have offered the opportunity to delegate the storage of individuals’ files, through various services that have been developed and diversified with competitive fees for data owners (e.g. copies of files stored in different storage locations). However, due to its complex structure, many unfortunate events have happened over the last few years. In 2015, lightning strikes engendered data loss on Google centers^[1]. The startup Front Edge CNC’ used to keep its online production data in Tencent Cloud Storage but realised in 2018 that it was completely lost^[2]. More recently, according to McAfee, 99% of misconfiguration incidents occurring in a public cloud environment are not detected, thus exposing enterprises and organisations to a huge risk of undetected data breaches^[3]. Therefore, it has become urgent to carefully design cloud storage solutions to overcome all possible unfortunate events such as the aforementioned ones.

An ideal solution will enable a simple deal between a client, who owns some files, and a cloud provider (also called cloud server), who offers safe and attractive cloud storage services. For instance, the cloud provider may propose to store copies of a file in addition to the file itself, and spread them across multiple servers, avoiding single point of loss. The cloud provider may also offer to decrease fees per copy, to encourage the client to adopt the replication process as much as possible. More precisely, both the client and cloud provider are financially incentivized: the client wants to save fees as much as possible while uploading files as many as possible, while the cloud provider wants to earn as much as possible while saving storage as much as possible. Those assumptions clearly motivate their behaviours. The rational cloud provider may claim to store the client’s files while actually not, and thus offering the free storage space to other clients. The malicious client may claim to upload copies of the files, with lower fees, but rather uploading different files where fees would have higher if behaving honestly.

This work is an extension of [1], in which a new solution was proposed for secure and efficient cloud storage for a client who owns some files stored on a cloud provider. Security is enhanced by allowing detection of a misbehaving cloud provider that does not store the client’s files correctly and prevention against a malicious client who tries to save fees. Informally, the cloud provider is asked to create copies of the client’s files stored across various locations and can be challenged to prove the client that all files and their copies are entirely stored. The client uploads encrypted files to the provider but does not have the responsibility of creating the copies, avoiding the client to upload fake copies (i.e. files that are not at all linked to the original ones). Efficiency is conserved even with improved security. In particular, experimental results presented for the first time in this paper show that the mechanisms used to preclude malicious behaviours incur low costs on the computational and communication processes.

1.1 Problem Statement

Let a client subscribe to data storage services offered by a cloud provider. Proof of Data Possession (PDP) and Proofs of Retrievability (POR) are cryptographic protocols proposed to enable the client to verify that the cloud provider actually proceeds as agreed, that is correctly stores the client’s data.

The latter protocol, POR [2], guarantees the client that her data is available in its entirety. The former protocol, PDP [3, 4], allows the client to verify that the stored data has not undergone any modifications. Recent PDP works [5, 6, 7] offer a replication feature: the cloud provider creates copies of the data and the client can check in a single instance that both the original and copied data are all correctly stored.

However, the aforementioned solutions do not reflect the actual framework. Limited bandwidth is offered for free and costs grow quickly with the increasing bandwidth. In most of existing works, the replication and uploading processes rely on the client, imposing huge burden and fees to the latter. In addition, fees for storage of extra replicas of a given file are less consequent than fees for storage of different files. Hence, a malicious client may attempt to upload different files while claiming that they are replicas of the same file. The cloud provider cannot observe such a trick since data is assumed to encrypted before being uploaded, and thus are not readable.

Limitations also raise on the cloud provider’s side. The latter may appear to be financially motivated and consequently act maliciously. For instance, it attempts to not store all file replicas and offers the resulting unoccupied storage space to other potential customers. Then, such a rational cloud provider creates the missing replicas on the fly when the client who owns the original file asks for storage verification. In addition, the client may put tacit trust on its cloud provider and neglect to carefully read the service level agreements [8]. Likely, the client does not take the time and effort to verify how the cloud provider deals in storing her data.

The design of an appropriate solution for secure data storage in the cloud is clearly encouraged by the aforementioned financial concerns. Clients are motivated by reducing the costs due to bandwidth and storage while the cloud provider is stimulated by partitioning data to make profit. Those concerns have been carefully studied and overcome in [9]. The authors presented an extension of POR, called Proof of Retrievability and Reliability (PORR), to encompass the correct storage verification of both file and its replicas at once. However, the main obstacle of the PORR instantiating in [9] is the private feature of verification: only the client is able to check that the cloud provider correctly stores her file and its replicas.

In [1], we proposed a new PORR protocol overcoming all the aforementioned challenges at once. Along with getting over malicious clients and rational providers, we overcame the likely laziness: the client can delegate the task of checking that the cloud provider has been acting honestly on her data.

1.2 Idea

Our solution is designed to enable a client to upload her file and the cloud provider to generate the replicas of this file. By doing so, we prevent malicious clients to upload different files and claim that there are all replicas of the same file.

Moreover, we offer the client the guarantee that the cloud provider correctly stores both the original file and its replicas at rest. By using slow functions, we prevent rational cloud providers to compute replicas of an original file on the fly when challenged to prove correct storage. Indeed, evaluating a slow function is noticeably slow while verifying its unique evaluation output is fast and easy. Therefore, if the cloud provider tries to generate a replica on demand, it will take a noticeable time to evaluate the slow function attached to the replica and output the unique solution, rather than just storing the replica along with the output from the evaluated slow function.

The cloud provider is challenged by a verifier, that can be anyone on behalf of the client. The verification allows a client to ensure that the cloud provider stores the original file and all replicas in their entirety.

Our PORR solution with public verification is a combination of the publicly verifiable POR protocol with RSA signatures from Shacham and Waters [10, 11] and of the slow exponentiation-based Verifiable Delay Functions (VDFs) in finite groups from [12].

We suggest an extension of the POR scheme built by Shacham and Waters [10, 11], where replicas of the challenged file are contained in the verification mechanism. Public verification allows anyone, on behalf of the client, to request the cloud provider a proof of correct storage. Such a feature overcomes a possible lack of data integrity awareness from the client. In order to stop the cloud provider to generate the file replicas on demand when being challenged by the verifier, we incorporate slow functions from [12], namely VDFs. Of course, storing VDF outputs must result into storage costs that are at least as high as storing replicas as required. In fact, rational cloud providers are expected to commit minimal computation resources when generating a correct response. Therefore, the cost of replying to a challenge on the fly should be more than the cost of storing the replicas correctly.

To our knowledge, Gritti [1] presented the first PORR protocol that both delegates the construction of the replicas to the cloud provider and that permits anyone to verify that the latter correctly stores the files and their replicas.

We give an overview of the PORR protocol in Figure 1. A client encodes and processes a file M as M^∗, and outsources it to the cloud provider. The latter commits to store M^∗ entirely across a set of r storage nodes. This means that M^∗ is updated to contain the original copy of M and r replicas. On inputs the public parameters, the verifier (possibly the client as in the figure) can efficiently launch challenge requests and verify the responses from the cloud provider. The cloud provider must store both the original file and its replicas at rest, at r storage nodes.

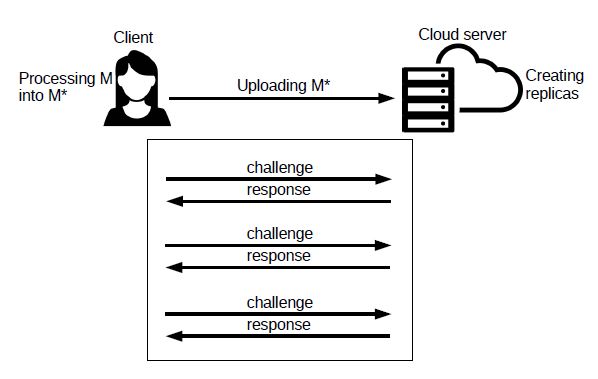Figure 1: PORR protocol: First the client prepares her file M by encrypting and encoding it, resulting into M^∗. Second, she uploads M^∗ to the cloud server along with some additional elements, such as a tag T. The cloud server generates the replicas based on the additional information. Later, and multiple times, the client and cloud server enter into a challenge-response protocol to allow the former to check whether the latter correctly stores her file and its replicas.

1.3 Related Work

We first present existing works on Provable Data Possession and Proof of Retrievability. We then move on Proof of Reliability, where several variants have been proposed based on different mechanisms, namely data replication, erasure codes, proof of location and proof of space. Finally, we review slow functions that allow to generate puzzles, and in particular Verifiable Delay Functions.

1.3.1 Provable Data Possession and Proof of Retrievability.

Provable Data Possession: The authors in [3] introduce the concept of Provable Data Possession (PDP), which enables a client to privately verify the integrity of her files stored at an untrusted cloud provider without the need to retrieve the entire files. Thereafter, the authors in [13] improve the efficiency of the previous PDP scheme [3] by using symmetric encryption. Subsequently, PDP constructions for static data have been proposed in the literature [14, 15, 16, 17]. PDP schemes with additional properties, such as data dynamicity, have been suggested in [18, 19, 20, 21, 22, 23]. Several works have been published recently [24, 25, 26, 27, 28, 29, 30], proposing PDP schemes preserving data privacy and publicly verifying data integrity.

Proof of Retrievability: Juels and Kaliski [2] defined Proof of Retrievability (POR), that is a similar concept to PDP. In POR, the client can correct existing erros and recover the whole files, in addition to check that the cloud provider stores her files in their entirety. Then, Shacham and Waters [10] propose two POR schemes: a first one with public verification built on BLS signatures, and a second one with private verification based on pseudo-random functions. Xu and Chang [31] improve Shacham-Waters POR schemes by achieving only a constant number of communication bits per verification rather than linear in the number of sectors. Subsequent works on distributed systems follow in [32, 33, 34], as well as POR protocols with data dynamicity in [35, 36].

1.3.2 Proof of Reliability.

Based on Data Replication: The authors in [5] extend the scheme from [3] by enabling the file owner to verify that at least k replicas are stored by the cloud provider. Chen and Curtmola [37, 38] propose a mechanism with a tunable masking feature in order to let the cloud provider be responsible of the repair operations and the client manage the process of repair. In [39], cross-client deduplication is enabled at the file level by extending [38]. In [6, 7], clients are able to modify and add some pieces of a given file, while to check the correctness of replications of this file. In [40], the replication process is made transparent in a distributed system for cloud storage by extending [18]. The aforementioned solutions, a similar framework is encountered: replicas are prepared by the client, and further sent to the cloud provider with the original files.

More recently, the Proof of Retrievability and Reliability (PORR) protocol is defined for the first time in [9] to illustrate the case where the cloud provider prepares the replicas rather than the client. Tunable puzzles are used for replicating the file, guaranteeing the the replicas are stored at rest. Nevertheless, only a private verifying process is available.

Based on Erasure Codes: HAIL [33] provides a high availability and integrity layer for cloud storage. By using erasure codes, data retrievability and reliability are guaranteed among distributed storage servers, and clients can detect and repair file corruption. The authors in [41] achieve a more efficient mechanism for repairs by extending HAIL [33] and moving bulk computations to the cloud provider. The authors in [42] present a scheme for remote data checking in network coding-based distributed storage systems. The scheme minimizes the communication overhead of the repair component compared to the erasure code-based approaches. The repair mechanism in [42] is improved in [22], such that the computation cost for the client is reduced. Following the idea of adding a third party auditor [22], Thao and Omote [43] offer a network codingbased scheme such that the repair mechanism is executed between the auditor and the cloud provider, and the client is let apart.

A proof of fault tolerance, as a protocol based on erasure codes, is proposed in [44]. The scheme uses technical characteristics of rotational hard drives to build a time-based challenge, such that the client can check that her encoded files are stored at multiple storage nodes within the same cloud provider. Thereafter, the authors in [45] construct POROS for erasure code-based cloud storage systems by combining POR with time-constrained operations. In order to set a time threshold for the response generation and thus to force the cloud provider to store replicas at rest, rotational hard drive-based ideas are leveraged similar to the ones in [44].

More recently, PORTOS [46] also uses erasure codes to guarantee data reliability, and ensures that the burden of replica generation as well as the repair operations are shifted to the cloud provider. Nevertheless, contrary to [44, 45], the solution in [46] does not rely on the technicity of rotational hard drive technology. Indeed, such method is inevitably dependent on the parameters of the underlying erasure code system. However, in [46], only the client can check the behaviour of the cloud provider in storing her files and replicas.

Proof of Location: Proofs of Location (PoL) [47, 48] have been introduced to prove the geographic position of data, such that whether certain servers in a given country store such data. A PoL scheme is presented in [48] as a combination of geo-location mechanisms and the Shacham-Waters POR schemes [10]. The PoL model looks similar to the PORR one, such that files are uploaded only once by the client to the cloud provider. Then, the cloud provider generates the file tags, prepares the replicas and scatters the latter across servers that are geo-located at different places. Individual POR instances are invoked by the client with all servers to verify whether the latter correctly store the files. On the contrary, PORR schemes must enable clients to launch a single instance to check that all file replicas are correctly stored instead of one instance per replica.

Proof of Space:    Proofs of Space (PoS) [49] allow the prover to reply correctly as long as a given amount of space or time per execution is invested. In our case, we require that the prover invests a minimum amount of space. In addition, we need to get a single instance to check that all file replicas are correctly stored, that is not made possible with PoS. Hence, the notion of PoS does not suit our requirements.

1.3.3     Slow Functions

Time-lock puzzles [50], benchmarking [51], timed commitments [52] and client puzzles [53, 54] rely on the sequential nature of large exponentiation in a finite group.

Dwork and Naor [53] design a slow function by extracting modular square roots. No algorithm is known for computing modular exponentiation which is sub-linear in the bit-length of the exponent. Nevertheless, the puzzle difficulty is limited to O(log p), meaning that a very large prime p (being the order of the group) must be chosen to produce a difficult puzzle. Lenstra and Wesolowski [54] consider the sequential nature of Dwork-Naor solution to suggest chaining a series of such puzzles together (e.g. for lotteries). However, this construction does not provide asymptotically efficient verification, hence it can rather be seen as a pseudo-Verifiable Delay Function (VDF).

Time-lock puzzles [50] involve computing an inherently sequential function, by repeating squaring in a RSA group. Used in the context of POR with data reliability guarantees, the cloud provider requires an apparent amount of time to solve those puzzles while the latter are efficiently solved by the client using a trapdoor. Moreover, storing the solution of a time-lock puzzle incurs extra storage costs that are at least as large as the required storage for replicas. The difficulty of a RSA-based puzzle can be easily adjusted by the client (who creates the puzzle) to cater for variable length and different cost metrics. However, such puzzles are not guaranteed to be publicly verifiable: the client (or a dedicated verifier) uses a secret element to prepare each puzzle and to verify the solution.

A given number of sequential steps are required for VDFs, resulting into a unique output verified in an efficient and public way. The construction of a VDF with a trusted setup was proposed [55]. The authors in [12] observe that the trusted setup can be discarded by choosing a sufficiently large random number N, such that N = pq with high probability, for p,q two large prime factors. Nevertheless, the adversary would benefit for parallelizing the arithmetic due to the large size of N, and the running time of the verifier would then increase. The authors in [12] rather suggest to build a VDF from exponentiation, based on the assumption that the adversary cannot run a long pre-computation from the publication of the public parameters to the evaluation of VDF. Hence, this solution achieves proofs that are shorter than the proofs in [55] at a similar level of security.

1.3.4    Work Comparison

In Table 1, we compare our work with main other ones, based on the specific features that enable secure cloud storage against malicious servers and clients. We omit the Proof-of-Space (PoS) mechanism for Proof of Reliability since it is too far-off our work.

Table 1: Comparing existing protocols similar to PORR.

Type	Work	Proof	Replicas?	Public?
			Where?	Private?
Original PDP	[3]	PDP	no replicas	private
	[13]	PDP	no replicas	private
Original POR	[2]	POR	no replicas	private
	[10]	POR	no replicas	private (pseudo)
	[10]	POR	no replicas	public (BLS)
Proof of	[5]	POR	replicas at	private
Reliability			client’s side
(data	[39]	POR	replicas at	private
replication)			client’s side
	[9]	POR	replicas at server’s side	private
	ours	POR	replicas at server’s side	public
Proof of	[33]	other	replicas at	private
Reliability			client’s side
(erasure	[46]	POR	replicas at	private
codes)			server’s side
Proof of	[48]	POR	replicas at	private
Reliability			server’s side
(proof of			but individual
location)			POR instances

Most of the compared works are based on PDP and POR proofs. When replica services are offered, we consider proof of correct data storage in a single instance for both original files and their copies (otherwise specified). Replica options are an important service to be offered by cloud providers, in order to avoid unfortunate data loss due to technical issues (e.g. single point of failure).

In almost all works, only private verification is offered. Private verification means that only the client can challenge the server for correct storage. We think that such an assumption is too strong as clients may be too lazy to do so. We suggest that delegating such a checking process to a third party will guarantee a better storage experience for both clients and cloud providers.

The closest work to ours is definitely the work from [9]. Indeed, the authors aim to develop a cloud storage solution to prevent both rational cloud providers and malicious clients. To do so, they combine POR instances with RSA-based puzzles [50].

One limitation in [9] is from the private aspect of POR instance verification. Indeed, either the client or someone in possession of the secret key can perform the verification of integrity of stored data. We aim to develop a publicly-verifiable PORR scheme, that allows everyone, using only public elements, to check that the cloud provider correctly stores original files and their replicas.

2  Contributions and Road Map

In [1], the first Proof of Retrievability and Reliability (PORR) with public verification was proposed. The original file of the client is first uploaded to a cloud provider. The replica plan has been agreed by both the client and cloud provider. Following that plan, replicas of the original file are prepared by the cloud provider. Anyone (and possibly the client) can challenge the cloud provider to check the integrity of the stored files and replicas.

In [1], the publicly verifiable RSA-based POR scheme from Shacham and Waters [10, 11] was combined with the exponentiation-based VDF construction from [12]. This allows us to define a common parameter setting, roughly a RSA-based one, while benefiting all the properties offered by the two schemes. Namely, the verifier can efficiently launch a large number of challenge requests and checks the cloud provider’s responses using only public elements, while the cloud provider is forced to store the client’s original file along with all the replicas at rest (otherwise being timely noticed).

In this paper, we provide the experimental analysis of our publicly verifiable PORR protocol. Implementation and evaluation results reveal realistic applications. Communication overhead between the client, the cloud provider and the verifier remains fair. Computation costs are affordable for the client and verifier, while they are made such that the cloud provider does not gain in computing the replicas on the fly from challenge requests. We also compare our solution with MIRROR [9], a PORR prototype with private verification, built upon Waters and Shacham’s POR [10] and RSA-based puzzles [50].

Therefore, our solution fits cloud-related bandwidth and storage requirements, while preventing malicious clients and rational cloud providers from being successful.

In the following Sections 3 and 4, we recall the definition and construction of Shacham-Waters POR [10, 11] and of VDF from [12]. The reader can directly jump to Section 5 if being familiar with concepts of POR and VDF. In Section 5, our publicly verifiable PORR protocol presented in [1] is described. In Section 6, we depict the implementation framework of our PORR and analyse the experimental results. We conclude this paper in the last section.

3 RSA-based POR with Public Verification

In this section, we recall the publicly verifiable RSA-based POR construction from [10, 11]. Since our choice of slow functions [12] is based on RSA and also publicly verifiable, such POR construction is welcomed. The RSA-based POR construction in [11] is an extension of the RSA-based PDP construction in [4].

3.1  Definition

A Proof Of Retrievability (POR) comprises five algorithms. The client runs the two first algorithms. A public and secret key pair (pk, sk) are generated by running the key generation algorithm. For each file M, the client computes a corresponding tag T. Using the secret key sk, the file and tag generation algorithm processes the file M, resulting into M^∗, and computes the tag T.

The client challenges the cloud provider when she wants to verify her files are stored in their entirety. A challenge set Q, selected when running the challenge generation algorithm, defines the file blocks that the cloud provider must prove to store correctly. From this challenge, the latter replies by running the response generation algorithm and shares the response resp with the client. The latter can then verifies resp by running the verification algorithm. The output of this algorithm tells the client whether or the cloud provider stores her files in their entirety.

In the above description, we suggest that the client verifies the cloud provider’s response. However, in a publicly verifiable case, anyone can verify resp since only public elements are required to run the verification algorithm. In a privately verifiable case, only someone with a secret element can check resp, the client in general would have such competency, but a private verifier can also be given a secret key. We only consider the first case in our paper.

POR protocols must be proved correct and sound. Correctness requires that for all key pairs (pk, sk) output by the key generation algorithm, for all file M ∈ {0,1}^∗, and for all pair (M^∗,T) output by the file and tag generation algorithm, the verification algorithm accepts with challenge and response respectively output by the challenge generation algorithm and the response generation algorithm. Soundness states that if a cheating cloud provider convinces the verifier that it is storing the file M, then it is actually storing the file M. Shacham and Waters formalize the notion of an extractor algorithm that interacts with the cheating cloud provider using the POR protocol.

3.2 Notations

The processed file M⁰ (obtained from applying an erasure code on the file M) is split into n blocks, and each block is then split into s sectors. Each sector m_i,j, for i ∈ [1,n] and j ∈ [1, s], is an element of Z_N. For instance, for a processed file M⁰ that is b-bit long, there are n = db/slog(N)e blocks.

A challenge is an l-element set Q = {(i,v_i)}. The size l of the set

Q is a system parameter. Each tuple (i,v_i) ∈ Q can be described as follows:

• The value i is a block index in [1,n].
• The value v_i is an element in E ⊆ Z_N. Let E ⊆ Z_N be the set of coefficients v_i chosen for verification requests. For instance, E = Z_N, such that coefficients v_i are randomly chosen from Z_N.

3.3 Construction

Let κ be the security parameter. Let κ₁ be a bit length such that the difficulty of factoring a (2κ₁ − 1)-bit modulus fits the security parameter κ. Let max(E) be the largest element in E. Let κ₂ be the bit length equal to dlog(l · max(E))e + 1 [10, 11].

The construction of publicly verifiable POR with RSA signatures given in [11] is as follows:

Key Generation: On input a security parameter κ, the randomized key generation algorithm outputs the public key and secret key pair (pk, sk) as follows. Let (spk, ssk) ← S.KeyGen(κ) be a random signing key pair. Choose two primes p and q at random such that p,q ∈ [2^κ1−1,2^κ1 − 1]. Let N = pq be the RSA modulus such that 2^κ1−2 < N < 2^κ1. Let G : {0,1}^∗ → Z^∗_N be a full-domain hash function, seen as a random oracle. Pick at random a prime e of length 2κ₁ + κ₂ bits, and set d = e⁻¹ mod φ(N).

Set the public key pk = (N,e,G, spk) and the secret key sk = (N,d,G, ssk).

File and Tag Generation: On inputs the secret key sk and the file

M, the file and tag generation algorithm outputs a processed file M^∗ and the tag T as follows:

1. Apply the erasure code on M to obtain M⁰.
2. Split M⁰ into n blocks for some integer n, each of them being s sectors long, resulting into a n × s ma-

trix {m_i,_j}_i∈[1,_n],_j∈[1,_s]. Each sector m_i,_j is an element of Z_N.

3. Choose a random file identifier id ∈ Z_N.
4. Pick at random s random numbers u₁,u₂, · · · ,u_s.
5. Let T₀ = id||n||u₁||u₂|| · · · ||u_s. Compute the file tag T = T0||Sigssk(t0).
6. For each i ∈ [1,n], compute σ_i = (G(id||i) · ^Qs_j=1 u^m_j ^i,j )^d mod N.
7. The processed file is M∗ = ({mi,j}i∈[1,n],j∈[1,s], {σi}i∈[1,n]).

Challenge Generation: On inputs the secret key sk and the tag T, the randomized challenge generation algorithm outputs the challenge set Q as follows:

1. Use the key spk to verify the signature on T. If the signature is invalid, then output 0 and halt.
2. Otherwise, recover id,n,u₁,u₂, · · · ,u_s.
3. Pick at random an l-element subset I from the set [1,n]. For each i ∈ I, choose a random element v_i ∈ E. Let

Q = {(i,v_i)}_i∈I.

Response Generation: On inputs the processed file M^∗ and the challenge set Q = {(i,v_i)}_i∈I, the deterministic response generation algorithm outputs a response resp as follows:

1. Compute µ_j = ^P_(i,_vi)∈Q v_im_i,_j ∈ Z for j ∈ [1, s] (note that there is no modular reduction).
2. Compute σ = Q(i,vi)∈Q σvi i mod N.
3. Set the response resp = ({µ_j}_j∈[1,s],σ).

Verification: On inputs the response resp, the deterministic verification algorithm checks first whether each µ_j is in the range [0,l · N · max(E)]. If some values are not in the range, then halt and output 0. Otherwise, check whether the equation σe = Q(i,vi)∈Q G(id||i)vi × Qsj=1 uµj j mod N. If so, then it outputs 1; otherwise, it outputs 0.

3.4       Security

The security for POR is linked to unforgeability, extractability and retrievability. Informally, the security proof is split in three parts such that:

• The first part shows that the verifier can not receive an illegitimate (i.e. forged) response from the adversary (i.e. the cheating cloud provider).
• The second part shows that there exists an extractor extracting a constant fraction δ of file blocks (previously encoded with an erasure code) as soon as there exists an adversary that succeeds the verification process a noticeable number of times. Indeed, all responses that have been checked should be legitimate.
• The last part shows that one can use an erasure code to rebuild the whole file M if the constant fraction δ of file blocks has been recovered.

The RSA-based POR construction has been proved correct and sound. We let the readers refer to [10, 11] for the formal security proof.

4 Verifiable Delay Functions From Exponentiation in a Finite Group

In order to prevent rational behaviour from cloud providers, we aim to use slow functions (also called puzzles). Slow functions are constructed such that:

• Puzzles and file blocks are combined, resulting into r correct replicas of the file M. Homomorphic properties required for compact proofs are preserved.
• The client can adjust the difficulty of the puzzles supply multiple cost metrics.
• The costs from the storage of the solution of the puzzle are at least as high as the storage needed for the replicas of the file M.
• The cloud provider needs more time to solve the puzzles than the client, since the latter has access to a trapdoor.

In this section, we recall the construction of VDFs [12] that we use in our PORR. In order to successfully combine Shacham-Waters POR with VDFs, we opt for the exponentiation-based version with bounded pre-computations in a RSA group. This version is secure against attackers with bounded pre-computations, from a generalization of exponentiation-based time-lock puzzles in groups of unknown order.

4.1 Definition

An algorithm is said to run with p processors in parallel time t if one can implement it on a PRAM machine with p parallel processors that run in time t. The total sequential time refers to the time required for computation on a single processor.

A Verifiable Delay Function (VDF) is composed of three algorithms, to set up the system, evaluate the slow function and verify a solution. On inputs a security parameter κ and a delay parameter t, the randomized setup algorithm outputs the public parameters pp containing an evaluation key ek and a verification key vk. This algorithm must be polynomial-time in κ. The delay parameter t must be sub-exponentially sized in κ.

On inputs the evaluation key ek and a puzzle x from some known sampleable set, the evaluation algorithm outputs the solution y and a (possibly empty) proof π. For all public parameters pp and for all puzzles x, the evaluation algorithm must run with poly(log(t),κ) processors in parallel time t. For a given puzzle x, there must be a unique output y whose verification will be correct.

On inputs the verification key vk, the puzzle x, the solution y and its proof π, the deterministic verification algorithm outputs either 1 if y is a valid solution for the puzzle x, or 0 otherwise. The verification algorithm must run in total time polynomial in log(t) and κ. This algorithm is much faster than the evaluation one.

The VDF is expected to be sequential where honest parties can compute (y,π) by running the evaluation algorithm in t sequential steps, while no parallel-machine adversary with a polynomial number of processors can make the distinction between the output y from a random value in many less steps. Moreover, the VDF is expected to be efficiently computable, where honest parties run the verification algorithm as fast as possible such that the total time should be O(polylog(t)). The VDF is finally expected to be unique where for all puzzles x, the value y is difficult to calculate such that the verification algorithm outputs 1 while y is not an output of the evaluation algorithm on inputs pp and x.

4.2 Notations

Given an integer n, let [1,n] denote the set of integers {1,2, · · · ,n}. Let L = {l₁ = 3,l₂ = 5, · · · ,l_t} be the first t odd primes. The parameter t is the provided delay parameter. Let P be the product of the primes in L, i.e. P = l₁ · l₂ · · · l_t. The parameter P is a large integer with about t logt bits.

4.3       Construction

Here, we describe in details the exponentiation-based solution for VDF in [12].

Setup: The trusted setup process is the following:

1. Set a RSA modulus N = pq (for instance, 4096 bits long) such that the prime factors p,q are strong primes. The factorization of N is only known by the trusted setup algorithm. Let H : Z → Z^∗_N be a random hash function.
2. For a given pre-processing security parameter B (for instance, B = 2³⁰), do the following:
   • Compute H and g_i = h¹_i ^/P ∈ Z^∗_N for i ∈ [1, B].
   • Set ek , H,g₁,g₂, · · · ,g_B) and vk

While the parameters of the verifier are short, the ones of the evaluator are not.

Evaluation: Solving a puzzle x works as follows:

1. Map the puzzle x to a random subset L_x ⊆ L of size κ and a random subset S _x of κ values in [1, B], using a random hash function.
2. Let P_x be the product of all the primes in L_x and let g = Qi∈S x gi.
3. The puzzle solution is y = g^P/Px .

The computation of the solution takes O(t logt) multiplications in Z^∗_N.

Verification: Verifying a solution y works as follows:

1. Compute P_x and S _x as in the evaluation algorithm on inputs ek and x.
2. Compute h = ^Q_{i∈S x} H(i).
3. Output 1 if and only if y^Px = h.

We observe that exactly one element y ∈ Z^∗_N will be accepted as a solution for a puzzle x. The verification process takes only O˜(κ) group operations.

4.4       Security

Security is defined in face of an attacker able to perform polynomially bounded pre-computations. A VDF scheme must satisfy:

Correctness and Soundness. Every output of the evaluation algorithm must be accepted by the verification algorithm. The solution y for a puzzle x is guaranteed to be unique because the evaluation algorithm evaluates a deterministic function on the sampleable set of puzzles. The proof π does not require to be unique but should be sound and a verifier cannot be convinced that some different output is the correct VDF outcome.

τ-Sequentiality. No adversary should be able to compute an output for the evaluation algorithm on a random puzzle in parallel time τ(t) < t, even with up to many parallel processors, and after a potentially large amount of pre-computations.

We let the readers refer to [12] for more details on the security models for VDFs.

The above construction does not satisfy the definition of a secure VDF presented in [12]. More precisely, an adversary who is able to run a large pre-computation once the parameters pp are known can break the above construction. There are various possible pre-computation attacks requiring tB group operations in Z

New parameters must be generated after B challenges; otherwise, the scheme is not secure. This is sufficient for our application of a VDF, for instance by choosing B = 2³⁰. Regarding experiments of other solutions [9, 45, 46], storage challenges never excess such B.

5 RSA-based PORR with Public Verification

In this section, we describe our RSA-based solution for Proof Of Retrievability and Reliability (PORR) with public verification, using exponentiation-based VDFs to prevent the cloud provider to generate replicas on the fly when being challenged.

A client encodes and then processes a file M into M^∗, and outsources the latter to the cloud provider. The cloud provider then commits to store M^∗ entirely across a set of r storage nodes with reliability guarantee R. This means that M^∗ contain the original copy of M along with replicas.

A PORR protocol is executed between a client and a cloud provider provided by its k storage nodes. The goal of such protocol is to enable either the client or anyone else to check the integrity and reliability of the processed file M^∗.

5.1       Definition

Informally, our PORR protocol combines the RSA-based POR scheme of Shacham and Waters [10] and the exponentiation-based VDF scheme from [12].

The Setup phase initiates the protocol. It corresponds to the key generation and file and tag generation algorithms of ShachamWaters POR scheme and to the setup algorithm of the VDF scheme. The client generates the parameters of the protocol, corresponding to the ones found in the two underlying schemes. She prepares her to-be-stored M by encrypting and processing it, and by generating the tag T and the authenticators σ_i for i ∈ [1,n] (where n is the number of blocks) as in the POR scheme [10]. According to the agreed number r of replicas that the cloud provider must store, the client also prepares the VDF puzzles x_i⁽_,^k_j⁾, for i ∈ [1,n], j ∈ [1, s] and k ∈ [1,r]. In other words, there is one challenge per sector per replica (we recall that there are s sectors per block).

Once the cloud provider receives the file-related elements to be stored, the Setup phase is over. It can then start the second phase, namely the Replica Generation phase, in order to create the r replicas of the original file M. To do so, the cloud provider evaluates the VDF puzzles x_i⁽_,^k_j⁾ by running the evaluation algorithm. It appends each solution y_i⁽_,^k_j⁾ with the corresponding sector replica m⁽_i,^k_j⁾, for i ∈ [1,n], j ∈ [1, s] and k ∈ [1,r].

The next three phases can be requested multiple times. There is an interaction between a verifier (the client herself or someone on her behalf) and the cloud provider. During the Challenge Generation phase, the verifier generates the challenge chal and sends it to the cloud provider, by running the challenge generation algorithm of Shacham-Waters POR scheme. During the Response Generation phase, the latter replies back to the client with a response resp by running the response generation algorithm of POR scheme. Finally, during the Verification phase, the verifier then checks resp using only public elements, using the verification algorithms of ShachamWaters POR scheme and of the VDF scheme. Indeed, verification exactly contains two steps: one check for POR and one check for VDF. If the output is 1, then the verifier is guaranteed that the cloud provider stores the file in its entirety along with its r replicas.

5.2       Construction

Here, we describe in details our publicly verifiable RSA-based PORR solution.

Setup: This phase includes the POR-based key, file and tag generations along with the VDF-based setup process.

Let κ be the security parameter. Let (S.KeyGen, S.Sign, S.Verify) be a digital signature scheme. Choose two primes p and q at random such that p,q ∈ [2^κ1−1,2^κ1 − 1]. Let N = pq be the RSA modulus such that 2^κ1−2 < N < 2^κ1. Let G : {0,1}^∗ → Z^∗_N be a full-domain hash function, seen as a random oracle. Pick at random a prime e of length 2κ₁ + κ₂ bits, and set d = e⁻¹ mod φ(N). Let t be the delay parameter and B be the security parameter for VDFs. Let L = {l₁ = 3,l₂ = 5, · · · ,l_t} be the first t odd primes and

P = l₁ × l₂ × · · · × l_t. Let H : Z → Z_N be a hash function, seen as a random oracle.

The client wishes to store a file M ∈ {0,1}^∗ at the cloud.

Without loss of generality, the file M is assumed to be encrypted and encoded (using the specific erasure code). Encryption guarantees confidentiality and encoding guarantees extractability and retrievability.

As in [10], the file M is first split into n blocks, and then split into s sectors. Let us denote a sector as m_i,j ∈ Z_N, for i ∈ [1,n] and j ∈ [1, s]. Bit representation of each sector m_i,j includes a characteristic pattern (e.g. a sequence of zero bits), in order to guarantee extractability [9]. Pattern length and file size are dependent such that the former should be larger than log₂(n · s).

The client runs the algorithm S.KeyGen(κ) and gets the signing and verification key pair (ssk, spk). She also chooses an identifier id ∈ Z_N for the processed file M^∗. She then picks at random s non-zero elements u₁,u₂, · · · ,u_s ∈ Z_N. The client computes T₀ = id||n||u₁||u₂|| · · · ||u_s and then T = T₀||^S.Sign_ssk(T₀). Moreover, the client calculates σ_i = (G(id||i) · ^Qs_j=1 u^m_j ^i,j )^d mod N for i ∈ [1,n]. We notice that all operations are done in the multiplcative group Z^∗_N of invertible integers modulo N.

Both the cloud provider and client have agreed to create r replicas of the file M and store all of them at rest. She computes h_i = H(i) and g_i = h¹_i ^/P for i ∈ [1, B]. She also chooses the values x_i⁽_,^k_j⁾ for i ∈ [1,n], j ∈ [1, s] and k ∈ [1,r].

           Finally,         the client uploads the processed file M^∗              =

({mi,j}i∈[1,n],j∈[1,s], {σi}i∈[1,n]) to the cloud provider. She also forwards the public parameters params =

(N,e,G, H, spk, L, P,T, {g_w}_w∈[1,_B], {x_i⁽_,^k_j⁾}_i∈[1,_n],_j∈[1,_s],_k∈[1,_r]) to the cloud provider and anyone interested in playing the role of the verifier.

The client keeps secret the tuple (N,d,G, ssk).

Replica Generation: This phase includes the evaluation process of the underlying VDF.

The cloud provider calculates the solution y⁽_i,^k_j⁾ for each x_i⁽_,^k_j⁾, and then build the replica ^m(_i,^k_j⁾ of the original sector m_i,j, for k ∈ [1,r].

First, the cloud provider maps x_i⁽_,^k_j⁾ to L_i⁽_,^k_j⁾ ⊆ L of size κ and the random subset S _i⁽_,^k_j⁾ of κ values in [1, B], using a random hash function. Second, it sets P⁽_i,^k_j⁾ as the product of all primes in L_i⁽_,^k_j⁾ and computes ^g(_i,^k_j⁾ = ^Q_w∈S i(,kj) g_w. Third, the cloud provider computes the solution ^y(_i,k_j) (k) P/P(i,kj) ∈ ZN. = (gi,j )

Finally, it computes m⁽_i,^k_j⁾ = m_i,j + y⁽_i,^k_j⁾ as the k-th replica of the sector m_i,j.

Challenge Generation: This phase corresponds to the challenge generation of POR.

First, the verifier (possibly the client) generates the challenge chal. Given T = T0||S.Sigssk(T0), check that S.Signssk(T0) is a valid signature by running the algorithm S.Verify_spk. If the signature is invalid then halt.

Thereafter, elements id,n,u₁,u₂, · · · ,u_s are recovered the verifier. The latter then sets I ⊂ [1,n] of l elements and randomly selects l elements v_i ∈ Z_N, for i ∈ I. Then, let Q = {(i,v_i)}_i∈I where i is defined as the index of the block m_i. A set R ⊂ [1,r] is also set by the verifier. Finally, let chal = (Q,R) be forwarded to the cloud provider.

Response Generation: This phase corresponds to the response generation of POR.

Upon reception of the challenge chal, the cloud provider creates its response resp. First, it computes µ_j = ^P_(i,_vi)∈Q v_im_i,_j ∈

Z and σ = Q(i,vi)∈Q(σi · Qsj=1 Qk∈R umj (i,kj))vi mod N. It sets resp = ({µ_j}_j∈[1,s],σ) and forwards it to the verifier.

Verification: This phase includes both POR- and VDF-based verification steps.

Upon reception of the response resp, the verifier verifies that whether each µ_j is in the range [0,l·N·max(Z_N)]. The verifier halts and outputs ) as soon as some values are not in the range. Otherwise, the verifier checks whether the following equation holds:

Sσe       =          Y G(id||i)vi × Yuµj j(1+|R|e)

(i,v_i)∈Q                            j=1

 Y Ys Y vi(h(i,kj) 1/P(i,kj) e)×u_j mod N(i,v_i)∈Q j=1 k∈R            (1)

The verifier outputs 1 if the equation holds. She outputs 0 otherwise.

5.3       Security

In this section, we first describe the possible misbehaving entities in PORR, w.r.t. the cloud provider and client. We then present the security goals of a PORR scheme and define the correctness requirements, according to the ones in [9]. Our PORR solution must guarantee three security goals, namely:

• Extractability: The client can recover the original file M in its entirety.
• Soundness of replica generation: The replicas of the original file M must be correctly generated.
• Storage allocation commitment: The cloud provider utilizes at least as much storage as required to store the original file M and its replicas.

Traditional security notions are either embedded in those security notions (e.g. integrity), or assumed to be guaranteed by default (e.g. confidentiality).

We also sketch the security proofs of our scheme according to their respective security goals. We let the reader reach [9, 10, 11, 45, 46] for more details about the PORR security models and proofs. Indeed, the extractability proof is based on the security of the original POR scheme [10, 11]. Proofs for soundness of replica generation and storage allocation commitment follow the same arguments than in MIRROR [9]. Those security goals are however made guaranteed based on the security of the VDF puzzles [45, 46] in our case rather than of the RSA-based puzzles [50] as in MIRROR.

5.3.1    Misbehaving Entities

Two entities, namely a cloud provider and a client, participate in our PORR protocol. Both are assumed to attempt malicious behaviours.

Rational Cloud Provider: If the cloud provider cannot save any costs by misbehaving, then it is likely to simply behave honestly. The advantage of an adversarial cloud provider depends on the ratio between costs for storage and accessibility to various resources (e.g. computing) and their availability. Hence, a cloud provider is restricted to a bounded number of concurrent threads of execution.

Therefore, we say that a cloud provider is rational when it can achieve cost savings by cheating. For instance, the cloud provider may attempt to get some storage space saved while the overall cost for operations has not increased. Such cost is limited to the number of storage servers along with limited computational and storage capacities of each server. If supplying computational resources incurs additional costs, then the cloud provider invests in extra computing resources if such a strategy would result in lower total costs (including the underlying costs of storage).

Let us assume that a rational cloud provider achieves to generate a valid response while not reliably storing the client’s data. If in order to reach such a behaviour, the cloud provider either provides more resources for storage or provides more resources for computing than resources when it follows the protocol honestly, then the cloud provider likely decides to not behave maliciously.

The client is protected from a misbehaving cloud provider that is not storing the file in its entirety by considering the extractability notion. The client is also protected from a misbehaving cloud provider that is not committing enough storage to keep all the file replicas by considering the storage allocation notion. Both properties guarantee both the integrity of the original file and its replicas. This means that the cloud provider invests enough redundancy to keep the client’s data safe.

Malicious client: We say that a client is malicious when she can encode additional data in the replicas by cheating. This additional data cannot be found in the original file.

A client may attempt to abuse on storing more data in the file replicas than what has been approved between the client and cloud provider. In particular, replicas may have a lower cost than their original files (e.g. Amazon S3). Therefore, additional data may be inserted into replicas by a malicious client.

The cloud provider is protected from such a misbehaving client by considering the correct replication notion.

The security model used to build our security proofs comes from [9, 45, 46]. We do not consider the confidentiality of the outsourced file: we simply assume that the client encrypts it before the start of the PORR protocol.

We first show the correctness of our PORR scheme. We then move forward to the security properties with relation to cheating cloud provider and client, namely extractability, storage allocation and correct replication.

Informally, our PORR must achieve the following properties:

• Extractability: The file can be recovered in its entirety if and only if at least a fraction δ is stored at the cloud provider.
• Storage allocation: Misbehavior will be detected with overwhelming probability if less than a fraction δ is stored at the cloud provider.
• Correct replication: The client does not participate in the replica generation. Moreover, the size of the file is independent of the size of the parameters needed to create the replicas.

5.3.2    Correctness

If both the cloud provider and the verifier are honest, then on input the challenge chal sent by the verifier (output by the challenge generation algorithm), the response generation algorithm (run by the cloud provider) generates a response resp such that the verification algorithm outputs “1” with probability 1. This means that an honest cloud provider should always be able to pass the verification of proof of data reliability. From it, the PORR scheme is said to be correct.

During the verification phase, if both the verifier and cloud provider are honest, then on input Q = {(i,v_i)}_i∈I generated by the verifier, the cloud provider should output a response resp such that the Equation (1) holds with probability 1.

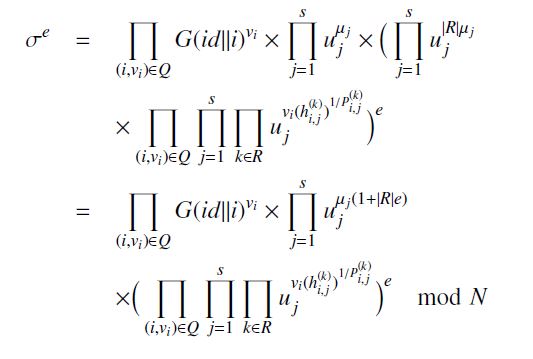5.3.3    Extractability

The client is protected against a malicious cloud provider that is not storing the file in its entirety, through the notion of extractability.

An honest client should recover her file M with high probability. Following the notion of extractability in [10, 11], if a cloud provider can convince a honest client with high probability that it stores the file M^∗ (i.e. the processed version of the original file M), then there exists an extractor algorithm that, given enough interaction with the cloud provider, can extract the file M.

Sketch of Proof.   Let us define a game between an adversary and an environment. The environment is a simulation of honest clients and honest verifiers. The adversary is allowed to submit requests to the environment to create new clients, along with their public and secret parameters, to let them prepare files and their replicas, and to verify correct storage. More precisely, the environment simulates honest client and verifier, and it further provides the adversary with oracles for the algorithms to set up the system, upload the file and replicas, generate the challenge and verify the response.

At the end, the adversary chooses a client with its file M and outputs a cloud provider who can execute the verification process with this client and the file M. A cloud provider is said to be admissible if the probability that the verifier does not abort is at least . The adversary thus picks the client along with the client’s secret tuple (N,d,G, ssk), the file M and the public parameters params, and simulates a cheating cloud provider. Let the latter succeed in making the verification algorithm yield “1” in an non-negligible  fraction of PORR executions. We say that the PORR scheme meets the extractability guarantee, if there exists an extractor algorithm such that given sufficient interactions with the cheating cloud provider, it recovers M.

The computations executed to upload the file M and to verify correct storage are similar operations to the ones in the publicly verifiable POR scheme in [10, 11]. Therefore, the extractability arguments given in [10, 11] apply to our PORR solution directly. An additional assumption is made on the existence of an erasure coding mechanism applied to the file, to guarantee the entire recovery of the file M from any file fraction δ. We let the reader refer to [10, 11] to obtain additional information on the choice of the erasure codes.

5.3.4    Soundness of Replica Generation

Contrary to extractability notion, soundness of replica generation aims to protect the cloud provider against a malicious client who tries to encode additional data in the replicas.

Sketch of Proof. The replica generation is said to be sound such that if the client is involved in the replica generation, then the cloud provider can get the assurance that the additional uploaded data represents indeed correctly built replicas that do not encode extra data. In our PORR, this situation is solved by not letting the client be fully involved in the replica generation. Indeed, while the client generates the puzzles whom solutions are created by the cloud provider, the latter is responsible of defining each replica with its puzzle solution.

The replica generation does not allow to encode a significant amount of extra data in the replicas. Indeed, the replication process takes as inputs elements whose size is independent of the file size. The replica generation is also said to be correct if replicas represent indeed copies of the uploaded file M. Indeed, the file M can be efficiently recovered from any replica M_k. There exists an efficient algorithm which given the file tags, the public parameters and any replica M_k outputs M.

5.3.5    Storage Allocation Commitment

Similarly to the extractability notion, the storage allocation commitment property aims to protect a client against a cloud provider who does not commit enough storage to store all replicas.

The storage allocation commitment notion forces the cloud provider to store the outsourced file and its replicas at rest. Therefore, a cheating cloud provider that participates in the above extractability game [10, 11] and devotes only a fraction of its storage space to store the file and the replicas entirely, cannot convince the verifier to accept its response with overwhelming probability.

Sketch of Proof. The storage allocation ratio of the cloud provider is defined as follows:

|st| ρ = |M| + |M₁| + · · · + |M_r|

where st corresponds to the storage of the cloud provider that has been allocated for storing the original file M and its replicas M₁, · · · , M_r. The file has been first encrypted and the replicas are copies of the processed file, thus they cannot be further compressed. We can assume that the cloud provider aims to save storage, thus it holds that 0 ≤ ρ ≤ 1. The storage allocation commitment ensures that δ ≤ ρ for a threshold 0 ≤ δ ≤ 1 agreed with the client (see the above extractability notion).

First, we want the cloud provider to use at least as much storage as needed to keep the file and its replicas. Second, we see our scheme as a POR protocol applied to both the original file and all the replicas. Let a challenge contain sectors that are not correctly stored. Then, our scheme guarantees that the cloud provider will fail with overwhelming probability unless the correct reconstruction of those sectors is possible.

Lastly, a malicious cloud provider should give a noticeable effort in reconstructing missing sectors. We can easily investigate such an effort as follows. Let the cloud provider store the whole file but only parts of the replicas. The cheating cloud provider will require a significantly higher effort in recomputing missing replicas, compared to an honest service provider that has all the replicas stored in their entirety. By using slow functions (here the VDFs), the time in getting back the missing parts of replicas is noticeable from the verifier’s point of view.

More precisely, the misbehaving cloud provider must compute the puzzle solutions y_i⁽_,^k_j⁾ in order to recompute the missing sectors.

Since those elements y⁽_i,^k_j⁾ are different for each replica, knowing (or reconstructing) one element y⁽_i,^k_j⁾ from one replica sector does not help the cloud provider in deriving elements from other replica sectors. A rational cloud provider should thus require a significantly higher effort compared to an honest cloud provider in recomputing missing replicas.

Given that the VDF evaluation function requires a noticeable amount of time and effort compared to the associated VDF verification function, this incurs additional (significant) computational overhead on the cloud provider to compute the puzzle solutions on the fly rather than storing them at rest.

Let δ be the threshold selected by the client (see Extractability). Let us assume that less than a fraction δ of all sectors of a replica is stored at the cloud provider. Thus, for each element y⁽_i,^k_j⁾ in the challenge, the probability to recompute it is at least 1 − δ. In addition, l · s sectors are contained in a challenge. Hence, the number of values to recompute is l · s · (1 − δ). Moreover, the costs from the time effort for recomputing these elements y⁽_i,^k_j⁾ exceed the costs from the storage of those elements. This is made possible by having a number of challenges linear in the security parameter κ. If so, then the overall probability to avoid these computations is negligible in κ.

6 Implementation and Evaluation

We are interested in implementing and evaluating our PORR solution in a realistic cloud framework. We also wish to compare our results with the ones from [9], since their solution is the closest one to ours.

In this section, we first describe MIRROR, the PORR scheme presented in [9]. We then describe our implementation setting, and we discuss our results and compare them with the ones from [9]. We choose to compare our results with MIRROR’s ones since, to our best of knowledge, MIRROR is the closest prototype to ours. Unlike existing schemes, the cloud provider replicates the data by itself in both MIRROR and our PORR. Therefore, expensive bandwidth resources are traded with cheaper computing resources.

As a summary, we evaluate an implementation of our PORR prototype within a realistic cloud setting and we compare the performance of it with MIRROR [9].

6.1       MIRROR

MIRROR [9] is the first scheme to enable the cloud provider to generate the replicas of the client’s files by itself. Such move permits to trade expensive bandwidth resources with cheaper computing resources. Cloud providers and clients are likely to adopt it easily since storage services are improved while financial costs are lowered.

The authors in [9] present new PORR definition and security model. Their definition extends Shacham-Waters POR from [10]. Their security model encompasses security risks that have not been covered in previous multi-replica POR schemes, namely security against malicious clients and rational cloud providers. We have sketched the security proofs of our PORR based on their model.

The authors give a solution for PORR, called MIRROR, and prove it secure according to their new security model. Their motivations mostly rely on business matters for cloud providers and financial incentives for clients. They propose a tunable replication scheme by combining Linear Feedback Shift Registers and RSA-based puzzles [50]. By doing so, the burden incurred by the construction of the replicas is shifted to the cloud provider. The latter swaps higher resources for bandwidth with lower resources for computation. In addition, a realistic cloud framework has been defined for the implementation and evaluation of MIRROR. The results show that MIRROR is applicable to real cloud environments.

The main difference between MIRROR and our PORR solution is the nature of the verification process, private and public respectively. The authors in [9] propose to use privately verifiable puzzles to prevent rational behaviour from cloud providers. Therefore, such feature forces the puzzle creator, namely the client, to check herself the solution generated by the cloud provider. We claim that such requirement is too strict on the client’s side. If we aim to design a solution for the general public, then we think about individuals that have limited knowledge on cloud storage security, thus that would not follow the process to prevent and/or detect malicious cloud provider behaviours. Instead, we suggest to use VDFs that offer public verification. This implies that anyone else on behalf of the client can verify that the cloud provider has been acting honestly.

6.2       Implementation

We implement our PORR scheme in order to analyze the computational efforts from honest and rational cloud providers, along with the ones from client and verifier.

We show that our protocol produces fair computational and communication overheads on the client, cloud provider and verifier, meaning that our solution is realistically applicable in cloud storage environments. Indeed, computation costs are affordable for the client and verifier, while they are made such that the cloud provider does not gain any advantage in computing the replicas on the fly from the verifier’s challenge requests. Therefore, our solution fits cloud-related bandwidth and storage expectations, while preventing malicious clients and rational cloud providers from being successful.

Our implementation setting follows the one in [9] for a more accurate and legitimate comparison. Our code is written in Python 3.8. The selected hash function is SHA-256. The whole test environment is deployed on a PC running an Intel Core i7-9700 with 32GB of memory. We create four Virtual Machines (VMs) to design our test environment, namely:

• One VM represents the client that owns files to be stored on a cloud storage server.
• One VM represents the cloud provider (server) that offers cloud storage services.
• Two VMs represent storage nodes, linked to the cloud provider, that guarantee data replication.

We depict the test environment topology in Figure 2.

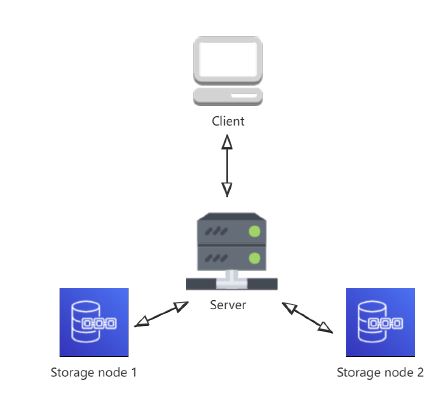Figure 2: Test environment topology

To emulate a realistic Wide Area Network (WAN), the communication between the various VMs is bridged using a 100 Mbps switch. All traffic exchanged in the environment is shaped with NetEm [56]. The setting parameters are the following:

• We set the packet loss rate at 0.1%, and the correlation rate of lost packets at 0.001% [57, 58, 59].
• We set the delay rate to fit normal distribution with a mean of 20ms and a variance of 4ms [60].
• We set the packet corruption rate at 0.1% [61].
• We set the rate of the package being out of order at 0.2% [62].

Each data point is averaged in our plots by five independent measurements. Where appropriate, we include the corresponding 95% confidence intervals.

Parameter selection. We select our parameters similarly to [9] in order to achieve a better comparison. Let the modulus N be 2048bit long (hence, 1024-bit primes p and q). We choose a block size equal to 8KB as such value offers the most balanced performance in average. This means that files of 64MB are split into n blocks where n = 8,000. Each block is then split into s sectors where s = 32. Then, r replicas are created for each file where r = 2. The cloud provider is thus expected to keep 8000 × 32 × 2 < 52 · 10⁴ file elements, namely the original file sectors and the replica sectors. The number of blocks per challenge will be set to |I| = 40.

We consider three network storage protocols, namely File Transfer Protocol (FTP), Server Message Block (SMB) and Network File System (NFS), to enable the client to access her files stored in the cloud, through a computer network. NFS is used on Unix operating systems and SMB on Windows operating systems. The deployment of FTP is wider, as long as the communication port is open. In order to select one of those three network storage protocols, we test their uploading speed. Figure 3 shows the uploading speed values (in MB per second) for network storage protocols FTP, SMB and NFS. Due to the instability of network transmission, the uploading speed results show some ups and downs. The average FTP speed is the fastest, at 17.4 MB per second, which is around 1 second faster than NFS and 3 seconds faster than SMB. Hence, FTP was chosen as the default setting.

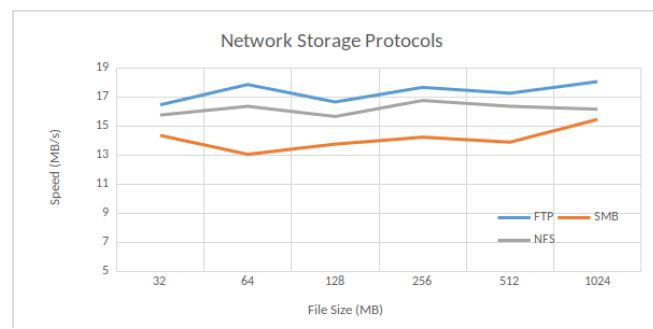Figure 3: Network Storage Protocols

We summarize our parameter selection in Table 2. When not specifically mentioned in Section 6.3, the default parameter values are kept as in Table 2 for our protocol evaluation.

Table 2: Parameter selection.

Parameter	Default value
RSA modulus size |N|	2048 bits
RSA prime size |p|	1024 bits
RSA prime size |q|	1024 bits
Pre-processing parameter B	230
Delay parameter t	216
File size	64MB
Block size	8192 Bytes
Sector size	256 Bytes
Number of replicas r	2
Number of challenges |I|	40
Network Storage Protocol	FTP

VDF implementation

We recall that our PORR scheme is based on the exponentiation-based VDF scheme [12]. The latter has the following characteristics.

The VDF evaluation algorithm runs with poly(log(t),κ) processors in parallel time t, where κ is the security parameter and t is the delay parameter. We say that an algorithm runs with p processors in parallel time t if one can implement it on a PRAM machine with p parallel processors running in time t.

The VDF verification algorithm runs in total time polynomial in log(t) and κ. This algorithm should be much faster than the evaluation one.

Our PORR scheme uses VDFs in order to allow the verifier to detect a cheating cloud provider computing the puzzle solutions on the fly rather than keeping them at rest. Therefore, we aim to notice a difference between the response time of a honest cloud provider and of a rational one. More precisely, a verifier should be able to observe a delay in responding from a cheating cloud provider. We choose a delay parameter t equal to 2¹⁶.

The security of the VDF scheme based on exponentiation [12] relies on the assumption that the adversary cannot run a long precomputation from the publication of the public parameters until the evaluation of the puzzles. Given the pre-processing parameter B, the VDF scheme is secure up to B puzzles. New public parameters must be generated once B puzzles have been used.

The authors in [12] suggest to set B = 2³⁰ for a reasonable trade-off between usability and security. Let us consider B = 2³⁰ and 64MB files. Up to 2000 files can be stored at the cloud with only one VDF instance. 2000 files roughly correspond to 128GB of data. Another VDF instance will be necessary if more files need to be stored. We recall that the setup algorithm runs in polynomial time in the security parameter κ, meaning that this algorithm is run easily and relatively fast.

We examine whether such condition on the pre-processing parameter B restricts the applicability of our PORR solution. In addition, we verify the costs incurred from computing and storing. Indeed, our results should convince us that our PORR solution fits real world requirements. We summarize our VDF implementation characteristics in Table 2.

6.3 Evaluation and Discussion

Response generation. We measure the time that the cloud provider takes in order to generate its response, according to different numbers of challenges. Results are shown in Figure 4.

We consider two types of cloud providers: a rational cloud provider and a honest cloud provider. The former needs more time to generate its response since it requires to compute puzzle solutions on the fly. On the other side, since the honest cloud provider has already computed the puzzle solutions and stores them at rest, its response generation is noticeably faster. Therefore, we are guaranteed that the verifier (and thus the client) will notice a rational cloud server from a honest cloud provider since the time difference for response generation is consequent.

The average response time of an honest cloud provider is less than 2 seconds when r = 2 in [9], and a delay of almost 1 second is observed from a rational cloud provider. In our case, if the cloud provider tries to compute the 2 replicas on the fly, then it needs to compute the solutions y of 2 puzzles x, meaning that it runs in parallel time t with poly(log(t),κ) processors twice.

From Figure 4, we notice that a rational server needs almost twice the time than a honest server to generate its response, for a given number of challenges. For instance, for 40 challenges, a rational server generates its response in 0.63 seconds while a honest server in 0.31 seconds. Moreover, the response generation time increases with the number of challenges.

MIRROR’s response generation depends on the bit size of the factors (that are elements needed to prepare the replicas) [9]. As long as the blind factors are greater or equal to 70 bits, the rational server should not gain any reasonable advantage in misbehaving. For instance, when the coefficients’ size is equal to 70 bits, a rational server in MIRROR needs around 1 second to generate its response based on 40 challenges. Since we do not use blind factors, a rational server in our PORR only requires 0.63 seconds.

For a higher security level, that is a bigger blind factors’ bit size

(say 200 bits), a MIRROR rational server generates its response in roughly 2.8 seconds. In our case, in order to reach a higher security level, we can increase the number of challenges. For instance, for a number of challenges equal to 200, a rational server needs 4.86 seconds to generate its response. Such time cost happens since the rational server must calculate puzzle solutions on the fly.

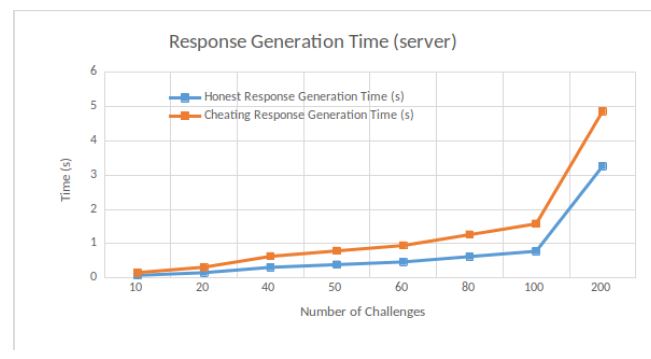Figure 4: Response Generation Time

File preparation.  We measure the time required to prepare a file before storing it on the cloud. Specifically, we measure the time for setup (i.e. key generation and tag generation) and replica generation (i.e. puzzle evaluation). Results are shown in Figure 5.

The time spent for preparing the file and its replicas increases exponentially with the size of the file. For instance, for a 16MB file and its 2 replicas, we need around 50 seconds while for a 256MB file, we require more than 700 seconds.

Moreover, file preparation takes around 180 seconds for a 64MB file and its 2 replicas in our case. We notice that setup and replica generation take around 500 and 700 seconds respectively in MIRROR [9], given the same file setting. Therefore, file preparation is almost 7 times faster in our PORR than in MIRROR for a 64MB file.

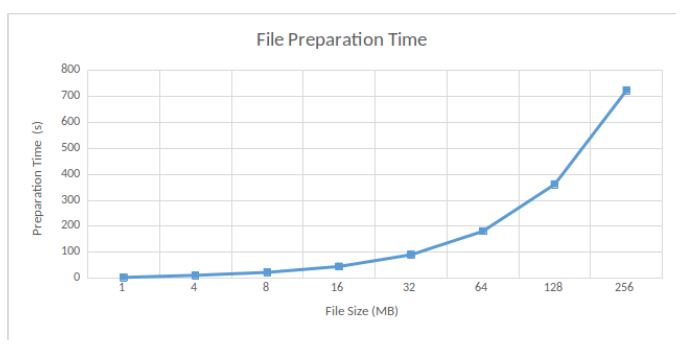Figure 5: File Preparation Time

Verification. We measure the time required to verify correct storage at rest. Specifically, we measure the time for response generation and response verification. We consider multiple file sizes, and thus multiple numbers of challenges, since the latter depend on the former. In particular, a large file means a bigger number of challenges. The number of challenges is calculated as the half of the file size (in MB). For example, 32 challenges are requested for a 64MB file. According to the default parameter settings, the verifier thus checks 128KB of data for each MB file data. Results are shown in Figure 6.

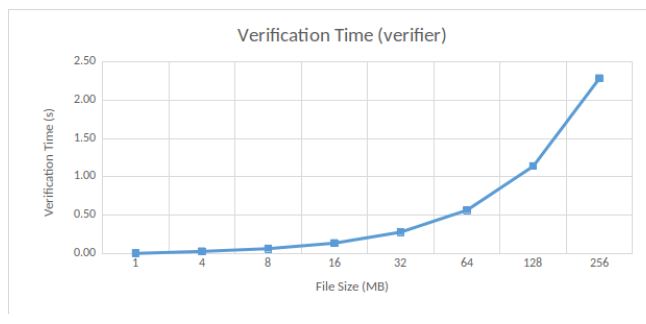
The verification time experienced by the client is 0.57 seconds in our case, while being 0.8 seconds in MIRROR [9]. The number of challenges increases with the file size, thus impacting the verification time. Given a file size of 128MB, the number of challenges is 64 and the verification time reaches 1.14 seconds. Note that the number of challenges in MIRROR is fixed at a value of 40, whatever the file size. Therefore, the verification time is constant, equal to 0.8 seconds.

Figure 6: Verification Time

Puzzle evaluation. We measure the time spent for puzzle evaluation only. We are interested in such measurement since this part takes the longest time in file preparation. Results are shown in Figure 7.

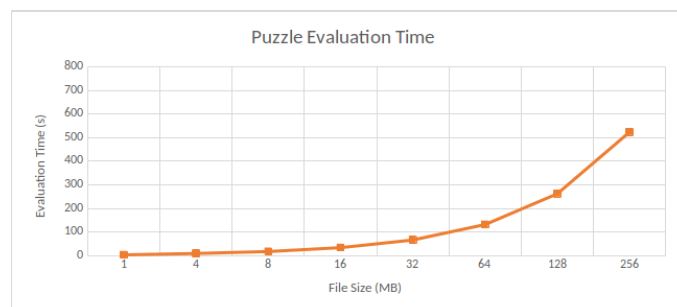
Figure 7: Puzzle Evaluation TimePuzzle evaluations contribute to almost 3/4 of the file preparation. In the default configuration, that is given a 64MB file, file preparation time reaches 180 seconds, where around 130 seconds are spent on puzzle evaluations. Since the number of sectors increases with the file size, this leads to the linear growth of puzzle evaluation time.

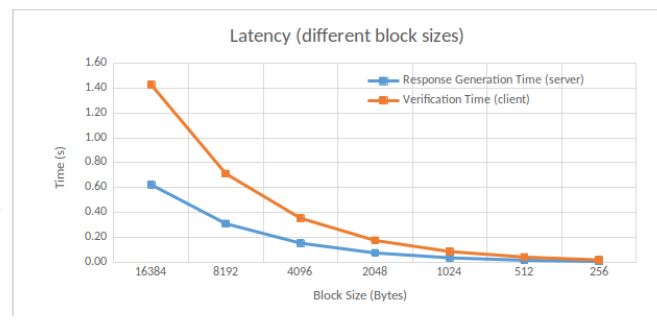
Latency w.r.t. block sizes. We measure the time required for response generation and verification, according to the block sizes. We choose a sector size of 256 Bytes. Results are shown in Figure 8. We notice that a smaller block size gives a shorter time. Indeed, block size and challenge number are related, meaning that response generation and verification are faster as the block size decreases.

Figure 8: Latency (blocks)

MIRROR [9] gets a similar trend to ours, but less obvious. In MIRROR, the verification time is around 1 second for a 1MB block size, and 1.1 seconds for a 2MB block size. In our case, the verification time is around 0.1 seconds for a 1MB block size, and 0.2 for a 2MB block size, thus an increase by 50%.

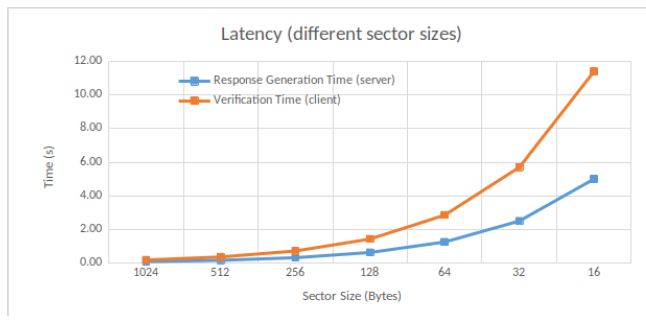
We measure the time required for response generation and verification, according to the sector sizes. We choose a block size of 8192 Bytes. For a given block size, a small sector size means a bigger number of sectors in that block. Therefore, the verification time is impacted since more data must be checked while the number of blocks and thus of challenges is fixed. Results are shown in Figure 9.

The authors in [9] do not explicitly analyze the effect of sector size of their protocol MIRROR. We expect that, for a given file, when the sector size decreases, its number increases, and thus impacts, with a rise, the server’s response time and verifier’s verification time.

Our default sector size is 256 Bytes, as a trade-off between efficiency and security. Verification is done in 0.36 seconds with such value. On the other size, a sector size equal to 32 Bytes results in getting a verification time 15 times slower.

Figure 9: Latency (sectors)

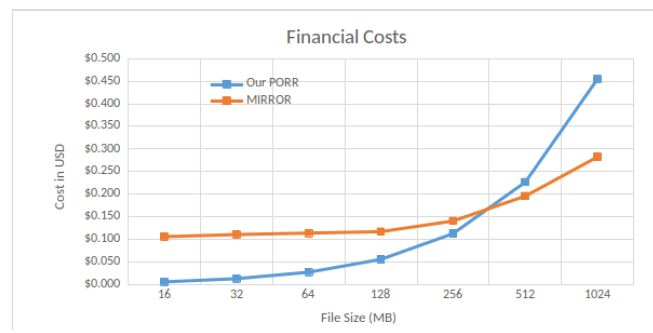
Financial costs. We compare the financial costs between our PORR and MIRROR [9], w.r.t. file preparation. The replication process (as named in MIRROR) roughly corresponds to our file preparation. Results are shown in Figure 10.

The graph records those cost differences between the two protocols. The Amazon EC2 processor rental price is US$ 0.404 per hour. Such price is thus US$ 0.000112 per second, and has been multiplied with our file preparation time.

Given a file of size 384MB, our PORR and MIRROR will both incur a cost equal to 0.18 USD. Our PORR protocol seems more interesting from a financial point of view with file sizes smaller than 384 MB, saving from 2 to 15 times compared to MIRROR. On the other side, MIRROR seems more attractive with larger file sizes.

Figure 10: Financial Costs

Additional remarks. In MIRROR [9], replicas are computed as the product of the original file sector and two blind factors. However, the cloud provider may just keep the factors in reserve, and multiply by the sector when requested for verification. The gain may not be substantial and a cloud provider may just store the replicas.

Our replicas are computed as the addition of the original file sector and one blind factor. Similarly to [9], the cloud provider may or may not just keep the factor and add the sector when challenged. Future task will investigate whether a better design can prevent such behaviour from the cloud provider.

Summary. Our results show that our PORR prototype manages to trade expensive bandwidth resources with cheaper computing resources. Those results are likely to be well accepted by cloud providers and clients with the promise of better storage services and lower financial costs. Moreover, some of those results, especially on both technical and financial aspects, show that our PORR is more competitive with small file sizes, compared to MIRROR [9]. Therefore, our PORR solution may become one of the economicallyviable, applicable systems that offer verifiable replicated cloud storage. In particular, our PORR fits the demands from indivudals and small businesses with lower file sizes to store on a cloud.

7        Conclusion

In this paper, we presented a recent PORR protocol, first proposed in [1], where one can check in a single instance that the cloud provider correctly stores an original file and its replicas. We combine our PORR with the slow function VDF to enable anyone to verify the cloud provider’s behaviour, not only the file owner.

Implementation and evaluation of our solution have been carried out. Results show that such design is well applicable in realistic cloud environments. Multiple results, on technical and financial aspects, show that our PORR is more competitive with small file sizes, compared to MIRROR [9] and with the noticeable advantage of offering public verification.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

We thank the reviewers for their valuable comments.

1.  C. Gritti, “Publicly Verifiable Proofs of Data Replication and Retrievability for Cloud Storage,” in 2020 International Computer Symposium (ICS), 431–436, 2020, doi:10.1109/ICS51289.2020.00091.
2. A. Juels, B. S. Kaliski, Jr., “Pors: Proofs of Retrievability for Large Files,” in Proceedings of the 14th ACM Conference on Computer and Communica- tions Security, CCS ’07, 584–597, ACM, New York, NY, USA, 2007, doi: 10.1145/1315245.1315317.
3. G. Ateniese, R. Burns, R. Curtmola, J. Herring, L. Kissner, Z. Peterson,
   D. Song, “Provable Data Possession at Untrusted Stores,” in Proceedings of the 14th ACM Conference on Computer and Communications Security, CCS ’07, 598–609, 2007, doi:10.1145/1315245.1315318.
4. G. Ateniese, R. Burns, R. Curtmola, J. Herring, O. Khan, L. Kissner, Z. Pe- terson, D. Song, “Remote Data Checking Using Provable Data Possession,” ACM Trans. Inf. Syst. Secur., 14(1), 12:1–12:34, 2011, doi:10.1145/1952982. 1952994.
5. R. Curtmola, O. Khan, R. Burns, G. Ateniese, “MR-PDP: Multiple-Replica Provable Data Possession,” in Proceedings of the 2008 The 28th International Conference on Distributed Computing Systems, ICDCS ’08, 411–420, IEEE Computer Society, Washington, DC, USA, 2008, doi:10.1109/ICDCS.2008.68.
6. A. F. Barsoum, M. A. Hasan, “Integrity Verification of Multiple Data Copies over Untrusted Cloud Servers,” in Proceedings of the 2012 12th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (Ccgrid 2012), CCGRID ’12, 829–834, IEEE Computer Society, USA, 2012, doi: 10.1109/CCGrid.2012.55.
7. A. Barsoum, M. Hasan, “Provable Multicopy Dynamic Data Possession in Cloud Computing Systems,” IEEE Transactions on Information Forensics and Security, 10, 485–497, 2015, doi:10.1109/TIFS.2014.2384391.
8. G. S. Prasad, V. S. Gaikwad, “A Survey on User Awareness of Cloud Se- curity,” Int. J. of Engineering and Technology, 7(2.32), 131–135, 2018, doi: 10.14419/ijet.v7i2.32.15386.
9. F. Armknecht, L. Barman, J.-M. Bohli, G. O. Karame, “Mirror: Enabling Proofs of Data Replication and Retrievability in the Cloud,” in Proceedings of the 25th USENIX Conference on Security Symposium, SEC’16, 1051–1068, USENIX Association, USA, 2016.
10. H. Shacham, B. Waters, “Compact Proofs of Retrievability,” in Proceedings of the 14th International Conference on the Theory and Application of Cryptology and Information Security: Advances in Cryptology, ASIACRYPT ’08, 90–107, Springer-Verlag, Berlin, Heidelberg, 2008, doi:10.1007/978-3-540-89255-7 7.
11. H. Shacham, B. Waters, “Compact Proofs of Retrievability,” Full version, 2008,
    https://hovav.net/ucsd/dist/verstore.pdf.
12. D. Boneh, J. Bonneau, B. Bu¨ nz, B. Fisch, “Verifiable Delay Functions,” CRYPTO 2018, 757–788, Springer-Verlag, Berlin, Heidelberg, 2018.
13. G. Ateniese, R. Di Pietro, L. V. Mancini, G. Tsudik, “Scalable and Efficient Provable Data Possession,” in Proceedings of the 4th International Confer- ence on Security and Privacy in Communication Netowrks, SecureComm ’08, 9:1–9:10, ACM, New York, NY, USA, 2008, doi:10.1145/1460877.1460889.
14. C. Wang, Q. Wang, K. Ren, W. Lou, “Privacy-preserving Public Auditing for Data Storage Security in Cloud Computing,” in Proceedings of the 29th Conference on Information Communications, INFOCOM’10, 525–533, IEEE Press, Piscataway, NJ, USA, 2010.
15. S. Yu, C. Wang, K. Ren, W. Lou, “Achieving Secure, Scalable, and Fine- grained Data Access Control in Cloud Computing,” in Proceedings of the 29th Conference on Information Communications, INFOCOM’10, 534–542, IEEE Press, Piscataway, NJ, USA, 2010.
16. Z. Hao, S. Zhong, N. Yu, “A Privacy-Preserving Remote Data Integrity Check- ing Protocol with Data Dynamics and Public Verifiability,” IEEE Trans. on Knowl. and Data Eng., 23(9), 1432–1437, 2011, doi:10.1109/TKDE.2011.62.
17. Y. Yu, M. H. Au, Y. Mu, S. Tang, J. Ren, W. Susilo, L. Dong, “Enhanced privacy of a remote data integrity-checking protocol for secure cloud storage,” International Journal of Information Security, 1–12, 2014, doi:10.1007/s10207- 014-0263-8.
18. C. Erway, A. Ku¨pc¸u¨, C. Papamanthou, R. Tamassia, “Dynamic Provable Data Possession,” in Proceedings of the 16th ACM Conference on Computer and Communications Security, CCS ’09, 213–222, ACM, New York, NY, USA, 2009, doi:10.1145/1653662.1653688.
19. Y. Zhu, H. Wang, Z. Hu, G.-J. Ahn, H. Hu, S. S. Yau, “Dynamic Audit Services for Integrity Verification of Outsourced Storages in Clouds,” in Proceedings of the 2011 ACM Symposium on Applied Computing, SAC ’11, 1550–1557, ACM, New York, NY, USA, 2011, doi:10.1145/1982185.1982514.
20. Y. Zhu, G.-J. Ahn, H. Hu, S. S. Yau, H. G. An, C.-J. Hu, “Dynamic Audit Services for Outsourced Storages in Clouds,” IEEE Transactions on Services Computing, 6(2), 227–238, 2013, doi:http://doi.ieeecomputersociety.org/10. 1109/TSC.2011.51.
21. C. Wang, Q. Wang, K. Ren, W. Lou, “Ensuring data storage security in cloud computing,” in in Proc. of IWQoS’09, 2009.
22. A. Le, A. Markopoulou, “NC-Audit: Auditing for Network Coding Storage,” CoRR, abs/1203.1730, 2012.
23. C. Wang, Q. Wang, K. Ren, N. Cao, W. Lou, “Toward Secure and Depend- able Storage Services in Cloud Computing,” IEEE Trans. Serv. Comput., 5(2), 220–232, 2012, doi:10.1109/TSC.2011.24.
24. B. Wang, B. Li, H. Li, “Oruta: privacy-preserving public auditing for shared data in the cloud,” IEEE Transactions on Cloud Computing, 2(1), 43–56, 2012, doi:http://doi.ieeecomputersociety.org/10.1109/TCC.2014.2299807.
25. B. Wang, B. Li, H. Li, “Knox: Privacy-preserving Auditing for Shared Data with Large Groups in the Cloud,” in Proceedings of the 10th International Con- ference on Applied Cryptography and Network Security, ACNS’12, 507–525, Springer-Verlag, Berlin, Heidelberg, 2012, doi:10.1007/978-3-642-31284- 7 30.
26. C. Wang, S. S. Chow, Q. Wang, K. Ren, W. Lou, “Privacy-Preserving Public Auditing for Secure Cloud Storage,” IEEE Transactions on Computers, 62(2), 362–375, 2013, doi:http://doi.ieeecomputersociety.org/10.1109/TC.2011.245.
27. X. Fan, G. Yang, Y. Mu, Y. Yu, “On Indistinguishability in Remote Data In- tegrity Checking,” 58(4), 823–830, 2015, doi:http://dx.doi.org/10.1093/comjnl/ bxt137.
28. B. Wang, B. Li, H. Li, “Panda: Public Auditing for Shared Data with Efficient User Revocation in the Cloud,” IEEE T. Services Computing, 8(1), 92–106, 2015, doi:10.1109/TSC.2013.2295611.
29. C. Gritti, W. Susilo, T. Plantard, “Efficient Dynamic Provable Data Possession with Public Verifiability and Data Privacy,” in E. Foo, D. Stebila, editors, In- formation Security and Privacy, 395–412, Springer International Publishing, Cham, 2015.
30. C. Gritti, R. Chen, W. Susilo, T. Plantard, “Dynamic Provable Data Possession Protocols with Public Verifiability and Data Privacy,” in J. K. Liu, P. Sama- rati, editors, Information Security Practice and Experience, 485–505, Springer
    ublishing, Cham, 2017.
31. J. Xu, E.-C. Chang, “Towards Efficient Proofs of Retrievability,” in Proceedings of the 7th ACM Symposium on Information, Computer and Communications Security, ASIACCS ’12, 79–80, Association for Computing Machinery, New York, NY, USA, 2012, doi:10.1145/2414456.2414503.
32. K. D. Bowers, A. Juels, A. Oprea, “Proofs of Retrievability: Theory and Implementation,” in Proceedings of the 2009 ACM Workshop on Cloud Com- puting Security, CCSW ’09, 43–54, ACM, New York, NY, USA, 2009, doi: 10.1145/1655008.1655015.
33. K. D. Bowers, A. Juels, A. Oprea, “HAIL: A High-availability and Integrity Layer for Cloud Storage,” in Proceedings of the 16th ACM Conference on Computer and Communications Security, CCS ’09, 187–198, ACM, New York, NY, USA, 2009, doi:10.1145/1653662.1653686.
34. Y. Dodis, S. Vadhan, D. Wichs, “Proofs of Retrievability via Hardness Ampli- fication,” in Proceedings of the 6th Theory of Cryptography Conference on Theory of Cryptography, TCC ’09, 109–127, Springer-Verlag, Berlin, Heidel- berg, 2009, doi:10.1007/978-3-642-00457-5 8.
35. Q. Wang, C. Wang, J. Li, K. Ren, W. Lou, “Enabling Public Verifiability and Data Dynamics for Storage Security in Cloud Computing,” in Proceed- ings of the 14th European Conference on Research in Computer Security, ESORICS’09, 355–370, Springer-Verlag, Berlin, Heidelberg, 2009.
36. E. Shi, E. Stefanov, C. Papamanthou, “Practical Dynamic Proofs of Retriev- ability,” in Proceedings of the 2013 ACM SIGSAC Conference on Computer &#38; Communications Security, CCS ’13, 325–336, ACM, New York, NY, USA, 2013, doi:10.1145/2508859.2516669.
37. B. Chen, R. Curtmola, “Towards Self-Repairing Replication-Based Storage Systems Using Untrusted Clouds,” in Proceedings of the Third ACM Confer- ence on Data and Application Security and Privacy, CODASPY ’13, 377–388, Association for Computing Machinery, New York, NY, USA, 2013, doi: 10.1145/2435349.2435402.
38. B. Chen, R. Curtmola, “Remote data integrity checking with server-side repair,” Journal of Computer Security, 25(6), 537–584, 2017, doi:10.3233/JCS-16868.
39. I. Leontiadis, R. Curtmola, “Secure Storage with Replication and Transparent Deduplication,” in Proceedings of the Eighth ACM Conference on Data and Application Security and Privacy, CODASPY ’18, 13–23, Association for Com- puting Machinery, New York, NY, USA, 2018, doi:10.1145/3176258.3176315.
40. M. Etemad, A. Ku¨ pc¸u¨ , “Transparent, Distributed, and Replicated Dynamic Provable Data Possession,” in M. J. J. Jr., M. E. Locasto, P. Mohassel, R. Safavi- Naini, editors, Applied Cryptography and Network Security – 11th International Conference, ACNS 2013, Banff, AB, Canada, June 25-28, 2013. Proceedings, volume 7954 of Lecture Notes in Computer Science, 1–18, Springer, 2013, doi:10.1007/978-3-642-38980-1\ 1.
41. B. Chen, A. K. Ammula, R. Curtmola, “Towards Server-Side Repair for Era- sure Coding-Based Distributed Storage Systems,” in Proceedings of the 5th ACM Conference on Data and Application Security and Privacy, CODASPY ’15, 281–288, Association for Computing Machinery, New York, NY, USA, 2015, doi:10.1145/2699026.2699122.
42. B. Chen, R. Curtmola, G. Ateniese, R. Burns, “Remote Data Checking for Network Coding-Based Distributed Storage Systems,” in Proceedings of the 2010 ACM Workshop on Cloud Computing Security Workshop, CCSW ’10, 31–42, Association for Computing Machinery, New York, NY, USA, 2010, doi:10.1145/1866835.1866842.
43. T. P. Thao, K. Omote, “ELAR: Extremely Lightweight Auditing and Repairing for Cloud Security,” in Proceedings of the 32nd Annual Conference on Com- puter Security Applications, ACSAC ’16, 40–51, Association for Computing Machinery, New York, NY, USA, 2016, doi:10.1145/2991079.2991082.
44. K. D. Bowers, M. van Dijk, A. Juels, A. Oprea, R. L. Rivest, “How to tell if your cloud files are vulnerable to drive crashes,” in Y. Chen, G. Danezis,
    V. Shmatikov, editors, Proceedings of the 18th ACM Conference on Computer and Communications Security, CCS 2011, Chicago, Illinois, USA, October 17-21, 2011, 501–514, ACM, 2011, doi:10.1145/2046707.2046766.
45. D. Vasilopoulos, K. Elkhiyaoui, R. Molva, M. Onen, “POROS: Proof of Data Reliability for Outsourced Storage,” in Proceedings of the 6th In- ternational Workshop on Security in Cloud Computing, SCC ’18, 27–37, Association for Computing Machinery, New York, NY, USA, 2018, doi: 10.1145/3201595.3201600.
46. D. Vasilopoulos., M. O¨ nen., R. Molva., “PORTOS: Proof of Data Relia- bility for Real-World Distributed Outsourced Storage,” in Proceedings of the 16th International Joint Conference on e-Business and Telecommunica- tions – Volume 2: SECRYPT,, 173–186, INSTICC, SciTePress, 2019, doi: 10.5220/0007927301730186.
47. Z. N. J. Peterson, M. Gondree, R. Beverly, “A Position Paper on Data Sovereignty: The Importance of Geolocating Data in the Cloud,” in Pro- ceedings of the 3rd USENIX Conference on Hot Topics in Cloud Computing, HotCloud’11, 9, USENIX Association, USA, 2011.
48. G. J. Watson, R. Safavi-Naini, M. Alimomeni, M. E. Locasto, S. Narayan, “LoSt: Location Based Storage,” in Proceedings of the 2012 ACM Workshop on Cloud Computing Security Workshop, CCSW ’12, 59–70, Association for Com- puting Machinery, New York, NY, USA, 2012, doi:10.1145/2381913.2381926.
49. S. Dziembowski, S. Faust, V. Kolmogorov, K. Pietrzak, “Proofs of Space,” in
    R. Gennaro, M. Robshaw, editors, Advances in Cryptology – CRYPTO 2015, 585–605, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015.
50. R. L. Rivest, A. Shamir, D. A. Wagner, “Time-Lock Puzzles and Timed-Release Crypto,” Technical report, USA, 1996.
51. J . Cai, R. J. Lipton, R. Sedgewick, A. C. . Yao, “Towards uncheatable bench- marks,” in [1993] Proceedings of the Eigth Annual Structure in Complexity Theory Conference, 2–11, 1993.
52. D. Boneh, M. Naor, “Timed Commitments,” in M. Bellare, editor, Advances in Cryptology — CRYPTO 2000, 236–254, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000.
53. C. Dwork, M. Naor, “Pricing via Processing or Combatting Junk Mail,” in Pro- ceedings of the 12th Annual International Cryptology Conference on Advances in Cryptology, CRYPTO ’92, 139–147, Springer-Verlag, Berlin, Heidelberg, 1992.
54. A. K. Lenstra, B. Wesolowski, “A random zoo: sloth, unicorn, and trx,” Cryptology ePrint Archive, Report 2015/366, 2015, https://eprint.iacr.org/ 2015/366.
55. B. Cohen, K. Pietrzak, “Simple Proofs of Sequential Work,” Cryptology ePrint Archive, Report 2018/183, 2018, https://eprint.iacr.org/2018/183.
56. NetEm, “NetEm, the Linux Foundation,” http://www.linuxfoundation. org/collaborate/workgroups/networking/netem, 2021, accessed on 11/04/2021.
57. T. Flach, N. Dukkipati, A. Terzis, B. Raghavan, N. Cardwell, Y. Cheng, A. Jain, S. Hao, E. Katz-Bassett, R. Govindan, “Reducing Web Latency: The Virtue of Gentle Aggression,” in Proceedings of the ACM SIGCOMM 2013 Confer- ence on SIGCOMM, SIGCOMM ’13, 159–170, Association for Computing Machinery, New York, NY, USA, 2013, doi:10.1145/2486001.2486014.
58. M. Dahlin, B. B. V. Chandra, L. Gao, A. Nayate, “End-to-End WAN Ser- vice Availability,” IEEE/ACM Trans. Netw., 11(2), 300–313, 2003, doi: 10.1109/TNET.2003.810312.
59. S. Sundaresan, W. de Donato, N. Feamster, R. Teixeira, S. Crawford, Pescape`, “Broadband Internet Performance: A View from the Gate- way,” SIGCOMM Comput. Commun. Rev., 41(4), 134–145, 2011, doi: 10.1145/2043164.2018452.
60. D. Dobre, G. Karame, W. Li, M. Majuntke, N. Suri, M. Vukolic´, “PoWerStore: Proofs of Writing for Efficient and Robust Storage,” in Proceedings of the 2013 ACM SIGSAC Conference on Computer and Communications Security, CCS ’13, 285–298, Association for Computing Machinery, New York, NY, USA, 2013, doi:10.1145/2508859.2516750.
61. D. Zhuo, M. Ghobadi, R. Mahajan, K.-T. Fo¨ rster, A. Krishnamurthy, T. An- derson, “Understanding and Mitigating Packet Corruption in Data Center Networks,” SIGCOMM ’17, 362–375, Association for Computing Machinery, New York, NY, USA, 2017, doi:10.1145/3098822.3098849.
62. V. Paxson, “End-to-End Internet Packet Dynamics,” SIGCOMM Comput. Com- mun. Rev., 27(4), 139–152, 1997, doi:10.1145/263109.263155.

(Click Here)