1. Introduction

The exploration of outer space, the planets closest and distant from us, requires the creation of compact, economical, reliable, low-maintenance (practically autonomous) and safe energy sources with a high energy density. Technologically mastered energy sources using the fission reaction of heavy atomic nuclei are attractive.

There are two directions of using space nuclear reactors. The first is related to the need to travel long distances. This is a nuclear electric propulsion system that combines the concepts of “nuclear space tug”, “interorbital tug”, “and transport and power module”. The second direction is associated with the supply of energy to the spacecraft, space or alien station and crew. It can be a low-power alien nuclear power plant (NPP) that provides power to the station, or a space NPP that provides power to a spacecraft. Its functions are not related to the movement of the spacecraft. This work is devoted to solving the second problem and is a continuation of the research published by the author earlier [1]. At present, the development of nuclear electric propulsion systems is being actively pursued, capable of operating in the mode of obtaining thrust (engine) and in the mode of generating electrical energy (NPP) [2, 3]. If it is necessary to supply power to stations located on other planets, it will be necessary to build a NPP (still of low power, that is, electric power up to 100 … 300 MW). The present work is devoted to this problem.

All reactors that have ever experienced severe accidents were considered safe. They met all the rules and regulations that were in force at the time of the accident on the territory of the country where these reactors were operated. Serious accidents occurred at the plutonium production reactor of the Windscale nuclear complex (Great Britain, 1957); Unit 2 of the Three Mile Island NPP (USA, 1979); 4th block of the Chernobyl NPP (USSR, 1986); four units of the Fukushima-1 NPP (Japan, 2011).

After a series of accidents at NPPs, the philosophy of ensuring the safety of nuclear power facilities was radically rethought. The first conceptual designs of nuclear reactors appeared, in which it is possible to exclude all accidents leading to unacceptable releases of radioactive substances outside the NPP.

A comprehensive solution to the following tasks was proposed:

• Provision of energy on the required scale;
• Economic efficiency;
• Safety;
• Provision (self-sufficiency) with fuel.

Safety is understood not only to exclude severe accidents at nuclear power facilities, but also to safely handle waste and create physical barriers to the theft of nuclear materials.

Nuclear power in the 20th century was not limited to terrestrial reactors. Nuclear power has entered low earth orbit. The first developments of NPPs were started simultaneously in the USSR and the USA in 1954 [4]. Space nuclear power was ahead of its time. Modern interplanetary spacecraft use radioisotope energy sources (less than 1 kW) [2]. Russia has experience in the development and use of nuclear electric propulsion systems and NPPs with electric power up to 6 kW in outer space. But such installations have not yet been in demand [2]. Until now, energy sources with a capacity of about 1 MW and more have not been in demand. The provision of spacecraft and orbital stations with energy is achieved through the use of solar batteries (the power of which is estimated at several kilowatts, but can reach ~ 10⁵ W), chemical sources of electric current (galvanic cells, batteries, fuel cells), radioisotope sources, nuclear reactors, etc. [5].

Despite the relatively low efficiency (up to 13% [5]), the preference is still given to solar panels. Their specific weight is 4.6 kg / kW; in the future it can be reduced by almost 2 times [5]. Flights to Mars, the creation of stations on the Moon and Mars will require much more energy (from 1 MW and more). Space nuclear power can easily solve this problem.

2. Background

2.1. Specific Requirements for a Space Reactor

Unlike ground-based nuclear power reactors for space reactors, it is necessary to provide a high density of energy release in the core with much lower safety requirements, and the possibility of long-term autonomous operation. For reactors and NPPs built on the surface of the planet, minimization of mass and size is not so urgent.

Relatively low safety requirements are associated with the fact that space reactors are designed to operate with an extremely low population density (crew of a ship or an orbital station; personnel of a station located on the planet under study). When placing a NPP on the surface of a planet (the Moon or Mars), it is advisable to bury the reactor under the soil layer. This is necessary to protect against meteorites in a highly rarefied atmosphere or in the absence of an atmosphere. With this arrangement of the reactor, a severe accident would not destroy or damage the entire space station. In addition, long-term dust storms are characteristic of Mars. Martian dust is iron oxide particles about 1.5 microns in size [6].

The situation is aggravated if the reactor is located on a spacecraft or orbital station. A severe accident of a space reactor will lead to huge economic losses. According to various estimates, the cost of the International Space Station is $ 150 billion. The cost of the Mir station is $ 4.2 billion (in 2001 prices). The commercial value of the Soyuz-2.1 disposable spacecraft (without additional modules) is about $ 35 million ($ 20-30 thousand per 1 kg of payload) [7]. The commercial value of the heavy rocket Proton (Russia) and Falcon 9 (USA, SpaceX) is $ 60-65 and $ 62 million, respectively [7]. The Soyuz-2.1 spacecraft is capable of putting up to 8.25 tons of cargo into low orbit, the Proton spacecraft – about 22 tons, the Falcon 9 – 22.8 tons [7]. NASA estimates the cost of a manned flight to Mars at between $ 400 billion and $ 1 trillion [8]. For comparison, the cost of building a land-based NPP with four VVER-1200 reactors (Turkish nuclear power plant “Akkuyu”) is $ 22 billion [9]. The cost of building a fast reactor BN-800 (4th power unit of the Beloyarsk NPP, Zarechny, Russia, electric capacity 880 MW) is estimated at $ 2 billion [10]. The cost of building BREST-OD-300 (Seversk, Russia) is estimated at $ 1.4 billion. [11] The high cost of the project is explained by the rise in prices for materials [11].

When designing space reactors, compactness is important: minimum weight and dimensions. This is achievable for liquid metal cooled reactors (LMR) operating on intermediate neutrons (in the resonance spectrum of neurons). One of the advantages of intermediate neutron LMRs is its relatively small size and lighter weight compared to light water reactors (LWRs). This is attractive for the use of LMRs as transport reactors (on ships of surface and submarine fleets, spaceships and space stations).

2.2. Existing Devices and Developments

The first space reactor on intermediate neutrons (SNAP-10A, thermal power 40 kW, electric power 500 … 650 W, thermoelectric power converter) was developed by Boeing by order of the Air Force and the US Atomic Energy Commission [12]. Highly enriched fuel was used in the core, the moderator was zirconium hydride, and the coolant was a eutectic alloy of sodium and potassium [12]. In the period from 1970 to 1988, 31 spacecraft with the fast reactor “Buk” (thermoelectric energy conversion, electric power 3 kW, service life up to 4400 hours) were launched into low-earth orbits in the USSR. Two experimental Soviet reactors on intermediate neutrons “TOPAZ” (thermionic energy conversion, electric power 5 kW) were launched into space in 1987 and 1988.

Modern concepts of space reactors, performing the functions of a tug, being developed from Russia and the United States, are guided by an electrical power of ~ 1 MW. In Russia, since 2010, research has been carried out within the framework of the project of the state corporations “Roscosmos” and “Rosatom” (“Creation of a transport and energy module based on a megawatt-class NPP”) [13]. The installations are designed for flights into deep space, to the Moon and Mars. For the same purposes, the USA is developing a nuclear electric motor plant “Kilopower” with an electric power of 1 kW (in the future, with an increase in power up to 2 MW) [14]. The service life of such installations is designed for 15 years [14].

At present, the development of nuclear electric propulsion systems is carried out in three directions: three types of installations are being developed [2, 3]:

• The first type is based on the concept of a reactor with direct conversion of thermal energy into electrical energy (thermal emission conversion) and an electric rocket motor;
• The installation of the second type is a reactor with machine energy conversion and an electric rocket engine;
• The installation of the third type should operate in two modes: obtaining traction in engine mode and generating electrical energy in a closed loop.

Several conceptual designs of new generation space NPPs have been developed in Russia [4, 15].

• Four projects with electrical capacity from 0.1 to 150 MW for operation as part of a transport an energy module for the study of distant planets of the solar system;
• Four projects of the Martian NPP with electric power from 25 to 500 kW;
• Four projects of the lunar NPP with electric power from 25 to 500 kW.

It is proposed to use a high-temperature fast reactor in all projects.

NASA and the US Department of Energy have selected three nuclear thermal propulsion concepts. The reactors are intended for deep space exploration (see [16] with reference to “World Nuclear News”). The concepts were developed by the following companies.

• “BWX Technologies” и “Lockheed Martin”;
• “General Atomics Electromagnetic Systems”, “X-energy” and “Aerojet Rocketdyne”;
• “Ultra Safe Nuclear Technologies”, “Ultra Safe Nuclear Corporation”, “GE Hitachi Nuclear Energy”, “GE Research”, “Framatome” и “Materion”.

Companies are encouraged to develop “different design strategies for specific performance requirements that could help deep space exploration” [16].

The plans of the Russian state corporation “Roscosmos” (within the framework of the “Nucleon” project) include the construction of a NPP on Mars to supply the future Russian Martian base with electrical energy [17]. The NPP is planned to be delivered to Mars orbit using the “Zeus” nuclear tug (nuclear rocket engine, 1 MW) [17]. The NPP will descend to the surface of the planet by parachute. Immediately after landing, the NPP will be ready for operation [17]. The developer of the project is the “Arsenal” design bureau (St. Petersburg). The “Arsenal” design bureau includes a pilot production plant. The plant is capable of performing a full cycle of work from the development of the corresponding (design, technological) documentation to the manufacture of finished products. The United States is planning to build a small NPP (with an electrical power of 10 kW, based on the “Kilopower” concept) on the Moon and Mars.

2.3. Operating Conditions

In the absence of a dense layer of the atmosphere in order to minimize the risk of damage to an alien NPP by meteorites, it should be buried in the soil of the planet [1]. In addition, it is necessary to take into account the daily and seasonal temperature drops on the planet’s surface [1]. According to [18, 19], daily temperature drops on the lunar surface average 300 ºС: from –173 ºС (at night) to +127 ºС (during the day). During eclipses (lasting about one and a half hours) the temperature of the lunar surface during the day decreases by 250 … 300 ºС. In lunar craters near the pole, a temperature of –249 ºС was recorded. On the other hand, at a depth of 1 m, the temperature of the lunar regolith is stable and amounts to –35 ºС [18, 19]. This is attractive for burying NPPs into the ground.

The seasonal change in the temperature of the atmosphere near the surface of Mars is 105 ºС: from –80… 125 ºС to + 20… 25 ºС. The maximum temperature spread is 178 ºС: from –143 ºС (in winter at the pole) to +35 ºС [18, 19]. In mid-latitudes, temperatures range from -50 °C in winter nights to 0 °C in summer days [18]. The average atmospheric pressure on the average radius of Mars is 636 Pa (data from NASA, 2004) [18]. Depending on the season, the pressure varies from 400 to 870 Pa [18]. Due to the large difference in altitude on Mars, the pressure at the surface varies greatly. In deep depressions (Hellas plain), atmospheric pressure is 1.24 kPa [20]. Atmospheric pressure on the lunar surface is about 10 nPa [21]. The lower layer of the Mars atmosphere contains carbon dioxide (95.32%), nitrogen (2.7%), argon (1.6%), other gases and traces of organic compounds [22]. The atmosphere of the Moon is composed mainly of hydrogen, helium, neon and argon [21].

One of the features of space NPPs operating in space far from the planet (relatively large gravitational mass) is associated with the absence of natural circulation of the coolant when the pumps fail. The high level of natural circulation in land-based reactors plays an important role (with rare exceptions) in ensuring their safety. An exception to this pattern is a fast reactor with a heavy coolant (lead or lead-bismuth alloy). For such reactors (for example, BREST-OD-300 [23]), a two-circuit energy conversion scheme is adopted, and water is used as a working fluid (in the second circuit). In emergency modes with depressurization of the steam generator tubes, a high level of natural circulation promotes the entrainment of water vapor bubbles into the core, which leads to an increase in reactivity and can lead to an accident.

In reactors located on Mars and the Moon, the level of natural circulation is noticeably lower than in terrestrial reactors. The reason lies in the lower value of the acceleration g of gravity. If on the surface of the Earth the average value of g is 9.81 m / s², then on the surface of Mars g ≈ 3.86 m / s², on the surface of the Moon g ≈ 1.61 m / s². The flow rate G of the coolant through the core in the natural circulation mode is determined by the formula [1]:

 G = [HgΔγ/Δp]^1/1,75,                         (1)

where H is the height of the natural circulation contour (thrust section), equal to the difference in heights between the average levels of the core and the intermediate heat exchanger for emergency cooling; Δγ is the difference in the density of the coolant at the inlet and outlet to the core; Δp is hydraulic pressure loss in the primary circuit.

In fig. 1 shows the qualitative dependence of the coolant flow rate in the natural circulation mode on the acceleration of the combined fall, all other things being equal (i.e., at HΔγ / Δp = const = B).

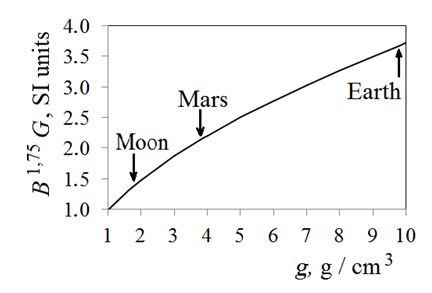Figure 1: Dependence of the coolant flow rate in the natural circulation mode on the acceleration of the consolidated fall

Based on the data in table 1, it can be concluded that for a space reactor located at a shallow depth under the surface of Mars or the Moon, acceptable values of the level of natural circulation are achievable to ensure safety in emergency modes with violation of forced circulation of the coolant. Circulation pumps can be eliminated in the design of low-power reactors located on the surface of planets with relatively high gravity.As noted in [1], “to compensate for the decrease in G, all other things being equal (in comparison with a ground-based reactor), it is necessary to increase H and, consequently, the total height of the NPPt”. For reactors located on Mars or the Moon, high values of the height of the natural circulation loop should be chosen. This is possible due to the deepening of the reactor into the soil of the planet. Table 1 shows the characteristic values of H for the lunar and Martian NPPs in relation to H₀ of a terrestrial-based reactor (according to [1]).

Table 1: Characteristic values of the height of the natural circulation contour of terrestrial, Martian and lunar-based reactors

The planet on which the reactor is located	H /H0	Typical values of H, m
Earth	1	5…10
Mars	2.54	up to 10
Moon	6.09	24…25

2.4. Possible Borrowing of Technologies of Ground-Based New Generation of Fast Power Reactors

The design of NPPs (installations capable of operating only in the mode of generating electrical energy) on other planets can be based on borrowing technologies from new generation of ground-based power reactors, taking into account the specifics of the operating conditions of the reactor.

Liquid metal cooled fast reactors (fast reactors or LMFRs) have a higher core energy density than light water reactors (LWRs) and have good potential for improving internal security. Currently, two directions of high-power, ground-based fast power reactors are being developed. The first direction (traditional) involves the use of a liquid sodium coolant. The second direction (innovative) involves the use of a liquid lead coolant. In 2021, Russia began construction of a pilot demonstration reactor BREST-OD-300 with a lead coolant and mixed mononitride fuel (UN-PuN) based on waste uranium and plutonium recovered from spent LWR fuel. Another advantage of fast reactors is the high value of the average number of neutrons ν_f produced during the fission of a heavy nucleus (Fig. 2). This is due to the relatively high kinetic energy of neutrons in the fast reactor.

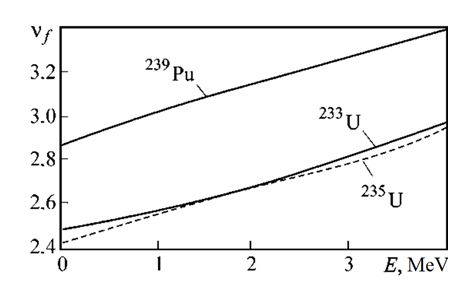Figure 2: Dependence of the average number of neutrons produced during nuclear fission on the kinetic energy of the neutron that caused the fission [24]

In space reactors, fuel based on highly enriched uranium (without plutonium in the launch load) is used. This is due to some of the properties of plutonium. When using plutonium-239 as the main fissile nuclide, the following advantages are achieved (in comparison with the fissile isotopes of uranium ²³³U and ²³⁵U):

• Maximum energy release;
• Maximum value of parameter ν_f ;
• when using mixed fuel (based on ²³⁸U and ²³⁹Pu), the reactor can operate for a long time (up to 20 years) in a self-fueling mode, i.e., the number of fissile nuclides in the core is constant and practically does not change over time (the BRC – breeding ratio in the core is approximately equal to 1).

These advantages are attractive for the use of mixed fuel (based on ²³⁸U and ²³⁹Pu) in terrestrial power engineering.

There are two significant disadvantages of plutonium fuel.

• A small fraction of β delayed neutrons produced during the fission of heavy nuclei (during the fission of uranium-235 β = 0.0065, plutonium-239 β = 0.0021 [25]) complicates reactor control and leads to a potential accident hazard (reactor is prompt critical) [24];
• Unpredictable behavior of the crystal lattice (when using metallic plutonium) and a spontaneous change in its shape during operation of the reactor leads to a noticeable change in the volume of fuel [26].

These disadvantages impede the use of plutonium-239-based fuel in transport reactors (space, ship, etc.).

One of the topical and fundamental tasks is the development of space NPPs, combining the advantages of new generation fast power reactors and existing or under development space reactors.

2.5. Tasks solved by a space NPP (based on data [2, 3])

In the near future, space NPPs with an electric power of up to 250 kW are designed to solve the problems of a global communication system, remote sensing of the Earth, environmental monitoring, warning of natural disasters, etc .; comprehensive study of the Earth and solar-terrestrial relations; detailed studies of planets and their satellites; explore the possibilities of industrial production in space; the task of cleaning from space debris; warnings about the approach of dangerous space objects. In the future, space nuclear power (the electric power of the reactor is from 5 to 40 MW) is designed to provide manned flights to the Moon and Mars; sending probes outside the solar system; delivery to Earth and processing of asteroids; combating natural disasters.

3. Materials and Methods

In addition to the general requirements for the choice of materials for space reactors, specific requirements must be taken into account, taking into account the extreme operating conditions. Extreme conditions include high temperatures (usually oriented at 3000 K), intense radioactive irradiation (neutron flux density 10¹⁴ s ^–1 cm ^–2), chemically active media (hydrogen in a nuclear rocket engine) [27, 28]. Most of the “traditional” materials for ground-based nuclear technology do not withstand these operating conditions.

In the manufacture of structural materials, preference is given to refractory metals (tungsten, molybdenum, chromium) [29]. Preferred fuels are carbides and nitrides of transition metals, ceramics [29]. To expand the temperature range of operation of fuel and structural materials, introduction phases are used [29-31]: ordered structures that are formed during the interaction of some metals with carbon, nitrogen, hydrogen and oxygen atoms. The disadvantage of interstitial phases is brittle fracture at relatively low temperatures (up to 1000 K) [29-31]. This drawback is eliminated by a special design technology. Materials must be in a compressive stress field. Tensile stresses should be minimized [29, 31].

3.1. “Traditional” promising fuel

Uranium dioxide is rightfully considered the most widespread nuclear fuel. The melting point of UO₂ is 2750 °C [32]. Such fuel is characterized by low density and thermal conductivity. Uranium mononitride melts congruently at 2850 °C if the nitrogen pressure in the system exceeds 250 kPa [32]. Low nitrogen pressure leads to the decomposition of UN to form a liquid uranium phase. The melting point of uranium monocarbide is 2275 °C [32]. Mononitride and monocarbide are characterized by high density and thermal conductivity. This is attractive for the use of such fuels in reactors with a high bulk heat density.

A mixture of uranium and zirconium hydride was used as fuel for the SNAP-10A space reactor. An alloy of uranium with molybdenum was used as fuel for the “Buk” reactor, a uranium dioxide was used for the “TOPAZ” reactor.

Fuel materials (introduction phases) are produced by interaction of heavy metals (Th, U, Pu) with non-metals (oxygen, carbon and nitrogen). The simplest ceramic compounds are UO₂, UC and UN. The advantages and disadvantages of these fuels are well understood. They were studied at the dawn of the development of fast reactors. In the BOR-60 reactor, fuel based on UC, UPuC and UNC was studied [33]. The fuel (UPu) C_{1 – x} N_x (where x < 0.8), PuO₂-MgO, PuN-CrN, (UZr) N [18, 33], UZrCN (uranium carbonitride) [34] was studied. It is proposed to use highly enriched uranium (up to 90% ²³⁵U) [34]. For a nuclear rocket engine, high-temperature fuel based on solid solutions of carbides is considered: UC-ZrC, UC-NbC and ZrC-NbC-UC [35]. The density of ZrC-NbC-UC is relatively low: 7.6 g / cm³, melting point 3520 K [35]. The carbonitride fuel UC-ZrC-ZrN is being investigated [35]. Fuel based on uranium-zirconium carbonitrides has the highest density among high-temperature fuels.

A space NPP is being developed in the United States. The NPP was developed on the basis of the “Kilopower” project. Uranium metal, UMo alloy, or uranium dioxide is considered as fuel [4]. The installation is designed to generate electricity (up to 10 kW) on the surface of Mars. The service life is 10 years.

So, in Russian space reactor designs, UZrCN carbonitride fuel is considered the most promising. The multi component composition opens up possibilities for optimizing the composition and properties of such a fuel. In the USSR, high-temperature and high-density carbonitride fuel based on highly enriched (96%) and low-enriched (less than 20%) uranium was developed for various types of reactors [36].

Scientists from Belarus, Russia and the United States are conducting joint computational and experimental studies of 0.9U-0.1Zr-0.5C-0.5N fuel (with 19.75% enrichment in ²³⁵U) with a density of 12 … 12.5 g / cm³ and thermal conductivity

λ = 11, 4 W m ^{– 1} K ^{– 1}

for the Russian high-flux research reactor SM-3 [36, 37].

3.2. New Promising Fuel

When designing Martian and lunar NPPs (in fact, space nuclear power plants), borrowing technical solutions suggests that the cermets fuel previously considered by the author for ground-based BN and BREST power reactors can be used in space NPPs [1]. This fuel is sintered pellets of mixed mononitride fuel micro grains (UN-PuN with additives of ²³⁷Np, ²⁴¹Am, ²⁴³Am long-lived waste) and uranium metal nanopowder. The composition of UN uses natural (²³⁵U content about 0.72%) or depleted (²³⁵U content about 0.4%) uranium. PuN uses plutonium recovered from LWR spent fuel and purified from the ²³⁸Pu isotope. Plutonium isotopic composition: 0.6 ²³⁹Pu – 0.25 ²⁴⁰Pu – 0.109 ²⁴¹Pu – 0.041²⁴²Pu. The Pu / (Pu + U) ratio does not exceed 0.2. The mass content of radioactive waste (²³⁷Np, ²⁴¹Am and ²⁴³Am) in fresh fuel is about 5%.The total content of fissile nuclides (²³⁵U, ²³⁹Pu and ²⁴¹Pu) in the fuel is about 16%.

The nanopowder occupies the voids between the micro grains of the ceramic. As a result, the porosity of the fuel is reduced to 5%. “The ratio of the volumes of micro grains of ceramics and metal nanopowder 20/75 corresponds to a mass ratio of 0.39. This is the maximum permissible mass content of metallic nanopowder in the fuel, associated with the limitation of the maximum permissible temperature” [1]. When using enriched uranium nanopowder, the reactor power at fixed dimensions can be increased by 40%.

The average density of such a fuel is about 16 g / cm³, the thermal conductivity is about 27.8 W  m ^–1 K ^–1, which significantly exceeds the corresponding values for mononitride and carbonitride. This contributes to the safe end of emergency situations, including those accompanied by a failure of the emergency protection (ATWS – anticipated transient without scram).

When the fuel temperature rises in emergency modes, melting of uranium nanopowder is possible. However, it will not go beyond the fuel element cladding. At the end of the emergency mode, the nanopowder will again go into the solid phase.

Uranium metal nanopowder acts as a getter of free nitrogen released from micro grains during reactor operation. Nitrogen migrates to the fuel element cladding. In the presence of free nitrogen, the corrosion rate of the inner surface of the shell increases. Getter binds free nitrogen, helping to minimize the rate of corrosion of the inner surface of the shell. After a long-term operation of the reactor, which “survived” emergency situations, uranium metal gradually loses its functions of an effective getter. Its functions in ensuring the safety of the reactor (due to its high thermal conductivity and density) are preserved.

Optimization of fuel properties is possible by changing the ratio of micro grains of mononitride and uranium nanopowder, as well as by changing the enrichment of uranium nanopowder.

From the point of view of ensuring safety in emergency situations (including the most dangerous of them – ATWS), it is sufficient to ensure the mass content of uranium nanopowder in the fuel at the level of 15 … 20%. From the point of view of maximizing the reactor power, it is advisable to increase the nanopowder content to the limiting value (39%). This value corresponds to the filling of the pores between the micro grains of the ceramic. When melting a nanopowder in emergency situations, liquid droplets should not completely surround the ceramic micro grains.

Particular attention is paid to solving the problem of non-proliferation of materials that can be used in the creation of weapons of mass destruction. As noted, when using a mixed mononitride fuel, a self-fueling regime is achieved, i.e., the breeding ratio in the core is approximately equal to 1. On the one hand, at all stages of the fuel cycle, the need to separate isotopes of heavy nuclei is completely eliminated. The burnout of the fissile isotopes of uranium (a small amount of ²³⁵U) and plutonium (²³⁹Pu, ²⁴¹Pu) is compensated by the production of ²³⁹Pu from ²³⁸U. On the other hand, NPP fuel contains material for direct use. This is attractive to the terrorist kidnappers. But terrorists are unlikely to be able to reach the Moon or Mars. If they can, then these will only mean that they are representatives of states with high technologies and (most likely) possessing nuclear weapons. If necessary, they will be able to produce the required amount of materials for direct use on Earth. It is extremely difficult to steal irradiated fuel characterized by a high background radiation, especially in space.

3.3. Traditional Coolants

The eutectic alloy NaK was used as a coolant for the first space reactors SNAP-10A, “Buk” and “TOPAZ”.

In fast space reactors of the second generation, it was proposed to use the eutectic alloy NaK (electric power 70 … 150 kW) and lithium (two reactors with electric power 80 … 150 and 160 … 400 kW) as a coolant [38]. The eutectic NaK and ⁷Li (not used in space) can be considered traditional coolants for space reactors with liquid metal cooling [39].

Alkali metals are characterized by the highest chemical activity. The activity towards oxygen increases from lithium to cesium. In the series of alkali metals from lithium to cesium (Li, Na, K, Rb, and Cs), the melting point decreases from Li to Cs, the chemical activity increases, and the hardness weakens. Of all alkali metals, only lithium interacts with water without exploding and has the highest melting point. There is practically no oxygen in the lunar and Martian atmosphere. Carbon dioxide (the main constituent of the Mars atmosphere [22]) oxidizes all alkali metals.

Table 2 shows the melting and boiling points of some liquid metal coolants with a relatively low fast neutron absorption cross section (according to [40–42]).

Table 2: Operating temperatures of some liquid metal coolants

Coolant	Melting point, ºС	Boiling point, ºС
Lithium	180.54	1339.85
Sodium	97.86	883.15
Potassium	63.7	758.85
Mercury	-36	357
Bismuth	271	1490
Lead	327.4	1740
77,2 % K – 22,8 % Na	−12.6	785
55,5 % Bi – 44,4 % Pb	123.5	1670

A NaK alloys are chemically active, low-melting, and flammable in air. With a mass fraction of potassium of 40 … 90%, the alloy remains liquid under normal conditions [41]. An alloy of 56% K and 44% Na is also a eutectic.

3.4. Alternative Coolants. Sodium, Potassium and Cesium Alloys

Is there an alternative to lithium-7 and NaK alloy used for cooling the core of space NPPs?

In the reactors of nuclear submarines, a coolant based on a eutectic alloy of blue bream with bismuth was used [43]. (Eutectic is a liquid solution that crystallizes at the lowest temperature for the alloys of this system.) The first such reactor (BM-40A) of the nuclear submarine “Lira” was lighter than traditional reactors of the LWR type by 300 tons at the same power (155 MW) [43]. An eutectic alloy of lead and bismuth provides a high level of inherent safety in relation to accidents [44]. The operating temperature range of such a coolant is wide: from 123.5 °C to 1670 °C [40, 41]. The technology of using such an alloy as a coolant for a nuclear reactor has been developed [43]. The PbBi eutectic alloy cooled reactor is intrinsically safe. In such a reactor, severe accidents can be excluded. The use of the PbBi coolant will require the reliable operation of the heating system of the idle reactor circuit.

Gallium has a maximum operating temperature range. The freezing point is 30 °C; the boiling point is 2230 °C [42]. Gallium is classified as a rare element. It is highly dispersed in the earth’s crust (on average, its mass content in the earth’s crust is about 19 ppm) [42]. Gallium is extracted from zinc and aluminum ores. Gallium is attractive as a high-temperature heat carrier. But gallium is a very expensive coolant. In addition, gallium is highly corrosive to traditional structural materials for fast reactors (AISI 316 SS, Russian stainless steel “12X18H9”) [44]. Gallium has never been used as a coolant in nuclear reactors [44]. Gallium is characterized by a relatively high fast neutron absorption cross section. When using mononitride fuel or cermets based on micro grains of mononitride and uranium metal nanopowder, it is possible to ensure a good balance of neutrons in the reactor core. The fuel self-sufficiency mode is easily achievable, i.e., the fuel breeding ratio in the core is slightly more than 1. However, the void reactivity effect is positive (when bubbles are drawn into the central part of the core) even in low-power reactors (electric power of 150 MW and more).

Among alkali metals, NaKCs alloys with different concentrations of components are attracted. Sodium, potassium and cesium are highly reactive. The NaKCs alloy forms a eutectic with a sodium content of 12% (at.), Potassium 47%, and cesium 41%. The properties of such an alloy are well studied [44–46]. The melting temperature of such an alloy (“Soviet alloy”) is minimal for all metals and is –78 ºС [47]. This eliminates the need for heating the coolant in the idle reactor. It is possible to exclude freezing of the coolant in emergency modes such as OVC WS (overcooling accident without scram). Alloy NaKCs with a certain content of components are characterized by a much lower chemical activity than their individual components. It was found experimentally that NaKCs alloys with a certain content of components “are capable of A NaK alloys are chemically active, low-melting, and flammable in air. With a mass fraction of potassium of 40 … 90%, the alloy remains liquid under normal conditions [41]. An alloy of 56% K and 44% Na is also a eutectic.

“NaKCs alloys with a certain content of components are capable of oxidizing in air at 300-1000 K without intensive release of aerosols and a noticeable increase in temperature” [48]. Eutectic alloy NaKCs does not ignite in the temperature range 293 … 973 K [45]. Thus, by changing the concentration of Na, K and Cs in the alloy, it is possible to control the properties of this alloy. The manufacturing technology of NaKCs alloys is presented in [45].

The melting point, density, electrical conductivity, electric potential, reactivity, plasticity, and flammability of the NaKCs alloy depend on the concentration of the components [45]. These differences are a consequence of differences in the interactions between the components of the alloy during its formation [45]. In addition to the eutectic, alloys 20% (at.) Na – 30% K – 50% Cs and 40% (at.) Na – 30% K – 30% Cs have been well studied. Melting point of 20% Na – 30% K – 50% Cs alloy is equal minus 37.90 ºС [45]. Melting point of 40% (at.) Na – 30% K – 30% Cs alloy is equal 0.00 ºС [45].

Ignition of liquid metal occurs due to a sharp violation of thermal equilibrium. This leads to a self-accelerating temperature rise [45]. The ability of a metal to ignite is largely determined by the characteristics of the oxide film formed on the surface [45].

When analyzing three-component systems (liquid alloys), appropriately delineated triangles are used (they are called Gibbs-Rosebohm triangles or Rosebohm triangles). On such a triangle for the NaKCs alloy, it is possible to distinguish the concentration range corresponding to the non-flammability of the alloy [48]. The boundary of the region is determined by the equation of an ellipse with the ratio of the semi axes 2.4 m center at the point corresponding to an alloy close to eutectic [48].

The center of the ellipse is determined by the content of sodium 12% (at.), potassium 44%, cesium 44% (or the mass content of 3.52% Na – 21.88% K – 74.60% Cs) [48]. The boundaries of the non-flammable range (% at.): 2 … 24 Na – 19 … 69 K – 19 … 69 Cs or (% wt.) 0.5 … 7.8 Na – 7.6 … 43.7 K – 46.5 … 89.2 Cs [48]. The region of non-flammability is determined by the inequality [48]:

(6C_Na – 1)² – 8C_KC_Cs + 1 ≤ 0,           (2)

where C_Na, C_K and C_Cs are the atomic concentrations of sodium, potassium and cesium, respectively.

Sodium and potassium are considered the most common in the earth’s crust (the mass content of sodium in the earth’s crust is 2.3%; potassium is 2.1% [49]). Cesium is a rare element (the mass content in the earth’s crust is 3 · 10^–4 % [42]). The volume of world production of cesium is small: 20 tons / year [49]. Increase in cesium production is possible. It can be extracted from spent nuclear fuel (~ 10 t / year).

In [50], with reference to [51], the total yield of relatively long-lived cesium isotopes during the fission of uranium and plutonium nuclei is given (Table 3). This yield is quite large: from 6.2 to 7.5%.

Table 3: Half-life and total (cumulative) yield of some isotopes of cesium during fission of heavy nuclei

Parameter	Cesium isotope
	133Cs	135Cs	137Cs
Half-life, years	Stable	2.3 · 106	30.0
The yield upon fission of 235U nuclei by a thermal neutron, %	6.6149	6.5803	6.2444
The yield upon fission of 235U nuclei by a fast neutron, %	6.6100	6.3696	5.9962
The yield upon fission of 239Pu nuclei by a thermal neutron, %	6.9034	7.2411	6.5090
The yield upon fission of 239Pu nuclei by a fast neutron, %	7.0466	7.5384	6.3534

The distribution of the yield w of fission fragments over the mass numbers A is determined by the presence of about magic, magic, and doubly magic nuclei. According to the shell structure (model) of the atomic nucleus, asymmetric fission is a consequence of the predominant formation of fission fragments with filled neutron and proton shells.

The w (A) curve corresponding to the fission of uranium or plutonium contains two maxima. This reflects the well-known fact that fission into two fragments with a mass ratio of 1.6 is most likely. The first maximum corresponds to the values А ≈ ≈ 90 … 100, the second corresponds to the values А ≈ 130 … 140 (Fig. 3). The yield of cesium isotopes illustrates the second (right) maximum.

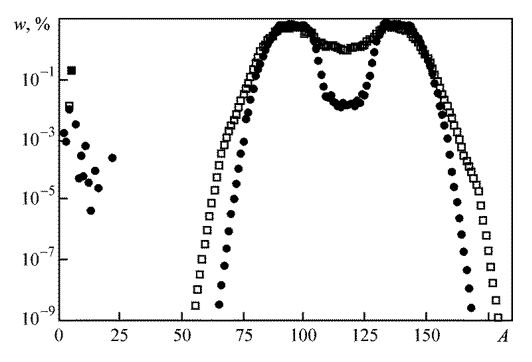Figure 3: Distribution of the yield of fission fragments of uranium 235U by atomic masses A [24]: □ – fission of nuclei by neutrons with an energy of 14.06 MeV; ● – fission of nuclei by neutrons with an energy of 0.0253 eV

Due to the wide range of operating temperatures at an extremely low freezing point and a relatively high boiling point (721 ºС [47]), the coolant based on the NaKCs eutectic is of great interest for space reactors. You can eliminate the need for heating the coolant in the idle reactor. Freezing of the coolant in OVC WS is excluded.Cesium is strongly activated in the core of a nuclear reactor [40, 44]). This is a serious problem that prevents the use of such alloys as coolants for ground-based power reactors. The use of cesium as a component of the NaKCs alloy, if it can be justified, is only by the non-flammability of such a coolant. However, the specific operating conditions of the reactor on the surface of Mars or the Moon (extremely low population density – the personnel of the alien station) make it possible to use radioactive waste from terrestrial nuclear power engineering as reactor materials (fuel and coolant).

The use of such a coolant will make it possible to exclude the combustion of the coolant (as a result of which the void reactivity effect is realized), and the boiling problem can be solved due to the optimal choice of the reactor layout parameters. For medium to high power LMFRs, there is a problem with the positive void reactivity effect. However, in low-power reactors, this effect is negative. It can be expected that the use of such a coolant will make it possible to create a safe space reactor.

3.5. The Research Methods

The author uses calculation and optimization methods and codes to substantiate the possibility of creating a space reactor for an alien NPP. The author’s codes [1] and well-known codes [52, 53] are used:

• FRISS-2D for simulation of emergency modes (including ATWS) [1];
• Multiple modernized calculation and optimization code Dragon-M [1];
• MCU code for precision neutron-physical calculation [52];
• WIMS code for neutron-physical calculation of a fuel element cell [53].

The FRISS-2D mathematical model is based on the solution of the following equations:

• Systems of equations of point neutron kinetics with a six-group description of delayed neutrons (for the relationship between power and reactivity);
• Non-stationary heat conduction equation, which is the heat balance equation, and the coolant energy equation (to determine the relationship between the reactor power and changes in the fuel and coolant temperatures);
• balance equation of reactivity (linking temperature changes with reactivity).

One of the versions of the FRISS-2D code can work as part of the Dragon-M computational and optimization code.

Dragon-M code is intended for solving mathematical programming problems in a deterministic setting and under conditions of uncertainty in the initial data. To solve optimization problems, the method of sequential linearization is used [54]. The code allows you to solve problems with a given criterion of optimality. The restrictions for the functionals characterizing the economic efficiency of the NPP, reliability and safety are considered. The emergency modes of the ATWS type of reactor operation are taken into account. Comprehensive optimization is carried out: the code contains modules for neutron-physical calculation (in the multi-group diffusion approximation), calculation of changes in the nuclide composition of fuel, thermal-hydraulic calculation, strength calculation, and assessment of the economic characteristics of NPPs. A homogeneous cylindrical reactor consisting of radial and axial zones differing in composition is considered. The control parameters include the geometric characteristics of the fuel element array, the fuel composition, the coolant flow rate, the dimensions of the reactor zones, etc.

The MCU code allows obtaining the solution of the stationary gas-kinetic equation of neutron transport (Boltzmann equation) by the Monte Carlo method.

In the calculations using the WIMS code (WIMS-D5B), the S4-approximation of the discrete ordinate method was chosen to solve the integral neutron transport equation (Peierls equation).

The author has developed the FRISS-2D, Dracon-M codes and a number of auxiliary codes. The author for the first time included in the optimization problem the constraints for functionals that simulate the safe termination of emergency processes (including ATWS). Limitations are considered for extreme temperatures of fuel, coolant, fuel-element cladding, power, pressure in the cavity for collecting gaseous fission products, etc.

As an optimality criterion, it is customary to consider the functional characterizing the economic efficiency of a NPP. The rest of the functionals can be taken into account among the limitations of the mathematical programming problem. However, when safety functionals are taken into account, the area of safe layouts in the space of control parameters is sometimes so small that the choice of the economic criterion of optimality does not matter. The criterion related to the safety of the reactor can be selected as the target functional (for example, the void reactivity effect). The control vector includes the characteristics of the core.

The FRISS-2D and Dracon-M codes assume that the reactor consists of several radial and axial zones of homogenized composition. The Dracon-M code has no analogues yet.

 With the help of the developed software, the author for the first time obtained the results of optimizing the safe layouts of ground-based and alien-based LMFRs, taking into account safe operation. In such reactors, severe accidents can be ruled out.

 The software developed by the author allows solving computational and optimization problems in conditions of uncertainty, including the uncertainty of emergency scenarios. This is important at the initial stages of nuclear reactor design (when its characteristics are not finally determined).

4. Results

4.1. Initial Provisions

The relatively low chemical activity of the NaKCs alloy in comparison with its components makes it possible to consider a two-circuit energy conversion scheme. The first circuit is filled with liquid NaKCs alloy, the second – with water. The transition to a two-circuit scheme will greatly simplify the design and reduce the cost of NPPs.

The most dangerous are emergency modes, accompanied by the failure of emergency protection (ATWS). As you know, all emergency modes of LMFR operation can be triggered by the following events.

• Draining the core or part of it (including entrainment of bubbles into the core) – modes of the LOCA WS (loss of coolant without scram) type;
• Input of limited value of positive reactivity – modes of TOP WS (transient overpower without scram) type;
• Violation of the forced circulation of the coolant in the primary circuit – modes of the LOF WS (loss of flow without scram) type;
• Violation of heat sinks from the first circuit to the second – modes of the LOHS WS type (loss of heat sink without scram);
• Overcooling of the primary coolant – modes of the OVC WS type.

The most dangerous are the combinations of these modes.

It is assumed that the reactor of the Martian NPP has an electrical capacity of 600 MW. (This is an abnormally high power for such a NPP.)

The traditional layout of the core is considered. It is assumed that there are two zones of profiling along the radius of the reactor. The initial loading of the reactor assumes the presence of enriched uranium and does not contain plutonium isotopes. Plutonium builds up as the reactor runs.

Both zones contain uranium mononitride fuel of different enrichment (11 and 15% for the central and peripheral zones, respectively) with the addition of long-lived transuranic elements (5% by weight ²³⁷Np, ²⁴¹Am and ²⁴³Am). A nanopowder of metallic uranium (39% by weight) with an enrichment of 16% in ²³⁵U is placed in the fuel pellet between the micro grains of the mononitride.

In order to increase the flow rate of the coolant in the natural circulation mode (when the main circulation pumps are de-energized), it is necessary to increase the effective height of the natural circulation circuit in comparison with ground-based NPPs. To ensure the required level of natural circulation up to 14 … 15% (which is required for the trouble-free completion of the LOF WS mode), it is necessary that the height difference between the averages levels of the core and the emergency cool-down heat exchanger be 23 … 25 m. This can be easily achieved when the reactor is buried under soil of the planet.

Ground-based fast reactors, cooled with sodium or NaK alloy, operate and operated at a pressure in the core close to the Earth’s atmospheric pressure (0.1 MPa). The average atmospheric pressure at the surface of Mars is about 636 Pa [18], i.e., almost 160 times less than at the surface of the Earth. The boiling point of the coolant decreases with decreasing operating pressure. For this reason, it is necessary to provide pressure in the core at the level of the earth’s atmosphere, i.e., 0.1 MPa. The result is a new type of reactor called the LMFR under pressure (PLMFR).

Reactors of the LMFR type with increased pressure in the core are being developed in Russia. An example is the lead-cooled BREST-OD-300 reactor under construction [23]. Under a thick and heavy layer of lead, the pressure in the core is about 1 MPa or 10 atm. This does not preclude the safety of the reactor.

4.2. Optimal Layout of the Martian Reactor

The calculations were performed using the Dragon-M code, which includes the FRISS-2D modules. The void reactivity effect was chosen as an optimality criterion. When the entire reactor is drained, it is negative. The WIMS code is used to calculate some of the coefficients of reactivity. The MCU code is used to refine the meaning of the void reactivity effect. (The diffusion approximation used in the Dragon-M code can lead to large errors in estimating this effect.)

It is assumed that the reactor core operates in a self-fueling mode. The breeding ratio in the core is slightly more than 1 (which is necessary to compensate for the production of “slag”).

Several layouts of the Martian reactor core were obtained. Two types of fuels based on cermets were considered. The first is a mixture of micro grains MN and nanopowder U, the second is a mixture of micro grains MOX and nanopowder U. The nanopowder fills the pores between micro grains of the ceramic. In both cases, the condition BRC ≈ 1 is satisfied. This limitation takes into account the minimum reactivity margin for fuel burnup.

The void reactivity effect was considered as an optimality criterion, realized when draining the reactor.

The core contains two radial zones surrounded by a reflector. The zones differ in the value of the fuel enrichment. The initial charge is formed from enriched uranium and does not contain plutonium. The fuel rods are located at the nodes of the triangular lattice. Perforated covers for fuel assemblies are used.

The reflector consists of two zones, assembled from assemblies containing steel tubes with long-lived radioactive waste (¹⁴C, ⁹⁹Tc). The assemblies are washed with a coolant. The first rows of assemblies (closest to the core) contain ⁹⁹Tc, while the far rows contain a mixture of ¹⁴C and ⁹⁹Tc powders. Carbon-14 slows down neutrons, which contributes to the creation of favorable conditions for the transmutation of ¹⁴C and ⁹⁹Tc. In addition, the presence of such nuclides in the reflector allows the thickness of the reflector to be reduced. The end reflectors are technetium-99 tablets. The height of the upper and lower reflectors is 20 cm each. The lower reflector may be absent.

Two optimal versions (A and B) of the MN-U-fuel core have been proposed.

Option A corresponds to the highest inlet temperature value. The total radius of the core and side shield is limited to 2.6 m. The thicknesses of the side and end reflectors are specified and did not change during the optimization process.

For both variants the diameter of the fuel pellet is 5 mm. The fuel rods are located at the nodes of the triangular lattice.

The grating spacing is 5.75 and 6.2 mm for two zones, respectively (Option A). The height of the fuel column is 1 m. The outer radius of the core is 2.15 m. The temperature at the entrance to the core is 198 ºС. Fuel enrichment with respect to ²³⁵U is 10.9 and 14.5% for the central and peripheral zones, respectively. The radius of the core is 129 cm. The radial dimensions of the two zones (with fuel of different enrichment) are 86.7 and 42.3 cm, respectively. When the reactor is operating at rated power, the maximum fuel temperature does not exceed 641 ºС, the coolant temperature does not exceed 516 ºС, and the fuel element cladding does not exceed 524 ºС. The presence of long-lived radioactive cesium-135 in the coolant (decaying into stable barium-135) and short-lived cesium-137 (decaying into metastable barium-135 and with the subsequent emission of γ-quanta) require taking into account the possibility of contamination of the coolant with barium. The melting point of barium is 727 ºС. There is no data on the formation of intermetallic compounds in the Ba-Na, Ba-K, Ba-Cs systems.

Thus, the presence of barium in the coolant can cause increased erosion of structural materials (in particular, fuel-element cladding). This is a payment for the use of “free” radioactive cesium-137 as part of the coolant. For this reason, the speed of the coolant in the core should be limited. In the considered options A and B, the average speed of the coolant does not exceed 3.2 and 3.5 m / s, respectively. (In sodium reactors, the average speed does not exceed 5 m / s.)

There are three ways to solve the problem:

• limiting the speed of the coolant in comparison with a sodium reactor;
• refusal to use cesium-137 as part of the coolant;
• use of cladding of fuel elements with tungsten sputtering (the technology is based on low-temperature plasma spraying of tungsten powder).

Options A and B are taught using the first path. In the options under consideration, the average speed of the coolant does not exceed 3.2 and 3.5 m / s, respectively. (In sodium reactors, the average speed does not exceed 5 m / s.)

Option B was obtained with the same lattice of fuel elements in two radial zones. This is a less compact core. The fuel element lattice spacing is 6.3 mm. Fuel enrichment in 235U in zones is 9.9 and 13.5%. The radius of the core is 144.5 cm. The radial dimensions of the two zones (with fuel of different enrichment) are 111.0 and 33.5 cm, respectively. The height of the fuel column is 0.92 m. The temperature at the inlet to the core is 198 ºС. When the reactor is operating at rated power, the maximum fuel temperature does not exceed 684 ºС, the coolant temperature does not exceed 502 ºС, and the fuel cladding does not exceed 527 ºС.

4.3. On the role of Doppler void and density coefficients and reactivity effects in ATWS

Doppler broadening of resonances in the energy dependence of the neutron-matter interaction cross sections plays an important role in ensuring the self-protection of reactors. This broadening is characterized by the Doppler effect and the coefficient of reactivity. If resonances are present in the energy dependence of the cross sections, then with increasing temperature they broaden (the width increases and the amplitude decreases). With a significant increase in temperature, narrow isolated resonances can overlap. If the kinetic energy of a neutron after collision (scattering) with a nucleus becomes comparable to the energy of some resonance, a nuclear reaction, in the energy dependence of which this resonance is present, is realized with a high probability (a neutron is captured by a nucleus, a compound nucleus is formed, decaying along some channel). If the kinetic energy of the neutron corresponds to the energy between resonances, where the cross section is close to zero, the neutron continues to slow down until its energy coincides with the energy of another resonance (up to the width of the level) and the neutron enters into a nuclear reaction.

If a neutron is captured by the uranium-238 nucleus, then one neutron decreases in the reactor. If a neutron is captured by a uranium-235 nucleus, then the fission of this nucleus with the production of new ν_f (as a rule, ν_f > 1) neutrons is possible, and the number of neutrons in the system increases. (In the resonance region, ²³⁸U nuclei practically do not fission.) Thus, broadening of resonances in the energy dependence of the cross sections for ²³⁸U leads to a decrease in the number of neutrons in the system, i.e., to a decrease in the effective neutron multiplication factor and reactivity. Broadening of resonances in the energy dependence of the fission cross section for fissile fuel nuclei (²³⁵U, ²³⁹Pu, etc.) promotes an increase in the number of fissions and, consequently, the number of neutrons, and hence, an increase in the effective neutron multiplication factor and reactivity. The first case corresponds to a negative Doppler reactivity effect, the second to a positive one. Thus, the sign and significance of the Doppler reactivity effect are mainly determined by the nuclei on which the broadening of resonances predominates.

If the reactor uses fuel with a relatively low enrichment in the fissile nuclide, then with an increase in the fuel temperature, the effect of broadening of resonances on the raw material nuclides (²³⁸U, etc.) dominates. This effect is negative. It has a beneficial effect on the safety of the reactor. In reactors with high enrichment (some research, transport), the dominant effect is associated with the broadening of resonances on the dependence of the fission cross section for fissile nuclides, which leads to an increase in the number of neutrons and a positive Doppler reactivity effect. For this reason, it is proposed to use fuel with a relatively low enrichment for LMFR (about 16%) in our space reactor.

It should be noted that in LMFRs, the negative Doppler reactivity effect can compensate for the positive void reactivity effect, since when the core is drained, the heat removal from the fuel elements deteriorates and the fuel temperature increases. Depending on the design of the LMFR and the type of emergency, the role of the Doppler coefficient of reactivity is different. The generally desirable negative Doppler coefficient of reactivity can in some cases exacerbate an accident. This remark applies primarily to LMFRs with medium to high power oxide fuels. This is well known. In such reactors, an increase in the absolute value of the negative Doppler coefficient leads to a favorable termination of emergencies caused by an unauthorized increase in the reactor power (for example, due to the introduction of limited positive reactivity or overcooling of the coolant), and the aggravation of emergency processes initiated by a decrease in the coolant flow rate (for example, as a result of blackout main circulation pumps).

It is known that the negative Doppler coefficient of reactivity helps to minimize the deviation of power and maximum fuel temperature from the nominal values. Fig. 4 illustrates the role of the Doppler coefficient of reactivity with decreasing and increasing maximum power W and maximum fuel temperature T_f. (These parameters are considered among the functionals of the optimization problem.) The dashed line corresponds to the values of these functionals in the nominal operating mode of the reactor. The arrows indicate the trend in the change in the functionals (ΔW or ΔT_f) with an increase in modulus of the negative Doppler coefficient of reactivity. It can be seen that the negative Doppler coefficient of reactivity, which is large in absolute value, plays a favorable role. For this reason, a negative Doppler factor contributes to the safe termination of the TOP WS emergency mode (initiated by injection of limited positive reactivity). Moreover, the higher this coefficient in absolute value, the smaller the deviation of the temperature and power of the reactor in emergency mode.

The nature of the change in the maximum fuel temperature over time during the LOF WS process depends on the type of fuel used (the relative amount of light and heavy atoms). As a consequence, the nature of the change in the maximum fuel temperature depends on the temperature difference between the fuel and the coolant in the nominal mode (before the start of the emergency). If this difference is large (for example, when using oxide fuel), the following scenario is realized. As the flow rate decreases, the coolant temperature rises and the temperature difference between the fuel and the coolant decreases. Consequently, the heat flux from the fuel to the coolant decreases. Under the influence of negative feedback on reactivity due to the thermal expansion of the core, the thermal power of the reactor decreases. The power decreases with time faster than the heat flux from the fuel to the coolant, i.e. more heat is removed from the fuel than is generated in it. As a result, the maximum fuel temperature decreases over time, which leads to a positive contribution to reactivity from the Doppler reactivity effect. To neutralize the latter, a higher temperature of the coolant and structural materials of the core is required. A negative Doppler coefficient of reactivity always prevents the power from deviating from the nominal value (in this case, it prevents it from decreasing) and leads to a stronger heating of the coolant. Thus, in order to increase the self-protection of a fast reactor with oxide fuel from accidents of the LOF WS type, it is necessary to decrease the negative Doppler coefficient of reactivity in absolute value. This fact was known at the dawn of the development of LMFR technologies and was described by many authors. However, the ATWS modes were not considered.

Figure 4: Influence of the Doppler coefficient of reactivity with decreasing (a) and increasing (b) functional W or Tf

In reactors with nitride or carbide fuel, one of these scenarios can be realized or an intermediate case, when the fuel temperature increases, reaches a maximum, and then decreases to a value below the nominal value. Different scenarios of changing the maximum fuel temperature can be realized in different grading zones.When using metallic fuel, the temperature difference between the fuel and the coolant in the nominal mode is small and the temperatures of the fuel and the coolant in the LOF WS process increase. In this case, negative Doppler reactivity coefficient and the effect of thermal expansion of the core prevent an increase in temperatures, and in order to increase self-protection from accidents, it is necessary to increase the negative Doppler coefficient in absolute value, i.e., the Doppler reactivity effect plays a favorable role. This is also known.

When using the fuel considered in this work (UN-PuN-U or UN-U) with a relatively high density and thermal conductivity, the role of the Doppler reactivity coefficient in the emergency modes LOF WS and TOP WS is the same. An increase in the absolute value of the negative Doppler coefficient of reactivity contributes to an increase in the self-protection of the reactor from such accidents.

The results of the analysis of the Doppler, void and density coefficients and reactivity effects are presented in [1]. In fig. 5 shows the dependence of the Doppler reactivity effect on the deviation of the fuel temperature from the nominal. Fig. 6 illustrates the dependence of the spectral component of the density effect on the density of the coolant. Zero density in Fig. 6 corresponds to the void reactivity effect.

Dependence 1 in Fig. 5 and 6 correspond to traditional mixed mononitride fuel (porosity 25%). Dependences 2, 3 and 4 correspond to fuel (5% porosity) based on a mixture of micro grains UN-PuN and metallic uranium nanopowder (dependence 2 corresponds to waste uranium in the composition of a nanopowder; 3 – enriched to 20% in ²³⁵U; 4 – enriched to 80% in ²³⁵U ). Obviously, the point of intersection of all straight lines corresponds to the reactor operating mode at rated power.

4.4. ATWS Analysis

The LOF WS emergency mode is initiated by de-energizing all main circulation pumps. For variant A, with a pump run-on time of 30 s, the maximum temperature of the heating medium reaches 694 ºС, which corresponds to a 27-degree boiling margin. For variant B it is 6 ºС higher than the boiling point. With an increase in the run-on time of the pumps to 40 s, the maximum temperature of the heat carrier is 709 ºС. In the steady-state mode of natural circulation, the maximum temperature of the heat carrier decreases by 68 and 58 ºС for options A and B, respectively. The maximum fuel temperature in the LOF WS transition mode (with a pump run-on time of 30 s) reaches 714 and 762 ºС for options A and B, respectively. The reactor power is reduced in LOF WS mode.

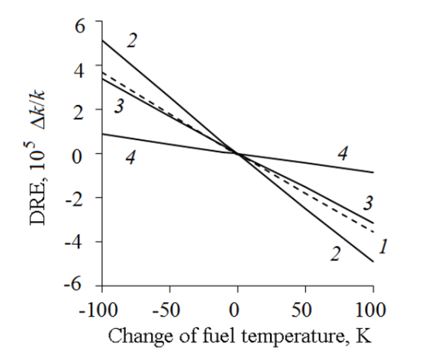Figure 5: Dependence of the Doppler reactivity effect (DRE) on the deviation of the fuel temperature from the nominal [1]

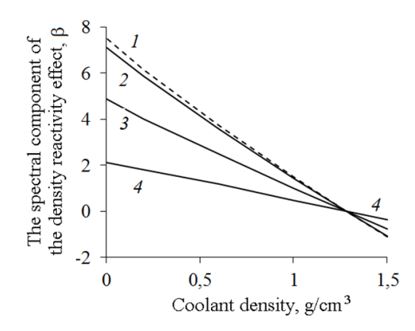Figure 6: Dependence of the spectral component of the density and void reactivity effects on the density of the coolant [1]

In OVC WS mode, the heating medium temperature decreases over time. A significant temperature margin is maintained until the coolant freezes. When the main circulation pumps are converted to increased performance (with an increase in flow rate by 20%), the maximum fuel temperature reaches 733 and 767 ºС for options A and B, respectively. The power increases by 58 and 24% (respectively) of the nominal. This is a hypothetical emergency that practically cannot be realized.  When a “cold” backup loop is connected (if it is provided), the maximum fuel temperature is 746 and 787 ºС for options A and B, respectively.The TOP WS emergency mode is initiated by the input of reactivity 0.9 β (where β is the effective fraction of delayed neutrons) for 10 s according to the linear law. This corresponds to the erroneous (unauthorized) removal from the core of both absorbing rods – reactivity compensators. The maximum fuel temperature increases in the transient mode to 777 and 789 ºС for options A and B, respectively. The maximum coolant temperature is 577 and 562 ºС for options A and B, respectively. The steady state power (under the action of reactivity feedbacks) is approximately 24% higher than the nominal power.

LOHS WS emergency mode is initiated by de-energization (or failure) of all secondary circulation pumps. Even if a coolant with a temperature equal to the outlet temperature is supplied to the entrance to the core, the emergency mode is not dangerous. Fuel temperature decreases over time. In the LOHS WS emergency mode, the maximum temperature of the coolant is 535 ºС. The maximum fuel temperature decreases over time.

When the LOF WS and OVC WS, LOHS WS and OVC WS modes are superimposed, their mutual neutralization is observed. The most dangerous is the overlap of the LOF WS, LOHS WS and TOP WS modes and the non-simultaneous overlap of LOF WS, TOP WS and OVC WS processes (with OVC lag). In this case, boiling of the coolant is possible.

Optimal configurations of the reactor with fuel based on oxide micro grains and uranium nanopowder have been obtained. The problem statement (optimality criterion, control parameters, constraints) is the same. The same scenarios for the development of emergency modes are postulated. It is a more heat-resistant fuel. Let us consider one of such layouts with the most compact core. Fuel enrichment in two zones is 12.5 and 19.8%, respectively. The diameter of the fuel pellet in both zones is the same and equal to 5.21 mm. The spacing of the fuel element lattice in the zones is 5.84 and 6.40 mm, respectively. The radial dimensions of the zones are 86.7 and 42.3 cm, respectively. The radius of the core is 129 cm. The height of the core is 1 m. The temperature of the coolant at the entrance to the core is 198 ºС. The maximum temperatures of fuel, coolants and fuel element cladding in the nominal mode do not exceed 938, 523 and 527 ºС, respectively. The void effect of reactivity is positive and dangerous. In the most dangerous combination of emergency modes, the coolant boils. The behavior of the reactor in ATWS is similar to that of using MN fuel without uranium nanopowder.

Thus, MN-U fuels are of the greatest safety interest.

4.5. Optimization of the Composition of the NaKCs Alloy

Multi component alloys of liquid metals have the greatest potential for regulating the properties of the LMFR coolant. If the problem of optimizing the ratio of the concentrations of the components of a binary alloy (for example, NaK used in space reactors) from the point of view of one or another quality criterion is quite trivial, then when switching to coolants based on three-component systems (for example, NaKCs), the solution of such a problem is laborious and can be associated with serious problems.

The complexity of solving such problems increases many times, if individual components of the alloy are capable of forming a eutectic, and if, at certain ratios of the concentrations of the constituent elements, a qualitative change in the chemical properties of the alloy is possible. First of all, these remarks refer to three-component alloys of alkali metals based on sodium, potassium and cesium, which, like individual components, including those forming binary eutectic alloys, can be considered as potential coolants for space reactors. Among the components of the NaKCs alloy, the eutectic is formed by the binary alloys NaK, NaCs, KCs [45, 55]. The melting point of the eutectic 21% (at.) Na – 79% Cs is equal to minus 31.70 ºС; the melting temperature of the eutectic 30% (at.) Na – 70% Cs is equal to minus 7.85 ºС [45]. The melting point of the eutectic 50% (at.) K – 50% Cs is equal to minus 37.90 ºС [45].

Optimization of the composition of the NaKCs alloy in terms of minimizing the cost of the coolant, increasing the internal self-protection against accidents LOHS WS, OVC WS and LOCA WS is of a conflict nature.

An increase in the concentration of cesium in the alloy is hindered by its high activability in the reactor core and its high cost. The problem is not relevant when using radioactive waste in the coolant of an alien reactor. An increase in the concentration of cesium in the NaKCs alloy leads to a decrease in the void reactivity effect (hence, to an increase in self-protection against a LOCA WS accident) and a deterioration in the self-protection against accidents of LOF WS and LOHS WS. Heavier elements (in comparison with sodium) slow down neutrons worse due to elastic scattering. The deceleration due to inelastic scattering is characterized by a high energy threshold. As a result, when the coolant is lost, the neutron spectrum in the reactor does not change significantly. As a result, the void reactivity effect is relatively small, and the danger of a LOCA WS emergency is less. The boiling points of the NaKCs alloy are lower than that of pure sodium, potassium (but higher than that of cesium).

The content of sodium and potassium in the alloy is higher than the content of cesium. As a result, the danger of accidents LOF WS and LOHS WS is higher. At the same time, the freezing point of the NaKCs eutectic is so low that this advantage can only be used in space. (For a Martian NPP buried in the ground, it is enough to ensure the coolant is non-freezing.) A slight change in the concentration of cesium in the NaKCs alloy will lead to an insignificant increase in the freezing point of the alloy (in comparison with the eutectic) from the point of view of ensuring self-protection from accidents with coolant cooling.

Thus, it makes sense to solve the problem of minimizing the concentration of cesium in the NaKCs alloy, provided that the main advantages of using such a coolant are retained: non-flammability and the elimination of freezing in the reactor. The first condition is determined by expression (1), the second – by the non-freezing of the alloy. The condition of non-flammability is more important when choosing a heat carrier. According to inequality (1), the alloy non-freezing is provided for a fairly wide range of cesium concentration in the alloy: from 19 to 69% (at.), Or from 46.6 to 89.2% (wt.). Non-freezing of the alloy is ensured at and near the eutectic point, i.e., with a slight deviation of the cesium concentration in the alloy from 73.8%, as well as with a small (ideally zero) cesium content in the NaKCs alloy. As noted earlier, in the absence of cesium, sodium and potassium can form eutectic alloys.

The optimization problem can be formulated as a continuous multi criteria problem with constraints for several functionals. These functionals include the maximum and minimum coolant temperatures, the maximum temperatures of the fuel and cladding of fuel elements, and the maximum power of the reactor in emergency modes of the ATWS type. The control parameters of the problem are the concentration of alloy components, the parameters of the reactor and core layout, the parameters of the lattice of the fuel elements, the flow rate of the coolant, the enrichment of the fuel, etc.

The solution to a multi criteria problem is a set of informal procedures. For example, the formation of a system of quality criteria (at the stage of setting the problem) and the choice of the most preferred solution (at the final stage of the solution) are not formalized and are subjective. To solve the problem, multiple correlation coefficients are introduced. This coefficient is equal to zero when the void reactivity effect and the cost of the coolant are selected as criteria. For the criteria related to the cost of the coolant and internal self-protection against accidents LOF WS and LOHS WS, the correlation coefficient is maximal and is equal to 1.

Let us analyze the preferred solutions, the number of which can be large. Let us choose nine solutions U₁, U₂, U₉, each of which is obtained under the condition that one or another quality criterion is preferable.

• The U₁ solution is obtained if the cost of the heat carrier is selected as the most preferable criterion: U₁ = {0% Cs, 0% K, 100% Na} (hereinafter, the mass content is indicated as a percentage);
• The U₂ solution meets the criteria of “cost of the coolant” and “internal self-protection against accidents OVC WS”: U₂ = {0% Cs, 78% K, 22% Na}, i.e. eutectic Na-K;
• The U₃ solution corresponds to the minimum void reactivity effect: U₃ = {100% Cs, 0% K, 0% Na};
• The U₄ solution corresponds to internal self-protection against accidents LOF WS and LOHS WS: U₄ = {0% Cs, 0% K, 100% Na};
• The U₅ solution corresponds to ensuring the non-flammability of the coolant: a set of optimal concentrations that satisfy condition (1), i.e., the optimality area, centered at the point 3.5% Na – 21.9% K – 74.6% Cs;
• The U₆ solution corresponds to the internal self-protection against accidents OVC WS: U₆ = {73.8% Cs, 22.0% K, 4.2% Na}, i.e. eutectic;
• The U₇ solution corresponds to internal self-protection against accidents OVC WS and non-flammability: U₇ = {73.8% Cs, 22.0% K, 4.2% Na}, i.e. eutectic;
• The U₈ solution corresponds to the non-flammability of the coolant and the minimum void reactivity effect: determined by condition (1) at the maximum cesium content – 89.2% Cs;
• The U₉ solution corresponds to the low cost of the coolant, the non-flammability of the coolant and the minimum void reactivity effect: determined by condition (1) with the minimum cesium content U₉ = {46.6% Cs, 46.3% K, 7.1% Na}, i.e. eutectic.

The next task is to determine the most preferable solution from options U₁, U₂, U₉.

Optimum corresponding to the low cost of the coolant; negative void reactivity effect; the best self-protection against accidents OVC WS, LOF WS, LOHS WS, LOCA WS (loss of coolant as a result of its combustion); and the minimum cost of the coolant can be determined unambiguously only when taking into account the weight coefficients reflecting the significance of all the listed criteria. (This is not a feature of the Martian reactors. This is a feature of the materials used in the core and the secondary circuit (mainly a non-flammable coolant with a relatively high boiling point and the lowest freezing point, with a small absorption and deceleration cross section for fast neurons) and the optimal layout of the core.) In other words, the determination of optimal control requires a preliminary ranking of the above criteria and emergency situations according to the degree of significance and danger. Obviously, this optimum belongs to the range of cesium concentration at which the NaKCs alloy does not ignite, i.e. 46.6 … 89.2% Cs. Internal self-protection against accidents such as ATWS and the negative void reactivity effect can be achieved by the optimal choice of the parameters of the layout, the fuel element array, and other design solutions. For this reason, the criterion of non-flammability, other things approximately equal, should be given preference when choosing a coolant for an alien reactor.

Using the well-known ideas and methods for solving discrete multi criteria problems, let us rank the options U₁, U₂, …, U₉ according to the degree of significance. The set of analyzed objects of the problem (U₁, U₂, …, U₉) is finite. Of these nine objects of the discrete optimization problem, a set of the most preferable solutions (objects) can be distinguished. This set includes options U₅, U₆, U₇, U₈ and U₉.

We will give preference to economic efficiency (in the problem under consideration, the goal is to minimize the cost of the coolant) and safety. In single power units (in the absence of massive construction of reactors on Mars), improving the economic characteristics is not so urgent. Giving preference to three criteria of the problem: non-flammability, the smallest void reactivity effect and the best self-protection against accidents LOF WS and LOHS WS, we can single out effective objects: U₅, U₆, U₇, U₈ and U₉. They are preferred. Thus, in the problem of finding the most preferred object, options U₁, U₂, U₃ and U₄ can be ignored.

Let F₁, F₂, and F₃ be dimensionless optimality criteria that determine non-flammability, the smallest PER and the best self-protection against accidents with a violation of heat removal (LOF WS and LOHS WS), respectively. Let’s define them. The area of effective objects is limited by three planes A, B and C (Fig. 7), corresponding to F_i  ³ L_i (where i = 1, 2, 3), where L_i is the minimum allowable value of the corresponding functional.

The lines of intersection of planes A and B; B and C; A and C, are parallel to the axes [0 F₁), [0 F₃) and [0 F₂), respectively. Point 0₂ meets the conditions: F₁ = L₁, F₂ = L₂ and F₃ = L₃. The goal of the problem is to maximize F_i under the condition F_i ³ L_i  (in the case under consideration, i = 1, 2, 3).

Let’s sort options U₅, U₆, U₇, U₈ and U₉ according to preference. Note that the solutions U₆ and U₇ are coincide (correspond to the eutectic). One of them (for example, U₆) can be excluded from consideration. Let’s write down the remaining objects in order of preference.

Figure 7: General view of the area of effective objects for choosing the preferred composition of the NaKCs alloy

• Object U₈ belongs to plane A (Fig. 7), i.e., for it F₃ = L₃. Object U₉ belongs to the F₃ axis, that is, to the planes B and C. For it, F₁ = L₁ and F₂ = L₂. Thus, object U₈ can be considered more preferable than U₉. Variants U₅ and U₇ lie inside the area of dominant objects at some distance from the border of this area. They satisfy the strict inequalities F_i > L_i (i = 1, 2, 3); moreover, U₅  dominates twice, i.e., according to two criteria: when maximizing F₁, and when maximizing F₂, and the U₇ variant dominates once: when the functional F₃ is maximized.From the point of view of maximizing the functional F₁: U₅ > U₆ > U₇ > U₈ > U₉ (here the symbol “>” means “more preferable”);
• From the point of view of maximizing the functional F₂: U₈ > U₅ > U₇ > U₉;
• From the point of view of maximizing the functional F₃: U₉ > U₇ > U₅ > U₈.

Thus, variant U₅ can be considered the most preferable object. If we consider all alloys based on sodium, potassium, and cesium with combinations of concentrations of components from region (1) “equally non-flammable”, then approaching the center of the non-flammable region inside (1) makes no sense, in other words, it makes no sense to maximize the functional F₁ inside the region (1). In this case, it is enough to satisfy the condition F_i ³ L_i and the most preferable solution should be considered U₇ (U₇ is equivalent to the object U₆), corresponding to the eutectic. Strictly speaking, the choice of the best solution from U₅ and U₇ should be carried out taking into account the coefficients of significance of the criteria F₁, F₂ and F₃.

Solution U₉ belongs to the line of intersection of planes B and C, that is, it is determined by the condition F₃ = L₃. A further increase in the economic efficiency of the reactor is possible with a comprehensive optimization of its parameters, which presupposes the search for the optimal control u, the components of which are not only the concentrations of sodium, potassium and cesium in the alloy, but also the parameters of the layout, the lattice of the fuel elements, the flow rate of the coolant, the enrichment of the fuel, etc.

So, the optimal composition of the NaKCs alloy can be obtained by solving the problem of multi criteria optimization. Moreover, the most preferable solutions may be different, and for alloys forming a eutectic, the optimum does not always coincide with the point of the eutectic.

5. Discussion

5.1. Further Prospects in Fuel Use

A two-circuit scheme of energy conversion with water in the second circuit was considered. Due to the relatively low chemical activity of the primary coolant (eutectic alloy NaKCs) during depressurization of the heat exchanger tubes, the interaction of NaKCs with water is not explosive. Water is the simplest and cheapest heat carrier. The technology of using water for cooling is well established. This applies to land-based reactors. The construction of a NPP on Mars will require large volumes of water. Water will have to be transported from Earth. This will increase the cost of the Martian NPP.

Among the possible innovations, it is possible to propose an increase in the proportion of long-lived radioactive waste (isotopes of neptunium and americium with an even number of neutrons) in the fuel composition by reducing the proportion of waste uranium. The fission cross section for ²³⁷Np, ²⁴¹Am and ²⁴³Am in the neutron energy range of more than 1.4 MeV is 2 – 3 times higher than that of ²³⁸U [51].

Figure 8: Dependence of the fission cross section on the kinetic energy of a neutron for 238U (curve 1) and some minor actinides: 237Np (2), 241Am (3), 243Am (4), 244Cm (5)

In fig. 8, according to [51], the dependences of the microscopic fission cross section σ_f on the kinetic energy E of the neutron for uranium-238 and some minor actinides are given.

When water is used in the second loop, the ingress of a small portion of the moderator into the core will lead to a decrease in reactivity and shutdown of the reactor. (Initiating event: emergency situation with depressurization of the tubes of the heat exchanger “liquid metal – water”.)

5.2. NPP with a Closed Gas Turbine Energy Conversion Cycle

What can be considered as an alternative to water (in the second circuit)? The atmosphere of Mars is 95.32% carbon dioxide [22]. Carbon dioxide was used as a coolant for the British nuclear reactors “Magnox”, AGR and the French reactor UNGG [56]. It is possible to offer a NPP with a closed gas turbine energy conversion cycle. In this case, carbon dioxide or unpurified air of Mars can serve as a coolant. A closed gas turbine cycle is proposed to be used in high-temperature gas-cooled reactors [57].

It is often proposed to use helium as a working medium for reactors of NPPs with a gas turbine energy conversion cycle. As is known, helium is the second most abundant in the Universe (after hydrogen) and makes up about 23% of the mass of the Universe. Natural helium consists of two stable isotopes with mass numbers 3 and 4. The fraction of ⁴He in the natural mixture of isotopes is 99.99986%) and can vary considerably within wide limits [58].

Helium (consisting mainly of the doubly magical isotope ⁴He) is not activated in the reactor core. Its practical use is hindered by its high cost and high fluidity [59]. For this reason, instead of helium, it is advisable to use expensive helium – xenon mixture [59]. Heat exchange equipment using a He-Xe mixture is the most compact [59].

In three-circuit NPPs with sodium reactors, the void reactivity effect can be realized in the following cases.

• Boiling of the coolant;
• Combustion of the coolant;
• Coolant leak (loss of coolant);
• Entrainment of gas from the argon bed into the core;
• Depressurization of fuel element cladding and release of gaseous fission products into the coolant.

In two-circuit NPPs with a gas turbine energy conversion cycle, another additional scenario for the implementation of the void reactivity effect appears: gas entrainment into the core when the gas heater tubes (liquid metal – gas heat exchanger) are depressurized.

Potential coolants of fast gas-cooled reactors (superheated water vapor, helium, carbon dioxide, dissociating gas, for example, N₂O₄ ↔ 2 NO₂, helium – xenon mixtures, etc), as well as working fluids of gas turbine plants, can be considered as the working fluid (coolant of the secondary circuit).

One problem with medium to high power LMFRs is the positive void reactivity effect. The most dangerous is the draining of the central part of the core (for example, when the working fluid is involved in the event of depressurization of the heat exchanger tubes). For the considered reactor, the void reactivity effect in the most dangerous scenario of its implementation reaches 6.1 β (slightly less than when using a sodium coolant).

When the steam generator pipes are depressurized, steam bubbles (the working fluid of the second circuit) emerging from them can be entrained by the coolant flow into the core. From the point of view of possible depressurization of the steam generator pipes, the most dangerous mode is LOF WS (or its overlap with TOP WS and LOHS WS), accompanied by the greatest increase in the temperature of the primary coolant.

When the main circulation pumps of the primary circuit are de-energized, the mode of natural circulation of the coolant is established. The higher the flow rates of the coolant in this mode, the greater the likelihood of the entrainment of bubbles in the core. Thus, the normally desired high level of natural circulation can worsen a steam generator pipe leakage accident.

The mechanism of the effect of bubbles (in the core) on reactivity is as follows. If water is used in the second loop, then, entering the core, water vapor (hydrogen) effectively slows down neutrons. Hydrogen also absorbs neutrons, but this effect is relatively small at LMFR energies. Deceleration of neutrons leads to a decrease in the average neutron energy in the core. In this case, the microscopic fission cross sections for all fissile nuclides (²³⁵U, ²³⁹Pu, etc.) increase significantly. As a result, the effective neutron multiplication factor and reactivity increase. This could lead to an accident.

If, as a working fluid (in the second circuit), a substance is used that strongly absorbs fast neutrons and weakly slows them down, then the result is exactly the opposite. Additional absorption of neutrons in the core leads to the shutdown of the reactor: the void effect is negative.

Let us assume that a substance that weakly interacts with neutrons is used as a working fluid. In this case, the void effect of reactivity is realized in “pure form”. Any coolant one way or another absorbs and slows down neutrons. The NaKCs alloy is no exception. When entering the core in the form of bubbles, the efficiency of absorption and slowing down of neutrons deteriorates. As a result of the worst absorption in the core, additional neutrons appear. This leads to increased reactivity and the possibility of an accident. As a result of the worst moderation of neutrons in the core, the neutron energy increases. This leads to intensification of the fission of raw material nuclides (²³⁸U) by neutrons with energies above 1.4 MeV (the fission threshold for most raw material nuclides). As a result, the reactivity and the risk of an accident increase.

Thus, it is necessary either to exclude the ingress of bubbles into the core, or to carefully select the materials of the reactor. It is preferable to use substances that efficiently absorb fast neutrons as a working fluid (secondary circuit). In this case, the void reactivity effect is negative.

Suppose, as a result of depressurization of the heat exchanger tubes, the material of the second circuit (working fluid) is drawn into the central part of the core (the most dangerous scenario). In fig. 9 shows the dependences of the neutron infinite multiplication factor k on the volumetric content ε of the working fluid of the second circuit in the coolant of the core. (Calculations were performed using the WIMS code [53]). As a working fluid, the following were considered: water vapor (fig. 9, curve 1), ⁴He (2), ³He (3), CO₂ (4), N₂ (5), N₂O₄ (6), air of the earth’s atmosphere (7) and Xe. Curve 8 corresponds to vacuum and is close to xenon. The dependence of k on the volume fraction f of gas when steam, He or CO₂ enters the core is non-monotonic, and it is possible to increase and decrease k, therefore, the scenario of the development of an emergency is less predictable.

Figure 9: Dependence of k on the volume fraction f of gas in the primary coolant during depressurization of the heat exchanger tubes and the entrainment of gas bubbles into the core

The ingress of carbon dioxide (Martian atmospheric air) into the central part of the core and the replacement of the liquid metal coolant with gas by 7 … 8% by volume, leads to a sharp decrease in the criticality of the reactor (k decreases by 2.4 times), i.e., to the shutdown of the reactor.As follows from the data in Fig. 9, with a small fraction ε of water vapor in the coolant, deceleration beyond the fission threshold of ²³⁸U, ²³⁷Np, ²⁴¹Am and ²⁴³Am prevails (k decreases). With an increase in the vapor fraction, a slowdown towards resonances is observed in the fission cross sections of ²³⁵U, ²³⁹Pu and ²⁴¹Pu (k increases). The key role in these processes is played by elastic deceleration on hydrogen nuclei in the composition of water. With a further increase in ε, an intense absorption of neutrons slowed down to resonances in the radiation capture cross section (on these nuclei and on hydrogen) is observed. When ³He (exotic), CO₂, N₂, N₂O₄ and air are used as a working medium, the deterioration of the conditions for heat removal from fuel elements can be compensated for by negative reactivity from the ingress of gas into the core.

The disadvantage of a NPP with a gas turbine energy conversion cycle is its large size. However, if a reactor of relatively small (according to earthly estimates) electrical power (500 … 600 MW) is built on the surface of another planet, this is not a serious problem.

5.3. Plans

The Russian design bureau “Arsenal” plans to implement the “Nucleon” project to build a NPP on Mars. It is assumed that the NPP will be fully built in terrestrial conditions, and not on Mars. The nuclear tug “Zeus” will deliver it to Mars [17]. The NPPs will start operating immediately after landing on Mars. Certain problems can arise here. The atmosphere of Mars is so rarefied that NPPs will be attacked by meteorites. Without special protection (containment), this can lead to damage or complete destruction of the NPP and reactor. (NASA’s MRO robotic interplanetary station, which orbited 60,000 times around Mars from 2006 to 2019, “received images of an unusual trail of recent meteorite impacts on the surface of Mars, similar to the traces of shots from a giant space shotgun” [60].)

It is advisable to use the Martian NPP “Nucleon” with an electrical capacity of about 1 MW at the initial stage of Mars exploration. It can be used, for example, to generate energy for the construction of NPPs of greater capacity, buried under the ground. Larger NPPs can be assembled from blocks built on Earth and delivered to Mars by a nuclear tug. If the concept of a NPP with a gas turbine energy conversion cycle is chosen as the basis, then carbon dioxide for the second circuit can be pumped from the Martian atmosphere.

There are at least three reasons for burying the Martian NPP under the ground.

• Burying the NPP under the ground is necessary to protect against meteorites and dust storms;
• It is necessary to ensure the required height of the natural circulation circuit (to ensure the natural circulation of the primary coolant in emergency LOF WS modes);
• It is also necessary to maintain a stable ambient temperature during NPP operation.

An erosion hazard for NPPs can be posed by Martian dust storms and tornadoes (particles consisting of iron oxide) [6]. Their speed reaches 100 m / s, duration from 50 to 100 days [6].

When building a NPP on Mars, the following factors should be taken into account.

• The soil of Mars is a rocky rock (basalt) with an admixture of iron oxide (that is, it does not differ much from the earth’s soil), covered with a layer of dust (consisting mainly of iron oxide);
• Mars is characterized by large daily and seasonal temperature drops;
• Mars is characterized by dust storms, meteorite attacks;
• In some regions of Mars (covering about 25% of the planet’s surface) volcanic and tectonic activity is pronounced [61].

It is possible to single out specific tasks that are not typical for ground-based NPPs. One of them is the production of oxygen from the atmosphere of Mars (from carbon dioxide) [62, 63]. Oxygen is needed to support the life of researchers working on Mars and as an oxidizer for traditional rocket (non-nuclear) fuel, if used. Another challenge is to provide energy to greenhouses for growing food crops. At the University of Dartmouth, by order of NASA, a project for a Martian greenhouse was developed [64]. The greenhouse will provide plant food for four astronauts daily for 600 days on Mars. [64] Another challenge is to provide energy for vehicles and machines for laying mines and tunnels.

Economic assessments of the construction of the considered rector (electric power of 600 MW) on Mars have not yet been carried out. It is obvious that the proposed concept of the core (and the reactor as a whole) in terms of construction costs significantly exceeds a NPP with a low-power reactor (~ 10 … 1000 kW). The diameter of the BN-600 reactor vessel is 12.8 m, the height is 12.6 m. (For comparison, the Hubble telescope is 13.3 m long and 4.3 m in diameter.) It is not yet possible to transport such a “product” to Mars. But at first glance, unsolvable problems have always stimulated and intensified scientific research in related fields. The coolant should be transported separately by elements in solid form (in the form of small briquettes). It is proposed to use long-lived cesium isotopes. This requires the use of special containers for the transport of cesium or full automation of loading and unloading a space tug. By the time a NPP of such a large capacity is in demand, a certain infrastructure and sources of electricity will already exist on Mars (for example, a low-power NPP). Robots will play an important role. The process of building a Martian NPP, filling it with coolant and other procedures can be fully robotized. It is advisable to make the reactor without a vessel. Instead of a body, a concrete shaft lined with a thin layer of steel (5 … 6 mm) can be used. The technology of creating such a mine (for the BREST-OD-300 reactor) exists in terrestrial conditions [23]. The lining of a concrete shaft can be made with steel or with a composite material. There is a technology for obtaining such a material. It is lightweight, durable, heat-resistant, radiation-resistant material. The material is reinforced with nanofibers of another polymer composite material with a high capture cross section for neutron and γ-radiation [65].

Concrete is required for the construction of the mine. It can be produced from Martian soil. There are many types of cement. As in terrestrial conditions, the technological process for the production of Martian cement consists of three main stages: extraction and processing of raw materials (CaO, Si₂O₃, Al₂O₃, Fe₂O₃); roasting of crushed and mixed raw materials to obtain clinker; and grinding of clinker, gypsum and additives. Gypsum can exist as minerals on Mars. Gypsum or its analog can be made artificially from Martian rock. Cement can be produced from Martian soil. It is not necessary to use earthy materials as additives. Mars has significant and accessible deposits of water ice [66]. In 2008, the Phoenix space probe (NASA) obtained water from soil samples collected from the surface of Mars [66].

6. Conclusion

The proposed innovations associated with the use of new nuclear fuel based on UN-PuN micro grains and non-powder of metallic uranium and a coolant based on the NaKCs alloy will make it possible to create an alien NPP within the framework of existing technologies. Computational and optimization studies demonstrate the possibility of creating a safe space reactor with an electric power of up to 600 MW. A reactor of such a relatively large capacity may be in demand only in the distant future. It is important to note that if it is possible to ensure the internal safety of a 600 MW reactor, then there will be no problems in ensuring the safety of a smaller reactor.

The following physical foundations of the concept of a Martian NPP can be noted:

• Fast reactor with electric power up to 600 MW (at the initial stage it is possible to restrict oneself to a much lower power, for example, 50 … 100 MW);
• Low-maintenance or maintenance-free (fully autonomous) NPP, operating without fuel replacement for 10 … 20 years;
• Coolant based on eutectic (or near eutectic) NaKCs alloy;
• Double-circuit power conversion scheme;
• As an option, a NPP with a gas turbine cycle (CO₂) energy conversion;
• Burying the NPP under the ground;
• Land-based factory fabrication of NPP modules and their transportation to Mars;
• Use of well-mastered technologies (it makes sense for the construction of a ground-based prototype of the Martian NPP).

LMFR type reactors are characterized by high safety potential. They are compact. The neutron spectrum (the absence of a neutron moderator and the fuel used) allows such a reactor to operate in the mode of self-supply of the core with fuel (the breeding ratio in the core is about 1), i.e., for a long time. Essentially, the Martian NPP will use a new type of nuclear reactor: a pressurized fast reactor (PLMFR).

The proposed new cermets fuel will allow not only to ensure accident-free completion of ATWS modes, but also to increase the content of fissile materials in the fuel elements of the core (hence, to increase the reactor power).

The power of the NPP will be determined by the range of tasks to be solved, including those unconventional for the terrestrial energy sector. For example, with the help of electricity generated by a NPP, the problem of producing oxygen from carbon dioxide will be solved. As Mars exploration progresses, the relevance of charging batteries for an increasing number of electric vehicles capable of moving across the surface of Mars will increase. There will be a need to provide power to electric machines for walking tunnels.

One should not be afraid of plutonium theft (material of direct use in weapons of mass destruction) from “fresh” fuel before the launch of the reactor. States whose representatives will visit Mars on their spacecraft (especially with a nuclear rocket engine) already possess nuclear weapons. In addition, the fuel cycle is protected from proliferation.

The coolant based on the NaKCs alloy is characterized by a much lower chemical activity compared to pure alkali metals. This allows us to consider a two-circuit energy conversion scheme (even with water in the second circuit). For Mars, a NPP with a gas turbine cycle (based on the use of carbon dioxide in the second loop) energy conversion with a low reactor power is more preferable.

The double-circuit scheme helps to simplify and reduce the cost of the NPP design. With such an energy conversion scheme, an additional scenario for the implementation of the void reactivity effect is possible. It is associated with the possible involvement of the working fluid in the reactor core. When carbon dioxide is used in the second circulation loop, the involvement of the working fluid into the core helps to reduce the reactivity and shutdown the reactor.

It is known that it is much easier to ensure the safety of a low-power reactor than a high-power reactor. The electric capacity of the 600 MW power units is unlikely to be in demand for the exploration of Mars in the near future. However, if it is possible to ensure the safety of such a reactor, then the safety of a reactor with a power of 10 times less does not pose a problem. The results are focused on the distant future.

Deepening under the ground, ground-based factory production of all modules and equipment, the use of well-mastered technologies are the general tasks of creating infrastructure facilities for the future Martian station.

It is obvious that the maximum use of the natural resources of the developed planet can significantly reduce research costs.

Obviously, for the implementation of the construction of a relatively large Martian NPP, international cooperation will be required. Before the construction of such a NPP on Mars, it is advisable to build a terrestrial prototype for testing technologies. Of course, the construction of a NPP on Mars with a reactor of electrical power of 600 MW may remain science fiction. But work on such an idea stimulates the development of new technologies that may be in demand in the future when exploring other planets.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The author is grateful to the head of the Department of Physics at the Bauman Moscow State Technical University, Corresponding Member of the Russian Academy of Sciences A.N. Morozov for comprehensive support.

1. V.S. Okunev, “Analysis of Reactivity Effects and Coefficients of a Space Nuclear Reactor Cooled by a Sodium-Potassium-Cesium Alloy”, AIP Conference Proceedings, 2318, 040007, 2021, https://doi.org/10.1063/5.0036182
2. A.S. Koroteev, “Analysis of Advanced Space Problems and the Place of Nuclear Power Propulsion Plants in their solution “, in 2005 International Conference Nuclear Power Engineering in Space-2005 (NPS-2005), Moscow, Podolsk, 2005, Plenary report 01.
3. A.S. Koroteev, “Actual problems of modern rocket and space technology”, Izvestiya RAN: Energetika, 5, 9-18, 2004.
4. Yu.G. Dragunov, B.A. Gabaraev, E.L. Romadova, “Space nuclear power: past, present, future”, in 2018 5th Int. Scientific and Technical Conf. Innovative Design and Technologies of Nuclear Power (ISTC NIKIET-2018), Moscow, 689-705.
5. V.N. Gushchin, “Fundamentals of Spacecraft Construction”, Moscow: Mashinostroenie, 2003.
6. M.T. Lemmon et. al., “Atmospheric Imaging Results from the Mars Exploration Rovers: Spirit and Opportunity”, Science, 2004, 306(5702), 1753-1756, DOI: 10.1126/science.1104474.
7. “The cost of the commercial launch of Soyuz with the Fregat block has become known”, RIA Novosti: Science (Moscow), 02 October 2018, https://ria.ru/20181002/1529826936.html
8. S. Kalashnikov, “The cost of a flight to Mars”, Ferra.ru (Moscow), May 10, 2017, https://www.ferra.ru/news/techlife/mars-cost-10-05-2017.htm
9. “Akkuyu NPP (Turkey)”, RIA Novosti (Moscow), December 10, 2017, https://ria.ru/20171210/1510584872.html
10. “The cost of building a fast breeder reactor BN-800 is estimated at 145.6 billion rubles (Russian)”, Moscow: TASS, January 19, 2018, https://tass.ru/ural-news/2597666
11. “The cost of building a fast reactor BREST is estimated at 100 billion rubles”, Moscow: TASS, June 8, 2021, https://tass.ru/ekonomika/11594071
12. R.F. Wilson, “SNAP 10A – A Status Report. / Book: Space Power Systems Engineering”, Progress in Astronautics and Rocketry, 1966, 16, 581-593, https://doi.org/10.1016/B978-1-4832-3056-6.50029-3
13. N. Yachmennikova. “Roskosmos will continue to create a space tug with a nuclear engine”, Rossiyskaya Gazeta RGRU, 04/29/2020, https://rg.ru/2020/04/29/roskosmos-prodolzhit-sozdanie-kosmicheskogo-buksira-s-iadernym-dvigatelem.html
14. “Nuclear Reactor for Mars Outpost Could Be Ready to Fly by 2022”, SPACE.com, 12 August 2019,
    https://www.youtube.com/watch?v=vQLStYhIR7Q
15. Yu.G. Dragunov, E.L. Romadova, L.A. Sleptsov, V.V. Kudinov, “Space Reactor Installation of a New Generation”,in 2012 Int. Scientific and Technical Conf. Innovative Design and Technologies of Nuclear Power (ISTC NIKIET-2012), Moscow.
16. NASA and US Department of Energy Selected Three Reactor Concepts for Thermal Nuclear Engines”, Atominfo.Ru, 15 July 2021, http://www.atominfo.ru/newsz03/a0869.htm
17. A. Demidov, “Roscosmos proposed to build a nuclear power plant on Mars”, Gazeta.ru (Moscow), July 10, 2021, https://www.gazeta.ru/science/news/2021/07/10/n_16224692.shtml
18. R.D. Williams, “Mars Fact Sheet”, National Space Science Data Center, NASA, Sept. 1, 2004, https://nssdc.gsfc.nasa.gov/planetary/factsheet/marsfact.html.
19. “Extreme Planet Takes Its Toll. Mars Exploration Rover Mission: Spotlight”, NASA, California Institute of Technology, Jet Propulsion Lab., June 12, 2007, https://mars.nasa.gov/mer/spotlight/20070612.html.
20. “Making a Splash on Mars”, NASA Science, June 29, 2000, https://science.nasa.gov/science-news/science-at-nasa/2000/ast29jun_1m/
21. S.A. Stern, “The Lunar atmosphere: history, status, current problems, and context”, Rev. Geophys, 1999, 37 (4), 453-491,
    DOI:10.1029/1999RG900005.
22. “Mars Pathfinder – Science Results”, Atmospheric and Meteorological Properties, https://mars.nasa.gov/MPF/science/atmospheric.html (дата обращения 7 ноября 2021)
23. V.V. Lemekhov, A.V. Moiseev, M.K. Sarkulov, V.S. Smirnov, O.A. Yarmolenko, Yu.V. Lemekhov, Yu.S. Cherepnin, V.P. Vasyukhno, D.A. Afremov, “Present-Day Status and Development Prospects of Fast-Neutron Lead-Cooled Reactors”, in. 2018 5th Int. Scientific and Technical Conf. Innovative Design and Technologies of Nuclear Power (ISTC NIKIET-2018), Moscow, 35-37.
24. V.S. Okunev, “Fundamentals of Applied Nuclear Physics and an Introduction to the Physics of Nuclear Reactors”, Moscow: Publishing house of Bauman Moscow State Technical University, 2015.
25. DOE Fundamental Handbook: “Nuclear physics and Reactor Theory”, DOE-HDBK-1019/1-93, U.S. Department of Energy, Washington, D.C. 20585, FSC-6910, 1, 32, 1993.
26. O.J. Wick (Ed), “Plutonium Handbook, A Guide to the Technology”, American Nuclear Society, 1980, 2.
27. N.M. Vlasov, I.I. Fedik, “Fuel elements of nuclear rocket engines”, Moscow: TsNIIatominform, 2001.
28. L.H. Caveny (ed.), “Orbit-Raising and Maneuvering Propulsion: Research Status and Needs”, Progress in Astronautics and Aeronautics. 89, New York: American Institute of Aeronautics and Astronautics, 1984, https://doi.org/10.2514/4.865633
29. I.I. Fedik, N.M. Vlasov, “New Materials in Space Nuclear Power Engineering”, Perspective Materials, 2001, 6, 24-30.
30. L.E. Von Toth, “Transition Metal Carbides and Nitrides”, New York – London: Academic Press, 1971.
31. M.L. Taubin, “Some Radiation Effects in the Interstitial Phases of ZrC, NbC, ZrN”, Atomic Energy 1990, 69 (3), 176-177.
32. A.E. Waltar, A.B. Reynolds, “Fast Breeder Reactors”, New York, Oxford, Toronto, Sydney, Paris, Frankfurt: PERGAMON PRESS, 1981.
33. IAEA-TECDOC-1083, “Status of liquid metal cooled fast reactor technology”, Vienna: IAEA, 1999.
34. N.N. Ponomarev-Stepnoy, V.S. Rachuk, V.P. Smetannikov, I.I. Fedik, “Space nuclear power and propulsion systems based on a reactor with external heat conversion of a solid-phase core”, in 2005 International Conference Nuclear Power Engineering in Space-2005 (NPS-2005), Moscow, Podolsk, 2005, Plenary report 07.
35. A.G. Lanin and I.I. Fedik, “Selecting and using materials for a nuclear rocket engine reactor”, Phys.-Usp, 2011, 54 305,
    DOI: https://doi.org/10.3367/UFNr.0181.201103f.0319
36. S.N.Sikorin, A.V.Kuzmin, S.G. Mandzik, S.A. Polozov, T.K. Grigorovich, Sh.T. Tukhvatulin, I.E. Galev, A.N. Bakhin, A.L. Izhutov, V.E. Alekseev, D. Kaiser, I. Bolshinsky, “Low Enriched Nuclear Fuel on the Basis Uranium Zirconium Carbonitride: Preparation to Reactor Test and Research on the Critical Assemblies”, in 2018 5th Int. Scientific and Technical Conf. Innovative Design and Technologies of Nuclear Power (ISTC NIKIET-2018), Moscow, 522-532.
37. A.N. Bakhin, I.E. Galev, D.S. Kiselev, D.M. Soldatkin, A.A. Urusov, D.A. Chesnokov, A.F. Ginevsky, Ya.S. Volgin, V.S. Volgin, “Study of Thermomechanical Strength of Uranium-Zirconium Carbonitride Fuel”, in 2018 5th Int. Scientific and Technical Conf. Innovative Design and Technologies of Nuclear Power (ISTC NIKIET-2018), Moscow, 533-543.
38. V.S. Vasilkovsky, P.V. Andreev, G.A. Zaritsky, N.N. Ponomarev-Stepnoy, G.V. Kompaniets, V.A. Usov, V.V. Vasilenko, A.Yu. Danilyuk, V.N. Zubrev, K.A. Pavlov, L.A. Rachev, V.P. Chupakhin, G.A. Shevtsov, V.V. Viter, M.V. Arakin, E.A. Ksenofontov, L.N. Tararin, B.I. Poletaev, E.G. Lyannoy, A.Yu. Pavlov, A.V. Romanov, “Problems of space energy and the role of nuclear power plants in their solution”, in 2005 International Conference Nuclear Power Engineering in Space-2005 (NPS-2005), Moscow, Podolsk, 2005, Plenary report 05.
39. A.A. Gafarov, A.B. Prishletsov, N.M. Rozhdestvensky, “Comparative analysis of transport and energy modules based on nuclear power plants with direct and dynamic energy conversion systems”, in 2005 International Conference Nuclear Power Engineering in Space-2005 (NPS-2005), Moscow, Podolsk, 2005, Section 1, report 01.
40. V.M. Borishansky, S.S. Kutateladze, I. I. Novikov, S. S. Fedynsky, “Liquid metal coolants”, Moscow: Atomizdat, 1976.
41. N.S. Akhmetov, “General and Inorganic Chemistry”, Moscow: Higher School, 2001.
42. L.M. Sulimenko, “Gallium. Popular library of chemical elements”, T. 1. M .: Nauka, 1983.
43. Yu. V. Apalkov, “Submarines of the Soviet fleet 1945-1991”, Moscow: Morkniga, 2012, 3, 229-233.
44. V.S. Okunev, “Some Issues of Using Liquid Metals and Their Alloys for Cooling Fast Reactors”, Moscow: Bauman Moscow State Technical University – Research Institute of Power Engineering, 2004.
45. E.V. Sulim, N.G. Bogdanovich, O.V. Starkov, E.A. Kochetkova, V.E. Levchenko, “Investigation of the properties of the ternary system of alkali metals sodium-potassium-cesium in the temperature range 293-973 K” , Obninsk (Russia): Institute of Physics and Power Engineering, 2007, FEI-3087.
46. A.G. Mozgovoy, V.V. Roshchupkin, S.N. Skovorodko, M.A. Pokrasin, A.I. Chernov, “Density and pressure of saturated vapors of liquid sodium-potassium-cesium eutectic”, High Temperature, 41(4), 560-562, 2004. http://mi.mathnet.ru/tvt1699
47. P.I. Bystrov, D.N. Kagan, G.A. Krechetova, E.E. Spielrain, “Liquid metal coolants for heat pipes and power plants”, Moscow: Nauka, 1988.
48. O.D. Kazachkovsky, A.V. Starkov, E.A. Kochetkova, N.G. Bogdanovich, E.V. Sulim, V.E. Levchenko, N.F. Lyubchenko, V.I. Zharinov, “Some features of the alloys of the sodium-potassium-cesium system”, Atomic Energy, 1992, 73 (6), 500-502.
49. J. Emsley, “The Elements”, Oxford: Clarendon Press, 1991.
50. V.S. Okunev, “Nuclear Power in Space: a Look into the Future”, AIP Conference Proceedings, 2171, 040001, 2019.
51. A. Koning, R. Forrest, M. Kellett, R. Mills, H. Henriksson, Y. Rugama (Ed.), “The JEFF Nuclear Data Library”, OECD 2006 NEA No. 6190, Nuclear energy agency organisation for economic co-operation and development, 2011, https://inis.iaea.org/collection/NCLCollectionStore/_Public/45/026/45026295.pdf
52. E.A. Gomin, “MCU-4 status”, VANT: Physics of nuclear reactors, 2006, 1, 6-32.
53. “WIMSD-IAEA Library”, IAEA, Nuclear Data Services, 2014, https://www.iaea.org/resources/databases/wimsd-iaea-library
54. N.I. Geraskin, Kuzmin A.M., Kashutin A.A, A.V. Kobiak, D.V. Morin, A.E. Novikov, V.S. Okunev, M.O. Shvedov, V.V. Khromov, “Complex Optimization of the Fast Reactors”, in 1990 proc. Of International Conference on the Physics of Reactors (PHYSOR-90), Marseille, Fr., 4.
55. I.S. Grigorieva, E.Z. Meilikhova (Ed.), “Physical quantities: Handbook”, Moscow: Energoatomizdat, 1991.
56. IAEA-TECDOC-1521, “Characterization, Treatment and Conditioning of Radioactive Graphite from Decommissioning of Nuclear Reactors”, Vienna: IAEA, 2006.
57. IAEA-TECDOC-1198, “Current Status and Future Developments of Modular High Temperature Gas C”ooled Reactor Technology”, Vienna: IAEA, 1999.
58. V.G. Fastovsky, A.E. Rovinsky, Yu.V. Petrovsky, “Inert gases”, Moscow: Atomizdat, 1972.
59. E.A. Manushin, “Gas turbines problems and prospects”, Moscow: Energoatomizdat, 1986.
60. A. Bina, E. Harrington, E. Pilles, L. Tornabelle, “A recent Cluster of Impacts”, 2017 (A HiRISE. Lunar & Planetary Laboratory. The University of Arizona), https://hirise.lpl.arizona.edu/ESP_047768_1995
61. S.C. Solomon, J.W. Head, “Evolution of the Tharsis Province of Mars: The Importance of Heterogeneous Lithospheric Thickness and Volcanic Construction”, J. Geophys. Res., 1982, 87(B12), 9755-9774, DOI:10.1029/JB087iB12p09755.
62. “A plant that extracts oxygen from carbon dioxide was created in the USA, Pasadena, USA”, Federal News Agency Regnum (Russia), May 30, 2019, https://regnum.ru/news/innovatio/2638707.html
63. A. Deryabin, “Decomposed CO2: Nizhny Novgorod residents figured out how to effectively decompose carbon dioxide”, Russian newspaper RGRU – Week – Volga region, 160, 22 July 2020, https://rg.ru/2020/07/22/reg-pfo/nizhegorodcy-pridumali-kak-effektivno-razlozhit-uglekislyj-gaz.html
64. K. Damadeo (Ed.), “NASA’s 2019 BIG Idea Challenge Winner Designs Best Planetary Greenhouse”, NASA, Space Tech, Apr 24, 2019, https://www.nasa.gov/feature/langley/nasa-s-2019-big-idea-challenge-winner-designs-best-planetary-greenhouse
65. P.V. Matyukhin. Heat-resistant polymeric composites for neutron and gamma protection. International research journal. 9(28), 39-40. DOI: 10.18454/IRJ.2227-6017.
66. Phoenix managed to get water from Martian soil. Lenta.ru. August 1, 2008. https://lenta.ru/news/2008/08/01/water/

(Click Here)