1 Introduction

Service-Oriented Computing (SOC) [1] is a paradigm for distributed computing, in which computation units are abstracted as services. The SENSORIA Reference Modelling Language (SRML) [2, 3] has been developed in the IST-FET integrated project SENSORIA [4], and it is a prototype domain-specific language for abstracting service-oriented systems at a high level abstraction. Hybrid systems arise in embedded control when discrete components are coupled with continuous components. Continuous time SRML [5] is an extension of SRML, and it aims at abstracting service-oriented systems in which hybrid systems are embedded. That is: the discrete components and continuous components are abstracted as components of services. Being different from SRML, continuous time SRML can be used to formally model services, whose components can perform both discrete processes and continuous processes that can be describe by differential equations.

In [6], we introduced the application of continuous time SRML through the case study of a Traffic Control System. In this paper, we give a novel systematic presentation of our approach from the semantic domain of continuous time SRML, to the case study, and finally to the test environment. Continuous time SRML is interpreted over Service-Oriented Hybrid Doubly Labeled Transition Systems [5] (SO-HL²TS). This kind of transition systems extends Service-

Oriented Doubly Labeled Transition Systems [7] (SO-L²TS), so that each state of a SO-L²TS is lifted to a function mapping a time interval to an infinite trace of state, over which the differential equations in continuous time SRML can be interpreted. Our approach includes two parts: specifying the system with continuous time SRML modules, and transforming the modules to a hybrid automaton-like Deterministic Finite Automaton (DFA). In order to test the system module, we combine IBM Websphere Integration Designer [8] (WID) and Matlab to form the test environment. WID is used to implement the continuous time SRML module, and Matlab [9] is used to compute the variables controlled by differential equations. Thus, the main contribution of this paper is to provide a way to test or verify the complex systems (like the Traffic Control System) that is specified with continuous time SRML.

This paper is arranged as follows: In Section 2, we introduce the related work such as hybrid automata, model checking tools and the early research of this topic. In Section 3, we introduce HL²TS, the semantic domain of continuous time SRML. In Section 4, we show the case study of the traffic control system. In Section 5, we introduce the testing environment and show the idea of implementing the traffic control system. In Section 6, we make a conclusion of this paper and introduce our future work.

2 Related work

SRML is brought forward in [7], and it is used to model important properties of services and the business conversations within and among services in SOC. A service specified with SRML can only perform discrete activities. Continuous time SRML extends the semantic domain and syntax of SRML, such that it could express differential equations which represents the continuous process performed by services. This essential property of continuous time SRML enables it be able to model the combination of serviceoriented systems and hybrid systems. We will introduce this in Section 3. Hybrid automata [10] are formal models for hybrid systems.

They abstract hybrid systems with graphs and workable representations. A hybrid automaton consists of a set of variables, a control graph, some essential conditions and a set of events. These compositions match the compositions of a service component that is specified with continuous time SRML. Thus, a service specified by continuous time SRML can be transformed to a hybrid automatalike DFA, this will be introduced in Section 4. Hybrid automata are interpreted over timed transition systems, while continuous time SRML is interpreted over SO-HL²TS. Timed transition systems abstract the duration of a continuous process as a parameter of a transition. In this way, it is simple and clear for abstracting continuous processes. SO-HL²TS specify continuous processes as traces of infinite states with definite initial states and finial states. This enables us to know the values of all the variable of an arbitrary state.

In [11], the author provides another way for modelling hybrid systems. In that paper, continuous processes are also interpreted over traces of states. This is the original idea from which the traces of states in SO-HL²TS come. But in [11], discrete processes are not modelled between traces of states. In [12], the author also provides rule schemata for verifying the hybrid systems. Moreover, based on this work, a model checking tools for hybrid systems, KeYmaera X, is brought forward in [13]. In [14], provides an approach for simulating embedded systems with Real-Time Maude. Compared with our approach for testing, this can be another way to test the traffic control model, but the interactions of a service would not be implemented as easy and explicate as that in WID.

3 Continuous time SRML and its semantic domain

Continuous time SRML models composite services, whose elementary components may involve in continuous time executions. The services in continuous time SRML are represented with service modules. A service module is composed of service components, external service interfaces and internal wires linking between them. In Figure 1, we see the compositions of a service module. In the service module, SC is a service component, EX-P is an external service interface (provides-interface), every EX-R is an external service interface (requires-interface), and every IW is an internal wire.

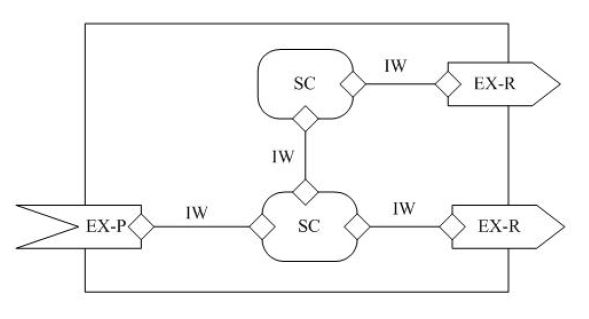Figure 1: A service module of continuous time SRML

In a service module of continuous time SRML, a service component is specified with a business role, an external service interface is specified with a business protocol, and an internal wire is specified with a connector. The full syntax of continuous time SRML can be found in [5], and they are interpreted over SO-HL²TSs.

SO-HL²TSs are extensions of HL²TSs [5, 15] such that they enrich HL²TSs with service-oriented features. HL²TSs extends the L²TS [16] in that it defines a set of functions Σ. These functions map from the real number domain to the state domain of the HL²TS and can be used to interpret the continuous processes described by differential equations. The following definition of HL²TS is from [5, 15].

Definition 1 (Hybrid Doubly Labeled Transition System) A Hybrid Doubly Labeled Transition System (HL²TS) is a tuple

hS, s₀,Σ, Act,R, AP, Li

where:

• S is a set of states;
• s₀ ∈ S is the initial state;
• Σ is a set of functions and for every function σ ∈ Σ there is r_σ ∈ R and r_σ ≥ 0, such that σ : [0,r_σ] → S;
• Act is a finite set of observable actions;
• R ⊆ {σ(r_σ) : σ ∈ Σ} × 2^Act × {σ(0) : σ ∈ Σ} is the transi-

α ⁰ α ⊂ Act, is tion relation. A transition σ(r_σ) −→ σ (0) with denoted by (σ(r_σ),α,σ⁰(0)) ∈ R ;

• AP is a set of atomic propositions;
• L : S → 2^AP is a labeling function such that L(s) is the subset of all atomic propositions that are true in state s.

In Definition 1, the set S of state can be finite or infinite; for every σ ∈ Σ, the real number r_σ is unique, and function σ on the interval [0,r_σ] represents the prolongation of states in the continuous process with the duration r_σ; function L is a state labeling function that defines which propositions are true in each state, and these propositions are from the fixed set of atomic propositions AP.

In order to add service-oriented features to HL²TSs, we refine HL²TSs with Service-Oriented Transition Systems (SO-TSs) [2]. SO-TSs are used that models the communications in serviceoriented systems during the computing processes. In a SO-TS, states and transitions are labelled with certain sub-sets of events that appear in the computing processes. With such refinements, we can obtain SO-HL²TSs. The following definition of SO-HL²TSs is from [5, 15].

Definition 2 (Service-Oriented Hybrid L²TS) A

Service-Oriented Hybrid

L²TS (SO-HL²TS) that refines a SO-TS hS, →, s₀,Gi is a tuple hS, s₀,Σ, Act,R, AP, L,TIMEi

where:

• Act = {e! : e ∈ E} ∪ {e¡ : e ∈ E} ∪ {e? : e ∈ E} ∪ {e¿ : e ∈ E};
• R ⊆ {σ(r_σ) : σ ∈ Σ} × 2^Act × {σ(0) : σ ∈ Σ} is such that:, σ(r_σ) → σ⁰(0) iff (σ(r_σ),α,σ⁰(0)) ∈ R for some α ∈ 2^Act
• AP = Act ∪ PLG;
• For every σ ∈ Σ and every ζ ∈ [0,r_σ], L : S → 2^AP is such that:

L(σ(ζ)) = {e!,e¡,e?,e¿ : e ∈ HST^σ(ζ)} ∪ PLG^σ(ζ)

In Definition 2, the set Act is refined with the sets of events that are published (denoted by e!), delivered (denoted by e¡), executed (denoted by e?)and discarded (denoted by e¿) respectively, E is the set of all the events. The set AP of atomic propositions is labelled with the set of actions and the set of pledges that associate with every interaction (the propositions that hold during the time when the interaction is valid). Every state is labelled with the actions whose associating events are from the history of the events of that state, and the pledges that hold in the state. We also specify the time in each state with the function TIME. The full definition can be seen in [5]

When applying a function σ ∈ Σ to its interval [0,r_σ], we obtain a infinite trace of states σ₀,…,σ_rσ. By connecting traces of states with possible actions, paths of states are formed. Because a trace of states represent the evolution of a continuous process, actions which represent the discrete processes can only take place at the initial and finial states of each trace. Thus, a transition in a path only exists between the last state of one trace and the first state of another trace. This can be seen in the definition of transition relation R in Definition 2. The following definition of traces and paths of states is from [5, 15].

Definition 3 (Paths of SO-HL²TSs ) Given a SO-HL²TS m = hS, s₀,Σ, Act,R, AP, L,TIME,Πi, paths of m are defined as follows:

• For every σ ∈ Σ, σ(0)…σ(r_σ) denotes the trace of states of σ where σ(0) is the first state of the trace and σ(r_σ) is the last state of the trace. σ(0)…σ(r_σ) includes all the states in the set {σ(ξ)|0 ≤ ξ ≤ r_σ}, which can be finite or infinite.
• ρ = (σ₁(0)…σ₁(r_σ1),σ₂(0)…σ₂(r_σ2),…) is a path of m if there exists an α ∈ 2^Act such that for every σ_i(r_σi ) and σ_i+1(0) with i ∈ N, there exists an α ∈ 2^Act such that

(σ_i(r_σi ),α,σ_i+1(0)) ∈ R;

• The states in a path are ordered lexicographically such that, for every i, j = 1,2,… and ζ ∈ [0,r_σi ],ξ ∈ [0,r_σj ], there is σ_i(ζ) ≺ σ_j(ξ) iff either i < j, or i = j and ζ < ξ;
• For the states in a path, there is:
  • for every i, j = 1,2,… and ζ ∈ [0,r_σi ],ξ ∈ [0,r_σj ], there is TIME^σi(ζ) ≤ TIME^σj(ξ) if i < j, and TIME^σi(ζ) < TIME^σj(ξ) if i = j and ζ < ξ;

In particular, if _TIME^σi(rσ_i ⁾ < TIME^σi+1(0) then the transition

(σ_i(r_σi ),α,σ_i+1(0)) takes time, otherwise if TIME^σi(rσ_i ⁾ = TIME^σi+1(0) the transition is executed in zero time;

• A path ρ terminates if it is a finite sequence σ₁(0)…σ₁(r_σ1),…,σ_n(0)…σ_n(r_σn ). In such case the first state of the trace σ₁(0) is denoted by firstρ and the last state σ_n(r_σn ) is denoted by lastρ;
• The concatenation of traces ρ₁ = (σ₁(0)…σ₁(r_σ1),σ₂(0)… σ₂(r_σ2),…) and ρ₂ = (ς₁(0)…ς₁(r_ς1),ς₂(0)…ς₂(r_ς2),…), denoted by ρ₁ ◦ ρ₂, is defined as follows:
  • ρ₁ ◦ ρ₂ = (σ₁(0)…σ₁(r_σ1),…,σ_n(0)…σ_n(r_σn ), ς₁(0)…ς₁(r_ς1)…) iff ρ₁ terminates at σ_n(r_σn ) and

(σ_n(r_σn ),α,ς₀(0)) ∈ R;

• ρ₁ ◦ ρ₂ = ρ₁ iff ρ₁ does not terminate;
• ρ₁ ◦ ρ₂ is not defined in other cases;

• λ is an empty hybrid trace such that for any arbitrary hybrid trace ρ, ρ ◦ λ = λ ◦ ρ = ρ.

The full semantics of continuous time SRML is defined based on Definition 2 and Definition 3, and can be found in [5].

4 Traffic control system and the transformation process

In order to show the application of continuous time SRML, we design a case study of a traffic control system to control the self-driving trains. A traffic control system includes a local traffic control center, a built-in intelligent driving system on a self-driving train, and a monitoring center. Suppose depending on the data obtained from the sensors on the train and the built-in intelligent driving system, the self-driving train can move on their own in most of the driving time without communicating to the outside. But when approaching train stations, they need to get additional information from the local traffic control center, e.g. to know if the station is free, in order to guarantee safe driving. In addition, the monitoring center needs to know the status of the train in some condition, so that they can react in time if the train is not driving safely. In our case study, we show in a traffic control system, how the intelligent driving system on a self-driving train communicates with the local traffic control center and the monitoring center when the train is approaching a train station. The control scheme of the intelligent driving system is adapted from the model of a train system in [17], which extends ETCS [18] level 3 for rail-road crossings.

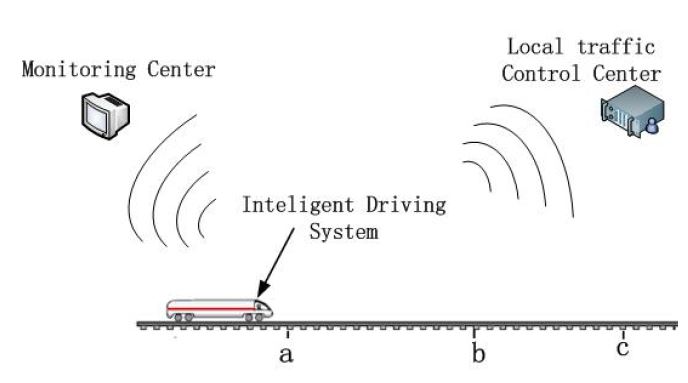Figure 2: A brief scenario of the traffic control system

Figure 3: Business Role IDS

Figure 2 shows a brief view of the scenario. In this figure, we assume that the train station is at point c, and on reaching point a, the train moves with a constant speed v₀. When the train reaches point a, as it needs to move at a lower speed, the intelligent driving system sends a request to the local traffic control center, to ask with which speed the train can move on. Based on the condition of the current traffic condition, the local traffic control center replies with the value of the proper speed. On receiving this message, the intelligent driving system sets a constant speed v₁ of this value to the train. If the local traffic control center finds the traffic is lighter and the train can move with a higher speed, it sends a message to the intelligent driving system with the value of the higher speed. On receiving this message, if the train hasn’t passed point b, the intelligent driving system sends another request to the local traffic control center, to ask with which lower speed it can move on in the future. Before the train reaches point b, this process can repeat for several times. When the train reaches point b, the intelligent driving system sends a request to the local traffic control center, to ask with which deceleration the train can brake. Based on the condition of the current traffic condition, the local traffic control center replies with the value of the proper deceleration. On receiving this message, the intelligent driving system sets the deceleration of the train to the required deceleration. After the train brakes, if the intelligent driving system receives the request from the monitoring center, it sends the current condition (position, speed, deceleration, and so on) of the train to the monitoring center.

We abstract the whole system with continuous time SRML as a traffic control service module, and abstract the intelligent Driving System with business role IDS, the Local Traffic Control Center with business protocol TCC, and the Monitoring Center with business protocol MOC. In this paper, we concentrate on the computational reality of a service module, and ignore the interactions caused by communications with the outside parties at the service interfaces, thus, we only make study to the business role IDS.

A business role includes a set of interactions and an orchestration in which these interactions are organized. An interaction consists of a type (e.g. s&r) and a name (e.g. VControl) and attributes of event types (e.g. receive) and parameters (e.g. newSpeed:speed). With this structure, we can specify events that associate with an interaction (e.g. VControl receive), and parameters that associate with an event (e.g. VControl receive.newSpeed). An orchestration of a business role includes a set of variables that is local to the service component abstracted by the business role, a set of initial values of the variables that identifies the initial state of the service component, and a set of transitions that model the activities performed by the service component. A transition consists of a trigger, a guard and an effect. A trigger is an event or a state condition that specifies the condition for the transition to occur. A guard is a condition that identifies the states in which the transition can occur. An effect is the proposition that is true in the state that follows the state specified by the guard condition, and represents the effect of the transition. In the declaration of a transition, we don’t model the actions caused by the transition (e.g. the assignments of local variables) because they are not considered in the verification procedure.

Figure 3 shows the specification of business role IDS. IDS contains four interactions and four transition rules. Interaction VControl denotes the communication between IDS and TCC: when the train reaches point a, the IDS sends a request to TCC to ask for a lower speed, and it can receive the reply from TCC with parameter newSpeed when the train is between point a and point b, the value of newSpeed is then assigned to local variable v₁; interaction VMoveOn denotes the communication between IDS and TCC: when the train is between point a and point b and the traffic is lighter, IDS can receive a message from TCC with parameter newSpeed, indicating that the train can move with a higher speed, the value of newSpeed is then assigned to local variable v₀; interaction Brake denotes the communication between IDS and TCC: when the train reaches point b, the IDS sends a request to TCC to ask for a braking deceleration, and it can receive the reply from TCC with parameter dec when the train is after point b, the value of dec is then assigned to local variable B; interaction BrakeInfo denotes the communication between IDS and MOC: when the train is between point b and point c, and it brakes, IDS can receive a request from MOC asking the current position of the train and the current time, and it replies to MOC with parameter currPos and currTime, which take the values of local variable C and t respectively. Transition Nego describes that the train changes its speed from v₀ to v₁ when it receives the slow down message from the local traffic control center; transition Cont describes that the train changes its speed from v₁ to v₀ when it receives the speed up message from the local traffic control center; transition Corr describes that the train brakes with the deceleration B when it receives the braking message from the local traffic control center; transition Stop describes that the train receives the request message from the monitoring center, and replies with its current position and the current time. In business roles, the continuous time executions are specified in the form of differential equations. (e.g. dC = v₀ in Figure 3). In general, in continuous time SRML, the n th derivative of variable a to time variable t, ^∂_∂ⁿ_tn^a , is denoted by dⁿa. The formal semantics of business roles can be found in [5].

Next we take transition Nego as an example to illustrate how a transition in IDS can be interpreted over a SO-HL²TSs: Suppose a SO-HL²TSs h = hS, s₀,Σ, Act,R, AP, L,TIME,Πi satisfies

IDS ( the satisfaction of a business role over a SO-HL²TS can be α ⁰              σ,σ⁰ ∈ Σ and found in [5]), σ(r_σ) −→ σ (0) is a transition in h ( α ∈ Act), if VControl receive ∈ α and σ(r_σ) |= dC = v₀, then σ⁰(0) · · · σ⁰(r_σ0) |= dC = v₁. Particularly, formula dC = v₁ represents the differential equation  v₁ , where t denotes the continuous time variable. Such a formula expresses that variable C changes according to the differential equation v₁ along the trace σ⁰(0) · · · σ⁰(r_σ0) of h.

In order to be able to test or verify the Traffic-Control module that is explained in this section, we show how to transform the business role IDS to a hybrid automata-like DFA. A Deterministic Finite Automata (DFA) [19] consumes a string of input symbols over a set of states, and it operates as follows: when inputting a symbol, the DFA transits from one state to another state, and it does the transitions until all input symbols have been consumed. In a business role, if we take the trigger and guard of every transition as an input symbol, and label the effect of every transition to a state, then we can construct a DFA based on the business role. According to the scenario of the traffic control system and the specification of business role IDS, we can construct the DFA shown in Figure 4.

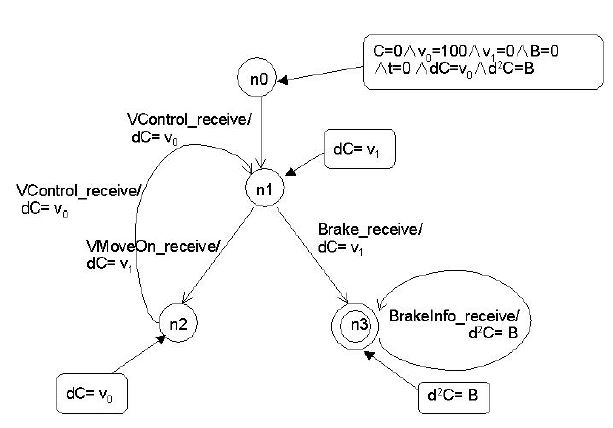Figure 4: The DFA for business role IDS

5 The testing environment

IBM WebSphere Process Server (WPS) is an integration platform for Service Oriented Architecture (SOA), and supports the Service Component Architecture (SCA) programming model. As a process engine, WPS provides a hosting environment for business processes and several Web-based applications. These features of WPS match the structure and the requirements of continuous time SRML modules, so we choose WPS as the basic testing environment.

As the implementing tools, we combine WID with Matlab. In

WID, an assembly editor is the central panel where service modules are built by creating and linking services components and service interfaces. A service component is specified with an implementation, some interfaces defining the inputs, outputs and faults of the service component, and zero or several references which denote the interface of other service components connecting to this service component. Service components can be implemented in various types, such as Java objects, business processes, and business state machines. We choose business state machines to implement our Traffic-Control module, because from Figure 5, we find that the hybrid automaton based DFA can be mapped to WID business state machines almost directly. Figure 5 shows the mapping relations between a continuous time SRML module and a WPS service module.

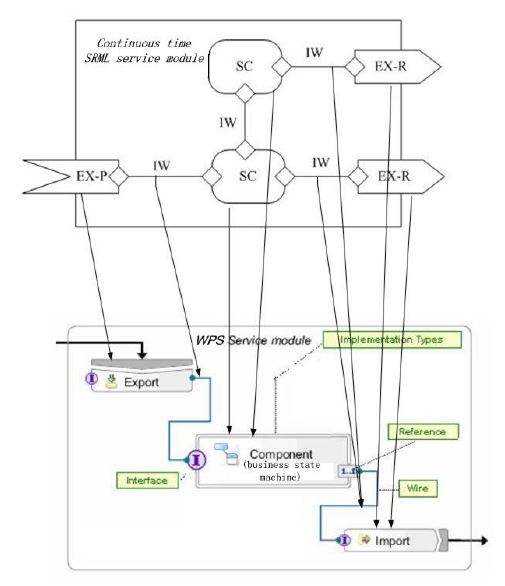Figure 5: Mappings from continuous time SRML module to WPS service module

In a service component, the continuous processes described with differential equations can be directly implemented with Java code when there are exact solutions of the differential equations. Otherwise, we need to solve the differential equations numerically.

In such case, we combine WID with Matlab to achieve our goal. Matlab [9] is a multi-paradigm numerical computing environment, and it allows interfacing with programs written in languages such as C, C++ and Java. In the latest versions of Matlab, there is a function to wrap programs to Java packages. This function enables us to write Matlab programs to solve the differential equations in the service components in WID, and pass the solutions to the service components by importing the programs packed into Java packages to WID. We’ll continue to do the implementation and testing in our future work.

6 Conclusion and future work

In this paper, we give a complete introduction to continuous time SRML, including the semantic domain of continuous time SRML, the application of continuous time SRML, and the testing environment. Continuous time SRML abstracts hybrid system-embedded service-oriented systems at a high level. The semantic foundation of continuous time SRML is SO-HL²TS, over which this modelling language is interpreted. The transitions of SO-HL²TSs enable continuous time SRML to model the communications between services or within a service; and the traces of states of SO-HL²TSs enable continuous time SRML to model the continuous processes performed by service components. Systems modelled with continuous time SRML can be transformed to hybrid automata-like DFA for testing and verification. This can be demonstrated by the case study of the Traffic Control System. By combining IBM WID and Matlab, we are able to implement the hybrid automata-like DFA.

In our future work, we will show the implementation of the hybrid automata-like DFA for the Traffic Control model, and provide the result of testing. We will also try to verify the Traffic Control system with KeYmaera X, which is a newly developed model checking tool for hybrid systems. For the transformation presented in Section 4, we are also working on a systematic approach so that this can be done automatically by programs. Further, we will try to enrich continuous time SRML with the expressions of actions, so that models specified with continuous time SRML match the business state machines of IBM WID better.

1. D. Georgakopoulos, M. Papazoglou, Service-Oriented Computing, The MIT Press, Cambridge, Massachusetts, 2009.
2. J. Fiadeiro, A. Lopes, J. Abreu, “A formal model for service-oriented in- teractions,” Science of Computer Programming, 77, 577–608, 2012, doi: 10.1016 2.003.
3. J. Fiadeiro, A. Lopes, L. Bocchi, J. Abreu, “The Sensoria Reference Modeling Language,” Lecture Notes in Computer Science, 6582, 61–114, 2011, doi:10.1007/978-3-642-20401-2 5.
4. M. Wirsing, M. Ho¨lzl, Rigorous Software Engineering for Service-Oriented Systems, Springer, 2011.
5. N. Yu, Injecting Continuous Time Execution into Service-Oriented Computing, Munich University , Ph.D. thesis, 2016.
6. N. Yu, M. Wirsing, “The Application of Continuous Time SRML,” in Proceedings of 2020 ICICSE&ICACTE, 99–103, 2020, doi:10.1145/3424311.3424316.
7. J. Abreu, Modelling Business Conversations in Service Component Architectures,University of Leicester, Ph.D. thesis, 2009.
8. IBM, IBM Integration Designer V8.5.5 documentation, https://www.ibm.com/support/knowledgecenter/SSTLXK 8.5.5/com.ibm.wbpm. wid.main.doc/kc-welcome.html, 2014.
9. MathWorks, https://www.mathworks.com/,2014-2021.
10. T. A. Henzinger, “The theory of hybrid automata,” in Proceedings of 11th Annual IEEE Symposium on Logic in Computer Science, 1996, doi:10.1109/ LICS.1996.561342.
11. K. Cordwell, A. Platzer, “Towards Physical Hybrid Systems,” in Proceedings of International Conference on Automated Deduction, CADE’19, 216–232, 2019, doi:10.1007/978-3-030-29436-6 13.
12. A. Platzer, Logical Foundation of Cyber-Physical Systems, Springer,Cham, 2018.
13. A. Platzer, KeYmaeraX: An aXiomatic Tactical Theorem Prover for Hybrid Systems, http://www.ls.cs.cmu.edu/KeYmaeraX/index.html, 2021.
14. M. Fadlisyah, E. A´ braham, P. C. Lepri, D. O¨lveczky, “A Rewriting-Logic- Based technique for modelling Thermal Systems,” in Proceedings of First International Workshop on Rewriting Techniques for Real-Time Systems, PTRTS 2010, 82–100, 2010, doi:10.4204/EPTCS.36.5.
15. N. Yu, M. Wirsing, “A SOC-Based Formal Specification and Verification of Hybrid Systems,” in Proceedings of the 22nd International Workshop on Algebraic Development Techniques (WADT2014), 151–169, 2015, doi: 10.1007/978-3-319-28114-8 9.
16. R. De Nicola, F. Vaandrager, “Three Logics for Branching Bisimulation,” Journal of the ACM, 42(2), 458–487, 1995, doi:10.1145/201019.201032.
17. A. Platzer, J. Ousel, “European Train Control System: A Case Study in Formal Verification,” in Proceedings of 11th International Conference on Formal Engineering Methods (ICFEM 2009), 246–265, 2009, doi:10.1007/ 978-3-642-10373-5 13.
18. The Worldwide Railway Organization (UIC), The European Train Control System, https://uic.org/etcs#Standards-and-Specifications, 2015.
19. J. E. Hopcroft, R. Motwani, J. D. Ullman, Introduction to Automata Theory, Languages, and Computation (3rd Edition)., Addison-Wesley Longmano., Inc., USA., 2006.

(Click Here)