1. Introduction

Being ready to perceive novel and unusual feelings, contradicting ideas initially estimated as the only correct ones, is an indicator of human intellectual and personal development. According to Vladimir Zinchenko, a person develops when he “rises above the available types of activity, chooses some, or builds a new one” [1].

The indicator under consideration, being an alternative thinking style, presupposes openness to all possible aspects of experience, including an unusual one; freedom from personal bias, stereotypes, prejudices and other external constraints. It admits a solution to problems opposite to generally accepted ones, based on the willingness of a person to “contradict himself”, being the basis for the formation of tolerance of any dissenting opinion and action in the future [2–12].

This readiness is one of the factors in overcoming stereotypes. Provided an individual considers a particular situation from different angles, takes into account various points of view on the essential relationships between concepts established in a situation, he will be able to at least partially decentralize his thinking, and overcome his initially unilateral perspectives.

Despite numerous studies somehow affecting the role and place of an alternative style of thinking in the intellectual development of a person [2, 3, 7, 8, 10, 13, 14], the patterns and possibilities of the formation of such a style in the educational space at school has not been considered as an object of special research. In particular, issues of the main conditions and possibilities for the formation of the considered phenomenon in school education, the stages and levels of such formation, the diagnostic means to achieve these levels, the nature of educational goals in various academic subjects targeting the actualization of alternative forms of educational and research activity, have not been considered by the scientists [14, 15].

As a result, purposeful formation of an alternative thinking style remains outside the attention of teachers and methodologists, leading to passive thinking in school students. In particular, they are not ready to transit from standard methods for performing educational and research activities to alternative methods. In other words, these standard methods for performing activities are fixed in their minds as rigid algorithms that do not allow any structural transformation.

Thus, the above conditions determine the relevance of the proposed research.

2. Problem Statement

 An alternative style of thinking can be effectively realized within the framework of mathematical content, since the presence of deep and often hidden connections between different branches of mathematics, different “mathematical languages” and general methods provide a possibility to correlate different perspectives on various mathematical concepts, facts and patterns. These possibilities are described in the works of many well-known mathematicians and methodologists [1, 4, 8, 15–20, etc.].

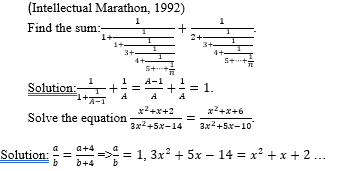
In particular, the actualization of the alternative style of thinking was very vividly illustrated in [15]. The great scientist correlated numbers and algebraic quantities: “Calculations are made either using numbers, as in ordinary arithmetic, or using species as in algebra. Both methods are based on the same principles and lead to one goal, but arithmetic using a specific and particular way, and algebra applying an indefinite and general way” [15]. However, “in arithmetic, when solving problems, one only passes from the given quantities to the sought ones; in algebra one works backwards, passing from the sought quantities, being considered as data, to the given values, being considered as the sought ones, in order to come to the conclusion or the equation, from which it would be possible to find the sought quantity” [15].

Newton implemented these considerations in finding a binominal series expansion of the function ( ,, and in calculating the area bounded by the curves   for various natural numbers n [21]. Newton was well aware that, according to the logic of his construction, the obtained expansion was hypothetical, and not a proven fact. Therefore, he proposes other ways to confirm the correctness of the obtained expansion, which are of interest in the context under consideration.

In particular, Newton applied Vièta’s method for square root extraction for numbers to polynomials [21]. Meanwhile, he formulated the rule for “square root extraction” from a polynomial, and he explained this rule with examples, in particular, an example of obtaining a binomial series for [21]

Despite the fact that there are tasks for actualizing an alternative style of thinking in modern textbooks in mathematics, preparation materials for the final certification of school students, and materials for various Olympiads, this orientation has not been fully implemented in mass practice of math education.

According to our observations and numerous publications, many school students realize the possibility of an alternative consideration of a particular problem situation only as reasoning that must be remembered and applied when solving problems of a specific type, rather than as a universal approach to its analysis   [9–11, 22–24]. To prevent this, an adequate pedagogical format, considering the purposeful actualization of an alternative style of thinking as one of the main tasks of school mathematics education, is urgent.

Considering the above, the purpose of this study is to define theoretical foundations for the formation of an alternative thinking style for school students in the educational process, and to develop an appropriate methodological structure to ensure such thinking goes beyond the range of stereotyped patterns and ideas.

3. Literature Review

Various aspects of an alternative thinking style, being an adequate indicator of personal intellectual development, have been considered by many scientists who associated it with the categories of decentralized, lateral, tolerant, or divergent thinking. The absence of this style is evident in the unilateral and tendentious thinking of a person using mainly stereotyped patterns and algorithms [2, 3, 8, 10, 17]. Therein, his ability for creative activity is poorly developed, which, in turn, negatively affects his ability to solve educational problems.

In this context, a special role is played by the mathematical content, which is characterized by a high degree of generalization, universality, and alternativeness of research and proof methods used. For example, one can mention the duality principle, which plays an important role in projective geometry. According to this, the projective space can be isomorphically mapped onto itself with the “transformation” of points in the plane, and vice versa. Obviously, the above regularity significantly helps to formulate statements of the mentioned theory, since any proof can automatically be applied to two different meaningful alternatives.

Accordingly, the targeted process of mathematics education creates the greatest opportunity for teaching generalized methods of mental activity to students, providing an opportunity for a multilateral analysis of the problem situations under consideration. It is convenient to organize such an analysis by changing the semantic status of the components of these situations. In this case, the initially key element of the task can be considered as an auxiliary element, and the initially auxiliary element as being a key one.

This approach appears in many psychological and pedagogical studies in various modifications. For example, the founder of Gestalt therapy, introduced thought experiments that contribute to the personal growth of a person (“feeling of opposing forces”, “attention and concentration”, etc.) [25]. The same procedures can be used in teaching mathematics. In particular, when solving geometrical problems, school students often consistently analyze the corresponding geometric configurations, highlighting the most promising one for further exploration, realizing the feeling of “background and figure” [8, 11, 22]. Having reconstructed the problem situation, students get the opportunity to actualize the “feeling of opposing forces” [1,11, 22, 26, 27].

The role of the considered characteristic of thinking in the development of scientific ideas was emphasized by many famous scientists [1, 18]. In particular, it is noted that the concepts and facts under consideration should be not investigated in the “normal”, correct, and usual form, but “in a critical situation, in fever and passion…” [28]. The authors also suggested paying special attention to characteristics that do not correspond to “the usual intuitive ideas, and allow us to look at well-known facts from a new angle, to see new and unexpected content therein” when conducting research [18]. Similar considerations in favor of the implementation of a “pathological” approach to the research subject are expressed by the famous mathematician in [1].

In a didactic context, updating the considered approach can be viewed as a kind of heuristic method used at the stage of problem solving [2, 3, 11, 22, 29]. In particular, this technique is the base of many non-standard math tasks. Mastering it, along with solving purely didactic problems, allows for the forming of a multilateral and “multidimensional” approach to the subject of study, “decentralizing” the viewpoint on the considered mathematical content and, thus, contributing to the formation of a sufficiently flexible and “variable” style of thinking of students.

From the foregoing, it follows that it is expedient to develop a special methodological structure that ensures the development of an alternative thinking style when teaching mathematics at school. The appropriate orientation should be a constant component of the educational process, one of the methods of cognition that allows for effectively organizing an educational heuristic search in the development of new subject content.

Based on the analysis of a number of studies in the context of the problem under consideration [2–4, 8, 11, 22, 25, 28, 30–33], and our own pedagogical experience, the following methodological provisions can be taken as the basis for such work:

• It is advisable to actualize and form an alternative thinking style for school students on the basis of special tasks implying an alternative consideration of a certain mathematical model and its components. These tasks should be interrelated with the general context of mathematical material, ensuring the effective achievement of the educational goals planned by the teacher.
• In accordance with active learning strategies, the implementation of the previous condition in the learning process presupposes an organization of adequate independent activity of students, during which certain connections and relations are established between the considered alternative positions, and a qualitatively new integrative knowledge arises. The highest developmental effect is present when the idea of applying some heuristic procedure comes directly from students in the form of conjecture and suppositions. George Pólya writes, “A conjecturing student associates himself therewith; his prestige and self-esteem depend on the outcome of the case to some extent, and he is eager to find out whether his guess turns out to be correct or not; he will be actively interested in his task and the work of class, he will not fall asleep, and will not be distracted by other tasks” [8].
• Actualization of various semantic positions, being complementary and mutually exclusive, presupposes interaction and cooperation of students’ efforts. According to Rada Granovskaya and Yuliya Krizhanovskaya, “during joint activities, the initial attitudes of some participants on the inability to solve the problem are removed. Interstimulation of partners … reduces self-criticism and prevents the displacement of original ideas into the subconscious” [3]. In particular, the so-called “effect of a teasing interlocutor” [33], which defends the position opposite to that of the author is very effective in the considered perspective. This approach makes it possible to impart a subjective-personal character to the educational exploratory process, which ensures the effective mastering of the corresponding heuristic techniques.
• The role of a teasing interlocutor can be effectively performed by a modern virtual educational environment, which allows for quickly moving and changing elements of a particular mathematical model when expedient. During the process it becomes possible to actualize alternative key elements for a relatively short period of time, and determine further prospects for their use when considering this specific task situation, or, to select the optimal alternatives [33].

The use of virtual educational and developmental environments can be implemented locally when organizing a heuristic search for a solution to a given specific problem, or it can become a means for full-fledged creative reflection on the meaningful links between its elements, due to their optimal dynamization and visualization. In the course of such work, it is given an initially boring (task) situation, after “having started to formulate and think it over” students see that “it acquires components, details, and new storylines, sometimes completely unexpected from the viewpoint of its initial perception” [33]. This approach is mentioned in a number of our publications [6, 30, 31, 34, 35].

4. Materials and Methods

The development of this research concept was carried out in line with the main trends in the system of mathematical education, in particular, problem-based and student-centered approaches, taking into account the specifics of the mathematical content [3, 4, 8, 9, 11, 22, 28, 34, 36–38]. The main instrument to implement these approaches is a system of special math tasks, leading to actualization of an alternative thinking style in school students regulated by a teacher. The study involved three clusters of materials.

Firstly, we have analyzed normative and program documents, educational standards of general secondary education, programs of mathematical disciplines, scientific and methodical works of leading domestic and foreign experts in the field of developmental psychology, didactics, theory and methods of mathematical education, materials on the history of mathematics, current textbooks, teaching aids, methodical recommendations, and educational software [1–3, 18, 21, 28, 33, 39]. The study of these materials indicates that the problem of the formation of alternative thinking in school students currently has not been singled out as a research subject for specialists in the field of mathematical education.

Secondly, we have conducted a longitudinal study of teaching mathematics in a number of educational institutions in Penza (Russia). The background competence of school students was revealed in terms of their readiness to manifest an alternative thinking style when solving exploratory math tasks. It was shown that about 80% of the school students surveyed in a number of Penza schools were not ready for consideration of variable alternatives to a given mathematical models, limiting themselves to analyzing the only possible alternative. Insufficient attention of teachers to the described component of educational and exploratory mathematical activity seems to be the main reason for such a problem.

Finally, the third cluster of materials comprised the results of an exploratory pedagogical experiment to determine the possibilities of introducing the developed mathematical content and make an assessment of its effectiveness in terms of creating the readiness of school students to apply an alternative thinking style when solving exploratory math tasks. The exploratory experiment was carried out in the course of a two-year mathematical training of school students at Lyceum No. 3 for gifted students of the Penza region, and a number of educational institutions in Penza. In total, the experiment included about 80 school students at the basic and senior levels of education.

The content of the materials being tested is partially presented in a number of our textbooks and articles [7, 11, 22, 30, 31].

The data collection technique was implemented using special educational and exploratory tasks. The results of their solving by school students were subjected to qualitative and quantitative analysis on the basis of a special quantitative scale at the background and productive stages. The following indicators were considered as the main characteristics of the alternative style of thinking: readiness to actualize unusual associative links; the ability to perceive the problem in an unusual way; readiness to build initially unobvious alternative constructions (an openness to an extraordinary combination of elements (“game-research”); the ability to alter actions; the ability to re-construct the acquired information in accordance with the structure of the problem domain [25]).

The data collection technique was implemented using special diagnostic approaches based on the use of two-level tasks. Each diagnostic task included two parts. In the first part, it was proposed to solve a task that involves finding a solution based on the actualization of an alternative task structure with a similar solution method. The second part included questions for which the students did not have clear guidelines. The purpose of posing these questions was to give students a certain “hint” about the possibility of developing the initial task. Attempts to find such answers testifies to the presence of a certain orientation of the students towards the search for alternatives. At the same time, students were required to set goals independently, (in particular, when they formulated tasks); focus on finding the most general way of action; effectively “translate” the information contained in the original problem into an alternative mathematical language; engage in full-fledged reflection on the revealed meaningful interrelationships.

The data collection technique was implemented using a special diagnostic intervention based on the use of two-level educational search tasks. Each diagnostic task included two parts. In the first part, it was proposed to solve a task that involves finding a solution based on the actualization of an alternative task structure with a similar solution method. The second part included questions for which the students did not have clear guidelines. The very purpose of posing these questions was to give schoolchildren a certain “hint” about the possibility of developing the initial task situation.

Already the presence of attempts to find such answers testifies to the presence of a certain orientation of the senior pupils towards the search for alternatives. At the same time, the ability to engage in relatively independent goal-setting was required (in particular, when drawing up tasks); focus on finding the most general approach; effective “translation” of the information contained in the original problem into an alternative mathematical language; full-fledged reflection on the revealed meaningful interrelationships (for example, when completing the definition of the task situation). The following are examples of such tasks for consideration.

Task 1:

• Let D be the point of the AC side in the ABC triangle; r, r1 and r2 the radiuses of the inscribed circles of the triangles ABC, ABD and BDC, accordingly. Prove that r < r1 + r2.
• Is it possible to extend the proved inequality to a larger number of inscribed circles? (You can, for example, divide the AC side into more parts, or take point D inside the ABC triangle).

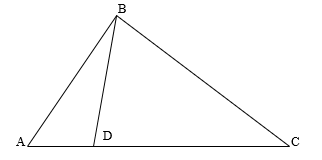Figure 1: Illustration of the task

Task 2:

• Prove that the bisector of the exterior angle at the vertex of an isosceles triangle is parallel to the base.
• How many ways of proof can you suggest? (The number of proposed and successfully implemented methods is considered).

To establish an ordinal measurement scale, a preliminary assessment of possible answers was carried out and a weighted assessment in points was made. Completion of only the first part of the assignment was assessed by one point, a purposeful attempt to answer the question of the second assignment added one more point, while the performance of the second part of the assignment was assessed by two points. If, when completing the second part of the tasks, the student offered at least three answer options, then one more point was added to the total number of points. Thus, the student could receive a maximum of four or five points for one task. The total grade that could be obtained for completing the entire work, including four tasks, did not exceed 18 points. Three   categories of students were identified. A student who received from 0 to 6 points corresponds to the initial level of the formation of an alternative style of thinking; students who received from 6 to 12 points were assigned to the intermediate level, and from 13 to 18 – to the high level.

Comparison of the results of the tasks performed by the students of the experimental and control groups showed that the purposeful use of the methodology for devising meaningful alternatives in the study of mathematical material significantly influenced the increase in the readiness of students to successfully solve mathematical search problems.

5. Research Results

5.1. Levels of formation of an alternative thinking style

With regard to mathematics, the characteristics defined above can be actualized in solving math tasks, the solution of which involves implementation of a certain set of intellectual procedures. These procedures are reflected in the exploratory activity of school students, corresponding to the levels of its development [16]. However, their status varies at different levels (Table 1).

Table 1: Levels of Formation

Levels of formation of an alternative thinking style	Object of the analysis	Dominant way for actualizing an alternative style of thinking	Selection criteria for an alternative search	Nature of the intellectual procedures involved
Initial	A particular task	External (based on strict external requirement)	Desire to “function” strictly within the prescribed range of choice	Random chaotic or systematic search for alternatives
Medium	General task situation	Mixed (result-oriented)	The choice is determined by different model representations of the task situation	Selection of a technique by analogy with the solution of “related” tasks, accompanied by its experimental verification
High	System of related tasks	Internal (search-oriented)	Independent and reasonable variation of the conditions and requirements of the task	Selection of a heuristic procedure generated by purposeful modification of the components of the task domain

This scale of levels allows us to outline a strategy for the consistent formation of an alternative style of thinking, based on the use of systems of special tasks which are presented below.

5.2. Substantive and Methodological Tools

5.2.1. Enumeration of Alternatives

We now consider the main methodological features of the formation of an alternative thinking style of school students during their moving up the “ladder of levels”.

At the initial level, alternativeness is directly related to the selection of possible task options, and its transformation. It is important that the expediency of such a choice should acquire a subjective personal meaning for a school student. According to Zinchenko, it means that the subject has a special type of “awareness of ignorance of some knowledge”, or “an emotional experience of ignorance of some knowledge”, as stated by Konstantin Pigrov. Johann Amos Comenius qualifies such awareness as the source of the thirst for knowledge.

Let us consider an example of actualizing an alternative thinking style of students by enumerating alternatives presented in a particular task situation.

There are three criteria for congruent triangles with different combinations of angles and sides of a triangle studied in school course of planimetry. If we enumerate possible combinations, we can formulate some more statements (with two angles and a side opposite to one of the angles; with two sides and an angle opposite to one of the sides; and with three angles).

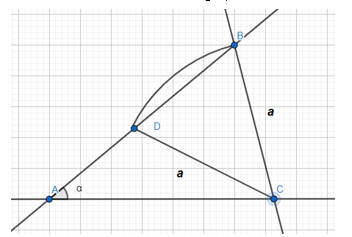Figure 2: Illustration of the task

The first criterion formulated by students can serve as a starting point for studying the sum of angles of a triangle.

In the second case, we consider the fourth criterion for congruent triangles with two possible solutions for constructing a triangle from the corresponding elements based thereon (Figure 2). The unambiguity of the solution can be provided by the additional condition of uniformity of the angles at the vertex B of one triangle, and the corresponding vertex D of another triangle.

Finally, the obvious inequity of a criterion for congruent triangles by three angles naturally raises the question of congruence of triangles.

The described alternatives matrix can be clearly presented for school students on the basis of a directive that includes all the selected cases (Table 2).

This example shows the possibility of actualizing an alternative thinking style of a student by enumerating various specific models of a common task, aimed at identifying all combinations with a minimum number of triangle elements, unambiguously determining its construction when considering standard mathematical material.

To conduct further exploratory activity, we should move away from traditional stereotypes and apply well-known heuristic procedures [2, 3, 8, 9, 11, 22, 26].

Table 2: An Example of a Directive for School Students

Criteria for congruent triangles	Constructing triangles given three elements	Solving triangles
1. Two triangles are congruent if two corresponding angles and the side in between are equal (a – side; a and γ – angles).	(Construction is possible and unambiguous at )	Angle a is found according to triangle angle sum theorem; side с is calculated by the law of sines; side b is found according to the law of cosines.

For example, we consider the replacement of structural components of the task domain. With regard to school mathematical content, the mentioned procedure can be actualized with the help of a specific teaching technique, namely, “he (she, it) does not know what he (she, it) really is.”

We illustrate this statement with the following artificially constructed example. Consider the usual quadratic equation . This equation obviously involves numbers and letters. Now we make an assumption that “numbers do not know that they are numbers, and letters do not know that they are letters.” In other words, “the number 6 does not know that it is a known number, the letter x does not know that it is an unknown number.” Let us find the number 6:

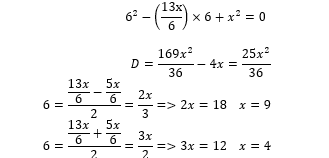This example illustrates the potential for an alternative search for thought, being opposite to the standard algorithm. According to Zinchenko, it is “at the junction of opposite processes of value comprehension and signification of meanings that new images are born, conveying certain meanings and making the meaning visible” [1].

The specificity of this approach is constant correlation of the original design for task solution with its alternatives forming the basis of this solution in a new semantic paradigm. The logic of an exploratory process using the adopted approach is shown in   Figure 3.

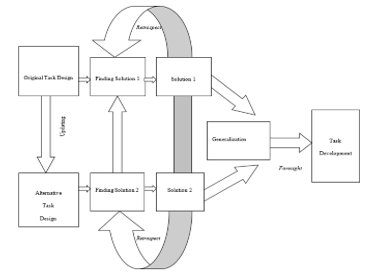Figure 3: Schematic for an exploratory process

This schematic demonstrates updating of possible alternative problem-solving in the process of sequential reformulation of the task situation, ensuring effectiveness of the exploratory process being implemented.

Here are some examples of such updating when solving non-standard tasks:

“The number does not know that it is a letter”

“Algebraic or numerical expressions do not know that they are letters”

Answer: x=2, x= – 4.

It is clear that the described principle of transition to meaningful alternatives can also be used when considering geometric configurations: “The angle does not know that it is exterior”; “The circle does not know that it is escribed,” etc.

Let us consider an example of the exploratory process to analyze one of configurations.

Example. Prove that the sum of angles DBE and CAM does not depend on the choice of the line l (Figure 4).

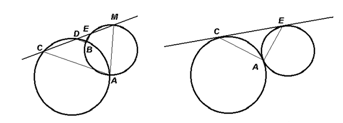Figure 4: Illustration of the task

It is proposed to consider the line СМ as a dynamic image that can move relative to circles, and turn into a tangent to both of them (“a secant does not know that it is a tangent”). Similarly, it’s possible to move from an intersection to an external contact of circles (“intersecting circles do not know that they are just tangent to each other”).

We obtain a chain of alternative configurations, which are degenerate cases of the initial one (Figure 3). The latter naturally leads to a derivative task situation.

Example. Find the angle CAE, where point A is the point of external contact of two given circles, and CE is their common tangent.

Solving the task, it is possible to assume that the angle CAE, considered as the sum of two angles, obtained at the intersection of the line CE and common tangent to two circles, is equal to 90°. As for the original geometric configuration, we consider the secant lines СМ and AB as analogs of common tangents in a degenerate alternative construction. As in the degenerate case, the solution consists of expressing the angles forming the angle CAM, via the angles of the triangle BDE.

Likewise, . Then, .

Finally, we get: .

Thus, we have shown that by highlighting the key link (determining the successful search) based on a meaningful analysis of the alternative configuration, one can successfully update the relevant considerations when examining the original one.

5.2.3. Structuring the Task

Since the use of an alternative style of reasoning is regarded by the student mainly as a local intellectual act in understanding the task situation at previous levels of mathematical development, then it is associated with the possibility of free and informed choice from a combination of implicitly presented meaningful alternatives at a higher level. It is quite obvious that in this case the heuristic potential for choosing alternatives increases significantly. Thenceforward, the larger set of heuristic procedures the student actualizes, and the more systemic they are, the more efficient a person’s intellectual development is.

Successful procedure for an informed alternative choice becomes one of the main instruments for maintaining an active exploratory activity in schoolchildren. One of the most effective methods for creating an opportunity for such a choice is a step-by-step transformation of components of a task situation as applied to mathematics education, leading to the construction of a sequence of new task structures, somehow related to the original one, which is accompanied by their comparative analysis. The advantage of such work stems from the fact that the initial intellectual activity of a student does not stop when the solution of the original problem is completed. Moreover, it receives an additional heuristic impulse during its transfer to new substantive content, ensuring full realization of his individual trajectory of development.

Transformation of task structures can be potentially implemented in many alternative formulations, determined by the choice of the involved techniques, or their expedient combinations. As a result of specially organized joint work of subjects of the educational process, one can obtain a whole cycle of alternative derivative tasks based on some initial mindset. The main methodological problem in this case is to ensure effective anticipation of the most promising and available areas of exploratory activity for implementation at the particular stage of training.

We consider one of such complexes, obtained by successive generalization of the following original situation.

Original Task. Construct a circle that is tangent to the lines m and n (m//n), and to the circle (O, r) lying between these lines.

Having changed the location of this circle (“the circle lying between two given lines does not know that in fact it does not lie between them”), we get the task:

Task 2. Construct a circle that is tangent to two different parallel lines, and a given circle.

If in Task 2 we consider that the lines coincide (“the lines do not know that they coincide”), then we get the following task:

Task 3. Construct a circle that is tangent to a given line at a given point M thereon, and a given circle that is tangent to this line.

Having ignored the condition of tangency of a given circle and line (“the circle that is tangent to the line does not know that it actually is not tangent to it”), we get the following task:

Task 4. Construct a circle that is tangent to a given line at a given point M thereon, and a given circle.

Having ignored the condition of tangency at a given point (“the circle does not know at what point it is tangent to the line”), we get the following task:

Task 5. Construct a circle that is tangent to a given line and a given circle.

Having replaced a line with a circle in Task 5 (“the circle does not know that it is the line”), we get the following task:

Task 6. Construct a circle that is tangent to two given circles, and to one of them at a given point.

Having replaced a circle with lines in Task 6 (“the circle does not know that it is two lines”), we get the following task:

Task 7. Construct a circle that is tangent to the lines m and n (m//n), and a line c intersecting the lines m and n at points K and L, KÎm, LÎn.

Using alternative task structures in the educational and exploratory work, ideologically related to the original task situation, a teacher gets the opportunity to stimulate an exploratory activity of school students, while enriching and improving their intellectual and personal potential.

It is important to note that similar procedures can be visualized quite effectively using a modern software environment. By selecting, swapping, and moving the initially actualized and background elements of considered mathematical structures with a manipulator, one can obtain alternative constructions that allow “seeing” a potentially successful area of an exploratory activity [6, 31, 32, 35].

6. Approbation

A unified, generally recognized methodological concept of the formation of an alternative style of thinking by students in mathematics lessons presumably is not provided in real school practice. The test of this hypothesis was carried out within the framework of the first stage of the experiment, the main task of which was: to study the nature of the spontaneous influence of the process of “natural” development of the content of school mathematics courses and the personality traits of the teacher on the effective actualization and formation of an alternative style of thinking in schoolchildren.

To confirm this fact, the results of the tests performed by 80 students of grades 3-4 of a number of schools in Penza (Russia) were analyzed. Control work included tasks that imply elements of the study of task structures and the feasibility of enumerating alternative options for the search process. Evaluation of their implementation in points took into account the characteristics of the levels of development of the alternative style of thinking presented above. The data obtained indicate that more than half of the surveyed schoolchildren can be assigned to the initial level of such development (52%), 39% to the average level, and only 9% to the high level. These data indicate that teaching mathematics in itself in accordance with the current curriculum does not yet provide a high level of development of the alternative style of thinking of schoolchildren.

Approbation of the proposed methodological solutions was carried out in two segments, differing from each other in the number of students involved and the nature of the experimental work.

1. A “free” experiment was carried out in several schools, gymnasiums and lyceums in Penza (№№ 3, 6, 11, 12, 42, 47), covering about 200 students. It was preceded by a lot of preparatory work. In the course of its implementation, we read a series of lectures for teachers in the field of advanced training, as well as mathematicians of the final year of Penza State University (as part of elective courses), in which the listeners were familiarized with the main theoretical provisions of the developed concept and a number of teaching materials.

Additional group and individual consultations were held with teachers who expressed their willingness to take part in the experiment. A special role in the implementation of this strategy was given to the initial and current diagnostics of relatively stable indicators of the development of an alternative style of thinking in order to clarify the individual educational trajectory of a particular student.

The experimental work was carried out for two years in accordance with the above recommendations, taking into account the achieved level of development of objective motivation. Throughout this period, regular observations of the course of the educational process were carried out, open lessons were organized, laboratory experiments and conversations with students were conducted.

Without purporting to be an exhaustive categorical conclusion, we consider it possible to note certain positive shifts in the development of the alternative style of schoolchildren’s thinking, which were found in a significant number of the schoolchildren who participated in the experiment. These schoolchildren have significantly increased their interest in solving tasks of a creative and research nature. Moreover, when performing such tasks, they in most cases independently transformed their conditions on the basis of implementing alternative search strategies possible in a given situation. In the course of studying the theory, the students involved in the experiment tried to “get ahead” of the teacher’s plan, “to see the goal from afar.” At the same time, a certain independence of judgment became more characteristic of them, expressed in a more critical and reflexive attitude to the decision made, the desire to supplement and improve it in relation to both the analyzed situation and a wider class of mathematical concepts.

2. The “local” experiment was carried out in one of the lyceums of the city of Penza, where one of the authors of the article worked for 10 years as a methodologist and teacher of mathematics. Purposeful experimental work in line with the studied issues was carried out at the Lyceum for three years from 2018 to 2020. At the beginning of this work, the teachers of mathematics of the experimental classes were given explanations of its goals and content, discussed the possibilities of implementation, and proposed educational materials that included systems of tasks of a special type corresponding to different levels of formation of an alternative style of thinking. Ongoing consultations were offered to teachers in the course of attending lessons, analyzing the results of control and cross-sectional works.

To partially confirm the effectiveness of the proposed tools, the results of 52 students in grades 3-4 were analyzed separately, some of whom worked according to the traditional method (27 students), and the other part according to the methodology proposed by the authors (25 students). At the first stage of the study, a number of introductory tests were carried out, consisting of tasks that imply elements of the study of task structures and the feasibility of enumerating alternative options for the search process. The distribution according to the levels of formation of alternative thinking of schoolchildren was carried out in accordance with the criteria reflected in the section “Materials and Methods”.

Table 3: The results before the experiment

Levels of formation of ATS	Before the experiment
	Experimental group		Control group
	Quantity	%	Quantity	%
Initial	12	48	12	44,4
Medium	8	32	10	37
High	5	20	5	18,6

Table 3 and Figure 5 show that the level of formation of the alternative style of thinking in both groups is rather low. About half of all subjects are at the elementary level, and only about 20% of students have reached a high level.

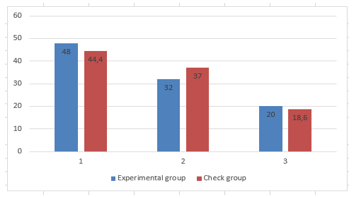Figure 5: The results before the experiment

The data obtained were statistically processed using Pearson’s chi square test (goodness of fit). The processing results are shown in Table 4.

Table 4: The results before the experiment

Levels off ATS	Qemp		Q1-Q2	(Q1-Q2)2	Q1+Q2
	Experimental group	Control group
Initial	12	12	0	0	24	0,00
Medium	8	10	-2	4	18	0,22
High	5	5	0	0	10	0,00
Σ	25	27				0,22

The data in the table indicate the absence of significant differences in the level of development of the alternative style of thinking among students in both groups (empirical value of Pearson’s criterion ). In other words, the nature of the distribution of schoolchildren according to the levels of development of this style was initially approximately the same.

Experimental work within the framework of this study was carried out for two years. In the course of teaching, the pupils of the experimental classes were offered the tasks described above, corresponding to their level of formation of an alternative style of thinking. For the initial level, emphasis was placed on an alternative enumeration of mathematical structures, to which tasks were added to replace the structural components of these structures. At the second and third levels, schoolchildren purposefully worked on a relatively independent compilation and analysis of task systems in accordance with the concept presented in the article.

As a result of the experimental work control measures were again carried out.

Comparison of the dynamics of changes in motivational characteristics in the selected groups of students (Table 5) showed that over the same time interval in the experimental classes, about 40% of students moved to a higher level of development of an alternative style of thinking, while the number and distribution of pupils at each of the levels in the second group changed insignificantly. A few students in this group even showed a slight decrease in interest in mathematics, explained by their future professional choice (not related to mathematical activity).

Table 5: The results after the experiment

Levels of formation of ATS	After the experiment
	Experimental group		Control group
	Quantity	%	Quantity	%
Initial	3	12	10	37
Medium	9	36	13	48,2
High	13	52	4	14,8

The data obtained were again subjected to statistical processing using Pearson’s chi square test (goodness of fit). The processed results are shown on Figure 6 and in Table 5.

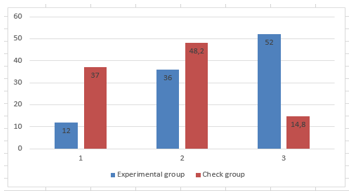Figure 6: The results after the experiment

The results of statistical processing of the data obtained indicate the appearance of significant differences in the analyzed indicator between the schoolchildren of the control and experimental groups (Pearson’s criterion = 9,26)

Table 6: The results after the experiment

Levels off ATS	Qemp		Q1-Q2	(Q1-Q2)2	Q1+Q2
	Experimental group	Control group
Initial	3	10	-7	49	13	3,77
Medium	9	13	-4	16	22	0,73
High	13	4	9	81	17	4,76
Σ	25	27				9,26

In other words, we found a significant difference between the distribution of characteristics of the formation of the alternative style of thinking of schoolchildren in the studied groups of schoolchildren. This difference indicates that the developed methodological solutions are more effective than the traditional ones in terms of the formation of the specified style.

In general, it can be stated that, as evidenced by the results of approbation, the described level-by-level strategy for the formation of an alternative style of thinking of schoolchildren in the process of teaching mathematics proved to be quite effective both in terms of the gradual formation of students’ readiness to overcome their initially one-sided attitudes, and in terms of the development of their cognitive activity generally.

7. Conclusions and Suggestions

In the course of the study, the author’s concept of the level-by-level formation of an alternative style of thinking of schoolchildren in mathematics lessons was developed. As the main means of such formation, it is advisable to consider special tasks that provide for the presence of alternative options for analyzing the elements of its subject area. Within the framework of this concept, the following scientific and methodological results were obtained:

• The important role of the alternative style of thinking is revealed, which underlies the realization of human intellectual activity and which ensures effective interaction with the environment and the ability to tolerantly respond to its diversity.
• It is shown that in the framework of mass school education, insufficient attention is paid to the formation of such a style. As a result, as many publications testify, many schoolchildren master the methods and techniques of educational and search activity as rigid algorithmic structures that hardly allow variation of semantic positions with respect to the concepts under consideration and the relations between them.
• A mathematics course has great potential in terms of the formation of an alternative style of thinking, as it is characterized by the presence of a variety of problem material, the mastering of which is possible from various positions and using various methods. For the full realization of this potential, an adequate pedagogical format is required, within which an alternative style of thinking can be actualized. As such a format, it is advisable to consider the joint activity of a teacher and students in solving special tasks that provide for the availability of alternative options for analyzing the elements of their subject area.
• When planning work on the development of an alternative style of thinking for schoolchildren in the process of teaching mathematics, it is advisable to single out a number of levels of formation of this style, the multifaceted characteristics of which are presented in the text of the article. This characteristic formed the basis for the development of diagnostic tools that ensure the assignment of a student to the appropriate level.
• The content of the work revealed the transition of schoolchildren up the “ladder of levels”. At the initial stage, such work is directly related to a basic enumeration of possible options for the state of a particular task structure and its possible transformation. At the next stage, a purposeful search for opportunities to connect the problem situation under consideration with a more familiar alternative problem structure by reformulating its condition is carried out, as well as identifying how promising this structure is in terms of choosing a possible search direction. Finally, at the third stage of the work, the alternative style of thinking is actualized as a result of a conscious free choice from a number of implicitly presented meaningful alternatives. Such a choice can be provided on the basis of a step-by-step transformation of the components of the task situation, leading to the construction of a sequence of new alternative task structures, which is accompanied by their comparative analysis.
• On the basis of the selected theoretical positions, teaching materials were developed, which were successfully tested in a number of schools in Penza (Russia) over a number of years. As evidenced by the results of approbation, subjected to statistical processing, the level-by-level strategy, as described by the author, for the formation of an alternative style of thinking for schoolchildren in the process of learning mathematics proved to be, on the whole, quite effective both in terms of forming students’ readiness to overcome their initially one-sided attitudes, and in terms of developing their cognitive activity on the whole.

At the next stage of the research, we plan to organize a wider pedagogical experiment to determine the optimal means of implementation of the proposed recommendations into a meaningful compilation of various programs in mathematics for different countries and regions.

1. M. Uzunoglu, M.S. Alam, “Dynamic modeling, design and simulation of a P 1. V.P. Zinchenko, Psychological Foundations of Pedagogy (Psychological and Pedagogical Bases for the Construction of Elkonin-Davydov System of Developmental Education), Moscow, Gardariki, 2002.
2. E. de Bono, Lateral Thinking: A Textbook of Creativity, London, Penguin Books, 1977.
3. R.M. Granovskaya, Yu.S. Krizhanovskaya, Creativity and Overcoming Stereotypes, St. Petersburg, OMS Publ., 1994.
4. M.A. Kholodnaya, Cognitive Psychology. Cognitive Styles, Moscow, Yurait Publ., 2018.
5. V.G. Thomas, B.A. Parsons, “Culturally responsive evaluation meets systems-oriented evaluation,” American Journal of Evaluation, 38(1), 7–28, 2016, doi: 10.1177/1098214016644069.
6. N.N. Khramova, M.M. Rodionov, “The development of thinking variability of schoolstudents in mathematics using 1C: Math designer,” Computer Science and Education, 7(256), 15–21, 2014.
7. W. Lake, M. Wallin, G. Woolcott, W. Boyd, A. Foster, C. Markopoulos, W. Boyd, “Applying an alternative mathematics pedagogy for students with weak mathematics: meta-analysis of alternative pedagogies,” International Journal of Mathematical Education in Science and Technology, 48(2), 215–228, 2017, doi:10.1080/0020739X.2016.1245876.
8. D. P?lya, Mathematical Discovery: On Understanding, Learning and Teaching Problem Solving, Moscow, Nauka, 1976.
9. M. Rodionov, Z. Dedovets, “The development of students’ intellectual tolerance in the process of teaching mathematics at secondary level,” London Journal of Research in Humanities and Social Sciences, 18(2), 1–11, 2018, https://journalspress.com/LJRHSS_Volume18/397_The-Development-of-Students-Intellectual-Tolerance-in-the-Process-of-Teaching-Mathematics-at-Secondary-Level.pdf.
10. M. Rodionov, Z. Dedovets, “The forming of students’ intellectual tolerance: theoretical study and implementation,” International Journal for Cross-Disciplinary Subjects in Education, 4(1), 775–781, 2014, doi: 10.20533 / ijcdse.2042.6364.2014.0259.
11. M.A. Rodionov, E.V. Marina, Formation of Variable Thinking of School Students in Solving Construction Problems: A Manual, Penza, PSPU Publ., 2006.
12. A.G. Stepanov, “The style of thinking in the formation system mythologemes paintings of socio-historical reality,” Bulletin of Chelyabinsk State University, 8(430), 29–34, 2019, doi: 10.24411/1994-2796-2019-10805.
13. M.A. Gadzhimuradov, Z.D. Gadzhieva, “Features of mathematical thinking and its development when learning geometry,” The World of Science, Culture and Education, 2(69), 189–191, 2018.
14. K.G. Kozhabaev, R.S. Gabdullin, “About pupils thinking development in the process of mathematics training,” Modern High Technologies, 5(3), 554–559, 2016, http://top-technologies.ru/ru/article/view?id=35952.
15. E.K. Galyamova, “Methodological peculiarities of the process of geometry teaching considering the cognitive styles,” Prepodavatel XXI Vek, 1(1), 153–158, 2019.
16. S.N. Lipatova, O.A. Milinis, “Psychological and pedagogical support of the development of students’s giftedness in the system of additional education: innovative model,” Otechestvennaya i Zarubezhnaya Pedagogika, 2(49), 200–210, 2018.
17. C. Plumpton, Generalization and structure. In Process of Learning Mathematics, L.R. Chapman, Ed., Oxford, Pergamon Press, 87–121, 1972.
18. H. Poincaré, The Foundations of Science (Science and Hypothesis. The Value of Science. Science and Method), Moscow, Nauka, 1990.
19. T.L. Killpack, L.C. Melón, “Toward inclusive STEM classrooms: What personal role do faculty play?” CBE Life Sciences Education, 15(3), 2016, doi:10.1187/cbe.16-01-0020.
20. E.Yu Ilaltdinova, V.V. Kisova, “Teaching talent and teaching intellect: theoretical and applied approaches design,” Vestnik of Minin University, 4(25), 2018, doi:10.26795/2307-1281-2018-6-4-9.
21. I. Newton, Mathematical Works. Transl. by D.D. Mordecai-Boltovsky, Moscow, Leningrad, ONTI Publ., 1937.
22. M.A. Rodionov, Formation of Search Motivation in the Process of Teaching Mathematics: A Manual for Students and Teachers, Penza, PSPU Publ., 2001.
23. M.K. Watfa, D. Audi, “Innovative virtual and collaborative teaching methodologies,” Behaviour & Information Technology, 36(7), 663–673, 2017, doi: 10.1080/0144929x.2016.1275806.
24. M.M. Thomson, D. DiFrancesca, S. Carrier, C. Lee, “Teaching efficacy: exploring relationships between mathematics and science self-efficacy beliefs, PCK and domain knowledge among preservice teachers from the United States,” Teacher Development, 21(1), 1–20, 2017, doi:10.1080/13664530.2016.1204355.
25. F. Perls, R. Hefferline, P. Goodman, Experiences in the Psychology of Self-Knowledge: A Workshop on Gestalt Therapy, Moscow, Gil-Estel Publ., 1993.
26. M. Rodionov, Z. Dedovets, E. Pavlova, N. Sharapova, I. Akimova, “Design and implementation of adaptive technology for teaching mathematics to school students based on integrated diagnostic approach to subject preparation and competence development,” Revista Amazonia Investiga, 9(26), 458–472, 2020, doi:10.34069/AI/2020.26.02.53.
27. M.A. Rodionov, E.V. Marina, Developmental Potential of Mathematical Tasks, and Possibilities for its Actualization in the Educational Process: A Manual, Penza, PSPU Publ., 2010.
28. I. Lakatos, Proofs and Refutations: The Logic of Mathematical Discovery, Moscow, Nauka, 1967.
29. J. Engelbrecht, A. Harding, “Interventions to improve teaching and learning in first year mathematics courses,” International Journal of Mathematical Education in Science and Technology, 46(7), 1046–1060, 2015, doi:10.1080/0020739X.2015.1070441.
30. T.A. Chernetskaya, M.A. Rodionov, “Interactive creative environments as a means for forming elements of mathematical research activity in schoolstudents,” Computer Science and Education, 3, 36–41, 2014.
31. V. Mkrttchian, G. Vishnevskaya, M. Rodionov, Avatar-Based Learning and Teaching in Modern Educational Environments: Emerging Research and Opportunities, Hershey, PA, IGI Global, Information Science Reference, 2018.
32. P.C. Abrami, R.M. Bernard, E. Borokhovski, D.I. Waddington, C.A. Wade, T. Persson, “Strategies for teaching students to think critically: a meta-analysis,” Review of Educational Research, 85(2), 275–314, 2015, doi:10.3102/0034654314551063.
33. H. Heckhausen, Motivation and Activity, Vol. 1, Moscow, Pedagogica, 1986.
34. M.A. Rodionov, I.V. Akimova, T.A. Chernetskaya, “Creation of the constructive creative environment on the basis of realization of interactive dynamic models,” In the World of Scientific Discoveries, 9(57), 21–34, 2014, doi:10.12731/wsd-2014-9-2.
35. M. Rodionov, Z. Dedovets, E. Pavlova, N. Sharapova, I. Akimova, “Design and implementation of adaptive technology for teaching mathematics to school students based on integrated diagnostic approach to subject preparation and competence development,” Revista Amazonia Investiga, 9(26), 458–472, 2020, doi:10.34069/AI/2020.26.02.53.
36. V.A. Mazilov, Yu.N. Slepko, “Pedagogical giftedness as a key prerequisite for efficient modern educational system,” Integration of Education, 23(1), 37–49, 2019, doi:10.15507/1991-9468.094.023.201901.037-049.
37. S. Abramovich, A.Z. Grinshpan, D.L. Milligan, “Teaching mathematics through concept motivation and action learning,” Education Research International, 7, 1–13, 2019, doi:10.1155/2019/3745406.
38. G.T. Klinkov, M.A. Rodionov, O.E. Kozlova, E.V. Veszetiu, E.V. Vovk, “Implementation of discussion technologies in a personality-centered professional education,” Revista Amazonia Investiga, 9(26), 82–87, 2020, doi: 10.34069/AI/2020.26.02.9.
39. K.W. Remijan, “Project-based learning and design-focused projects to motivate secondary mathematics students,” Interdisciplinary Journal of Problem-Based Learning, 11(1), 2017, doi:10.7771/1541-5015.1520.

(Click Here)