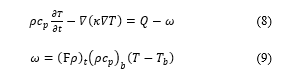1. Introduction

Ventricular tachycardia (VT) is generally related to severe structural heart diseases (SHD) and accounts for an elevated risk of sudden cardiac death in patients with the heart failure [1]. It is also reported that for patients hospitalized with AMI, 5% to 10% of them have ventricular fibrillation (VF) or sustained VT prior to hospital presentation, and another 5% have VF or sustained VT after hospital arrival, most within 48 hours of admission [2]. A report about the incidence and case-fatality of ventricular events in hospital mentioned that the hospital case-fatality rates (CFRs) of VT declined from 27.7% to 6.9% and the incidence rates (IRs) declined from 14.3% to 10.5% from 1986 to 2009. This report concluded that the CFRs and IRs of VT are decreased, but it’s still necessary to timely identify and treat patients with these serious ventricular arrhythmias [3]. Implantable cardioverter defibrillators (ICDs) remain the main method for the primary and secondary prevention of sudden cardiac death associated with these arrhythmias [4]. However, ICDs can only be used for treatment, not for the prediction or prevention of ventricular arrhythmia [4]. ICDs are effective but their shocks are painful and can lead to post-traumatic stress disorders [5]. As a first line drug for arrhythmias, amiodarone can reduce arrhythmias for some patients but have limited efficacy for long-term management [6].

Radiofrequency (RF) catheter ablation has been proved as an effective treatment method for ventricular arrhythmias [7]. Particularly, the use of RF to treat atrial fibrillation (AF) has a history of more than 20 years [8]. Catheter ablation causes partial necrosis of lesion and therefore restore normal heart rhythms. Unipolar ablation (UA) is the standard configuration of catheter ablation, i.e., a singular electrode and a sheet ground on body surfaces [9]. UA is routinely used in clinical practice, but the effect and the treatment process of UA are expected to be improved [10][11]. Bipolar ablation (BA) can deliver concentrated energy between two electrodes. BA’s focused energy delivery shortens ablation durations and minimizes lesion width; therefore, this reduces the potential of adjacent tissue injury. Although BA is still under study, it has been shown to be more effective than UA [12].

Computer simulation is an additional method for the study on the mechanisms of cardiac arrhythmias and the procedure of catheter ablation [13]. In [14], the author reported a systematic study on the effectiveness of different ablation line patterns based on a biophysical model. Analysis with a two-dimensional finite element method can also predict temperature distributions in ablation or hyperthermia [15], [16].

Due to the difference in density and other properties, the thermal and electrical conductivities of myocardial fat are significantly different in myocardium, blood  and pericardial fluid [10]. In view of the low electrical conductivity of fat, the therapeutic effects of UA and BA may vary in different myocardial fat’s thickness and  myocardial impedance. Theoretically, when the thickness of cardiac fat increases, the voltage of myocardium would decrease because the impedance of fat is larger, and the electric current decreases as the impedance increases when the ablation power keeps the same value, and vice versa. As a result, the performance of ablation is reduced correspondingly. At present, the main research on radiofrequency ablation is the occurrence of complications and improvement of catheter ablation. However, there are few studies about the effect of myocardial fat’s thickness and myocardial impedance on catheter ablation.

In this study, we conducted computer simulation to investigate the heating effects of UA and BA at different values of myocardial impedance and fat layer’s thickness. To validate the results of computer simulation, we performed an in vitro experiment by using a swine’s heart for comparison.

2. Methods and Materials

2.1. Configurations of Myocardial Fat Thickness and Impedance

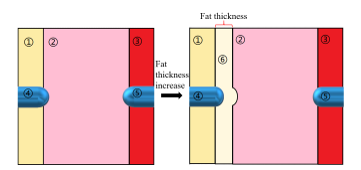Figure 1: 2D model. ① Pericardial fluid, ②Myocardium, ③Blood, ④ Positive electrode, ⑤ Negative electrode, ⑥ Fat.

We created a two-dimensional (2D) myocardial model based on the cross-section of the heart with a fat layer between the pericardial fluid and the myocardium as illustrated in Figure 1. To reflect most clinical conditions, fat thickness of 0-2mm was set [17]. Considering the pressure of the electrode on myocardium, the fat layer under the electrode invades has a distortion as the semidiameter of the electrode [18]. In this model, we set up a thin layer of pericardial fluid and blood with a thickness of 3 mm, and for myocardium, the thickness is 10 mm [10], [19]. The ablation electrodes have a radius of 1.155 mm (7 Fr). The influence from blood and water flow was not considered to simplify this study.

In general, as the heating temperature of radiofrequency ablation does not exceed 100°C, the conductivity of body tissue in the model increases with temperature up to 100° C as follows,

where  is impedance, max the increasing percentage of at 100°C,  the length and  the area. As the conductivity is proportional to impedance [18], we adopted the function of electricity in radiofrequency ablation, and impedance was considered increasing by 5%, 10%, 15% and 20% during the heating period, i.e.,   = 5 , 10 , 15 , and 20 . By

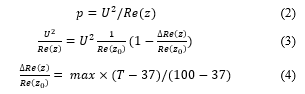
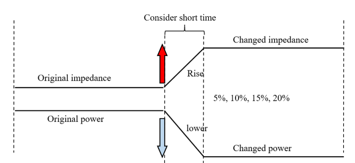Figure 2: The power changed by increased myocardial impedance.

where  is power, and  voltage [20]. We calculated  from  and , and we also hypothesized that the rate of increase of impedance approximately equals to the decreasing rate of power at a constant voltage. In this study,  was set to calculate power. Figure 2 showed the variation of power with impedance.

2.2. Numerical Analysis

In this study, we used the Finite Element Toolbox in MATLAB^TM R2020b (Mathworks Inc., USA) to construct computer models and perform computer simulation. The simulation is converted to a procedure resolving partial differential equations, i.e., parabolic and elliptic functions in partial differential equation (PDE). Boundary conditions have been set to create electric and thermal fields [21]. The electrical frequency in radio frequency ablation is about 500 kHz. The biological medium can be considered almost totally resistive [10][15] because the human’s body scales is about 0.5 m, which is much less than the wavelength of radio frequency wave. This means we can use a quasi-static approach to solve the electrical problem. Laplacian equation serves as the governing equation for calculating the electric potential within a 2D heterogeneous model [10].

where  is the potential, and  the permittivity varying spatially due to the heterogeneity of tissues. From the solution of (5),  the electric field E is got, and the specific absorption rate (SAR)  can be expressed as follows,

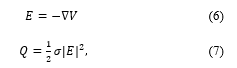where  is the electric conductivity. Based on SAR, i.e.,  obtained above, and Penne’s bioheat transfer equation as follows[15][22], we can obtain temperature distributions.

Table 1: Parameters used in the computer simulation Parameters Pericardial effusion 1.35 118.00 0.63 Myocardial 0.61 113.00 0.60 Fat 0.05 20.00 0.22 Blood 1.10 118.00 0.54   , Conductivity;  electric constant; , Thermal Conductivity; ,Density; , Specific heat capacity

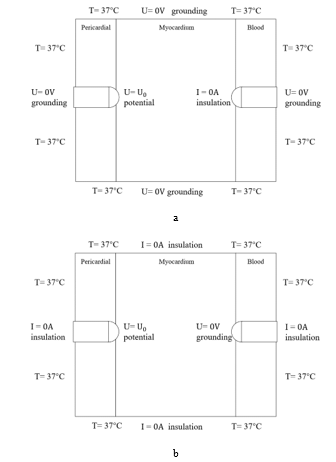Figure 3: The boundary conditions of electric and thermal fields for UA (a) and BA (b).

In equation (8),  is the density,  the constant pressure specific heat capacity,  thermal conductivity,  temperature, and  SAR  calculated by equation (7). In equation (9),  is the heat taken away by the blood flow rate , and  blood temperature, with an initial temperature of myocardium (37°C). 2-D FEM can be used to solve equations (5)-(9) numerically. Spatially and temporally variable physical parameters like current, potential and heat are mapped to first-order triangular elements [23]. Then, equations (5)-(8) are discretized, converted into a matrix notation and solved with  finite element method (FEM). Equation (8) is discretized spatially and temporally; therefore, a transient state is hypothesized to resolve this problem. Finally we got the temperature distribution [15].

We employed two boundary conditions including Dirichlet and Neumann boundary conditions. For the configurations of electric field, Dirichlet boundary condition is used to constrain the potential of electrode, and Neumann boundary condition is used to calculate electric currents, mainly setting the outer boundaries to be of air insulation. Figure 3 shows the boundary conditions in computer simulation, including the initial temperature and electrodes boundary conditions.

The initial temperature in BA and UA is 37°C. It is hypothesized that the temperature in the perpendicular direction of the model is the same, so that the temperature conduction is only affected by the electrode and the initial temperature in the 2D model. For the bipolar model in Figure 3(b), the left and right electrodes are positive and grounded (U=0V), respectively; for the unipolar model shown in Figure 3(a), the positive electrode is the same as that of the bipolar model, but the negative electrode is insulated (I=0A). Table 1 listed the parameters used in the computer simulation [10], [18].

2.3. Experiment

We conducted an in vitro experiment to perform catheter ablation  using a swine’s heart, thus we can validate the results of computer simulation. A glass tank filled with water at normal temperature(22 ) was employed to simulate the environment of human tissue, and a swine’s myocardium was used to perform UA and BA. The  power of  30W lasts for 30s and 50W for 10s. Figure 4 shows the experiment results of swine’s myocardium after ablation.

Table 2 lists the experiment results for the models with 2 mm’s  fat layer and without fat, including the lesion depth and width in swine’s myocardium under different parameters of ablation durations and powers. The power and duration of heating commonly used in clinical practice were used in the experiment. Based on the experimental results, even though the cooling effect of water may reduce the efficiency of ablation, the transmural damage was obtained in the myocardium with a thickness of 8 mm. The heating effects of BA are better than those of UA in any ablation configurations. The existence of myocardial fat has a significantly stronger effect on the results of BA, and we usually don’t use 50W power in BA heating for 30s because the power is too strong, and may put patients at risk if the heating time is too long.

Table 2: Experiment Result Compared with Simulation Result

Experiment Result (environmental temp.: 22 )
Power/time	Lesion thickness (without fat)
	Uni. Diameter(mm)	Uni. Depth(mm)	Bi. Diameter(mm)	Bi. Depth(mm)
30W/ 30s	6.0	3.0	6.0	8.0
50W/ 10s	7.0	5.0	—	—
Power/time	Lesion thickness (with 2mm fat)
	Uni. diameter(mm)	Uni. depth(mm)	Bi. diameter(mm)	Bi. depth(mm)
30W/ 30s	6.5	3.0	5.5	5.0
50W/ 10s	7.5	4.5	—	—
Simulation Result (environmental temp.: 22 )
Power/time	Lesion thickness (without fat)
	Uni. diameter(mm)	Uni. depth(mm)	Bi. diameter(mm)	Bi. depth(mm)
30W/ 30s	6.5	3.5	6.5	10.0
50W/ 10s	7.0	5.5	—	—
Power/time	Lesion thickness (with 2mm fat)
	Uni. diameter(mm)	Uni. depth(mm)	Bi. diameter(mm)	Bi. depth(mm)
30W/ 30s	6.5	3.5	6.0	5.5
50W/ 10s	7.5	5.0	—	—

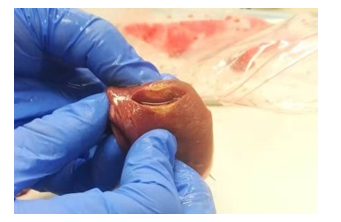Figure 4: The results of a 30s 30w unipolar ablation experiment performed by a physician using an in vitro swine’s myocardium. The lesion has a diameter of 6.00mm, and a depth of 3.00mm.

3. Results

Table 2 lists the simulation results obtained under the same configurations. Through comparison, the lesion thicknesses in the simulation are nearly the same but better than those in experiments. This may attribute to that the ablation parameters were more ideal in simulation. As the lesion thickness is the main therapeutic effect index in catheter ablation, we may believe the results are basically the same.

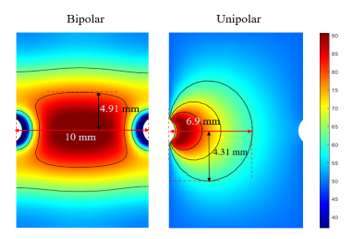Figure 5: Simulation under 16W ablation for 120 s.

Simultaneously, in order to further ensure the accuracy of the simulation results, we also set the same ablation parameters based on a research report published in 2014 to validate the simulation [10]. We set an ablation configuration with a power of 16W ablation for 120 s. The results of the study are shown in Figure 5. Our simulation results are similar to those in [10], so we can ensure that our simulation results are basically consistent with the experiment and related research.

In this study, we selected central regions from the experimental results for calculating transmural lesion ratios (TLR), a 10 mm×5 mm red rectangle shown in Figure 6. Thus we have:

We also visualized the temperature distribution in order to better observe heating areas as shown in Figure 6. The colormap was changed from colorful to gray levels from 0 to 255, and we found the appropriate threshold value to differentiate the temperature after testing, regions at 37 to 59  corresponded to the gray levels from 0 to 93 are marked in black, 60 to 100 corresponded to the gray levels from 94 to 254 marked in gray, and more than 100  corresponded to the gray level 255  marked in white.

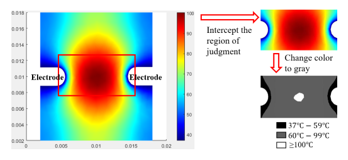Figure 6: The visualization of temperature distribution.

At regions above 100 , the blood vaporizes and clots to form a thrombus. This is a situation that needs to be avoided during therapy. In the study, the simulation temperature may be too high due to the absence of cooling liquid, and we treat this as a tissue necrosis.

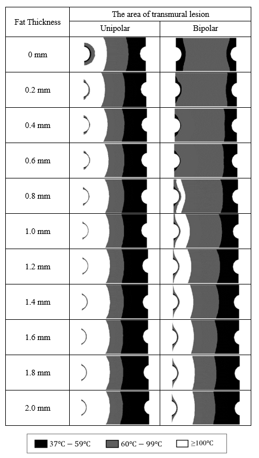Figure 7: The area of transmural lesion of UA and BA under different fat thickness.

Figure 7 shows simulated heating results under the heating power of 30 W in UA and BA with ablation time of 60s. We observed that when the fat thickness is less than 1 mm, BA has obvious advantages over UA. BA can effectively control the high temperature range and maintain a wall penetration effect. When the fat thickness is greater than 1 mm, the controllability of BA gradually decreases. This heating results of UA are almost unaffected by fat thickness, but the local temperature is too high and transmural effect is not ideal in the UA.

Figure 8 shows the TLR of simulation under UA and BA with the variation of myocardial fat’s  thickness. Both UA and BA’s heating effects show an overall reduced trend. The TLR of BA are better than that of UA, but with the increasing of the fat’s thickness, the TLR of BA decline slightly faster. When the fat’s thickness is 0.2 mm, as heat begins to transfer to the fat, the temperature around the fat rises, leading to a sudden improvement in transmural heating effects. The TLR of UA also tends to be stable when the fat’s thickness is over 0.2 mm.

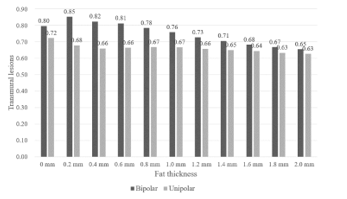Figure 8: TLR of UA and BA under different fat thickness.

In this study, we considered the myocardial impedance increased 5%, 10%, 15% and 20% from the original impedance when the ablation power is 30W and sustains for 60 s. Figure 8 shows the TLR of simulated UA and BA under different heating time with increased impedance.

Figure 9 shows that the transmural lesions of both UA and BA generally decrease as the impedance increases. For BA, heating effect is poor at the beginning because the heat is still in the accumulation stage. When the heating duration is 30s to 40s, the transmural lesion increases rapidly and stabilizes after more than 40s. The final transmural effect of BA is stronger than that of UA. For UA, transmural lesion increases slowly and steadily. This indicates UA did not change drastically when impedance changed. As a result, the ablation effect of BA is more sensitive to myocardial impedance.

4. Discussion

This study compared the impact of myocardial fat’s thickness and impedance changes on the heating effect of catheter ablation. From the simulation, we roughly identified a range of fat thickness, i.e., a fat thickness less than 1 mm, that BA has obvious advantages, including controllable temperature and a well transmural effect over UA. Because the UA has a radial range of action, fat does not change the direction of current conduction and UA is basically stable from the variation of fat’s thickness and myocardial impedance. Therefore, UA is nearly unaffected by external conditions in case of excessive myocardial fat or impedance uncertainty.

In terms of ablation effect, we found BA demonstrated better results. The heat diffuses from the middle to ensure higher transmural ability, and the dispersed heat also reduces the burning temperature and ensures safety. Thus, for patients with lower BMI, BA might be a better choice. Less myocardial fat can reduce heat accumulation and lead to lower myocardial impedance. On the other hand, since the conductivity of fat is lower than that of

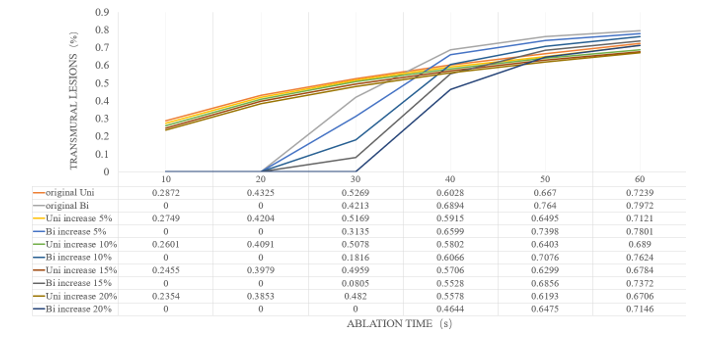Figure 9: TLR of UA and BA under different impedance during ablation time.

myocardium,  pericardial effusion and blood, fat thickness may be positively correlated with myocardial impedance, but their relationship remains to be determined by further studies.

In addition to the influence from myocardial fat’s thickness and myocardial impedance, we also studied the ablation time to further understand the heating duration and characteristics of UA and BA. We found that BA is more sensitive to time variations. As far as the simulation conclusion is concerned, UA has a better ablation than effect 30s ago, and the BA effect is significantly improved, which is better than UA after 30 s. Time may be an important variable that affects BA. High-power and short-term ablation is the goal pursued by catheter ablation, but cooling water is necessary under UA in case of increasing power. Otherwise, blood steam evaporation may occur. Thus BA may avoid blood steam evaporation.

Using a 2D model for biological research has some advantages over 3D model because the calculation time of 2D model is greatly shortened. In contrast, the calculation time of a 3D model is longer, but the simulation results are closer to actual situations. Furthermore, flow of blood and cooling water can be easily introduced in a 3D model [24], [25]. These are hard to be set in a 2D model [26]; therefore, they are not considered in this study.

5. Conclusions

We perform a study about the effect of myocardial fat’s thickness and myocardial impedance on catheter ablation using computer simulation. The results indicate that the thickness of fat layer and myocardial impedance change may have influence on the heating performance of BA to a certain degree. Therefore, for patients with lower BMI, BA might be a better choice. The effect of UA is more stable for patients with higher BMI. We also proved that the BA has better ablation effects compared with those of UA when there are small variations of myocardial fat’s thickness and myocardial impedance.

6. Future Work

In the future, we will extend the 2D cardiac model to a 3D cardiac model and consider the influence of blood flow and electrode types on the performance of UA and BA.

Acknowledgements

This research is partially supported by Japan Society For The Promotion of Science Kakenhi Basic Research Fund 18K11532& 21K10287, and 2021 Competitive Research Fund of The University of Aizu P-5.

1. W.G. Stevenson, K. Soejima, “Catheter Ablation for Ventricular Tachycardia,” Circulation, 115(21), 2750–2760, 2007, doi:10.1161/CIRCULATIONAHA.106.655720.
2. S.M. Al-Khatib, W.G. Stevenson, M.J. Ackerman, W.J. Bryant, D.J. Callans, A.B. Curtis, B.J. Deal, T. Dickfeld, M.E. Field, G.C. Fonarow, A.M. Gillis, C.B. Granger, S.C. Hammill, M.A. Hlatky, J.A. Joglar, G.N. Kay, D.D. Matlock, R.J. Myerburg, R.L. Page, “2017 AHA/ACC/HRS Guideline for Management of Patients With Ventricular Arrhythmias and the Prevention of Sudden Cardiac Death: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines and the Heart Rhythm Society,” Journal of the American College of Cardiology, 72(14), e91–e220, 2018, doi:10.1016/J.JACC.2017.10.054.
3. H. V. Tran, A.S. Ash, J.M. Gore, C.E. Darling, C.I. Kiefe, R.J. Goldberg, “Twenty-five year trends (1986-2011) in hospital incidence and case-fatality rates of ventricular tachycardia and ventricular fibrillation complicating acute myocardial infarction,” American Heart Journal, 208, 1–10, 2019, doi:10.1016/J.AHJ.2018.10.007.
4. K. Shivkumar, “Catheter Ablation of Ventricular Arrhythmias,” Https://Doi.Org/10.1056/NEJMra1615244, 380(16), 1555–1564, 2019, doi:10.1056/NEJMRA1615244.
5. M.O. Sweeney, “The Contradiction of Appropriate Shocks in Primary Prevention ICDs,” Circulation, 122(25), 2638–2641, 2010, doi:10.1161/CIRCULATIONAHA.110.000208.
6. G.H. Bardy, K.L. Lee, D.B. Mark, J.E. Poole, D.L. Packer, R. Boineau, M. Domanski, C. Troutman, J. Anderson, G. Johnson, S.E. McNulty, N. Clapp-Channing, L.D. Davidson-Ray, E.S. Fraulo, D.P. Fishbein, R.M. Luceri, J.H. Ip, “Amiodarone or an Implantable Cardioverter–Defibrillator for Congestive Heart Failure,” Http://Dx.Doi.Org/10.1056/NEJMoa043399, 352(3), 225–237, 2009, doi:10.1056/NEJMOA043399.
7. L.S. Klein, H.T. Shih, F.K. Hackett, D.P. Zipes, W.M. Miles, “Radiofrequency catheter ablation of ventricular tachycardia in patients without structural heart disease.,” Circulation, 85(5), 1666–1674, 1992, doi:10.1161/01.CIR.85.5.1666.
8. M. Haïssaguerre, P. Jaïs, D.C. Shah, A. Takahashi, M. Hocini, G. Quiniou, S. Garrigue, A. Le Mouroux, P. Le Métayer, J. Clémenty, “Spontaneous Initiation of Atrial Fibrillation by Ectopic Beats Originating in the Pulmonary Veins,” Http://Dx.Doi.Org/10.1056/NEJM199809033391003, 339(10), 659–666, 2009, doi:10.1056/NEJM199809033391003.
9. X. Zhu, D. Yang, W. Lu, W. Chen, D. Wei, K. Fukuda, H. Shimokawa, “Computer simulation of cathode ablation for atrial fibrillation,” Proceedings – 2014 IEEE International Conference on Computer and Information Technology, CIT 2014, 721–725, 2014, doi:10.1109/CIT.2014.37.
10. A. González-Suárez, M. Trujillo, J. Koruth, A. d’Avila, E. Berjano, “Radiofrequency cardiac ablation with catheters placed on opposing sides of the ventricular wall: Computer modelling comparing bipolar and unipolar modes,” Http://Dx.Doi.Org/10.3109/02656736.2014.949878, 30(6), 372–384, 2014, doi:10.3109/02656736.2014.949878.
11. R.R. Tilz, A. Rillig, A.M. Thum, A. Arya, P. Wohlmuth, A. Metzner, S. Mathew, Y. Yoshiga, E. Wissner, K.H. Kuck, F. Ouyang, “Catheter ablation of long-standing persistent atrial fibrillation: 5-year outcomes of the hamburg sequential ablation strategy,” Journal of the American College of Cardiology, 60(19), 1921–1929, 2012, doi:10.1016/J.JACC.2012.04.060.
12. G. SIVAGANGABALAN, M.A. BARRY, K. HUANG, J. LU, J. POULIOPOULOS, S.P. THOMAS, D.L. ROSS, A. THIAGALINGAM, P. KOVOOR, “Bipolar Ablation of the Interventricular Septum is More Efficient at Creating a Transmural Line than Sequential Unipolar Ablation,” Pacing and Clinical Electrophysiology, 33(1), 16–26, 2010, doi:10.1111/J.1540-8159.2009.02602.X.
13. B. Avitall, “Computer simulation of ventricular tachyarrhythmias during coronary artery ligation and release,” Journal of Electrocardiology, 12(1), 17–22, 1979, doi:10.1016/S0022-0736(79)80040-0.
14. A.F. Members, A.J. Camm, G.Y.H. Lip, R. De Caterina, I. Savelieva, D. Atar, S.H. Hohnloser, G. Hindricks, P. Kirchhof, E.C. for P.G. (CPG), J.J. Bax, H. Baumgartner, C. Ceconi, V. Dean, C. Deaton, R. Fagard, C. Funck-Brentano, D. Hasdai, A. Hoes, P. Kirchhof, J. Knuuti, P. Kolh, T. McDonagh, C. Moulin, B.A. Popescu, Ž. Reiner, U. Sechtem, P.A. Sirnes, M. Tendera, et al., “2012 focused update of the ESC Guidelines for the management of atrial fibrillationAn update of the 2010 ESC Guidelines for the management of atrial fibrillationDeveloped with the special contribution of the European Heart Rhythm Association,” European Heart Journal, 33(21), 2719–2747, 2012, doi:10.1093/EURHEARTJ/EHS253.
15. N. Tsuda, K. Kuroda, Y. Suzuki, “An inverse method to optimize heating conditions in RF-capacitive hyperthermia,” IEEE Transactions on Biomedical Engineering, 43(10), 1029–1037, 1996, doi:10.1109/10.536904.
16. P.M. Van Den Berg, A.T. De Hoop, A. Segal, N. Praagman, “A Computational Model of the Electromagnetic Heating of Biological Tissue with Application to Hyperthermic Cancer Therapy,” IEEE Transactions on Biomedical Engineering, BME-30(12), 797–805, 1983, doi:10.1109/TBME.1983.325081.
17. J.-W. Jeong, M.H. Jeong, K.H. Yun, S.K. Oh, E.M. Park, Y.K. Kim, S.J. Rhee, E.M. Lee, J. Lee, N.J. Yoo, N.-H. Kim, J.C. Park, “Echocardiographic Epicardial Fat Thickness and Coronary Artery Disease,” Circulation Journal, 71(4), 536–539, 2007, doi:10.1253/CIRCJ.71.536.
18. M. Trujillo, E.B.-I.J. of Hyperthermia, undefined 2013, “Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency,” Taylor & Francis, 29(6), 590–597, 2013, doi:10.3109/02656736.2013.807438.
19. C.E. Hamner, D.D. Potter, K.R. Cho, A. Lutterman, D. Francischelli, T.M. Sundt, H. V. Schaff, “Irrigated radiofrequency ablation with transmurality feedback reliably produces cox maze lesions in vivo,” Annals of Thoracic Surgery, 80(6), 2263–2270, 2005, doi:10.1016/J.ATHORACSUR.2005.06.017.
20. C. Luca. Electrical impedance: principles, measurement, and applications. CRC Press, 2012.
21. P. George F., and William G. Gray. Finite element simulation in surface and subsurface hydrology. Elsevier, 2013.
22. M. Ezzat, N. AlSowayan, … Z.A.-M.-H. and M., undefined 2014, “Fractional modelling of Pennes’ bioheat transfer equation,” Springer, 50(7), 907–914, 2014, doi:10.1007/s00231-014-1300-x.
23. T. Nakata, N. Takahashi, “Direct finite element analysis of flux and current distributions under specified conditions,” IEEE Transactions on Magnetics, 18(2), 325–330, 1982, doi:10.1109/TMAG.1982.1061870.
24. A. González-Suárez, E. Berjano, J.M. Guerra, L. Gerardo-Giorda, “Computational Modeling of Open-Irrigated Electrodes for Radiofrequency Cardiac Ablation Including Blood Motion-Saline Flow Interaction,” PLOS ONE, 11(3), e0150356, 2016, doi:10.1371/JOURNAL.PONE.0150356.
25. J.M. GUERRA, E. JORGE, S. RAGA, C. GÁLVEZ-MONTÓN, C. ALONSO-MARTÍN, E. RODRÍGUEZ-FONT, J. CINCA, X. VIÑOLAS, “Effects of Open-Irrigated Radiofrequency Ablation Catheter Design on Lesion Formation and Complications: In Vitro Comparison of 6 Different Devices,” Journal of Cardiovascular Electrophysiology, 24(10), 1157–1162, 2013, doi:10.1111/JCE.12175.
26. L. Zou, L. Jing, V. Cvetkovic, “Shear-enhanced nonlinear flow in rough-walled rock fractures,” International Journal of Rock Mechanics and Mining Sciences, 97, 33–45, 2017, doi:10.1016/J.IJRMMS.2017.06.001.

(Click Here)