Model Reduction H? Finite Frequency of Takagi-Sugeno Fuzzy Systems
Adv. Sci. Technol. Eng. Syst. J. 6(5), 53–58 (2021);
DOI: 10.25046/aj060507
The daily treats model reduction finite frequency (FFMR) design for Takagi Sugeno (T S) systems. This work is to FFMR design in such a way whether augmented model is steady get a reduced H? index in FF areas with noise is established as a prerequisite. To highlight the importance of suggested process, a practical application has been made.
1. Introduction
Fuzzy models T-S [1] call for wide observation of various practical industrial applications, mainly as the recognized T-S samples actually approximate nonlinear shapes. The essential characteristic on the sample TS is its general estimation of a nonlinear function. There are large number of results of literature that treat the globally difficulties utilizing the TS fuzzy samples, see [2]–[7].
The our existing sources on model reduction problem and disturbances are based on the whole full frequency (EF) area, which will give several types of model reduction design [8]–[13]. However, most practical industrial applications work in a FF domain. So far, a few applications have been made [14]–[19]. Thus, for this we will present new approaches to solve these problems.
The primary goal of our work is to define a fuzzy model reduction of discrete Model over FF ranges such a way that the augmented model is steady get a reduced H∞ index in FF areas with disturbance is established as a prerequisite. we have also presented an example of simulation in order to exemplify the efficiency of the suggested method.
Notations :
- ”T” : Matrix transposition
- ” ∗ ” : Matrix symmetry
- M > 0 : matrix M is positive
- sym[D] : D + D∗
- HeD∗
2. Problem statement
2.1 System formulation
Envisage the nonlinear model presented by :
Rule x: IF ζ1(µ) is T1i,… ζn(µ) is Tin THEN
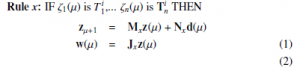
with z(µ) is the input; w(µ) is deliberate output; Mx, Nx and Jx are system parametres; ζ1(µ) ,…, ζn(µ) the premise variables. d(µ) is a known disturbance signal located in a following FF areas
We describe the nonlinear system (1) employ singleton fuzzifer, center-average and inference product by the following relation :
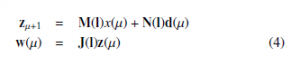
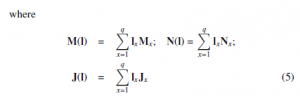
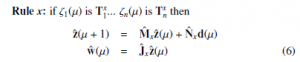
with zˆ(µ) is state MR vector; wˆ (µ) is the output MR function, Mˆ x, Nˆ x and Jˆx are parameters should exist defined.
We get defuzzified for system (6) as following :
Definition 2.1 [20] Consider β > 0, if the following inequality is verified:
From Parseval function [21], we get :
We express the question of this work by : we design an appropriate fuzzy MR system (7) such that a error model is well-posed, stable satises the FF index:
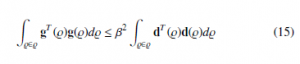
2.2 Preliminaries
Lemma 2.2 [22] Let Φ ∈ Rm, L ∈ Rm×m and S ∈ Rp×m. Then, The following equations are the same:
- Φ∗LΦ < 0, ∀Φ , 0 : SΦ = 0
- S⊥TLS⊥ < 0
- ∃θ ∈ R : L − θSTS < 0
- ∃D ∈ Rm×p : L + DS + STDT < 0
Lemma 2.3 Error system (10) is stable and FF in (15) is fulfilled, on condition that there are B, 0 < C, satisfying
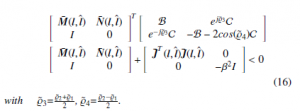
Proof 2.4 The substantiation of Lemma 2.3 is defined in appendix.
3. FF performance analysis
Theorem 3.1 Error model (10) is stable, FF index (15) is fulfilled, on condition that there are X, B, C, E, Z, T satisfying C > 0,
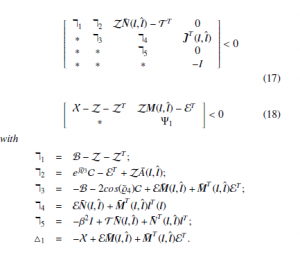
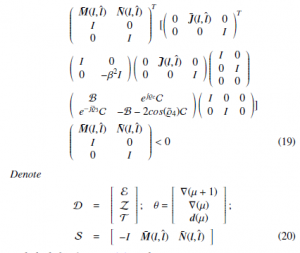
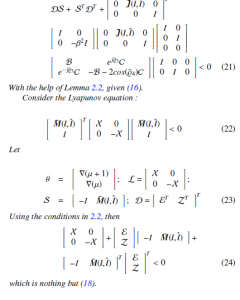
which is nothing but (18).
4. FF performance Design
Theorem 4.1 Error model (10) is stable, FF index (15) is fulfilled,
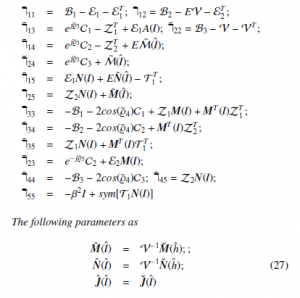
Proof 4.2 Parameterise slack matrices E, Z, T in Theorem 3.1 as
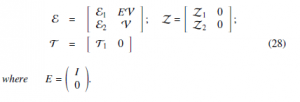
Moreover, the Theorem 4.3 is to solve the FFMR problem in the FF Therefore, us find Theorem 4.1. index (15).
Theorem 4.3 Error model (10) is stable, FF index (15) is fulfilled, Remark 4.5 If us pick C = 0, we mastery employ theorem 4.3 to
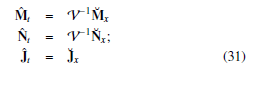
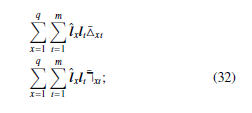
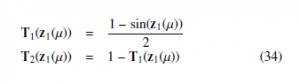
Proof 4.4 We propose the following equations :
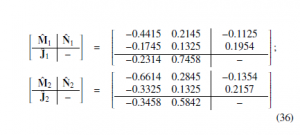
The comparison result with the technique proposed in Theorem 4.3 illustrate in Table 1, that indicate the little conservation of the method suggest in the paper.
The initial cases are proposed null. Figure 1 illustrate the errors e(k) from various approaches. It illustrate the FF method have the best performance in comparison with the EF approach.
Table 1: H∞ performance apply from various approaches
| Frequency | Methods | βmin | Max error |
| −π ≤ % ≤ π | [12] | 0.9715 | 0.0915 |
| −π ≤ % ≤ π | Th4.3 (Q=0) | 0.5514 | 0.0423 |
| Th4.3 | 0.1305 | 0.0088 |
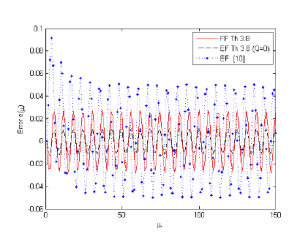
Figure 1: Error response of gµ.
The ratio W(µ) is presented as :
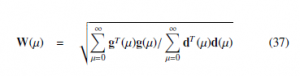
Figures 2 indicate the the ratio in (37), we could notice whether the error model is stable, knowing that the initial Condition are null, that indicate the little conservation of the method suggest in the paper.
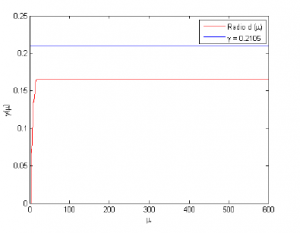
Figure 2: Value of W(µ).
6. Conclusion
This work, we dealt with problematic for the FF model reduction design of nonlinear systems over FF ranges. We have suggested a model reduction process in order to minimize the conservatism design using the frequency information of the disturbances and we have assumed that the disturbances are known in a recognized FF domain. Also, systematic techniques have been suggested for the generation of a model reduction which ensures asymptotic stability and FF H∞ index, at the basis of a more general linearization procedure.
7. Appendix
Multiply equation (16) of for right and by its transposition d(µ)
to the left, we get
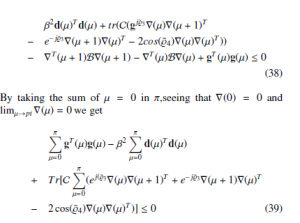
From Parseval function [21], we get :
seeing that, (40) and the FF of signal input %˜1 ≤ %˜ ≤ %˜2, thus (15) is fulfilled.
- T. Takagi, M. Sugeno, ” Fuzzy identification of systems and its applications to modeling and control,” IEEE transactions on systems, man, and cybernetics,
SMC-15(1), 116-132, 1985, doi: 10.1109/TSMC.1985.6313399 - H. Zhang, Y. Shi, A. S. Mehr, ”On H? filtering for discrete time Takagi Sugeno fuzzy Systems,” IEEE Transactions on Fuzzy Systems, 20(2), 396- 401, 2011, doi: 10.1109/TFUZZ.2011.2175933
- A. Benzaouia, A. Hmamed, A. EL Hajjaji, ” Stabilization of controlled posi- tive discrete-time T-S fuzzy systems by state feedback control,” International Journal of Adaptive Control and Signal Processing, 24(12), 1091-1106, 2010, doi: 10.1002/acs.1185
- H. Gao, Y. Zhao, J. Lam, K. Chen, ”H? fuzzy filtering of nonlinear systems with intermittent measurements,” IEEE Transactions on Fuzzy Systems, 17(2), 289-299, 2009.
- L. Zhang, H. Yang, Q. Mao, ”T S fuzzy system identification based on C Express Letter, 13(1), 51-58, 2019.
- M. Nentwig, P. Mercorelli. ”hrottle valve control using an inverse local linear model tree based on a fuzzy neural network,” 7th International Conference on Cybernetic Intelligent Systems, IEEE, 1-6, 2008, doi: 10.1109/UKRI-CIS.2008.4798943
- M. Schimmack, F. Po¨ schke, H., Schulte, P. Mercorelli, ”Observer Strategies for Virtual Sensing of Embroidered Metal-Polymer Heater Structure,” 23rd International Conference on Methods & Models in Automation & Robotics (MMAR) IEEE, 887-892, 2018, doi: 10.1109/MMAR.2018.8486033
- A. C. Antoulas, ”An overview of approximation methods for large-scale dynamical systems,” Annual reviews in Control, 29(2), 181-190, 2005, doi: 10.1016/j.arcontrol.2005.08.002
- K. Glover, ”All optimal Hankel-norm approximations of linear multivariable systems and their L,?-error bounds”. International journal of control,” 39(6), 1115-1193, 1984, doi: 10.1080/00207178408933239
- G. Lastman, ”Reduced-order aggregated models for bilinear time-invariant dynamical systems,” IEEE transactions on automatic control, 29(4), 359-361, 1984, doi: 10.1109/TAC.1984.1103534
- B. Moore, ”Principal component analysis in linear systems: Controllability, observability, and model reduction,” IEEE transactions on automatic control, 26(1), 17-32, 1981, doi: 10.1109/TAC.1981.1102568
- L. Wu, X. Su, J. Qiu, ”Model approximation for discrete-time state-delay systems in the T–S fuzzy framework,” IEEE Transactions on Fuzzy Systems, 19(2), 366-378, 2011, doi: 10.1109/TFUZZ.2011.2104363
- D. Wang, A. Zilouchian. ”Model reduction of discrete linear systems via frequency-domain balanced structure,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 47(6), 830-837, 2000, doi: 10.1109/81.852936
- X. Du, G. H. Yang, ”H? model reduction of linear continuous-time systems over finite-frequency interval,” IET control theory & applications, 4(3), 499-508, 2020, doi : 10.1049/iet-cta.2008.0537
- X. Li, S. Yin, H. Gao, ”Passivity-preserving model reduction with finite frequency H? approximation performance,” Automatica, 50(9), 2294-2303, 2014, doi: 10.1016/j.automatica.2014.07.001
- D. W. Ding, X. J. Li, X. Du, X. Xie,” Finite-frequency model reduction of Takagi-Sugeno fuzzy systems,” IEEE Transactions on Fuzzy Systems, 24(6), 1464-1474, 2016, doi: 10.1109/TFUZZ.2016.2540060
- A. El-Amrani, B. Boukili, A. El-Hajjaji, A. Hmamed, ”H? model reduc- tion for T-S fuzzy systems over finite frequency ranges,” optimal control applications and methods, 39(4), 1479-1496, 2018, doi : 10.1002/oca.2422
- D. W. Ding, X. Xie, X. Du, X. J. Li, ”Finite-frequency model reduction of discrete-time T–S fuzzy state-delay systems,” Neurocomputing, 203, 121-128, 2016, doi: https://doi.org/10.1016/j.neucom.2016.03.053
- A. El-Amrani, A. El Hajjaji, I. Boumhidi, A. Hmamed, A. Aitouche, ”Finite Frequency Approach for H? model reduction of 2D continuous systems,” 27th Mediterranean Conference on Control and Automation (MED) IEEE, 177-182, 2019, doi: 10.1109/MED.2019.8798569
- X. Su, L. Wu, P. Shi, Y. D. Song, ”H? model reduction of Takagi-Sugeno fuzzy stochastic systems”, IEEE transactions on systems, man, and cybernetics. Part B, Cybernetics: a publication of the IEEE Systems, Man, and Cybernetics Society, 42(6), 1574-1585, 2012, doi: 10.1109/tsmcb.2012.2195723
- A. V. Oppenheim, A. S. Willsky, S. H. Nawab. ”Signals and Systems”, 2nd l, Boston University, 1-987, 1996.
- M. J., Lacerda, R. C. F., Oliveira, P. L. D., Peres, ”Robust H2 and H1 filter design for uncertain linear systems via LMIs and polynomial matrices,” Signal
Processing, 91(5), 1115-1122, 2011, doi: 10.1016/j.sigpro.2010.10.013