1. Introduction

       X-ray lasers are a class of lasers in which gain has been demonstrated over various discrete wavelengths ranging from 3.56nm to 46.9nm. Because of the very short-duration and high-energy excitation pulses required to generate these lasers [1], [2], photo excitation method [3], Electron collisional pumping method (ECP), charge transfer technique, electron collisional recombination process and dielectronic recombination pumping are examples of X-ray pumping procedures which using picoseconds chirped pulse amplification (CPA) pulses [4]-[6]. Globally it’s often observed that carbon is abundant element in astrophysical sits having the atmosphere. Emission lines of C-like ions are functionalized at prosopopoeia of the solar, astrophysical and melting plasmas whose illustrating needed exact atomic calculations; where the soft X-ray and XUV regions most of the data was found[7], [8]; thus Electron Collisional Pumping was functionalized to generate   soft X-ray lasers after pumping methods[9], [10].

The process of pumping was illustrated as following:

X_lⁿ⁺ + e               X_uⁿ⁺

where X_lⁿ⁺ is a n-frequencies of atom ionization of the element X that pumping occurrence from lower level “l” to an excited level “u” in the same element atoms.

Theoretically there are more works done for computing the energy states, transition possibilities’ and oscillator powers for Zn (XXV) [11]-[17]; while the gain for the same element not have more studies. The goal of this thesis is to utilize the atomic calculations such as energy states, oscillator powers and spontaneous radiative decay rates which calculated by using (FAC) program depending on  Dirac equation for sixty nine thin-structure states to compute reduced populations and gain coefficients of C-like Zn excited states through a broad extent of electron densities (10⁺²⁰ to10⁺²³) and at several electron temperatures (700, 800, 900, 1000, 1100, 1200, 1300, 1400 & 1500).These calculations might support the experimentalists for generating soft X-ray lasers.

2. Calculations equations used for Gain Coefficient determination

      To calculate gain coefficient firstly energy levels, weighted oscillator strength and radiative rate for allowed transitions should be calculated; then the reduced population should calculated by solving coupled rate equation [18], [19]. After calculating the reduced population, it used to solve the Doppler broadening equation to obtain the gain coefficient.

    Laser emission from Zn (XXV) ions plasma was investigated by studying the relation between several plasma temperatures and electron densities.

According to equation (1)

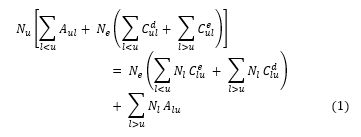   Since  and  are the fractional populations of levels  successively,  represents Einstein coefficient for spontaneous radiative decay from u to l;  represents the electron density and are the rate coefficients for collisional excitation and de-excitation successively. The actual population density  of the  state can be computed from relation (2) [20][21].

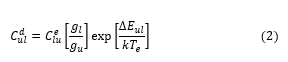  Since  and represents a statistical weights of lower and upper states, successively.

The electron impact excitation rates identified by the effective collision strengths

[20]Where;

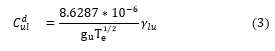The measured population density  of the was calculated [20],

Since is the number of ions which achieved at the ionization stage  [20],

Since is the electron density, is the average degree of ionization and is the fractional abundance of the ionization levels were calculated [20]. Where the populations computed from Equation (1) is equal the unit;

where the populations density calculated by Equation (1) is equal unit,

By computation the state’s population density, the values   and  can be determined.

To prove that when inversion factor (F<0) gives positive gain equation (7) was used[22];

Since  and  are the reduced populations of the upper state and lower state successively. Then Eq. (7) used to compute the gain coefficient (α) for Doppler broadening of the various transitions in the Zn (XXV) ion.

Since M is the ion mass, is the transition wavelength in (nm), and is the ion temperature in eV.

3. Results and discussions

3.1. Energy states

With utilizing (FAC) [23] energy state measures for the 1s² 2s² 2pnl (n=3, l=s, p & d) and ml (m=4,l=s, p, d &f ) configurations in C-like Zn⁺³⁰ was obtained, this data presented in Tables (1); which shows the 69 energy levels of transition configurations:

Table (2) presented the comparison between our calculations of energy levels for Zn (XXV) the theoretical calculations by Bhatia, Seely and Feldman [12] and the actual results computed by NIST [24].

In table (2), the calculated data for energy levels of Zn (XXV) comparing to experimental values in NIST at (2p_1/2 2p_3/2)₁ and (2p_1/2 2p_3/2)₂ by 0.05 and 0.04 successively; and it differs than the theoretical work of Bhatia at (2p_1/2 2p_3/2)₁ and (2p_1/2 2p_3/2)₂ by 0.05 Ryd and 0.04 Ryd successively also; which proved that our calculations are in well agreement with other works.

3.2. Level population

Where increasing the excited electrons in higher energy states than in ground state causes the production of Laser in the XUV and soft X-ray spectral area;

Table 1: Energy states and definitions for Zn (XXV)

* Ryd is Rydberg constant

Schematic diagram of population inversion (Source of figure: https://spie.org/publications/fg08_p94_lasers?SSO=1)

Table 2: The comparison between our calculations of energy levels

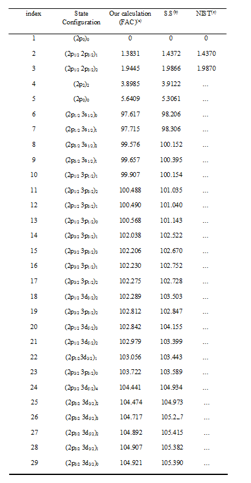Note: (a) present thesis results calculated by (FAC), (b) S.S data is the work done by Bhatia et al. & (c) NIST data.

Thus the process of the reduced population densities was computed for sixty nine thin structure states starting from 1s² 2s² 2pnl (n=3, l=s, p&d) and ml (m=4, l=s, p, d &f) configurations. The determination was done by applying the coupled rate Eq. (1) simultaneously using MATLAB version 7.10.0 (R2010a) computer program [25][17].

Figure (1 to 4) illustrate the reduced population for states (2p_3/23s_1/2)_2, (2p_1/23p_3/2)_1, (2p_3/23p_3/2)_3, (2p_3/23p_3/2)_1, (2p_3/23d_5/2)_4, and (2p_3/23d_3/2)₃at various temperatures (800,900,1000,1100)eV; so it can explain the behavior of states populations’ density for several ions; where at low electron densities the reduced population densities are proportional to the electron densities, and the excitation process for an excited state is followed immediately by radiation decay. These results were agreed with the results of Feldman et.al. [11,17,24]. At electron density 10⁺¹⁹ various peaks were appeared; which means that radiative transitions dominant the de-excitation due its higher energy and fast decay time.

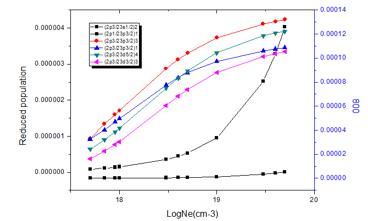Figure 1: Reduced population of Zn⁺³⁰ states at electron temperature 800eV.

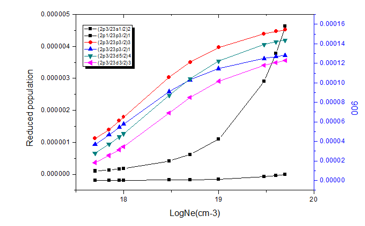Figure 2: Reduced population of Zn⁺³⁰ states at electron temperature 900eV.

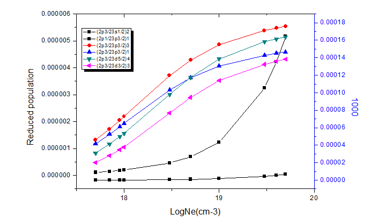Figure 3: Reduced population of Zn⁺³⁰ states at electron temperature 1000eV.

  Let the population of energy E_l be N_l and the population of energy E_u be N_u. The energy between the ground state E_u and excited state E_l is a photon with energy (E_u-E_l) is required to stimulated the transition; however, by using optical pumping electrons from ground state which jumping to excited state by absorbing photons. The stimulated emission and absorption probabilities` per occupied state are the same, therefore we must have a mechanism where N_u > N_l. The reduced populations’ density were computed as a function of electron density then drawn at different plasma temperatures for Zn (XXV) ion. Figure (5, 6) illustrate (2p_1\23p_1\2)₁, and (2p_1\23p_3\2)₁   states for Zn (XXV) were studied at temperatures (700, 800, 900, 1000, 1100, 1200, 1300, 1400&1500) eV.

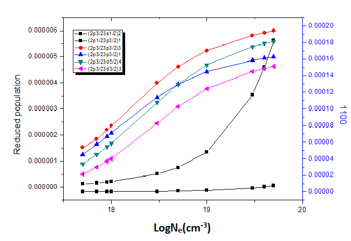Figure 4: Reduced population of Zn⁺³⁰ states at electron temperature 1100eV.

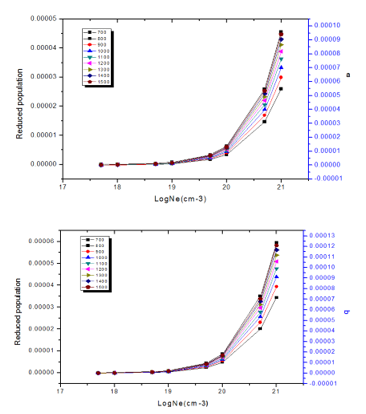Figure 5: Reduced population of level (a) (2p_1\23p_1\2)₁, (b) (2p_1\23p_3\2)₁ for Zn (XXV) after electron collisional pumping as a function of the electron density at temperatures (700, 800, 900, 1000, 1100, 1200, 1300, 1400&1500) eV.

3.3. Radiative lifetime

During the excitation process the electrons transferred from ground state to excited population states, after time electron transition reversed through the depopulation process; the time of reversing the transition in the inverse process called radiative life time. The radiation process of X-ray depending on stimulated emission of radiation from upper to lower states; then using these transition to calculate the life time. By using equation (9) the atomic transfer probability is related to the life time u of an exited state

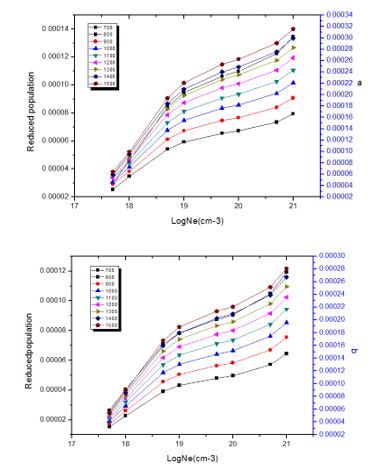Figure 6: Reduced population of level (a) (2p_3\23p_3\2)₃, (b) (2p_3\23p_3\2)₁ for Zn (XXV) as a function of the electron density at different electron temperatures (700,800, 900, 1000, 1100, 1200, 1300, 1400&1500) eV.

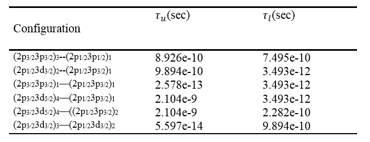
Table 3. Illustrate the results of (2p_1/23d_3/2)₂–(2p_1/23p_3/2)_1, (2p_3/23d_5/2)₄—(2p_1/23p_3/2)₁and (2p_3/23d_5/2)₄—((2p_1/23p_3/2)₂radiative life time is longer than the lifetime of the lower state.

Table 3. Radiative lifetime for Zn³⁰⁺ laser levels

3.4. Inversion factor

According to equation (7) the reduced population for lower states and upper states was calculated and demonstrate in the equation to calculate the inversion factor and it’s found that the inversion factor is larger than zero. By using electron collisional pumping process the pumping quanta can be transferred to other state as a result of collision process, and this cause population inversion from the upper states to the lower states; whence this population inversion achieved appositive gain via F<0[21].

3.5. Gain coefficient

The gain process is the measure of the part of medium energy transferred to the emitted radiation which causes the amplification of the emitted radiation leading to strength optical power.

To calculate the gain the MATlab version the program was used to solve the coupled rate equation; this by using A_ul (spontaneous decay rates), C^e_lu (electron collisional excitation rate coefficients) and C^d_ul (electron collisional deexcitation rate coefficients).

This data is computed by MATlab to solve coupled rate equation to calculate the population inversion; then calculating the inversion factor which F< 0.

Finally the Doppler broadening equation was solved for various transitions to give the gain coefficient; then by plotting the relation between gain and electron density at different temperature to obtain the most intense laser transitions.

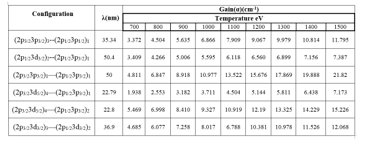
The figures (7, 8, 9, 10 & 11) illustrates the proportional relation between gain and electron density; and also have proportional relation between gain and temperature. According to the collected data it’s found that the largest gain occur at temperature (1100eV) which give gain height of (13.522cm^-1) at wavelength (50nm); this transition is at (2p_3/23p_3/2)₁—(2p_1/23p_3/2)₁ which refers to them by (16<>9). The smallest gain occur at temperature (800eV) which give gain  height of (2.5530cm^-1) at wavelength (22.79nm); this gain transition at (2p_3/23d_5/2)₄—(2p_1/23p_3/2)₁which describe them as (22<>10); the gain of these transition at (22<>10) and at (16<>9) was  plotted against electron densities at different temperatures. See Figure (11).

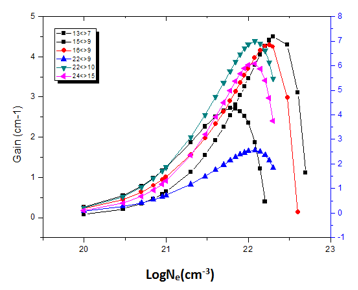Figure 7: Electron density versus Gain coefficient at temperature 800 eV.

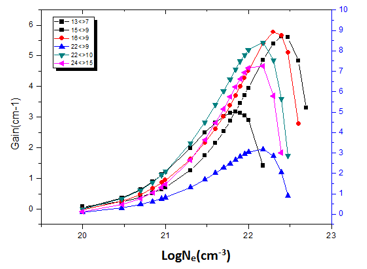Figure 8: Electron density versus Gain coefficient at temperature 900 eV.

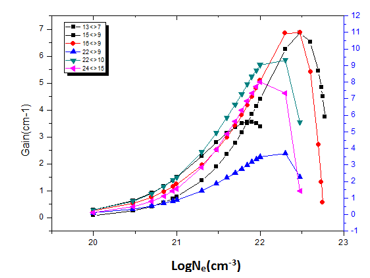Figure 9: Electron density versus Gain coefficient at temperature1000 eV.

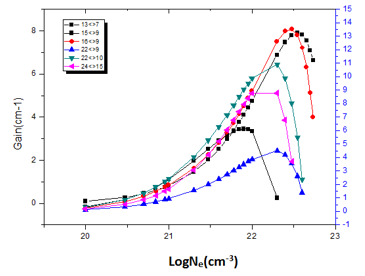Figure 10: Electron density versus Gain coefficient at temperature1100 eV.

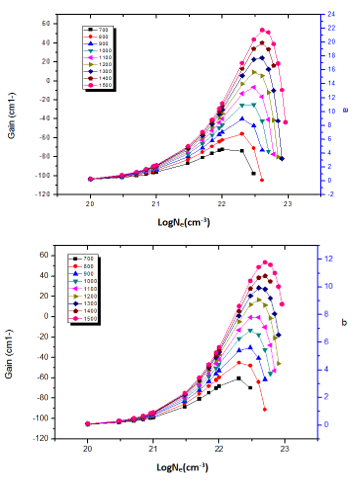Figure 11: Gain coefficient for (a) (2p_3/23p_3/2)₁—(2p_1/23p_3/2)₁ and (b) (2p_3/23p_3/2)₃—(2p_1/23p_1/2)₁ transitions against electron density (Ne) at different electron temperature.

Table 4: configuration states, wavelength and maximum gain coefficient at various temperatures.

4. Conclusions

The electron collisional pumping is appropriate for achieving population inversion. The  comparison of present thesis data with the previous experimental calculated data by NIST and with the theoretical calculated data by Bhatia,Seely&Feldman  was illustrated that energy levels of Zn (XXV) differs than experimental values of NIST at (2p_1/2 2p_3/2)₁ and (2p_1/2 2p_3/2)₂ by 0.05 and 0.04 successively; and differs than the theoretical work of Bhatia at (2p_1/2 2p_3/2)₁ and (2p_1/2 2p_3/2)₂ by 0.05 Ryd and 0.04 Ryd successively also; which proved that our calculations are in well agreement with other works. The results gave spectral region between 22 and 50 nm in the XUV region for the Zn³⁰⁺ion.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors thanks both Prof. Dr. Souad ElFeky, Dr. Nagy Emara, and NILES their promotion and support.

1. W..T. Silfvast, Cambridge University press, second edi, 2000.
2. B.N. Wellegehausen, B., Eichmann, H., Meyer, S., Momma, C., Mossavi, K., Welling, H., &Chichkov, “Generation of coherent VUV and XUV radiation. In ICONO’95: Fundamentals of Laser-Matter Interaction.,” International Society for Optics and Photonics., 2796, 132–139, 1996.
3. A. Verma, R. Kumar, A. Parashar, “Enhanced thermal transport across a bi-crystalline graphene–polymer interface: an atomistic approach,” Physical Chemistry Chemical Physics, 21(11), 6229–6237, 2019.
4. R.E. King, G.J. Pert, S.P. McCabe, P.A. Simms, A.G. MacPhee, C.L.S. Lewis, R. Keenan, R.M.N. O’Rourke, G.J. Tallents, S.J. Pestehe, “Saturated x-ray lasers at 196 and 73 Å pumped by a picosecond traveling-wave excitation,” Physical Review A, 64(5), 53810, 2001.
5. A. V Vinogradov, I.I. Sobel’man, E.A. Yukov, “Population inversion of transitions in neon-like ions,” Soviet Journal of Quantum Electronics, 7(1), 32, 1977.
6. B.A. Norton, N.J. Peacock, “Population inversion in laser-produced plasmas by pumping with opacity-broadened lines,” Journal of Physics B: Atomic and Molecular Physics, 8(6), 989, 1975.
7. G. Tachiev, C.F. Fischer, “Breit-Pauli energy levels and transition rates for the carbonlike sequence,” Canadian Journal of Physics, 79(7), 955–976, 2001.
8. K.M. Aggarwal, F.P. Keenan, A.Z. Msezane, “Oscillator strengths for transitions in C-like ions between K XIV and Mn XX,” Astronomy & Astrophysics, 401(1), 377–383, 2003.
9. V.A. Bhagavatula, “Soft x?ray population inversion by resonant photoexcitation in multicomponent laser plasmas,” Journal of Applied Physics, 47(10), 4535–4537, 1976.
10. J. Nilsen, P. Beiersdorfer, S.R. Elliott, T.W. Phillips, B.A. Bryunetkin, V.M. Dyakin, T.A. Pikuz, A.Y. Faenov, S.A. Pikuz, S. Von Goeler, “Measurement of the Ly-? Mg resonance with the 2s? 3p Ne-like Ge line,” Physical Review A, 50(3), 2143, 1994.
11. U. Feldman, G.A. Doschek, J.F. Seely, A.K. Bhatia, “Short wavelength laser calculations for electron pumping in Be I and BI isoelectronic sequences (18? Z? 36),” Journal of Applied Physics, 58(8), 2909–2915, 1985.
12. A.K. Bhatia, J.F. Seely, U. Feldman, “Atomic data and spectral line intensities for the carbon isoelectronic sequence (Ar XIII through Kr XXXI),” Atomic Data and Nuclear Data Tables, 36(3), 453–494, 1987, doi:https://doi.org/10.1016/0092-640X(87)90012-X.
13. A. Verma, A. Parashar, “Molecular dynamics based simulations to study the fracture strength of monolayer graphene oxide,” Nanotechnology, 29(11), 115706, 2018, doi:10.1088/1361-6528/aaa8bb.
14. A. Verma, A. Parashar, “Molecular dynamics based simulations to study failure morphology of hydroxyl and epoxide functionalised graphene,” Computational Materials Science, 143, 15–26, 2018.
15. V. Singla, A. Verma, A. Parashar, “A molecular dynamics based study to estimate the point defects formation energies in graphene containing STW defects,” Materials Research Express, 6(1), 15606, 2018.
16. A. Verma, A. Parashar, M. Packirisamy, “Atomistic modeling of graphene/hexagonal boron nitride polymer nanocomposites: a review,” Wiley Interdisciplinary Reviews: Computational Molecular Science, 8(3), e1346, 2018.
17. U. Feldman, J.F. Seely, G.A. Doschek, A.K. Bhatia, “3 s–3 p laser gain and x?ray line ratios for the carbon isoelectronic sequence,” Journal of Applied Physics, 59(12), 3953–3957, 1986.
18. U. Feldman, A.K. Bhatia, S. Suckewer, “Short wavelength laser calculations for electron pumping in neon?like krypton (Kr XXVII),” Journal of Applied Physics, 54(5), 2188–2197, 1983.
19. U. Feldman, J.F. Seely, A.K. Bhatia, “Scaling of collisionally pumped 3 s?3 p lasers in the neon isoelectronic sequence,” Journal of Applied Physics, 56(9), 2475–2478, 1984.
20. W.H. Goldstein, J. Oreg, A. Zigler, A. Bar-Shalom, M. Klapisch, “Gain predictions for nickel-like gadolinium from a 181-level multiconfigurational distorted-wave collisional-radiative model,” Physical Review A, 38(4), 1797, 1988.
21. A. V Vinogradov, V.N. Shlyaptsev, “Calculations of population inversion due to transitions in multiply charged neon-like ions in the 200–2000 Å range,” Soviet Journal of Quantum Electronics, 10(6), 754, 1980.
22. I.I.S. Man, Introduction to the theory of atomic spectra, International series of Monographs in Natural Philosophy, Vol. (40), Pergamon Press.
23. [FAC Code. http://kipac-tree.stanford.edu/fac].
24. NIST [http:///F:/NIST/NIST%20ASD%20Levels%20Output32.htm].
25. R.D. Neidinger, “Introduction to automatic differentiation and MATLAB object-oriented programming,” SIAM Review, 52(3), 545–563, 2010.

Citations by Dimensions

Citations by PlumX

Google Scholar

Crossref Citations

1. Robinson Lawrance, Nishith Kumar Reddy Gorla, "System-Level Test Case Design for Field Reliability Alignment in Complex Products", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 6, pp. 55–64, 2025. doi: 10.25046/aj100605
2. Jenna Snead, Nisa Soltani, Mia Wang, Joe Carson, Bailey Williamson, Kevin Gainey, Stanley McAfee, Qian Zhang, "3D Facial Feature Tracking with Multimodal Depth Fusion", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 5, pp. 11–19, 2025. doi: 10.25046/aj100502
3. Koji Oda, Toshiyasu Kato, Yasushi Kambayashi, "Evaluation of a Classroom Support System for Programming Education Using Tangible Materials", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 5, pp. 21–29, 2024. doi: 10.25046/aj090503
4. Ajla Kulaglic, Zeynep Örpek, Berk Kayı, Samet Ozmen, "Analysis of Emotions and Movements of Asian and European Facial Expressions", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 1, pp. 42–48, 2024. doi: 10.25046/aj090105
5. Lucksawan Yutthanakorn, Siam Charoenseang, "Augmented Reality Based Visual Programming of Robot Training for Educational Demonstration Site", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 5, pp. 8–16, 2023. doi: 10.25046/aj080502
6. Fadwa Bouhannana, Akram El Korchi, "Application of Lean Practices in Food Supply Chain: The Case of Morocco", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 4, pp. 101–110, 2023. doi: 10.25046/aj080412
7. Seungjea Lee, Moonwoo Park, "A Numerical Study on The Change in Safety Factor (FOS) According to Slope Angle Change for The Establishment of Photovoltaic Facilities Using SRM (Strength Reduction Method)", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 178–185, 2023. doi: 10.25046/aj080320
8. Chanuka Bandara, Yehan Kodithuwakku, Ashan Sandanayake, R. A. R. Wijesinghe, Velmanickam Logeeshan, "Design and Implementation of an Automated Medicinal-Pill Dispenser with Wireless and Cellular Connectivity", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 161–169, 2023. doi: 10.25046/aj080318
9. Mohammed Mahfuz Hossain, Thomas Ortmeyer, Everett Hall, "Human-Centered Design, Development, and Evaluation of an Interface for a Microgrid Controller", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 80–88, 2023. doi: 10.25046/aj080310
10. Yu Yan, Eric Wallace Cooper, Richard Lee, "Inferring Student Needs Based on Facial Expression in Video Images", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 19–28, 2023. doi: 10.25046/aj080303
11. Ossama Embarak, "Multi-Layered Machine Learning Model For Mining Learners Academic Performance", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 850–861, 2021. doi: 10.25046/aj060194
12. Abdulrasaq Jimoh, Samson Oladayo Ayanlade, Emmanuel Idowu Ogunwole, Dolapo Eniola Owolabi, Abdulsamad Bolakale Jimoh, Fatina Mosunmola Aremu, "Metaheuristic Optimization Algorithm Performance Comparison for Optimal Allocation of Static Synchronous Compensator", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 1, pp. 116–124, 2023. doi: 10.25046/aj080114
13. Mikhail Lavrentiev, Dmitry Kuzakov, Andrey Marchuk, "Optimizing Sensors Locations for Tsunami Warning System", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 256–261, 2022. doi: 10.25046/aj070629
14. Rafia Akhter, Fred Beyette, "Detection of Event-Related Potential Artifacts of Oddball Paradigm by Unsupervised Machine Learning Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 157–166, 2022. doi: 10.25046/aj070517
15. Erick Esparza Tapia, Eva Selene Hernández Gress, Martin Flégl, "Sensitive Analysis in Holding and Penalty Costs for the Stochastic Sequencing Problem in Agile Manufacturing", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 62–72, 2022. doi: 10.25046/aj070509
16. Hiroaki Hanai, Akira Mishima, Atsuyuki Miura, Toshiki Hirogaki, Eiichi Aoyama, "Realization of Skillful Musical Saw Bowing by Industrial Collaborative Humanoid Robot", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 1–9, 2022. doi: 10.25046/aj070501
17. Aicha Lamjahdi, Hafida Bouloiz, Maryam Gallab, "Heuristic Analysis of Overall Performance Measurement Perception and Management in Automotive Industry", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 1–11, 2022. doi: 10.25046/aj070301
18. Mauricio Mamani, Mario Chauca, Edward Huamani, Richard Gonzales, "Associated Risk Factors for the Development of Extensively Resistant Pulmonary Tuberculosis in the First Level of Health Care: From a Public Health Perspective", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 6, pp. 119–129, 2021. doi: 10.25046/aj060616
19. Ruben Chambilla, Daniel Tomiuk, Cataldo Zuccaro, Michel Plaisent, Prosper Bernard, "Antecedents to Learners’ Satisfaction with Serious Games: An Investigation Using Partial Least Square", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 6, pp. 43–53, 2021. doi: 10.25046/aj060607
20. Sarina Abdul Halim-Lim, Nurul Najihah Azalanzazllay, Anjar Priyono, Guven Gurkan Inan, Muhammad Iqbal Hussain, "Lean Six Sigma Implementation in the Food Sector: Nexus between Readiness-Critical Success Factors", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 6, pp. 12–21, 2021. doi: 10.25046/aj060603
21. Jotje Rantung, Frans Palobo Sappu, Yan Tondok, "Real-time Measurement Method for Fish Surface Area and Volume Based on Stereo Vision", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 141–148, 2021. doi: 10.25046/aj060516
22. Prattana Deeprasertkul, Royol Chitradon, "A Monthly Rainfall Forecasting from Sea Surface Temperature Spatial Pattern", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 101–106, 2021. doi: 10.25046/aj060513
23. Chia-En Yang, Yang-Ting Shen, Shih-Hao Liao, "SyncBIM: The Decision-Making BIM-Based Cloud Platform with Real-time Facial Recognition and Data Visualization", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 16–22, 2021. doi: 10.25046/aj060503
24. Takashi Sasaoka, Hiroto Hashikawa, Akihiro Hamanaka, Hideki Shimada, Keisuke Takahashi, "Study on Deformation Behavior of Sediments and Applicability of Sealants in Seabed Mining", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 170–175, 2021. doi: 10.25046/aj060420
25. Jose María Sierra-Fernández, Agustin Agüera-Pérez, Jose Carlos Palomares-Salas, Manuel Jesús Espinosa-Gavira, Olivia Florancias-Oliveros, Juan José González de la Rosa, "Web-based Remote Lab System for Instrumentation and Electronic Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 100–109, 2021. doi: 10.25046/aj060412
26. Mohammad AL-Tahat, Issam Jalham, Abbas Al-Refaie, Mohammed Fawzi Alhaj Yousef, "Activity-Based Cost Estimation Model for The Extrusion of Variant Aluminum Profiles", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 3, pp. 172–181, 2021. doi: 10.25046/aj060320
27. Chibuzo Victor Ikwuagwu, Ikechukwu Emmanuel Okoh, Stephen Aroh Ajah, Cosmas Uchenna Ogbuka, Godwin Ogechi Unachukwu, Emenike Chinedozi Ejiogu, "Development of Electric Power Availability Recorder for Accurate Energy Billing of Unmetered Facilities", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 3, pp. 7–14, 2021. doi: 10.25046/aj060302
28. Nadia Jmour, Slim Masmoudi, Afef Abdelkrim, "A New Video Based Emotions Analysis System (VEMOS): An Efficient Solution Compared to iMotions Affectiva Analysis Software", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 990–1001, 2021. doi: 10.25046/aj0602114
29. Showkat Ahmad Dar, S Palanivel, "Performance Evaluation of Convolutional Neural Networks (CNNs) And VGG on Real Time Face Recognition System", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 956–964, 2021. doi: 10.25046/aj0602109
30. Tamer Saraçyakupoğlu, "Usage of Additive Manufacturing and Topology Optimization Process for Weight Reduction Studies in the Aviation Industry", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 815–820, 2021. doi: 10.25046/aj060294
31. Md Mahmudul Hasan, Nafiul Hasan, Mohammed Saud A Alsubaie, "Development of an EEG Controlled Wheelchair Using Color Stimuli: A Machine Learning Based Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 754–762, 2021. doi: 10.25046/aj060287
32. Asep Herry Hernawan, Deni Darmawan, Asyifa Imanda Septiana, Idriyani Rachman, Yayoi Kodama, "Developing Kamishibai and Hologram Multimedia for Environmental Education at Elementary School", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 656–664, 2021. doi: 10.25046/aj060276
33. Khalil Ibrahim Mohammad Abuzanouneh, Khalil Hamdi Ateyeh Al-Shqeerat, "Development and Improvement of Web Services Selections using Immigrants Scheme of Multi-Objective Genetic Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 412–422, 2021. doi: 10.25046/aj060248
34. Dejun Chen, Congcong Xiong, Li Guo, Ming Zhong, "A Hybrid NMF-AttLSTM Method for Short-term Traffic Flow Prediction", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 175–184, 2021. doi: 10.25046/aj060220
35. Kamel Fahmi Bou-Hamdan, "Design and Implementation of an Ultrasonic Scanner Setup that is Controlled using MATLAB and a Microcontroller", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 85–92, 2021. doi: 10.25046/aj060211
36. Yousra Karim, Abdelghani Cherkaoui, "Fuzzy Analytical Hierarchy Process and Fuzzy Comprehensive Evaluation Method Applied to Assess and Improve Human and Organizational Factors Maturity in Mining Industry", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 75–84, 2021. doi: 10.25046/aj060210
37. Isman Khazi, Andras Kovacs, Ulrich Mescheder, Ali Zahedi, Bahman Azarhoushang, "Fusion of Optical and Microfabricated Eddy-Current Sensors for the Non-Destructive Detection of Grinding Burn", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1414–1421, 2021. doi: 10.25046/aj0601160
38. Helen Leligou, Despina Anastasopoulos, Anita Montagna, Vassilis Solachidis, Nicholas Vretos, "Combining ICT Technologies To Serve Societal Challenges", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1319–1327, 2021. doi: 10.25046/aj0601151
39. Almahasees Zakaryia, Al-Taher Mohammad, Helene Jaccomard, "Evaluation of Facebook Translation Service (FTS) in Translating Facebook Posts from English into Arabic in Terms of TAUS Adequacy and Fluency during Covid-19", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1241–1248, 2021. doi: 10.25046/aj0601141
40. Anas Najdawi, Zakariya Chabani, Raed Said, "Factors Impacting Digital Payment Adoption: An Empirical Evidence from Smart City of Dubai", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1208–1214, 2021. doi: 10.25046/aj0601137
41. Akintunde Alayande, Somefun A.O, Tobiloba Somefun, Ademola Ademola, Claudius Awosope, Obinna Okoyeigbo, Olawale Popoola, "Transient Stability Enhancement of a Power System Considering Integration of FACT Controllers Through Network Structural Characteristics Theory", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 968–981, 2021. doi: 10.25046/aj0601107
42. Syeda Nadiah Fatima Nahri, Shengzhi Du, Barend Jacobus van Wyk, "Active Disturbance Rejection Control Design for a Haptic Machine Interface Platform", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 898–911, 2021. doi: 10.25046/aj060199
43. Walvies Mc. Alcos, Mirador G. Labrador, "A Surface Plasmon Resonance (SPR) and Water Quality Monitoring: A System for Detecting Harmful Algal Bloom", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 770–775, 2021. doi: 10.25046/aj060185
44. Javier Stillig, Nejila Parspour, "Novel Infrastructure Platform for a Flexible and Convertible Manufacturing", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 356–368, 2021. doi: 10.25046/aj060141
45. Deisy Chipana-Collahua, Mariluz Chipana-Collahua, Rosa Villegas-Ortiz, Brian Meneses-Claudio, Hernan Matta-Solis, "Type 2 Diabetes Risk and Physical Activity in outpatients treated in Health Centers in a District of North Lima, 2020", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1651–1656, 2020. doi: 10.25046/aj0506196
46. Nesma N. Gomaa, Khaled Y. Youssef, Mohamed Abouelatta, "On Design of IoT-based Power Quality Oriented Grids for Industrial Sector", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1634–1642, 2020. doi: 10.25046/aj0506194
47. Angelina Ervina Jeanette Egeten, Harjanto Prabowo, Ford Lumban Gaol, Meyliana, "Features Preference using Conjoint Analysis Method for E-marketplace Social Care System", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1593–1597, 2020. doi: 10.25046/aj0506190
48. Amancio Izquierdo-Príncipe, Jaqueline Garcia-Núñez, Brian Meneses-Claudio, Hernan Solis-Matta, Lourdes Matta-Zamudio, "Quality of Nursing Care in Hospitalized Patients of the Carlos Lanfranco La Hoz Hospital, 2019", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1335–1339, 2020. doi: 10.25046/aj0506159
49. Marouane EL Midaoui, Mohammed Qbadou, Khalifa Mansouri, "A Novel Approach of Smart Logistics for the Health-Care Sector Using Genetic Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1143–1152, 2020. doi: 10.25046/aj0506138
50. Rushikesh Kulkarni, Kiyoshi Honda, "Estimating LAI of Rice Using NDVI Derived from MODIS Surface Reflectance", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1047–1053, 2020. doi: 10.25046/aj0506127
51. Majdouline Meddad, Chouaib Moujahdi, Mounia Mikram, Mohammed Rziza, "Optimization of Multi-user Face Identification Systems in Big Data Environments", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 762–767, 2020. doi: 10.25046/aj050691
52. Abdeslam Amri, Zakaria Abidli, Mounir Bouzaaboul, Rabea Ziri, Ahmed Omar Touhami Ahami, "Burnout Among Primary School Teachers in the Wazzane Region in Morocco: Prevalence and Risk Factors", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 636–641, 2020. doi: 10.25046/aj050677
53. Ignacio Alvarez-Placencia, Diana Sánchez-Partida, Patricia Cano-Olivos, José-Luis Martínez-Flores, "Inventory Management Practices during COVID 19 Pandemic to Maintain Liquidity Increasing Customer Service level in an Industrial Products Company in Mexico", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 613–626, 2020. doi: 10.25046/aj050675
54. Jojo Blanza, Lawrence Materum, "Interface for Visualization of Wireless Propagation Multipath Clustering Outcomes", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 544–549, 2020. doi: 10.25046/aj050665
55. Zakaryia Almahasees, Helene Jaccomard, "Facebook Translation Service (FTS) Usage among Jordanians during COVID-19 Lockdown", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 514–519, 2020. doi: 10.25046/aj050661
56. Viktor Butenko, Liana Gusakova, Dmitry Durov, Boris Safoklov, Oleg Dolgov, "Method for Improving the Quality of the Product Obtained by Abrasive Treatment with Impregnated Tools", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 398–402, 2020. doi: 10.25046/aj050647
57. Gede Putra Kusuma, Jonathan, Andreas Pangestu Lim, "Emotion Recognition on FER-2013 Face Images Using Fine-Tuned VGG-16", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 315–322, 2020. doi: 10.25046/aj050638
58. Hanny Juwitasary, Christian Christian, Edi Purnomo Putra, Hilman Baskara, Mohammad Wildan Firdaus, "The Effect of E-Service Quality on Customer Satisfaction and Loyalty (Case Study at E-Marketplace XYZ in Indonesia)", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 206–210, 2020. doi: 10.25046/aj050624
59. Simona Kirilova Filipova-Petrakieva, "Applications of the Heuristic Optimization Approach for Determining a Maximum Flow Problem Based on the Graphs’ Theory", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 175–184, 2020. doi: 10.25046/aj050621
60. Fei Gao, Jiangjiang Liu, "Effective Segmented Face Recognition (SFR) for IoT", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 36–44, 2020. doi: 10.25046/aj050605
61. Pamela Zontone, Antonio Affanni, Riccardo Bernardini, Leonida Del Linz, Alessandro Piras, Roberto Rinaldo, "Supervised Learning Techniques for Stress Detection in Car Drivers", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 22–29, 2020. doi: 10.25046/aj050603
62. Nhu-Tung Nguyen, Dung Hoang Tien, Do Duc Trung, "Development of the Surface Roughness Model in the Grinding Processes", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1184–1188, 2020. doi: 10.25046/aj0505143
63. Thi Anh Van Nguyen, Khac Hieu Nguyen, "The Impact of Innovation on the Performance of Manufacturing Enterprises in Vietnam", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 984–990, 2020. doi: 10.25046/aj0505120
64. Proud Arunrangsiwed, Yothin Sawangdee, "Overcome Discrimination: A Logistic Regression with 10-year Longitudinal Investigation of Emo Kids’ Facebook Posts", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 637–644, 2020. doi: 10.25046/aj050578
65. Imad El Hajjami, Bachir Benhala, Hamid Bouyghf, "Shape Optimization of Planar Inductors for RF Circuits using a Metaheuristic Technique based on Evolutionary Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 426–433, 2020. doi: 10.25046/aj050553
66. Nhu-Tung Nguyen, Dung Hoang Tien, Do Duc Trung, "Multi-Objective Optimization when Surface Grinding the 3X13 Steel by Combining the General Reduced Gradient Algorithm and Harmonic Mean Method", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 395–400, 2020. doi: 10.25046/aj050550
67. Altamashuddinkhan Nadimalla, Siti Aliyyah Masjuki, Siti Asmahani Saad, Maisarah Ali, Shuhairy Norhisham, "The Relation of Compression Strength with Modulus of Rupture and UPV of Concrete Containing M-sand as Fine Aggregate", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 39–46, 2020. doi: 10.25046/aj050506
68. Rohith Raj S, Pratiba D, Ramakanth Kumar P, "Facial Expression Recognition using Facial Landmarks: A Novel Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 24–28, 2020. doi: 10.25046/aj050504
69. Anubha Gautam, Parshram Sharma, Yogendra Kumar, "Mitigating Congestion in Restructured Power System using FACTS Allocation by Sensitivity Factors and Parameter Optimized by GWO", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 01–10, 2020. doi: 10.25046/aj050501
70. Moulay Smail Bouzakraoui, Abdelalim Sadiq, Abdessamad Youssfi Alaoui, "Customer Satisfaction Recognition Based on Facial Expression and Machine Learning Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 594–599, 2020. doi: 10.25046/aj050470
71. Kanishk Rai, Keshav Kumar Thakur, Preethi K Mane, Narayan Panigrahi, "Design of an EEG Acquisition System for Embedded Edge Computing", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 119–129, 2020. doi: 10.25046/aj050416
72. Zakaria Aitelcadi, Mohamed Reda Mesradi, Redouane El Baydaoui, Ahmed Bannan, Abdennacer Ait Ayoub, Kamal Saidi, Saad Elmadani, "Monte Carlo Estimation of Dose in Heterogeneous Phantom Around 6MV Medical Linear Accelerator", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 478–486, 2020. doi: 10.25046/aj050359
73. Krina B. Gabani, Mayuri A. Mehta, Stephanie Noronha, "Racial Categorization Methods: A Survey", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 388–401, 2020. doi: 10.25046/aj050350
74. Rajesh Kannan Megalingam, Raviteja Geesala, Ruthvik Rangaiah Chanda, Nigam Katta, "Multimode Control and Simulation of 6-DOF Robotic Arm in ROS", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 3, pp. 306–316, 2020. doi: 10.25046/aj050340
75. Suharjito, Atria Dika Puspita, "Face Recognition on Low Resolution Face Image With TBE-CNN Architecture", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 730–738, 2020. doi: 10.25046/aj050291
76. Zulmandakh Otgongerel, Gaemyoung Lee, Ankhzaya Baatarbileg, "The Capacity Factor of Renewable Energy Power Plants During Electric Power Peak Times in Jeju Island", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 545–550, 2020. doi: 10.25046/aj050268
77. Marwa Daghari, Hedi Sakli, "Antenna Radiation Performance Enhancement Using Metamaterial Filter for Vehicle to Vehicle Communications Applications", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 344–350, 2020. doi: 10.25046/aj050245
78. Jorge Castro-Bedriñana, Doris Chirinos-Peinado, Felipe Zenteno-Vigo, Gianfranco Castro-Chirinos, "Satisfaction of Old Graduates of Zootechnical Engineering for Improvement of Educational Quality at the UNCP", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 166–173, 2020. doi: 10.25046/aj050221
79. Sherif Gamal Abd-Elhamid, Reham Mohamed Galal Ebrahim El-Tahawy, Mohamed Nour El-Din Fayed, "Dynamic Behavior of Multi-Story Concrete Buildings Based on Non-Linear Pushover & Time History Analyses", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 143–153, 2020. doi: 10.25046/aj050219
80. Jorge Castro Bedriñana, Doris Chirinos Peinado, Richard Peñaloza-Fernández, "Lead Bioaccumulation in Root and Aerial Part of Natural and Cultivated Pastures in Highly Contaminated Soils in Central Andes of Peru", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 126–132, 2020. doi: 10.25046/aj050216
81. Djurayeva Nigora Avazovna, "Ontological and Epistemological Issues of Studying the Development of Uzbekistan in the Context of Globalization from the Point of View of the Paradigm of Civilizations", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 2, pp. 28–34, 2020. doi: 10.25046/aj050204
82. Rasha Attia Ahmed Attia, Reham Mohamed Galal Ebrahim El-Tahawy, Mohamed Nour El-Din Fayed, "Seismic Response Modification Factor for Special Concrete Structures Based on Pushover & Non-linear Time History Analyses", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 1, pp. 436–445, 2020. doi: 10.25046/aj050156
83. Argha Sarkar, Padarthi Venkataramana, Nimmala Harathi, Thummuru Jyothsna, Neeruganti Vikram Teja, "Design and Optimization of ZnO Nanostructured SAW-Based Ethylene Gas Sensor with Modified Electrode Orientation", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 1, pp. 263–266, 2020. doi: 10.25046/aj050133
84. Youness Frichi, Fouad Jawab, Said Boutahari, "An Exploratory Qualitative Study of the Influence of Hospital Logistics Factors on Quality of Care and Patient Satisfaction at Public Hospitals in Morocco", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 414–422, 2019. doi: 10.25046/aj040652
85. Sunarsih, Sutrisno, "Multi-period Quadratic Programming Model for Sewon-Bantul Facultative Ponds Optimization", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 397–401, 2019. doi: 10.25046/aj040650
86. Omar Freddy Chamorro Atalaya, Nel Yuri Huaita Ccallo, Luis Enrique Rojas Vicuña, Rudy Jesús Capa Ilizarbe, José Arturo Pillco Torres, José Jean Franco Ramos Rupay, "Experimental Analysis in Alternate Current and Direct Current of the Operating Parameters of a Universal Single-Phase Engine", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 360–370, 2019. doi: 10.25046/aj040646
87. Naga Rama Devi Vedala, Yadla Saritha, Ankam Ankamma Rao, Gaddam Sridhar, "Study of MX/M/1 Queueing System with Vacation, Two kinds of Repair facilities and Server Timeout", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 339–342, 2019. doi: 10.25046/aj040643
88. Omar Freddy Chamorro Atalaya, Dora Yvonne Arce Santillan, Jorge Isaac Castro Bedriñana, Teodoro Neri Díaz Leyva, Denisse Marie Barrientos Pichilingue, "Comparative Analysis of Student Dissatisfaction of the Continuing Academic Semesters at UNTELS", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 203–207, 2019. doi: 10.25046/aj040626
89. Naima Essadi, Adil Anwar, "Coordination between Heterogeneous Models Using a Meta-model Composition Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 147–157, 2019. doi: 10.25046/aj040618
90. Mikhail Lavrentiev, Dmitry Kuzakov, Andrey Marchuk, "Fast Determination of Tsunami Source Parameters", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 6, pp. 61–66, 2019. doi: 10.25046/aj040608
91. Lajmi Imen, Masmoudi Wassim, Elleuch Mounir, Chtourou Hedi, "Improvement opportunities of a Simulation/Expert System Approach for Manufacturing System Sizing: A review and proposal", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 213–223, 2019. doi: 10.25046/aj040527
92. Omar Freddy Chamorro Atalaya, Teodoro Neri Díaz Leyva, Dora Yvonne Arce Santillan, Jorge Isaac Castro Bedriñana, Denisse Marie Barrientos Pichilingue, Avid Roman-Gonzalez, "Satisfaction of the Graduate for the Continuous Improvement of Educational Quality in UNTELS", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 151–157, 2019. doi: 10.25046/aj040520
93. Seema Saxena, Vikramjeet Singh, Rajesh Kumar Gupta, Nitin Kumar Mishra, Pushpinder Singh, "Green Inventory Supply Chain Model with Inflation under Permissible Delay in Finite Planning Horizon", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 5, pp. 123–131, 2019. doi: 10.25046/aj040516
94. Ahmad Fauzan Zakki, Aris Triwiyatno, Bandi Sasmito, Krismon Budiono, "Design and Control of Autonomous Surface Vehicle to Support Bathymetry Survey in the Coastal Environment", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 458–461, 2019. doi: 10.25046/aj040455
95. Constantina Costopoulou, Maria Ntaliani, Filotheos Ntalianis, "An Analysis of Social Media Usage in Winery Businesses", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 380–387, 2019. doi: 10.25046/aj040446
96. Takahiro Ishizu, Makoto Sakamoto, Masamichi Hori, Takahiro Shinoda, Takaaki Toyota, Amane Takei, Takao Ito, "Hidden Surface Removal for Interaction between Hand and Virtual Objects in Augmented Reality", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 359–365, 2019. doi: 10.25046/aj040444
97. Maryam Butt, Golshah Naghdy, Fazel Naghdy, Geoffrey Murray, Haiping Du, "Investigating The Detection of Intention Signal During Different Exercise Protocols in Robot-Assisted Hand Movement of Stroke Patients and Healthy Subjects Using EEG-BCI System", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 300–307, 2019. doi: 10.25046/aj040438
98. Darya Denisenko, Nikolay Prokopenko, Nikolay Butyrlagin, "All-Pass RC-Filters Architecture with Independent Adjustment of the Main Parameters Based on Differential Difference Amplifiers", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 4, pp. 65–72, 2019. doi: 10.25046/aj040409
99. Yuliana Tanulia, Abba Suganda Girsang, "Sentiment Analysis on Twitter for Predicting Stock Exchange Movement", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 3, pp. 244–250, 2019. doi: 10.25046/aj040332
100. Sohail Akhtar, Adarsh Tandiya, Medhat Moussa, Cole Tarry, "An Efficient Automotive Paint Defect Detection System", Advances in Science, Technology and Engineering Systems Journal, vol. 4, no. 3, pp. 171–182, 2019. doi: 10.25046/aj040323