1. Introduction

Despite the proven efficiency of cryptography in protecting the security of information during communication, this protection is not guaranteed after the sent information is received and decrypted. On the other hand, Steganography introduced innovative ways to hide the existence of the secret information into innocent looking cover media in such a way that the resultant stego-media is hardly distinguishable from the original one. This makes it almost impossible to discover the concealed information or even suspect its existence. The first use of steganography dates back to the fifth century BC as documented in “Histories” of Herodotus [1]. The story happened during the conflict between Persia and Greece when Demaratus sent a secret message to warn the Spartans about the surprise attack planned by Xerxes, the tyrant king of Persia. The message was carved on a wooden tablet and covered with wax. Being apparently blank, the tablet was not intercepted by the Persian guards along the road. When the tablet reached its destination, the message was revealed after scrapping the wax off. With the element of surprise lost, the Persian fleet was lured in the harbor and damaged in less than a day. A modern model for a steganographic system was formulated by Simmons in terms of a prisoner’s problem [2]. It assumes that Alice and Bob are trying to prepare an escape plan and need to exchange messages without drawing the attention of the warden. So, they embed their secret messages some cover-object using a secret key. Only using the same key, the message can be extracted from the transmitted stego-object.

In the digital era, modern steganographic techniques use a variety of digital media for the purpose of data hiding. Examples of such media include: images [3], audio tracks [4], video files [5], 3D Objects [6], and even file systems [7]. Recently, researchers attempted to use Deoxyribonucleic Acid (DNA) sequence data as a cover medium. In 1999, a paper published in Nature [8] presented one of the earliest methods for using biological DNA as a cover for the purpose of information hiding. The authors used a synthesized a DNA strand to encode the secret data that was then copied and camouflaged within an enormous number of similarly sized fragments of human DNA. Later, a small amount of the resultant DNA-containing solution was printed as a dot on a period in a typed letter. When mailed, the recipient of the letter was able to successfully recover the secret message after laboratory analysis. Another interesting example is live data storage, where digital data can be stored in the genome of a living organism; preserved for thousands of years and protected even from nuclear explosions [9]. The authors of [10] proposed a watermarking technique for RNA sequences in such a way the functionality of the organism remains intact. The main application for such a technique is protecting genetic discoveries such as gene therapy, transgenic crops, and tissue cloning. A similar approach was proposed in [11] where the message is encrypted before hiding and block-sum checking is used to detect errors in mutations.

Another category of DNA-based steganographic methods was motivated by the huge publicly available genomic databases that store DNA sequence data on digital files following a simple format. In [12], the authors proposed that both the sender, and the receiver should agree or share a reference sequence before the communication takes place. The secret message can then be embedded into the reference sequence using one of three different methods. With the help of the reference sequence, the reverse of the hiding process can be performed by the rreceiver to extract the hidden message. However, communicating a sequence twice can draw suspicion and may affect the security of the steganographic channel itself. Secondly, the reference sequence is randomly modified without any consideration to the biological functionality of the DNA sequence. Addressing this later point, the authors of [13] introduced a hiding method that exploits the codon redundancy feature of DNA to hide data into sequence data without affecting the type nor the structure of protein it encodes for. Reversible hiding techniques, on the other hand, works in a way such that the cover sequence can be recovered from the stego-DNA sequence. an example of such technique was proposed in [14] where the cover sequence is coded into symbols that have integer values and the hiding process is then implemented using multilevel histogram shifting. Other methods added the power of encryption to provide more security to the hidden messages [15]. Some of these ciphers are actually bio-inspired and can be used to represent the message into a DNA sequence such as [16], [17] and [18]. A more recent research investigated using DNA steganography and PCR technology for the purpose of quantum key distribution (QKD) [19]. The authors of [20] provide a more comprehensive review on recent DNA-based steganographic methods.

In this paper, we present a method for securely hiding information into DNA sequences. The method is an extension of the work published by the author in [21]. The original research hides a secret message into a reference DNA sequence where both the message and the reference sequences are divided into random-length splices that are eventually merged to form the setgo-sequence. Before embedding, the binary message is encrypted and encoded into a DNA sequence using an 8×8 playfair cipher. In order to perform the extraction process correctly, it was proposed to add a header section before the embedded message to store the length of the hidden message. In this research, however, we propose a novel splicing technique based on the genes detected in the cover sequence. Therefore, the need for the message-size header information is eliminated. Finally, since the message splices are replacing the non-coding regions of the cover, the resultant stego-sequence is shorter. Although the aforementioned modifications don’t increase the hiding capacity but it enhances both applicability and security of the method. The rest of the paper is organized as follows: section 2 provides a brief overview on some useful characteristics of DNA sequence data. Section 3 describes the details of the hiding and the extraction modules of the proposed method. In section 4, the performance of the proposed approach is measured, analyzed, and compared with some other techniques. Finally, section 5 concludes the paper.

2. DNA Sequence Data

The genetic information of all living organisms, as well as viruses, is stored in DeoxyriboNucleic Acid (DNA) molecules. A DNA molecule consists of two polynucleotide strands coiled around each other in the form of double helix structure. Each individual strand of DNA is made up with 4 different types of nucleotides. Nucleotides can contain either a purine base : adenine (A) and guanine (G) or pyrimidine base: thymine (T) and cytosine (C). In nature, A pairs only with T and G pairs only with C [22]. As a data medium, DNA can be represented as string of characters over the alphabet {A, C, G, T}. Using some coding rule, a DNA string can be converted into a string of binary digits where each base is mapped into two bits. Figure 1 shows an example of such coding rule along with a sample sequence encoded using this rule.

Figure 1: An example digital coding of DNA sequence data

The information stored in the DNA molecule plays a vital role in controlling all aspects of cell functionality. Through the complicated process of Central Dogma, the DNA sequence is read, copied, and eventually translated into a chain of amino acids that forms a protein [23]. Although the reading and the copying process is made one base at a time, the translation process reads the sequence into units of three adjacent nucleotides; called codons. With only 4 possible bases; there are 64 (4³) distinctive ways to form 3-base long codons. As shown in figure 2, a three-letter abbreviation designates the type of amino acid molecule as in “Phe” and “Leu”. Notice that some codons code for more than one amino acid. This is a feature called codon degeneracy [22]. Furthermore, three of the codons; indicated as STOP, identifies the end of the protein chain and doesn’t actually code for any amino acid.

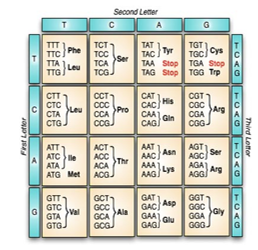Figure 2: The genetic code table

In fact, not all parts of the DNA sequence code for proteins. That segment of the DNA that code for a protein is called a gene and hence other segments are referred to as non-coding regions. Genes can be identified by searching the DNA sequence for open reading frames (ORF). An ORF is a long stretch of codons that is preceded by a start codon (ATG) and will be uninterrupted by stop codons (TGA, TAG or TAA) [24]. This searching process proceeds by dividing the DNA sequence into a set of consecutive, non-overlapping triplets. This can start at the first, the second, or the third base in the sequence resulting in three different reading frames in that direction. The reading frame that has the potential to be translated into protein is identified as an ORF. Since DNA is double stranded and either strand could include a gene, there is a total of six reading frames: three in forward direction and three in the reverse complement direction. Figure3 shows an example of a sample a sample sequence and the three reading frames in its forward direction. The potential ORFs found in each frame are highlighted well. Notice that this sequence has three potential genes, one in each reading frame. The gene identified in frame 2 for instance consists of exactly three codons in between the start and the stop codons.

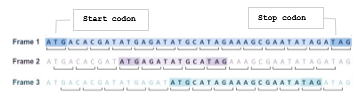Figure 3: An example of Open Reading Frames (ORF) for gene identification

3. The Steganographic method

A steganographic communication channel consists of two main processes: hiding and extraction. Whereas the hiding process is normally carried out by the sender, the extraction process is performed by the receiver to reveal the secret message. As shown in figure 6, the proposed hiding process starts with ciphering the message and encoding it into a DNA sequence. Next, the cover sequence is spliced to identify the ORFs. The embedding process then moves forward by infusing the message sequence into the cover sequence splices. On the other side of the communication, the receiver extracts the secret message from the stego-sequence simply by reversing the hiding steps. Here we assume that both of the sender and the receiver share a secret key in advance. This key is used in different steps of the hiding process to make sure that only the intended recipient will be able to retrieve the hidden message.

3.1. The Hiding Process

The detailed steps of the hiding process are listed in Algorithm 1. It starts with an encryption step that utilizes a DNA-inspired implementation of Playfair cipher [17]. The classical Playfair cipher uses a 5 by 5 table to substitute a pair of letters (digraph) and with another one following a few simple rules. This implementation was originally proposed to work plaintext consisting only of alphabets without punctuation, or even numerical values. The cipher also requires a preprocessing step in order to remove spaces and handle double-letter digraphs. However, in [17], the author proposed using a randomly constructed 8×8 matrix representing the 64 different DNA codons. This technique is capable of ciphering any type of digital data not only text. In addition, the preprocessing step is no longer required since the digraphs are represented over the DNA not English alphabet. The final output of this cipher can be coded back into characters or left in its DNA data representation. In this research, we decided to use the cipher proposed in [17] to encrypt the secret message and use its intermediate DNA representation of the cipher-text. The encrypted message sequence is then infused into the cover sequence following a structured splicing methodology.

The splicing process is performed on both the cover and the message sequences. However, the splicing is carried out differently on each one of them. First, the cover sequence (C) is divided into coding and non-coding regions through an ORF analysis. Guided by the ORF result, the coding genes (C_g) are identified, and the cover sequence is spliced out at those specific locations. On the other hand, the message sequence (M) is randomly spliced into random-length segments (m_i) similar to the insertion method proposed in [12]. Finally, the message splices and the cover genes are merged to form the stego-sequence (S). The merging process is done in a very special way. As shown in figure 4, the merging process starts with a message segment followed by the first cover gene and then another message segment that is followed by the second cover gene and so on.

In fact, the base composition of message sequence can vary depending on several factors such as the message content, the secret key, and binary coding rule. Therefore, and like any random sequence, a message sequence will comprise of coding and non-coding regions as well. This may introduce a challenge in the extraction process on how to distinguish between a cover gene and a message gene. Therefore, we suggest adding a separator codon at the end of each message segment to uniquely identify the start of a cover gene.

Figure 4: Merging message splices with cover genes.

Theoretically, this codon can be any of the 63 codons (except the start codon). However, we suggest using one of the three stop codons (STOP) to avoid forming new genes in the message sequence that may overlap with the cover genes causing issues during the extraction process. Figure 6 shows an example of such a situation. The figure shows four ORFs (highlighted in blue). The first two of them are part of the message sequence, while the other two are cover genes since they are proceeded with the stop codon (TAA in this case).

Figure 5: An example of a ORFs formed in message splices.

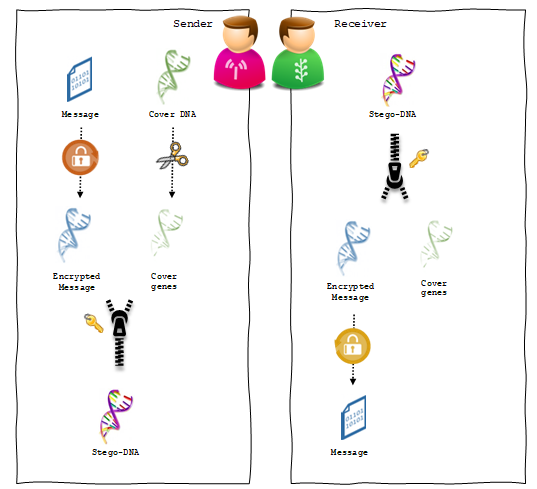Figure 6: The main steps of the proposed steganographic channel

3.2. The Extraction Process

The extraction is obviously the reverse process of hiding. As listed in Algorithm 2, the message retrieval starts with sequence splitting based on the specified reading frame. The locations of the start and the stop codons of the genes can then be identified. It is expected to find more genes in the stego-sequence than those used from the cover during the hiding process. As mentioned above, depending on the message contents and the randomness of the encryption algorithm, the message sequence can form new genes. Therefore, the proposed algorithm checks, for every detected gene, the codon that proceeds its start codon. If it is the specified STOP codon utilized during the hiding process, the gene will be skipped and the message segment that follows will be extracted. Otherwise, this detected gene actually belongs to the message sequence.

Figure 7 uses the same stego-sequence example shown in figure 6. Here only the highlighted segments belong to the message sequence. Notice how the first message segment spans the range of bases from 1 to 357 but when extracted, it will be concatenated from four different segments because of the two ORFs formed in its content. Furthermore, since the third and the fourth detected ORFs are cover genes, the segment following each one of them is extracted and appended to the message sequence extracted so far. Once all ORFs are processed, all segments of the message will be extracted, concatenated, and deciphered. Thus, there is no need to embed any header information to store the length of the hidden message as required in [21]. It is important to mention that, the extraction process here is done blindly without the need to reference the reference cover sequence.

Algorithm 1: Message Hiding
Input: C : A reference DNA sequence, used as a cover Msg : a secret message Key :  a secret key-word Result: S : A Stego-DNA sequence
1. Message Ciphering
1.1 Encode Msg into MsgDNA using a DNA binary coding rule
1.2 Build an 8×8 codon matrix
1.3 Shuffle the matrix based on the Key
1.4    for each pair of codons in MsgDNA do
if the pair appears on the same row of the matrix, replace each codon with its immediate right with wrap around
else if the pair appears on the same column of the matrix, replace each codon with its immediate below with wrap around.
else replace the pair with the pair at the corners of the rectangle defined by the original pair.
end
end
1.5 Build a column-wise square matrix filled with bases in MsgDNA in reverse order
1.6 for each column and row in sequence matrix do
1.6.1 Rotate circular upward on the column
1.6.2 Rotate circular left on the row
end
1.7 Rearrange encrypted message into a linear sequence Msgcph
2. Cover Splicing
2.1 Locate genes in C considering one of the ORFs.
2.2 Let be the detected cover genes.
3. Message Splicing:
3.1 Let i be a value derived from Key
3.2 Generate a sequence of random numbers  using i as the seed
3.3 Find the smallest integer tm such that :
3.4 if tm < tc
Divide Msgcph into tm -1 segments with lengths  respectively and keep the residual part of Msgcph in
else
return. end
4. Segment merging:
4.1 Initialize S as an empty sequence
4.2 for each k = 1 to tm -1 do
Append  to S
Append STOP to S
Append  to S
4.3 Append  to S
5. return S
End
Algorithm 2: Message retrieval
Input: S : A Stego-DNA sequence Key :  a secret key-word Result: Msg : the embedded secret message
1. ORF Splicing
1.1 find location of genes in S for the specified ORF
1.2 Let be the detected cover genes
1.3 Let  return the location of the start codon for the gene
1.4 Let  return the location of the stop codon for the gene
2. Message extraction:
2.1 Initialize Msgcph as an empty sequence
2.2 let k = 1
2.3 for k = 1 to t -1
if  is proceeded by STOP extend Msgcph by adding the bases from  to
Else
extend Msgcph by adding the bases from  to
End
End
2.4 Append the bases following  to Msgcph
3. Message Deciphering:
3.1 Build an 8×8 codon matrix
3.2 Shuffle the matrix based on the Key
3.3 for each pair of codons in MsgDNA do
if the pair appears on the same row of the matrix, replace each codon with its immediate right with wrap around
else if the pair appears on the same column of the matrix, replace each codon with its immediate below with wrap around.
else replace the pair with the other pair at corners of the rectangle defined by the original pair.
end
End
3.4 Build a column-wise square matrix filled with bases in MsgDNA in reverse order
3.5 for each column and row in sequence matrix
Rotate circular upward on the column
Rotate circular left on the row
End
3.6 Rearrange deciphered message into a linear sequence MsgDNA
3.7 Convert  MsgDNA into Msg using the specified coding rule
4. return Msg
end

Figure 7: An example of detecting and extracting message splices.

4. Performance Analysis

4.1. Hiding Capacity

Usually, the hiding capacity of a steganographic technique is measured by the maximum number of bits that can be hidden into the cover media. For DNA data, this capacity is measured in bit-per-nucleotide (bpn) which reflects how many bits can be hidden for each nucleotide in the cover sequence. Since the proposed algorithm requires only that the number of message segments should be less than or equal to the number of genes in the cover sequence, this doesn’t impose any restrictions on the length of message. Theoretically, fine tuning the embedding parameters would allow us to hide a message sequence that is as long as the cover sequence itself. Furthermore, since each encoded nucleotide in a message sequence represents 2 bits, the hiding capacity of the proposed method can be expressed as follows:

where C represents the cover sequence and |C| refers to the length of C in base pairs (bp).

4.2. Security

Generally speaking, the harder for an attacker to crack the implementation of a steganographic method, the more secure this approach is. Therefore, the proposed method was designed in way that the details of the hiding process are based on several parameters the attacker needs to guess correctly in order to extract the hidden message. Beside the value of the secret key, the attacker needs to know: the binary rule used to encode the DNA nucleotides, the random number generator used during the message splicing, the ORF selected for cover splicing, and the stop codon used to separate between message and cover segments.

First, given the fact that there are only 4 nucleotides, there are 4! = 24 possible binary coding rules. So, the probability of a successful guess on this parameter is 1/24 . Similarly, there are 6 different ORFs and 3 different stop codons. This makes the probability of predicting each one of them to be 1/6 and 1/3 respectively. More importantly, to find the sequence of numbers generated to randomly slice the message sequence, an attacker may need to make a number of guesses [12] up to the value computed in (2). Where n represents the length of the message sequence and is the set of all k-combinations of n.

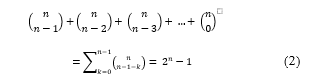Since the summations of the k’s can be as long as the cover sequence, the probability of a successful guess for this parameter can reach   , where C represents the cover sequence and |C| refers to the length of C in base pairs (bp). In conclusion, the probability of cracking the hiding process of the proposed method can be estimated as follows:

Considering the fact that |C| may reach hundreds of thousands bases, it is almost impossible for an attacker to retrieve the hidden message based on a successful guess. In addition, the message itself is protected by a powerful cipher that adds another layer of security to the hidden message in case the steganographic method fails.

5. Results and Discussions

In this section, the proposed method is tested using 10 different cover sequences. The discussion is then followed by a comparison with some existing methods based on different performance measures.

5.1. Experimental results

The sequence data was drawn from the Genbank database on the National Center for Biotechnology Information (NCBI) website using their unique accession numbers. The downloaded files in the FASTA format which is a text-based format that starts with a single-line description followed by lines of sequence data using the {A, C, T, G} alphabet. Furthermore, in this set of experiments, we choose to randomly generate 30KB of textual data and use it as a sample secret message. However, this should not limit the applicability of the proposed algorithm to hide any type of digital data as long as it is encoded using a rule similar to the one given in Fig. 1.

Table 1 summarizes the experimental results for 10 sequences using the secret key “12345”. It lists the lengths of the cover- and stego- sequences as well as the number of ORFs detected in the first reading frame of the sequences in each case. The payload is computed as the ratio of message to cover nucleotides in the stego-sequence. Notice that the results show an increase in the number of genes detected in the stego-sequence compared with those of the cover sequence. That was expected because the encoded message sequence will probably form some genes that will add to the detected ORFs in the resultant stego-sequence. For example, in the case of the AAEX03000038 sequence, the message was sliced into 343 segments. this means that only 342 genes out of the 364 cover genes are needed for hiding. However, during the extraction process, 657 genes were detected in the stego-sequence representing not only cover genes but also genes formed by the message content.

Furthermore, the embedding process was not successful for sequences AAEX03000001, AAEX03000010, and AAEX03000999 because none of them has enough ORFs to hide the message segments. For example, AAEX03000999 is a sequence that is 22,099 bases long with only 48 ORFs. Since the message is sliced into 832 segments, we need at least 831 cover genes to infuse those segments into. It is also worth to notice that the number of message segments changes in each case. In fact, in our implementation, the randomness of the splicing process does not only depend on the secret key, but also on the number of bases in the longest ORF in the identified the cover sequence.

5.2. Comparisons

In this set of experiments, the performance of the proposed technique was compared with some existing methods in terms of capacity, blind extraction, and security against brute force attacks. With blind extraction we mean that the original cover sequence is not required during the extraction process to retrieve the embedded message. With non-blind methods, the cover sequence needs to be communicated in advance which can draw suspicion and affect the security of the channel.

The results listed in table 2, show that the insertion method proposed in [12] may be more robust to brute-forth attacks than the proposed method, but it is not blind. On the other hand, the proposed method achieves a higher hiding capacity than all the methods in [12] while maintaining the advantage of blind extraction. The same is true for the GCBC method, despite it is also a blind technique, its hiding capacity is less than that offered by the proposed method. The methods proposed in [12] were not evaluated in terms of robustness, so there is no way to compare them to the proposed method in that regard. However, it is obvious though that they did not succeed to offer a better hiding capacity. Finally, although the technique introduced in [21] offers the same hiding capacity, the details of the proposed method added more parameters to the hiding process that enhanced its security.

Table 1: Experimental results for hiding 30KB of text

Cover Sequence			Number of message segments	Stego-Sequence
Accession number	Length (bp)	Number of detected ORFs		Length (bp)	Number of detected ORFs	Payload (bpn)
AL645637	207,629	588	222	147,239	525	1.69
AC168892	197,841	563	452	167,027	743	1.49
AAEX03000080	305,811	823	437	162,125	750	1.54
AAEX03000038	133,800	364	343	157,811	657	1.59
AC153526	200,117	521	281	151,259	592	1.65
AC168874	206,488	523	466	169,277	771	1.48
AL645625	226,754	553	490	178,616	790	1.40
AAEX03000001	24,025	59	526	—	—	—
AAEX03000010	44,186	98	403	—	—	—
AAEX03000999	22,099	48	832	—	—	—

Table 2: A comparison with some existing techniques

Author	Method	Capacity (bpn)	Security (Pbf)	Blind?
[12], 2010	Insertion	0.58		No
	Complementary	0.07		No
	Substitution	0.82		No
[15], 2016	Generic Complementary Base Substitution (GCBS)	1.5		Yes
[16], 2018	Noncircular type (NHS)	1.243	NA	yes
	Circular type (CHS)	1.865	NA	yes
[21], 2020	Random Splicing	2		yes
Proposed	ORF-guided Splicing	2	x	yes

6. Conclusions

This paper describes a steganographic method that extends the work presented in [21] and uses DNA sequence data for data hiding purposes. The proposed technique consist of two processes: hiding and extraction. The hiding module starts with an encryption step that encodes the secret message as a DNA sequence. The cover sequence is then spliced into coding and non-coding segments in a given reading frame. The encrypted sequence is also spliced; but is a random fashion, and infused into the cover’s gene-coding segments. The extraction module, on the other hand, reverses the hiding process starting from gene detection and ending with a decryption step.

The proposed method is blind, which means that parties of the communication don’t need to exchange anything in advance other than the secret key. Experimental results showed a superior performance of the proposed technique in terms of capacity and security. The proposed method achieved a hiding capacity of 2 bit per nucleotide, which is the highest among all methods except [21]. However, the proposed technique succeeded to eliminate the need for embedding header information about the size of the hidden message in [21]. Furthermore, the proposed method showed strong robustness against attacks making it almost unbreakable. Not to mention the ciphering step that protects the contents of the secret message in case the steganographic shield was cracked.

This research can be extended in one of two directions. First, introducing randomness in the merging process of the message and cover segments. That is, message segments can be infused in a random order in between the cover ORFs. Secondly, encryption techniques other than the play-fair cipher can be explored as well.

Conflict of Interest

The authors declare no conflict of interest.

1. Herodotus, Herodotus : The History, University of Chicago Press, 1987.
2. G. Simmons, “The Prisoners’ Problem and the Subliminal Channel,” Advances in Cryptology, Springer, 51-67, 1984, doi:10.1007/978-1-4684-4730-9_5.
3. A. Cheddad, J. Condell, K. Curran, and P. Mc Kevitt, “Digital Image Steganography: Survey and Analysis of Current Methods,” Signal Processing, 90, 727-752, 2010. doi: 10.1016/j.sigpro.2009.08.010.
4. P. Balgurgi, S. Jagtap, “Audio Steganography used for Secure Data Transmission,” in International Conference on Advances in Computing. Advances in Intelligent Systems and Computing, 2013, doi:10.1007/978-81-322-0740-5_83.
5. M. Sadek, A. Khalifa, M. Gad-El Haaq, “Robust Video Steganography Algorithm using Adaptive Skin-tone Detection,” Multimedia Tools and Applications, 76(2), 2017, doi:10.1007/s11042-015-3170-8.
6. Y. Tsai, I. Chi, C. Chan, “A Vertex-Based 3D Authentication Algorithm Based on Spatial Subdivision,” Symmetry, 10(10), 2018, doi:10.3390/sym10100422.
7. J. MacLean, D. Dampier, J. Davis, “Methods of Information Hiding and Detection in File Systems,” in Fifth International Workshop on Systematic Approaches to Digital Forensic Engineering (SADFE), 66-69, 2010, doi:10.1109/SADFE.2010.17.
8. C. Clelland, R. Taylor, C. Bancroft, “Hiding Messages in DNA Microdots,” Nature, 399, 533-534, 1999, doi:10.1038/21092.
9. S. Jiao, R. Goutte, “Hiding Data in DNA of Living Organisms,” Natural Science, 1(3), 181-184, 2009, doi:10.4236/ns.2009.13023.
10. D. Heider, M. Pyka, A. Barnekow, “DNA Watermarks in Non-Coding Regulatory Sequences,” BMC Research Notes, 2(125), 2009, doi:10.1186/1756-0500-2-125
11. D. Na, “DNA Steganography: Hiding Undetectable Secret Messages Within the Single Nucleotide Polymorphisms Of A Genome and Detecting Mutation-Induced Errors,” Microb Cell Fact, 19(128), 2020, doi:10.1186/s12934-020-01387-0
12. H. Shiu, K. Ng, J. Fang, R. Lee, C. Huang, “Data Hiding Methods based upon DNA Sequences,” Information Sciences., 180(11), 2196-2208, 2010. doi: 10.1016/j.ins.2010.01.030.
13. A. Khalifa, “LSBase: A Key Encapsulation Scheme to Improve Hybrid Crypto-Systems using DNA Steganography,” in 8th International conference on Computer and Engineering, 105-110, 2013, doi:10.1109/ICCES.2013.6707182.
14. S. Lee, “Reversible Data Hiding for DNA Sequence using Multilevel Histogram Shifting,” Security and Communication Networks, 2018. doi:10.1155/2018/3530969.
15. A. Khalifa, A. Elhadad, S. Hamad, “Secure Blind Data Hiding into Pseudo DNA Sequences Using Playfair Ciphering and Generic Complementary Substitution,” Applied Mathematics & Information Sciences, 10(4), 2016, doi:10.18576/amis/100427
16. M. Sabry, M. Hashem, T. Nazmy, M. Khalifa, “A DNA and Amino Acids-Based Implementation of Playfair Cipher,” (IJCSIS) International Journal of Computer Science and Information Security, 8(3), 129-136, 2010.
17. S. Hamad, “A Novel Implementation of an Extended 8×8 Playfair Cipher Using Interweaving on DNA-encoded Data,” International Journal of Electrical and Computer Engineering, 4(1), 93-100, 2014, doi:10.11591/ijece.v4i1.4969.
18. M. Biswas, K. Alam, S. Tamura, Y. Morimoto, “A Technique for DNA Cryptography based on Dynamic Mechanisms,” Journal of Information Security and Applications, 48, 2019, doi: 10.1016/j.jisa.2019.102363.
19. M. Cui, Y. Zhang, “Advancing DNA Steganography with Incorporation of Randomness,” ChemBioChem, 21(17), 2503-2511, 2020, doi:10.1002/cbic.202000149.
20. D. Zebari, H. Haron, S. Zeebaree, “Security Issues in DNA Based on Data Hiding: A Review,” International Journal of Applied Engineering Research, 12(24), 15363-15377, 2017.
21.  A. Khalifa, “A Blind DNA-Steganography Approach using Ciphering and Random Sequence Splicing,” in 10th International Conference on Information Science and Technology (ICIST), 86-90, 2020, doi:10.1109/ICIST49303.2020.9202036.
22. A. Ghosh, M. Bansal, “A glossary of DNA structures from A to Z,” ACTA Crystallography D, Biological Crystallography, 59(4), 620-626, 2003, doi:10.1107/s0907444903003251.
23. F. Crick, “Central Dogma of Molecular Biology,” Nature, 227, 561–563, 1970, doi:10.1038/227561a0.
24. M. Adam, H. Ardinger, R. Pagon, et al, Gene Reviews, University of Washington, 1993-2021.

(Click Here)