1. Introduction

The advent of many electric vehicles implies some environmental changes, however, the conversion of a number of motorists to electric vehicles implies a growth in electricity demand and adds additional constraints on the power grid. Figure 1 shows the growth (estimated by the french grid operator) in the number of EVs and their demand for electricity on the French electrical grid in the coming years

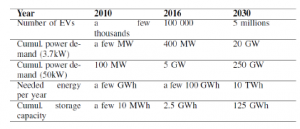
Figure 1: Evolution of EV energy needs (France)

The need for electricity corresponds to the virtual demand (in the scenario where all electric vehicles charge simultaneously), the calculation of the annual energy needed is based on a scenario of 15kWh/100 km and 13,000 km/year (source: ENT2008, datas in perpetual variation) and on a storage possibility of 20kWh of on-board batteries (again, these data are constantly changing). On the basis of these elements, we note that the energy required to recharge the vehicle is always moderate compared to the total annual electricity consumption (consumption of electric vehicles in 2030: 10 TWh, -total grid consumption in 2016: 470 TWh), while the electricity needs can be very large (several tens to several hundreds of GW, compared to the total installed power in 2016 of 130 GW). The development of EVs seems feasible without significantly increasing electricity production, but the punctual need for energy can be problematic if judicious recharging methods are not planned. A research work carried out in Spain in 2011 [1], shows the interest of smart charging planning methods. In this work, a simple decrease in the concurrency factor can decrease the additional costs of EVs by 60-70%. On the other hand, the application of strategies that allow charging during off-peak hours could also avoid up to 35% of the necessary additional expenses. In conjunction with this limited increase in electricity consumption, it is important to highlight the storage opportunities that several million EVs will provide, and the new possibilities for controlling an increasingly intermittent electricity grid. In this paper, we will develop the implementation of a smart parking with renewable energy generation and fixed storage taking into account the constraints of the grid, while showing the difficulties encountered due to interoperability issues. The load management of an EV fleet is a subject that is widely covered in the literature, around five main axes: bi-directional charging [2], decentralised [3], mobility management [4], [5], integration of renewable energies [6], adding ancillary services to the grid [7].

Many algorithms based on different methods have been developed and tested in simulation for the intelligent management of energy flows in a network with multiple sources and loads. Multi-agent systems (MAS) allow the decentralisation of the energy management system based on the collaboration of different actors. Initially designed to model the collective behaviour of groups of individuals evolving together while being able to make their own choices, MAS are today frequently used for energy management systems in micro-grids with several sources [8]. The energy management of a system is usually carried out by an EMS (Energy Management System) with centralised control. The use of multi-agent systems is tantamount to decentralising energy control by giving decisionmaking power to different actors. Another application example is given by Taesic Kim et al. in their paper [9]. It is an application on a micro-grid composed of a set of dwellings, each with production, storage and load devices (domestic, electric car …). An SMA solution is proposed to optimise the energy flows within the network in order to minimise peak load, reduce the energy costs of the inhabitants and maximise the energy efficiency of the storage system. Despite their wide use, the use of SMAs is controversial in the scientific community, as the results of the interaction between agents are sometimes unpredictable, therefore predicting the behaviour of the overall system from these constituent entities can become very complex.

Fuzzy logic is an extension of classical logic which allows the imprecision of data to be taken into account and thus seeks to come closer (to some extent) to the flexibility of human reasoning. It is based on Lotfi Zadeh’s mathematical theory of fuzzy sets, which presents an extension of classical set theory to imprecisely defined sets. As opposed to Boolean logic, fuzzy logic allows to add a degree of truth to a condition, which allows this condition to be in a state different from true or false. In their paper [10], Kyriakarakos et al. give an example of the use of fuzzy logic for energy management in a microgrid with multi-source power supply for remote areas. The network in question consists of an AC bus on which are connected production elements : PV panels with their inverter, wind generator, hydrogen fuel cell, loads : seawater desalination module, various domestic loads, an electrolyser to create hydrogen from water, and an electrochemical storage battery connected through an AC/DC converter. Simulations have shown that the use of fuzzy logic for energy control makes it possible to respect the constraints imposed for a much smaller system dimensioning and therefore to save a lot of energy and money. Another example of fuzzy logic energy management including intelligent load management of electric vehicles is given in [11]. The performance of the algorithm is evaluated from the point of view of peak consumption and charging cost. Fuzzy logic makes it possible to implement inference systems with seamless, flexible and non-linear decision making, closer to human behaviour than conventional logic. Moreover, the rules are expressed in natural language. This has many advantages, such as including the knowledge of a non-computer expert at the heart of a decision-making system or even modelling certain aspects of natural language more finely. However, fuzzy logic has some drawbacks, such as not being able to predict that the system will behave optimally. Performance will therefore have to be measured a posteriori and adjustments will be made by trial and error. For these reasons, fuzzy logic hasn’t been chosen for this specific experimentation.

Artificial neural networks (ANN) are a family of bio-inspired algorithms : their principle is borrowed from the functioning of biological neurons (in a simplistic way). They are designed to reproduce certain characteristics of biological memories by the fact that they are parallel, capable of learning, able to store information in the connections between neurons, able to process incomplete information. An example of the use of neural networks for the control of a generator in a micro-grid is given in [12]. The system is a micro-grid for the production of energy and drinking water for regions isolated from the power grid; it is composed of solar photovoltaic panels, a diesel generator, an electrochemical storage battery, a desalination unit, and conventional domestic loads. A neural network is used to control the diesel generator (On/Off and intensity) in order to minimise dependence on the generator, greenhouse gas emissions and engine wear due to incomplete combustion. Another example is given in [13], where the design and validation of an innovative control system based on an artificial neural network for a hybrid micro-grid is proposed. The use of neural networks for energy flow management is however complex to implement and may require a large computing capacity.

In this paper, we will develop a supervision method for the intelligent charging of electric vehicles based on dynamic programming. This optimization method, developed by Richard Bellman in 1957, consists in solving a global problem by breaking it down into subproblems, each with its own solution. After presenting the concept of the microgrid, this method will be developed in section III of this paper. The results obtained will be presented and analysed

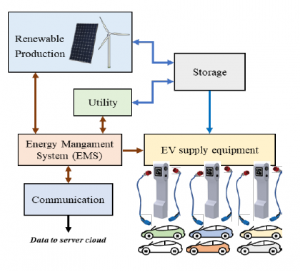
Figure 2: Experimental bench structure

2. Context and Experimental Bench

Dropbird is working on EV charging station management solutions and also on a planned charging organization in order to improve the performance of charging sites. The objective is to ensure maximum access to energy for EV users and to reduce the negative consequences for parking lot/network managers. This objective can manifest itself in two ways: with a given set of constraints, ensure that a maximum number of EVs can be charged or, with a given amount of EVs, minimize the strain on the power grid.

In order to carry out our studies, a flexible experimental environment has been created. It consists of an energy management system connected to multiple elements: EVSEs, DN, ESS, PV, remote control as shown in figure 2. Despite the fact that the environment is experimental, the users are various real local workers so the user satisfaction has to be respected the owned data is limited. The only data gathered on the PEV is the vehicle characteristics (battery capacity) and the initial SoC. Communication is also allowed between the EMS and the DN to receive requests of load demand response.

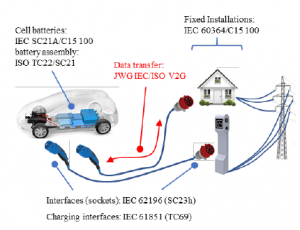
Figure 3: Normative context

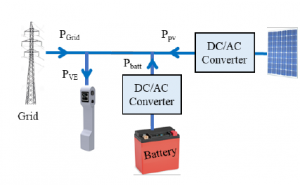
Figure 4: Energy flow within the experimental micro-grid

The development of such an experimental platform requires to meet normative constraints and standards. The main international standards associated to EV charging can be seen in figure 3.

Figure 4 sums up the energy flows exchanged by the different equipments connected to the micro-grid.

3. Algorithm structure

The energy management algorithms developed here are primarily EV recharge control algorithms; however, they are intended to control not only the EVSEs but also all elements of the system. We can speak of an EMS (energy management system) that will interact with the different elements described in figure 2: the EMS communicates with the EVSEs of course, but also with the inverter of the solar production, the fixed storage system, the distribution grid manager. The figure 5 shows the exchanges of measurements or control between the EMS and the other elements: an instantaneous measurement of the photovoltaic production, of the battery state of charge, of the charge power of each connected EV is transmitted to the EMS at each time step of the algorithm.

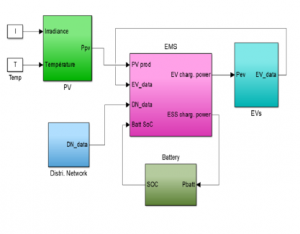
Figure 5: Information and control links

4. Dynamic Programming

Energy management in a parking lot with renewable energy sources consists in making a sequence of decisions spread over a day. The behavior of the users not being modeled, a simulation on an indeterminate day (working week or weekend) is rational. The concepts of artificial intelligence and more particularly of decision support are perfectly adapted to our problem. Enumeration (the simplest principle) is used [14].

4.1        Choosing the right energy management tool

In order to develop an independent intelligent energy management system, different strategies based on artificial intelligence were analyzed in simulation: multi-agent systems, fuzzy logic, artificial neural networks and dynamic programming.

4.2        Energy management uses

The method, defined by Bellman and used for sequential optimization problems, was developed in the 1980s to manage water reservoirs in hydroelectric installations [15]. Since the beginning of the 2000s, it has been used for the optimized use of energy in electric vehicles (such as the simultaneous management of several motors) [16]–[17], and, recently, for the management of electric energy storage from wind power and the management of a fleet of electric vehicles in [18], [19].

4.3        Principle

Bellman’s principle of optimality forms the basis of the concept of dynamic programming. This principle states that ”every optimal policy is composed of optimal sub-policies”. The simplest (and most time-consuming) way to construct an optimal decision-making scenario is to list all possible choices at each step time and determine the least costly path. The number of possible paths can be considerably reduced using Bellman’s principle by considering only the optimal subpaths at each computational step. As we elaborate the different possible paths, at each time step k, we keep only the best path that allows us to reach this state at this time: x(k). To use this method, it is necessary to discretize the time in time steps k, with 1¡k¡N, as well as each of the state variables x₁, x₂, x₃, x₄, x₅.

Dynamic programming is both a mathematical optimization method and a computer programming method. It is an algorithmic method for solving optimization problems.

Dynamic programming is used in particular for problems requiring a sequential decision-making sequence. It allows to determine the optimal trajectory by considering the problem as an optimal path to compute, and by decomposing it into sub-paths.

For example, if you want to solve the following optimization problem :

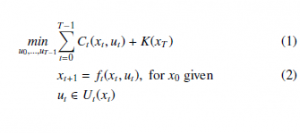
where

• C_t(x,u) is the cost to go from t to t + 1 starting from the state x by applying the u command;
• K(x) is the final cost for the final state x;
• f_t is the dynamic function of the system;
• U_t(x_t) is the set of possible commands at time t starting from state x.

Problem can be written as follows :

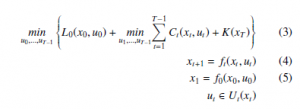
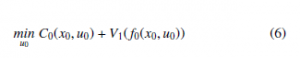
Where V₁(x) is the value for the problem starting from the state x₁ = x at time t = 1.

The optimal value V_t0(x) starting from the state x at time step t can thus be written :

5. Simulations and Results

5.1        Validation of the operation of the dynamic programming algorithm

Before carrying out complex simulations using dynamic programming algorithms, a first series of tests was performed on a simple case that is easy to grasp in order to verify the behavior of the system controlled by the dynamic programming algorithms, and to validate that its behavior seems intuitively coherent. For this purpose, a simulation with a single EV (always connected) and a fixed battery was carried out, with the parameter to minimize the cost of charging. The simulation does not take into account photovoltaic production. The electricity tariff is variable depending on the time of day and defined so that the EV is not able to charge 100% while the cost is at its lowest (consistent with the values of nominal charging power and battery capacity). Thus, to enable the EV to charge at minimum cost, the system must necessarily be controlled so that the storage battery also charges during the low cost period, and provides the EV with this low-cost energy purchased from the EV outside the off-peak period. The state of charge of the battery must also be the same at the beginning and end of the simulation.

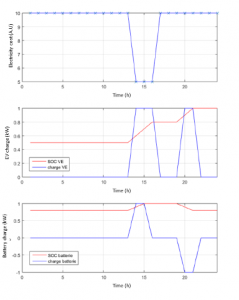
Figure 6: Test of the dynamic algorithm : after DP algorithm has been implemented, a simple intuitive case has been used to check its correct behaviour. The figure shows the battery is charged when electricity price is low according to cost function as long as it is possible

The results of the simulation are given in figure 6. The first graph describes the variation of the hourly rate of electricity for our simulation, the second graph represents the charge of the electric vehicle in blue (1 for in charge and 0 for no charge) and the variations of the state of charge of its internal battery in red. The third graph represents the charge and the variation of the state of charge for the fixed storage battery. It is immediately apparent that the algorithm controlled the system logically: the EV was charged when energy was cheapest (cost function to be minimized: total price of recharge). Since this was not enough time for the EV to receive enough energy to fully charge, the fixed battery was used well: it was also recharged when electricity was cheap, so that enough energy was stored to complete the charge of the EV outside the period of low price, and end the day with exactly the same level of charge as at the beginning. The timing of the energy delivery is random, from a cost minimization point of view, so it makes no difference whether the EV is charged with battery energy before or after the off-peak period, since the battery starts the day with a fairly high state of charge (70 percent), and no setpoint has been implemented for this action. This result allows to validate this first test of consistency of the dynamic programming algorithms.

In this paper, a simulation based on elementary rules makes it possible to judge the efficiency of the dynamic programming algorithms implemented: cases 1 and 2 are designed by implementing simply-expressed rules to control the system.

• In case 1, the EV is always charged at nominal power as long as the demand exists (presence of EV and SoC less than 1), the power taken from the grid corresponds to the difference between the demand and what can be produced by the solar panels.
• In case 2, the EV is also charged at constant nominal power, the fixed batteries tend to compensate for solar production (they produce if the power demanded Pve is higher than the power of the solar panels Ppv and are charged otherwise). The energy in the fixed batteries must be the same at the beginning and end of the day (battery state of charge at 70%) to justify the consistency of the simulation, and to compare with the case without fixed storage.
• In the third case, a decision-making process is based on a single decision at each time step: charging EVs at rated power or not charging, which allows the cost matrix to be filled quickly (no use of the fixed battery). The cost function chosen is to minimize the total energy consumed by the network, as modeled by equation14.

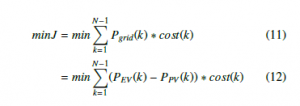
• A fourth case is also added for comparison purposes, similar to case 3, but this time to minimize the cost of energy over a day, as modeled by equation12.

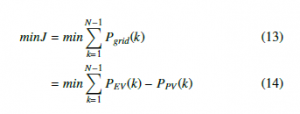
5.2        Simply-expressed rules (cases 1 and 2)

For the first case, the results are given in the figure 7 : in blue, the photovoltaic production over the day, in cyan the hourly energy pricing, which was defined in collaboration with the distribution network manager in order to limit the consumption of the EVs over 3 periods corresponding to morning, midday, and evening peaks. All the electric vehicles arrive at 6:00 am and are automatically charged without planning as soon as they arrive (red curve on the figure). The charging is not optimized and does not take into account the pricing or the photovoltaic production.

For the second case, the fixed storage battery is added, allowing to store the energy produced by the solar panels in order to increase the self-consumption of renewable energy. The first graph of the figure 8 shows the use of the battery (in red, the power supplied by the battery, and in green the state of charge). On the second graph, we find the behavior of case 1, since it is still a simulation without load planning intelligence.

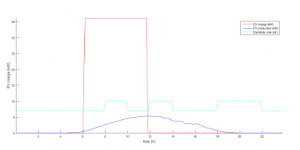
Figure 7: Reference case 1 : without battery

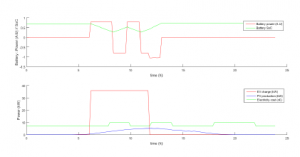
Figure 8: Reference case 2 : with battery

5.3        Minimizing energy consumption

We have now integrated the dynamic scheduling algorithm to plan the charging in an intelligent way. In the figure 9, we can see on the top graph the hourly charging, and on the bottom one, we find in green the PV production, in blue the charging power, and in red, the state of charge of the EV batteries. In this case, the algorithm is designed to minimize energy consumption, so EV charging is favored during the time slots when renewable production is at its maximum.

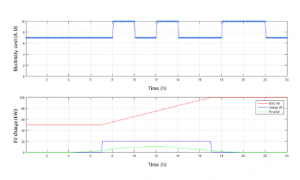
Figure 9: Results for minimal energy consumption

5.4        Minimizing charging cost

For the last case, the cost function to minimize is the total cost. Thus, we can see on the figure 10 that EV charging is planned on periods when electricity is cheaper and renewable generation is also available.

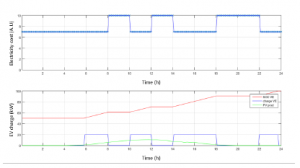
Figure 10: Results for minimal charging cost

5.5        Experimental test

The developed dynamic programming algorithm has been implemented and tested for minimizing charging cost in a real parking lot with 22kW AC EVSEs, which is illustrated on figure 11. The experimentation environment has been created and developed on the experimental site of the French distribution network operator. We also developed a supervision interface to remotely monitor the system and energy supply strategies. Figure 12 shows the web monitoring interface. Experimental data is confidential but the first experimental results are consistent with the simulations.

Figure 11: Experimental environment : part of the EVs, EVSEs and PV panels used for our study

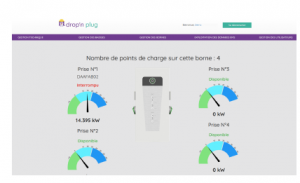
Figure 12: Screen capture of the web monitoring interface used for experimental data

6. Limits of deterministic model

Difficulties in using a deterministic model for inconsistencies with reality and planning is due to a lack of access to system data. Unlike the EV driver, the operator responsible for managing the charging stations is unable to easily visualize the SoC visible on the dashboard. Data exchanges between the EV and the EV charging infrastructure (IRVE) are governed by the IEC 61851 standard (and soon by the IEC 15118 standard). However, the access to the SoC through the EVSE will not be facilitated by EV manufacturers. This decision, political and commercial above all, limits the development of smart charging stations. The relevance of the criteria to be used for efficient load planning is discussed in [20]. The need to have access to certain data (arrival / departure of VE, SoC, etc.) for robust management algorithms is also mentioned. The unpredictable behaviour of people using ESVEs is considered a non-deterministic aspect.

6.1        Data gathering

In order to compensate for the lack of information described above, a system for collecting data from users can be set up. In the case of a fleet of electric vehicles of a company or that of people having a subscription to a public or private parking, the collaboration of the people in charge of the recharging of the electric vehicles and their agreement to provide the data necessary for the correct sequencing of the algorithm is the main drawback of this method. One solution to retrieve the data is that each user declares the EV’s expected departure time, model and state of charge. Without going through a declarative process, an experiment was carried out to recover useful data for recharging EVs. The company Dropbird was tested a communication system between the EV and the EVSE through on-board diagnostics (OBD). The first tests carried out seem very promising.

6.2        Users behaviour modelling

Modelling user behavior is a key issue, whether access to the SoC is available or not. So far, all users have been modelled as arriving at the same time to charge their EV. This particular case is not realistic. Also, an optimization taking into account more realistic user behaviour was carried out. An optimized management law for a family of random cases (in the sense of ”average”) is preferred over the search for a list of optimal choices for a given case. An identification of the recurring behaviours of the users will be carried out from real behaviour data, which will make it possible to create a matrix of transitions between the different possible states. Each transition will be associated with a probability of passing from one state to another (present/absent) depending on the arrival time, presence time and/or state of charge.

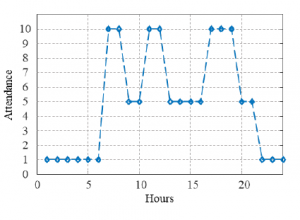
Figure 13: Attendance factor added to model to take into account the probability of a new incoming vehicle to the parking, depending on the time of the day

6.3        Users behaviour quick approximation

A study of fictitious cases was carried out with the aim of making a first approximation of user behavior. Fictitious users whose behaviour is modelled by several random variables (initial state of charge, battery capacity, arrival time) were simulated.

Fictitious users whose behaviour is modelled by several random variables were simulated: initial state of charge, battery capacity, arrival time. These variables are initialized for each EV when it arrives by picking a random value from a range of realistic values. An

“attendance” variable was defined on the basis of our observations. This variable gives the probability that an EV will arrive to recharge, depending on the time of day, as illustrated to the Figure 13.

In order to observe the impact of user behaviour on the load planning and to compare the planning in cases where access to the state of charge is possible or not, a simulation was carried out on a parking lot. not having renewable energies. Figure 14 shows, for different scenarios, the distribution of the final state of charge and the final energy on board for all the electric vehicles that have used the parking lot during the day. For the same user behaviour but with different management methods, 3 simulations were performed. In Fig. 14a), the state of charge of the incoming vehicles is unknown to the parking manager, the energy is allocated first to the earliest arrived EV.

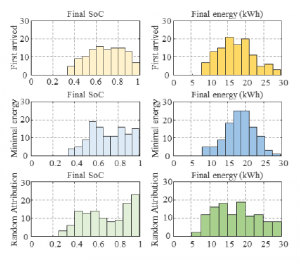
Figure 14: Number of EVs for each value of final energy and final SOC at departure time, for three different strategies of allocation of available energy : first come first served (a), minimum energy (b), random (c)

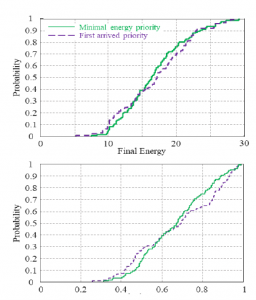
Figure 15: Cumulative probability of EV final Energy / final SOC at departure time. Cumulative distribution is given for 2 strategies : priority to first arrived or priority to lowest energy

In Figure 14 (b), it is considered that the SoC and the battery capacity of each EV are accessible. The energy is then allocated to the EV with the lowest autonomy, that is to say to the EV with the minimum stored energy. In Fig. 14c), the SoC of the incoming vehicles is unknown. Energy is assigned to the EV when it comes to connect. To allow another waiting EV to start charging, we must wait for an EV to reach full charge or for an EV start. The choice is made randomly if several EVs are on standby. The simulation of figure 14b) shows that it is possible to significantly reduce the number of EVs with final energy less than 15 kWh (the distribution is shifted to the right). Figure 15 compares more explicitly the cases illustrated in Figures 14 (a and b).

In figure 13, the criterion used is the energy available in the EVs from the car park (at the end of charging). The distribution of this data is used to qualify our load planning algorithm. This distribution is given for 2 planning algorithms: in red for the case where the energy allocation is given to the EV with the minimum energy (the SoC is accessible) and in blue for the case where the energy allocation is given on first arrival (the SoC is not accessible). A criterion corresponding to a range of approximately 100 km is set, i.e. approximately a minimum energy at the end of charging of 15kWh. For the case without access to the SoC, this value is guaranteed for 60% of the EVs, while for the case with access to the Soc, this value is guaranteed for 70% of the EVs. To ensure a minimum energy level for each EV at the end of charging, knowledge of SoC is essential.

7. Conclusion and perspectives

In this paper, the optimization of energy flows within a network of micro-parking lots with EV charging stations and energy production was carried out using dynamic programming algorithms. Their proper functioning has been first validated in simulation by considering a predetermined use. The implementation of the algorithms in a real experimental demonstrator has been made. The first results obtained validate the effectiveness of the algorithms. This is the first step in a long process, the final objective of which is the creation of an energy management system. The final objective is to propose an optimal management law for all types of car parks equipped with recharging infrastructures, taking into account their specificity. Among the work to be developed, we can cite the increasing complexity of dynamic simulation by adding degrees of freedom, but also the strengthening of the study of user behavior in order to define random cases based on reality.

1. L. Pieltain Fernandez, T. Gomez San Roman, R. Cossent, C. Mateo Domingo,
   P. Frias, “Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks,” 26(1), 206–213, doi:10.1109/TPWRS.2010.2049133.
2. G. B. Shrestha, B. C. Chew, “Study on the optimization of charge-discharge cycle of electric vehicle batteries in the context of Singapore,” 1–7, IEEE, 2007, doi:10.1109/AUPEC.2007.4548023.
3. Z. Ma, D. Callaway, I. Hiskens, “Decentralized charging control for large pop- ulations of plug-in electric vehicles: Application of the Nash certainty equiva- lence principle,” 191–195, IEEE, 2010, doi:10.1109/CCA.2010.5611184.
4. S. Deilami, A. S. Masoum, P. S. Moses, M. A. S. Masoum, “Real-Time Coordination of Plug-In Electric Vehicle Charging in Smart Grids to Min- imize Power Losses and Improve Voltage Profile,” 2(3), 456–467, doi: 10.1109/TSG.2011.2159816.
5. D. Dallinger, D. Krampe, M. Wietschel, “Vehicle-to-Grid Regulation Reserves Based on a Dynamic Simulation of Mobility Behavior,” IEEE Transactions on Smart Grid, 2(2), 302–313, 2011, doi:10.1109/TSG.2011.2131692.
6. A. Y. Saber, G. K. Venayagamoorthy, “Resource Scheduling Under Uncer- tainty in a Smart Grid With Renewables and Plug-in Vehicles,” 6(1), 103–109, doi:10.1109/JSYST.2011.2163012.
7. E. Sortomme, M. A. El-Sharkawi, “Optimal Scheduling of Vehicle-to-Grid En- ergy and Ancillary Services,” IEEE Transactions on Smart Grid, 3(1), 351–359, 2012, doi:10.1109/TSG.2011.2164099.
8. J. Lagorse, D. Paire, A. Miraoui, “A multi-agent system for energy management of distributed power sources,” 35(1), 174–182, doi:10.1016/j.renene.2009.02. 029.
9. T. Kim, J. Yun, W. Qiao, “A multiagent system for residential DC microgrids,” in 2015 IEEE Power & Energy Society General Meeting, 1–5, IEEE.
10. G. Kyriakarakos, A. I. Dounis, K. G. Arvanitis, G. Papadakis, “A fuzzy logic energy management system for polygeneration microgrids,” 41, 315–327, doi: 10.1016/j.renene.2011.11.019.
11. N. J. Schouten, M. A. Salman, N. A. Kheir, “Energy management strategies for parallel hybrid vehicles using fuzzy logic,” 11(2), 171–177.
12. A. Al-Alawi, S. M Al-Alawi, S. M Islam, “Predictive control of an integrated PV-diesel water and power supply system using an artificial neural network,” 32(8), 1426–1439, doi:10.1016/j.renene.2006.05.003.
13. Y. Ates, O. Erdinc, M. Uzunoglu, B. Vural, “Energy management of an FC-UC hybrid vehicular power system using a combined neural network-wavelet trans- form based strategy,” 35(2), 774–783, doi:10.1016/j.ijhydene.2009.11.021.
14. Louis Frecon, Manuel d’intelligence artificielle, presses polytechniques et universitaires romandes edition, 2009.
15. Yakowitz, Dynamic programming applications in water resources ». Water Resources Research, water resources research edition, 1982.
16. X. Zeng, J. Wang, “A Parallel Hybrid Electric Vehicle Energy Management Strategy Using Stochastic Model Predictive Control With Road Grade Preview,” IEEE Transactions on Control Systems Technology, 23(6), 2416–2423, 2015, doi:10.1109/TCST.2015.2409235.
17. X. Zeng, J. Wang, “Optimizing the Energy Management Strategy for Plug-In Hybrid Electric Vehicles With Multiple Frequent Routes,” IEEE Transactions on Control Systems Technology, 27(1), 394–400, 2019, doi:10.1109/TCST. 2017.2768042.
18. J.-M. Kang, I. Kolmanovsky, J. W. Grizzle, “Dynamic optimization of lean burn engine aftertreatment,” Journal of Dynamic Systems, Measurement, and Control, 123(2), 153–160, 2001.
19. Chan-Chiao Lin, Huei Peng, J. Grizzle, Jun-Mo Kang, “Power manage- ment strategy for a parallel hybrid electric truck,” 11(6), 839–849, doi: 10.1109/TCST.2003.815606.
20. C.-C. Lin, H. Peng, J. W. Grizzle, “A stochastic control strategy for hybrid electric vehicles,” in American Control Conference, 2004. Proceedings of the 2004, 5, 4710–4715, IEEE, 2004.

(Click Here)