1. Introduction

FECG reflects electrical activity of fetal heart. It can be used to discover Fetal Heart Rate (FHR) and multiple pregnancies and to establish if the fetus is in distress. It is also useful in function parameter analysis of heart for the prevention of neonatal diseases [1]. The two methods used for obtaining FECG are the use of electrodes applied on the scalp of the fetus and through non-invasive recording by placing electrode on mother’s abdomen. Invasive recordings achieve better quality but the process is regretfully difficult and only applicable during labor [2]. In contrast, the recording by noninvasive means has the advantage of being simple, noninvasive and can be applied throughout gestational period. That is why medical workers and pregnant women have deeply welcomed it [3].

The major drawback of noninvasive FECG (NI-FECG) recording is contamination with various forms of noise like maternal ECG (MECG), electromyogram (EMG), baseline wandering, power line interference, etc.[4], [5].

Research is ongoing on methods of extracting FECG from AECG. MECG is the most influential interference noise signal present in the AECG which has been suppressed using various techniques such as adaptive filters [4], [5] and wavelet transform [6]-[9] among other methods [9], [7]. Two things characterize adaptive filters. First, the type of unit sample response based on which we have Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. Second, the optimization algorithm used. Gradient-based optimization algorithms are popular, but they have the problem of convergence at local minimum for multimodal error surfaces [10]. Attempts to solve the problem of local minima and achieve global optimum solution has led many researchers to introduce the use of global optimization techniques for adaptive filter optimization such as Genetic Algorithm (GA) [11], Simulated Annealing (SA) [12], Tabu Search (TS) [13], Differential Evolution (DE) [14], Particle Swarm Optimization (PSO) [15], Ant-colony (ACO) [16], Artificial intelligence [17] Modified firefly and modified ABC algorithms [18].

In this work, LMS algorithm with its exploitation ability, robustness, ease of implementation, low computational complexity and unbiased convergence [19] is combined with MFO which has high global search (exploration) capability. MFO has the additional advantages of simplicity, flexibility and ease of implementation. Due to these advantages, it has been successfully applied in many optimization applications [20]. Some of these include scheduling [21], classification [22], power energy [23], medical [24], and image processing [25]. However, from available literature, this is the first time MFO is being used for FECG Extraction.

2. Fetal ECG Monitoring

Figure 1 illustrates the method of FECG monitoring. Two electrodes are placed on the body of a pregnant woman; one each on her chest and abdomen. Three signals are recorded by the electrode placed on the abdomen. One of them is the corrupted version of the maternal ECG (MECG) signal, i.e. . The second is FECG signal  and the third is noise from various sources denoted as .  Equations (1) to (3) describe the relationship between these signals.

MECG as recorded by the abdominal electrode is corrupted due to the nonlinear transformation it undergoes as it travels from the chest to the abdomen.

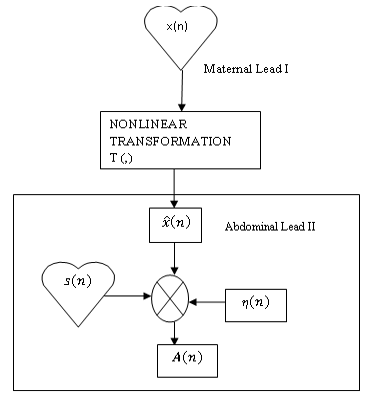Figure 1: Fetal ECG Monitoring

3. Proposed Extraction Algorithm

The proposed method of adaptive filtering as depicted in Figure 2 consists of two adaptation algorithms; the LMS alone and LMS/MFO. These algorithms (implemented one after the other) were used to update the weights of Finite Impulse Response Filter based on the error signal (desired signal). Here the noisy abdominal signal is given as input and a thoracic electrode output signal is given as reference input to the filter. Since the signal of interest is the fetal heartbeat, maternal heart beat is considered as the interference noise to the signal. The primary signal is the fetal electrocardiogram measured from the abdominal electrode. It consists of mainly maternal heartbeat which dominates the fetal heartbeat and some residual measurement noises. The reference signal is taken from the chest of the mother through thoracic electrode which consists of actual maternal heart beat with some additive noise. Adaptation algorithm here uses the error signal as its input and updates the filter coefficients based on the parameters defined to the filter. The output obtained by the filter should be approximately equal to the noise i.e. the maternal heart beat in the primary signal so that the error signal obtained should be fetal heart signal. The error signal obtained finally corresponds to the fetal heart beat signal but corrupted with residual noises which are in turn eliminated by filtering them out adaptively.

3.1. Configuration of the Adaptive Filter

The configuration of the adaptive filter is shown in Figure. 3. The filter is shown to be operating in time domain.

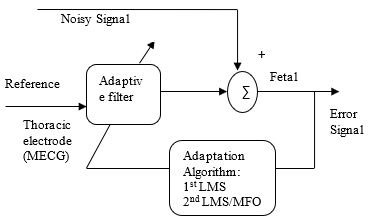Figure 2: Block diagram of proposed algorithm

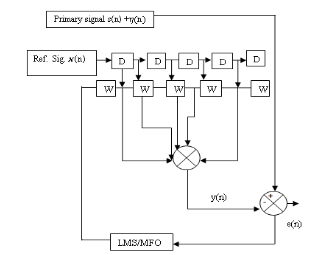Figure 3: Adaptive filter structure

In Figure 3,  is the primary signal while the primary noise is , and the two are uncorrelated.  is the reference signal and it is strongly correlated with  but uncorrelated with . The output error  is given by

The error signal serves as the input to the adaptation algorithm [26]-[28] which subsequently adjusts the adaptive filter coefficient vector    depending on some measurements standard. The adaptation process is geared towards minimizing the error signal (in this case the fetal ECG).

 According to [26]-[28], the mean square error (MSE) is a measure that shows how effectively a system adapts to a specified solution. The final value of MSE can be used to decide on proficiency of the adaptation algorithm. Consequently, a least value signifies the efficiency of the algorithm and in contrast, a high value normally signifies the inability of the algorithm to model the specified system or the initial state of the adaptive filter is inappropriate starting point to ensure the adaptive filter convergence. The mean square error is given by

where E[.] indicates expectation operation. For noise cancellation, the goal is to have a system output best fit in the least squares sense of the signal s(n) . The mean square of error is of interest and can be obtained as follows

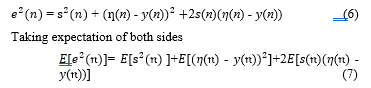Since  is uncorrelated with both  and

Adapting the filter minimizes the mean square of error. This has no effect on the input signal .

If the means square error is minimized, output of the filter,  will be a best least square match to  We can rewrite (4) as

Minimization of the mean square error makes e(n) to be the most suitable match of the signal s(n) in the least squares sense. This is achieved by adaptive filtering with no a priori information about the signal and noise statistic.

3.2. Least Mean Square Algorithm

The popularity of LMS as an adaptive filter algorithm is due to its simplicity, robustness, ease of implementation, low computational complexity, stability and unbiased convergence as reported by [19]. From Figure 3

where  is a vector representation of the adaptive filter weights and  is a vector of the corresponding delayed values of x(n) as depicted in Figure 3. That is,

where µ is called the step-size, w(n) represents the new coefficient values for the next time interval, x(n) is the filter (reference) input signal, y(n) represent the filtered output, s(n) is the desired response and e(n) is the error function. The convergence of  to the optimum solution and the convergence speed depend on the value of step-size parameter µ.

3.3. Moth-Flame Optimization Algorithm (MFO)

Moth-flame optimization (MFO) was initiated by Mirjalili in 2015 [29]. It is among the latest metaheuristic population-based methods. It is an optimization design to mimic the behavior of moth, a type of butterfly species flying in night towards a moon in a straight line known as transverse orientation for navigation. However, turn to spiral motion when encountered with shorter light source. Consequently, this led to the formulation of an interestingly new optimization algorithm. Additionally, MFO was designed to achieve exploration and exploitation goal as it combines population-based algorithm and local search strategy. Also, to prevent the solution being trapped in local minima, the optimal solutions were maintained in each repetition as reported in [29]. The algorithm uses the explorative as well as exploitative search to get an optimized solution.

 In the introduced MFO, a moth is considered to be a candidate solution and the position of moth at different search space as problem’s variables. Hence, the moth can fly in hyper dimensional space or 3D dimensions and changing their position vectors. Since MFO is population-based, matrix representation of the swarm of moths can be made as in (18)

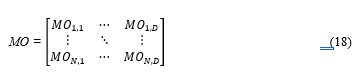    We can evaluate the fitness of each moth by means of the fitness function. The fitness is stored in a matrix as in (19)

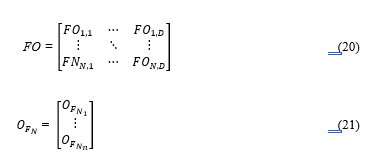
     The matrix of (20) stores moths best positions in each dimension as flames, while the generated corresponding fitness values are stored as in (21).

      The spiral movement of the moth around the flame is represented in (22)

here,    indicate the spiral motion,  is a constant associated with the shape of the spiral movement.  is a random variable used to select the position of a moth from the flame  represents the closest position while  represents the farthest position of the moth. Equation (22) is used to update the position of the moths with the best moth position updating the flame position. Furthermore, the number of flames is decreased in each iteration using (23)

where ceil,     and    denote round to whole number, the current iteration number and the total number of iterations respectively. MFO process is elucidated in Table 1.

MFO algorithm is illustrated in Table 1. The next stage describes the implementation   of MFO in the proposed work.

Table 1: The MFO Process [29]

Initialization of the Moths
For  I =1:N
	For j = 1:D then
			MOi, j = random position between given bounds ;
	End
O = Fitness value
End
C = 1
While  M   = | – M  cos(2
	If
		MOi  = Fitness value ( MOi )
	Elseif
			FO = Quick Sort (MO) = Quick Sort ( )
	Else
			FO = Quick Sort (M  , M  ) = Quick Sort(  ,  )
	End
	Update b and t M   = | – M   cos (2
	Update number of flames
End
Exit

3.4. MFO Adaptive Filtering

It is noteworthy that we are using the moth flame optimization algorithm to optimize the LMS adaptive filtering algorithm. The moths here represent the filter coefficients to be updated. This means for each filter coefficient ( ), there is a moth and the position of the filter coefficient is considered as the position of the moth. This is because the moth is taken to be candidate solution in the search space and when the moth changes position, the filter coefficient is adjusted. The process continues repeatedly until the best coefficients are obtained as in MFO process in Table 1. The number of dimensions,  since the filter coefficients ( ) would be placed in a real world environment.  The position matrix representing the moth based on filter coefficient ( ) is given by (24).

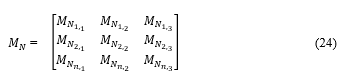here, n is a number representing the length of the coefficient vector ( ) in the network. The fitness value of the current filter coefficient ( ) is generated by using its distance from the destination. Equation (25) is used to generate the said fitness value.

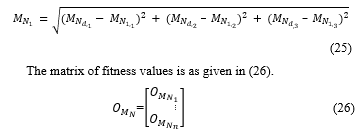The flame matrix gives the position matrix of the best neighbor filter coefficient ( ) to be selected in the route by any filter coefficient ( ) given by (27) and corresponding fitness value matrix generated using the (25) is given in the (28).

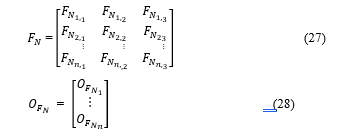The position of the filter coefficient ( )  to be selected next in the route is given by the (29).

The new position obtained using the (12) need not be the exact position of the filter coefficient ( ), so the filter coefficient ( ) nearest to the updated position is to be selected, so the (12) is applied to generate the matrix in (30).

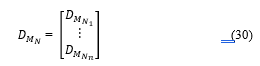For the updated matrix   to be generated, a quick sort can be performed on matrix . The algorithm would then select or  according to the fitness value. In other words, filter coefficients ( ) with lower fitness values (which are better) are selected. The estimation error is thus decreased to minimal value.

4. Simulation, Results and Discussion

4.1. Generation of Synthetic Signals

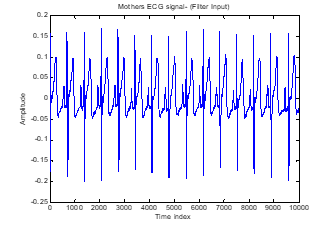
A sampling frequency of 4 KHz is used to simulate the maternal ECG shown in Figure 4. Other important parameters for the signal are the approximate heart rate of 89 bmp (beats per minute) and the peak voltage of 3.5 mV.

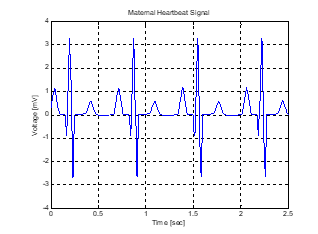Figure 4: Maternal Heartbeat Signal

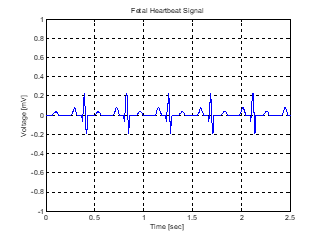Figure 5: Fetal Heartbeat Signal (Targeted Signal)

The FHR is normally higher than the maternal heart rate, with the former ranging from 120 bpm to 160 bpm. For the simulated FECG signal the heart rate is 139 bpm and the peak voltage is 0.25 mV. [30]

The signal obtained from the abdominal electrode is a noisy signal and is shown in Figure 6. This is to be filtered and given as input to the adaptive noise canceller.

The signal recorded by the thoracic electrode is given as reference signal [30] as shown in Figure 7. This is given as reference input to the adaptive noise canceller.

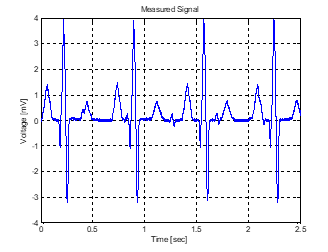Figure 6: Abdominal ECG Signal

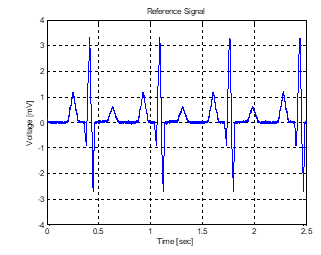Figure 7: Measured Maternal Electrocardiogram (Reference) Signal

4.2. Simulation using Synthetic Signals

Figure 8 is the result obtained by training the adaptive noise canceller with LMS algorithm. In fetal ECG extraction QRS complex detection is important so that R-R interval and R peaks can properly be identified. In this case two R peaks indicated by arrows are poorly extracted that may hinder proper monitoring of fetal heart status.

Figure 9 to Figure 13: The results show that with moth population between 20 and 80, the first p-waves are missing or not clearly defined. However, all the waves were recovered and R-R interval clearly seen when the moth population was increased to 100. Also, the expected FHR was equally recovered. The FHR was recovered using (31).

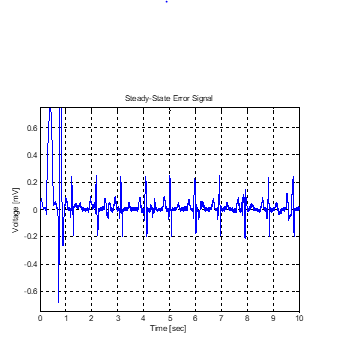Figure 8: Result obtained by LMS

where  is the R-R  interval and t is the time interval.

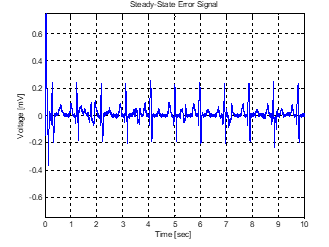Figure 9:  LMS/MFO result at 100 moth pop.

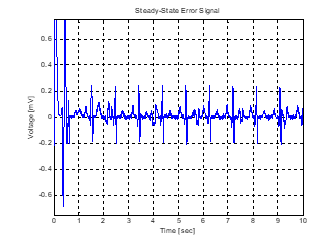Figure 10: LMS/MFO result at 80 moth pop.

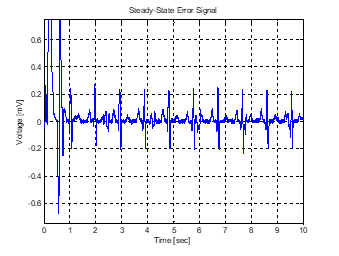Figure 11: LMS/MFO result at 60 moth pop.

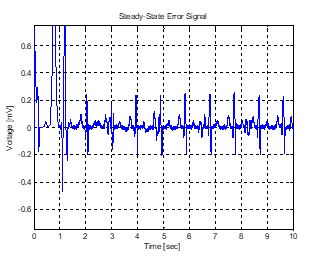Figure 12: LMS/MFO result at 40 moth pop.

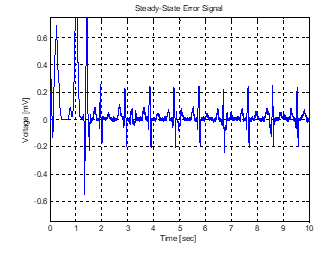Figure 13:  LMS/MFO result at 20 moth pop.

Table 2 shows the results of magnitude of Mean Square Error (MSE) obtained at different moth population (between 20 and 100) at a fixed number of iterations. Table 3 shows the SNR before the application of the proposed technique and after. The SNR is calculated using (34).

SNR= 10 log₁₀ (P_s / P_n)                 (34)

where Ps is the signal power, in this case the power of fetal ECG signal  which was obtained using  and  is the noise power which represents the power of both deformed maternal ECG and white Gaussian noise. It was obtained using

The result in Table 2 shows that the MSE is low with high population of moth (i.e. 100). The obtained mean square error values show that system has converted to a solution. Table 3 indicates a decrease of MSE and increase of SNR when the proposed algorithm was applied as required.

Table 2: Mean Square Error (MSE) Values at different Moth Population and fixed iteration number

Moth Pop	MSE	ITER
100	0.0215	20
80	0.0224	20
60	0.0224	20
40	0.0224	20
20	0.0224	20

Table 3: SNR and MSE for LMS and proposed LMS/MFO

Method	SNR	MSE
LMS	0.1028	0.0275
Proposed LMS/MFO	10.280	0.0215

Table 4 gives performance comparison of the proposed algorithm with conventional LMS and some existing methods. The proposed method shows improvement in SNR and decrease in MSE.

Table 4: comparison of MSE and SNR

Methods	MSE	SNR (dB)
Wavelet Transform [31]	Not reported	-2.457
Wiener Method [32]	Not reported	-10.9838
ICA [33]	Not reported	-3.1313
SVD [32]	Not reported	-12.7980
LMS	0.0275	0.1028
Proposed LMS/MFO	0.0215	10.280

 

4.3. Analysis Using Real ECG Signal

To establish the efficacy of the proposed approach a real abdominal ECG and thoracic ECG data were obtained from Physionet developed by MIT-BIH. Figure 14 and Figure 15 are the abdominal and thoracic ECG signals respectively. After the application of the proposed algorithm, Fetal ECG was extracted as in Figure 16. The R peaks that are used to determine the FHR were efficiently localized.

Figure 14: Real abdominal ECG

Figure 15: Real thoracic ECG

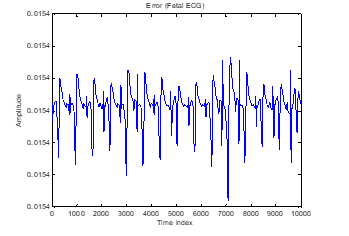Figure 16: Extracted fetal ECG

4.4. Performance Comparison with Existing Techniques

The results obtained using proposed LMS/MFO extraction method was compared with selected existing methods and the result is summarized in Table 4.

According to [34], actual comparison of the existing techniques for FECG extraction is still difficult due to the differences in dataset, evaluation techniques, etc used by individual researchers. It is thus easier to use specific criteria like improvement in SNR, computational complexity, etc. the following rather subjective criteria were proposed.

Overall performance: This has to do with the robustness of the technique. Performance can be classified as low, medium or high.

Low: Performance is classified as low when the technique is not suitable for FECG extraction but may be used to eliminate specific types of noise like power line interference, baseline wandering, etc. Low performance techniques are primarily capable of NI-FECG preprocessing.

Medium: In this case, techniques are suitable for advanced preprocessing. They are capable of removing most noise types in NI-FECG preprocessing.  These include EMG, myopotentials, motion artifacts, among others. Medium performance techniques partly remove MECG thereby enabling the detection of FQRS (Fetal QRS) and consequently the determination of FHR.

High: High performance techniques are the strongest in terms of NI-FECG processing. A high performance technique supplies information on FHR and FECG morphology (PR, QT, ST, etc.).

Improvement in SNR: Like with overall performance, techniques are categorized into three (i.e. low, medium and high) in terms of SNR improvement. It is noteworthy that SNR accurately verifies proficiency of a technique with respect to some reference value. However, when it comes to clinical applications the use of SNR may not be very helpful. Techniques that show very high performance in the improvement of SNR may not be good in FQRS detection.

Computational Complexity: This is an assessment of the computational requirements of a particular technique. Computational complexity requirements may be high, medium or low. Of course, low is the best.

FHR (R-R): This is an assessment of the credibility of a technique under investigation in terms of its ability to determine FHR based on R-R interval. Four classes are identified, viz. inaccurate, moderately accurate and very accurate.

Inaccurate: This is when a technique is not capable of effectively removing artifacts and noise for proper detection of the R-R interval. When an inaccurate technique is used to process NI-FECG, the result cannot be used for monitoring FHR.

Moderately accurate: This is when a technique effectively removes most common noises, thus enabling the detection of R-R interval. Of course, the noises are not effectively removed resulting in undetected and false-detected complexes. For moderately accurate techniques, maximum sensitivity is 80%, maximum PPV (positive predictive value) is 90%, maximum accuracy is 80% and probability of correct detection of beats (F1) is 85%.

Accurate: These techniques permit precise FHR detection. Maximum sensitivity is 85%, maximum PPV, 95%, maximum accuracy, 85% and maximum F1, 95%.

Very accurate: This class of techniques permits a very precise detection of FHR. For very accurate techniques, the maximum sensitivity is 95%, maximum PPV is 95%, maximum accuracy is 95% and maximum F1 is 95%. For values above this (say 99% PPV) a technique is still considered very accurate.

Morphological analysis (T/QRS; QT): This is a measure of the effectiveness of a technique being investigated for an in-depth analysis of the morphology of FECG. Three classes are identified.

Insufficient: When the quality of FECG extracted by a technique is not sufficient for morphological analysis.

Moderately accurate: This is when a technique allows for morphological analysis. The problem, in this case, is that SNR, age of gestation, position of fetus, etc. significantly affect the efficacy of the method except for some tested real data. Thus, for monitoring of T/QRS or QT interval, a moderately accurate technique cannot be used.

Promising: A promising technique has a very high potential of being used for morphological analysis.

Table 4: Comparison with some existing methods

Technique	Fetal Heart Rate, FHR (R-R)	Morphological Analysis (T/QRS; QT)	Overall Performance	Improvement in SNR	Computational Complexity
Wavelet Transform [35]	Moderately Accurate	Insufficient	Medium	Medium	Low
Independent Component Analysis [36]	Accurate	Moderately accurate	Medium	Medium	Medium
Singular Value Decomposition [37]	Inaccurate	Insufficient	Low	Low	Low
Sequential Total Variation Denoising [38]	Accurate	Insufficient	Medium	Medium	Medium
Template Subtraction [39]	Moderately accurate	Insufficient	Medium	Low	Low
Proposed  Method	Very Accurate	Promising	High	High	Low

5. Conclusion

A new algorithm for FECG extraction has been presented. The algorithm which combines MFO algorithm and LMS adaptive filtering has two inputs, viz. the abdominal signal which is the major signal of interest and the thoracic signal which serves as the reference input.

The hybrid algorithm has been shown to be better than the LMS adaptive algorithm. Results have shown improvement in the detection of R-peaks of fetal ECG much better with 100 moth population. The superiority of the new approach has been shown quantitatively by MSE and SNR calculation.

 A decrease of mean square error of 0.0215 was observed with the proposed algorithms and improvement of signal to noise ratio of 10.28 was also observed.

 Comparison with existing methods shows better performance of the proposed approach.

Further research should focus on applying this method for multifetal ECG separation and the use of statistical method of analysis e.g. anova method for comparison of result.

1. M. Ahmadi, M. Ayat, K. Assaleh, H. Al-Nashash, “Fetal ECG signal enhancement using polynomial classifiers and wavelet denoising,” in 2008 Cairo International Biomedical Engineering Conference, CIBEC 2008, 2008, doi:10.1109/CIBEC.2008.4786095.
2. R. Sameni, Extraction of Fetal Cardiac Signals from an Array of Maternal Abdominal Recordings, 2008, doi:10.13140/RG.2.2.14830.41285.
3. A.K. Barros, A. Cichocki, “Extraction of specific signals with temporal structure,” Neural Computation, 13(9), 1995–2003, 2001, doi:10.1162/089976601750399272.
4. E.R. Ferrara, B. Widrow, “Fetal Electrocardiogram Enhancement by Time-Sequenced Adaptive Filtering,” IEEE Transactions on Biomedical Engineering, BME-29(6), 458–460, 1982, doi:10.1109/TBME.1982.324973.
5. A. Khawaja, Automatic ECG analysis using principal component analysis and wavelet transformation, University Publishing Karlsruhe, Karlsruhe, 2007.
6. J.H. Nagel, “Progresses in Fetal Monitoring by Improved Data Acquisition,” IEEE Engineering in Medicine and Biology Magazine, 3(3), 9–13, 1984, doi:10.1109/MEMB.1984.5006080.
7. E.C. Karvounis, C. Papaloukas, D.I. Fotiadis, L.K. Michails, “Fetal heart rate extraction from composite maternal ECG using complex continuous wavelet transform,” in Computers in Cardiology, 737–740, 2004, doi:10.1109/cic.2004.1443044.
8. S. Wu, Y. Shen, Z. Zhou, L. Lin, Y. Zeng, X. Gao, “Research of fetal ECG extraction using wavelet analysis and adaptive filtering,” Computers in Biology and Medicine, 43(10), 1622–1627, 2013, doi:10.1016/j.compbiomed.2013.07.028.
9. A.U. Jibia, A. Inuwa, “Fetal Electrocardiogram Extraction Using BFOA-Based Adaptive Filter,” ATBU Journal of Science, Technology and Education, 3(4), 30–43, 2016.
10. E.C. Karvounis, M.G. Tsipouras, D.I. Fotiadis, K.K. Naka, “An automated methodology for fetal heart rate extraction from the abdominal electrocardiogram,” IEEE Transactions on Information Technology in Biomedicine, 11(6), 628–638, 2007, doi:10.1109/TITB.2006.888698.
11. J.H. Holland, “Genetic algorithms,” Scientific American, 267(1), 66–72, 1992, doi:10.1038/scientificamerican0792-66.
12. S. Chen, B.L. Luk, “Adaptive simulated annealing for optimization in signal processing applications,” Signal Processing, 79(1), 117–128, 1999, doi:10.1016/S0165-1684(99)00084-5.
13. A. Kalinli, N. Karaboga, “A parallel tabu search algorithm for digital filter design,” COMPEL – The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 24(4), 1284–1298, 2005, doi:10.1108/03321640510615616.
14. R. Storn, K. Price, “Differential Evolution – A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces,” Journal of Global Optimization, 11(4), 341–359, 1997, doi:10.1023/A:1008202821328.
15. R. Eberhart, J. Kennedy, “New optimizer using particle swarm theory,” in Proceedings of the International Symposium on Micro Machine and Human Science, IEEE: 39–43, 1995, doi:10.1109/mhs.1995.494215.
16. M. Dorigo, M. Birattari, T. Stützle, “Ant Colony Optimization,” Computational Intelligence Magazine, IEEE, 1, 28–39, 2006, doi:10.1109/MCI.2006.329691.
17. G. Chandrasekaran, S. Periyasamy, K. Panjappagounder Rajamanickam, “Minimization of test time in system on chip using artificial intelligence-based test scheduling techniques,” Neural Computing and Applications, 32(9), 5303–5312, 2020, doi:10.1007/s00521-019-04039-6.
18. G. Chandrasekaran, S. Periyasamy, P.R. Karthikeyan, “Test scheduling for system on chip using modified firefly and modified ABC algorithms,” SN Applied Sciences, 1(9), 2019, doi:10.1007/s42452-019-1116-x.
19. N. Sireesha, K. Chithra, T. Sudhakar, “Adaptive filtering based on least mean square algorithm,” in International Symposium on Ocean Electronics, SYMPOL, IEEE Computer Society: 42–48, 2013, doi:10.1109/sympol.2013.6701910.
20. M. Shehab, L. Abualigah, H. Al Hamad, H. Alabool, M. Alshinwan, A.M. Khasawneh, Moth–flame optimization algorithm: variants and applications, Neural Computing and Applications, 32(14), 9859–9884, 2020, doi:10.1007/s00521-019-04570-6.
21. N. Jangir, M.H. Pandya, I.N. Trivedi, R.H. Bhesdadiya, P. Jangir, A. Kumar, “Moth-Flame optimization Algorithm for solving real challenging constrained engineering optimization problems,” in 2016 IEEE Students’ Conference on Electrical, Electronics and Computer Science, SCEECS 2016, Institute of Electrical and Electronics Engineers Inc., 2016, doi:10.1109/SCEECS.2016.7509293.
22. A.A. Elsakaan, R.A. El-Sehiemy, S.S. Kaddah, M.I. Elsaid, “An enhanced moth-flame optimizer for solving non-smooth economic dispatch problems with emissions,” Energy, 157, 1063–1078, 2018, doi:10.1016/j.energy.2018.06.088.
23. H.M. Zawbaa, E. Emary, B. Parv, M. Sharawi, “Feature selection approach based on moth-flame optimization algorithm,” in 2016 IEEE Congress on Evolutionary Computation, CEC 2016, Institute of Electrical and Electronics Engineers Inc.: 4612–4617, 2016, doi:10.1109/CEC.2016.7744378.
24. I.N. Trivedi, A. Kumar, A.H. Ranpariya, P. Jangir, “Economic Load Dispatch problem with ramp rate limits and prohibited operating zones solve using Levy flight Moth-Flame optimizer,” in 2016 International Conference on Energy Efficient Technologies for Sustainability, ICEETS 2016, Institute of Electrical and Electronics Engineers Inc. 442–447, 2016, doi:10.1109/ICEETS.2016.7583795.
25. M. Wang, H. Chen, B. Yang, X. Zhao, L. Hu, Z.N. Cai, H. Huang, C. Tong, “Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses,” Neurocomputing, 267, 69–84, 2017, doi:10.1016/j.neucom.2017.04.060.
26. N. Karaboga, “A new design method based on artificial bee colony algorithm for digital IIR filters,” Journal of the Franklin Institute, 346(4), 328–348, 2009, doi:10.1016/j.jfranklin.2008.11.003.
27. B. Widrow, S.D. Stearns, Adaptive Signal Processing, Prentice-Hall, Inc., USA, 1985.
28. J.-W. Lee, G.-K. Lee, “Design of an Adaptive Filter with a Dynamic Structure for ECG Signal Processing,” International Journal of Control, Automation, and Systems, 3(1), 137–142, 2005.
29. S. Mirjalili, “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge-Based Systems, 89, 228–249, 2015, doi:10.1016/j.knosys.2015.07.006.
30. B. Widrow, C.S. Williams, J.R. Glover, J.M. McCool, R.H. Hearn, J.R. Zeidler, J. Kaunitz, E. Dong, R.C. Goodlin, “Adaptive Noise Cancelling: Principles and Applications,” Proceedings of the IEEE, 63(12), 1692–1716, 1975, doi:10.1109/PROC.1975.10036.
31. H. Hassanpour, A. Parsaei, “Fetal ECG extraction using wavelet transform,” in CIMCA 2006: International Conference on Computational Intelligence for Modelling, Control and Automation, Jointly with IAWTIC 2006: International Conference on Intelligent Agents Web Technologies …, IEEE Computer Society, 2006, doi:10.1109/CIMCA.2006.98.
32. C. Engineering, Fetal Ecg Extraction Using Wiener , Svd and ICA Algorithms, National Institute of Technology, Rourkella, Odisha, 2013.
33. P.D. Kushwaha, R. Narvey, D.K. Verma, “Extraction Methods of Fetal ECG from Mother ECG Signal in Pregnancy,” International Journal of Advanced Research in Computer and Communication Engineering, 2(6), 2411–2418, 2013.
34. R. Jaros, R. Martinek, R. Kahankova, Non-adaptive methods for fetal ECG signal processing: A review and appraisal, Sensors (Switzerland), 18(11), 2018, doi:10.3390/s18113648.
35. N. Para, . S. Wadhawani, “Fetal ECG Extraction using Wavelet Transform,” International Research Journal of Engineering and Technology, 5(7), 2577–2581, 2018.
36. E. Ahuja, F.I. Shaikh, “A Novel Approach to FEG Extraction based on Fast ICA,” International Research Journal of Engineering and Technology, 3(4), 2450–2453, 2016.
37. L. De Lathauwer, B. De Moor, J. Vandewalle, “Fetal electrocardiogram extraction by blind source subspace separation,” IEEE Transactions on Biomedical Engineering, 47(5), 567–572, 2000, doi:10.1109/10.841326.
38. K.J. Lee, B. Lee, “Sequential total variation denoising for the extraction of fetal ECG from single-channel maternal abdominal ECG,” Sensors (Switzerland), 16(7), 2016, doi:10.3390/s16071020.
39. A. Agostinelli, A. Sbrollini, L. Burattini, S. Fioretti, F. Di Nardo, L. Burattini, “Noninvasive Fetal Electrocardiography Part II: Segmented-Beat Modulation Method for Signal Denoising,” The Open Biomedical Engineering Journal, 11(1), 25–35, 2017, doi:10.2174/1874120701711010025.

(Click Here)