1. Introduction

Today, with the complex growth of VLSI technology, it is very difficult to hand design analog integrated circuits with multiple parameters and purposes. The characterization of complicated tradeoffs between conflicting and nonlinear performances while ensuring the required design specifications makes the design of analog circuits a tedious and time-consuming process. In this regard, due to their design difficulty and complexity, analog circuits have been attracted a lot of optimization attention. In general, optimization is often a time-consuming process having several contradictory criteria as well as a wide variety of design parameters. However, the design of electronic circuits is carried out by optimizing the circuit parameters to be able to rapidly design high-performance circuits [1]. For instance, finding passive elements values and transistor sizes and bias currents, so it can meet output performances such as gain, frequency band, power consumption, etc.

Several metaheuristics have been developed in the literature, which can be divided into two principal categories [2]: Single solution based methods, such as Taboo Search (TS) [3], Local Search (LS) [4], Simulated Annealing (SA) [5], or population based approaches like, Ant Colony Optimization (ACO)[6], Whale Optimization Algorithms (WOA)[7], Grey Wolf Optimizer (GWO), Particle Swarms Optimization (PSO)[8], Hybrid PSO-GWO [9], Non-dominated Sorting Genetic Algorithm (NSGA II)[10], Multiobjective Genetic Algorithm (MOGA)[11], Strength Pareto Evolutionary Algorithm (SPEA2)[12], etc. Single solution based techniques do not offer good results for problems where different types of variables, objectives and constraint functions (linear or non-linear constraints) are used [8]. Moreover, their efficiency highly depends on their parameters, the search space dimension and the number of variables. The population based techniques are generally classified into two groups, Particle Swarms (PS) and Evolutionary Algorithms (EA). PS give good results for problems that are not so difficult [13], but their performance also depends on their parameters and the complexity of the problem, especially for multi-objective optimization problems (MOP) [5, 13]. However, EAs are optimization techniques based on biological evolution and natural selection of species [14], are population-based, where each individual represents a possible solution. The initial population is generated randomly. At every new generation, the population iteratively evolves by the mutation, the crossover and the selection operators on each individual, and only non-dominated solutions meeting the constraints, will survive. Hence, such algorithms are well-known for their efficiency when solving complex MOP, Unlike PS, EAs do not need big parameter adjustments.

In this paper, we apply EAs for the optimal design of the current conveyor (CCII). The used EAs are NSGA II, MOGA and SPEA2, which allows the simultaneous optimization of multiple conflicting targets resulting into a set of Pareto Front (PF) solutions. Hence, the main objective to optimize the size of the MOS transistors transistors, using these algorithms, to achieve the high performances of the CCII. The CCII is one of the best known current mode circuits, making it the objective of several applications, such as filters, oscillators, etc., [15]. As far as we know, few works have been reported until now on CCII optimization by the EAs. In [16], the MOPSO with Crowding Distance (CD) was used for the optimization of the CCII, the differential CCII and the current feedback operational amplifier (CFOA) for low voltage low power applications, the MOPSO-CD was used as a part of a simulation-based tool to find the optimal sizing transistors that operate in weak inversion. In [17], the NSGA II and the decomposition-based multi-objective EA (MOEA/D) were used for the optimization of other purposes of the CCII, i.e., current gain and offset. However, the high-performance CCII design requires that the input parasitic resistance be small and its cut-off frequency be high. For this reason, we have chosen in this work these two characteristics as objectives to be optimized. All EAs generate Pareto fronts and simulations are carried out on Cadence using 0.18µm CMOS process. The simulation results are conform to those obtained by the optimization.

This paper is structured as follows: Section 2 gives an overview of the EAs, Section 3 is dedicated to the EAs validation using usual test functions. Section 4 presents the CMOS CCII. Section 5, is devoted to the results and discussion. A conclusion is given at the end.

2. Evolutionary Algorithms

2.1    MOGA

The MOGA was introduced in [11], as a new variant of the Golberg approach [18]. It uses the concept of dominance and a randombased fitness assignment. The non-dominanted solutions are ranked into groups, which are assigned the same rank in each group. The pseudo-code of MOGA is given by algorithm 1.

Algorithm 1: MOGA Pseudo Code

Generate the initial population P_i; Evaluate of P_i; while the stopping criteria is not met do

2.2     NSGA II

NSGA-II, which was proposed in [10] as a modified version of NSGA, is among the most commonly used and effective EAs due to its simplicity and effectiveness. The basic operation of the NSGA-II is : A random population is created. This generated population is sorted using the notion of dominance. A fitness function is assigned to each solution. Therefore, it is assumed that physical fitness is minimized. At first, selection, mutation and crossover operators are used to create a new population from the first. The NSGA II algorithm uses the notion of elitism, to compare the current population with previously found best non-dominated solutions.

NSGA II relies on two major procedures: crowding distance and fast non-dominated sorting. Both procedures ensure elitism and feasibility of solutions. Algorithm 2 represents the NSGA II pseudo-code.

Algorithm 2: NSGA II Pseudo Code

Generate randomly the initial population P_i while the stopping criteria is not satisfied do while population in not classified do

Search for non-dominated individuals;

Fitness calculation;

2.3     SPEA2

SPEA2 is a MO algorithm introduced in [12] as an improved version of SPEA. It is based on the notion of dominating fitness evaluation to to generate the PF. SPEA2 uses elitist concept maintaining an external archive of non-dominated solutions. It also uses a nearest neighbor density estimation method, and an improved archive Truncation approach.

The SPEA2 is given by algorithm 3.

Algorithm 3: SPEA2 Pseudo Code

Generate randomly population P_i;

Evaluate objective and create external Archive A_i ; for i = 1, i ≤ Max iterations do

3. EA robustness

Before using the proposed algorithms, we evaluated performances using multi-objective standards ZDT functions [19].

Each ZDT function includes two objectives f₁ and f₂ with 30 variables, which demonstrates the high complexity of such test functions. All tests are carried out with the algorithms parameters of 1000 iterations and a population size of 50 and a crossover probability of 0.8 and a mutation probability of 0.1. The ZDT benchmark functions and their expressions are given in the appendix.

Figure 1 shows the PFs obtained for the three chosen algorithms.

As can be clearly seen the generated PFs with the all proposed methods achieve good approximations to the exact benchmark functions PFs. Therefore, we can confidently use them for the optimization problems of the CCII optimal design with guaranteed results.

Figure 1: Evaluation of algorithms by ZDT benchmark functions

4. CMOS Current Conveyor

In this section, we studied the current conveyor shown in Figure 2, it has three active ports X, Y and Z, and its main function consists of

• Current follower between ports X and Z, which can be provided by the translinear loop formed by transistors M1- M4.
• Voltage follower between ports X and Y, which can be provided by M5-M6 and M7-M8 current mirrors.

The present current conveyor topology is the most used one for its good performances and the interest of using a translinear loop [20]. Therefore, the design optimization of the CCII is performed considering its main objective functions : the parasitic resistance at the port X (R_X) and the cut-off frequency (f_-3dB). Recall that the aim is to minimize the first objective to obtain low input resistance and to maximize the second objective to get high bandwidth.

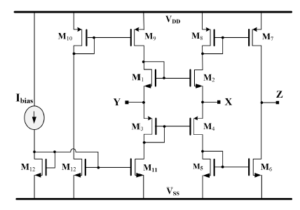
Figure 2: CMOS Current conveyor.

The CCII sizing is performed as in [14], using CMOS 0.18 µm process, and with the following conditions V_DD = V_SS = ±1.8V. All the transistors are characterized by their geometrical parameters: the channel length L and the gate width W.

The CCII optimal sizing issue is treated as a MOP. The aim is to find the best trade-off between a small R_X and a high f_-3dB as a function of the transistors parameters. The problem constraints are given by Eqs. 4 and 5 bellow corresponding to the saturation transistor regime [15].

The design problem can be formulated as:

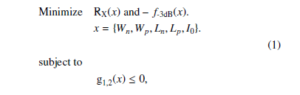
• The resistance R_X is

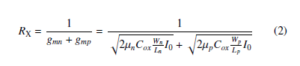
g_mn(p) is the transconductance for N(P) channel transistor. µ_n (µ_p) and C_ox are the electrons (holes) mobility and the gate oxide capacitance per unit area, respectively. I₀ is the bias current.

• The cut-off frequency f_-3dB is

2π The saturation constraints g₁ and g₂ are given by :

• The constraint of M₂ and M₈ transistors:

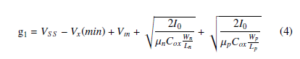
• The constraint of M₄ and M₅ transistors:

where V_tn(V_tp), V_DD(SS) are the threshold voltage for NMOS(PMOS) and the supply voltage, respectively. W_n (W_p), L_n (L_p) are the gate width and the channel length for n-channel (p-channel) transistors, respectively.

5. Results and discussion

All the CCII transistors with the same channel type have the same parameters (W_n, L_n for NMOS and W_p, L_p for PMOS). To respect the industrial design constraints, we also used identical channel length (L) for all transistors.

5.1     CCII optimization results

The optimal MOS transistors sizes are reached using EAs by minimizing R_X and maximizing f_-3dB in two ways:

First, the optimization process is performed by MOGA, SPEA2 and NSGA II using three I₀ values, i.e., 20µA, 40µA and 80µA. For these experiments, we use the minimum channel length L_n = L_p = L_min. The generated PFs (R_X and –f_-3dB) by the algorithms for different bias currents are shown in Figure 3. From this figure, we can see that the best trade-off between R_X and –f_-3dB is obtained for the PF with the large bias current I₀=80µA. Therefore, designers have to select the best trade-off solution depending on the circuit design and its application requirements.

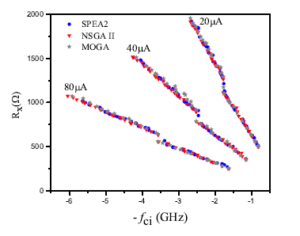
Figure 3: Pareto fronts obtained by the three algorithms for three bias currents

Second, the optimization process is performed by the same algorithms using three channel lengths L_min, 2L_min and 3L_min. For these experiments, we use I₀ = 80µA. The generated PFs for these cases are shown in Figure 4. From this figure, we can see that the best trade-off between performances is achieved for the PF with a minimum channel length L_min. Unlike digital circuits, the channel length for analog circuits is usually at least 3L_min, which is why we tested all three channel lengths. This relatively large channel lengths minimizes the effects of channel modulation.

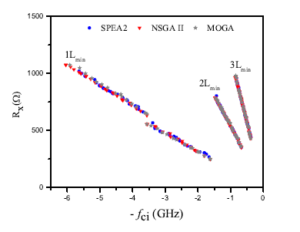
Figure 4: Pareto fronts obtained by the three algorithms for three channel lengths.

Based on the results in both scenarios, we can see that the best performances are obtained with a smaller channel length and a higher bias current. Considering the effects of channel modulation, power consumption and the circuit design and application requirements, IC designers should select the appropriate solution.

We run all algorithms 10 times, to evaluate the weakness and strength of each algorithm in all the performed experiments. To evaluate the diversity and the distribution of Pareto solutions, we use the hyper volume metric [21]. This metric shows the covered area by the Pareto front. In case of minimization, of the problem, the lager hyper-volume value, the good is the quality of Pareto front solutions.

The hypervolume results are shown in Table 1. The optimization procedure required a mean CPU time of approximately 6.707 s, 67.25 s, and 148.412 s for NSGA II, MOGA and SPEA2, respectively.

Compared to the others algorithms, the NSGA II has the rapid CPU time and a good convergence rate confirmed by the higher hypervolume value.

Table 1: The Hypervolume Values.

		SPEA2	MOGA	NSGA II
	20 µA 40 µA	0.750 0.825	0.752 0.824	0.752 0.826
	80 µA	0.873	0.875	0.876
	1  Lmin 2  Lmin 3  Lmin	0.873 0.824 0.782	0.875 0.823 0.784	0.876 0.825 0.785

5.2     CCII validation results

Table 2 presents the solutions to be validated by the CADENCE tool, they are defined by their cutoff frequencies, their values of R_X and the corresponding transistors parameters. They are randomly chosen from the PF that corresponds to I₀ = 80µA and L_n=L_p=L_min.

Table 2: Parameters to be validated by Cadence, obtained in the PF that gives the best trade-off (R_X,f_-3dB).

	Test	Wn(µm)	Wp(µm)	f-3dB(GHz)	RX(Ω)
MOGA	1	1.08	4.26	5.11	926.5
	2	3.77	13.38	3.08	481.26
SPEA2	1	0.86	3.54	5.63	1018.6
	2	4.30	17.85	2.66	439.07
NSGA II	1	0.80	3.08	6.04	1073.3
	2	4.65	15.77	2.64	443.26

Figures 5–8 show the simulation results of the selected solutions in table 2. The maximum (minimum) deviation between the simulation and the theoretical results is 10.1% (1%) and 9.4% (4.7%) for R_X and f_-3dB, respectively. This interval of variations is quite narrow and makes it possible to consider that the simulation results are in good agreement with the theoretical ones, obtained by the algorithms.

Table 3 presents a qualitative comparison of the obtained CCII performance with works previously published but with 0.35µm process. From the data given in this table, it is clear that the achieved performances are higher than reported, i.e, very higher frequency and much lower power consumption and good X-port resistance.

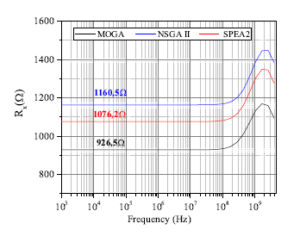
Figure 5: Cadence simulation results of parasitic resistance for the used algorithms (Tests 1 in table 2).

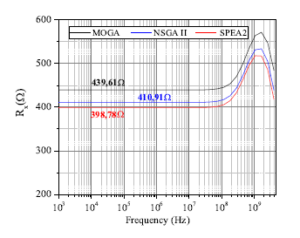
Figure 6: Cadence simulation results of parasitic resistance for the used algorithms (Tests 2 in table 2).

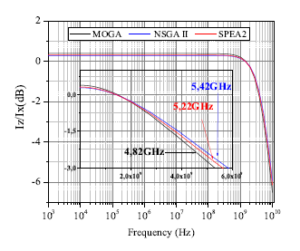
Figure 7: Cadence simulation results of cut-off frequency for the used algorithms (Tests 1 in table 2).

Table 3: CCII performance comparison with works previously published. This work [22] [23] [24] Algorithms NSGA II PSO-2S MODE EGO-PEI Technology (µm) CMOS 0.18 CMOS 0.35 CMOS 0.35 AMS 0.35 VDD/VSS (V) ±1.8 ±2.5 ±2.5 – Ibias (µA ) 80 300 300 – Power (µW ) 288 1500 1500 – f-3dB(max) (GHz) 6.04 2.121 2.132 1.2255 RX(min) ( Ω) 247 225 221 259.53

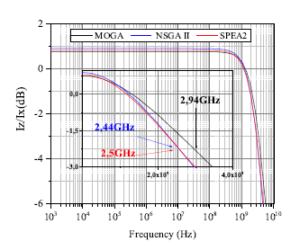
Figure 8: Cadence simulation results of cut-off frequency for the used algorithms (Tests 2 in table 2).

6. Conclusion

In this paper, we presented the usefulness of applying EAs, namely MOGA, SPEA2 and NSGA II, for the automatic optimization of high performances CCII. Several optimization experiments were carried out with three bias currents and three channel lengths, minimizing the parasitic resistance and maximizing the cut-off frequency. In all experiments, the achieved results show that these methods can provide Pareto Fronts with greater solutions diversity. The simulations are performed by Cadence using the CMOS 0.18µm process, showing good accuracy with the theoretical results. The best performances achieved with EAs in this work can be summarized in a power consumption of 288µW, a minimum parasitic resistance of about 247Ω and a maximum frequency of about 6.04GHz.

Appendix

• ZDT1 function:

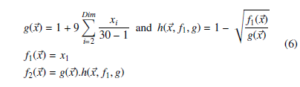
• ZDT2 function:

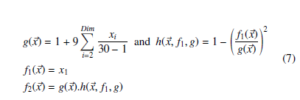
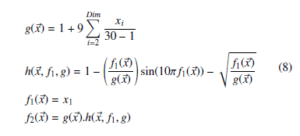
1. B. Liu, G. Gielen, F. V. Fernandez, Automated design of analog and high-frequency circuits, Springer, 2014.
2. M. Fakhfakh, A. Sallem, M. Boughariou, S. Bennour, E. Bradai, E. Gaddour, M. Loulou, “Analogue circuit optimization through a hybrid approach,” in Intelligent Computational Optimization in Engineering, 297–327, Springer, 2011.
3. A. Gharbi, M. Benrejeb, P. Borne, “A taboo search optimization of the control law of nonlinear systems with bounded uncertainties,” International Journal of Computers Communications & Control, 11, 224–232, 2016, doi: 10.15837/ijccc.2016.2.2010.
4. C. Dai, Y. Wang, L. Hu, “An improved -dominance strategy for many-objective optimization problems,” Soft Computing, 20, 1105–1111, 2016, doi:10.1007/s00500-014-1570-8.
5. F. Y. Vincent, A. P. Redi, Y. A. Hidayat, O. J. Wibowo, “A simulated annealing heuristic for the hybrid vehicle routing problem,” Applied Soft Computing, 53, 119–132, 2017, doi:10.1016/j.asoc.2016.12.027.
6. Q. Yang, W. Chen, Z. Yu, T. Gu, Y. Li, H. Zhang, J. Zhang, “Adaptive Multi-modal Continuous Ant Colony Optimization,” IEEE Transactions on Evolutionary Computation, 21(2), 191–205, 2017, doi:10.1109/TEVC.2016.2591064.
7. A. Lberni, M. A. Marktani, A. Ahaitouf, A. Ahaitouf, “Adaptation of the Whale Optimization Algorithm to the Optimal Sizing of Analog Integrated Circuit: Low Voltage Amplifier Performances,” in 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), 1–6, 2020, doi:10.1109/ICECOCS50124.2020.9314428.
8. M. Fakhfakh, Y. Cooren, A. Sallem, M. Loulou, P. Siarry, “Analog cir- cuit design optimization through the particle swarm optimization technique,” Analog integrated circuits and signal processing, 63, 71–82, 2010, doi: 10.1007/s10470-009-9361-3.
9. A. Lberni, M. A. Marktani, A. Ahaitouf, A. Ahaitouf, “Application of hpsgwo to the optimal sizing of analog active filter,” in International Conference on Electronic Engineering and Renewable Energy, 309–315, Springer, 2020.
10. K. Deb, A. Pratap, S. Agarwal, T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, 6(2), 182–197, 2002, doi:10.1109/4235.996017.
11. T. Murata, H. Ishibuchi, “MOGA: multi-objective genetic algorithms,” in Proceedings of 1995 IEEE International Conference on Evolutionary Computation, volume 1, 289–, 1995, doi:10.1109/ICEC.1995.489161.
12. E. Zitzler, M. Laumanns, L. Thiele, “SPEA2: Improving the strength Pareto evolutionary algorithm,” TIK-report, 103, 2001, doi:10.3929/ ethz-a-004284029.
13. A. Sallem, B. Benhala, M. Kotti, M. Fakhfakh, A. Ahaitouf, M. Loulou, “Ap- plication of swarm intelligence techniques to the design of analog circuits: evaluation and comparison,” Analog Integrated Circuits and Signal Processing, 75, 499–516, 2013, doi:10.1007/s10470-013-0054-6.
14. A. Lberni, A. Ahaitouf, M. A. Marktani, A. Ahaitouf, “Sizing of second generation current conveyor using evolutionary algorithms,” in 2019 International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), 1–5, 2019, doi:10.1109/ISACS48493.2019.9068896.
15. A. Lberni, M. A. Marktani, A. Ahaitouf, A. Ahaitouf(in press), “International Journal of Computer Aided Engineering and Technology,” .
16. A. Lberni, A. Sallem, M. A. Marktani, A. Ahaitouf, N. Masmoudi, A. Ahaitouf, “An efficient Multi-Objective Simulation-based Approach for Low Voltage Low Power Analog ICs,” in 2020 IEEE International Conference on Design Test of Integrated Micro Nano-Systems (DTS), 1–5, 2020, doi:10.1109/DTS48731. 2020.9196166.
17. I. Guerra-Gomez, E. Tlelo-Cuautle, T. McConaghy, G. Gielen, “Optimizing cur- rent conveyors by evolutionary algorithms including differential evolution,” in 2009 16th IEEE International Conference on Electronics, Circuits and Systems- (ICECS 2009), 259–262, 2009, doi:10.1109/ICECS.2009.5410989.
18. D. Golberg, S. Mahfoud, “A Genetic algorithm for parallel simulated anneal- ing,” in Proceedings of international conference on parallel problem solving from nature. Netherland, 1992.
19. E. Zitzler, K. Deb, L. Thiele, “Comparison of multi-objective evolutionary algorithms: Empirical result,” Evolutionary computation, 8, 173–195, 2000, doi:10.1162/106365600568202.
20. M. A. Yakout, T. A. Alawadi, “A novel simple BiCMOS Current Controlled Current Conveyor for RF applications,” International Journal of Electronics Letters, 8, 1–16, 2019, doi:10.1080/21681724.2019.1600726.
21. G. Chen, J. Qian, Z. Zhang, Z. Sun, “Applications of novel hybrid bat algorithm with constrained Pareto fuzzy dominant rule on multi-objective optimal power flow problems,” IEEE Access, 7, 52060–52084, 2019, doi: 10.1109/ACCESS.2019.2912643.
22. A. El Dor, M. Fakhfakh, P. Siarry, “Performance optimization of CMOS second generation current conveyors using a multi-swarm algorithm,” AEU- International Journal of Electronics and Communications, 68, 496–503, 2014, doi:10.1016/j.aeue.2013.12.007.
23. A. El Dor, M. Fakhfakh, P. Siarry, “Multiobjective differential evolution algorithm using crowding distance for the optimal design of analog circuits,” Journal of Electrical Systems, 12(3), 612–622, 2016.
24. N. Drira, M. Kotti, M. Fakhfakh, P. Siarry, E. Tlelo-Cuautle, “Pseudo Expected Improvement Based-Optimization for CMOS Analog Circuit Design,” in 2019 16th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), 137–140, 2019, doi:10.1109/SMACD.2019.8795259.

(Click Here)