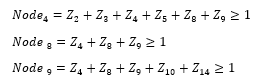1.Introduction

Electric power system is a complex system with multiple sections, subsections and various components. Any analysis or model to set up a power system or upgrade the existing one must be very robust and adequate. Considering optimal location of distributed generator within distribution arm of electric power system [1, 2], reconfiguration of a section of power system [3-5], etc., all these required robust model and methodology to successfully obtain useful results.

In Nigeria, most of the power system network is overseen physically which is an issue. This physical management of the power network brought about constraints, in order to solve this challenge, the obvious path to take will be the incorporation of smart devices into the network to monitor, operate and control the power system which will increase interaction between the utility and the grid.

Phasor measurement unit is the leading device for monitoring power system network which is based on global positioning system technique. The phasor measurement unit measures different locations where it is installed which are time-synchronized to communicate the condition of the power system in real time to help operators with more instant and accurate information. By placing phasor measurement units in several buses in a power network the system becomes more stable and reliable. However, Phasor measurement units are expensive so it is not economical to place a unit on every node in a power network [6]. Thus, an appropriate approach is essential to reduce the quantity of phasor measurement units while sustaining the power network to be observed completely.

Phasor measurement unit (PMU) has certain variations as follows from standard Supervisory Control and Data Acquisition (SCADA) measures. Synchro phasors provide phasor details while traditional state estimate (SE) utilizes voltage magnitude, branch current magnitudes, and active power and reactive power measurements for infusion, voltage phasor at neighbouring nodes without PMU can be directly calculated utilizing the phase angle information.  PMU information gives 30-70 samples every second, while SCADA devices mainly give new data samples every 4-5 seconds. Therefore, dynamic observability is given of the effect of irregularities that spread through critical sections of the network [7, 8].

In [9, 10], the authors carried out a study to investigate an ideal method for placing PMUs in any power system network. They proposed a method known as inverse of connectivity which utilizes the information of connectivity and the inability to monitor any node in the power system network. They chose the ideal bus to place the PMUs basically by selecting adjacent buses through weighing factors to observe a minimal connectivity buses; this procedure continues until the power system network is observable. In [11] the authors worked on calculated allocation of PMU to observe the power system taking consideration of redundancy measurement. In this research they tackled the ideal PMU allocation issue with binary valued factors actualized by a dual-stage branch and bound formulation, but their approach did not consider Zero injection node (ZIN). In stage one of the suggested formulations, GA is worked out by depth foremost search technique. When a first whole number solution is gotten, stage two includes breadth foremost search system to find the solution position. Beginning from a subjective introductory position, the executed formulation finds other solutions at the most minimal target capacity worth guaranteeing global optimality [12]. In this way, the reliance of the suggested two-stage branch and bound by the foremost position provides the ability to the end-user to distinguish ideal arrangements without the existence of spiral nodes in the power network [13,14].

In [15], the authors used topology-based method and genetic algorithm to solve the optimal PMU placement problem. In their approach they put into consideration zero-injection nodes in the network for finding solution to the optimal PMU placement problem. The outcome was compared to previously applied method.  They achieved complete observability of the power system utilizing GA which solved the optimal PMU placement problem successfully [15]. Measurement redundancy was not considered in this research.

In [16], the authors analyse techniques used for observing the most topological network, while recursive tabu search which is obtained when numerical and tabu search method are combined was developed to attain maximum observability of a power system with full redundancy.  This optimizing approach executed the solution better than the previous solution that was achieved by greedy algorithm. The process put into consideration different approaches as well as moving target search (MTS) to achieve the least quantity of PMUs to solve the optimization problem [17]. Though Placement of PMU in ZIN was not allowed in the initialization it was validated through simulation results that the recursive tabu search was more efficient that the MTS approach. Authors [18,19] gives more detailed comparisons of the recursive tabu search and other methods.

In [20-23], the authors presented the cost of installing different PMUs in a power network and the reliant factors such as branch neighbouring numbers at the node and the communicating situations. They utilized the particle swarm optimization tool to attain the best solution proving the optimization to be better than conventional techniques. The authors did not only determine the highest number of PMUs that can observe the system, they also determined the cost of installing the least quantity of different PMUs and chose the best with least cost [24].

This study serves as a pioneer study for placement of PMU in the new NG 52 bus, as there is no previous study before it. In this study, optimal placement of PMU considering normal operation and ZIN is proposed. The uniqueness in this algorithm used to place PMU on the 52 bus network is the combination of distinct values of the chromosome, mutation function, mutation rate, selection function and crossover function.

This research paper is systematized in four sections. The “introduction” gives a brief description of PMU, also a review on existing works. The “Materials and Method” section shows the GA steps and the parameters used. Details of the inequality constraint and connectivity matrix for IEEE 14-bus and NG 52-bus was presented in PMU placement formulation. Measurement redundancy presents the BOI and SORI used to check the quality of each placement set. The “results and discussion” presented the outcome of the simulation. In “conclusion” the procedures and the outcomes are summarized.

2. Materials and Method

This section presents the placement formulation used in obtaining the minimum amount of PMU, the procedure of the Genetic algorithm, and the measurement redundancy.

2.1. PMU Placement Formulation

The purpose of the optimal PMU placement is to obtain the least quantity of PMUs needed and its position in the network in order to obtain complete observability of the network. The goal here is to minimize the utilization of PMUs and make the whole power system fully observable. The formulated objective function is therefore given as:

subject to:

where  is a number of network nodes and  is a binary connectivity matrix. Entries for matrix  are defined by equation 3:

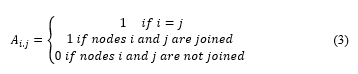Meanwhile [Z] is defined as a binary decision variable vector given in equation 4 where  and :

[b] is a column vector where

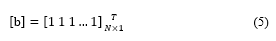2.2. Genetic Algorithm Approach

For this research, genetic algorithm was selected as the optimization solver for optimal placement of PMUs on the Nigerian 330kV network. Genetic algorithm operates on a population made up of certain outcomes whereby the number of outcomes is known as population size. Every outcome is named an individual. Every single outcome has in it a chromosome. The chromosome is defined as a collection of features that characterize the individual. Each separate chromosome has a collection of genetic factors. Each genetic factor is often interpreted as being a sequence of zeros and ones. Every individual has a fitness value, too. An objective function is employed to locate the fittest characters. The objective function outcome is the fitness value which signifies the outcome’s performance. The greater the fitness value, the greater the outcome is in effectiveness.

In the breeding process the characters are known as parents. Any pair nominated parents within the breeding population will give dual offspring. Through breeding just fine-quality characters, a finer quality offspring is produced better than their parents. That will eliminate the bad individuals from producing more bad people. Through having fine-quality characters chosen and paired, there would be better chances of only having the good individuals and tossing bad individuals out. Eventually, the ideal or appropriate solution will end in the cycle. But the offspring already produced utilizing the chosen parents still have their parents’ features, and no more without alterations. There is no difference added to it and therefore the latest offspring would still have the same disadvantages in its parents. Some improvements must be added to each offspring to produce new characters to solve these problems. The group of all freshly produced characters would be the recent population and will substitute the existing population that was formerly utilized. Each produced population is called a generation. The method of exchanging the existing population with the current one is known as replacement. Figure 1 gives a rundown of the genetic algorithm phases.

Figure 1: Process flow of genetic algorithm

The genetic algorithm flow chart is outlined in Figure 1. Simulation results obtained on the premise that each PMU has the highest quantity of channels and the cost is the same for each PMU.

The Genetic algorithm procedure for the OPP problem is given below:

• Study the configuration arrangement of the power network
• Take variable/chromosome size equal to quantity of nodes
• Create the initial population
• For each selected variable, calculate the objective function
• Apply tournament selection function
• Apply single point crossover function
• Apply a uniform mutation function and a mutation rate of 0.01
• Go back to calculate the objective function if the number of generations are completed.

Two experimental cases are used to show the feasibility of the proposed approach in achieving the optimal PMU placement problem. All cases are described by using IEEE 14 and Nigeria 52 bus network model as demonstrated below and simulated utilizing MATLAB, respectively.

Case 1: not considering standard measurement for maximum network observability

In this scenario, measurements of the ZIN and the power flow are not taken into account. Furthermore, no PMU is pre-assigned to the radial node which is incident. The binary connectivity matrix A is generated from Figure 2 by use of equation 3 as follows:

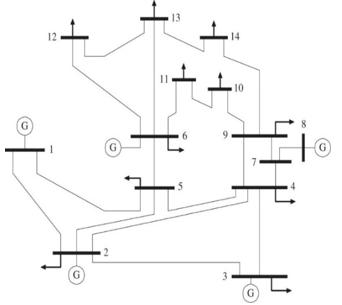Figure 2: IEEE14 test bus system

Connectivity matrix [A] for IEEE-14 bus system =

The final inequality constraints of matrix A are formulated as shown in the expression below with respect to each node:

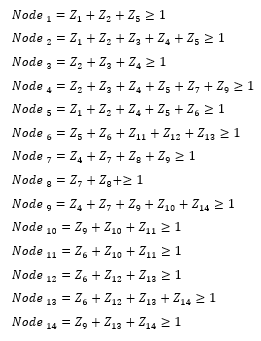Case 2: Consideration of ZIN for maximum network observability

      According to Figure 2, node 7 is ZIN, node 8 is radial node. Since node 8 is a radial node, it is chosen to be integrated with the ZIN in accordance with Rule A as stated in the suggested approach section. This integration procedure indicates the node 7 constraint is eliminated from the equation and node 8 is now joined to node 4 and node 9. Following, because this procedure includes a radial bus, it is important to pre-assign a PMU to one of the nodes incidents to it.

However, because neither node 4 nor node 9 is a ZIN, there is no pre-placement of a PMU to enable more potential solutions. In the situation of node 4 being a ZIN a PMU would be pre-assigned to node 9 in order to guarantee that node 8 is observed as shown in Figure 3.

Figure 3:  Illustration of ZIN integration

This change of topology implies that the node constraints for nodes 4,7,8, and 9 have been modified. Remember that the node 7 constraint is removed because it no doesn’t occur after the change of topology. For the meantime, the node constraints 4,8, and 9 are revised to show the modification of topology that was made during the integration process. The modified constraints are given as follows:

A minimum of three PMUs must be installed at node 2, 6, and 9 to guarantee maximum network observability from these newly created constraints.

Thus, the same model is applied to Nigeria 330kV new 52-bus system for total observability on the quantity of PMUs needed.  Measurements of the ZIN and power flow are not considered in this case.

2.3. Measurement Redundancy

Because Genetic algorithm is a heuristic technique, there will be an amount of PMU placement group that includes exact quantity of the least PMUs necessary for total observability. To ensure to assessing the efficiency of each PMU allocation group, measurement redundancy method of bus observability index (BOI) and system of redundancy index (SORI) are used. The BOI is specified as the quantity of times the PMUs placement set observes a node, while the SORI refers to the BOI summation for all nodes. The PMU allocation group which holds the maximum quantity of SORI signifies that the PMU allocation group has a superior performance and more efficient solution for likely contingencies compared to the PMU allocation group which has a lower quantity of SORI.  Hence, this principle will be utilized in this research to test and compare the PMU allocation sets generated in terms of measurement redundancy from the suggested technique and previous studies. The following definitions in equations 6 and 7 refer to the BOI and SORI:

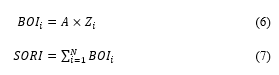3. Results and Discussion

This section sets out the outcomes gotten from MATLAB software simulations. The proposed technique is implemented on   IEEE 14-bus, and the Nigeria 330KV network for the purpose of verifying the operation of the suggested approach to solve the optimal PMU placement problem. The purpose of the suggested approach is to achieve the least quantity of PMUs which maintain total observability while maximizing the redundancy of measurements.  Because genetic algorithm is meta-heuristic, it is anticipated to have various allocations of PMUs and to distinguish the efficiency of each PMU allocation set having the exact quantity of PMUs, the set with the most SORI will be chosen as the ideal outcome. The PMUs allocation set with the most measurement redundancy, as stated above, indicates that it is superior to the PMU allocation sets with lower measurement redundancy. Furthermore, in order to assess the efficiency of the suggested approach in finding solution to the optimal PMU placement problem, the SORI outcome for the PMU allocation set acquired from the suggested approach is compared with previous research. The suggested approach is implemented to find solution to the problem by taking consideration of two cases namely normal operation, and zero injection cases for IEEE 14 bus system and NG 52 bus system.

Case 1: Normal Operation

IEEE 14-Bus

Table 1 shows the result obtained for the IEEE-14 bus system, with respect to number of required PMU, the position of the PMU and other indices that were used in the model.

Table 1: PMU Locations for IEEE 14 Bus- Normal Operation

Network	IEEE 14-bus
Number of PMU	4
PMU Positions	2, 6, 7, 9
SORI	19
Npmu/NBus	0.286

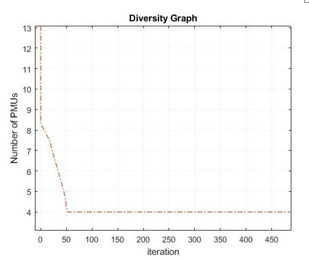Figure 4: IEEE 14-bus graph considering normal operation

As can be observed, Figure 4 shows the iteration against the number of PMUs. It can be observed that at zero iteration the number of PMUs is over 14 and as the iteration increases the number of PMU decreases until it gets to 52 iterations where the constraint converges.

NG 52-Bus

The values of the parameters used in obtaining the number of PMUs required for NG 52-bus including their locations are given in Table 2.

Table 2: PMU Locations for NG 52-Bus Normal Operation

Network	NG 52-bus
Number of PMU	17
PMU Positions	3, 4, 6, 8, 10, 16, 19, 24, 26, 27, 32, 35, 39, 41, 42, 46, 51
SORI	71
Npmu/NBus	0.32692

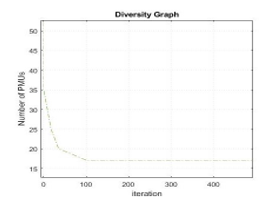Figure 5:  Diversity graph for NG 52-bus considering normal operation

The Figure 5 shows the iteration against the number of PMUs. It can be observed that at zero iteration the number of PMUs is over 52 and as the iteration increases the number of PMU decreases until it gets to 102 iterations where the constraint converges.

Table 3: BOI and SORI for Normal Condition

	IEEE14	NG 52
Number of PMU	4	17
PMU Location	2, 6, 7, 9	3, 4, 6, 8, 10, 16, 19, 24, 26, 27, 32, 35, 39, 41, 42, 46, 51
BOI	1, 1, 1, 3, 2, 1, 2, 3, 1, 1, 1, 1, 1, 1	2, 2, 3, 1, 1, 1, 1, 1, 2, 1, 4, 1, 2, 1, 1, 1, 1, 3, 1, 1, 2, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3
SORI	19	71

Case 2: Zero Injection Node (ZIN) for IEEE 14-Bus

Table 4 shows the quantity of PMUs needed for the IEEE 14-bus system that can accomplish total observability, which is less than 25% of the number of nodes in the system that needs to be observed as shown in Figure 6. The BOI result is shown in Table 5.

Table 4: PMU Locations for IEEE14-Bus Considering ZIN

Network	IEEE 14-bus
Number of PMU	3
PMU positions	2, 6, 9
SORI	16
Npmu/NBus	0.2308

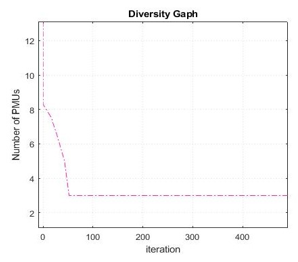Figure 6:  Diversity graph for IEEE 14-bus considering ZIN

Figure 6 shows the iteration against the number of PMUs. It can be observed that at zero iteration the number of PMUs is over 13 and as the iteration increases the number of PMU decreases until it gets to 52 iterations where the constraint converges.

Table 5: BOI and SORI Considering ZIN

	IEEE14
Number of PMU	3
PMU location	2, 6, 9
BOI	1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1
SORI	16

The outcomes of the simulation of the proposed method validate the results from previous studies as shown in Tables 6 and 7. The methodology designed can optimally position the PMU in strategic nodes and show substantial improvements in comparison with existing works.

Table 6: Comparison with previous study considering normal operation

Methods	IEEE14
Proposed method	NPMU: 4 SORI: 19
Binary particle swarm optimization	NPMU: 4 SORI: 19
Integer Linear Programming	NPMU: 4 SORI: 19
Differential Evolution	NPMU: 4 SORI: 19
Evolutionary Search	NPMU: 4 SORI: 19
Binary Search Algorithm	NPMU: 4 SORI: 19

Table 7: Comparison with Previous Study Considering ZIN

Methods	IEEE14
Proposed method	NPMU: 3 SORI: 16
Binary particle swarm optimization	NPMU: 3 SORI: 16
Integer linear programming	NPMU: 3 SORI: 16
Evolutionary Search	NPMU: 3 SORI: 16
Binary Search Algorithm	NPMU: 3 SORI: 16

Having established the authenticity of the proposed method, the authors therefore deployed the proposed method to ascertain the number of PMU required on NG 52 bus system (appendix) as well as optimal location of the PMUs installation. The results for the NG 52-bus shows that PMU is required to be placed at 17 nodes for maximum observability. These nodes are, 3-Ikot-Ekpene, 4-Port-Hacourt, 6-Ikeja-West, 8-Aja, 10-Ajaokuta, 16-Aladja, 19-Aliade, 24-Kanji, 26-Onitsha, 27-Benin North, 32-Damaturu, 35-Egbema, 39-Ganmo, 41-Yola, 42-Gwagwalada, 46-Kaduna, 51-Jebba.

4. Conclusion

This study explores the capability genetic algorithm to optimally site PMU for electric power system network. From the outcome of this algorithm, it can be concluded that the utilization of optimization technique in the Nigerian power system network for complete   observability in the most economical way will precisely position PMU in strategic nodes. This greatly improves the efficiency of the outputs and increase the grid monitoring rate. There are endless prospects for installing PMU in the national grid, as it can also be used to control the entire power system. The technique formed to handle ZIN succeeded in producing comparable results with other available techniques. For IEEE 14 and NG 54 bus reached the convergence of their constraint at 52 and 102 iterations respectively. The suggested approach also shows that to find ideal PMU location, it can be combined with the power flow calculation.

Conflicts of Interest

The authors declare that there is no conflict of interest.

Funding Statement

This research work and publication charge is fully funded by Covenant University Centre for Research, Innovation and Discovery (CUCRID).

Acknowledgments

Covenant University is acknowledged for her financial support.

1. T. Somefun, C. Awosope, A. Abdulkareem, and A. Alayande, “Deployment of Power Network Structural Topology to Optimally Position distributed Generator within Distribution System,” Journal of Engineering Science and Technology Review, 13, 12-17, 2020. DOI: 10.25103/jestr.131.02
2. T. E. Somefun, “Critical Review of Different Methods for Siting and Sizing Distributed Generators,” TELKOMNIKA (Telecommunication Computing Electronics and Control), 16, 2018. DOI: 10.12928/telkomnika.v16i5.9693
3. A. Y. Abdelaziz, R. A. Osama, S. M. Elkhodary, and E. F. El-Saadany, “Reconfiguration of distribution systems with distributed generators using Ant Colony Optimization and Harmony Search algorithms,” in 2012 IEEE Power and Energy Society General Meeting, 2012, 1-8. DOI: 10.1109/PESGM.2012.6345125
4. M. E. Baran and F. F. Wu, “Network reconfiguration in distribution systems for loss reduction and load balancing,” IEEE Transactions on Power delivery, 4, 1401-1407, 1989. DOI: 10.1109/61.25627
5. R. J. C. Gallano and A. C. Nerves, “Multi-objective optimization of distribution network reconfiguration with capacitor and distributed generator placement,” in TENCON 2014 – 2014 IEEE Region 10 Conference, 2014, 1-6. DOI: 10.1109/TENCON.2014.7022365
6. M. M. Amin, H. B. Moussa, and O. A. Mohammed, “Wide area measurement system for smart grid applications involving hybrid energy sources,” Energy Systems, 3, 3-21, 2012. doi.org/10.1007/s12667-011-0047-4.
7. M. Laouamer, R. Mohammedi, A. Kouzou, and A. Tlemçani, “Optimal Placement of PMUs in Algerian Network Using Genetic Algorithm,” in 2018 15th International Multi-Conference on Systems, Signals & Devices (SSD), 2018, 947-951. DOI: 10.1109/SSD.2018.8570652
8. M. Mehdinejad, B. Mohammadi-Ivatloo, R. Dadashzadeh-Bonab, and K. Zare, “Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms,” International Journal of Electrical Power & Energy Systems, 83, 104-116, 2016. doi.org/10.1016/j.ijepes.2016.03.039
9. S. Akhlaghi, “Optimal PMU placement considering contingency-constraints for power system observability and measurement redundancy,” in 2016 IEEE Power and Energy Conference at Illinois (PECI), 2016, 1-7. DOI: 10.1109/PECI.2016.7459251
10. R. Sodhi, S. Srivastava, and S. Singh, “Optimal PMU placement method for complete topological and numerical observability of power system,” Electric Power Systems Research, 80, 1154-1159, 2010. DOI: 10.1016/j.epsr.2010.03.005
11. G. C. Sushma and T. Jyothsna, “A Genetic Algorithm Approach Considering Zero Injection Bus Constraint Modeling for Optimal Phasor Measurement Unit Placement,” International Journal of Energy and Power Engineering, 12, 800-806, 2018. doi.org/10.5281/zenodo.2021557
12. R. Babu and B. Bhattacharyya, “Strategic placements of PMUs for power network observability considering redundancy measurement,” Measurement, 134, 606-623, 2019. doi.org/10.1016/j.measurement.2018.11.001
13. A. Y. Amira and G. Fathi, “Optimal PMU placement for full network observability case of the tunisian network,” in Eighth International Multi-Conference on Systems, Signals & Devices, 2011, 1-5. DOI: 10.1109/SSD.2011.5986789
14. S. S. Noureen, V. Roy, and S. B. Bayne, “Phasor measurement unit integration: A review on optimal PMU placement methods in power system,” in 2017 IEEE Region 10 Humanitarian Technology Conference (R10-HTC), 2017, 328-332. DOI: 10.1109/R10-HTC.2017.8288967
15. P. P. Bedekar, S. R. Bhide, and V. S. Kale, “Optimum PMU placement considering one line/one PMU outage and maximum redundancy using Genetic algorithm,” in The 8th Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI) Association of Thailand-Conference 2011, 2011, 688-691. DOI: 10.1109/ECTICON.2011.5947933
16. N. C. Koutsoukis, N. M. Manousakis, P. S. Georgilakis, and G. N. Korres, “Numerical observability method for optimal phasor measurement units placement using recursive Tabu search method,” IET Generation, Transmission & Distribution, 7, 347-356, 2013. DOI: 10.1049/iet-gtd.2012.0377
17. L. Tang and J. Wu, “A new method of optimal PMU configuration considering vulnerability of power system and economy,” Power System Technology, 36, 260-264, 2012.
18. N. H. Rahman and A. F. Zobaa, “Optimal PMU placement using topology transformation method in power systems,” Journal of advanced research, 7, 625-634, 2016. doi.org/10.1016/j.jare.2016.06.003
19. R. Ramachandran and S. Karthick, “Optimal PMU Placement for Tamil Nadu Grid Under Controlled Islanding Environment,” Procedia Technology, 21, 240-247, 2015.doi.org/10.1016/j.protcy.2015.10.021
20. N. Xia, H. B. Gooi, S. Chen, and M. Wang, “Redundancy based PMU placement in state estimation,” Sustainable Energy, Grids and Networks, 2, 23-31, 2015. doi.org/10.1016/j.segan.2015.03.002
21. P. Gopakumar, M. J. B. Reddy, and D. K. Mohanta, “Novel multi-stage simulated annealing for optimal placement of PMUs in conjunction with conventional measurements,” in 2013 12th International Conference on Environment and Electrical Engineering, 2013, 248-252. DOI: 10.1109/EEEIC.2013.6549625
22. A. Y. Abdelaziz, A. M. Ibrahim, and R. H. Salem, “Optimal PMU Placement for Complete Observability Using Heuristic Methods.” Conference: the Fifteenth International Middle East Power Systems Conference, MEPCON’2012At: Alexandria, Egypt, 8-22
23. R. H. Shewale, B. K. Kethineni, U. P. Balaraju, S. Bhil, and P. D. More, “Optimal placement of phasor measurement unit for power system observability by heuristic search method,” International Journal of Advanced Technology and Engineering Research, 2, 128-133, 2012. DOI: 10.1109/CIASG.2011.5953335
24. M. Shafiullah, M. I. Hossain, M. Abido, T. Abdel-Fattah, and A. Mantawy, “A modified optimal PMU placement problem formulation considering channel limits under various contingencies,” Measurement, 135, 875-885, 2019. doi.org/10.1016/j.measurement.2018.12.039

(Click Here)

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country