1. Introduction

Advantages of the adaptive linear filters are simply used in various applications. However, the linear models underperform when comparing with the nonlinear models. Over the last few years, the spline adaptive filter (SAF) structure [1], [2] i.e. Hammerstein spline filtering [3] in cascade architecture [4] has been applied in many practical engineering fields as for example. SAFs based on the set-membership approach [5] and infinite impulse response [6] have been introduced for using in the impulsive noise environment.

In some particular nonlinear problems, the Hammerstein SAF (HSAF) [3], the combined Wiener-Hammerstein SAF [1], and cascade SAFs or sandwich SAF models [4] based on the least mean square (LMS) can operate effectively to identify for nonlinear systems identifications. It provides a good potential for low cost implementation in hardware. Based on the normalised version of LMS (NLMS) on HSAF have been performed in [7]-[10]. In [7], the authors have pointed out the derivation of HSAF on NLMS. In [8], the authors have proposed the performance analysis of HSAF based on the stochastic gradient algorithm. To counteract with impulsive noises, the sign normalised Hammerstein spline adaptive filtering has been proposed in [9] and its performance shown in [10].

In order to reduce the computational requirements of NLMS, the simplifications of NLMS approach in the form of a sign algorithm has been presented in several applications [11]-[16]. To further diminish and protect the impulse noise, the sign normalised SAF [11], [12] and sign subband adaptive filterings with variable step-size parameter [13]- [15] have been designed. In [16], the robust shrinkage normalised version of sign algorithm has been implemented.

Recently, an approach based on the stochastic gradient method for improving the convergence rate based on SAFs has been established in [3], [17]-[19] resulting in the low computation and high performance. For nonlinear systems, the authors in [17] have presented NLMS for SAF. In [18], the adaptive step-size mechanism for SAF has been proposed with the fast convergence and robustness. In [19], the authors have proposed the normalised version of least mean square algorithm for spline adaptive filtering based on the adaptive step-size method with the averaging energy on the previous and present errors and their properties of stability analysis have been introduced.

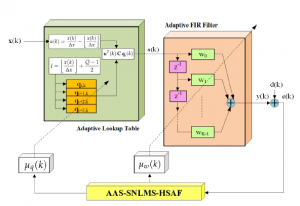
Figure 1: Proposed Adaptive Averaging Step-size Sign Normalised Least Mean Square algorithm for Hammerstein Spline Adaptive Filtering (AAS-SNLMS-HSAF).

In this paper, we propose a statistical behaviour analysis of a Hammerstein spline adaptive filter based on the sign version of normalised least mean square algorithm with adaptive averaging step-size (AAS-SNLMS-HSAF). To enhance the convergence speed with low computational complexity, the adaptive averaging step-size algorithm is suggested.

Also, the performance analysis of sign version of NLMS-HSAF based on adaptive step-size mechanism using averaging energy of errors are derived. We encounter the relationship between the step-size parameter and the mean square error from the analysis that can be examined numerically in the computer simulations for an example of system identification.

This paper is organised as following. Section 2 clarifies the HSAF structure based on LMS approach in brief. Section 3 introduces the constraint criterion of the cost function based on the stochastic gradient descent with the adaptive averaging step-size mechanism. The energy of errors is exploited to update the variant of step-size parameter. Section 4 explains how to derive the convergence analysis of HSAF-based algorithm that consists of the convergence properties and the mean square behaviour analysis. Furthermore, the simulation experiment design and experimental results are detailed in Section 5 and Section 6. Finally, Section 7 discusses and Section 8 concludes the proposed algorithm.

2. Hammerstein Spline Adaptive Filtering

The structure of Hammerstein spline adaptive filtering (HSAF) is depicted in Figure 1. It consists of a nonlinear model controlled by adaptive lookup table (LUT) [20] in which the adaptive control points vector is interpolated by the spline function and adaptive linear finite impulse response (FIR) filter [7].

The vectors x_k and s_k at symbol k appear the input and output vectors of adaptive LUT as

where y_k is the HSAF output, d_k is the desired signal and w_k is the adaptive FIR coefficient vector.

By using the chain rule, the cost function in (5) is derivative with respect to (w.r.t.) w_k, q_i,k. The result is set to zero to find optimal points. So, the adaptive FIR coefficient vector w_k and the update control points coefficient vector q_i,k are demonstrated in the recursive form as

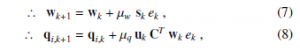
where µ_w and µ_q are the fixed step-size parameters.

3. Proposed Adaptive Averaging Step-size Sign Normalised Least Mean Square Algorithm

We extend the scope of sign algorithm into Hammerstein spline adaptive filtering (HSAF) based on the normalised version of LMS, named SNLMS-HSAF derived by minimised absolute a posteriori error as shown in Figure 1.

The constraints of this optimisation problem are formulated as

where µ_wk is an adaptive step-size of w_k and sgn{·} is the sign function. The regularisation parameter ε is a small constant.

Similarly, the constraints of the cost function regarding with q_i,k can be shown as

where µ_qk is an adaptive step-size of q_i,k and the regularisation parameter ε is a small constant.

To enhance the performance by reducing computational complexity, we modify an estimation of the energy of errors for updating average step-size parameter from the present and previous errors of systems [21].

Since, the adaptive averaging step-size µ_wk of w_k can be implemented following [19]

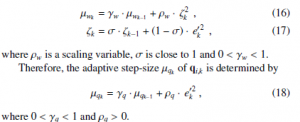
The summary of the proposed sign normalised version of least mean square algorithm using adaptive averaging step-size approach for HSAF (AAS-SNLMS-HSAF) is presented in Table. 1.

4. Convergence Analysis

In this section, we focus on the derivation and analysis of the relationship between the step-size and the mean square error. These approaches are to ensure the optimal convergence at the steady-state condition.

4.1        Convergence Properties

According to enhance the performance of SNLMS-HSAF-based algorithm, we examine the optimal learning rate of step-size parameters for adaptive FIR coefficient vector w_k and update control points vector ^q_i,k as follows.

We determine the a posteriori error e⁰_k as

Correspondingly, we investigate the convergence properties of the update control points vector q_i,k using Taylor series expansion of estimated a posteriori error e⁰_k as

Similarly, we take the norm of both sides (28), the adaptive step-size µ_qk of update control points coefficient vector q_i,k can be

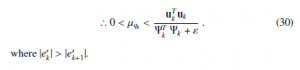
where |e⁰_k| > |e⁰_k+1|.

4.2        Mean Square Behaviour Analysis

In this section, we investigate the convergence analysis in forms of the mean square error performance in the steady-state condition.

Remark 1: We assume that the estimated coefficient error vector V_wk is under the independent and identically distributed condition with zero mean and finite variance.

We consider following [4] the estimated coefficient error vector V_wk involved the adaptive FIR vector w_k as

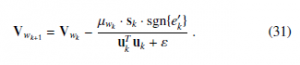
Table 1: Proposed adaptive averaging step-size algorithm based on sign normalised least mean square algorithm for HSAF (AAS-SNLMS-HSAF).

1: ALGORITHM AAS-SNLMS-HSAF ()
2:	w(0) = δ · [1 0 …0]T , uk = [u3k u2k uk 1]T xk = [ xk xk−1 … xk−K+1 ] qi,k = [ qi,k qi+1,k qi+2,k qi+3,k ]
3:	FOR k = 1 TO K − 1.
4:	sk = uTk Cqi,k
5:	uk = ∆skx − j∆skxk
6:	j i = ∆skxk + Q2−1
7:	e0k = dk − yk = dk − wTk+1 sk
8:	µwk = γw · µwk−1 + ρw · ζk2
9:	ζk = σ · ζk−1 + (1 − σ) · e0k2
10:	µqk = γq · µqk−1 + ρq · e0k2
11:	s ·sgn{e0 wk+1 = wk + µwk uk Tk uk+εk}
12:	uTk ·C·wk·sgn{e0k} qi,k+1 = qi,k + µqk uTk uk+ε
13:	NEXT k
14: END ALGORITHM

We can also determine the squared coefficient error vector as

By taking the expectation on the left-side of (33) and using (35) at the steady state condition, we can see that

Please note that (40), an approximation of (39), is valid only for small step-size parameter.

In a similar way, we consider the estimated coefficient error vector V_qk concerned with the update control points vector q_i,k as

where q_opt ∈ R^N is the optimal control points vector and V_qk ∈ R^N.

We can then rewrite the update control points vector q_i,k in (15) by using the coefficient error vector V_qk as follows.

where Ψ_k is defined in (29).

We calculate the a posteriori error with the updated control points vector q_i,k as

where µ_qk  1 is assumed.

Therefore, the excess MSE ξ_ex^q with the update control points coefficient vector q_i,k can be expressed by

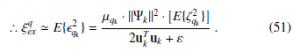
Notice that (51) is an approximation of (50) is only applicable for small values of the step-size parameter.

5. Simulation Experiment Design

In this section, the experiments are conducted with the system identification through computer simulations to verify the proposed nonlinear adaptive filtering. Flow chart of the proposed AAS-SNLMS for HSAF is shown in Figure 2.

The input color signal x_k composes of 10,000 samples by averaging over 100 Monte Carlo trials can be generated by the following equation as [3]

where ϕ is a unitary variance of zero mean white Gaussian noise and ω is a parameter to determine the correlation level between adjacent samples [2], where 0 ≤ ω < 1.

In these experiments, we set ω = 0.15,0.75 and signal to noise ratio (SNR) is of 20, 25, 30dB. As shown in [3], simulation parameters are comprised of w₀ = [0.6, −0.4, 0.25, −0.15, 0.1, −0.05, 0.001] .

The target function of nonlinear memoryless determined by a 23-point LUT of update control points vector q₀ is interpolated by a uniform third degree spline function using an interval sampling ∆x = 0.2 [3] q₀ = {−2.20, −2.00, −1.80, −1.60, −1.40, −1.20, −1.00, −0.80, − 0.91, −0.40, −0.20,0.05,0.0, −0.40,0.58,1.00,1.00, 1.20,1.40,1.60,1.80,2.00,2.20} .

The constant matrix C is called a Catmul-Rom spline matrix as For HSAF models, the initial parameters are in the following terms: δ = 0.001, number of tap length M = 7, number of control points Q = 23, µ_w = 1.15 × 10⁻³,4.25 × 10⁻³, and µ_q = 1.15 × 10⁻³,2.55 × 10⁻³.

Other initial parameters of the proposed adaptive averaging step-size sign normalised least mean square algorithm based on the Hammerstein spline adaptive filtering (AAS-SNLMS-HSAF) consists of µ_w(0) = 7.5 × 10⁻⁴,7.5 × 10⁻³,7.5 × 10⁻² and µ_q(0) = 5.5 × 10⁻⁴,5.5 × 10⁻³,5.5 × 10⁻². And the fixed parameter for adaptive averaging step-size approach of the adaptive FIR vector w_k and the update control points q_i,k are set as: γ_w = 0.97, γ_q = 0.975, σ = 0.975, ρ_w = 2.75 × 10⁻³, ρ_q = 2.95 × 10⁻³, and ε = 1 × 10⁻⁶.

6. Experimental Results

The first experiment is carried out to show the effectiveness of the proposed AAS-SLMS algorithm for HSAF performs against the white Gaussian noise. In particular, the mean square error (MSE) of HSAF-based algorithm with the different of ω = 0.15,0.75 with S NR = 25,30dB presented in Figures 3 and 4 that manifests the proposed AAS-SNLMS-HSAF and the conventional least mean square algorithm based on Hammerstein spline adaptive filtering (LMS-HSAF) [3] with the two different choices of ω given in (52). It shows that the MSE directions of the proposed AAS-SNLMSHSAF algorithm can achieve faster convergence rate compared with to the LMS-HSAF algorithm at the steady state condition.

In addition, Figure 5 shows the trajectories of µ_wk of tapweight vector w_k at different initial value of step-size as µ_w(0) = 1.75 × 10⁻²,1.75 × 10⁻³,1.75 × 10⁻⁴ at ω = 0.75 with S NR = 20dB. Figure 6 conducts the step-size curves µ_qk of control point q_i,k at different initial step-size µ_q(0) = 1.55 × 10⁻²,1.55 × 10⁻³,1.55 × 10⁻⁴ at the same environment.

Figure 7 depicts the trajectories of µ_wk of tap-weight vector w_k at different initial value of step-size as µ_w(0) = 7.5 × 10⁻²,7.5 × 10⁻³,7.5 × 10⁻⁴ at ω = 0.75 with S NR = 25dB. Figure 8 shows the step-size curves µ_qk of control point q_i,k at different initial step-size µ_q(0) = 5.5 × 10⁻²,5.5 × 10⁻³,5.5 × 10⁻⁴ at the same environment.

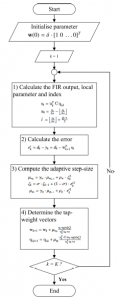
Figure 2: Flow chart of proposed AAS-SNLMS-HSAF algorithm

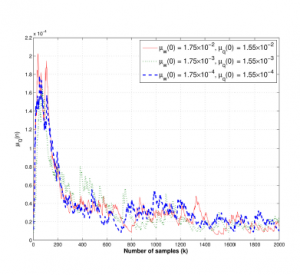
Figure 9 presents the trajectories of µ_wk of tap-weight vector w_k at different initial value of step-size as µ_w(0) = 1.75 × 10⁻²,1.75 × 10⁻³,1.75 × 10⁻⁴ at ω = 0.75 with S NR = 30dB.

Figure 10 shows the step-size curves µ_qk of control point q_i,k at different initial step-size µ_q(0) = 1.55×10⁻²,1.55×10⁻³,1.55×10⁻⁴ in the same environment.

Considering the learning rate of the proposed step-size mechanism in terms of both the adaptive step-size parameter µ_wk of w_k and the adaptive step-size µ_qk of q_i,k with different SNR values, they can quickly converge to steady-state conditions compared with the fixed step-size.

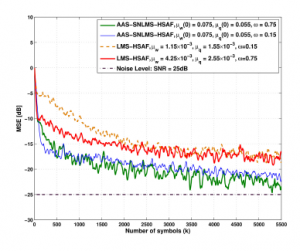
Figure 3: MSE of proposed AAS-SNLMS-HSAF with the different initial stepsize of µ_w(0),µ_q(0) and LMS-HSAF [3] with the fixed step-size µ_w and µ_q, when ω = 0.15,0.75 and SNR = 25dB.

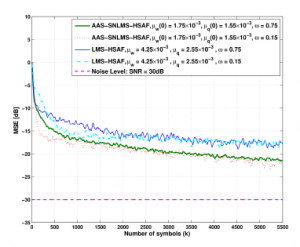
Figure 4: MSE of proposed AAS-SNLMS-HSAF with the different initial stepsize of µ_w(0),µ_q(0) and LMS-HSAF [3] with the fixed step-size µ_w and µ_q, when ω = 0.15,0.75 and SNR = 30dB.

In the second experiment, the electrocardiogram (ECG) [22] from the MIT-BIH Atrial Fibrillation Database [23], [24] is used as a real biomedical input signal, shown in Figure 11. ECG is sampled at 250Hz. Figure 12 shows the proposed AAS-SNLMS-HSAF and LMS-HSAF [3] using the ECG dataset with the different ω can achieve better convergence rate compared with the LMS-HSAF algorithm, even the ECG input signal is small.

Figure 13 demonstrates the trajectories of µ_wk of coefficient vector w_k at different ω = 0.15,0.75 and the initial value of step-size µ_w(0) = 1.75 × 10⁻³ and µ_q(0) = 1.55 × 10⁻³ with S NR = 25dB using the ECG dataset at [24]. Figure 14 presents the the learning curves of µ_qk of control point q_i,k at the same environment. It reveals

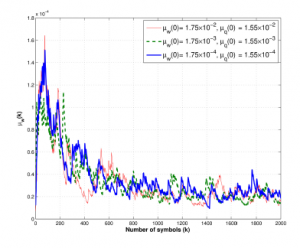
Figure 5: Trajectories of step-size µ_wk of coefficient vector w_k with the different initial step-size parameters µ_w(0), when ω = 0.75 and SNR = 20dB.

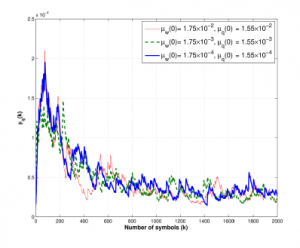
Figure 6: Trajectories of step-size µ_qk of control points coefficient vector q_i,_k with the different initial step-size µ_q(0), when ω = 0.75 and SNR = 20dB.

that the proposed adaptive step-size algorithms for both µ_wk and µ_qk can converge to equilibrium points using the real ECG dataset.

7. Discussion

The comparison over 100 Monte Carlo trials shows the robustness and superiority of the proposed AAS-SNLMS algorithm over the conventional LMS algorithm for HSAF model. The learning curves of adaptive step-size µ_wk and µ_gk of the proposed AAS-SNLMS algorithm after 10,000 iterations can expedite the convergence rate even the initial values are varied.

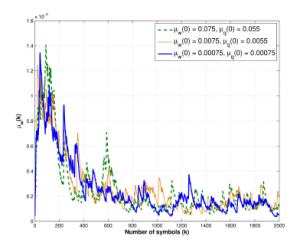
Figure 7: Trajectories of step-size µ_wk of coefficient vector w_k with the different initial step-size µ_w(0), when ω = 0.75 and SNR = 25dB.

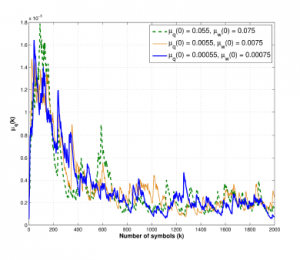
Figure 8: Trajectories of step-size µ_qk of control points coefficient vector q_i,_k with the different initial step-size µ_q(0), when ω = 0.75 and SNR = 25dB.

8. Conclusion

This paper presents a sign algorithm based on the normalised least mean square with Hammerstein adaptive filtering by applying an adaptive averaging step-size scheme. The proposed algorithm is developed using the minimised absolute a posteriori squared error. We modify an adaptive averaging step-size mechanism by using the energy of the estimated a posteriori error to update the step-size variant.

Furthermore, we derive the behaviour and mean square performance analysis of a sign algorithm based on the normalised version of least mean square algorithm for Hammerstein spline adaptive

Figure 9: Trajectories of step-size µ_wk of coefficient vector w_k with the different initial step-size µ_w(0), when ω = 0.75 and SNR = 30dB.

.

Figure 10: Trajectories of step-size µ_qk of control points coefficient vector q_i,_k with the different initial step-size µ_q(0), when ω = 0.75 and SNR = 30dB.

filtering with the adaptive averaging step-size algorithm. That leads to discover the relationship between the step-size parameter and the mean square error from the analysis. Experimental results clearly show that the proposed algorithm outperforms the conventional least mean square based on the Hammerstein adaptive filter approach.

Hammerstein models are being particularly interested in fields of engineering such as adaptive signal processing, biomedical engineering and data analysis in the nonlinear processes.

Conflict of Interest

The authors declare no conflict of interest.

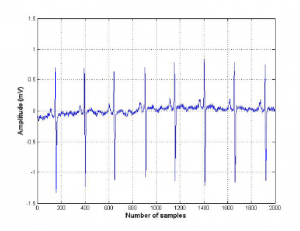
Figure 11: Electrocardiogram (ECG) input signal from MIT-BIH Atrial Fibrillation Database at [24].

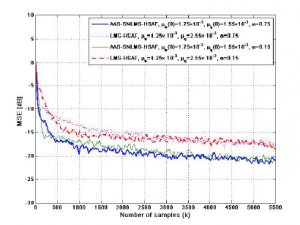
Figure 12: MSE of proposed AAS-SNLMS-HSAF and LMS-HSAF [3] using ECG input signal, when ω = 0.15,0.75 and SNR = 25dB.

1. M. Scarpiniti, D. Comminiello and A. Uncini, “Convex Combination of Spline Adaptive Filters”, in 2019 IEEE European Signal Processing Conference (EU- SIPCO), 1-5, 2019, doi:10.23919/EUSIPCO.2019.8903134.
2. M. Scarpiniti, D. Comminiello, R. Parisi and A. Uncini, “Nonlin- ear spline adaptive filtering,” Signal Processing, 93(4), 772-783, 2013, doi:10.1016/j.sigpro.2012.09.021.
3. M. Scarpiniti, D. Comminiello, R. Parisi and A. Uncini, “Hammerstein uniform cubic spline adaptive filtering : learning and convergence properties,” Signal Processing, 100, 112-123, 2014, doi:10.1016/j.sigpro.2014.01.019.
4. M. Scarpiniti, D. Comminiello, R. Parisi and A. Uncini, “Novel cascade spline architectures for the identification of nonlinear systems,” IEEE Transactions on Circuits and Systems I: Regular Papers, 62(7), 1825-1835, 2015, doi: 10.1109/TCSI.2015.2423791.
5. C. Liu and Z. Zhang, “Set-membership normalised least M-estimate spline adaptive filtering algorithm in impulsive noise,” Electronics Letters, 54(6), 393-395, 2018, doi:10.1049/el.2017.4434.
6. C. Liu, C. Peng, X. Tang and X. Liu, “Two Variants of the IIR Spline Adaptive Filter for Combating Impulsive Noise”, EURAZIP Journal on Advances in Signal Processing, 8, 1-15, 2019, doi:10.1186/s13634-019-0605-9.
7. S. Prongnuch, S. Sitjongsataporn and T. Wiangtong, “Hammerstein Spline Adaptive Filtering based on normalized Least Mean Square Algorithm”, in 2019 IEEE 2019 International Symposium on Intelli- gent Signal Processing and Communication Systems (ISPACS), 2019, doi:10.1109/ISPACS48206.2019.8986401.
8. S. Prongnuch and S. Sitjongsataporn, “Stability and Steady-State Performance of Hammerstein Spline Adaptive Filter Based on Stochastic Gradient Algo- rithm ”, International Journal of Intelligent Engineering and Systems, 13(3), 112-123, 2020, doi:10.22266/ijies2020.0630.11.
9. C. Liu, Z. Zhang and X. Tang, “Sign Normalised Hammerstein Spline Adaptive Filtering Algorithm in an Impulsive Noise Environment”, Neural Processing Letters, 50, 477-496, 2019, doi:10.1007/s11063-019-09996-6.
10. C. Liu, Z. Zhang and X. Tang, “Steady-state Performance for the Sign Nor- malised algorithm based on Hammerstein Spline Adaptive Filtering”, in 2019 IEEE International Conference on Control, Automation and Information Sci- ences (ICCAIS), 2019, doi:10.1109/ICCAIS46528.2019.9074547.
11. C. Liu, Z. Zhang and X. Tang, “Sign Normalized Spline Adaptive Filtering Algorithms Against Impulsive Noise”, Signal Processing, 148, 235-240, 2018, doi:10.1016/j.sigpro.2018.02.022.
12. S. Zhang, J. Zhang, and H. Han, “Robust Shrinkage Normalized Sign Algo- righm in an Impulsive Noise Environment”, IEEE Transactions on Circuits and Systems, 64(1), 91-95, 2017, doi:10.1109/TCSII.2016.2546905.
13. K. Xiong, S. Wang and B. Chen, “Robust Normalized Least Mean Absolute Third Algorithm”, IEEE Access, 7, 10318-10330, 2019, doi:10.1109/ACCESS.2019.2891549.
14. P. Wen and J. Zhang, “Robust Variable Step-size Sign Subband Adaptive Filter Algorithm against Impulsive Noise”, Signal Processing, 139, 110-115, 2017, doi:10.1016/j.sigpro.2017.04.012.
15. J. Kim, J. Choi, S.W. Nam, J. Chang, “Delayless Block Individual- Weighting-Factors Sign Subband Adaptive Filters With an Improved Band- Dependent Variable Step-Size”,IEEE Access, 8, 185796 – 185803, 2020, doi:10.1109/ACCESS.2020.3029269.
16. S. Zhang, J. Zhang and H. Han, “Robust Shrinkage Normalized Sign Algorithm in An Impulsive Noise Environment”, IEEE Transactions on Circuits and Sys- tems II: Express Briefs, 64(1), 91-95, 2017, doi: 10.1109/TCSII.2016.2546905.
17. S. Guan and Z. Li, “Normalized Spline Adaptive Filtering Algorithm for Non- linear System Identification”, Neural Processing Letter, 46(2), 595-607, 2017, doi:10.1007/s11063-017-9606-6.
18. S. Sitjongsataporn, W. Chimpat, “Adaptive Step-size Normalised Least Mean Square Algorithm for Spline Adaptive Filtering”, in 2019 IEEE International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), 544-547, 2019, doi:10.1109/ITC-CSCC.2019.8793383.
19. A. Saengmuang and S. Sitjongsataporn, “Convergence and Stability Analysis of Spline Adaptive Filtering based on Adaptive Averaging Step-size Normalized Least Mean Square Algorithm ”, International Journal of Intelligent Engineer- ing and Systems, 13(2), 267-277, 2020, doi:10.22266/ijies2020.0430.26.
20. S. Prongnuch and R.E. Valmoria, “Applied of Co-design in Reconfigurable Sys- tem for Remote Image Noise Filtering via Ethernet Technology”, in 2013 IEEE International Science, Social Science, Engineering and Energy Conference, 92-98, 2013.
21. S. Sitjongsataporn, “Advanced Adaptive DMT Equalisation: Algorithms and Implementation”, LAP LAMBERT Academic Publishing, 2011.
22. G.B. Moody and R.G. Mark, “A New Method for Detecting Atrial Fibrillation using R-R Intervals”, Computers in Cardiology, 10, 227-230, 1983.
23. A. Goldberger, L. Amaral, L. Glass, J. Hausdorff, P.C. Ivanov, R. Mark, J.E. Mietus, G.B. Moody, C.K. Peng, and H.E. Stanley, “PhysioBank, Phys- ioToolkit, and PhysioNet: Components of a New Research Resource for Com- plex Physiologic Signals”, Circulation [Online], 101(23), e215–e220, 2000, doi:10.1161/01.cir.101.23.e215.
24. G. Moody and R. Mark, “MIT-BIH Atrial Fibrillation Database”, 2000, [On- line]. Available: https://physionet.org/content/afdb/1.0.0/. [Accessed Jan. 8, 2021], doi:10.13026/C2MW2D.

(Click Here)

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country