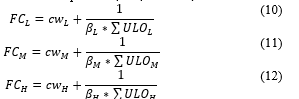1.Introduction

In general, learning groups are designed to be heterogeneous. That is, a class is inhabited by students with various types of learning and characters. There are students with a fast learning type. While others are slow and even very slow. Therefore, it is difficult for teachers to follow an approach that is suitable for every student. In an effort to reach all students, teachers often design class lectures and activities. To remedy this situation requires personal support and guidance so that individual needs and difficulties can be addressed. However, given the number of students a class has, it is not easy for a teacher to deal with the diversity of levels and needs of students at all times [1].

Curriculum Sequencing (CS) is a technique to give students flexibility in planning the most appropriate sequence of individual learning tasks [2]. Produce an individual learning method in which each student dynamically chooses the most optimal teaching operation through presentations, examples, questions, or problems. Meanwhile [3] found the optimal learning sequence through the pretest to identify the weaknesses of students. Thus, CS aims to replace the rigid, generic, modeled learning structure set by the instructor or pedagogical team, with a more flexible and personalized learning path.

CS development according to [4] must consider students’ learning abilities, background, and motivation. Even for certain students, the requirements can change according to their increased knowledge due to learning. According to [5] states that CS not only helps students find the most efficient and appropriate learning path but also helps instructors to organize program structures, content, or learning objects and make improvements. Meanwhile [6] stated that individualization of teaching materials was a challenge in choosing the right LO and making the LO sequence easy to learn. Thus, optimal results will be obtained because the learning path of learning is following students’ abilities. Learning paths that have been developed have not used cognitive classification as a controller of the learning object ontology of a subject. The Evolutionary Computing (EC) algorithm approach has been widely used in solving Curriculum Sequencing problems.

According to [7] the EC method that is most widely used to solve CS problems is grouped into two main approaches, namely the social sequencing approach and the individual sequencing approach. Genetic Algorithm (GA) is a metaheuristic method which is famous because it has good performance for various types of optimization problems. There have been many GA studies in the CS domain including [8]-[11].

In [12] present a Personalized e-Course Composition approach based on Particle Swarm Optimization (PC2PSO). A binary particle encoding is used, in which each dimension determines whether the object of learning is included in sequence (1) or (0). The initial particles are generated randomly. The fitness function is used to determine Gbest and Pbest based on the level of compatibility between the pedagogical targets of students and the learning concept: learning material, level of compatibility, difficulty level, the time limit for learning, and student checks on the material that has been studied. Comparative evaluation in terms of average fitness and stability functions shows that the PSO method is better than the GA method. While the newer optimization method is swarm intelligence.

Swarm intelligence is an optimization method based on a distributed agent system, where each agent has simple abilities that can solve complex problems together. The approach to swarm intelligence is very different from EA because swarm intelligence emphasizes cooperation rather than competition. To support the concept of cooperation, each agent has a simple ability to learn from experience and also communicate with fellow agents. Metaheuristic methods based on the concept of swarm intelligence are Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO).

The PSO algorithm was originally proposed in 1995 [13]. In the PSO, each particle represents the solution to the problem. Particle learning consists of two factors, namely particle experience called cognitive learning and the combination of learning from the whole swarm is called social learning. Cognitive learning as Pbest is the best position that a particle has ever reached, while social learning as Gbest is the best position of all particles in the swarm. One of the uses of PSO in the e-education domain includes research conducted by [14] using the PSO method to offer formative value in e-assessment and turn it into a learning tool.

This research proposes a learning path model based on the cognitive classification of Revised Bloom’s Taxonomy and an ontology of learning objects. Cognitive classification is based on RBT into three cognitive classes (Cognitive Low (CL), Cognitive Medium (CM), and Cognitive High (CH)). Hybrid Particle Swarm Optimization (HPSO) algorithm is used to solve combinatorial problems, namely learning object ontology with Discrete PSO which is controlled by cognitive class using Binary PSO. So that a learning path model will be produced that is following the cognitive abilities of students through optimization of the assessment of the LO relationship between RBT and the ontology of a subject.

2. Literature Review

2.1. Learning Object

Primary reference sources in the form of journals and dissertations, and secondary sources in the form of books, many have provided explanations about learning objects. However, in general, there is a common view of the concept of learning objects. The definition of a learning object is broadly described as all entities that are related or used as learning and training materials. From this understanding, all general and conventional learning materials such as worksheets, modules, handouts, etc. are also included in the learning object category. Researcher [15] as well as a learning practitioner defines learning objects as each learning resource in the form of a digital entity that can be used repeatedly as a learning resource. While other researchers [16] presented various definitions of LO, the simplest description refers to data objects, content, or information.

The Institute of electrical and electronics engineer (IEEE) defines learning objects, namely as any digital or non-digital entity that can be used, then reused and can become a reference for technology-assisted learning. Thus LO is any entity (digital or non-digital) that can be reused or referenced including multimedia content, instructional content, software, people, organizations, or events for technology-supported learning. This definition leaves room for the entire curriculum to be seen as an LO.

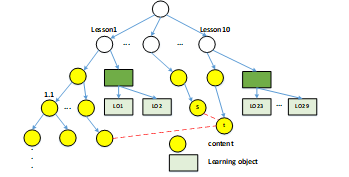Figure 1:  Examples of learning object structures

Figure 1 shows that in one topic or one subject, the description of the content of the course is followed by the related learning material. In other words, subject content is usually arranged based on ontology, where the yellow circle represents the learning content while the blue rectangle represents LO [17].

2.2. Particle Swarm Optimization

The PSO algorithm works based on particles in the population that work together to solve existing problems disregarding the physical position. The PSO algorithm combines local and global search methods that balance exploration ability to conduct investigations in different areas of the search area to get the best optimal value and exploitation ability to concentrate around the search area for fix solution. The similarity of PSO and GA is that the system starts with a population formed from random solutions, then the system seeks optimization through random generation changes [18]. Each particle holds traces of position in the search space as the interpretation of the best solution (fitness) that had been achieved.

The basis of the PSO algorithm consists of three steps, namely determining the particle position and velocity, updating the velocity, and updating the position [19]. Each particle tries to update its position using information such as the current position, the current velocity, the distance between the current position to Pbest, and the current position to Gbest which mathematically updates the particle velocity calculated (1).

The achievement of the results is obtained from a new velocity calculation for each parallel based on the distance from the Pbest it has and the distance from the Gbest position updating the particle position  is shown in (2).

Personal best (Pbest) according to [20] is the best value that a particle has, the value in the next time step, t + 1, where t ∈ [0,…, N], update Pbest is shown in (3),

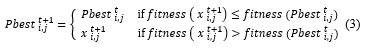While the Global best (Gbest) is the best value that takes into account all particles in the population calculated using (4)

, where  and

Each iteration, each particle is given information about the latest Gbest value so that a one-way information sharing mechanism occurs to carry out the process of finding the best solution with a fast convergence shift.

2.2.1. Binary Particle Swarm Optimization (BPSO)

In [21] developed PSO to operate in binary search space because real value domains can be converted into binary valued domains. The proposed algorithm is called the PSO binary algorithm (BPSO) in which particles represent positions in binary space and the particle position vectors can take a binary value 0 or 1 where . In this case, it maps from the binary space of the dimension  (an eg string of bits of length n) to the real number  (where f is the fitness function and  is the set of real numbers). That means that the position of the particle must belong to  to be calculated by the fitness function [22]. In BPSO, the particle velocity  is connected to the probability that the particle position  is 0 or 1. Equation (1) for updating the particle velocity is still used in BPSO. Then the sigmoid function shown in (5) is used to update the particle velocity.

The position of the particle  is influenced by (6), where  is a random number selected from the distribution (0, 1) and  of the sigmoid function.

2.2.2. Discrete Particle Swarm Optimization (DPSO)

In 2000, Clerc modified the DPSO algorithm formulated by Kennedy and Eberhart. Clerc modifies the representation of the position of the particle, the shape of the velocity produced by the particle, and the effect of velocity on the position of the particle. This modification hopes that it can be applied to problems with discrete models, especially combinatorial types [23]. The velocity update formula that has been modified by Clerc is defined in (7), while for fixed position updates using (1).

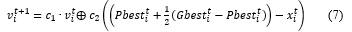3. Methodology

The Hybrid Particle Swarm Optimization algorithm is applied to overcome combinatorial problems in a more practical and orderly manner in determining learning pathways. Determination of the order of learning objects through LO ontology based on cognitive classes from the learning vector quantization method and using RBT to assess connection quality. The expected result is that each student gets a recommendation for a learning path that is appropriate to their cognitive level.

The model used in this study consists of three components, cognitive classification with LVQ, learning object ontology based on RBT, and hybrid discrete particle swarm optimization. The general architecture of the proposed model can be seen in Fig. 1.

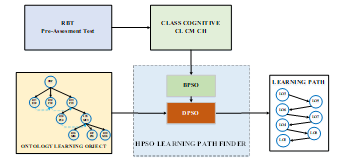Figure 2: The Architecture of The proposed Model

3.1. Particle Representation BPSO

The representations of the particles of the three cognitive classes (CL, CM, CH) were arranged according to a predetermined LO sequence. Each cognitive class is placed in 8 data slots, so it takes 24 data slots. The Cognitive Low class on particles 7 and 8, the Cognitive Medium class on particles 1, 4, 8, and the Cognitive High class on particles 1, 2, 4, have a value of 0. This value of 0 indicates that the value at the position of these particles can change from 0 becomes 1 depending on the speed and position of the particles. Meanwhile, the value of particles with a value of 1 is determined as LO which must be followed and the calculation is carried out which is not affected by the particle velocity. The updated particle velocity and position of the CL cognitive class are presented in Figure 3.

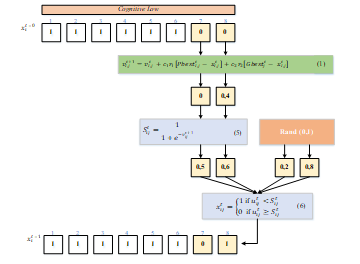Figure 3: Update velocity and position in cognitive class

3.2. Particle Representation DPSO

LO particles consist of eight particles arranged based on object-oriented programming lessons that have been determined based on the depth and breadth analysis of RBT, namely Table I. The representation of LO-LO sequence particles is shown in Figure 4 randomly from three groups of particles.

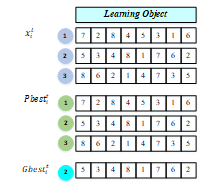Figure 4: Learning Object Particle Representation

Update the position of the learning object using (1) while for speed update using (7). The process of updating the speed of learning objects begins with the process of reducing Gbest with Pbest, where   [5 3 4 8 1 7 6 2] is used as a reference in the transposition process. The transposition stage starts with a shift in the learning object starting from (1,5) and several times the position shift from position (2,6) – (3,4) – (5,7) – (6,7) and stops at the position shift ( 7,8) after equal to the reference value  [5 3 4 8 1 7 6 2]. Based on (7) the temporary velocity value is multiplied by 0.5 to produce the velocity, namely (1.5) (2,6) (3,4).

3.3. BPSO – DPSO Integration

HPSO is the part that performs the process of determining the learning path, consisting of BPSO and DPSO. Cognitive classes (CL, CM, and CH) are represented as particles in the BPSO method and ontology learning objects are represented as particles in the DPSO method. The integration of BPSO and DPSO through the fitness function will produce a learning path model that is suitable for students’ cognitive abilities.

Figure 5 shows the process of updating the speed and position of particles for DPSO and BPSO in each iteration so that it will ensure changes in LO and cognitive class (CL, CM, CH). Update the velocity and position of DPSO particles on the learning object update through (7) to update the particle velocity, and use (2) to update the position. Meanwhile, the update of the speed and position of BPSO particles in the cognitive class is through (1) to update the speed, (5) to calculate the sigmoid value, and (6) to update its position.

3.4. The Proposed HPSO Algorithm

The fitness function is used as a measuring tool to select the best object from a set of existing objects. The fitness function is identical to the objective function of the optimized problem, which is to make the best individual learning route according to their cognitive abilities. The objective function is determined based on the highest fitness value. The higher the fitness value, the results are closer to the objective function.

The objective function defined in this research is to create individual learning paths or routes based on student cognitive data, namely CL, CM, and CH with the learning object ontology of a subject. Thus, the fitness function is to find the best Connection Weight (CW) value between LO in ontology-based on students’ cognitive classes, namely CL, CM, and CH as illustrated in Figure 6.

Connection Weight ( ) was used to assess the relationship of LO in RBT ontology as cognitive level evaluators (8).

This study uses Distance by Bloom (DBB) to measure the cognitive distance depth and breadth ( between LO using (9),

Equation (10),(11),(12) , ,  is fitness function to determine LO relationships in CL,CM,CH class,

with:

 is 0 -1.

     is connection weight for each class cognitive

    is unsed LO for each class cognitive.

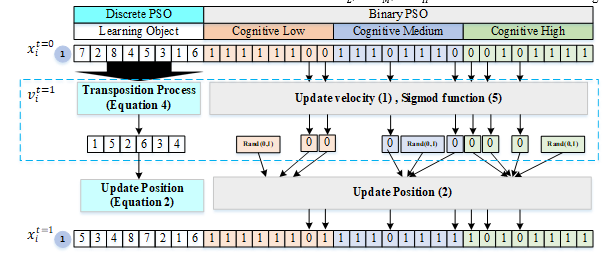Figure 5: DPSO-BPSO integration in updating the velocity and position of particles

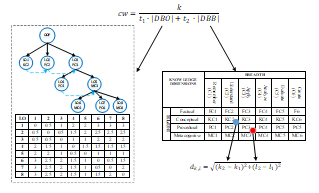Figure 6: Illustration of Determining the Fitness Function

The objective function value is calculated for all the particles generated earlier. The PBest position is determined from the objective function value obtained. The initial velocity of the particles is the absolute difference between the initial position and the personal best position of the particles. The particle with the maximum objective function value is the GBest particle and the corresponding position is the global best position [24]. The calculation of the fitness function stops until the iteration value limit has been determined.

The Hybrid Particle Swarm Optimization algorithm with a learning object transposition function is presented in detail in Table 1.

Table 1: HPSO Algorithm

Algorithm 1: HPSO for recommendation learning path

Result: Learning path based on students’ cognitive class

Initialization; Transposition() posx=1; for i = 1 To Gbest for j = 1 To Pbest                 if Gbest(i) = Pbest(j) And i<>j then tmp = Pbest(j); Pbest(j) = Pbest(i); Pbest(i) = temp; trsp1(posx) = i; trsp2(posx) = j; posx = posx + 1;   end next j next i vc = posx * 0.5; for i = 1 To vc – 1 indx1 = trsp1(i); indx2 = trsp2(i); tmp = Pbest(indx1); Pbest(indx1) = Pbest(indx2); Pbest(indx2) = tmp; next i end Function   while (true) do for i = 1 To LO call: Transposition();            if (dbb(i) > 0 && dbo(i) > 0) then cwIndex(i) = k / ( t1 * dbo(i)) + (t2 * dbb(i))            end        cw(i) += cwIndex(i); tempFitness(i)=cw(i) + (1 / beta * unLo(i));        f(i) += tempFitness(i); if (f( ) <= f( ) then         Pbest(i) = f( ); if (f( ) > f( ) then         Pbest(i) = f( ); end Gbest(i) = max(Pbest(i)); next i end

4. Results

Testing the HPSO algorithm to recommend a learning path model that suits the CL, CM, and CH cognitive classes through steps, i.e:

1. Testing the next computational program, test the consistency of the PBest fitness function for each population to become GBest through five particle populations, ten particle populations (ten LO groups), and fifteen populations (fifteen LO groups).
2. Groups of students in cognitive classes CL, CM, and CH will get the best learning path recommendations based on their respective GBest.

4.1. Connection Weight for Fitness Fuction

A CW calculation process occurs when one LO is paired together with CL of value 1.  The calculation starts with finding the DBO, DBB, and CW values of each LO. In the state of one LO paired together with CL is 0 then the LO is not used in the connection weight calculation process. The mechanism for testing connection weight according to in accordance with the procedure shown in Figure 7.

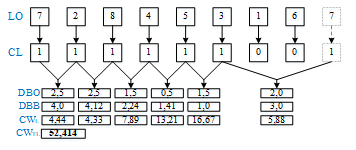Figure 7: Representation of Connection Weight

The fitness function in the CL,CM,CH-class is calculated using (10),(11),(12) ,the  fitness value data with 15 groups of particles is shown in Figure 8.

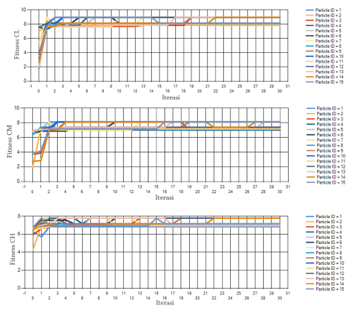Figure 8:  Pbest Values for Each Cognitive Class

Pbest tests through the fitness function in the CL, CM, and CH classes show that the higher the iteration used, the more optimal the solution will be from the system, marked with the increasing fitness results. This is due to the increasing number of iterations used to make the particles move to find the optimal solution so that the particles can find the optimal solution.

4.2. Learning Path Recommendation

Gbest is the best value that takes into account all particles in Gbest the population in each CL, CM, and CH class. Each iteration, each participant is given information about the latest Gbest value so that there is a mechanism for sharing one-way information to carry out the process of finding the best solution with a fast convergence movement.

Learning path recommendations based on the Gbest values shown in Table 2 indicate that an increase in the number of particles affects the value of the resulting learning path sequence, but is still within the schema of each cognitive class.

Table 2: Learning Path Recommendation

No	Class Cognitive	Number Of Particles	Learning Path
			HPSO	Manual Set
1	CL	10	1-3-2-5-4-6-7-8	1-2-3-4-5-6-7-8
2		15	1-2-3-5-4-6-7-8
3	CM	10	3-5-6-7-4-2-8-1	1-2-3-4-5-6-7-8
4		15	3-5-7-6-2-4-8-1
5	CH	10	8-5-7-6-4-3-1-2	1-2-3-4-5-6-7-8
6		15	8-5-7-6-4-3-2-1

The HPSO algorithm can create learning pathways by CL, CM, and CH cognitive classes. The cognitive class CL tendency of its learning path (1-3-2-5-4-6-7-8) shows the order of the basic LO to a higher LO. Whereas the cognitive class CH of the learning path tendency (8-5-7-6-4-3-1-2) shows a sequence of high LO to the basic LO. In CM cognitive class the tendency of learning path is (3-5-7-6-4-2-8-1). The similarity of the learning path sequence based on the number of CL cognitive particles is 87.5%, CM is 75%, and CH is 87.5%, so the average similarity of the learning path sequence is 83.3%.

The results of the learning path model research using HPSO have been presented and explained to three education experts. The recommendation of three education experts stated that cognitive classification with LVQ and the logical flow learning path model was acceptable. Researchers can prove the use of RBT through the results of learning paths based on cognitive low (CL), cognitive medium (CM), and cognitive high (CH). The HPSO learning pathfinder is a very important part of combining the output of the LVQ cognitive classification with the ontology learning object.

The advice given from education experts is as follows, the dynamics of the interrelation between the depth of the material and the breadth of the material can be determined by the teacher or teacher based on competency targets to produce a learning path in accordance with the characteristics of students. This research can be developed in the realm of attitudes and skills in accordance with learning evaluation competencies, namely, attitudes, knowledge, and skills.

5. Conclusion

The Hybrid Particle Swarm Optimization method, which consists of DPSO for learning object ontology and BPSO in cognitive classes, can be applied more practically and regularly to produce a learning path recommendation. Based on experimental studies and verification of education experts, the HPSO algorithm in this research can recommend a suitable learning path for students classified in the CL, CM, and CH cognitive classes.

Further research is the integration of the Learning Vector Quantization method with Hybrid Particle Swarm Optimization in a platform that is supported by the provision of standard learning object ontologies that can be the right and efficient solution in the development of smart e-learning mode during the Covid-19 pandemic.

Acknowledgment

Director General of Higher Education of the Ministry of Education and Culture Indonesia, National Competitive Research Program for Doctoral Dissertation Research (PDD) in 2020.

1. Á. Santos, A. Gomes, A. Mendes, “A taxonomy of exercises to support individual learning paths in initial programming learning,” Proceedings – Frontiers in Education Conference, FIE, (October), 87–93, 2013, doi:10.1109/FIE.2013.6684794.
2. L. De-Marcos, C. Pages, J.J. Martínez, J.A. Gutiérrez, “Competency-based learning object sequencing using particle swarms,” Proceedings – International Conference on Tools with Artificial Intelligence, ICTAI, 2, 111–116, 2007, doi:10.1109/ICTAI.2007.14.
3. C.M. Chen, “Intelligent web-based learning system with personalized learning path guidance,” Computers and Education, 51(2), 787–814, 2008, doi:10.1016/j.compedu.2007.08.004.
4. D. Hauger, M. Köck, “State of the art of adaptivity in e-learning platforms,” LWA 2007 – Lernen – Wissen – Adaptivitat – Learning, Knowledge, and Adaptivity, Workshop Proceedings, 355–360, 2007.
5. S. Al-Muhaideb, M.E.B. Menai, “Evolutionary computation approaches to the Curriculum Sequencing problem,” Natural Computing, 10(2), 891–920, 2011, doi:10.1007/s11047-010-9246-5.
6. V. Shmelev, M. Karpova, A. Dukhanov, An Approach of Learning Path Sequencing Based on Revised Bloom’s Taxonomy and Domain Ontologies with the Use of Genetic Algorithms, Elsevier Masson SAS, 2015, doi:10.1016/j.procs.2015.11.081.
7. S. El Lakkah, M.A. Alimam, H. Seghiouer, “Adaptive e-learning system based on learning style and ant colony optimization,” 2017 Intelligent Systems and Computer Vision, ISCV 2017, 2017, doi:10.1109/ISACV.2017.8054963.
8. A. Hovakimyan, S. Sargsyan, S. Barkhoudaryan, “Genetic algorithm and the problem of getting knowledge in e-learning systems,” Proceedings – IEEE International Conference on Advanced Learning Technologies, ICALT 2004, 336–339, 2004, doi:10.1109/ICALT.2004.1357431.
9. K. Seki, T. Matsui, T. Okamoto, “An adaptive sequencing method of the learning objects for the e-learning environment,” Electronics and Communications in Japan, Part III: Fundamental Electronic Science (English Translation of Denshi Tsushin Gakkai Ronbunshi), 88(3), 54–70, 2005, doi:10.1002/ecjc.20163.
10. A. Samia, B. Mostafa, “Re-use of resources for adapted formation to the learner,” ISCIII’07: 3rd International Symposium on Computational Intelligence and Intelligent Informatics; Proceedings, 213–217, 2007, doi:10.1109/ISCIII.2007.367391.
11. A. Dukhanov, M. Karpova, V. Shmelev, “An automation of the course design based on mathematical modeling and genetic algorithms,” Proceedings – Frontiers in Education Conference, FIE, 2015-Decem(December), 7–10, 2015, doi:10.1109/FIE.2015.7344325.
12. C.M. Chen, “Ontology-based concept map for planning a personalised learning path,” British Journal of Educational Technology, 40(6), 1028–1058, 2009, doi:10.1111/j.1467-8535.2008.00892.x.
13. J. Kennedy, R. Eberhart, Particle swarm optimization, IEEE International Conference on Particle Swarm Optimization, 4, 1942–1948, 1995, doi:10.1109/ICNN.1995.488968.
14. M.-I. DASCĂLU, “Application of Particle Swarm Optimization to Formative E-Assessment in Project Management,” Informatica Economica, 15(1), 48–61, 2011, doi:DAOJ.
15. D.A. Wiley, “Learning Object Design and Sequencing Theory,” Learning Object Design and Sequencing Theory, (June), 142, 2000, doi:10.1017/CBO9781107415324.004.
16. R. McGreal, “Learning Objects: A Practical Definition,” International Journal of Instructional Technology and Distance Learning, 1(9), 21–32, 2004, doi:10.1002/tl.37219925103.
17. J. Wang, T. Mendori, J. Xiong, “A Language Learning Support System using Course-centered Ontology and its evaluation Computers & Education A language learning support system using course-centered ontology and its evaluation,” Computers & Education, 78(September 2014), 278–293, 2015, doi:10.1016/j.compedu.2014.06.009.
18. X. Li, K. Deb, “PSO Niching algorithms Using Different Position Update Rules,” IEEE Congress on Evolutionary Computation, 2010.
19. J. Kennedy, E.C. Russell, Y. Shi, Swarm Intelligence, Academic Press, USA, 2001, doi:10.1007/978-3-540-74089-6.
20. F. van den Bergh, A.P. Engelbrech, “New Locally Convergent Particle Swarm,” IEEE International Conference on Systems, Man and Cybernetics, 3, 1–5, 2002.
21. J. Kennedy, R.C. Eberhart, “A discrete binary version of the particle swarm algorithm,” IEEE, International Conference on Systems, Man, and Cybernetics, 5, 4104–4108, 1997, doi:10.1109/ICSMC.1997.637339.
22. A.P. Engelbrecht, Computational Intelligence An Introduction, Second Edi, John Wiley & Sons Ltd, England, 2007.
23. M. Clerc, Discrete Particle Swarm Optimization Illustrated by the Traveling Salesman Problem, Springer Verlag, Berlin Heidelberg, 2004, doi:10.1007/978-3-540-39930-8_8.
24. M.K. Marichelvam, M. Geetha, Ö. Tosun, “An improved particle swarm optimization algorithm to solve hybrid flowshop scheduling problems with the effect of human factors – A case study,” Computers and Operations Research, 114, 104812, 2020, doi:10.1016/j.cor.2019.104812.

(Click Here)

(Click Here)