1.Introduction

Standard floating point has been useful over the years, but unknowable error is inherent in the standard system. Though not indicated in standard floating point, a calculated result may have an insufficient number of significant bits. This paper, which is an extension of work originally presented in [1], uses a bounded floating-point (BFP) software model that emulates the BFP hardware implementation to identify the accurate significant bits of a calculated result, thus unmasking standard floating-point error.

2. Background – Standard Floating Point

2.1. Standard Floating-Point Format

Computer memory is limited; thus, real numbers must be represented in a finite number of bits. The need to represent a range of real numbers within a limited number of bits and to perform arithmetic operations on those real numbers, led to the early development of, and use of, floating-point arithmetic. The formulaic representation employed is reminiscent of scientific notation with a sign, an exponent, and a fraction [2]. Through the efforts of William Morton Kahan and others, a standard for floating point was published in 1985 by the Institute of Electrical and Electronics Engineers (IEEE) [3]. The current version is IEEE 754-2019 – IEEE Standard for Floating-Point Arithmetic [4], which has content identical to the international standard ISO/IEC 60559:2020 [5].

The standard floating-point format is shown in Figure 1. The sign of the value is represented by a single bit, S. The offset exponent is E with a length of e. The significand, T, has a length of t. The overall length of the representation is k.

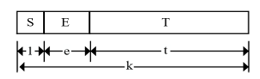Figure 1: Standard Floating-Point Format

The IEEE 754-2019 standard defines floating-point formats and methods for both base two and base ten. However, this work only addresses base two floating point. The formats most commonly used require 32 bits or 64 bits of storage, which are known as single precision and double precision, respectively.

The decimal equivalent of the standard representation is shown in (1), where S, T, t, and E are defined above and O is the exponent offset. For binary floating point, O is nominally 2^e-1-1.

                            (-1)^S ∙ (1+T/2^t) ∙ 2^E-O                                                             (1)

The expression (1) is used in expressing the value of the standard floating-point representation in various number bases, typically for the display of the value in number base ten.

2.2. Standard Floating-Point Representation Error

Floating-point error is the difference between the representation of the actual standard floating-point value and the infinitely accurate real value to be represented. It must be clearly stated that the IEEE floating point standard does not specify any mechnism for indicating nor defining floating-point error. Floating-point error is invisible to implementations of the IEEE floating-point standard.

Standard floating-point error occurs because only a limited number of real numbers can be expressed with the finite number of bits available.

Because binary floating point represents real numbers with a fixed number of bits, numbers that cannot be represented with a limited set of powers of two cannot be represented exactly [6]. As Goldberg succinctly describes it, “Squeezing infinitely many real numbers into a finite number of bits requires an approximate representation” [7]. Therefore, there are a finite number of values that can be represented with floating point, but an uncountably infinite number of values [8] that cannot be exactly represented with floating point. For instance, the values 0.1, 0.22, and transcendental values, such as π, cannot be accurately represented with binary standard floating point, but the values 0.5, 0.125. and 942.625 can be exactly represented with standard binary floating point. Thus, only those real numbers which can be represented with a constrained sum of the powers of two can be represented with no error. All other representations must have error.

Therefore, we can define floating-point representation error as the difference between the representation value, see (1), and the infinitely accurate real value represented.

2.3. Standard Floating-Point Operational Error

Accuracy in floating-point computations may be measured or described in terms of ulps, which is an acronym for “units in the last place.” Kahan originated the term in 1960, and others have presented refined definitions [9], [7]. An ulp is expressed as a real function of the real value represented. Rounding to the nearest value, for instance, can introduce an additional error of no more than ±0.5 ulp.

The real solution to the floating-point error issue is knowing the number of significant bits of a computational result. The number of significant bits can be known by using BFP. When BFP identifies sufficient significant bits, a decision may be made, or an opinion may be formed.

Usually, the error of a single computation is insignificant, with the exception being catastrophic cancellation error. However, with large, complex floating-point computations, error can accumulate and can reduce the significant bits to an unacceptable level [10], [11]. Loss of significant bits may be propagated through recursive repetition. BFP tracks the current number of significant bits through recursion [12], [13]. Examples of such recursive calculations are spatial modeling of explosions [14], dynamic internal stress [15], weather [16], etc.

The repetition of such calculations accumulates floating-point error. Unfortunately, there are two types of error, rounding and cancellation, and these errors are incompatible since rounding error is linear and cancellation is exponential. However, just as apples and oranges cannot be added by species, they can be added by the “genus” fruit. In order to accumulate cancellation and rounding errors we must find a similar “genus” before such error can be accumulated. This genus in the BFP system is the logarithm of the accumulated error stored in the defective bits field D (Figure 3), which captures both the accumulated rounding error and cancellation error.

Three operations that must be performed during floating-point operations introduce error. These operations are the following: alignment, normalization (causing cancellation error), and truncation (leading to rounding error).

Alignment occurs during add operations (which include both positive and negative numbers) when one exponent is smaller than the other and the significand must be shifted until the exponents are equal or “aligned” [17].

Cancellation error occurs because the resulting significand after a subtraction, including the hidden bit, must lie between 1.0 and 2.0. If the operands of a subtract have similar values, significant bits of the result may be defective, or “cancelled” [2], [18]. This is called cancellation error, and when that error is significant it is called “catastrophic cancellation” [7]. Jorgensen mathematically defines “similar values” [6].

Rounding error occurs because nearly all floating-point operations develop more bits than can be represented within the floating-point format, and the additional bits must be discarded [4]. The floating-point standard describes how these discarded bits can be used to “round” the resulting value but necessarily must introduce error into the resulting representation of the real value [2].

Standard floating point provides no means of indicating that a result has accumulated error [4]. Therefore, such errors are invisible unless they cause a catastrophe. Even then the cause can only be traced to floating-point failure with substantial effort, as stated by Kahan in the conference article entitled “Desperately needed remedies for the undebuggability of large floating-point computations in science and engineering” [19].

Misuse of floating point and the accumulation of floating-point error has been expensive in terms of election outcomes [20], financial disruption [21], [22], and even lives lost [23].

This computational weakness has been known since the early days of computing and continues until today. Even as early as 1948 Lubken had noted that: “…it is necessary at some intermediate stage to provide much greater precision because of large loss of relative accuracy during the process of computation” [10]. To this day, floating-point error is a known problem. [13], [24], [11].

3. Background – Bounded Floating Point (BFP)

The BFP system is an extension or annex to the standard floating point format, which may be implemented in hardware, software, or a combination of the two. BFP calculates and saves the range of error associated with a standard floating-point value, thus retaining and calculating the number of significant bits [25], [26]. BFP does not minimize the floating-point error but identifies the error inherent within standard floating point.

BFP extends the standard floating-point representation by adding an error information field identified as the “bound” field B. The bound field B contains subfields to retain error information provided by prior operations on the represented value, but the field of primary importance is the “Defective Bits” field D. This field identifies the number of bits in the represented value that are no longer of significance, consequently defining the number of bits in the result that are significant. The value of D is not an estimate but rather is calculated directly from standard floating-point internals such as normalization leading zeros and alignment of exponent differences. (See Appendix). BFP identifies and reports floating-point error and has no direct means of reducing that error. Because it is a direct calculation, the bound is neither optimistic nor pessimistic. However, the conversion between binary significant bits and decimal significant digits is not one-to-one and introduces a small error of less than 1 decimal ulp on conversion.

BFP retains the exception features of standard floating point, such as detection of infinity, operations with not a number (NaN), overflow, underflow, and division by zero. Though zero is a special case in the standard, the standard does not detect zero as long as any bits remain in the significand. However, BFP exactly identifies zero when the significant remaining bits in the significand are all zero, as shown in the test results below.

3.1. Bounded Floating-Point (BFP) Format

The bound field B, as seen in Figures 2 and 3, is a field added, to the format of standard floating point to describe the bounds of the error of the represented value. The bound field B contains and propagates information about the accuracy of the value that is being represented by creating and maintaining a range in which the infinitely accurate value represented must reside.

Figure 2: BFP Format

3.2. Bound Field Specifics

Figure 3 presents the subdivisions incorporated into the bound field format.

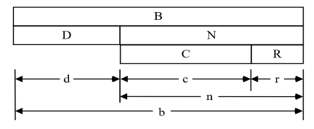Figure 3: Format of Bound Field and Subfields

The bound field B is of width b. The bound field B consists of two fields, the defective bits field D of length d and the accumulated rounding error field N of length n. The value of the defective bits is the number of bits of the representation that are not significant, that have no value. The defective bits field D stores the logarithm of the upper bound of the error represented in units in the last place (ulps) and, in effect, determines the number of significant bits of the result.

The accumulated rounding error, stored in the N field, is the sum of the rounding error in fractions of an ulp.

The accumulated rounding error field N consists of two fields, the rounding error count field C, of width c, and the rounding bits field R, of width r. The fraction of an ulp represented in the accumulated rounding error is R/2^r ulp.

The decimal equivalent of the BFP representation is shown in the expression of (2), which is equivalent to the expression (1) above.

                              (-1)^S ∙ ((T+2^t)/2^t) ∙ 2^E-O                                          (2)

The IEEE standard [4] defines “precision” as the capacity of the significand plus one (for the hidden bit). This capacity-type precision is defined as the maximum number “of significant digits that can be represented in a format, or the number of digits to that (sic) a result is rounded” [4]. In contrast, BFP identifies the actual number of bits that are significant (have meaning). These significant bits (SB) are a subset of the IEEE precision, p. The BFP’s defective bits field D represents the number of bits of the representation that are not significant, where D = t + 1 – SB. In IEEE standard representation, the value of D is not known, nor is the number of significant bits.

BFP provides a means of specifying the number of significant bits required in a BFP calculation. Additionally, when there are fewer significant bits than specified or required, BFP represents this condition with the quiet not-a-number representation, “qNaN.sig,” indicating excessive loss of significance.

3.3. Alignment

For addition and subtraction, when the exponents of the two operands are unequal, the significand of the smaller operand must be right shifted by the exponent difference. This is known as alignment [2], [17], [27], [28].

To perform alignment, the significand of the operand with the smallest value is right shifted by the exponent difference [26].

In standard floating point, the bits that cannot fit within the space of the standard floating-point format are used to determine the guard bit, the rounding bit, and the sticky bit.

In BFP, the bits that cannot fit within the space of the BFP format are used to calculate the accumulated rounding error field N.

The bits that cannot fit within the space of the BFP format due to alignment shift are retained in the R_PN field and X_PN field of the post normalization result configuration of Figure 4. As in standard floating-point format, if alignment shifts one or more bits out of the range of the arithmetic unit, the sticky bit is set to one.

3.4. Dominant Bound

The results of BFP binary functions (functions with two operands) retain only the number of significant bits as the aligned operand with the least number of significant bits. For BFP this means the result having the larger number of defective bits.

For binary functions the dominant bound is selected from the larger of the largest operand bound or the adjusted (aligned) bound of the smallest operand. For add (and subtract) operations, the binary point of the smaller operand must be aligned by the exponent difference [26]. The adjusted bound of the smallest operand is derived by subtracting the exponent difference from the smallest operand bound defective bits and shifting the significand of the smallest operand to the right by the exponent difference. This shift will reduce the number of defective bits in the significand of the operand with the smaller value by the exponent difference, perhaps even to zero.

The resulting bound is obtained by accounting for the changes to the dominant bound by the effects of normalization and the accumulation of rounding error. (See Appendix for more details.)

3.5. Normalization and Cancellation

Floating-point results must be normalized to align the binary point to values between 1.0 and 2.0 [28]. The result of a floating-point operation may not meet this requirement and, therefore, may require that the result be “normalized” by shifting right or left to meet this requirement [27]. The exponent and the associated number of defective bits must be adjusted by the amount of this shift. Since the most significant bit is always one when the normalized value is between 1.0 and 2.0, it need not be stored. It is known as the “hidden bit.”

Figure 4 illustrates the format of the post normalization result in which H_PN is the hidden bit field, T_PN is the resulting normalized significand (which is placed in the T field of the standard floating result of Figure 2), R_PN is the most significant bits of the excess bits and is the resulting rounding bits field (which is added to the accumulated rounding error field N, of Figure 3), and X_PN is the extended rounding error. X_PN serves as the source for the BFP “sticky bit,” as used in standard floating point.

Figure 4: Post normalization result configuration

Normalizing by left shifting shifts information into the least significant bits, possibly adding to the unknown bits that already exist. In BFP this must be added to the defective bits unless the result is known to be “exact.” Exactness is identified by BFP as having zero defective bits (e.g. referring to Figure 3, when the defective bits field D of the dominant bound is equal to zero.)

3.6. Zero Detection

The number of remaining significant bits is the difference between number of bits available in the representation (t+1) minus the number of defective bits D. The number of bits to be shifted to normalize is the number of leading zeros of the result. If all of the significant bits are zero, the resulting value must be zero.

BFP detects this condition and sets all fields of the BFP result to zero.

3.7. Accumulation of Rounding Error and Contribution to Defective Bits

Referring to Figures 2, 3, and 4, the accumulated rounding error N is computed by adding the resulting rounding bits R_PN of Figure 4, to the accumulated rounding error N of Figure 3, contributing a fraction of an ulp. If the extended rounding error X_PN of Figure 4, is not zero, an additional one is added to the accumulated rounding error N of Figure 3, functioning as a sticky bit. The carries out of the rounding bits field R of Figure 3, add to the rounding error count C of Figure 3. The rounding error count is the accumulated rounding error in ulps.

The rounding error count C cannot, however, contribute directly to the value of the defective bits field D because of the difference of scaling, linear versus exponential. For example, when there are 2 defective bits, there must be at least 4 accumulated rounding errors to advance the defective bits to 3, and 8 to advance to 4, etc. In other words, when the logarithm of the rounding error count field C is equal to the defective bits field D, the value of the defective bits is increased by one.

3.8. Resulting Range

The BFP range relative to zero is defined by a lower bound (3) and an upper bound (4), as follows:

                             (-1)^S · ((T+2^t)/2^t) · 2^E-O                                               (3)

                         (-1)^S · ((T+2^t+2^D-1)/2^t) · 2^E-O                           (4)

The infinitely accurate real value represented by a BFP value is within this range. This is the same as in standard floating point except that the term 2^D-1 provides the upper bound where the value of the defective bits field D is the number of bits that are no longer significant.

4. BFP Solutions to Standard Floating-Point Problems

Not only does BFP deliver all of the advantages of standard floating point, but it also delivers solutions to problems inherent in standard floating point.

4.1. Exact Equality Comparison and True Detection of Zero

Standard floating point requires additional code to be written to decide as to whether a comparison result is within error limits. BFP inherently provides this equality comparison.

Standard floating point cannot provide true zero detection as BFP does, which is demonstrated in the square root test of Section 8 below.

4.2. Number of Significant Bits

Standard floating point has no means to indicate the number of bits that are significant, but BFP identifies and indicates the number of significant bits. Further, BFP allows programmatic specification of the required number of significant bits. When the required number of significant bits are not available, BFP provides notification.

4.3. Mission Critical Computing

In some computing applications, such as mission-critical computing, computations need to be extremely accurate. But standard floating point cannot determine any accuracy loss. In contrast, BFP provides calculations – in real time – that can be depended upon to have the required number of significant bits.

4.4. Modeling and Simulation

Computational modeling and simulation, supported by constantly improving processor performance, often requires solving large, complex problems during which error may accumulate. This error, though not identified in standard floating point, is reported when the BFP extension is utilized.

4.5. Unstable Matrices

In numerical computation “stability” implies that small changes in the data translate into small changes in the result. Significant problems arise when small changes in the data, such as rounding error, create substantial error in the results. This occurs in matrix calculations, for instance, when solving simultaneous linear equations, when the roots may be similar or equal. BFP is used in this work to determine when a matrix is invertible, while assuring that the requirement for accuracy is met.

5. Standard Floating-Point Error Mitigation

5.1. Error Analysis Versus Direct Testing

Algorithmic error analysis can be used to identify error that occurs when using standard floating point. Though it is costly, it is commonly used for complex computing in critical systems, the failure of which may have severe consequences. In contrast, BFP directly, and in real time, tests calculation results, thus removing the need for costly error analysis.

5.2. Software Testing of Floating Point

Standard floating point problem in that it has no indication of accuracy errors is challenging to detect, diagnose, and repair.. BFP detects accuracy errors in real time, thus providing a response to the plea of “Desperately Needed Remedies for the Undebuggability of Large Floating-Point Computations in Science and Engineering” [19].

5.3. Stress Testing of Floating-Point Software

Stress testing may also be used to determine error that accumulates when using standard floating point. In general, stress testing is a form of intense testing used to establish failure points or useful operating limits of a given system. It involves testing beyond normal operational capability, often to a breaking point, in order to observe the performance limits.

Stress testing, as commonly applied to software, determines data value limits (boundary value testing) or performance (memory required, response time, latency, throughput, and time required to complete the calculation). Chan describes software stress testing as a method for accelerating software defect discovery and determining failure root cause and assisting problem diagnosis [29]. However, determining the accuracy of floating-point calculations or diagnosing accuracy failures in floating-point calculations, in intermediate results, or in final results is problematic using standard floating point [19]. In fact, floating-point errors are invisible in standard floating point, as there is nothing within the IEEE Standard that describes or limits floating-point error.

BFP provides a new and unique method of stress testing. Stress testing floating-point application software using BFP determines the accuracy at any point in a calculation, or even at the point of failure of a given computation, by executing computations with successively higher values of required significant bits and analyzing failure points. This reduces the cost of diagnosis and repair of floating-point calculation failures [19].

5.4. Other Mitigation Techniques

Other real-time techniques attempt to mitigate error, but only do so by increasing the overhead. Some of these techniques have the goal of computing results within error bounds, such as interval arithmetic [30] and real-time statistical analysis [31], [32]. But these require two floating point operations and require the storage of two floating point values and, thereby, increase the needed time and memory.

Parallel computation with higher precision standard floating point [33] can also be used to mitigate error. In addition to substantially increasing overhead, only the probability of error is reduced. There is no indication of that amount of error, whereas BFP identifies the remaining significant bits.

6. Software Model Solutions Using BFP

This work presents a software model of the BFP hardware system as described in detail in [25], [26]. When using standard floating point, there are certain problem areas that are prone to floating-point error. This work provides results from computations using BFP compared to computations using standard floating point in three of these well-known floating-point problem areas.

6.1. 80-Bit BFP

The BFP software model used in the following examples is configured by the field sizes of the BFP data structure, which is an 80-bit BFP configuration. The sign, exponent, and significand fields of the BFP format are identical to the corresponding fields in the standard 64-bit floating-point format. This permits conversion from 64-bit standard floating point to 80-bit BFP with a single instruction that stores the standard floating-point value directly into the corresponding fields of the BFP structure.

The BFP model contains the basic operations BFPAdd, BFPSub, BFPMult, BFPDiv, and BFPSqrt.

The following experiments were conducted on an ACER Aspire PC with an Intel Core i5 7th gen processor, using GNU Compiler Collection (GCC) version “(i686-posix-dwarf-rev0, Built by MinGW-W64 project) 8.1.0” [34].

6.2. Significant digits

In computers, binary floating-point calculations are performed with a collection of binary bits. But to be useful in the scientific and engineering world, outputs from, and inputs to, the human interface must be in decimal digits. In other words, the calculated results must be displayed in decimal digits, and decimal information must be suppled to the processing unit. However, there is no direct mapping between binary floating-point values and the decimal representation of these values [35]. The fixed number of binary bits available in the double-precision (64-bit) floating-point format can represent a range of decimal values with as few as 15 or as many as 17 decimal digits [13].

External representations of BFP results, as shown below in Tables 1-14, are constrained to the actual number of significant decimal digits of the real number represented; i. e. only the digits having significance are displayed. This contrasts with standard floating point in which decimal digits of unknown significance are displayed, which results, at times, in the display of multiple incorrect digits (digits without significance). The display of these insiginifcant decimal digits obtained by the use of standard floating point is shown in the Tables 1-14 below.

6.3. Significant Bits

The number of significant bits is identified by the binary BFP representation of an infinitely accurate real value. The number of significant bits, SB_, is calculated as the total bits available, p, minus the number of defective bits, D, as shown in (5)

                                      SB = p – D                                                                   (5)

where p = t + 1.

BFP provides a default value for the required number of significant bits. Alternatively, a special command can specify the required number of significant bits. Whether the BFP default value is applied or the commanded value is applied, the required number of significant bits may not be generated in a calculation. In this case, a special not-a-number code “qNaN.sig” is produced, which is visible when externally displayed.

6.4. Modeling Overview

The following demonstrations address three problems presented above, which are floating-point error diagnosis, true detection of zero, and unstable matrices. The first utilizes Kahan’s thin triangle problem where the area of a thin triangle is diminished until a specified number of significant bits is not met. The second is an illustration of zero detection by BFP, which uses an expression that mathematically evaluates to zero; however, standard floating point does not generate zero. The third demonstration solves for a matrix determinate identifying that the matrix is unstable.

7. Modeling Stress Testing – The Heron and Kahan Thin Triangle Problems

7.1. The Thin Triangle

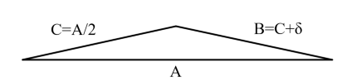
Knowing the length of three sides of a triangle (Figure 5) is sufficient to determine the area of the triangle without knowledge of the angles [36]. Work from early in the first millenium CE, attributed to Heron, produced an area formula that has become known as “Heron’s Formula.” In 2014, Kahan produced an improved area formula.

 Figure 5: Thin Triangle

The thin triangle problem considered here is from “Miscalculating area and angles of a needle-like triangle.” [37]. This work extends the 1976 work of Pat H. Sterbenz who suggested a method to make Heron’s Formula more accurate [38]. In that work Sterbenz states:

“However, we can produce a good solution for the problem if we assume that A, B, and C are given exactly as numbers in (floating point).” (Emphasis added)

However, when using standard floating point, A, B, or C may not be exact. And standard floating point does not provide any indication that A or B or C is exact. But BFP establishes exactness, where a representation is exact if and only if the dominate bound defective bits field D is zero; this indicates that there are no insignificant bits in the representation. Using the BFP extension of standard floating point, this work shows when A or B or C is not exact.

In the tests shown below, values were chosen to reflect a thin triangle in which one side of the triangle, side C, is one half the length of the base A and in which the other side of the triangle, side B, is equal to the length of side C plus delta (δ). By injecting 1 ulp error in any one of the values, the values are no longer exact. In the tests below, a 1 ulp error was injected into A. And the injection of this small error into only one of the values causes the equation to produce a result that does not meet the required significant digits for a specified δ and a required number of significant digits.

In the examples, the value for A was increased by 1 ulp of error by adding one to the significand. For the equivalent result, in BFP the defective bits D value was set to 1 indicating that there is 1 ulp of error.

In the tests below, the area of the triangle is influenced by the value for δ. When δ is zero, the area of the triangle is zero.

Tables 1-14 present stress test results for Heron’s and Kahan’s area algorithms for thin triangles, A=2.0 + 1 binary ulp, C=1.0 and B= C+ δ, with decreasing values of δ and increasing values of the required number of significant digits. Results are presented for 64-bit (double precision) and 128-bit (quad precision) standard floating point and 80-bit BFP. Each test is conducted until the particular algorithm fails to provide the required number of signicant digits, at which point BFP displays “qNaN.sig.” Tables 6, 7, and 14 present results for when δ is sufficiently small that the areas are significantly zero as detected by BFP.

The second row of each table (excluding Tables 6, 7, and 14) shows the results for the required significant digits immediately prior to the failure point (one decimal ulp prior to not meeting the required number of significant digits as determined by the BFP calculations). The third row of each table lists the results at the failure point, where BFP shows that the required number of significant digits has not been met.

The BFP output conversion routine only displays those digits known to be correct to + or – 1 in the last digit presented.

7.2. Heron’s Formula

Heron’s formula is shown in (6):

Area = SQRT(S(S-A)(S-B)(S-C))                                      (6)

where S= (A + B + C)/2.

The Heron stress test determines, for a specific triangle, where (6) fails for a specific number of required significant digits. For each of the triangles in the test reported in Tables 1-7 (using a given value of δ for each triangle), the required number of significant digits is increased until BFP indicates by qNaN.sig that (6) cannot be solved for the specific triangle while achieving the specified number of required significant digits.

In Tables 1-7 standard floating-point results for Heron’s area algorithms for each required number of significant digits, 14, 13, …7 are benchmarked against BFP results. Heron’s area formula (6) was solved for successively smaller values of δ until the BFP calculation indicated (by qNaN.sig) that the required number of significant digits was not met.

Table 3, for example, shows that for δ =0.0001, a 10-digit result is obtained successfully, but requiring 11 significant digits fails.

7.3. Kahan’s Formula

In 2014, Professor William M. Kahan demonstrated that the Heron formula yielded inaccurate results when computed with a modern computer using floating point. Kahan contributed (7), which provides more accurate results for the area of thin triangles than (6) [37].

Area = SQRT(A+(B+C))(C-(A-B))(C+(A-B))(A+(B-C)))/4     (7)

      where A ≥ B ≥ C

The stress tests of Tables 8-14 determine, for a specific triangle, where (7) fails for a specific number of required significant digits. For each of the triangles (using a given value of δ for each triangle), the required number of significant digits is increased until BFP indicates by a qNaN.sig that (7) cannot be solved for the specific triangle while achieving the specified number of required significant digits.

Tables 8-14 list the standard floating-point computations benchmarked against the BFP computations of (7) for thin triangles for the required significant digits, which present results similar to the Heron solutions of (6).

For example, Table 10 shows that for δ =0.0001, an 11-digit result is obtained successfully, but requiring 12 significant digits fails. This demonstrates that the Kahan algorithm (7) provides more significant digits than does the Heron algorithm (6) as shown in Table 3 (described above).

Double precision (64-bit) floating point can represent up to 15 significant decimal digits. BFP computations with inexact values shows that neither (6) or (7) is capable of producing a thin triangle area result accurate to 15 significant digits, as shown Tables 1-14.

7.4. Stress Tests Summary

In summary, Tables 1-14 show that BFP identifies the failure point at the largest number of significant digits for a given δ that does not meet the required number of significant digits. BFP identifies the smallest δ that retains the required number of significant bits. And BFP identifies when the area of a thin triangle is significantly zero when standard floating point does not.

Table 1: Stress Test One of Heron’s Formula for Area of Thin Triangle

For δ =0.01, A=2.0 + 1 ulp, B=1.01, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
11	0.10012367040315583000000	0.10012367040315691503050	0.100123670403
12	0.10012367040315583000000	0.10012367040315691503050	0.100123670403
13	0.10012367040315583000000	0.10012367040315691503050	qNaN.sig
14	0.10012367040315583000000	0.10012367040315691503050	qNaN.sig

Table 2: Stress Test Two of Heron’s Formula for Area of Thin Triangle

For δ = 0.001, A=2.0 + 1 ulp, B=1.001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
10	0.03162672524840082900000	0.03162672524839554108590	0.031626725248
11	0.03162672524840082900000	0.03162672524839554108590	0.031626725248
12	0.03162672524840082900000	0.03162672524839554108590	qNaN.sig
13	0.03162672524840082900000	0.03162672524839554108590	qNaN.sig

Table 3: Stress Test Three of Heron’s Formula for Area of Thin Triangle

For δ = 0.0001, A=2.0 + 1 ulp, B=1.0001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
9	0.01000012498670694800000	0.01000012498671860350864	0.01000012498
10	0.01000012498670694800000	0.01000012498671860350864	0.01000012498
11	0.01000012498670694800000	0.01000012498671860350864	qNaN.sig
12	0.01000012498670694800000	0.01000012498671860350864	qNaN.sig

Table 4: Stress Test Four of Heron’s Formula for Area of Thin Triangle

For δ = 0.00001, A=2.0 + 1 ulp, B=1.00001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
8	0.00316228161305403100000	0.00316228161297345549598	0.00316228161
9	0.00316228161305403100000	0.00316228161297345549598	0.00316228161
10	0.00316228161305403100000	0.00316228161297345549598	qNaN.sig
11	0.00316228161305403100000	0.00316228161297345549598	qNaN.sig

Table 5: Stress Test Five of Heron’s Formula for Area of Thin Triangle

For δ = 0.000001, A=2.0 + 1 ulp, B=1.000001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
7	0.00100000012506975620000	0.00100000012499986718749	0.0010000001
8	0.00100000012506975620000	0.00100000012499986718749	0.0010000001
9	0.00100000012506975620000	0.00100000012499986718749	qNaN.sig
10	0.00100000012506975620000	0.00100000012499986718749	qNaN.sig

Table 6: Stress Test Six of Heron’s Formula for Area of Thin Triangle

For δ=0.0000001, A=2.0 + 1 ulp, B=1.0000001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
7	0.00031622777041308547000	0.00031622776996968458842	0.0
8	0.00031622777041308547000	0.00031622776996968458842	0.0
9	0.00031622777041308547000	0.00031622776996968458842	0.0
10	0.00031622777041308547000	0.00031622776996968458842	0.0

Table 7: Stress Test Seven of Heron’s Formula for Area of Thin Triangle

For δ=0.00000001, A=2.0 + 1 ulp, B=1.00000001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
1	0.00009999999982112643300	0.00010000000012499999867	0.0
2	0.00009999999982112643300	0.00010000000012499999867	0.0
3	0.00009999999982112643300	0.00010000000012499999867	0.0
4	0.00009999999982112643300	0.00010000000012499999867	0.0
5	0.00009999999982112643300	0.00010000000012499999867	0.0
6	0.00009999999982112643300	0.00010000000012499999867	0.0
7	0.00009999999982112643300	0.00010000000012499999867	0.0
8	0.00009999999982112643300	0.00010000000012499999867	0.0

Table 8: Stress Test One of Kahan’s Formula for Area of Thin Triangle

For δ=0.01, A=2.0 + 1 ulp, B=1.01, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
12	0.10012367040315807000000	0.10012367040315691503050	0.1001236704031
13	0.10012367040315807000000	0.10012367040315691503050	0.1001236704031
14	0.10012367040315807000000	0.10012367040315691503050	qNaN.sig
15	0.10012367040315807000000	0.10012367040315691503050	qNaN.sig

Table 9: Stress Test Two of Kahan’s Formula for Area of Thin Triangle

For δ=0.001, A=2.0 + 1 ulp, B=1.001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
11	0.03162672524839731100000	0.03162672524839554108590	0.0316267252483
12	0.03162672524839731100000	0.03162672524839554108590	0.0316267252483
13	0.03162672524839731100000	0.03162672524839554108590	qNaN.sig
14	0.03162672524839731100000	0.03162672524839554108590	qNaN.sig

Table 10: Stress Test Three of Kahan’s Formula for Area of Thin Triangle

For δ=0.0001, A=2.0 + 1 ulp, B=1.0001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
10	0.01000012498672915600000	0.01000012498671860350864	0.010000124986
11	0.01000012498672915600000	0.01000012498671860350864	0.010000124986
12	0.01000012498672915600000	0.01000012498671860350864	qNaN.sig
13	0.01000012498672915600000	0.01000012498671860350864	qNaN.sig

Table 11: Stress Test Four of Kahan’s Formula for Area of Thin Triangle

For δ=0.00001, A=2.0 + 1 ulp, B=1.00001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
9	0.00316228161301892240000	0.00316228161297345549598	0.003162281612
10	0.00316228161301892240000	0.00316228161297345549598	0.003162281612
11	0.00316228161301892240000	0.00316228161297345549598	qNaN.sig
12	0.00316228161301892240000	0.00316228161297345549598	qNaN.sig

Table 12: Stress Test Five of Kahan’s Formula for Area of Thin Triangle

For δ=0.000001, A=2.0 + 1 ulp, B=1.000001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
8	0.00100000012506975620000	0.00100000012499986718749	0.00100000012
9	0.00100000012506975620000	0.00100000012499986718749	0.00100000012
10	0.00100000012506975620000	0.00100000012499986718749	qNaN.sig
11	0.00100000012506975620000	0.00100000012499986718749	qNaN.sig

Table 13: Stress Test Six of Kahan’s Formula for Area of Thin Triangle

For δ=0.0000001, A=2.0 + 1 ulp, B=1.0000001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
7	0.00031622777041308547000	0.00031622776996968458842	0.00031622777
8	0.00031622777041308547000	0.00031622776996968458842	0.00031622777
9	0.00031622777041308547000	0.00031622776996968458842	qNaN.sig
10	0.00031622777041308547000	0.00031622776996968458842	qNaN.sig

Table 14: Stress Test Seven of Kahan’s Formula for Area of Thin Triangle

For δ=0.00000001, A=2.0 + 1 ulp, B=1.00000001, C=1.0
Significant Digits Required	Area Using Double Precision	Area Using Quad Precision	Area Using BFP
1	0.00010000000093134947000	0.00010000000012499999867	0.0
2	0.00010000000093134947000	0.00010000000012499999867	0.0
3	0.00010000000093134947000	0.00010000000012499999867	0.0
4	0.00010000000093134947000	0.00010000000012499999867	0.0
5	0.00010000000093134947000	0.00010000000012499999867	0.0
6	0.00010000000093134947000	0.00010000000012499999867	0.0
7	0.00010000000093134947000	0.00010000000012499999867	0.0
8	0.00010000000093134947000	0.00010000000012499999867	0.0

Table 15: Zero Detection – Standard Floating point (SFP) vs. Bounded floating point (BFP)

Function	GCC 64-bit Floating Point	GCC 128-bit Floating Point	80-bit BFP
sqrt(pi*pi)-pi	2.27682456e-017	-1.2246467991e-16	0.0
sqrt(pi)*sqrt(pi)-pi	-1.96457434e-016	-1.2246467991e-16	0.0

8. Modeling Square Root Problem – Zero Detection

Zero detection is important because standard floating point does not always accurately identify when the result of a subtraction is a zero.

In standard floating point, even a one ulp error may cause a significantly erroneous result. Standard floating point does not reliably provide zero as a result when subtracting significantly equal values. For example, when subtracting two values representing infinitely accurate numbers, if a one ulp error has been introduced into one of the floating-point values, the floating-point subtraction result will not be zero. Detection of this condition requires external testing of the comparison result. In contrast, BFP provides zero detection by detecting whether the significant bits of a comparison result are equal to zero. Using the software model, we examine a simple expression that should evaluate exactly to zero. Standard floating point does not solve this simple calculation correctly but BFP does.

Table 15 demonstrates BFP’s zero detection capability as compared to the results of calculating the same expression (that mathematically equates to zero) in standard double capacity precision (64-bit) and quad capacity precision (128-bit) floating point [13].

9. Modeling Unstable Matrices

BFP can be used to determine if a determinant is significantly zero. Thus, BFP can be used to identify an unstable matrix, as shown in Table 16.

Common matrix expressions require the application of the inverse of a matrix. The inverse of matrix A is denoted as A^-1. The inverse of a matrix may be calculated only if the determinant of that matrix (|A|) is not equal to zero. Thus, it is important to know if the determinant is zero. But standard floating point may not properly yield zero because of floating-point error. To address this problem, many supplementary methods have been developed to determine if a matrix is invertible. Because these supplementary methods are otherwise unnecessary for the computation of the equation, they add unnecessary overhead in terms of computation time and memory space. Moreover, requiring the addition of code to enable these methods makes the code more complex and more prone to error.

However, if the software is written in BFP, this calculation is made directly during the solving of the equation. In solving the linear equation, Ax=b, the inverse of the A matrix is multiplied by the b vector. This produces a new vector, which is the solution to the equation. When BFP calculates the determinant, it identifies – during the calculation – if the determinant is zero. Thus, BFP efficiently identifies whether the equation can be solved, without requiring additional code as the supplementary methods do.

Table 16: Comparison of Determinant Calculation of an Unstable Matrix

Matrix	Standard 64-bit Floating Point	Standard 128-bit Floating Point	80-bit BFP
cavity01	4.9359402474e-045	4.9359402474e-45	0.0

Table 16 presents the comparison of the calculations of the determinant of an unstable matrix using 64-bit standard floating point, 128-bit standard floating point, and 80-bit BFP. The determinant is calculated using the upper triangle method, Gaussian Elimination [39].

The matrix selected, cavity01, is from the Matrix Market [40]. It was located searching the Matrix Market with the term “unstable.”^[1] The matrix selected is a sparce 317×317 matrix with 7,327 entries.

Table 16 shows that both 64-bit and 128-bit standard floating point provide a non-zero value for the determinant, where BFP does return zero, because at some point in the calculation the significant bits were all zero. Thus, using BFP identifies the problem efficiently during the calculation. Using standard floating point requires the incorporation of one of the supplementary methods into the code to prevent division by zero. Consequently, BFP directly determines if a matrix is not invertible.

Moreover, when the matrix is properly invertible, using BFP provides the accuracy of the result. The use of BFP identifies how many significant digits are in the result. In an example, a requirement is that the accuracy must be more than three significant digits. Even if the matrix is valid, there may be less than three significant digits remaining in the results, which BFP identifies.

Consequently, when BFP is used during matrix calculations, it not only determines if the matrix is invertible, but it also assures that the requirement for accuracy is met.

10. Summary

BFP adds a field to the standard floating point format in which error may be accumulated. The upper bound of that error is stored as the logarithm of that bound.

BFP makes floating-point error quantifiable and visible. It allows exact equality comparison. It provides notification when insufficient significant digits have been retained during floating-point computations. When implemented in hardware it affords real-time fail-safe calculations for mission critical applications.

Though designed for hardware implementation, a software model emulating the BFP functions was used in this paper. The BFP software model has been applied to three problems as follows:  the failure of standard floating point to exactly detect zero in the presence of floating-point error, the failure of standard floating point to identify the number of significant digits (if any) of a result, and the lack of the ability to diagnose standard floating point accuracy errors.

This paper shows that BFP solves these problems by calculating and propagating the number of significant bits as described by the BFP algorithms presented. Three examples have been used, which are a precision stress test, true floating point zero detection, and detection of an unstable matrix.

The precision stress test of an algorithm increases the required precision for that algorithm under specific parameters until that required precision cannot be met. The algorithm parameters may be adjusted as well to determine the operational envelope for that algorithm for a given required precision.

Standard floating point does not return precisely zero when significantly similar, yet different numbers are subtracted. An example is provided where an expression clearly evaluates to zero, yet standard floating point does not return zero but BFP does return zero. Using this property of BFP, we evaluate the determinant of a matrix known to be unstable and note that BFP evaluates the determinant as zero.

Properly implemented in hardware, BFP will reduce the time and cost of the development of scientific and engineer calculation software and will provide run-time detection of floating-point error. This hardware implementation has begun using Verilog HDL.

11. Appendix – Post Revision Result Format

11.1. Bound Description

Definitions are from, or amended from, [26].

An 80-bit model was chosen to allow for using 64-bit standard floating point and a 16-bit bound field B. Table 17 specifies subfield widths for a 80-bit BFP model.

Table 17: 80-Bit Model Field Widths

Subfield Widths

#define r 4

#define d 6

#define c d

#define n (c+r)

#define b (d+n)

11.2. Notation Used

Each algorithm is preceded by a list of definitions of the variables (for example, Op1Exp) used in the algorithm. Each definition (for example, first operand exponent) is followed by an alphanumeric identifier (for example, 51A). That identifier refers to the patent reference number of [26]. Further, a letter (E, B, D, N, R, or C) may follow the identifier definition (for example, first operand exponent E). This refers to a specific portion of the data format identified in Figures 1 and 3.

11.3. Dominant Bound

The dominant bound (DominantBound) is the larger of the largest operand bound (HiOpBound) and the adjusted bound of the smallest operand (AdjBoundLoOp). This is the bound of the operand with the least number of significant bits.

The dominant bound (DominantBound) is determined from the first operand bound (Op1Bound), the second operand bound (Op2Bound), the exponent difference (ExpDelt), and the condition (Op2Larger) in which the magnitude of the second operand (Op2) is greater than the magnitude of the first operand (Op2).

11.4.           Finding the Exponent Difference

The exponent difference (ExpDelt) is the magnitude of the difference between the first operand exponent (Op1Exp) and the second operand exponent (Op2Exp).

The exponent difference (ExpDelt) is determined from the first operand (Op1Exp) and the second operand (Op2Exp), as in Algorithm 1.

Algorithm 1: Finding Exponent Difference
Result: Exponent Difference Op1 := first operand, 201; Op2 := second operand, 202; Op1Exp := first operand exponent E, 51A; Op2Exp := second operand exponent E, 51B; ExpDelt := exponent difference, 321; Op2Larger := second operand > first operand, 302; SmallerExp := smallest exponent E, 51E; LargerExp := largest exponent E, 51D;
begin
	Op2Larger := |Op2| > |Op1| if Op2Larger then
		LargerExp := Op2Exp; SmallerExp := Op1Exp;
	else
			LargerExp := Op1Exp; SmallerExp := Op2Exp;
	end ExpDelt := LargerExp – SmallerExp
end

11.5. Finding the Dominant Bound

As shown in Algorithm 2, the dominant bound (DomBound) is derived from the first operand bound B (Op1Bound), the second operand bound B (Op2Bound), the exponent difference (ExpDelt), and the second operand larger (Op2Larger).

Algorithm 2: Finding the Dominant Bound

Result: Dominant Bound

Op1Bound := the first operand bound B, 52A; Op2Bound := the second operand bound B, 52B; LoOpBound := smallest operand bound B, 52D; HiOpBound := largest operand bound B, 52E; LoOpBoundeBadBits := smallest operand bound defective bits D, 54A; AdjLoOpBoundBadBits := adjusted smallest operand bound defective bits D, 54B; ClampedBadBits := clamped defective bits D, 54G; LoOpBoundAccRE := smallest operand bound accumulated rounding error N, 55A; AdjBoundLoOp := adjusted bound B of the smallest operand, 52F; HiOpBoundLargest := largest operand bound B is greatest, 431; DominantBound := dominant bound, the bound of the operand with the least number of significant bits after alignment, 52H;

Begin

Op2Larger := |Op2| > |Op1| if Op2Larger then

LoOpBound := Op1Bound;

HiOpBound := Op2Bound;

else

LoOpBound := Op2Bound; HiOpBound := Op1Bound

end

AdjLoOpBoundBadBits := LoOpBoundeBadBits – ExpDelt if AdjLoOpBoundBadBits < 0  then

AdjLoOpBoundBadBits := 0;

end

AdjLoOpBoundBadBitsE           := ClampedBadBits |&| LoOpBoundAccRE; HiOpBoundLargest := HiOpBound > AdjBoundLoOp; if HiOpBoundLargest  then

DominantBound := HiOpBound;

else

DominantBound := AdjBoundLoOp;

end

end

Where ‘|&|’ is the field concatenation operator.

11.6. Result Bound Calculation

The resulting bound of a calculation is determined by one of two mutually exclusive calculations, the bound calculation algorithm of Algorithm 3 or the bound rounding algorithm of Algorithm 4. When there is a subtract operation and the operands are sufficiently similar, the intermediate result has leading zeros (is not normalized). Under this condition the bound calculation algorithm determines the bound of the result. Otherwise, the bound rounding algorithm determines the result.

In any case, exact operands produce an exact result [6].

Operations other than add or subtract return the dominant bound.

11.7. Bound Cancellation Algorithm

The result bound B (ResultBound) is determined from either the cancellation adjusted bound B  (AdjCaryBound) or the carry adjusted bound B (AdjCaryBound). The result bound B requires the dominant bound (DominantBound), the significand capacity (SigCap), and the number of leading zeros (LeadZeros).

Algorithm 3 accounts for compensating errors.

Algorithm 3: Bound Cancellation
Result: Result Bound from Cancellation
Cancellation := cancellation detected, 620; DomBadBits := dominant bound defective bits D, 54C; LeadZeros := number of leading zeros prior to normalization, 711; SigCap := significand capacity, the number of bits in the significand (t+1), includes hidden bit H, 805; AdjBadBits := adjusted defective bits D, 54D; MaxedBadBits := max defective bits detected, 617; ResultBadBits := resulting defective bits D, 54H; DomAccRE := dominant bound accumulated rounding error N, 55B; CancAdjBound := cancellation adjusted bound B, 52J; ResultBound := result bound B, 52C;
if Cancellation then
	AdjBadBits := DomBadBits + LeadZeros; MaxedBadBits := SigCap <= AdjBadBits;
	if MaxedBadBits then
		ResultBadBits := SigCap;
	else
			ResultBadBits := AdjBadBits;
	end CancAdjBound := ResultBadBits |&| DomAccRE ResultBound := CancAdjBound
end

11.8. Bound Rounding Algorithm

The adjusted value of R is added to the dominate bound to provide the adjusted bound.  When the logarithm of C is equal to D, 1 is added to D and C is set to zero in the resulting bound.

There is an externally applied limit, Required Significant Bits, which is defaulted and programmable. On external representation, when the available significant bits value (t+1-D) is less than or equal to the Required Significant Bits, “sNaN.sig” is displayed. A special command is provided that tests for this condition of an individual BFP value to produce a signaling exception sNaN.sig, which can be detected and serviced like any other hardware exception such as sqrt(-1) or x/0.

When there are significant bits and they are all zero, the value represented is truly zero and the resulting value is set to all zeros. (Zero has no significant bits/digits). This is true zero detection unavailable with standard floating point nor Interval Arithmetic (IA).

Algorithm 4: Bound Rounding
Result: Result Bound from Rounding
NormalizedRE := normalized rounding error R, 57A; StickyBit := significand excess, logical OR of all bits of the normalized extension X, 741; RESum   := rounding error sum B, 52K; RESumCount := updated accumulated rounding error extension count C from the rounding error sum B, 54K; RESumFraction := updated accumulated rounding error rounding bits R from the rounding error sum B, 57B; Log2RESum := rounding count logarithm, 61; LogOvrflw := log count overflow, 651; AdjBadBits := incremented defective bits D, 54E; MaxBadBits := max defective bits, 662; LimAdjBadBits := clamped incremented defective bits D, 54J; AdjBadBitsBnd := defective bits adjusted bound B, 52L; AdjCaryBound := carry adjusted bound B, 52M;
if not Cancellation then
	RESum := DominantBound + NormalizedRE + StickyBit; Log2RESum := Log2(RESumCount); CntOvrflw := Log2RESum >= DomBadBits; AdjBadBits := LogOvrflw + DomBadBits; MaxBadBits := AdjBadBits >= SigCap;
	if MaxBadBits then
		LimAdjBadBits := SigCap;
	else
			LimAdjBadBits := AdjBadBits;
	End AdjBadBitsBnd := LimAdjBadBits |&| RESumFraction
	if LogOvrflw then
		AdjCaryBound := AdjBadBitsBnd;
	else
			AdjCaryBound := RESum;
	End ResultBound := AdjCaryBound
end

Conflict of Interest

The authors whose names are listed immediately below report the following details of affiliation or involvement in an organization or entity (True North Floating Point) with a financial or non-financial interest in the subject matter or materials discussed in this manuscript.

Alan A. Jorgensen; Connie R. Masters, Andrew C. Masters

Acknowledgment

We would like to acknowledge Professor Emeritus William Kahan for his personal informative discussion of the prior efforts to encapsulate floating point error.

[1] This particular matrix is available in compressed form from ftp://math.nist.gov/pub/MatrixMarket2/SPARSKIT/drivcav_old/cavity01.mtx.gz, accessed 4 August 2020.

1. A. Jorgensen, A. Masters, R. Guha, “Assurance of accuracy in floating-point calculations – a software model study,” 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 471-475, 2019, DOI: 10.1109/CSCI49370.2019.00091.
2. J. Muller, B. N., F. de Dinechin, C.-P. Jeannerod, V. Lefevre, G. Melquiond, N. Revol, D. Stehle, S. Torres, Handbook of floating-point arithmetic, Boston: Birkhauser, 2010, DOI 10.1007/978-0-8176-4705-6.
3. T. Haigh, “A. M. Turing Award: William (“Velvel”) Morton Kahan,” Association for Computing Machinery, 1989, https://amturing.acm.org/ award_winners/kahan_1023746.cfm, accessed 24 February 2019.
4. IEEE Standard for Floating-Point Arithmetic, IEEE Std 754-2019, 1-84, 22 July 2019, DOI: 10.1109/ IEEESTD.2019.8766229.
5. ISO/IEC 9899:2018, Information technology – programming languages – C, Geneva, Switzerland: International Organization for Standardization, 2018.
6. A. A. Jorgensen, A. C. Masters, “Exact floating point,” to be published Springer Nature – Book Series: Transactions on Computational Science & Computational Intelligence, Ed, H. Arabnia, ISSN 2569-7072, 2021.
7. D. Goldberg, “What every computer scientist should know about floating-point arithmetic,” ACM Computing Surveys 23.1, 5-48, 1991.
8. G. Cantor, Ueber eine elementare Frage der Mannigfaltig-keitslehre, Jahresbericht der Deutschen Mathematiker-Vereinigung, (1891) 1: 75–78; English translation: W. B. Ewald (ed.) From Immanuel Kant to David Hilbert: a source book in the foundations of mathematics, Oxford University Press, 2, 920–922, ISBN 0-19-850536-1,1996.
9. W. M. Kahan, “A logarithm too clever by half,” 9 August 2004, http://people.eecs.berkeley. edu/~wkahan/ LOG10HAF.TXT, accessed 26 February 2019.
10. S. Lubkin, “Decimal point locations in computing machines,” Mathematical tables and other aids to computation, 3(21), 44-50, 1948, DOI:10.2307/ 2002662, www.jstor.org/stable/2002662, accessed 20 Nov. 2020.
11. M. Frechtling, P. H. Leong, “MCALIB: measuring sensitivity to rounding error with monte carlo programming,” ACM Transactions on Programming Languages and Systems, 37(2), 5, 2015, DOI: 10.1145/2665073.
12. S. Ardalan, “Floating point error analysis of recursive least squares and least mean squares adaptive filters,” IEEE Trans. Circuits Syst., CAS-33, 1192-1208, Dec. 1986, DOI: 10.1109/TCS.1986.1085877.
13. N. J. Higham, Accuracy and stability of numerical algorithms, Second Edition, Philadelphia, PA: SIAM, 2002, DOI 10.1137/1.9780898718027, accessed 6 August 2020.
14. C. Lea, H. Ledin, “A review of the state-of-the-art in gas explosion modelling,” February 2002, UK Health and Safety Laboratories, http://www.hse.gov.uk/research/hsl_pdf/2002/hsl02-02.pdf, accessed 24 March 2019.
15. W. Lai, D. Rubin, E. Krempl, Introduction to Continuum Mechanics, Fourth Edition, Amsterdam, Netherlands, Elsevier, 2009, ISBN 0750685603.
16. Weather Prediciton Center, O. P. Center, N. H. Center, H. F. Center, Unified Surface Analysis Manual, November 21 2013, National Weather Service, https://www.wpc.ncep.noaa.gov/sfc/UASfcManualVersion1.pdf, accessed 24 March 2019.
17. M. Ercegovac, T. Lang, Digital arithmetic, Morgan Kaufmann Publishers, San Francisco, 2004, ISBN-13: 978-1-55860-798-9.
18. N. Higham, Accuracy and stability of numerical algorithms, Philadelphia, PA: SIAM, 1996, ISBN 0-89871-521-0.
19. W. Kahan, “Desperately needed remedies for the undebuggability of large floating-point computations in science and engineering,” IFIP Working Conference on Uncertainty Quantification in Scientific Computing (2011): 2012, https://people.eecs.berkeley.edu/~wkahan/Boulder.pdf, accessed 29 August 2019.
20. D. Weber-Wulff, “Rounding error changes Parliament makeup,” 7 April 1992, Mathematik Institut fuer Informatik Freie Universitaet Berlin Nestorstrasse 8-9, http://mate.uprh.edu/~pnegron/notas4061/ parliament.htm, accessed 25 March 2019.
21. K. Quinn, “Ever had problems rounding off figures? This stock exchange has,” 8 November 1983, p. 37, The Wall Street Journal, https://www5.in.tum.de/~huckle/Vancouv.pdf, accessed 25 March 2019.
22. B. Eha, “Is Knight’s $440 million glitch the costliest computer bug ever?” 9 August 2012, Cable News Network, https://money.cnn.com/2012/08/09/technology/knight-expensive-computer-bug/index.html, accessed 24 February 2019.
23. “Report to the chairman, subcommittee on investigations and oversight, committee on science, space, and technology,” House of Representatives, United States General Accounting Office Washington, D.C. 20548, Information Management and Technology Division, https://www.gao.gov/assets/220/215614.pdf, accessed 25 March 2019.
24. C. Daramy-Loirat, D. Defour, F. de Dinechin, M. Gallet, N. Gast, C. Lauter, J. M. Muller, “CR-LIBM: a correctly rounded elementary function library,” Proc. SPIE 5205, Advanced Signal Processing Algorithms, Architectures, and Implementations XIII, 5205, 458–464, December 2003, DOI: 10.1117/12.50559.
25. A. A. Jorgensen, “Apparatus for calculating and retaining a bound on error during floating point operations and methods thereof,” U. S. Patent 9.817.662, 14 November 2017.
26. A. A. Jorgensen, “Apparatus for calculating and retaining a bound on error during floating point operations and methods thereof,” U. S. Patent 10,540,143, 21, January 2020.
27. D. E. Knuth, The art of computer programming (3rd ed.), II: Seminumerical Algorithms, Addison-Wesley, Boston, Massachusetts, United States, 1997, ISBN: 978-0-201-89684-8.
28. D. Patterson, J. Hennessy, Computer organization and design, the hardware software interface, 5th edition, Waltham, MA: Elsevier, 2014, ISBN: 978-0-12-407726-3.
29. H. A. Chan, “Accelerated stress testing for both hardware and software,” Annual symposium reliability and maintainability, 2004 – RAMS, Los Angeles, CA, IEEE, 346–351, DOI: 10.1109/RAMS.2004.1285473.
30. H. Dawood, Theories of interval arithmetic: mathematical foundations and applications, Saarbrücken, LAP LAMBERT Academic Publishing, ISBN 978-3-8465-0154-2, 2011.
31. G. Masotti, “Floating-point numbers with error estimates,” Computer-Aided Design, 25(9) 524-538, 1993, DOI: 10.1016/0010-4485(93)90069-Z.
32. G. Masotti, 2012, “Floating-point numbers with error estimates (revised),” https://arxiv.org/abs/1201.5975, arXiv:1201.5975v1 accessed 9 January 2021.
33. F. Benz, A. Hildebrandt, S. Hack, “A dynamic program analysis to find floating-point accuracy problems,” ACM SIGPLAN Notices, PLDI 2012, 47(6) 453–462, 2012, DOI: 10.1145/2345156.2254118.
34. GNU, 2020, “GCC, the GNU Compiler Collection,” Free Software Foundation, 2020-11-16, https://gcc.gnu.org/, accessed 8 January 2020.
35. I.B. Goldberg, “27 bits are not enough for 8-digit accuracy,” Comm, ACM 10:2, 105–106, 1967, DOI: 363067.363112.
36. W. Dunham, Journey through genius: the great theorems of mathematics, John Wiley & Sons, Inc., New York, 1990, http://jwilson.coe.uga.edu/ emt725/References/ Dunham.pdf, ISBN-13: 978-0140147391, accessed 5 November 2020.
37. W. Kahan, “Miscalculating area and angles of a needle-like triangle,” 4 September 2014, https://people.eecs. berkely.edu/~wkahan/Triangle.pdf, accessed 14 August 2019.
38. P. H. Sterbenz, Floating-point computation, Prentice-Hall, Inc., Englewood Cliffs, N.J., 1976, ISBN 0-13-322495-3.
39. Å. Björck, Numerical methods in matrix computations, Switzerland, Springer, 2015, ISBN-13: 978-3-319-05089-8.
40. Matrix market, National Institute of Standards and Technology, Computational Sciences Division, 2007, https://math.nist.gov/ MatrixMarket/index.html, accessed 4 August 2020.

(Click Here)

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country