1. Introduction

The development of personality is impossible to imagine without the presence of situations of intellectual tension in the conditions of uncertainty and lack of future activities prediction, opportunities to overcome the problem areas that arise in an education and in real life. The presence of such problem areas and situations of overcoming is directly related to the development of complex knowledge and is an important attribute of qualitative changes in the development of personality [1]-[3]. The methodology and guide for the study of such content of education are the functional characteristics of the state and order parameters in the transitions from chaos to the equilibrium setting of systems of different types (fractal objects and processes [4], Benard’s cells [5], turbulence and lasers, chemical effects of Zhabotinsky-Belousov [6], the theory of dissipative structures, nonlinear dynamics [7], etc.). It is quite significant that in this case, the transition from chaos to order (and vice versa) occur through the universal mechanisms of system complexity. In particular, this can be implemented, for example, through a cascade of doubling bifurcations period, implementing the scenario of P. F. Verhulst in the development of M. Feigenbaum tree [8], or by opening a step-by-step process of moving to the object essence by means of mathematical and computer modeling. Thus, the introduction of the processes of mastering complex knowledge into student’s mathematical education creates the conditions for synergy manifestation in teaching mathematics and, thereby, contributes to the development of intellectual operations of thinking and creative independence of students [9]. Later the similar scientific facts will be called as “modern achievements in science”. So, it should be characterized by applied effect, visual modeling, need for computer and mathematical modeling together the possibility of adapting the basic constructs for school mathematics with synergistic effects for personal development and research activity.

In this article we study one of the “problem areas” of mathematics, which concerns the problem of measuring and understanding the complex concept essence of surface area with intelligent system support. Although for some reason, the essence of this concept remains inaccessible to the student (as the limit of the areas of multi-faceted complexes of tangent planes fragments on the crumbling triangulations of three-dimensional surface of mathematical object). It will be one of the personal trajectories by student’s choice of research activity with intelligent system support. Therefore, it is necessary to be able to stage-by-stage design of cognitive activity of students to develop the manifestations variety of surface area concept as an extension of Vygotsky’ zones of immediate development [10]. Namely, functional parameters and regularities of approximation will be revealed and the areas of layered multi-faceted complexes will be investigated at the limit grinding of regular and irregular triangulations of the lateral surface of Schwartz cylinder [11, 12] by means of computer and mathematical modeling using intelligent system. So, it will be checking the personal opportunities and skills in dynamics and perspectives of student’s research activity. is become the managing instrument for defining of zones of immediate development of the person (create, check, direct, evaluate, create on new stage). Moreover, it will be constructing of Schwartz cylinder’s fractal surface as an indirect synergetic effect of student’s research activities as new mathematical and computer design result. Methods of fractal analysis of technological constructs of Schwartz cylinder research [4, 8, 13, 14] are used.

The development of intelligent learning systems based on artificial intelligence methods is a promising direction in solving complex problems of managing students’ research activity, aimed on increasing their self-organization and self-learning levels with a continuous decrease of teacher participation degree [15]. Intelligent management of learning process in “teacher – computer – student” triad requires a hybrid approach in mathematical and computer modeling. It integrates the functions of expert systems, fuzzy logic, artificial neural networks and genetic algorithms taking into account the research interests and preferences of students [16]. The using of intelligent systems in education (neural networks, fuzzy logic, cellular automata, hybrid expert systems with fuzzy logic, etc.) is actively implemented in tools environments development and software systems for evaluating student’s knowledge and competence [17]-[21]. However, the use of intelligent systems for managing students’ research activities has not been considered in educational practice.

2. Methodology, Methods and Technologies

In modern psychological and pedagogical research, learning is considered as an intellectual process that al lows you to de sign and implement in dividual educational routes de pending on the le vel of subject training and individual psychological characteristics of students in a hybrid learning environment. Hybrid neural network of intelligent system support of student’s research activity is defined by an expert system information support (big data, methods, instruments, etc.) on neural layers depending from student’s research activity results and personal changes in scientific thinking. Thus, it becomes possible to di versify the in dividual trajectories of students’ research activity depending on their interests and scientific experience. The leading role in the analyzed aspect is played by the synergetic approach in education, which determines the design of individual educational environments consisting of educational elements of different levels based on the processes of self-organization of its subjects. The synergetic approach is based on the mechanisms of interdisciplinary interaction in order to create new, more complex structures with a new quality [7, 22, 14, 23, 24]. The possibility of setting and solving the individualization problems of ma thematical education and motivation to study mathematics both at school and at university in modern Russia can be based on the actualization of leading pedagogical technologies (visual modeling and founding person’s experience [10, 25], theory of multi-stages ma thematical and in formational tasks [1, 14, 23], learning complex knowledge [26]) and the adaptation processes of complex knowledge learning (including modern achievements in science) to the development of ma thematical methods (parametrization, se arch of generalized constructs, ma thematical modeling, ets.) by the most accessible for these purposes means, methods and selection. It is necessary to design techniques and methods of re flection and research of technological parameters of generalized construct against the background of the adaptation system and obtaining new results: in our case, the generalized construct of scientific knowledge as an example of in dividual trajectories of student’s realization – the concept of surface area is in directly up dated through computer and ma thematical modeling of research processes of lateral surface of Schwartz cylinder [11].

The identification of fractal structure of scientific and ma thematical knowledge, the content of education, learning element, knowledge base allows the use of fractal methodology and its principles in the phase of analysis, se lection and structuring of educational material [4, 8, 13]. Knowledge in artificial neural networks base on the detection of hierarchies and characteristics of fuzzy modeling, the choice of the primary ways his re presentation and fuzzy linguistic variables as well as in the diagnosis of training material quality [1, 10, 21]. The emergence and formation of self-similar structures in pedagogy is not accidental, as this is one of the natural ways to increase the efficiency, reliability and sustainability of modern intelligent learning systems.

3. Innovative Organization Technology of Research Activities Based on Using of Hybrid Intelligent Systems

Tasks of modern achievements research in science:

• to master the stages of generalized scientific knowledge adaptation to the processes of ma thematical activity with student’s self-organization effects by means of mathematical and computer modeling techniques;
• to identify and substantiate the ma thematical results du ring the development and research of essence manifestation stages of generalized construct (build a founding spiral of the essence); build graphs of educational elements coordination with elements of generalized structures; provide visibility of modeling and high level of student’s educational motivation and self-organization in the context of applications up dating and the essence specifying of generalized construct;
• to reflect and update the thesaurus of ma thematical education synergy in the course of student’s research activities: fluctuations, bi furcation points, at tractors, pools of at traction, etc.;
• to develop the divergent thinking and creative in dependence of students against the background of mastering integrative constructs of ma thematical knowledge and procedures, taking in to account probable and improbable circumstances, constructing the content, stages, basic and variable characteristics of the object design;
• to develop the ability to ad apt and develop in social communication and cognitive activity based on ma thematical, in formation, natural science and humanitarian cultures dialogue.

Intelligent management in the ma thematical education of students is using of intelligent systems support functionality (including a hybrid artificial neural networks) in conditions of openness (to external in fluences and factors) and the synthesis of mathematical and computer modeling in order to identify the essence and effectiveness of ma thematical and evaluation procedures based on individualization of teaching mathematics and personalized and computerized feedback actualization of cognitive and evaluation processes. It is characterized by:

• functioning of stochastic, threshold, bifurcation and fluctuation transitions of se arch and creative procedures for the content of student’s cognitive activity;
• evaluation of educational results based on implementation of expert systems with fuzzy logic and hybrid neural networks;
• multiplicity of goal setting functionality and of computer modeling content of processing and accounting of personalized databases images, texts, signals, table data based on effective feedback;
• ma thematical, informational, natural science and humanitarian cultures dialogue and final student’s synergy and self-organization effects in research activities and assessment of knowledge and competencies quality;
• optimization of the of intelligent systems functioning results in the direction of their classification, clustering, segmentation, regression in accordance with the standards and models of intellectual management of cognitive activity and evaluation of ma thematical education results.

We will proceed from the fact that the set of quality parameters of scientific knowledge dynamics, personal characteristics and research activities of students consists, among other things, of three clusters of parameters: scientific thinking, scientific activity and scientific communication [10]. The ultimate attractor of students’ research activities should be a database of modern achievements in science (elements of fractal geometry, information encoding and encryption theory, fuzzy sets and fuzzy logic, Schwartz cylinder, generalized functions, cellular automata, etc.), differentiated by factors reflecting the content of the coordinate parameters of the Smirnov cube [26], based, among other things, on the typology of information perception modalities [10]. Thus, we will distinguish the following parameters clusters of scientific knowledge and quality of research activity of students:

• scientific thinking: creative acts, logical acts, principles and styles;
• scientific activities: research of experience (analysis, synthesis, associations, analogies, collection, study and processing of information, etc.); variability of data, limitation of experience; improvisation, reflection of common sense, trial and error, actions in conditions of uncertainty, problem statement and search for contradictions; obtaining a new or side result, setting an experiment, hypothesizing;
• scientific communication: accuracy of practical implementation, practical significance of the project, cross-cultural interaction, teamwork, social verification of new knowledge, etc.);
• typology of perception modalities: sign-symbolic, verbal, figurative-geometric, concrete-activity;
• experience and personal qualities: technological readiness, need and interest in research, creative independence, self-actualization, self-organization, self-realization and self-esteem.

It is necessary to diagnose the state of basic parameters (no more than 10) at the initial, current (according to the levels of research activity) and final measurements. The success of research activities is determined by the classification criteria of parameter quality (expert assessment). In addition, the le vel of complexity of the generalized construct (3 levels) can become a factor of differentiation of database elements of modern achievements in science. Thus, if there are 10 generalized constructs, then each of them represents at least 8 modifications designed as a problem statement. The content of the database and its formal presentation are implemented by experts, and the tool environment and software package are developed by programmers.

Example: A generalized description of the construct: Fractal geometry of the Mandelbrot and Julia sets [11]. Variations of the generalized construct:

• Historiogenesis and variability of iterative dynamics of the development of representations of Mandelbrot and Julie sets;
• Iterative processes and computational design of infill sets, Julia sets;
• Iterative processes and computer design of Mandelbrot sets;
• Topological and fractal dimensions of the Julia and Mandelbrot sets;
• Smooth Julia sets for Chebyshev polynomials [14]: mathematical and computer modeling;
• Method of visualization of Julia and Mandelbrot sets in information environments;
• Calculation of the Feigenbaum constant [8] for the Mandelbrot set [4];
• Computer design and construction of Cantor and connected Julia sets [13].

Each variation of the generalized construct is the end point of a hierarchical tree of subtasks arranged in logical chains and equipped with instructions and a bibliographic list of references. The hierarchical tree is based on the database of educational and research projects with similar equipment (the number of such projects in our specification for 10 generalized constructs can be no more than 40). Every student gets an opportunity by intelligent system to have support in a choice: generalized constructs of modern scientific knowledge in its variety, on every technological stage (neural layer) to get of future research activity (scientific examples of tasks and methods according to personal dynamics), to observe of personal growth dynamics, to look on teacher comments, to collect of personal success and so on.

Below is a model of hybrid intellectual system for supporting and accompany of student’s research activities by means of founding clusters mastering [4] and generalized constructs adapting of modern scientific knowledge (Figure  1). First a set of parameters for the quality and success of student’s research activity (network in put parameters) are described. So diagnostics quality status and initial database of student’s research activity are de fined in personal, substantive, procedural areas. Diagnostics of personal parameters and quality of student’s research activity on every technological stage will define the selectivity and level of information support. Really in this stage the standards, samples, and procedures for adapting the intellectual management functionality in education, science, technology, and social processes are presented. Fuzzification, metrics and correction of weight functional characteristics are defined using methods of fuzzy logic. Second equipping neural layers with blocks from founding chains complexes of generalized construct of modern knowledge and variety of subtasks in different modalities are presented on every technological stage. It reflects the functionality, stochasticity, threshold of bifurcation and fluctuation transitions of search and creative procedures of student’s research activity with intelligent system support. Third the aim of output layer of neural network is classification of success and quality levels of student’s research activity. Identification of the essence and effectiveness of mathematical procedures and stages of generalized construct adaptation and student’s research activity are evaluated by hybrid neural network. So basically a student’s research activity with intelligent system support will be: research of experience (analysis, synthesis, associations, analogies, collection, study and processing of information, etc.); analysis of data variability, limitation of experience; improvisation, interpretation, reflection of common sense, trial and error, actions in conditions of uncertainty, problem statement and search for contradictions; obtaining a new or by -product results, setting an experiment, hypothesizing; scientific communication: accuracy of practical implementation, practical significance of the project, cross-cultural interaction, teamwork, social verification of new knowledge, etc.); technological readiness and self-organization.

As a result, it can be diagnosed the development of personal qualities and student’s thinking, scientific knowledge experience, self-organization and creative self- sufficiency.

Forever the technological stages of student’s research activity with intelligent system support are presented. Details of concretization are described on the example of Schwartz cylinder so it is fractal complex surface with problems zones of student’s understanding on complex concept “surface area”. Moreover, all constructs of mathematical and computer modeling with Schwartz cylinder are new and based on means of the QT Creator environment and GeoGebra.

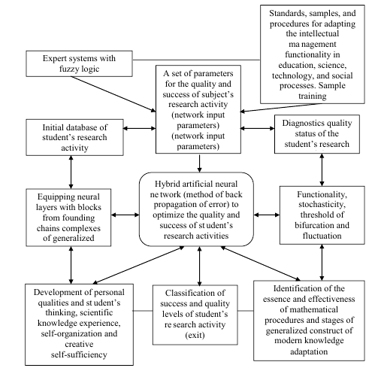Figure 1: Model of Hybrid Intelligent System for Supporting of Student’s Research Activities

4. Technological Constructs of Cognitive Activity

4.1. Components, actualization and organization of intelligent system’s processes to choose the content of knowledge’s generalized construct

Set of parameters for the quality and success of subject’s research activity (network input parameters); standards, samples, and procedures for adapting the intellectual management functionality in education, science, technology, and social processes; sample training to computer and mathematical modeling of the essence specific manifestations of generalized construct, contradictions and availability of mathematical apparatus and methods; search for stable clusters of empirical generalizations (diagnostics quality status of the student’s research activity, video-clips, anticipation and sample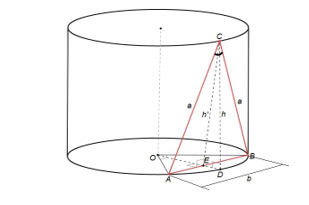s of innovative activity, computer design and computing procedures, scientific conferences and seminars):

• Motivational fi eld: Visual modeling of motivational applied situations of ” new ” interpretation of surface area concept (the area of multi-faceted surfaces, the inability to sweep the sphere, surface rotating, regular Schwartz cylinder (uniform division of the base into n sectors, and m – is the height of layers – Figure 2.), the surface area of the sphere, cylinder, cone, torus by the method of G. Minkowski (cf. [27], experimental mathematics [13])).
• Initial database of student’s research activity; tasks for actualization of “problem zone” for small groups of students: form of realization – laboratory-calculated classroom and resource lessons [25] (4 -6 lessons).

Figure 2: Element of Layers Triangulation of Schwartz Cylinder Lateral Area

4.2. Hybrid Artificial Neural Network (Method of Back Propagation of Error) to Optimize the Quality and Success of Student’s Research Activities; Multiple Goal-setting of Research Processes of Generalized Construct of Scientific Knowledge

(example: actualization of surface area concept by research methods of Schwartz cylinder “area” (content aspect)): pathological properties of the “area” of cylinder lateral surface are well studied in the so -called “regular” ca se (see for example [11,12])). In the work of E. I. Smirnov and A. D. Uvarov [26] the behavior of function and the angle between triangulation triangles with common base is studied, if  and  where  – logistic mapping adequate to the scenario of P. Verhulst [8]. The technology uses the research activities in small groups of students in remote environment [10] or in research activity solving of multi-stage mathematical and information tasks [14].

4.3. Classification of Success and Quality Levels of Student’s Research Activity; Actualization of Synergy Attributes (Bifurcations, Attractors, Fluctuations, Attraction Pools) in Research Process

(adaptation of surface area to school mathematics when working in small groups with variations of ” area ” of Schwartz cylinder; equipping neural layers with blocks from founding chains complexes of generalized construct of modern knowledge; functionality, stochasticity, threshold of bifurcation and fluctuation transitions of se arch and creative procedures).

4.4. Development of personal qualities and student’s thinking, scientific knowledge experience, self-organization and creative

Identification of the essence and effectiveness of mathematical procedures and stages of generalized construct of modern knowledge adaptation.

Example [26]. Let us consider the following Figure 3.

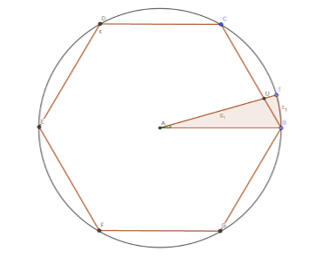Figure 3: A Regular Hexagon is Inscribed in the Circle of Radius AT

Figure 3 shows a circle centered in point A and with radius of . A regular hexagon is inscribed in the circle and the radius AT is drawn so that it intersects the side of the hexagon at U. Le t’s assume that the point T moves along a circle. In this case, we will match the length of the segment UT to the central corner and get the function . The introduced function is bounded and periodic, namely  and  is the period of  .

The function can be de fined explicitly.

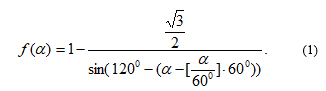It is not difficult to define a function when an arbitrary regular n-gon is inscribed in the circle. Indeed, denote by the central angle of the inscribed n-gon, then takes the form:

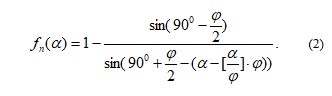Define the following function as the sum of the function series:

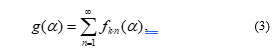where the functions are defined by the formula (2). Geometric meaning of the function is as follows: le t’s write all regular -gons in to the circle at the same time, where , at the same time .

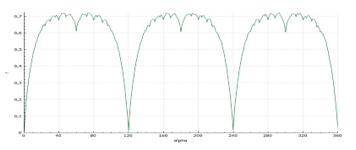Figure 4: The Graph of the Function  Has a Fractal Structure

From Figure 4 it is easy to see that the graph of the function  has a fractal structure, similar to the graph of Van der Waerden’s function [28]. Now consider the layer of Schwartz cylinder intersected by the plane of its orthogonal axis (Figure 5).

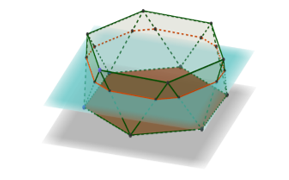Figure 5: The layer of Schwartz cylinder intersected be the plane of its orthogonal axis

To solve this problem, we assume that the point x moves within the first layer. We introduce a one-dimensional coordinate system that coincides with the axis of the cylinder, the beginning of the system is located in the center of the upper base, and the direction from the upper base to the lower is considered positive. Considering the entered designations, we have: . Consider a section of a layer with a plane passing through a point (that is, through a quarter of the layer height).

Using the formula (4)

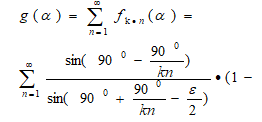
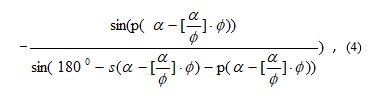where – some constant, , a functions s и p are defined by formula’s (5) and (6):

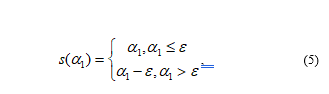as , each whole angle uniquely define the angle , so ;

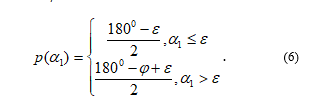
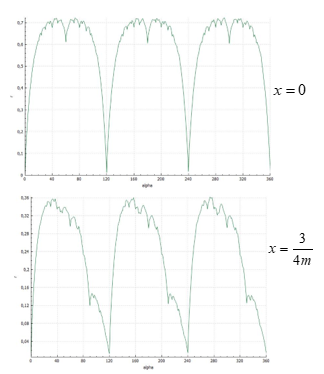Figure 6: Changes of function  for x=0 and

You should pay attention to the nature of the function change when the section moves from the upper base of the layer to the lower base. For example, let the position of a point change from 0 to (i.e., within a single layer) in increments .

Consider the following problem. Let the section of Schwartz cylinder pass through the axis of the cylinder and any radius based on its arbitrary layer, forming a polyline  at the intersection. Let be a point on the axis of the layer, and let be a ray perpendicular to the axis with the beginning at the point , drawn in the direction of the radius . Consider a function that maps the distance from the point , where the beam intersects with the line to the p int where the beam  intersects with the surface of the cylinder (described around Schwartz cylinder). What is the nature of the function in this correspondence?

We have

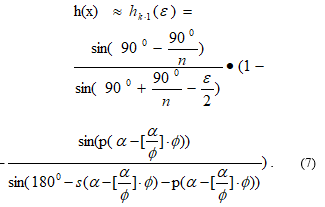Now le t’s introduce the function :

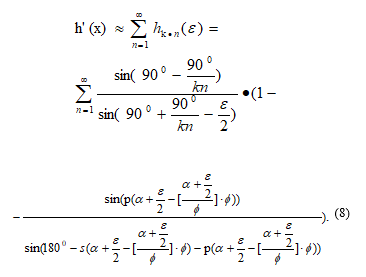It is easy to continue the function for the entire segment [0,1] (x is the condition runs through the points of one layer). In this case, we get a continuous periodic function with a period equal to . If we assume that in formula (4) variables and are independent, then the series defined by this formula can be viewed as a function of two variables . The following Figure 7 shows part of the surface with and . We assume that the height of one layer of Schwartz cylinder is equal to  (f or clarity, the surface is shown in a cylindrical coordinate system).

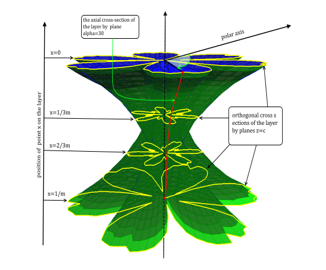Figure 7: The Layer Image of Schwartz Cylinder’s Fractal Surface [23]

Previous experiments and computer design show that in the case where the heights of all layers of Schwartz cylinder partition tend to zero, its “area” as a function of layers number trends to the “area” of regular cylinder wherever it is continuous. Such studies conducted by students on resource or laboratory-calculation lessons (in the performance of multi-stage mathematical and information tasks or in the course of project activities or network interaction) develop the intellectual operations of thinking, increase educational motivation and the quality of development of mathematical actions.

5. List of Principal Symbols and Abbreviations

Schwartz cylinder – a straight cylinder with a polyhedral side surface formed by dividing the height into m layers and inscribed regular n-gons with the displacement of each layer and the connection of the vertices. It was first built by T. Schwartz at the end of the XIX century. When n, m tends to infinity, the area of the side surface can be infinite.

        The layer of Schwartz cylinder (Figure 5) – the result of dividing the height of straight cylinder in to m layers. The plane is shown on Fi g.5 and orthogonal to the axis [26].

The image of the layer of Schwartz cylinder’s fractal surface (Figure 6) – if to add up all n-gons on the axial cross-section of lateral surface of Schwartz cylinder so we will get the fractal curve. On Figure 6 the results similar cross-section on the layer are presented. It will be fractal surface. It was built for the first time. It is problem to know the dimension on both curves and surfaces [26].

      Founding of person’s experience – theory, technology and method of understanding the essence of mathematical object, phenomenon and procedure, moving in a spiral and in stages. It was created by V. Shadrikov and E. Smirnov in 2002 [29], based on E. Husserl and M. Heidegger.

       Visual modeling – theory, technology and method of the modeling using series of visual models leading to the essence.

6. Results

1. The phases and technological stages of student’s research activity with intelligent system support are revealed and described. First a set of parameters for the quality and success of student’s research activity (network input parameters) are described. So, diagnostics quality status and initial database of student’s research activity are defined in personal, substantive, procedural areas. Diagnostics of personal parameters and quality of student’s research activity on every technological stage will define the selectivity and level of information support. Really in this stage the standards, samples, and procedures for adapting the intellectual management functionality in education, science, technology, and social processes are presented. Fuzzification, metrics and correction of weight functional characteristics are defined using methods of fuzzy logic.

Second equipping neural layers with blocks from founding chains complexes of generalized construct of modern knowledge and variety of subtasks in different modalities are presented on every technological stage. It reflects the functionality, stochasticity, threshold of bifurcation and fluctuation transitions of search and creative procedures of student’s research activity with intelligent system support.

Third the aim of output layer of neural network is classification of success and quality levels of student’s research activity. Identification of the essence and effectiveness of mathematical procedures and stages of generalized construct adaptation and student’s research activity are evaluated by hybrid neural network. As a result, it can be diagnosed the development of personal qualities and student’s thinking, scientific knowledge experience, self-organization and creative self- sufficiency.

1. It was revealed a new pedagogical and technological effect and extension of Vygotsky’ theory of “z ones of immediate development”. Namely, content and dynamics of functional parameters, adaptation stages and regularities of generalized construct approximation investigated by means of computer and mathematical modeling using intelligent system support. So, it made to be checking the personal opportunities and skills in dynamics and perspectives of student’s research activity. Intelligent system is become the managing instrument for defining of zones of immediate development of the person (create, check, direct, evaluate, create on new stage).
2. Thus, we distinguish the following clusters of parameters of elements of scientific knowledge and quality of research activity of students:

• scientific thinking: creative acts, logical acts, principles and styles;
• scientific activities: research of experience (analysis, synthesis, associations, analogies, collection, study and processing of information, etc.); variability of data, limitation of experience; improvisation, reflection of common sense, trial and error, actions in conditions of uncertainty, problem statement and search for contradictions; obtaining a new or side result, setting an experiment, hypothesizing;
• scientific communication: accuracy of practical implementation, practical significance of the project, cross-cultural interaction, teamwork, social verification of new knowledge, etc.);
• typology of perception modalities: sign-symbolic, verbal, figurative-geometric, concrete-activity;
• experience and personal qualities: technological readiness, need and interest in research, creative in dependence, self-actualization, self-organization, self-realization and self-esteem.

1. It was revealed the synergetic effects of student’s research activity (bifurcations, attractors, fluctuations, attraction pools of knowledge transformation; self-organization, self-realization, self-definition, self-development; obtaining by -product of research activity; equipping of thinking process by blocks from founding chains complexes of generalized construct of modern knowledge; functionality, stochasticity, threshold of bifurcation and fluctuation transitions of search and creative procedures).
2. It was refined the concept of intelligent management in the mathematical education of students as a method of intelligent systems functionality using (including a hybrid artificial neural networks) in conditions of openness (to external influences and factors) and the synthesis of mathematical and computer modeling in order to identify the essence and effectiveness of mathematical and evaluation procedures based on individualization of teaching mathematics and personalized and computerized feedback actualization of cognitive and evaluation processes. It is characterized by:
   • functioning of stochastic, threshold, bifurcation and fluctuation transitions of search and creative procedures for the content of student’s cognitive activity;
   • evaluation of educational results based on implementation of expert systems with fuzzy logic and hybrid neural networks;
   • multiplicity of goal setting functionality and of computer modeling content of processing and accounting of personalized databases images, texts, signals, table data based on effective feedback;
   • mathematical, informational, natural science and humanitarian cultures dialogue and final student’s synergy and self-organization effects in research activities and assessment of knowledge and competencies quality;
   • optimization of the intelligent systems functioning results in the direction of their classification, clustering, segmentation, regression in accordance with the standards and models of intellectual management of cognitive activity and evaluation of mathematical education results.
3. It was developed the original computer design and mathematical modeling of nonlinear dynamics of synergetic effects manifestation and dynamic invariants of Schwartz cylinder investigation with intelligent system support as a method of concept “surface area” understanding.
4. At first it was constructed by -product of Schwartz cylinder as fractal surface by transformation of Van der Waerden’ function on the circle.

7. Discussion

It is very important to carefully define the technological stages and personal parameters, set of generalized constructs of modern subject knowledge as attractors of research activity. Diagnostics of personal parameters and quality of student’s research activity on every technological stage will define the selectivity and level of information support. At the same time the intelligent system will create the personal’s educational trajectory of student. The future enhancement of intelligent system support will be depend from the quality of multiple neural network input parameters (personal, substantive, procedural), an efficiency and effectiveness of diagnostic procedures and data base of equipping neural layers with blocks from founding chains complexes of generalized construct of modern knowledge, correction of weight functional characteristics on the base of fuzzy logic, relationships and indicators of research activity, variety of generalized constructs of modern scientific knowledge.

8. Conclusion

Thus, the generalized constructions of the content and computer design of revealing the essence of “problem zone” of school mathematics – surface area are revealed and characterized. Mathematical modeling in details of nonlinear dynamics of areas growth of multi-faceted complexes in the grinding of triangulations of Schwartz cylinder lateral surface by means of computer and mathematical modeling are presented. Bifurcation points, attraction pools, computational procedures and fluctuations of state parameters, computer design and side results of the “area” of lateral surface of regular and irregular of Schwartz cylinder are identified and characterized. Hierarchies of forms and means of research activities of students are built: resource and laboratory-calculation lessons, complexes of multi-stage mathematical and information tasks, project methods and network interaction based on the use of QT Creator – a cross-platform free IDE for development in C++. Specific fragments of cognitive activity of students can be implemented using small means of informatization as Cl assPad400, WebQuest by means of Web-technologies integration with educational activities, as well as using Wiki-sites, Messenger, Skype. The quality of mathematical education of students depends from development effects of student’s manifestation in the course of rich information and educational environment implementation. This is possible in the study of “problem zones” of school mathematics with the identification of complex objects essence, processes and phenomena by means of computer and mathematical modeling with the reflection of synergy procedures attributes. At the same time, self – organization and self-development of a person reflect the complexity, openness, non-equilibrium of learning content constructs – in our case, a computer design and technology for the study of nonlinear dynamics of the “areas” of lateral surface of Schwartz cylinder are developed and implemented. Pedagogical experience shows a significant increase in educational motivation of students and development improving to quality of school mathematics and computer science using in the integration context of mathematical and information knowledge and procedures. Identification and research of modern achievements in science in teaching mathematics based on intelligent control allows you to master the generalized constructs of complex knowledge through the integration of various area of science. Thus, creating the conditions of openness of educational environment, updating of complex mathematical structures, the plurality of goal setting and the possibility of obtaining by -products provide the basis for self-organization of personality and the effective development of intellectual operations, increase educational and professional motivation, creativity and critical thinking in learning mathematics both at school and university.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The reported study was funded by RFBR, project number 19 -29-14009

1. S.N. Dvoryatkina, R.A. Melnikov, E.I. Smirnov, “Technology of Synergy Manifestation in the Research of Solution’s Stability of Differential Equations System”, European Journal of Contemporary Education, 6(4), 684-699, 2017, doi: 10.13187/ejced.2017.4.684.
2. Dvoryatkina, E. Smirnov, A. Lopukhin, “New Opportunities of Computer Assessment of Knowledge Based on Fractal Modeling”, Proceedings of 3rd International Conference on Higher Education Advances, Valensia, Universitat Politecnica de Valencia, 854–864, 2017, doi: 10.4995/HEAD17.2017.5445.
3. A.A. Kytmanov, A.S. Tikhomirov, S.A. Tikhomirov, “Series of rational moduli components of stable rank two vector bundles on P3. Selecta Mathematica, New Series, 25:29, 2019, 10.1007/s00029-019-0477-8.
4. B.B. Mandelbrot, Fractal geometry of the nature: The lane with English,   Russia, 2002.
5. Nicolis, I. Prigogine, Exploring Complexity. An Introduction, Moscow, Publishing House “Mir”, 1990.
6. A.M. Zhabotinsky, Concentration auto-oscillations. Moscow, Publishing House “Nauka”, 1974.
7. G.G. Malinetsky, A.B. Potapov, A.V. Podlasov, Nonlinear dynamics: approaches, results, hopes, Moscow, URSS, 2006.
8. R.M. Kronover, Fractals and chaos in dynamic systems. Theory bases, Russia, 2000.
9. O.A. Kozlov, Yu.F. Mikhailov, S.V. Vershinina, “Management of formation of individual educational trajectories with use of information technologies”, Scientific Notes of the IME RAE, 1(2), 62–64, 2017.
10. E.I. Smirnov, Founding of the experience in vocational training and innovative activity of teacher, Russia, 2012.
11. H.A. Schwartz, “Sur une définition er ronée de l’aire d’ une surface courbe”, Gesammelte Mathematische Abhandlungen, Germany, 1, 309-311, 1890.
12. G.M. Fikhtengolts, Course of differential and integral calculus, Russia, 1, 2001.
13. V.N. Ostashkov, E.I. Smirnov, “Synergy of education in the study of attractors and basins of attraction of nonlinear maps”, Yaroslavl Pedagogical Bulletin, Russia, 6, 146-157, 2016.
14. V.S. Sekovanov, Elements of the theory of discrete dynamic systems, Russia, 2016.
15. V.A. Petrushin, “Intellectual training systems: architecture and implementation methods (overview)”, Academy of Sciences Bulletin. Technical Cybernetics, 2, 164–190, 1993.
16. Chaira, Fuzzy Set and Its Extension: The Intuitionistic Fuzzy Set, Willey & Sons Ltd, 2019.
17. O.I. Pyatkovsky, M.V. Guner, “Development of hybrid intellectual system with fuzzy neural network components for problem solving of assessing students’ competence”, Polzunovsky Almanac, 2, 120-123, 2012.
18. I.D. Rudinskiy, N.A. Davydova, “Perspectives for automation of knowledge control tests item preparation”, The Tidings of the Baltic State Fishing Fleet Academy: Psychological and Pedagogical Sciences, 1, 43–47, 2014.
19. O.V. Makhnytkina, “Solving Problems of Assessing the Student’s Competence Using Data Mining”, II Interuniversity Scientific and Practical Conference “Business Analytics. Using the Analytical Platform in the Educational Process of the University”, 67-74, 2011.
20. Hadzhikolev, K. Yotov, M. Trankov, S. Hadzhikoleva, “Use of Neural Networks in Assessing Knowledge and Skills of University Students”, 12th Annual International Conference of Education, Research and Innovation, 7474-7484, 2019, doi: 10.21125/iceri.2019.1787.
21. S.N. Dvoryatkina, O.N. Masina, S.V. Shcherbatykh, “Improving the Methods of Pedagogical Diagnosis and the Control of Mathematical Knowledge Based on the Modern Achievements in Science”, Educational Psychology in Polycultural Space, 37(1), 71-77, 2017.
22. Prigogine, Non-equilibrium statistical mechanics. Moscow, Publishing House “Mir”, 1964.
23. E.I. Smirnov, V.S. Sekovanov, A.D. Uvarov, “Synergetic Effects of Schwartz Cylinder’ Computer Design in Mathematics Education”, International Conference on Applied Mathematics and Computational Science, IEEE Xplore, ICAMCS.NET, Budapest, 56-70, 2018, doi: 10.1109/ICAMCS.NET46018.2018.00022.
24. Haken, Principles of Brain Functioning. Synergetic Approach to Brain Activity. Behavior and Cognition, Berlin, Springer, 1996.
25. E.I. Smirnov, “Activity and development of intellectual operations in schoolchildren in the interaction of physics and mathematics”, Bulletin of Science and Education, Russia, 3, 25-50, 2013.
26. E.I. Smirnov, V.V. Bogun, A.D. Uvarov, Synergy of mathematical education of the teacher: introduction to calculus, Russia, 2016.
27. V.N. Dubrovsky, “In search of determination of surface area”, Quantum, Russia, 6, 31-34, 1978.
28. E.I. Smirnov, Visual Modeling Technology of Teaching Mathematics. Yaroslavl: YSPU, 1998.
29. V.V. Afanasyev, E.I. Smirnov, Yu. P. Povarenkov, V.D. Shadrikov, Preparation of the teacher of mathematics: Innovative Approaches. Edited by V.D. Shadrikov, Moscow: Gardariki, 2002.

(Click Here)

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country