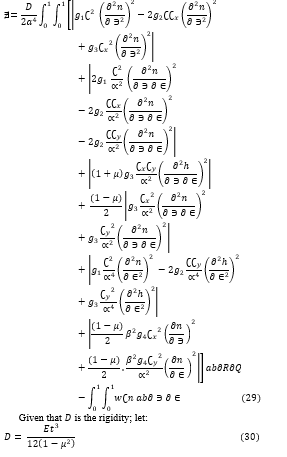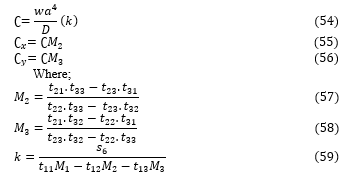1.Introduction

Plates, generally well-known structural element have been extensively used in different fields like engineering, and other industries due to their high strength, lightweight, load resistance characteristic and their cost benefits, as recorded in [1]. Plates are widely used in structural engineering, aerospace engineering, mechanical engineering, etc., for the construction of buildings, retaining walls, ships, bridges, railways, etc., [2 – 3].
Plates have been classified based on thickness as: thick, moderately thick, and thin plates [4], based on material composition as: isotropic and anisotropic plates, based on shape as: circular, rectangular, triangular, elliptical, and skew plates, [5]. The edges of plates can be of different kinds of supports such as: simply supported support, point and fixed supports, etc. as seen in [6].
The analysis or solutions of plates help to determine the stability of plates, and it entails the determination of displacements, stresses, moments, etc., at a different portion of the plate, [7]. Also, the analysis of plates can be due to bending, buckling, and vibration caused forces. It is generally known that the bending of plates relates to the deflection of the plate at a right angle (90o) to the plate plane due to the influence of forces and moments [8].
It is the depth of plates that mainly affects their bending characteristics compared to other surface dimensions like: length and breadth [9].
There have been different theorems: the classical plate theory (CPT) and refined plate theory (RPT) developed and applied in the analysis of the different categories of plates by many researchers. The classical plate theory (CPT), which was developed by [10 – 11], is based on the assumption that the line which is normal to the mid-surface remains so, before and after deformation. The classical plate theory (CPT) is mainly used in the analysis of thin plates and has also been used by [12 – 14] in the analysis of solutions involving plates and shells, respectively. But it has been found to be inadequate by [15] for the analysis of thick plates as its neglects the effect of shear deformation – a gap that led to the development of refined plate theory by researchers. The Refined Plate Theory (RPT) is used for the analysis of thick plates [16], and it addresses the gap in classical plate theory (CPT).
The RPT comprises First-Order Shear Deformation Theory (FSDT – which has a correction factor as a limitation, and Higher-Order Shear Deformation Theories (HSDT), etc., taking into account the effect of shear deformation and has been applied by different researchers in analyzing thick plates. Authors in [17 – 18] revealed that the limitations in CPT and FSDTs led to the formulation of higher-order shear deformation theory (HSDT). There have been various studies on the bending analysis of thick rectangular plates with different boundary conditions using refined plated theory with different methods and techniques.
This present paper is aimed at bridging the gap in the literature by applying the polynomial shear deformation theory in obtaining the displacements, bending moment, and stresses of the thick rectangular plate. This theory, which is based on a traditional fourth-order shear deformation plate, is presented and applied in a bending analysis of thick rectangular plates using the Energy-variational approach. The investigation has conducted on the plate that has three edges clamped and the other opposite edge free of support (CCFC). Furthermore, derivation of general governing equations for the plate and numerical solutions for deformation, moment, and stress distributions of different points of the plate with a uniformly distributed transverse load is presented.
The physical interpretation of CCFC plate is that, the three clamped edges are supported by a beam and continuous over the span of the plate while the remaining one is free of support i.e. hang without support (Eg. Cantilever). This makes the study very significant because such BC exist depending on the type of beam/column support in the plate structure i.e. it contains different support case of the plate structure than other BCs. So, whenever such case (CCFC) as explained occurs in the structure, analyzing the plate as if is any other BC like SSSS, CCCC etc.(22, 27, 28 and 29) will not account for all the forces (stresses) acting on it. This is because, forces are generated due to the applied load on the structure thereby will introduce significant errors in the analysis and not predict an accurate or reliable result for the design if they are not considered. Thus, for a safe structural design of plate (slab) in a building or any type of structure with CCFC BCs, plate analysis with CCFC BCs like this is required.
The aim of this study is to determine the bending analysis of an isotropic rectangular plate for the effects of aspect ratio and displacement on the moment, shear force, stresses, and stress resultant of a thick rectangular plate. The study sought to achieve the aim through the following objectives:
To generate the potential energy of a thick plate in line with the work of authors in [5].

To formulate the general governing equations of the plate and obtain equations for the coefficients of deflection and shear deformation slope for x and y coordinates.

To determine the expressions for the in-plane and out of plane displacement, bending moment, shear force and stresses of the thick rectangular plate.

Previous Works

The authors in [19] used Fourier trigonometric series to analyze the bending of rectangular plates on elastic foundations. They developed the deflection equation, which was in the form of trigonometric series using the Navier solution to the plate. The constraint of the trigonometric series is that it is tedious and rigorous for the formulation of shape functions for the analysis of rectangular plates. The authors in [20] stated that the constraint of the trigonometric series is that it is very strenuous for the formulation of shape functions relating to plates with unsymmetrical boundary conditions.
The authors in [21] used Mindlin’s plate higher-order shear deformation theory to generate governing equations for the bending analysis of thick rectangular plates with clamped supports at all its edges (CCCC). Their developed theory involved the decoupling method and improvement on Navier’s solutions with partial differential equations, which reduced the complexity involved in obtaining coefficients of plates. In as much as their results showed great accuracy when compared with past results of other studies, their study did not address plate with the CCFC edge condition and didn’t make use of the direct variation energy method, which is less rigorous.
In [16], the authors used polynomial shape function for the analysis of rectangular isotropic thick plates. They used the direct variation energy method to obtain displacement coefficients without the need for correction factor for plates with CCCS and SSFS edge conditions, respectively. Their results (displacements and stresses), which they found to be adequate after comparing with results from previous works but did not include the CCFC plate’s edge condition as it was not included in their study.
In [17], the authors used exponential function in shear deformation to determine the bending solution of the thick isotropic square and rectangular plates with simply supported supports. They applied the refined shear deformation theory and exponential functions in the form of thickness coordinate to obtain transverse shear deformation and rotary inertia without the need for a correction factor. They found their results: displacements, stresses, and frequencies to be satisfactory after comparing with other refined and exact theories. They only considered the boundary condition (SSSS) using the exponential function and not the polynomial displacement function in an energy method, which is less cumbersome.
The authors in [22] worked on the bending solutions of a thick rectangular plate with CCCC edge conditions. They used refined plate theory (RPT) – polynomial shear deformation theory (PSDT) with the Ritz energy method in their analysis without considering correction factor, and they obtained the coefficients for displacement by putting the total static energy equations to direct variation. They found out that their results (displacements and stresses) were accurate after comparing with results from other previous studies. The authors in [23] used the same boundary condition to study the bending behavior of the elastic rectangular thick plate using the Bergan-Wang approach. They found out that their approach can be used to determine the deflection of plates and analysis of thin, moderately thin, and thick plates, respectively. The authors in [22] used an assumed shape function, which is not a close-form solution, while the authors in [23] didn’t use the Energy method, which is more simplified. Both authors did not consider the plate with the CCFC edge condition in their analysis.
In [24], the authors did a study on bending solutions of the thick plate using a numerical method – based on the 3-D theory of elasticity. They used the method: spline collocation in two coordinate directions for their analysis. They concluded their approach to be useful in determining the distribution of displacements and stresses in thick rectangular plates, with hinged or clamped edge conditions. Their study did not cover the plate with the CCFC edge condition, and also they made use of a numerical method which, unlike the analytical approach, cannot determine the value of deflection at any given point in the plate.
The author in [25] used HSDT with stretching effect to determine bending characteristics of exponentially graded material plates. In his study, he made the assumption that the modulus of elasticity varies exponentially through the plate thickness direction. He found that his theory satisfied the shear stress-free condition at the top and bottom surface of the plates without considering the correction factor. He found out from his study that his theory was satisfactory after compared with previous studies and then concluded that the theory is suitable for predicting bending behavior of exponentially graded material plates. It can be seen from his study that he used shear strain shape function – a new higher-order shear deformation theory and not a polynomial displacement function in the energy method.
The authors in [26] have used PSDT for the analysis of rectangular plates. They obtained the expression for the critical lateral load that induces deflection and shear as a solution to the bending problem of rectangular plates with all four edges clamped (CCCC) and plate with free of support at the third edge and the other edges clamped (CCFC) using third-order shear deformation theory for thick rectangular plate respectively. They did not analyze the effect of displacement, moment, and stresses in predicting responses of the applied load on the plate structure.
Apart from the distinctiveness of the present study with respective individual previous works, there exists an aspect of the distinctiveness of the present study over the previous works put together. This lies in the type of shape functions, and plates support boundary conditions. Unlike the previous works that assumed the displacement function, the present work obtains the exact formulation of the total potential energy from a principle of static elastic theory to get a close form solution of the polynomial displacement function. Except for the author in [26], none of the researchers could determine the analytical solution of bending moment and stresses used in predicting the bending behavior of an elastic thick rectangular CCFC plate. These aspects cannot be overlooked.

Methodology

Assumptions

Considering the following assumptions, the total potential energy of a thick rectangular plate will be formulated. They include:
The material of the plate is elastic and homogeneous in nature.
The vertical line that is initially normal to the middle surface of the plate before bending is neither straight nor normal to the middle surface after bending.
The effect of the strain and stress normal to the x-y plane on the gross response of the plate is small and can be neglected. Thus, the in-plane displacements, u and v, are differentiable in x, y, and z coordinates, while the deflection, w, is only differentiable in x and y coordinates.

Displacement, Strain and Stress Relationships

Figure 1 shown the two in-plane displacements: in-plane displacement in the direction of x coordinates (u) and in-plane displacement in the direction of y coordinates (v) are represented in Equations (1) and (2) (see the author in [1]):

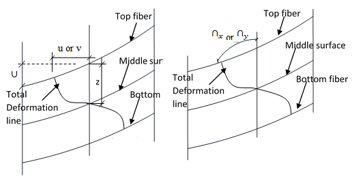Figure 1: Deformation of a section of a thick Plate

The shear deformation profile of plate section S(z) is given (see the author in [5]) as:

where;
∩_x and ∩_y is the shear deformation slope in x and y axis respectively.
It is assume from this work that the out-of-plane displacement (∪) is only differentiable in x and y coordinates.ie. (∪=∪(x,y).
The normal stress along x-axes (ε_x) becomes:

The normal stress along y-axes (ε_y) gives:

The shear strain along (x-y), (x-z) and (y-z) respectively are given in the Equation (6), (7) and (8) respectively as:

Similarly, the stress normal to x-axes is defined as:

the stress normal to y-axes is defined as:

Considering the relationship between the strain and stress in the plate, the shear strain in x-y plane is given as:

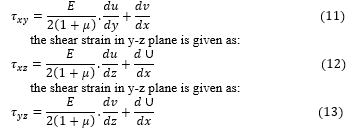Substituting Equation (1), (2), (4) and (5) into Equation (9), we have:

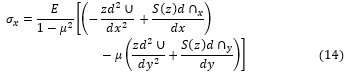Substituting Equation (1), (2), (4) and (5) into Equation (10), we have:

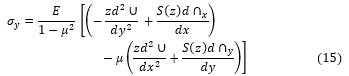
Substituting Equation (1), (2) and (6) into Equation (11), we have:

Substituting Equation (1), (2) and (7) into Equation (12), we have:

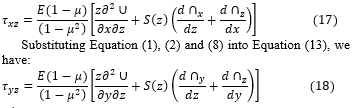
where:
the symbol ∪ denotes out-of-plane displacement
the symbol F(z) denotes Shear deformation profile
the symbol ∩_x denotes shear deformation rotation along x axis
the symbol ∩_y denotes shear deformation rotation along y axis
the symbol μ denotes poison ratio
the symbol E denotes modulus of elasticity of the plate
the symbol σ_x denotes stress normal to x axis
the symbol σ_y denotes stress normal to y axis
the symbol τ_xy denotes shear stress along x-y axis
the symbol τ_xz denotes shear stress along x-z axis
the symbol τ_yz denotes shear stress along y-z axis
the symbol ε_x denotes normal strain along x axis
the symbol ε_y denotes normal strain along y axis
the symbol γ_xy denotes shear strain along x-y axis
the symbol γ_xz denotes shear strain along x-z axis
the symbol γ_yz denotes shear strain along y-z axis

Total Potential Energy Equation

The total potential energy expression (∄), was formulated in accordance to the kinematics and constitutive relation in the previous section (see [27]).

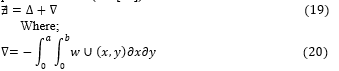
Where w is the uniformly distributed load.

The non-dimensional values of quantities along the x and y-axis respectively is presented below.

where;
a,b and t are the length,breath and thickness of the plate while ∋,∈and s are the non-dimensional value of length, breath and thickness of the plate.

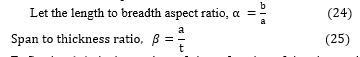
Deflection (∪), is the product of shape function of the plate and deflection coefficient:

Similarly;
The shear deformation rotation along x-axis becomes:

Similarly, the shear deformation rotation along y-axis becomes:

where,
n is the shape function of the plate
∁ is the coefficient of deflection
∁_x is the coefficient of shear deformation along x axis
∁_y is the coefficient of shear deformation along y axis
By substituting Equation 23, 24, 25, 26, 27 and 28 into 22, gives:

Governing Energy Equation

The elastic plate presented plate in figures 1 and 2 under bending subjected to uniformly distributed load was used to obtain the displacement – strain relationships in terms of curvatures.

3.4.1. General Governing Equation

The total potential energy shall be minimized with respect to the deflection w, shear deformation along the x axis, ∩_x and shear deformation along y axis∩_y. Minimizing or differentiating total potential energy equation with respect to ∪,∩_x,and ∩_y is said to be the direct variation.

By solving the resulting three simultaneous governing equation the actual deflection ∪, shear deformation along the x axis, ∩_x and shear deformation along the y axis, ∩_y was gotten as:

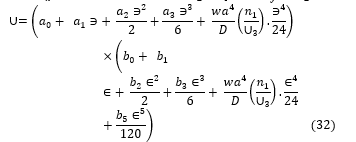
The general polynomial shear deformation function (Rotation equation for the y-axis) of a rectangular plate as was obtained and presented:

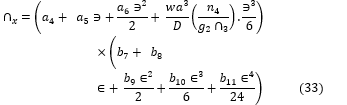The general polynomial shear deformation function (Rotation equation for the y-axis) of a rectangular plate as was obtained and presented:

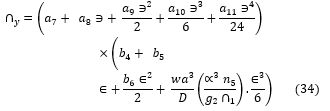
The support conditions of the plate consideration is presented in the Figure 2.

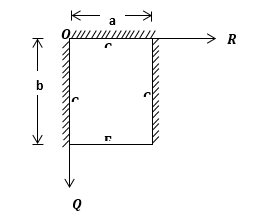Figure 2: CCFC Rectangular Plate

3.4.2. Direct Governing Equation

The direct variation method was used to obtain the direct governing differential equation by differentiating the total potential energy with respect to the coefficient of deflection (∁), coefficient of shear deformation with respect to x-axis 〖(∁〗_x) and coefficient of shear deformation with respect to y-axis〖 (∁〗_y). Minimizing the Energy expression (∄) with respect to the coefficient of deflection (∁), coefficient of shear deformation with respect to x-axis 〖(∁〗_x) and coefficient of shear deformation with respect to y-axis〖 (∁〗_y):

The solution of Equation (35) yields the three Equations of equilibrium which is presented as:

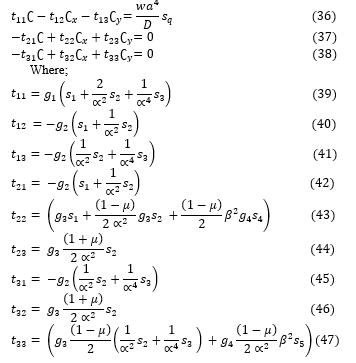Given that s_1,s_2,s_3,s_4,s_5 and s_q are the stiffness coefficients, let:

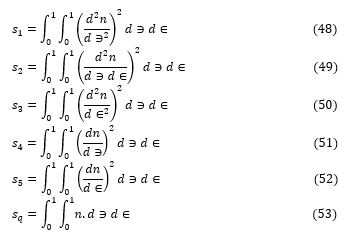Solving Equation (36), (37) and (38) simultaneously, gives Equation (54), (55) and (56):

Displacement, Stresses, Bending moment and Shear force Equations

The equations for the moment (M_x and M_y), shear force (Q_x and Q_y), in-plane displacement (u and v), deflection (∪) and the stress of isotropic rectangular thick plate was derived according to [28] by substituting the Equation (54), (55) and (56) where appropriate.
Substituting Equation (54) into (26), gave:

The bending moment along y-axes:

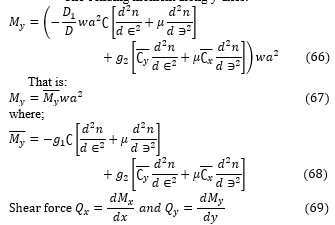Thus, the shear force along x-axes:

The in-plane displacement along x-axes:

Results and Discussions

The numerical analysis of a CCFC rectangular plate of various span-thickness ratios is presented in Table 2 to 6. A third-order polynomial displacement function for the analysis CCFC as was derived in Equation (32) in line with the work of [29] is presented in Equation 83 to 94:

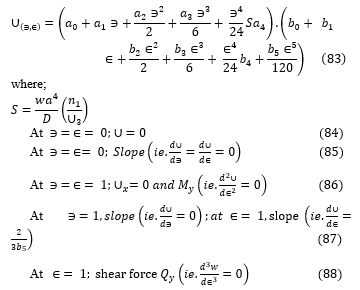
Substituting Equations (84 to 88) into Equation (83) and solving gives the following constants:

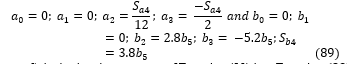
Substituting the constants of Equation (89) into Equation (83) gives;

The values stiffness coefficient obtained from the above expression is presented in Table 1. Table 2 contains the result of bending moment, shear force, and their resultants of a square CCFC rectangular plate at different span to thickness aspect ratio. These numerical values of the design factors of these quantities (∪ ̅, M ̅ and Q ̅) for a square thick plate is obtained using Equation (60) to (75) as obtained from this study. Table 3 contains the result of the values of displacement (u, v and ∪) and the stresses characteristics (σ_x,σ_y,τ_xy,τ_xz and τ_yz ) of a square CCFC rectangular plate at different span to thickness aspect ratio using Equation (60), (70) and (77). These numerical values were obtained from the Equation (60), (78) to (82). Table 4 contains the result of the value of displacement (u, v and ∪) and the stresses characteristics (σ_x,σ_y,τ_xy,τ_xz and τ_yz ) for length to breadth ratio of 1.5 for CCFC rectangular plate at different span to thickness aspect ratio. These numerical values were obtained from the Equation (60), (78) to (82). Table 5 contains the result of the values of displacement (u, v and ∪) and the stresses characteristics (σ_x,σ_y,τ_xy,τ_xz and τ_yz ) for length to breadth ratio of 2.0 for CCFC rectangular plate at different span to thickness aspect ratio. These numerical values were obtained from the Equation (60), (78) to (82). A comparative analysis of results obtained from this work is presented in Table 6 and Figure 3. This is determined the correctness of the results from the present studies, comparison was made between values from the present study and those of past scholars. Table 2 presents the result of the comparison done with the work of [30] for CCFC rectangular thick plate of 2.0 lengths to breadth ratio of various aspect ratios and the corresponding percentage difference between the values of centroidal deflection. Figure 3 contains a graph of the deflection versus span to the thickness aspect ratio of CCFC thick plate of length to breadth ratio of 2.0. This shows the comparison between the present work and that of the author in [30].

Discussion

The numerical results of stiffness coefficient of the plate is obtained from Equation (31) to (36).
Table 1: Stiffness coefficient, s values for CCFC boundary conditions

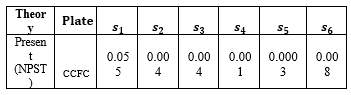
Table 2: Bending Moments, Shear Force and Stress resultants of CCFC plate for b/a = 1. 0

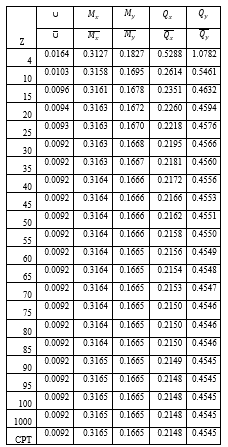
It is seen from Table 2 that as the deflection (∪), bending moment (M_x and M_y) and (Q_x and Q_y) decreases, the span to thickness ratio increases. These continue until failure occurs in the plate structure. This means that, the load that causes the plate to deflect also causes the plate material to bend simultaneously. It is observed that the value of deflection varies less as the span to thickness increase, this equal to the value of the CPT at span to thickness ratio of 100 and above. Table 2 reveals that the values of deflection at both the x and y axis decrease as the span-thickness ratio increases with a constant value of 0.0092 at the span-thickness ratio of 30.
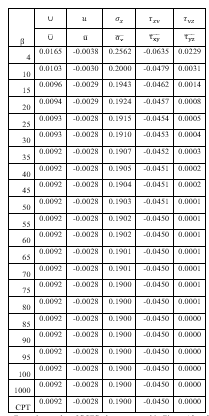
Table 3: Displacement and Stresses of CCFC plate for length to breadth ratio of 1.0

From the results of SCFS plate presented in Figure 12 to 20, it shows that the values of critical lateral imposed load q_iw decrease as the length-width ratio increases, this continues until failure occurs. This means that an increase in plate length increases the chance of failure in a plate structure. Meanwhile the values of critical lateral imposed load q_ip increase as the length-width ratio increases, this continues until safety is ensured.
From a critical look at Table 3, it is shown that the value of displacement (u, v and ∪) characteristics decreases with increases in the value of the span-thickness ratio. It is also observed in the Tables that the displacement (u, v and ∪) and stresses characteristics increases as the value of the length to breadth ratio increases. This means that, the in-plane displacement is functions of x, y and z as it varies with the plate thickness while the deflection is only a function of x and y and did not vary linearly with the thickness of the plate thickness. Also, it was deduced that the normal stress (σ_x and σ_y) and shear stress characteristics (τ_xy,τ_xz and τ_yz ) also decreases as the span-thickness ratio increases. It is also observed in the Table 3 that the stresses characteristics (σ_x,σ_y,τ_xy,τ_xz and τ_yz )increases as the value of the length to breadth ratio increases.
It can be seen that, at span to thickness ratio between 4 and 15, the value of transverse shear stress along y and z axes (τ_yz) varies between 0.022904 and 0.001370. These values of transverse shear stress (τ_yz) decrease between 0.000765 and 0.000100 at the span to thickness between 20 and 55 respectively. Hence, the value of transverse shear stress (τ_yz) is about 0.000084 and 0.00003, at the span to thickness between 60 and 100. The value becomes almost constant or equal to the value from CPT. This value becomes negligible as the value span to thickness increases. The values of transverse stress for span-thickness ratios of 100 and above are equal to the value from CPT.
In summary, there are three categories of rectangular plates. The plates whose vertical shear stress do not vary well from zero will be classified as thin plates because its value is almost equal to the value of the CPT. In between the thin and thick plate is the classified as moderate thick plate. Since the plate whose transverse shear stress varies very much from zero is categorized as thick plates. Therefore, the span-to-depth ratio for these categories of rectangular plates are: Thick plate∶a/t≤ 15; moderately thick plate: 20 ≤ a/t ≤ 55; thin plate: a/t≥60. This confirmation can be used to show the boundary between thin and thick plate. Thus, it can be deduced from this research work that thick plate is the one whose span-depth ratio value is 4 up to 15.
Table 4: Displacement and Stresses of CCFC plate for length to breadth ratio of 1.5

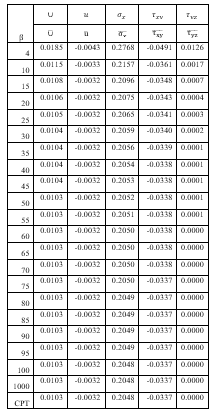
From a critical look at Table 4, it is shown that the non-dimensional displacement (u, v and ∪) characteristics decrease with increases in the value of the span-thickness ratio. It is also observed in the Tables that the displacement (u, v and ∪) and stresses characteristics increase as the value of the length to breadth ratio increases. This means that, the in-plane displacement are functions of x, y and z as it vary with the plate thickness while the deflection is only a function of x and y and did not varies linearly with the thickness of the plate thickness. Also, it was deduced that the normal stress (σ_x and σ_y) and shear stress characteristics (τ_xy,τ_xz and τ_yz ) also decrease as the span-thickness ratio increases. It is also observed in the Table 4 that the stresses characteristics (σ_x,σ_y,τ_xy,τ_xz and τ_yz )increase as the value of the length to breadth ratio increases.
It can be seen that, at span to thickness ratio between 4 and 10, the value of transverse shear stress along y and z axes (τ_yz) varies between 0.012564 and 0.001667. These values of transverse shear stress (τ_yz) decrease between 0.000724 and 0.000100 at the span to thickness between 15 and 40. Hence, the value of transverse shear stress (τ_yz) is about 0.000079 and 0.000016, at the span to thickness between 45 and 100. The value becomes almost constant or equal to the value from CPT. This value becomes negligible as the value span to thickness increases. The values of non-dimensional value of transverse stress for span-thickness ratios of 100 and above are equal to the value from CPT.
In summary, there are three categories of rectangular plates. The plates whose vertical shear stress does not very well from zero will be classified as thin plates because its value are almost equal to the value of the CPT. In between the thin and thick plate is the classified as moderate thick plate. Since the plate whose transverse shear stress varies very much from zero is categorized as thick plates. Therefore, the span-to-depth ratio for these categories of rectangular plates are: Thick plate∶a/t≤ 10; moderately thick plate: 15 ≤ a/t ≤ 40; thin plate: a/t≥45. This confirmation can be used to show the boundary between thin and thick plate. Thus, it can be deduced from this research work that a thick plate is the one whose span-depth ratio value is 4 up to 10.
Table 5: Displacement and Stresses of CCFC plate for length to breadth ratio of 2.0

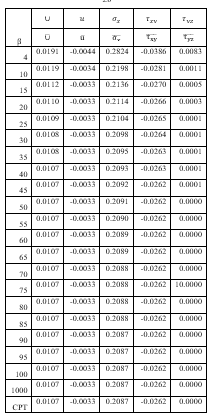
From a critical look at Table 5, it is shown that the non-dimensional displacement (u, v and ∪) characteristics decrease with increases in the value of the span-thickness ratio. It is also observed in the Tables that the displacement (u, v and ∪) and stresses characteristics increase as the value of the length to breadth ratio increases. This means that, the in-plane displacement are functions of x, y and z as it vary with the plate thickness while the deflection is only a function of x and y and did not varies linearly with the thickness of the plate thickness. Also, it was deduced that the normal stress (σ_x and σ_y) and shear stress characteristics (τ_xy,τ_xz and τ_yz ) also decrease as the span-thickness ratio increases. It is also observed in the Table 4 that the stresses characteristics (σ_x,σ_y,τ_xy,τ_xz and τ_yz )increase as the value of the length to breadth ratio increases.
It can be seen that, at span to thickness ratio between 4 and 10, the value of transverse shear stress along y and z axes (τ_yz) varies between 0.008325 and 0.001101. These values of transverse shear stress (τ_yz) decrease between 0.000478 and 0.000118 at the span to thickness between 15 and 30 respectively. Hence, the value of transverse shear stress (τ_yz) is about 0.000087 and 0.000011, at the span to thickness between 35 and 100. The value becomes almost constant or equal to the value from CPT. This value becomes negligible as the value span to thickness increases. The values of non-dimensional value of transverse stress for span-thickness ratios of 100 and above are equal to the value from CPT.
In summary, there are three categories of rectangular plates. The plates whose vertical shear stress do not vary well from zero will be classified as thin plates because its value are almost equal to the value of the CPT. In between the thin and thick plate is the classified as moderate thick plate. Since the plate whose transverse shear stress varies very much from zero is categorized as thick plates. Therefore, the span-to-depth ratio for these categories of rectangular plates are: Thick plate∶a/t≤ 10; moderately thick plate: 10 ≤ a/t ≤ 30; thin plate: a/t≥35. This confirmation can be used to show the boundary between thin and thick plate. Thus, it can be deduced from this research work that thick plate is the one whose span-depth ratio value is 4 up to 10.
In the classical plate theory (CPT), it is assumed that the plane cross sections initially normal to the plate’s mid-surface before deformation remain plane and normal to the mid-surface after deformation , and the length of such elements is not altered [31]. This is the result of neglecting the transverse shear strains, therefore value of vertical shear stress from CPT analysis is zero. Any plate whose span-to-thickness ratio is such that the value of transverse shear stress from thick plate analysis is approximately zero can be idealized as thin plate. Analyzing such plate with classical plate theory will not introduce significant errors.
Thus, these plates can be classified as moderately thick plate. Hence, analyzing them with classical plate theory will introduce significant errors. When the span-to-thickness ratio is less than 15, the value of vertical shear stress is significant even when corrected to 4 decimal places. This range of span-to-thickness ratio produces plate classified as thick plate. It is also, showed that at span-thickness ratio above 100, the values obtained from the models used herein coincide exactly with values from CPT. This is quite expected since we assumed in CPT analyses that at span-thickness ratios from 100 and above, a plate can be taking as being thin.
Table 6: Comparative analysis of results from the present work and literature for 2.0 aspect ratio (α)

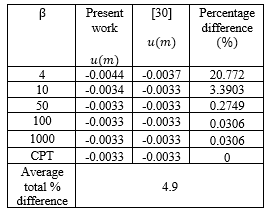
From Table 6, it is shown that the present study predicts slightly higher values of in-plane displacement along the direction of x coordinate with highest percentage difference of 20.8% which occur at length to breadth aspect ratio of 4. This proves the safety of the present model. The present study converges with the work as value of span to thickness ratio increases and becomes the same or equal to CPT value at span to thickness ratio of 100. The rate of convergence can be seen in Figure 3. The total average percentage difference between the present study and the author in [30] is 4.9%. This means that at about 95 % confidence level, the values from the present study are the same with those of [30]. This higher confidence level proved that the polynomial shear deformation theory can be used with confidence for stress and bending analysis of thick rectangular plate clamped on three edges, and free at the other remaining edge.

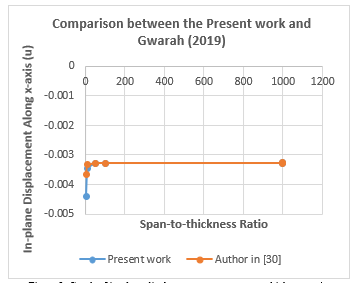Figure 3: Graph of in-plane displacement versus span-to-thickness ratio

 

Conclusion

Stress analysis of thick rectangular plate using higher order polynomial shear deformation theory has been investigated. From the study this conclusion has been drawn:
It is concluded that the values of transverse shear stress obtained by this theory achieve accepted vertical shear stress to the thickness of plate variation and satisfied the transverse flexibility of condition at the top and bottom faces of the plate while predicting the flexural characteristics for an isotropic rectangular CCFC plate.
The result moment and stresses obtained by present work using polynomial shear deformation theory agreed well with those of refined plate theory, but varied more with value of CPT. This validates the efficacy of the present theory in the thick plate analysis.
The governing differential equations and associated boundary conditions obtained are variationally consistent and can be used with confidence in the analysis of rectangular thick plate.

Recommendation of Future Scope of Studies

This lies in the establishment shear deformation/displacement function for free vibration and buckling analysis of rectangular or circular thick plate. Then determining the displacement and stress parameters for the plate using virtual work principles.

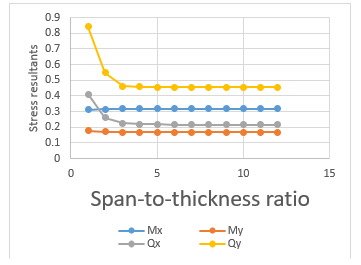Figure 4: Graph of span to thickness ratio versus stresses of a square plate

 

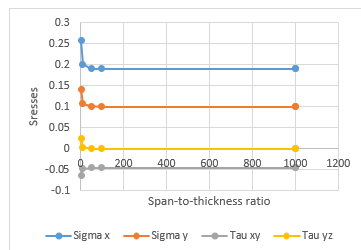Figure 5: Graph of span to thickness ratio versus stresses for length to breadth ratio of 1.0

Figure 6: Graph of span to thickness ratio versus stresses for length to breadth ratio of 1.5

 

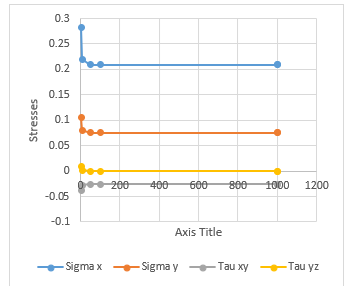Figure 7: Graph of span to thickness ratio versus stresses for length to breadth ratio of 2.0

Conflict of Interest Statement

There is no conflict of interest associated with this work.

1. F.C. Onyeka, F.O. Okafor, H.N. Onah, “Displacement and stress analysis in shear deformable thick plate,” International Journal of Applied Engineering Research, 13(11), 9893-9908, 2018, https://www.ripublication.com/ijaer18/ijaerv13n11_161.pdf
2. H.O. Ozioko, O.M. Ibearugbulem, J.C. Ezeh, U.C. Anya, “Algorithm for exact solution of thick anisotropic plates,” Scholar Journal of Applied Sciences and Research, 2(4), 11 – 25, 2019, https://www.innovationinfo.org/articles/SJASR/SJASR-4-225.pdf
3. Y.M. Ghugal, P.D. Gajbhiye, “Bending analysis of thick isotropic plates by using 5th order shear deformation theory,” Journal of Applied and Computational Mechanics, 2(2), 80 – 95, 2016, https://jacm.scu.ac.ir/article_12366_b9e3037fda12c4f05a83ea31f80271e6.pdf
4. K. Chandrashekhara, “Theory of plates. University Press (India) Limited,” 2001.
5. N.P. Kruyt, et al., “A strain–displacement–fabric relationship for granular materials. International journal of solids and structures, 165, 14-22, 2019. https://doi.org/10.1016/j.ijsolstr.2019.01.028
6. K. Shwetha, V. Subrahmanya, P. Bhat, “Comparison between thin plate and thick plate from navier solution using matlab software,” International Research Journal of Engineering and Technology (IRJET), 5(6), 2675 – 2680, 2018, https://www.irjet.net/archives/V5/i6/IRJET-V5I6500.pdf
7. Md. Roknuzzaman, Md.B. Hossain, Md.R. Haque, T.U. Ahmed, “Analysis of rectangular plate with opening by finite difference method,” American Journal of Civil Engineering and Architecture, 3(5), 165 – 173, 2015, doi: 10.12691/ajcea-3-5-3
8. P.S. Gujar, K.B. Ladhane, “Bending analysis of simply supported and clamped circular plate,” International Journal of Civil Engineering (SSRG-IJCE), 2(5), 45 – 51, 2015, DOI: 10.14445/23488352/IJCE-V2I5P112
9. O.M. Ibearugbulem, J.C. Ezeh, L.O. Ettu, “Pure bending analysis of thin rectangular SSSS plate Using Taylor-Mclaurin series,” International Journal of Civil and Structural Engineering, 3(4), 685 – 691, 2013, DOI: 10.6088/ijcser.201203013062
10. G.R. Kirchhoff, “U’’ber das Gleichgewicht and die bewegung einer elastschen scheibe,” Journal f’’ ur die reine und angewandte Mathematik,, 40, 51-88 (in German), 1850, DOI:10.1515/crll.1850.40.51
11. G.R. Kirchhoff, “U’’ber die Schwingungen einer kriesformigen elastischen scheibe,” Annalen der Physik und Chemie, 81, 258 – 264 (in German), 1850.
12. G.O. Mathieu, D. Tyekolo, S. Belay, “The nonlinear bending of simply supported elastic plate,” Rudn Journal of Engineering Researches, 18(1), 58-69, 2017, DOI: 10.22363/2312-8143-2017-18-1-58-69
13. D. W. Zietlow, D. C. Griffin, T. R. Moore, “The limitations on applying classical thin plate theory to thin annular plates clamped on the inner boundary,” AIP Advances, 2, 042103, 2012, https://doi.org/10.1063/1.4757928
14. S.P. Timoshenko, S. Woinowsky-Krieger, “Theory of plates and shells,” McGraw-Hill/Springer, New York, NY, USA, 1959.
15. B.O. Mama, C.U. Nwoji, C.C. Ike, H.N. Onah, “Analysis of simply supported rectangular Kirchhoff plates by the finite Fourier sine transform method,” International Journal of Advanced Engineering Research and Science, 4(3), 285 – 291, 2017, DOI: 10.22161/ijaers.4.3.44
16. J.C. Ezeh, O.M. Ibearugbulem, L.O. Ettu, L.S. Gwarah, I.C. Onyechere, “Application of shear deformation theory for analysis of CCCS and SSFS rectangular isotropic thick plates,” Journal of Mechanical and Civil Engineering (IOSR-JMCE), 15(5), 33 – 42, 2018, DOI: 10.9790/1684-1505023342
17. A.S. Sayyad, Y.M. Ghugal, “Bending and free vibration analysis of thick isotropic plates by using exponential shear deformation theory,” Applied and Computational Mechanics, 6, 65–82, 2012, https://www.kme.zcu.cz/acm/acm/article/view/171
18. C. Onyechere, O.M. Ibearugbulem, U.C. Anya, L. Anyaogu, C.T.G. Awodiji, “Free-vibration study of thick rectangular plates using polynomial displacement functions,” Saudi Journal of Engineering and Technology, 2020, 10.36348/sjet.2020.v05i02.006
19. S.P. Timoshenko, S. Woinowsky-Krieger, “Theory of Plates and shells (2nd Ed.),” Auckland: McGraw-Hill Inc, 1959.
20. F.O. Okafor, O.J. Udeh, “Direct method of analysis of an isotropic rectangular plate using characteristic orthogonal polynomials,” Nigerian Journal of Technology, 34(2), 232-239, 2015, http://dx.doi.org/10.4314/njt.v34i2.3
21. Y. Zhong, Q. Xu, “Analysis bending solutions of clamped rectangular thick plate,” Hindawi Mathematical Problems in Engineering, 20, 1- 6, 2017, https://doi.org/10.1155/2017/7539276
22. O.M. Ibearugbulem, J.C. L.O. Ettu, L.S. Gwarah, “Bending analysis of rectangular thick plate using polynomial shear deformation theory,” IOSR Journal of Engineering (IOSRJEN), 8(9), 53-61, 2018, http://www.iosrjen.org/Papers/vol8_issue9/Version-3/J0809035361.pdf
23. K. Hassan, S. Guirguis, H. El-Hamouly, “Bending of an elastic rectangular clamped plate using Bergan-Wang approach,” African Journal of Engineering Research, 5(1), 7 – 17, 2017, http://www.netjournals.org/z_AJER_16_024.html
24. A.Y. Grigorenko, A.S. Bergulev, S.N. Yaremchenko, “Numerical solution of bending problems for rectangular plates,” International Applied Mechanics, 49(1), 81 – 94, 2013, https://doi.org/10.1007/s10778-013-0554-1
25. B.S. Reddy, “Bending behaviour of exponentially graded material plates using new higher order shear deformation theory with stretching effect,” International Journal of Engineering Research, 3(1), 124-131, 2014.
26. F.C. Onyeka, O.M. Ibearugbulem, “Load analysis and bending solutions of rectangular thick plate,” International Journal on Emerging Technologies, 11(3), 1103–1110, 2020.
27. F.C. Onyeka, F.O. Okafor, H.N. Onah, “Application of exact solution approach in the analysis of thick rectangular plate,” International Journal of Applied Engineering Research, 14(8), 2043-2057, 2019, http://www.ripublication.com/ijaer19/ijaerv14n8_39.pdf
28. F.C. Onyeka, O.T. Edozie, “Application of higher order shear deformation theory in the analysis of thick rectangular plate,” International Journal on Emerging Technologies, 11(5), 62–67, 2020.
29. O.M. Ibearugbulem, F.C. Onyeka, “Moment and stress analysis solutions of clamped rectangular thick plate,” European Journal of Engineering Research and Science, 5(4), 531-534, 2020, https://doi.org/10.24018/ejers.2020.5.4.1898
30. L.S. Gwarah, “Application of shear deformation theory in the analysis of thick rectangular plates using polynomial displacement functions,” A published PhD. thesis presented to the school of Civil Engineering, Federal University of Technology, Owerri, Nigeria, 2019, https://futospace.futo.edu.ng/bitstream/handle/123456789/2956/Gwarah_Application_2019.pdf?sequence=1&isAllowed=y
31. E. Ventsel, T. Krauthammer, “Thin plates and shells theory, analysis and applications,” Maxwell Publishers Inc; New York, 2001.

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country