1. Introduction

With the development of industry and technology, various industrial rotating machines have become capable of handling high speeds and heavy loads, which cause massive mechanical and thermal loads, resulting in their breakdown [1]. When a rotating machine fails, fault diagnosis is very important as time and economic loss can occur. Therefore, a countermeasure is required to check the condition of rotating machines and to diagnose faults. According to statistical data, 45%–55% of failures in rotating machines are due to faults in the bearings [2]. Monitoring the condition of the rotating machine to detect its faults helps reduce losses [3]-[5].

Machine learning algorithm is a common method of diagnosing faults of rotating machines.

In general, the fault diagnosis method of rotating machines using a machine learning algorithm is divided into four steps: (1) data acquisition, (2) feature extraction, (3) machine learning algorithm training (neural network training), and (4) classification [6]-[9].

The data acquisition step is the process of obtaining a signal that indicates the state of a rotating machine using a sensor. A noise-measuring device, the electric current signals of the motor, and vibration signals are used to obtain signs that indicate the state of the rotating machine [10]-[12]. Among them, the commonly used method detects the fault of the rotating machine by obtaining vibration signal data that are the easiest to measure and can clearly indicate the state of the rotating machine [13].

In the feature extraction step, signs that indicate the state of the rotating machine are extracted from the vibration signals. In general, a signal measured from the rotating machine consists of a mixture of noise and a sign indicating the state of the rotating machine. If vibration signals containing noise are used as input values in the machine learning algorithm, it is difficult to accurately diagnose the state of the rotating machine due to the noise. Hence, noise should be removed from the vibration signals through feature extraction to use them as input values for the machine learning model.

The most common feature extraction methods use filters and signal decomposition [14]-[16]. The widely used methods of diagnosing faults in vibration signals include empirical mode decomposition (EMD) technique, which uses intrinsic mode function (IMF) to decompose the signals, and wavelet transform method, which uses the wavelet function to decompose the signals.

The EMD technique yields outstanding performance when detecting faults of rotating machines [17]. However, it requires to combine sub-band signals because the sub-bands decomposed by IMF are generally not orthogonal to each other [18].

The wavelet transform method has the advantage of adjusting the cycle and amplitude to show the features more clearly in the vibration signals of rotating machine and to remove the noise included in the vibration signals [19], [20].

In the machine learning algorithm training step, the algorithm is trained by using the features extracted from the vibration signals as input values for the machine learning algorithm. Among the various machine learning algorithms, the algorithms using deep learning show better performance, and among the deep learning algorithms, convolution neural network (CNN) shows superior performance.

In the classification step, the test data, which are not used in the training step, are used to classify the state of the rotating machine, and the indicator showing the performance of the model can be derived.

Eren used CNN to diagnose faults of rotating machines but diagnosed their faults based solely on the performance of the CNN model without considering the method of removing the noises [21]. Meanwhile, Yuan used discrete wavelet transform and CNN to improve the performance of the existing rotating machine fault diagnosis model. However, there was a limitation in showing the suitable performance in a poor environment where noise can be measured substantially because the experiment was conducted without reflecting noise [22].

In this study, we used continuous wavelet transform method, to decompose vibration signals into noise, and signals indicating the state of the rotating machine to detect its faults, and extracted signals that can be used to detect the faults of the rotating machine, from the decomposed signals. The extracted features were used as input values of CNN, a deep-learning technique, to classify the faulty state of the rotating machine. Furthermore, we added white Gaussian noise to investigate the effectiveness of the corresponding algorithm through performance comparison between the model and conventional machine learning methods in a poor environment where a large amount of noise can be observed.

2. Theory

2.1. Continuous wavelet transform

The advantage of the wavelet transform method is that the wavelet function with dynamic resolution can be used to efficiently analyze the vibration signals, unlike Fourier transform, which cannot accurately display the characteristics of non-cyclic signals due to the fixed resolution [23][24]. The time series analysis using the wavelet transform is defined as follows.

In Eq. (1), the signal is decomposed by shifting the wavelet function to the time axis by  and scaling by a. If the mother wavelet is given, then continuous wavelet transform (CWT) of the signal f(t) is defined by Eq. (2).

The wavelet coefficient obtained in Eq. (2) indicates the similarity between f(t) and . The wavelet transform produces the decomposition of the time scale of f(t), but the time-frequency region can be obtained by the pseudo-frequencies.

The relationship between the scale and the pseudo-frequencies changes depending on the center of the wavelet function, performance of the scale, and sampling cycle and maximizes the spectrum of the wavelet function with the given scale. The relationship of these parameters is expressed by Eq. (3).

In Eq. (3),  denotes the center frequency,  is the sampling cycle, and  shows the result of the pseudo-frequency. The entire signal is synthesized by applying the inverse continuous wavelet transform (ICWT) defined in Eq. (4) as follows:

here,  is the acceptance constant obtained when the mother wavelet satisfies all requirements.

2.2. Convolutional Neural Network

CNN was inspired by the principle of recognizing objects in the visual cortex of the brain and was derived from the field of deep learning. It consists of convolutional layer, pooling layer, and fully connected layer [25].

The main function of a convolutional layer is to obtain a feature map through the convolutional operation of filter for the input. The convolutional layer typically consists of learnable kernel and bias. The size of the kernel corresponds to the size of the filter, and the depth of the kernel corresponds to the number of channels in the feature map. The input of the convolutional layer can be calculated by the weight and the inner product of cognitive region, as expressed by Eq. (5).

      In Eq. (5),  refers to the convolutional value of ith channel in the convolutional layer l,  refers to the ith output of the pooling layer l-1,  refers to the kernel of the convolutional layer l,  refers to the bias of the jth channel in the convolutional layer l, and * refers to the convolutional operation.

      After the convolutional operation is completed, the value of convolutional layer is calculated according to the activation function. The role of the activation function is to perform the nonlinear projection for the input of the neuron. Rectified linear unit (ReLU), one of activation functions, is used for pattern recognition. The ReLU function shows excellent performance in accelerating convergence and solving vanishing gradient problems. Therefore, the ReLU is used as the activation function of a convolutional layer, and the output of convolutional layer 1 can be expressed by Eq. (6).

Here,  represents the output of the jth channel in the convolutional layer l, and ( ) refers to the activation function.

      After the convolutional layer operation, the pooling layer is used to extract additional features. It plays a role of reducing the dimensions of the output of the previous layer. Therefore, the key purpose of this layer is to reduce the volume of data to reduce the computation time on the computer. Types of pooling layer include max pooling, average pooling, logarithmic pooling, and weight pooling.

      Max pooling is used to classify operation because it can speed up the convergence and improve the generalization. Max pooling function can be expressed by Eq. (7).

       represents the window of the pooling layer that can shift to a certain step, and  correspond to the dimensions of the pooling layer. Further,  refers to the output of jth channel in the convolutional layer, and  refers to the overlap between the pooling layer and the channel’s output.

      In general, the CNN model contains multiple convolutional and pooling layers and extracts feature maps sequentially. The extracted feature map is transformed into a vector, which is used as an input of a fully connected layer. The main function of the fully connected layer is to extract additional features and connect the output step to the softmax classifier. A fully connected layer usually consists of 2 or 3 hidden layers, and all neurons of a hidden layer can be shown by Eq. (8).

       refers to the weight matrix of the fully connected layer,  represents the bias, and  represents the activation function of the fully connected function.

2.3. Batch normalization

In general, as the depth of the neural network structure increases, the distribution of features changes, and the overall distribution gradually approaches both ends of the nonlinear function value interval. This phenomenon is called gradient diffusion, which causes a problem with the convergence of the model. To resolve this problem, the Google DeepMind team proposed batch normalization technique in 2014 [26].

The key purpose of the batch normalization technique is to revert the distribution of all neurons to the standard normal distribution through a specific normalization method. Batch normalization can re-parameterize almost all neural networks and, thus, can be used for any hidden layer. Batch normalization, which optimizes neural networks, can improve the performance of neural networks, such as faster convergence, faster learning time, ability to allow higher learning rate, and easier initialization of weights.

First, normalization can make each scalar feature with the mean 0 and the unit variance, as expressed in Eq. (9).

However, if Eq. (9) is used to directly normalize the features of a certain layer, the learned features can be affected, thereby reducing the performance of the neural network. To overcome this problem, each normalized  is modified based on two adjustment parameters,  and , aiming at scaling and shifting the normalized values. This process can be expressed by Eq. (10).

here,  and  are parameters that can be used to learn the method of recovering the characteristic distribution of the existing neural network. By setting  and , the existing activation can be restored. In this case, the activation values are stably distributed during learning.

Second, because the mini-batch technique is used in training process, the specific activation  that possesses the B value in the mini-batch is , and the corresponding transformation is . Therefore, the batch normalization transform →  can be represented by Eqs. (11), (12), (13), and (14).

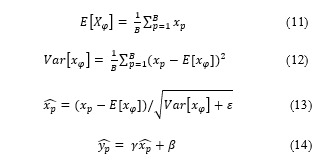here,  is a constant and is used to avoid undefined gradient values.

3. Experiment setup

This study required constructing a variety of dataset to enhance the accuracy of the fault detection of the rotating machine. Thus, we utilized the Case Western Reserve University Bearing Fault Database, which is widely used for fault detection of conventional rotating machines [27]. Because various researchers have conducted experiments using this database, there are several advantages: the data are reliable, and the performance comparison can be conducted with other learning algorithms. As shown in Figure 2, the test bench consists of a motor on the left, a torque transducer/encoder on the center, and a dynamometer on the right.

The vibration signals were measured in a total of four types: normal, ball fault, inner race fault, and outer race fault. The levels of crack consisted of 0.007, 0.014, and 0.021 inch, and the levels of load consisted of 0 HP, 1 HP, 2 HP, and 3 HP.

Figure 1 shows the fault detection process of rotating machine using vibration signals. Data having cracks of 0.007 inch were used, and the dataset was classified into Case 1 (0 HP), Case 2 (1 HP), Case 3 (2 HP), and Case 4 (3 HP), depending on the level of load. Each case consisted of 4,368 data: 1,092 for normal data, 1,092 for ball faults, 1,092 for inner race faults, and 1,092 for outer race faults. In addition, white Gaussian noise was increased in the vibration signals having cracks of 0.007 inch to verify the robustness to noise by CWT. As shown in Figure 3, the sample data were constructed to train the CNN model by performing the segmentation with 4,392 signals where white Gaussian noise was added in the actual vibration signals. For each sample data, continuous wavelet functions, such as morse, morlet, and bump wavelet, were applied, and CWT was used. The conversion to images with the size of 224 × 224 was performed to use them as inputs of CNN after signal preprocessing, as shown in Figure 2.

Figure 1: Experiment setup

The CNN was constructed with 8 3 × 3 filters for the first layer of the CNN model, 16 3 × 3 filters for the second layer, and 32 3 × 3 filters for the third layer. Additional features were extracted through the fully connected layer, and the faults of rotating machine were classified using the softmax classifier. After the convolutional operation was completed in each layer, batch normalization and max pooling, a type of pooling layer, were applied.

To conduct the training of the constructed CNN model, 70% of 4,368 data in the entire dataset were used for the training process of the CNN model, and the rest were used to validate the trained CNN model. To validate the performance of the trained model, comparative analysis was performed with the DNN technique, a conventional vibration signal analysis method using artificial neural network (ANN).

Figure 2: Representation of proposed fault diagnosis structure

4. Simulation

As shown in Fig 3, CWT was performed through the continuous wavelet functions—namely, morse, morlet, and bump wavelet—using the white Gaussian noise-added vibration signals, and the results were used as input values of the CNN model.

To compare the performance of the generated CNN model, comparative analysis was performed using the ANN model by extracting statistical parameters, such as peak, entropy, skewness,
kurtosis, variance, and rms, and using them as the input values of the ANN, as shown in Figure 4.

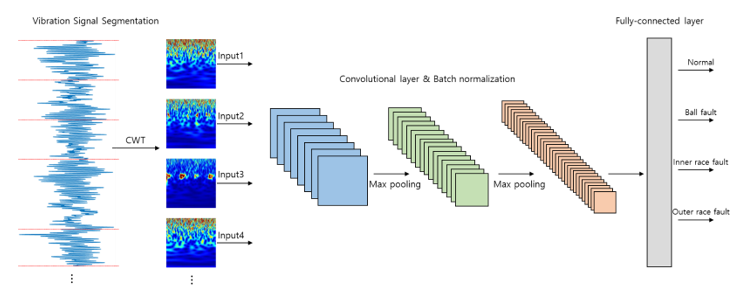Figure 3: The process of fault diagnosis in vibration signal using CWT & CNN.

Figure 4: Result of fault diagnosis (accuracy & loss) – (a) Case1(=0HP), (b) Case2(=1HP), (c) Case3(=2HP), (d) Case4(=3HP)

To compare the performance of the CNN model and the CWT for noise removal, we compared the accuracy and loss for each signal-to-noise ratio (SNR) level with those of the existing method, in which the parameters are extracted from the vibration signals and then used as inputs of the ANN, as shown in Figure 4.

When the SNR was 1 dB in the Case 1 (0 HP) dataset, the accuracy of the CNN model using morlet wavelet was 95.31% with a loss of 0.05869, that of the CNN model using bump wavelet was 90.25% with a loss of 0.11, and that of CNN model using morse wavelet was 90.13% with a loss of 0.124. Therefore, the performance was excellent compared to that of the ANN model. Furthermore, when the SNR level was reduced step by step, the CNN model using CWT showed that the accuracy converged to 100% at the SNR level of 8 dB, whereas the ANN model showed that the accuracy converged to 100% when the SNR level was 15 because of performance degradation in the denoising function.

In terms of loss, the CNN model using CWT showed the convergence close to 0 when the SNR level was 11 dB. However, the model using the ANN showed the convergence to 0 when the SNR level was 18 dB, indicating that the performance was lower than that of the CNN model.

When SNR was 1 dB in the Case2 (1 HP) dataset, the accuracy of the CNN model using morlet wavelet was 72.82% with a loss of 0.6254, that of the CNN model using bump wavelet was 86.12% with a loss of 0.3602, and that of the CNN model using morse wavelet was 86.09% with a loss of 0.3597. The differences were not large compared to those of the ANN model (accuracy: 71.7% and loss: 0.1388). When the SNR level was reduced, the accuracy converged to 100% at the SNR level of 10 dB in the CNN model using CWT. Conversely, the accuracy converged to 100% when the SNR level became 14 dB in the ANN model. Furthermore, in terms of loss, the CNN model using CWT showed the convergence to 0 when the SNR level was 10 dB, whereas the ANN model showed the convergence to 0 when the SNR level was 14 dB.

When the SNR level was 1 dB in the Case 3 (2 HP) dataset, the accuracy of the CNN model using morlet wavelet was 87.04% with a loss of 0.31, that of the CNN model using bump wavelet was 86.72% with a loss of 0.409, and that of the CNN model using morse wavelet 86.61% with a loss of 0.1232. Therefore, the performance was excellent compared to that of the ANN model (accuracy: 71.9% and loss: 0.1432).

When the SNR level was 1 dB in the Case 4 (3 HP) dataset, the accuracy of the CNN model using morlet wavelet was 85.13% with a loss of 0.2947, that of the CNN model using bump wavelet was 83.37% with a loss of 0.34924, and that of the CNN model using morse wavelet was 85.03% with a loss of 0.4238. Meanwhile, the accuracy and loss of the ANN model were 69.3% and 0.1431, respectively. As the noise signal decreased, the CNN model using CWT showed that the accuracy and the loss converged to 100% and 0, respectively, when the SNR level was 10 dB. However, the ANN model showed that the accuracy converged to 100% when the SNR level was 14 dB, and the loss converged to 0 when the SNR level was 16 dB. Based on these results of the vibration signal analysis, we have confirmed that the CNN model using CWT is more robust to noise than the existing method. Furthermore, we used the pooling layer and batch normalization to reduce the training time of the CNN model and improve the performance, thereby confirming the effectiveness and stability of the method, in comparison with the conventional signal analysis method.

5. Conclusion

In this study, vibration signal analysis was conducted to diagnose faults of rotating machines. Furthermore, to investigate the performance in actual work site environment, we conducted vibration signal analysis. Hence, we added white Gaussian noise in the vibration signals step by step and applied CWT. Subsequently, we extracted the images to use them as input values of the CNN. When we added the white noise from 1dB to 20dB to vibration signal, the proposed method converged to 100% accuracy from 8dB at no load, at 10dB at presence of load. The analysis results confirmed that CWT-applied CNN model showed superior performance compared to the existing signal analysis method.

6. Acknowledgment

This work was supported by the Technology Innovation Program (or Industrial Strategic Technology Development Program) (Grant number: No.20010132, development of the systematization platform for expending the industry of xEV parts) and 2019 Industrial Employment Crisis Area Technology (Grant number: P075100005, ESS Safety certification system for ships and international testing laboratory) funded By the Ministry of Trade, Industry & Energy(MOTIE, Korea).

1. A. H. Bonnett, G. C. Soukup, “Cause and analysis of stator and rotor failures in three-phase squirrel-cage induction motors”, IEEE Transaction on Industry Applications, 28(4), 921-937, 1992, 10.1109/PAPCON.1991.239667
2. Nandi, S., Toliyat, H. A., & Li, X., “Condition monitoring and fault diagnosis of electrical motors – a review”, IEEE Transactions on Instrumentation and Measurement, 65(11), 2646-2656, 2005, 10.1109/CMD.2008.4580260
3. B. Dolenc, P. Boskoski, D.Juricic , “Distributed bearing fault diagnosis based on vibration analysis”, Mech. Syst. Signal Process, 66-67, 521-532, 2016, https://doi.org/10.1016/j.ymssp.2015.06.007
4. L. Barbini, A.J. Hillis, J.L. du Bois, “Amplitude-cyclic frequency decomposition of vibration signals for bearing fault diagnosis based on phase editing”, Mech. Syst. Signal Process, 103, 76-88, 2018, https://doi.org/10.1016/j.ymssp.2017.09.044
5. E. EI-Thalji, Jantunen, “A summary of fault modeling and predictive health monitoring of rolling bearings”, Mech. Syst. Signal Process, 60-61, 252-272, 2015, https://doi.org/10.1016/j.ymssp.2015.02.008
6. W.K. Xi, Z.X. Li, Z. Tian, et al., “A feature extraction and visualization method for fault detection of marine diesel engines”, Measurement, 116, 429-437, 2018, https://doi.org/10.1016/j.measurement.2017.11.035
7. J.B. Yu, J.X Lv, “Weak fault feature extraction of rolling bearings using local mean decomposition-based multilayer hybrid denoising”, IEEE Trans. Instrum. Meas., 66(12), 3148-3159, 2017, 10.1109/TIM.2017.2751878
8. M. Amar, I. Gondal, C. Wilson, “Vibration spectrum imaging: a novel bearing fault classification approach”, IEEE Trans Ind. Electron., 51(1), 494-502, 2015, 10.1109/TIE.2014.2327555
9. B. Madahian, L.Y. Deng, R. Homayouni, “Development of a literature informed Bayesian machine learning method for feature extraction and classification”, BMC Bioinform, 16. , 2015, https://doi.org/10.1186/1471-2105-16-S15-P9
10. Chacon, J.L.F., Kappatos, V., Balachandran, W., & Gan, T.-H., 2015 “A novel approach for incipient defect detection in rolling bearings using acoustic emission technique”, Applied Acoustics, 89, 88-100., 2015, https://doi.org/10.1016/j.apacoust.2014.09.002
11. S. Singh, Kumar, A., & Kumar, N., ” Motor current signature analysis for bearing fault detection in mechanical system”, Procedia Materials Science, 6, 171-177, 2014, https://doi.org/10.1016/j.mspro.2014.07.021
12. J. Zarei, Tajeddini, M. A., & Karimi, H. R., “Vibration analysis for bearing fault detection and classification using an intelligent filter”, Mechatronics, 24(20), 151-157, 2014, https://doi.org/10.1016/j.mechatronics.2014.01.003
13. Kharche, P., P., & Ksgirsagar, S. V., “Review of fault detection in rolling element bearing”, International Journal of Innovative Research in Advanced Engineering, 1(5), 169-174, 2014, https://ijirae.com/images/downloads/vol1issue5/JNME10092(33).pdf
14. W. He. Z.N. Jiang., K. Feng, “Bearing fault detection based on optimal wavelet filter and sparse code shrinkage”, Measurement, 42(7), 1092-1102. 2009, https://doi.org/10.1016/j.measurement.2009.04.001
15. X. L. An, H. T. Zeng, W. W. Yang, et al., 2017, “Fault diagnosis of a wind turbine rolling bearing using adaptive local iterative filtering and singular value decomposition”, T. I. Meas. Control., 39(11), 1643-1648, 2017, https://doi.org/10.1177/0142331216644041
16. X. An, Weiwei Yang, Xuemin An, “Vibration signal analysis of a hydropower unit based on adaptive local iterative filtering”, P. I. Mech. Eng. C-J Mec. 231(7), 1339-1353, 2017, https://doi.org/10.1177/0954406216656020
17. Y. Li, M. Xu, X. Liang, “Huang Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings”, IEEE Trans. Ind. Electron., 61(8), 6506-6517, 2017, 10.1109/TIE.2017.2650873
18. J.P. Yang, P.Z. Li, Yang, et al., “An improved EMD method for modal identification and a combined static-dynamic method fir damage detection”, Sound Vib., 240, 242-260, 2018, https://doi.org/10.1155/2014/317954
19. Q.B. He, “Vibration signal classification by wavelet packet energy flow manifold learning”, J. Sound Vib., 332(7), 1881-1894, 2013, https://doi.org/10.1016/j.jsv.2012.11.006
20. Q. Pan, L. Zhang, G. Dai, H. zhang, “Two denoising methods by wavelet transform”, IEEE Trans. Signal Processing, 47(12), 3401-3406, 1991, https://doi.org/10.1109/78.806084
21. Eren L., “Bearing Fault Detection by One-Dimensional Convoltional Neural Networks”, Mathematical Problems in Engineering, https://doi.org/10.1155/2017/8617315
22. Yuan Xie, Tao Zhang, “Feature Based on DWT and CNN for Rotating Machinery Fault Diagnosis”, IEEE Trans. CCDC, 29, 3861-3866, 2017 10.1109/CCDC.2017.7979176
23. V. Pichot, J.M. Gaspoz, S. Molliex, A. Antoniadis, Wavelet transform to quantify heart rate variability and to assess its instantaneous changes, J. Appl. Physiol.86(3), 1081–1091, 1991, http://dx.doi.org/10.1152/jappl.1999.86.3.1081
24. L.G. Gamero, J. Vila, F. Palacios, Wavelet transform analysis of heart rate variability during myocardial ischaemia, Med. Biol. Eng. Comput. 40, 72–78, 2002, http://dx.doi.org/10.1007/BF02347698.
25. X. Li, W. Zhang, Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction, Reliab. Eng. Syst. Saf. 182 208–218, 2019, http://dx.doi.org/10.1016/j.ress.2018.11.011.
26. J. Wang, S. Li, B. Han, et al., Construction of a batch-normalized autoencoder network and its application in mechanical intelligent fault diagnosis, Meas. Sci. Technol. 30, 1–14, 2019, http://dx.doi.org/10.1088/1361-6501/aaf319.
27. K.A. Loparo, “Bearing fault diagnosis based on wavelet transform and fuzzy inference”, Mechanical System and Signal Processing, 2005, https://doi.org/10.1016/S0888-3270(03)00077-3

Citations by Dimensions

Citations by PlumX

Google Scholar

Crossref Citations

1. Mya Soe Soe Moe, Win Mar Oo, "Hybrid Feature Selection for Anomaly Detection in IoT Network Intrusion Detection Systems", Advances in Science, Technology and Engineering Systems Journal, vol. 11, no. 2, pp. 17–29, 2026. doi: 10.25046/aj110203
2. Vikas Thammanna Gowda, Landis Humphrey, Aiden Kadoch, YinBo Chen, Olivia Roberts, "Multi Attribute Stratified Sampling: An Automated Framework for Privacy-Preserving Healthcare Data Publishing with Multiple Sensitive Attributes", Advances in Science, Technology and Engineering Systems Journal, vol. 11, no. 1, pp. 51–68, 2026. doi: 10.25046/aj110106
3. David Degbor, Haiping Xu, Pratiksha Singh, Shannon Gibbs, Donghui Yan, "StradNet: Automated Structural Adaptation for Efficient Deep Neural Network Design", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 6, pp. 29–41, 2025. doi: 10.25046/aj100603
4. Glender Brás, Samara Leal, Breno Sousa, Gabriel Paes, Cleberson Junior, João Souza, Rafael Assis, Tamires Marques, Thiago Teles Calazans Silva, "Machine Learning Methods for University Student Performance Prediction in Basic Skills based on Psychometric Profile", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 4, pp. 1–13, 2025. doi: 10.25046/aj100401
5. khawla Alhasan, "Predictive Analytics in Marketing: Evaluating its Effectiveness in Driving Customer Engagement", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 3, pp. 45–51, 2025. doi: 10.25046/aj100306
6. François Dieudonné Mengue, Verlaine Rostand Nwokam, Alain Soup Tewa Kammogne, René Yamapi, Moskolai Ngossaha Justin, Bowong Tsakou Samuel, Bernard Kamsu Fogue, "Explainable AI and Active Learning for Photovoltaic System Fault Detection: A Bibliometric Study and Future Directions", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 3, pp. 29–44, 2025. doi: 10.25046/aj100305
7. Surapol Vorapatratorn, Nontawat Thongsibsong, "AI-Based Photography Assessment System using Convolutional Neural Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 2, pp. 28–34, 2025. doi: 10.25046/aj100203
8. Khalifa Sylla, Birahim Babou, Mama Amar, Samuel Ouya, "Impact of Integrating Chatbots into Digital Universities Platforms on the Interactions between the Learner and the Educational Content", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 1, pp. 13–19, 2025. doi: 10.25046/aj100103
9. Ahmet Emin Ünal, Halit Boyar, Burcu Kuleli Pak, Vehbi Çağrı Güngör, "Utilizing 3D models for the Prediction of Work Man-Hour in Complex Industrial Products using Machine Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 6, pp. 01–11, 2024. doi: 10.25046/aj090601
10. Joshua Carberry, Haiping Xu, "GPT-Enhanced Hierarchical Deep Learning Model for Automated ICD Coding", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 4, pp. 21–34, 2024. doi: 10.25046/aj090404
11. Haruki Murakami, Takuma Miwa, Kosuke Shima, Takanobu Otsuka, "Proposal and Implementation of Seawater Temperature Prediction Model using Transfer Learning Considering Water Depth Differences", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 4, pp. 01–06, 2024. doi: 10.25046/aj090401
12. Brandon Wetzel, Haiping Xu, "Deploying Trusted and Immutable Predictive Models on a Public Blockchain Network", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 72–83, 2024. doi: 10.25046/aj090307
13. Anirudh Mazumder, Kapil Panda, "Leveraging Machine Learning for a Comprehensive Assessment of PFAS Nephrotoxicity", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 62–71, 2024. doi: 10.25046/aj090306
14. Nguyen Viet Hung, Tran Thanh Lam, Tran Thanh Binh, Alan Marshal, Truong Thu Huong, "Efficient Deep Learning-Based Viewport Estimation for 360-Degree Video Streaming", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 49–61, 2024. doi: 10.25046/aj090305
15. Sami Florent Palm, Sianou Ezéckie Houénafa, Zourkalaïni Boubakar, Sebastian Waita, Thomas Nyachoti Nyangonda, Ahmed Chebak, "Solar Photovoltaic Power Output Forecasting using Deep Learning Models: A Case Study of Zagtouli PV Power Plant", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 41–48, 2024. doi: 10.25046/aj090304
16. Taichi Ito, Ken’ichi Minamino, Shintaro Umeki, "Visualization of the Effect of Additional Fertilization on Paddy Rice by Time-Series Analysis of Vegetation Indices using UAV and Minimizing the Number of Monitoring Days for its Workload Reduction", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 29–40, 2024. doi: 10.25046/aj090303
17. Henry Toal, Michelle Wilber, Getu Hailu, Arghya Kusum Das, "Evaluation of Various Deep Learning Models for Short-Term Solar Forecasting in the Arctic using a Distributed Sensor Network", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 12–28, 2024. doi: 10.25046/aj090302
18. Tinofirei Museba, Koenraad Vanhoof, "An Adaptive Heterogeneous Ensemble Learning Model for Credit Card Fraud Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 01–11, 2024. doi: 10.25046/aj090301
19. Toya Acharya, Annamalai Annamalai, Mohamed F Chouikha, "Optimizing the Performance of Network Anomaly Detection Using Bidirectional Long Short-Term Memory (Bi-LSTM) and Over-sampling for Imbalance Network Traffic Data", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 144–154, 2023. doi: 10.25046/aj080614
20. Renhe Chi, "Comparative Study of J48 Decision Tree and CART Algorithm for Liver Cancer Symptom Analysis Using Data from Carnegie Mellon University", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 57–64, 2023. doi: 10.25046/aj080607
21. Ng Kah Kit, Hafeez Ullah Amin, Kher Hui Ng, Jessica Price, Ahmad Rauf Subhani, "EEG Feature Extraction based on Fast Fourier Transform and Wavelet Analysis for Classification of Mental Stress Levels using Machine Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 46–56, 2023. doi: 10.25046/aj080606
22. Nizar Sakli, Chokri Baccouch, Hedia Bellali, Ahmed Zouinkhi, Mustapha Najjari, "IoT System and Deep Learning Model to Predict Cardiovascular Disease Based on ECG Signal", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 08–18, 2023. doi: 10.25046/aj080602
23. Zobeda Hatif Naji Al-azzwi, Alexey N. Nazarov, "MRI Semantic Segmentation based on Optimize V-net with 2D Attention", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 4, pp. 73–80, 2023. doi: 10.25046/aj080409
24. Kohei Okawa, Felix Jimenez, Shuichi Akizuki, Tomohiro Yoshikawa, "Investigating the Impression Effects of a Teacher-Type Robot Equipped a Perplexion Estimation Method on College Students", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 4, pp. 28–35, 2023. doi: 10.25046/aj080404
25. Yu-Jin An, Ha-Young Oh, Hyun-Jong Kim, "Forecasting Bitcoin Prices: An LSTM Deep-Learning Approach Using On-Chain Data", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 186–192, 2023. doi: 10.25046/aj080321
26. Kitipoth Wasayangkool, Kanabadee Srisomboon, Chatree Mahatthanajatuphat, Wilaiporn Lee, "Accuracy Improvement-Based Wireless Sensor Estimation Technique with Machine Learning Algorithms for Volume Estimation on the Sealed Box", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 108–117, 2023. doi: 10.25046/aj080313
27. Chaiyaporn Khemapatapan, Thammanoon Thepsena, "Forecasting the Weather behind Pa Sak Jolasid Dam using Quantum Machine Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 54–62, 2023. doi: 10.25046/aj080307
28. Der-Jiun Pang, "Hybrid Machine Learning Model Performance in IT Project Cost and Duration Prediction", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 2, pp. 108–115, 2023. doi: 10.25046/aj080212
29. Ivana Marin, Sven Gotovac, Vladan Papić, "Development and Analysis of Models for Detection of Olive Trees", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 2, pp. 87–96, 2023. doi: 10.25046/aj080210
30. Paulo Gustavo Quinan, Issa Traoré, Isaac Woungang, Ujwal Reddy Gondhi, Chenyang Nie, "Hybrid Intrusion Detection Using the AEN Graph Model", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 2, pp. 44–63, 2023. doi: 10.25046/aj080206
31. Víctor Manuel Bátiz Beltrán, Ramón Zatarain Cabada, María Lucía Barrón Estrada, Héctor Manuel Cárdenas López, Hugo Jair Escalante, "A Multiplatform Application for Automatic Recognition of Personality Traits in Learning Environments", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 2, pp. 30–37, 2023. doi: 10.25046/aj080204
32. Ossama Embarak, "Multi-Layered Machine Learning Model For Mining Learners Academic Performance", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 850–861, 2021. doi: 10.25046/aj060194
33. Fatima-Zahra Elbouni, Aziza EL Ouaazizi, "Birds Images Prediction with Watson Visual Recognition Services from IBM-Cloud and Conventional Neural Network", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 181–188, 2022. doi: 10.25046/aj070619
34. Roy D Gregori Ayon, Md. Sanaullah Rabbi, Umme Habiba, Maoyejatun Hasana, "Bangla Speech Emotion Detection using Machine Learning Ensemble Methods", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 70–76, 2022. doi: 10.25046/aj070608
35. Bahram Ismailov Israfil, "Deep Learning in Monitoring the Behavior of Complex Technical Systems", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 10–16, 2022. doi: 10.25046/aj070502
36. Deeptaanshu Kumar, Ajmal Thanikkal, Prithvi Krishnamurthy, Xinlei Chen, Pei Zhang, "Analysis of Different Supervised Machine Learning Methods for Accelerometer-Based Alcohol Consumption Detection from Physical Activity", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 147–154, 2022. doi: 10.25046/aj070419
37. Nosiri Onyebuchi Chikezie, Umanah Cyril Femi, Okechukwu Olivia Ozioma, Ajayi Emmanuel Oluwatomisin, Akwiwu-Uzoma Chukwuebuka, Njoku Elvis Onyekachi, Gbenga Christopher Kalejaiye, "BER Performance Evaluation Using Deep Learning Algorithm for Joint Source Channel Coding in Wireless Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 127–139, 2022. doi: 10.25046/aj070417
38. Zhumakhan Nazir, Temirlan Zarymkanov, Jurn-Guy Park, "A Machine Learning Model Selection Considering Tradeoffs between Accuracy and Interpretability", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 72–78, 2022. doi: 10.25046/aj070410
39. Ayoub Benchabana, Mohamed-Khireddine Kholladi, Ramla Bensaci, Belal Khaldi, "A Supervised Building Detection Based on Shadow using Segmentation and Texture in High-Resolution Images", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 166–173, 2022. doi: 10.25046/aj070319
40. Tiny du Toit, Hennie Kruger, Lynette Drevin, Nicolaas Maree, "Deep Learning Affective Computing to Elicit Sentiment Towards Information Security Policies", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 152–160, 2022. doi: 10.25046/aj070317
41. Kaito Echizenya, Kazuhiro Kondo, "Indoor Position and Movement Direction Estimation System Using DNN on BLE Beacon RSSI Fingerprints", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 129–138, 2022. doi: 10.25046/aj070315
42. Jayan Kant Duggal, Mohamed El-Sharkawy, "High Performance SqueezeNext: Real time deployment on Bluebox 2.0 by NXP", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 70–81, 2022. doi: 10.25046/aj070308
43. Sreela Sreekumaran Pillai Remadevi Amma, Sumam Mary Idicula, "A Unified Visual Saliency Model for Automatic Image Description Generation for General and Medical Images", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 2, pp. 119–126, 2022. doi: 10.25046/aj070211
44. Idir Boulfrifi, Mohamed Lahraichi, Khalid Housni, "Video Risk Detection and Localization using Bidirectional LSTM Autoencoder and Faster R-CNN", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 6, pp. 145–150, 2021. doi: 10.25046/aj060619
45. Seok-Jun Bu, Hae-Jung Kim, "Ensemble Learning of Deep URL Features based on Convolutional Neural Network for Phishing Attack Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 291–296, 2021. doi: 10.25046/aj060532
46. Osaretin Eboya, Julia Binti Juremi, "iDRP Framework: An Intelligent Malware Exploration Framework for Big Data and Internet of Things (IoT) Ecosystem", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 185–202, 2021. doi: 10.25046/aj060521
47. Arwa Alghamdi, Graham Healy, Hoda Abdelhafez, "Machine Learning Algorithms for Real Time Blind Audio Source Separation with Natural Language Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 125–140, 2021. doi: 10.25046/aj060515
48. Baida Ouafae, Louzar Oumaima, Ramdi Mariam, Lyhyaoui Abdelouahid, "Survey on Novelty Detection using Machine Learning Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 73–82, 2021. doi: 10.25046/aj060510
49. Radwan Qasrawi, Stephanny VicunaPolo, Diala Abu Al-Halawa, Sameh Hallaq, Ziad Abdeen, "Predicting School Children Academic Performance Using Machine Learning Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 08–15, 2021. doi: 10.25046/aj060502
50. Fatima-Ezzahra Lagrari, Youssfi Elkettani, "Traditional and Deep Learning Approaches for Sentiment Analysis: A Survey", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 01–07, 2021. doi: 10.25046/aj060501
51. Zhiyuan Chen, Howe Seng Goh, Kai Ling Sin, Kelly Lim, Nicole Ka Hei Chung, Xin Yu Liew, "Automated Agriculture Commodity Price Prediction System with Machine Learning Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 376–384, 2021. doi: 10.25046/aj060442
52. Hathairat Ketmaneechairat, Maleerat Maliyaem, Chalermpong Intarat, "Kamphaeng Saen Beef Cattle Identification Approach using Muzzle Print Image", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 110–122, 2021. doi: 10.25046/aj060413
53. Anjali Banga, Pradeep Kumar Bhatia, "Optimized Component based Selection using LSTM Model by Integrating Hybrid MVO-PSO Soft Computing Technique", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 62–71, 2021. doi: 10.25046/aj060408
54. Md Mahmudul Hasan, Nafiul Hasan, Dil Afroz, Ferdaus Anam Jibon, Md. Arman Hossen, Md. Shahrier Parvage, Jakaria Sulaiman Aongkon, "Electroencephalogram Based Medical Biometrics using Machine Learning: Assessment of Different Color Stimuli", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 3, pp. 27–34, 2021. doi: 10.25046/aj060304
55. Nadia Jmour, Slim Masmoudi, Afef Abdelkrim, "A New Video Based Emotions Analysis System (VEMOS): An Efficient Solution Compared to iMotions Affectiva Analysis Software", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 990–1001, 2021. doi: 10.25046/aj0602114
56. Bakhtyar Ahmed Mohammed, Muzhir Shaban Al-Ani, "Follow-up and Diagnose COVID-19 Using Deep Learning Technique", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 971–976, 2021. doi: 10.25046/aj0602111
57. Showkat Ahmad Dar, S Palanivel, "Performance Evaluation of Convolutional Neural Networks (CNNs) And VGG on Real Time Face Recognition System", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 956–964, 2021. doi: 10.25046/aj0602109
58. Dominik Štursa, Daniel Honc, Petr Doležel, "Efficient 2D Detection and Positioning of Complex Objects for Robotic Manipulation Using Fully Convolutional Neural Network", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 915–920, 2021. doi: 10.25046/aj0602104
59. Md Mahmudul Hasan, Nafiul Hasan, Mohammed Saud A Alsubaie, "Development of an EEG Controlled Wheelchair Using Color Stimuli: A Machine Learning Based Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 754–762, 2021. doi: 10.25046/aj060287
60. Abraham Adiputra Wijaya, Inten Yasmina, Amalia Zahra, "Indonesian Music Emotion Recognition Based on Audio with Deep Learning Approach", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 716–721, 2021. doi: 10.25046/aj060283
61. Antoni Wibowo, Inten Yasmina, Antoni Wibowo, "Food Price Prediction Using Time Series Linear Ridge Regression with The Best Damping Factor", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 694–698, 2021. doi: 10.25046/aj060280
62. Javier E. Sánchez-Galán, Fatima Rangel Barranco, Jorge Serrano Reyes, Evelyn I. Quirós-McIntire, José Ulises Jiménez, José R. Fábrega, "Using Supervised Classification Methods for the Analysis of Multi-spectral Signatures of Rice Varieties in Panama", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 552–558, 2021. doi: 10.25046/aj060262
63. Phillip Blunt, Bertram Haskins, "A Model for the Application of Automatic Speech Recognition for Generating Lesson Summaries", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 526–540, 2021. doi: 10.25046/aj060260
64. Sebastianus Bara Primananda, Sani Muhamad Isa, "Forecasting Gold Price in Rupiah using Multivariate Analysis with LSTM and GRU Neural Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 245–253, 2021. doi: 10.25046/aj060227
65. Prasham Shah, Mohamed El-Sharkawy, "A-MnasNet and Image Classification on NXP Bluebox 2.0", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1378–1383, 2021. doi: 10.25046/aj0601157
66. Alisson Steffens Henrique, Anita Maria da Rocha Fernandes, Rodrigo Lyra, Valderi Reis Quietinho Leithardt, Sérgio D. Correia, Paul Crocker, Rudimar Luis Scaranto Dazzi, "Classifying Garments from Fashion-MNIST Dataset Through CNNs", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 989–994, 2021. doi: 10.25046/aj0601109
67. Md Mahmudul Hasan, Nafiul Hasan, Mohammed Saud A Alsubaie, Md Mostafizur Rahman Komol, "Diagnosis of Tobacco Addiction using Medical Signal: An EEG-based Time-Frequency Domain Analysis Using Machine Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 842–849, 2021. doi: 10.25046/aj060193
68. Reem Bayari, Ameur Bensefia, "Text Mining Techniques for Cyberbullying Detection: State of the Art", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 783–790, 2021. doi: 10.25046/aj060187
69. Inna Valieva, Iurii Voitenko, Mats Björkman, Johan Åkerberg, Mikael Ekström, "Multiple Machine Learning Algorithms Comparison for Modulation Type Classification Based on Instantaneous Values of the Time Domain Signal and Time Series Statistics Derived from Wavelet Transform", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 658–671, 2021. doi: 10.25046/aj060172
70. Carlos López-Bermeo, Mauricio González-Palacio, Lina Sepúlveda-Cano, Rubén Montoya-Ramírez, César Hidalgo-Montoya, "Comparison of Machine Learning Parametric and Non-Parametric Techniques for Determining Soil Moisture: Case Study at Las Palmas Andean Basin", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 636–650, 2021. doi: 10.25046/aj060170
71. Imane Jebli, Fatima-Zahra Belouadha, Mohammed Issam Kabbaj, Amine Tilioua, "Deep Learning based Models for Solar Energy Prediction", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 349–355, 2021. doi: 10.25046/aj060140
72. Ndiatenda Ndou, Ritesh Ajoodha, Ashwini Jadhav, "A Case Study to Enhance Student Support Initiatives Through Forecasting Student Success in Higher-Education", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 230–241, 2021. doi: 10.25046/aj060126
73. Lonia Masangu, Ashwini Jadhav, Ritesh Ajoodha, "Predicting Student Academic Performance Using Data Mining Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 153–163, 2021. doi: 10.25046/aj060117
74. Revanna Sidamma Kavitha, Uppara Eranna, Mahendra Nanjappa Giriprasad, "A Computational Modelling and Algorithmic Design Approach of Digital Watermarking in Deep Neural Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1560–1568, 2020. doi: 10.25046/aj0506187
75. Xianxian Luo, Songya Xu, Hong Yan, "Application of Deep Belief Network in Forest Type Identification using Hyperspectral Data", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1554–1559, 2020. doi: 10.25046/aj0506186
76. Sara Ftaimi, Tomader Mazri, "Handling Priority Data in Smart Transportation System by using Support Vector Machine Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1422–1427, 2020. doi: 10.25046/aj0506172
77. Othmane Rahmaoui, Kamal Souali, Mohammed Ouzzif, "Towards a Documents Processing Tool using Traceability Information Retrieval and Content Recognition Through Machine Learning in a Big Data Context", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1267–1277, 2020. doi: 10.25046/aj0506151
78. Lubna Abdelkareim Gabralla, "Dense Deep Neural Network Architecture for Keystroke Dynamics Authentication in Mobile Phone", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 307–314, 2020. doi: 10.25046/aj050637
79. Puttakul Sakul-Ung, Amornvit Vatcharaphrueksadee, Pitiporn Ruchanawet, Kanin Kearpimy, Hathairat Ketmaneechairat, Maleerat Maliyaem, "Overmind: A Collaborative Decentralized Machine Learning Framework", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 280–289, 2020. doi: 10.25046/aj050634
80. Helen Kottarathil Joy, Manjunath Ramachandra Kounte, "A Comprehensive Review of Traditional Video Processing", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 274–279, 2020. doi: 10.25046/aj050633
81. Andrea Generosi, Silvia Ceccacci, Samuele Faggiano, Luca Giraldi, Maura Mengoni, "A Toolkit for the Automatic Analysis of Human Behavior in HCI Applications in the Wild", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 185–192, 2020. doi: 10.25046/aj050622
82. Fei Gao, Jiangjiang Liu, "Effective Segmented Face Recognition (SFR) for IoT", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 36–44, 2020. doi: 10.25046/aj050605
83. Pamela Zontone, Antonio Affanni, Riccardo Bernardini, Leonida Del Linz, Alessandro Piras, Roberto Rinaldo, "Supervised Learning Techniques for Stress Detection in Car Drivers", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 22–29, 2020. doi: 10.25046/aj050603
84. Kodai Kitagawa, Koji Matsumoto, Kensuke Iwanaga, Siti Anom Ahmad, Takayuki Nagasaki, Sota Nakano, Mitsumasa Hida, Shogo Okamatsu, Chikamune Wada, "Posture Recognition Method for Caregivers during Postural Change of a Patient on a Bed using Wearable Sensors", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1093–1098, 2020. doi: 10.25046/aj0505133
85. Daniyar Nurseitov, Kairat Bostanbekov, Maksat Kanatov, Anel Alimova, Abdelrahman Abdallah, Galymzhan Abdimanap, "Classification of Handwritten Names of Cities and Handwritten Text Recognition using Various Deep Learning Models", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 934–943, 2020. doi: 10.25046/aj0505114
86. Khalid A. AlAfandy, Hicham Omara, Mohamed Lazaar, Mohammed Al Achhab, "Using Classic Networks for Classifying Remote Sensing Images: Comparative Study", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 770–780, 2020. doi: 10.25046/aj050594
87. Khalid A. AlAfandy, Hicham, Mohamed Lazaar, Mohammed Al Achhab, "Investment of Classic Deep CNNs and SVM for Classifying Remote Sensing Images", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 652–659, 2020. doi: 10.25046/aj050580
88. Chigozie Enyinna Nwankpa, "Advances in Optimisation Algorithms and Techniques for Deep Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 563–577, 2020. doi: 10.25046/aj050570
89. Rajesh Kumar, Geetha S, "Malware Classification Using XGboost-Gradient Boosted Decision Tree", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 536–549, 2020. doi: 10.25046/aj050566
90. Nghia Duong-Trung, Nga Quynh Thi Tang, Xuan Son Ha, "Interpretation of Machine Learning Models for Medical Diagnosis", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 469–477, 2020. doi: 10.25046/aj050558
91. Oumaima Terrada, Soufiane Hamida, Bouchaib Cherradi, Abdelhadi Raihani, Omar Bouattane, "Supervised Machine Learning Based Medical Diagnosis Support System for Prediction of Patients with Heart Disease", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 269–277, 2020. doi: 10.25046/aj050533
92. Sathyabama Kaliyapillai, Saruladha Krishnamurthy, "Differential Evolution based Hyperparameters Tuned Deep Learning Models for Disease Diagnosis and Classification", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 253–261, 2020. doi: 10.25046/aj050531
93. Haytham Azmi, "FPGA Acceleration of Tree-based Learning Algorithms", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 237–244, 2020. doi: 10.25046/aj050529
94. Hicham Moujahid, Bouchaib Cherradi, Oussama El Gannour, Lhoussain Bahatti, Oumaima Terrada, Soufiane Hamida, "Convolutional Neural Network Based Classification of Patients with Pneumonia using X-ray Lung Images", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 167–175, 2020. doi: 10.25046/aj050522
95. Young-Jin Park, Hui-Sup Cho, "A Method for Detecting Human Presence and Movement Using Impulse Radar", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 770–775, 2020. doi: 10.25046/aj050491
96. Tran Thanh Dien, Nguyen Thanh-Hai, Nguyen Thai-Nghe, "Deep Learning Approach for Automatic Topic Classification in an Online Submission System", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 700–709, 2020. doi: 10.25046/aj050483
97. Anouar Bachar, Noureddine El Makhfi, Omar EL Bannay, "Machine Learning for Network Intrusion Detection Based on SVM Binary Classification Model", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 638–644, 2020. doi: 10.25046/aj050476
98. Adonis Santos, Patricia Angela Abu, Carlos Oppus, Rosula Reyes, "Real-Time Traffic Sign Detection and Recognition System for Assistive Driving", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 600–611, 2020. doi: 10.25046/aj050471
99. Amar Choudhary, Deependra Pandey, Saurabh Bhardwaj, "Overview of Solar Radiation Estimation Techniques with Development of Solar Radiation Model Using Artificial Neural Network", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 589–593, 2020. doi: 10.25046/aj050469
100. Maroua Abdellaoui, Dounia Daghouj, Mohammed Fattah, Younes Balboul, Said Mazer, Moulhime El Bekkali, "Artificial Intelligence Approach for Target Classification: A State of the Art", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 4, pp. 445–456, 2020. doi: 10.25046/aj050453