Some Results on Fixed Points Related to 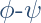 Functions in JS – Generalized Metric Spaces
Functions in JS – Generalized Metric Spaces
Volume 6, Issue 1, Page No 112-120, 2021
Author’s Name: Eriola Sila1,a), Sidita Duraj2, Elida Hoxha1
View Affiliations
1Department of Mathematics, Faculty of Natural Science, University of Tirana, Tirana, 1054, Albania
2Department of Mathematics, Faculty of Natural Science, University “Luigj Gurakuqi”, Shkoder, 4000, Albania
a)Author to whom correspondence should be addressed. E-mail: Roliaerjola.liftaj@fshn.edu.al
Adv. Sci. Technol. Eng. Syst. J. 6(1), 112-120 (2021); ![]() DOI: 10.25046/aj060112
DOI: 10.25046/aj060112
Keywords: JS – generalized metric space, Nonlinear contraction, Fixed point, Ultra – altering distance function, Coincidence point
Export Citations
In this paper are shown some new results on fixed point related to a φ – ψ contractive map in JS – generalized metric spaces X. It proves that there exists a unique fixed point for a nonlinear map f:X→X, using two altering distance functions. Furthermore, it gives some results which related to a couple of functions under some conditions in JS – generalized metric spaces. It provides a theorem where is shown that two maps F,g:X→X under a nonlinear contraction using ultra – altering distance functions ψ and φ, which are lower semi – continuous and continuous, respectively, have a coincidence point that is unique in X. In addition, there is proved if the maps F and g are weakly compatible then they have a fixed point which is unique in JS – generalized metric space. As applications, every theorem is illustrated by an example. The obtained theorems and corollaries extend some important results which are given in the references.
Received: 16 November 2020, Accepted: 21 December 2020, Published Online: 15 January 2021
1.Introduction
The study of fixed point in metric space has an important role in Functional Analysis. It is developed in two directions during the years which are the improving contraction conditions and changing axioms of metric space with the intention to generalize fixed points results in this space. As a result, there are given many new spaces such as generalized metric space [1], cone metric space [2], rectangular metric space [3].
In [4], authors introduced the concept of JS – metric space. It generalizes well-known concepts of metric structures like metric spaces, b – metric spaces [5], metric – like spaces [6], etc. There are many articles which are worked on these spaces, like [7]-[10].
In [11], authors expanded the Banach contraction introducing the concept of weakly contractive function in Hilbert spaces.
Many authors have used these functions in many other spaces like [12]-[14].
In [15], authors provided some theorems related to fixed points of mappings in generalized metric spaces introducing the concept of altering distance functions.
In [16], authors generalized some theorems on fixed point for contractive functions of type Kannnan, Chatteria and Hardy – Rogers in generalized metric space.
This paper generalizes some important results on fixed point for weakly contractive functions and functions with altering distance between points, giving some new theorems on fixed point for φ-ψ contractive functions in JS – generalized metric spaces.
Furthermore, it proves a theorem on common fixed points of two φ-ψ contractive functions on JS – generalized metric spaces.
2.Preliminaries
Let X be a set which is not empty and D_JS be a non – negative function of cartesian product X×X .
For each ϑ∈X, let define the set
C(D_JS ,X,ϑ)={ {x_n }⊂X: lim┬(n→∞)〖D_JS (〗 x_n,ϑ)=0}
Definition 2.1 [4] The map D_JS that satisfies the conditions:
(〖D_JS〗_1) D_JS (x,x ̃ )=0 yields x=x ̃
(〖D_JS〗_2) D_JS (x,x ̃ )=D_JS (x ̃,x)
(〖D_JS〗_3) There exists a constant ρ>0, such that for x_n∈ C(D_JS,X,ϑ), it yields
D_JS (x,x ̃ )≤ρ lim┬(n→+∞)〖D_JS (〗 x_n,x ̃)
for all (x,x ̃ )∈ X×X, is called JS – generalized metric.
The couple (X,D_JS) is called s JS – generalized metric pace.
In [4], authors showed that JS – generalized metric space are metric space, b – metric space, dislocated metric space, etc.
Remark 2.2 [4] As it can be seen in JS – generalized metric space, the map D_JS (x ̃,x ̃) maybe not zero.
Remark 2.3 [4] When the set C(D_JS,X,ϑ) does not contain any element for all ϑ∈X, the couple (X,D_JS) is JS – generalized metric space satisfying only (D_JS1) and (D_JS2).
Definition 2.4 [16] Let (X,D_JS) be a JS – generalized metric space and {x_n }_(n∈N) is in X and ϑ∈X. If {x_n }_(n∈N) is in C(D_JS,X,ϑ), it is called D_JS – convergent to ϑ∈X.
Remark 2.5 [16] If a constant sequence is D_JS – convergent to c∈ X then D_JS (c,c)=0.
Proposition 2.6 [16] A necessary and sufficient condition that the set C(D_JS,X,ϑ) is not empty is that D_JS (ϑ,ϑ)=0
Proposition 2.7 [4] Let the pair(X,D_JS) be a JS – metric generalized space and {x_n }_(n∈N) in X and ϑ,ϑ ̅∈X. If {x_n }_(n∈N) is D_JS – convergent to ϑ and ϑ ̅ then ϑ=ϑ ̅.
Definition 2.8 [16] The sequence {x_n }_(n∈N) in a JS – generalized metric space (X,D_JS)is called D_JS – Cauchy if D_JS (x_n,x_m) converges to 0 when m,n tent to +∞.
Definition 2.9 [16]A JS – generalized metric space (X,D_JS) is named D_JS– complete if each D_JS – Cauchy sequence in X is D_JS – convergent in X.
Example 2.10 Take X=[0,c] where c∈R and D_JS be a non – negative function of cartesian product X×X , where
D_JS (x,x ̃ )={■(max{x,x ̃},&(x,x ̃)≠(0,0) @x/2,&(x,0)@x ̃/2,&(0,x ̃))┤
Since the map D_JS accomplishes (〖D_JS〗_1) and (〖D_JS〗_2) in trivially manner, it is a JS – generalized metric.
Consequently, it needs to verify that (〖D_JS〗_3 ) is satisfied only for x∈X that D_JS (x,x)=0. But D_JS (x,x)=0 implies x=0.
If 〖〖(x〗_n)〗_(n∈N)⊂X converges to 0 then lim┬(n→+∞)〖D_JS (x_n,0)=0〗.
Taking n∈N and x ̃∈X,
D_JS (x_n,x ̃ )={■(max{x_n,x ̃ },&for〖 x〗_n≠0 @x ̃/2,&for x_n=0)┤.
As a result, the inequality x ̃/2<D_JS (x_n,x ̃ ) is true.
From this, it yields D_JS (0,x ̃ )=x ̃/2<lim┬(n→+∞)sup D_JS (x_n,x ̃ ).
So, (X,D_JS) is JS – generalized metric. However, it is not neither metric space nor dislocated metric space because it doesn’t accomplish the third condition of their metric, for x,x ̃∈X-{0} and x^*=0, because
D_JS (x,0)+D_JS (0,x ̃ )=x/2+x ̃/2<max{x,x ̃ }=D_JS (x,x ̃).
Definition 2.11 [15] The function ψ:R^+→R^+ that satisfies the conditions:
ψ is non-decreasing and continuous
ψ(s)=0 if and only if s=0.
ψ(s)≥Ms^μ,for every s>0 where M>0,μ>0 are constants
is called altering distance.
Definition 2.12 [15] A function ψ:R^+→R^+ that accomplishes the conditions:
ψ is non – decreasing
ψ(s)>0 if s>0 and ψ(0)=0
is called ultra – altering distance.
The set of ultra-altering distances is denoted Ψ.
Let g,F two functions of X in itself.
Definition 2.13 [17] The point ξ∈X which completes the equality g(ξ)=F(ξ) is called coincidence point of g,F.
Definition 2.14 [18] The functions g,F that satisfy gFξ=Fgξ, for each ξ that is coincidence point of g and F, are called weakly compatible.
Definition 2.15 [18] The point ξ∈X, in which ξ=F ξ=g ξ, is called common fixed point of maps g,F.
Theorem 2.16 ([16], Corollary 5.5) Let f of set X in itself where(X,D_JS)is D_JS – generalized metric space which is complete and
D_JS (fx,fx ̃ )≤κmax{D_JS (x,x ̃ ),D_JS (x,Tx),D_JS (x ̃,Tx ̃ ),(D_JS (x,fx ̃ )+D_JS (x ̃,fx))/2}
If there exists a ς∈X that δ(D_JS,f,ς)<+∞, then the sequence 〖〖{f〗^n ς}〗_(n∈N) D_JS – convergences to a point ϑ in X.
When D_JS (ϑ,fϑ)<+∞ then ϑ is fixed point of function f. Furthermore, for ϑ^’∈X which is another fixed point of function f, such that D_JS (ϑ’,fϑ’)<+∞, it yields ϑ= ϑ’.
3.Main results
Fixed point results related to φ- ψ contractions in JS – generalized metric spaces
Definitions 3.1.1 Define the set
δ(D_JS,f,ς)=sup{D_JS (f^l ς,f^m ς),l,m≥0}
where ς∈X.
Theorem 3.1.2 Let (X,D_JS) be JS – generalized metric space which is complete and f:X→X a function that satisfies the following condition:
ψ(D_JS (fx,fx ̃ ))≤ψ(M_JS (x,x ̃ ))-φ(M_JS (x,x ̃ )) (3.1)
where
M_JS (x,x ̃ )=maximum{D_JS (x,x ̃ ),D_JS (x,fx),D_JS (x ̃,fx ̃ ),
D_JS (x,fx ̃ ),D_JS (x ̃,fx)},
for every x and x ̃ from X and φ,ψ from Ψ, where ψ is continuous and φ is lower semi – continuous.
If there exists a ς∈X that δ(D_JS,f,ς)<+∞, then the sequence 〖〖{f〗^n ς}〗_(n∈N) D_JS – convergences to a point ϑ in X.
When D_JS (ϑ,fϑ)<+∞ then ϑ is fixed point of function f. Furthermore, for ϑ^’∈X which is another fixed point of function f, such that D_JS (ϑ’,fϑ’)<+∞, it yields ϑ= ϑ’.
Proof. Let take ς∈X that δ(D_JS,f,ς)<+∞. Applicating (3.1) for i,j,n∈N, it yields
ψ(D_JS (f^(n+i) ς,f^(n+j) ς))
≤ψ(M_JS (f^(n+i-1) ς,f^(n+j-1) ς))-φ(M_JS (f^(n+i-1) ς,f^(n+j-1) ς))
≤ψ(M_JS (f^(n+i-1) ς,f^(n+j-1) ς)) (3.2)
M_JS (f^(n+i-1) ς,f^(n+j-1) ς)=maximum{█(D_JS (f^(n+i-1) ς,f^(n+j-1) ς),D_JS (f^(n+i-1) ς,f^(n+i) ς),@D_JS (f^(n+j-1) ς,f^(n+j) ς),D_JS (f^(n+i-1) ς,f^(n+j) ς),@D_JS (f^(n+j-1) ς,f^(n+i) ς) )}
≤δ(D_JS,f,f^(n-1) ς)
Consequently,
ψ(D_JS (f^(n+i) ς,f^(n+j) ς))≤ψ(M_JS (f^(n+i-1) ς,f^(n+j-1) ς))≤ψ(δ(D_JS,f,f^(n-1) ς)).
Using the non-decreasing monotony of ψ it results
D_JS (f^(n+i) ς,f^(n+j) ς)≤ M_JS (f^(n+i-1) ς,f^(n+j-1) ς)≤ δ(D_JS,f,f^(n-1) ς) (3.3)
for every i,j∈N,n∈N.
δ(D_JS,f,f^n ς)=sup{D_JS (f^(n+i) ς,f^(n+j) ς),i,j∈N}≤ δ(D_JS,f,f^(n-1) ς).
As a result, the sequence 〖{δ(D_JS,f,f^n ς)}〗_(n∈N) is non – increasing and bounded.
Consequently, it D_JS – converges and lim┬(n→+∞)〖δ(D_JS,f,f^n ς)=l≥0〗.
In addition, from (3.3) the following inequality
δ(D_JS,f,f^n ς)≤M_JS (f^(n+i-1) ς,f^(n+j-1) ς)
≤δ(D_JS,f,f^(n-1) ς) (3.4)
Taking the limit in (3.4) when n→+∞ and i,j∈N, it yields
lim┬(n→+∞)〖M_JS (f^(n+i-1) ς,f^(n+j-1) ς)=l≥0〗.
Furthermore, from
δ(D_JS,f,f^n ς)=sup{ D_JS (f^(n+i) ς,f^(n+j) ς),i,j∈N},
it implies:
for each natural number k, there exist i(k) and j(k) that the inequality
l-1/k< D_JS (f^(n+i(k) ) ς,f^(n+j(k) ) ς)≤l (3.5)
holds.
Taking the limit in (3.5) when k→+∞, it yields
lim┬(n→∞)〖D_JS (f^(n+i(k) ) ς,f^(n+j(k) ) ς)=l〗.
Furthermore, since φ is lower semi – continuous and ψ is continuous, taking the limit in
ψ(D_JS (f^(n+i(k)) ς,f^(n+j(k)) ς))≤ψ(M_JS (f^(n+i(k)-1) ς,f^(n+j(k)-1) ς))-φ(M_JS (f^(n+i(k)-1) ς,f^(n+j(k)-1) ς))
it implies ψ(l)≤ψ(l)-φ(l).
Consequently, φ(l)=0. Since φ is in Ψ, it implies l=0.
So
lim┬(n→+∞)〖δ(D_JS,f,f^n ς)=0〗 (3.6)
Since δ(D_JS,f,f^n ς)=sup{D_JS (f^(n+i) ς,f^(n+j) ς),i,j∈N}, it is true that
0≤D_JS (f^(n+i) ς,f^(n+j) ς)≤δ(D_JS,f,f^n ς),
for every i,j∈N.
Taking the limit when i,j →+∞ , it implies
lim┬(i,j→+∞)〖D_JS (f^(n+i) ς,f^(n+j) ς)=0〗 (3.7)
Since the sequence 〖{f^n ς}〗_(n∈N) is D_JS – Cauchy, there exists a point ϑ∈X, that accomplishes:
lim┬(n→+∞)〖D_JS (f^n ς,ϑ)=0〗 (3.8)
Let prove now that f(ϑ)=ϑ.
D_JS (fϑ,ϑ)≤ρ lim┬(n→+∞)〖D_JS (fϑ,f^(n+1) ς)〗
Taking (3.1) for x=ϑ and x ̃=f^n ς, it implies
ψ(D_JS (fϑ,f^(n+1) ς)≤ψ(M_JS (ϑ,f^n ς))-φ(M_JS (ϑ,f^n ς)) (3.9)
where
M_JS (ϑ,f^n ς)=maximum〖{D_JS (ϑ,f^n ς),D_JS (ϑ,fϑ),D_JS (〗 f^n ς,f^(n+1) ς),
D_JS (ϑ,f^(n+1) ς),D_JS (f^n ς,fϑ)}
Taking limit in M_JS (ϑ,f^n ς) when n →+∞ and from (3.7) and (3.8), it yields
lim┬(n→+∞)〖M_JS (ϑ,f^n ς)〗=maximum{0,D_JS (ϑ,fϑ),0,0,D_JS (ϑ,fϑ)}=D_JS (ϑ,fϑ)
Taking limit in (3.9) it implies
ψ(D_JS (fϑ,ϑ)≤ψ(D_JS (ϑ,fϑ))-φ(D_JS (ϑ,fϑ))
Consequently φ(D_JS (ϑ,fϑ))=0 and
D_JS (ϑ,fϑ)=0 (3.10)
From this, it yields fϑ=ϑ.
If ϑ’ is another point that fϑ’=ϑ’ and D_JS (ϑ’,ϑ’) is finite, then D_JS (ϑ’,ϑ’)=0.
Indeed, applicating (3.1) for x and x ̃ equal to ϑ’, it yields ψ(D_JS (ϑ’,ϑ’)=ψ(D_JS (fϑ’ ,fϑ’ ))
≤ψ(M_JS (ϑ’ ,ϑ’ ))-φ(M_JS (ϑ’ ,ϑ’ ))
where
M_JS (ϑ’ ,ϑ’ )=maximum{ D_JS (ϑ’ ,ϑ’ ),D_JS (ϑ’ ,fϑ’ ),D_JS (ϑ’ ,fϑ’ ),
D_JS (ϑ’ ,fϑ’ ),D_JS (ϑ’ ,fϑ’ )}=D_JS (ϑ’ ,ϑ’ )
As a result ψ(D_JS (ϑ’ ,ϑ’ )≤ψ(D_JS (ϑ’ ,ϑ’ ))-φ(D_JS (ϑ’ ,ϑ’ )) ,
which implies φ(D_JS (ϑ’ ,ϑ’ ))=0 and〖 D〗_JS (ϑ’ ,ϑ’ )=0.
Furthermore, D_JS (ϑ ,ϑ)=0, because f(ϑ)= ϑ.
Due to the fact D_JS (ϑ,ϑ’ )=D_JS (fϑ,fϑ’ ), it yields
ψ(D_JS (fϑ ,fϑ’ )≤ψ(M_JS (ϑ,ϑ’ ))-φ(M_JS (ϑ,ϑ’ )) (3.11)
where
M_JS (ϑ,ϑ’ )=maximum{ D_JS (ϑ,ϑ’ ),D_JS (ϑ ,fϑ ),D_JS (ϑ’ ,fϑ’ ),
D_JS (ϑ,fϑ’ ),D_JS (ϑ’ ,fϑ)}=maximum〖{D_JS (ϑ,ϑ’ ),0,0,〗 D_JS (ϑ,ϑ’ ),D_JS (ϑ’ ,ϑ)}=D_JS (ϑ,ϑ’ )
From (3.11), it implies
ψ(D_JS (ϑ,ϑ’ )≤ψ(D_JS (ϑ,ϑ’ ))-φ(D_JS (ϑ,ϑ’ )).
As a result φ(D_JS (ϑ ,ϑ’ ))=0 and D_JS (ϑ,ϑ’ )=0 and ϑ=ϑ’ .
Remark 3.1.3 Theorem 3.1.2 generalizes Theorem 2.18 (Theorem 1.9) in [19].
Example 3.1.4 Let be X=[0,1] and a non – negative D_JS of X×X, where
D_JS (x,y)={■(maximum{x,x ̃},&x≠0 ,x ̃≠0@x/2,&x∈X ,x ̃=0@x ̃/2,&x=0 ,x ̃∈X)┤.
(X,D_JS) is a JS – generalized metric space as it is shown in Example 2.10.
Let f:X→X be a map such that f(x)=x^2/(2(1+x)) and the functions φ,ψ∈Ψ, φ(s)=s/2, ψ(t)=3s/2.
For x≠x ̃ and x≠0, x ̃≠0
D_JS (f(x),f(x ̃ ))=maximum{x^2/2(1+x) ,x ̃^2/2(1+x ̃ ) }.
Taking x<x ̃, D_JS (f(x),f(x ̃ ))=x ̃^2/2(1+x ̃ )
M_JS (x,x ̃ )=maximum{D_JS (x,x ̃ ),D_JS (x,fx),D_JS (x ̃,fx ̃ ),
D_JS (x,fx ̃ ),D_JS (x ̃,fx)},
D_JS (x,x ̃ )=maximum{x,x ̃ }=x ̃,D_JS (x,f(x))=maximum{x,x^2/2(1+x) }=x,
D(x ̃,f(x ̃ )=D(x ̃,x ̃^2/2(1+x ̃ ) )=x ̃,
D_JS (x,f(x ̃ ))=maximum{x,x ̃^2/2(1+x ̃ ) }={■(x ̃^2/2(1+x ̃ ) @x)┤ ,
D_JS (f(x),x ̃ )=maximum{x ̃,1/2 x^2/((1+x) )}=x ̃.
Case 1. If D_JS (f(x ̃ ),x)=1/2 x ̃^2/((1+x ̃ ) ), then
M_JS (x,x ̃ )=maximum{x ̃,x,1/2 x ̃^2/((1+x ̃ ) )}=maximum〖{x ̃,1/2 x ̃^2/((1+x ̃ ) )}=x ̃ 〗
ψ(D_JS (f(x),f(x ̃ ))=ψ(x ̃^2/2(1+x ̃ ) )=3/2 x ̃^2/2(1+x ̃ ) =(3x ̃^2)/4(1+x ̃ ) .
ψ(M_JS (x,x ̃ ))-φ(M_JS (x,x ̃ ))=ψ(x ̃ )-φ(x ̃ )=(3x ̃)/2-x ̃/2=x ̃
Since 3/4 x ̃^2/((1+x ̃))<x ̃, the condition of Theorem 3.1.2 is accomplished.
Case 2. If D(x,f(x ̃ )) is x, then
M_JS (x,x ̃ )=maximum{x ̃,x}=x ̃
ψ(D_JS (f(x),f(x ̃ ))=3/2 x ̃^2/2(1+x ̃ ) =(3x ̃^2)/4(1+x ̃ ) .
ψ(M(x,x ̃ ))-φ(M(x,x ̃ ))=ψ(x ̃ )-φ(x ̃ )=(3x ̃)/2-x ̃/2=x ̃
Since 3/4 x ̃^2/((1+x ̃))<x ̃, the condition of Theorem 3.1.2 is completed.
Therefore, the function f:X→X has a fixed point which is 0.
Corollary 3.1.5. Let (X,D_JS ) be a JS – generalized metric space which is complete and fa function of X in itself satisfying the condition
D_JS (fx,fx ̃)≤M_JS (x,x ̃ )-φ(M_JS (x,x ̃ )),
where
M_JS (x,x ̃)=maximum{█(D_JS (x,x ̃ ),D_JS (x,fx),D_JS (x ̃,fx ̃ ),@D_JS (x,fx ̃ ),D_JS (x ̃,fx) )},
for every x,x ̃∈X and φ is from Ψ, and lower semi – continuous.
If there exists ς∈X that δ(D_JS,f,ς)<+∞, then 〖〖{f〗^n ς}〗_(n∈N) D_JS – convergences to a point ϑ in X.
When D_JS (ϑ,fϑ)<+∞ then ϑ is fixed point of function f. Furthermore, for ϑ^’∈X which is another fixed point of function f, such that D_JS (ϑ’,fϑ’)<+∞, it yields ϑ= ϑ’.
Proof. Replacing ψ(s)=s∈Ψ in above theorem, the proof is clear.
Corollary 3.1.6 Let (X,D_JS ) be a JS – generalized metric space which is complete and f a function of X in itself satisfying the condition
D_JS (fx,fx ̃)≤ κM_JS (x,x ̃)
where
M_JS (x,x ̃)=maximum{█(D_JS (x,x ̃ ),D_JS (x,fx),D_JS (x ̃,fx ̃ ),@D_JS (x,fx ̃ ),D_JS (x ̃,fx) )},
for every x,x ̃∈X and κ∈├]0,1┤[.
If there exists ς∈X that δ(D_JS,f,ς)<+∞, then 〖〖{f〗^n ς}〗_(n∈N) D_JS – convergences to a point ϑ in X.
When D_JS (ϑ,fϑ)<+∞ then ϑ is fixed point of function f. Furthermore, for ϑ^’∈X which is another fixed point of function f, such that D_JS (ϑ’,fϑ’)<+∞, it yields ϑ= ϑ’.
Proof. Taking ψ(s)=s and φ(s)=(1-κ)s∈Ψ in inequality (3.1), the proof is clear.
Remark 3.1.7 Corollary 3.1.5 is a generalization of Theorem 2.16 which is the result of [16] as Corollary 5.5 and Corollary 3.8 in [20].
Common fixed point related to φ-ψ contractive functions in JS – generalized metric space.
Theorem 3.2.1 Let (X,D_JS ) a JS – generalized metric space which is complete and F,g:X→X such that FX is a subset of gX and the set gX is closed in X and
ψ(D_JS (Fx,Fx ̃ )≤ψ(M_JS (gx,gx ̃ ))-φ(M_JS (gx,gx ̃ )) (3.12)
where
M_JS (gx,gx ̃ )=maximum{D_JS (gx,gx ̃ ),D_JS (gx,Fx),D_JS (gy,Fx ̃ )}
for x and x ̃ in X and φ and ψ in Ψ, ψ is continuous and φ is lower semi – continuous.
If there exist ς∈X such that δ(D_JS,F,ς)<+∞ and δ(D_JS,g,ς)<+∞ then the sequence 〖〖{γ〗_n}〗_(n∈N)=〖{gς_(n+1)}〗_(n∈N)=〖{Fς_n}〗_(n∈N), where γ_1=Fς=gς_1, D_JS – converges to a point ϑ in X.
If δ(D_JS,F,ϑ)<+∞ and δ(D_JS,g,ϑ)<+∞ then the maps F, g have a unique coincidence point in X.
Furthermore, they have a unique common fixed point in X,
if they are weakly compatible.
Proof. Let take ς∈X such that δ(D_JS,F,ς)<+∞ and δ(D_JS,g,ς)<+∞. For ς∈X, due to FX⊂gX then Fς∈gX. Consequently, there exists ς_1∈X,gς_1=Fς.
Reasoning in the same manner for ς_1 and so on, there can be defined the sequences 〖{ς_n}〗_(n∈N) and 〖{γ_n}〗_(n∈N) such that
γ_n= gς_(n+1)= Fς_n (3.13)
for n=0,1,2,…
If there exists any n∈N, such that γ_n=γ_(n+1) then gς_(n+1)=Fς_n=γ_n=γ_(n+1)=Fς_(n+1).
So, ς_(n+1) is the required point for g and F.
Let suppose now that the terms of 〖{γ〗_n} are diferent from each other.
Consequently,
D_JS (γ_n,γ_(n+1) )>0. (3.14)
ψ(D_JS (γ_n,γ_(n+1) ))=ψ(D_JS (〖Fς〗_n,Fς_(n+1) ))
≤ψ(M_JS (〖gς〗_n,〖gς〗_(n+1) ))-φ(M_JS (〖gς〗_n,〖gς〗_(n+1) )) (3.15)
where
M_JS (〖gς〗_n,〖gς〗_(n+1) )=maximum{D_JS (〖gς〗_n,〖gς〗_(n+1) ),D_JS (〖gς〗_n,〖Fς〗_n ),D_JS (〖gς〗_(n+1),〖Fς〗_(n+1) )}=maximum{D_JS (〖gς〗_n,〖gς〗_(n+1) ),D_JS (〖gς〗_n,〖gς〗_(n+1) ),D_JS (〖gς〗_(n+1),〖gς〗_(n+2) )}=maximum{D_JS (〖gς〗_n,〖gς〗_(n+1) ),D_JS (〖gς〗_(n+1),〖gς〗_(n+2) )}=maximum{D_JS (γ_(n-1),γ_n ),D_JS (γ_n,γ_(n+1) )}
Case 1. D_JS (〖gς〗_n,g_(ςn+1) )=D_JS (γ_n,γ_(n+1) ),then replacing it in (3.15), it yields
ψ(D_JS (γ_n,γ_(n+1) ))≤ψ(D_JS (γ_n,γ_(n+1) ))-φ(D_JS (γ_n,γ_(n+1) ))
So φ(D_JS (γ_n,γ_(n+1) ))=0 and consequently D_JS (γ_n,γ_(n+1) )=0, which is absurd due to (3.14).
Case 2. M_JS (〖gς〗_n,〖gς〗_(n+1) )=D_JS (γ_(n-1),γ_n ) then replacing it in (3.15), it yields
ψ(D_JS (γ_n,γ_(n+1) ))≤ψ(D_JS (γ_n,γ_(n-1) ))-φ(D_JS (γ_n,γ_(n-1) ))
≤ψ(D_JS (γ_n,γ_(n-1) )) (3.16)
Due to non-decreasing monotony of ψ, it implies
D_JS (γ_n,γ_(n+1) )≤ D_JS (γ_n,γ_(n-1) ),
for all n∈N.
This shows that 〖{D_JS (γ_n,γ_(n+1) )}〗_(n∈N) is non-increasing and lower bounded because D_JS (γ_n,γ_(n+1) )≥0.
Consequently, the sequence 〖{D_JS (γ_n,γ_(n+1) )}〗_(n∈N) converges to l≥0, lim┬(n→+∞)〖D_JS (γ_n,γ_(n+1) )〗=l.
Taking the limit in (3.16) when n→+∞, it yields
ψ(l)≤ψ(l)-ϕ(l).
Consequently, φ(l)=0 and l=0.
So,
〖 lim┬(n→+∞)〗〖D_JS (γ_n,γ_(n+1) )〗=0 (3.17)
Denote
〖 c〗_k=sup{D_JS (γ_i,γ_j ),i,j>k} (3.18)
c_k is finite for every k∈N because δ(D_JS,F,ς)<+∞ and δ(D_JS,g,ς)<+∞.
Since the sequence 〖{c_k}〗_(k∈N) is non – increasing, lower bounded from zero, it is convergent to a point ζ,
lim┬(k→+∞)〖c_k 〗=ζ≥0 (3.19)
From (3.17), it yields:
for each p∈N, there exist i_p,j_p>p, such that
〖 c〗_p-1/p<D_JS (γ_(i_p ),γ_(j_p ) )<c_p (3.20)
Taking limit in (3.20) when p→+∞ and using (3.19), it yields
lim┬(p→+∞)〖D_JS (γ_(i_p ),γ_(j_p ) )〗=ζ (3.21)
Knowing that D_JS (γ_(i_p ),γ_(j_p ) )= D_JS (〖Fς〗_(i_p-1),〖Fς〗_(j_p-1) ), it implies
ψ(D_JS (ς_(i_p ),ς_(j_p ) ))=ψ (D_JS (〖Fς〗_(i_p-1),〖Fς〗_(j_p-1) )≤ψ (M_JS (〖gς〗_(i_p-1),〖gς〗_(j_p-1) ))-φ(M_JS (〖gς〗_(i_p-1),〖gς〗_(j_p-1) )) (3.22)
where
M_JS (〖gς〗_(i_p-1),〖gς〗_(j_p-1) )=maximum{█(D_JS (〖gς〗_(i_p-1),〖gς〗_(j_p-1) ),D_JS (〖gς〗_(i_p-1),〖Fς〗_(i-1) ),@D_JS (〖gς〗_(j_p-1),〖Fς〗_(j_p-1) ) )}=maximum{█(D_JS (γ_(i_p-2),γ_(j_p-2) ),D_JS (γ_(i_p-2),〖gς〗_(i_p-1) ),@D_JS (γ_(j_p-2),ς_(j_p-1) ) )}
From (3.17) and (3.19), it yields
lim┬(p→+∞)〖M_JS (〖gς〗_(i_p-1),〖gς〗_(j_p-1) )〗=maximum{ζ,0,0}=ζ
Taking the limit in (3.22) when p→+∞ and from (3.21), it implies
ψ(ζ)≤ψ(ζ)-φ(ζ)
Consequently, φ(ζ)=0 and ζ=0.
So,
lim┬(k→+∞)〖c_k 〗=0 (3.23)
From (3.18) and (3.23), it yields lim┬(i,j→+∞)〖D_JS (γ_i,γ_j )〗=0, which means that the sequence 〖{γ_n}〗_(n∈N) is D_JS– Cauchy in X.
Since γ_n=〖gς〗_(n+1)=Fς_n, it yields 〖{γ_n}〗_(n∈N)⊂g(X). Since the set g(X) is closed, there is ϑ∈gX such that lim┬(n→+∞)〖γ_n 〗=ϑ . Consequently, lim┬(n→+∞)〖〖gς〗_(n+1) 〗=lim┬(n→+∞)〖Fς_n 〗=ϑ .
Since ϑ∈gX then there is μ∈X,gμ=ϑ.
The other step is to show that Fμ=ϑ.
Knowing D_JS ( ϑ,Fμ)≤lim┬(n→+∞)〖D_JS (Fς_n,Fμ)〗 and applying x=ς_n and x ̃=μ at (3.12), it implies
ψ(D_JS (Fς_n,Fμ))≤ψ(M_JS (gς_n,gμ))-φ(M_JS (gς_n,gμ)) (3.24)
where
M_JS (gς_n,gμ)=maximum{D_JS (gς_n,gμ),D_JS (gς_n,Fς_n ),D_JS (gμ,Fμ)}=maximum{D_JS (gς_n,ϑ),D_JS (gς_n,Fς_n ),D_JS (ϑ,Fμ)}
Since
lim┬(n→+∞)〖D_JS (gς_n,ϑ)=0〗
and
lim┬(n→+∞)〖D_JS (gς_n,Fς_n )〗=lim┬(n→+∞)〖D_JS (γ_(n-1),γ_n )=0〗,
it implies lim┬(n→+∞)M(gς_n,gμ)= D_JS (ϑ,Fμ).
Taking limit in (3.24) when n→+∞, it yields
ψ(D_JS (ϑ,Fμ))≤ψ(ϑ,Fμ)-φ(ϑ,Fμ)
As a result φ(ϑ,Fμ)=0.
Consequently, ϑ=Fμ.
The following step is to prove that ϑ is unique.
Suppose that there exists another point of coincidence ϑ^’≠ϑ of g and F.
So, there exists μ_1∈X which accomplishes Fμ_1=gμ_1=ϑ’
ψ(D_JS (ϑ,ϑ^’ ))=ψ(D_JS (Fμ,Fμ_1 ))
≤ψ(M_JS (gμ,gμ_1 ))-φ(M_JS (gμ,gμ_1 )) (3.25)
For
M_JS (gμ,gμ_1 )=maximum{D_JS (gμ,gμ_1 ),D_JS (gμ,Fμ),D_JS (gμ_1,Fμ_1 )}
=maximum〖{D_JS (ϑ,ϑ^’ ),〗 D_JS (ϑ,ϑ),D_JS (ϑ’,ϑ^’ )} (3.26)
D_JS (ϑ,ϑ)=D_JS (Fμ,Fμ)
ψ(D_JS (ϑ,ϑ))=ψ(D_JS (Fμ,Fμ))
≤ψ(M_JS (gμ,gμ))-φ(M_JS (gμ,gμ)) (3.27)
where
M_JS (gμ,gμ)=maximum{D_JS (gμ,gμ),D_JS (gμ,Fμ),D_JS (gμ,Fμ)}=max〖{D_JS (ϑ,ϑ),〗 D_JS (ϑ,ϑ),D_JS (ϑ,ϑ)}=D_JS (ϑ,ϑ)
Replacing M_JS (gμ,gμ)=D_JS (ϑ,ϑ) in (3.27),
it implies
ψ(D_JS (ϑ,ϑ))≤ψ(D_JS (ϑ,ϑ))-φ(D_JS (ϑ,ϑ))
So, φ(D_JS (ϑ,ϑ))=0 and
D_JS (ϑ,ϑ)=0 (3.28)
Using the same method, it can be proved that
D_JS (ϑ’,ϑ’)=0 (3.29)
Replacing (3.28) and (3.29) in (3.26) and then in (3.25) it yields
M_JS (gμ,gμ_1 )=D_JS (gμ,gμ_1 )=D_JS (ϑ,ϑ^’ )
ψ(D_JS (ϑ,ϑ^’ ))≤ψ(D_JS (ϑ,ϑ^’ ))-φ(D_JS (ϑ,ϑ^’ ))
From this, it implies φ(D_JS (ϑ,ϑ^’ ))=0 and D_JS (ϑ,ϑ^’ )=0. Consequently ϑ=ϑ^’.
Furthermore, let prove that if g and F are weakly compatible then Fϑ=gϑ.
From D_JS (Fϑ,ϑ)=D_JS (Fϑ,Fμ) and (3.12), it implies
ψ(D_JS (Fϑ,ϑ))=ψ(D_JS (Fϑ,Fμ))
≤ψ(M_JS (gϑ,gμ))-φ(M_JS (gϑ,gμ)) (3.30)
M_JS (gϑ,gμ)=maximum{D_JS (gϑ,gμ),D_JS (gϑ,Fμ),D_JS (gϑ,Fμ)}=maximum〖{D_JS (Fϑ,ϑ),〗 D_JS (Fϑ,Fϑ),D_JS (ϑ,ϑ)}
From (3.28), it is known that D_JS (ϑ,ϑ)=0. Using the same method as in (3.28), it can be proved that D_JS (Fϑ,Fϑ)=0.
Consequently, M_JS (gϑ,gμ)=D_JS (Fϑ,ϑ)
Replacing this equality in (3.30), it implies
ψ(D_JS (Fϑ,ϑ))≤ψ(D_JS (Fϑ,ϑ))-φ(D_JS (Fϑ,ϑ))
From this φ(D_JS (Fϑ,ϑ))=0 and D_JS (Fϑ,ϑ)=0.
So, Fϑ=ϑ=gϑ and ϑ is unique.
Remark 3.2.2 Since JS – generalized metric spaces are metric spaces, b – metric spaces, dislocated metric spaces, partial metric spaces it implies that Theorem 3.2.1 is true in these spaces.
Example 3.2.3 Let be X=[0,a], where a∈R and D_JS the JS – generalized metric defined at Example 2.10 and the functions φ,ψ∈Ψ, φ(s)=1/5 s, ψ(s)=s/2.
Let g,F:X→X two functions where g(x)=x/2 and F(x)=ln(1+x/4).
The functions g,F complete the condition of Theorem 3.2.1.
Indeed,
D_JS (Fx,Fx ̃ )=D_JS (ln(1+x/4),ln(1+x ̃/4) )=maximum{ ln(1+x/4),ln(1+x ̃/4)}
Since x≠x ̃, it is supposed that x<x ̃ without restricting anything.
From monotony of logarithmic function
D_JS (Fx,Fx ̃ )=D_JS (ln(1+x/4),ln(1+x ̃/4) )=ln(1+x ̃/4).
M_JS (g(x),g(x ̃))=maximum{D_JS (g(x),g(x ̃)),D_JS (g(x),F(x)),D_JS (g(x ̃),F(x ̃))}
D_JS (g(x ̃),g(x))=maximum{g(x ̃ ),g(x)}=x ̃/2
D_JS (F(x),g(x))=max{F(x),g(x)}=1/2 x.
D_JS (F(x ̃),g(x ̃))=max{F(x ̃ ),g(x ̃ )}=x ̃/2
M_JS ├ (g(x),g(x ̃))=1/2 x ̃
ψ(D_JS (Fx,Fx ̃ ))=ψ(ln〖(1+1/4 x ̃ ))<ψ(1/4 x ̃ )=1/8 x ̃ 〗.
ψ(M_JS (gx,gx ̃ ))-φ(M_JS (gx,gx ̃ ))=ψ(x ̃/2)-φ(x ̃/2)=(3x ̃)/20
Since
ψ(M_JS (gx,gx ̃ ))-φ(M_JS (gx,gx ̃ ))-ψ(D_JS (Fx,Fx ̃ ))>(3x ̃)/20-x ̃/8=x ̃/40>0,
then g,F have a common fixed point 0.
Corollary 3.2.4 Let (X,D_JS ) be a JS – generalized metric space which is complete and g,F:X→X such that gX is closed and FX is a subset of gX and
D_JS (Fx,Fx ̃ )≤M_JS (gx,gx ̃ )-φ(M_JS (gx,gx ̃ )) (3.31)
where
M_JS (x,x ̃ )=max{D_JS (gx,gx ̃ ),D_JS (gx,Fx),D_JS (gx ̃,Fx ̃ )}, for x,x ̃ in X and φ in Ψ is lower semi – continuous.
If there exist ς∈X such that δ(D_JS,F,ς)<+∞ and δ(D_JS,g,ς)<+∞ then the sequence 〖〖{γ〗_n}〗_(n∈N)=〖{gς_(n+1)}〗_(n∈N)=〖{Fς_n}〗_(n∈N), where γ_1=Fς=gς_1, D_JS – converges to a point ϑ in X.
If δ(D_JS,F,ϑ)<+∞ and δ(D_JS,g,ϑ)<+∞ then the maps F, g have a unique coincidence point in X.
Furthermore, they have a unique common fixed point in X,
if they are weakly compatible.
Proof. Taking ψ(s)=s in (3.12), the corollary is true.
Corollary 3.2.5 Let (X,D_JS ) be a JS – generalized metric space which is complete and g,F:X→X such that gX is closed set and FX is a subset of gX in X and
D_JS (Fx,Fx ̃ )≤κmax{D_JS (gx,gx ̃ ),D_JS (gx,Fx ̃ ),D_JS (gx ̃,Fx)}
where κ∈├]0,1┤[ for x and x ̃∈X.
If there exist ς∈X such that δ(D_JS,F,ς)<+∞ and δ(D_JS,g,ς)<+∞ then the sequence 〖〖{γ〗_n}〗_(n∈N)=〖{gς_(n+1)}〗_(n∈N)=〖{Fς_n}〗_(n∈N), where γ_1=Fς=gς_1, D_JS – converges to a point ϑ in X.
If δ(D_JS,F,ϑ)<+∞ and δ(D_JS,g,ϑ)<+∞ then the maps F, g have a unique coincidence point in X.
Furthermore, they have a unique common fixed point in X,
if they are weakly compatible.
Proof. Taking ψ(s)=s, φ(s)=(1-κ)s in (3.12), the corollary is true.
Corollary 3.2.6 Let (X,D_JS ) be a JS – generalized metric space which is complete and F,g:X→X such that FX⊂gX and gX is closed set in X and
D_JS (Fx,Fx ̃ )≤κ_1 D_JS (gx,gx ̃ )+κ_2 D_JS (gx,Fx)+κ_3 D_JS (gx ̃,Fx ̃ )
where 0〖<κ〗_1+κ_2+κ_3<1, for x and x ̃ from X.
If there exist ς∈X such that δ(D_JS,F,ς)<+∞ and δ(D_JS,g,ς)<+∞ then the sequence 〖〖{γ〗_n}〗_(n∈N)=〖{gς_(n+1)}〗_(n∈N)=〖{Fς_n}〗_(n∈N), where γ_1=Fς=gς_1, D_JS – converges to a point ϑ in X.
If δ(D_JS,F,ϑ)<+∞ and δ(D_JS,g,ϑ)<+∞ then the maps F, g have a unique coincidence point in X.
Furthermore, they have a unique common fixed point in X,
if they are weakly compatible.
Proof. Taking 〖κ=κ〗_1+κ_2+κ_3,κ∈├]0,1/3┤[, it implies
κ_1 D_JS (gx,gx ̃ )+κ_2 D_JS (gx,Fx)+κ_3 D_JS (gx ̃,Fx ̃ )≤κ(D_JS (gx,gx ̃ )+D_JS (gx,Fx)+D_JS (gx ̃,Fx ̃ ))≤κ∙3∙M_JS (gx,gx ̃).
Replacing φ(s)=(1-3κ)s and ψ(s)=s in (3.12), the corollary holds.
Conclusions
In this paper are given some theorems and corollaries on fixed points for weakly contractive functions and for contractive functions with altering distance between points in JS – generalized metric spaces. Furthermore, in it are proved some results related to common fixed points of two φ-ψ contractive functions on JS – generalized metric spaces. Since JS – generalized metric spaces are metric spaces, b – metric spaces, dislocated metric spaces, partial metric spaces, it implies that all obtained results are true in above mentioned spaces. In additions, some important results given in this paper are generalizations of some known references. Concretely, Theorem 3.1.2 generalizes Theorem 1.9 in [19]. Corollary 3.1.5 is a generalization of Corollary 3.8 in [20] and Corollary 5.5 in [16].
- K. Wlodarczyk, R. Plebaniak, “Generalized uniform spaces, uniformly locally contractive set-valued dynamic systems and fixed points,” Fixed Point Theory and Applications, 2012, doi:10.1186/1687-1812-2012-104.
- L.G. Huang, X. Zhang, “Cone metric spaces and fixed point theorems of contractive mappings,” Journal of Mathematical Analysis and Applications, 2007, doi:10.1016/j.jmaa.2005.03.087.
- M. Arshad, J. Ahmad, E. Karapınar, “Some Common Fixed Point Results in Rectangular Metric Spaces,” International Journal of Analysis, 2013, doi:10.1155/2013/307234.
- M. Jleli, B. Samet, “A generalized metric space and related fixed point theorems,” Fixed Point Theory and Applications, 2015, doi:10.1186/s13663-015-0312-7.
- S. Czerwik, “Contraction mappings in b-metric spaces,” Ostraviensis, 1993.
- A. Amini-Harandi, “Metric-like spaces, partial metric spaces and fixed points,” Fixed Point Theory and Applications, 2012, doi:10.1186/1687-1812-2012-204.
- E. Karapınar, B. Samet, D. Zhang, “Meir–Keeler type contractions on JS-metric spaces and related fixed point theorems,” Journal of Fixed Point Theory and Applications, 2018, doi:10.1007/s11784-018-0544-3.
- K. Chaira, A. Eladraoui, M. Kabil, A. Kamouss, “Fisher Fixed Point Results in Generalized Metric Spaces with a Graph,” International Journal of Mathematics and Mathematical Sciences, 2020, doi:10.1155/2020/7253759.
- P. Agarwal, M. Jleli, B. Samet, P. Agarwal, M. Jleli, B. Samet, JS-Metric Spaces and Fixed Point Results, 2018, doi:10.1007/978-981-13-2913-5_9.
- A. Shoaib, Q. Mehmood, “Fixed Point Results in Js Multiplicative Metric Spaces,” Turkish Journal of Analysis and Number Theory, 6(6), 2019, doi:10.12691/tjant-6-6-3.
- Y.I. Alber, S. Guerre-Delabriere, Principle of Weakly Contractive Maps in Hilbert Spaces, 1997, doi:10.1007/978-3-0348-8910-0_2.
- S. Cho, “Fixed point theorems for generalized weakly contractive mappings in metric spaces with applications,” Fixed Point Theory and Applications, 2018(1), 3, 2018, doi:10.1186/s13663-018-0628-1.
- P.N. Dutta, B.S. Choudhury, “A Generalisation of Contraction Principle in Metric Spaces,” Fixed Point Theory and Applications, 2008(1), 406368, 2008, doi:10.1155/2008/406368.
- G.V.R. Babu, T.M. Dula, “Fixed points of generalized TAC-contractive mappings in b-metric spaces,” Matematicki Vesnik, 69(2), 2017.
- S.N. Ješić, N.A. Ćirović, D. O’Regan, “Altering Distances and a Common Fixed Point Theorem in Menger Probabilistic Metric Spaces,” Filomat, 31(2), 175–181, 2017.
- Y. ElKouch, E.M. Marhrani, “On some fixed point theorems in generalized metric spaces,” Fixed Point Theory and Applications, 2017(1), 2017, doi:10.1186/s13663-017-0617-9.
- H. Rahimi, G. Soleimani Rad, “Note on ‘common fixed point results for noncommuting mappings without continuity in cone metric spaces,’” Thai Journal of Mathematics, 11(3), 2013.
- L.B. Ćirić, J.S. Ume, “Some common fixed point theorems for weakly compatible mappings,” Journal of Mathematical Analysis and Applications, 314(2), 2006, doi:10.1016/j.jmaa.2005.04.007.
- E. Karapınar, P. Salimi, “Dislocated metric space to metric spaces with some fixed point theorems,” Fixed Point Theory and Applications, 2013(1), 222, 2013, doi:10.1186/1687-1812-2013-222.
- T. Senapati, L.K. Dey, D. Dolićanin-Ðekić, “Extensions of Ćirić and Wardowski type fixed point theorems in D-generalized metric spaces,” Fixed Point Theory and Applications, 2016(1), 33, 2016, doi:10.1186/s13663-016-0522-7.
Citations by Dimensions
Citations by PlumX
Google Scholar
Scopus
Crossref Citations
No. of Downloads Per Month
No. of Downloads Per Country
