1. Introduction

This paper is an extension of work originally presented in the International Electrical Engineering Congress [1], which has been proposed the variable leaky mechanism based on the least mean square (LMS) algorithm for spline adaptive filter. The combination of a linear finite impulse response (FIR) filter and a nonlinear adaptive lookup table (LUT) based on the spline interpolation is called the spline adaptive filtering (SAF) with the adaptation process [2]. It is a class of nonlinear adaptive filtering with a spline function [1]-[12].

According to the practical models, the linear adaptive filter should be inadequate [3]. The models of nonlinear dynamic systems have demonstrated with more robust performance. Linear adaptive filtering should be insufficient in real-world models. Moreover, many dynamic systems using model of nonlinear structure have been extended to the operating model.

Based on the SAF, many research works have achieved efficiently in the practical system identification. In [2], the authors have presented the sign approach with the normalized version of least mean square (NLMS) based on Wiener spline adaptive filter in order to fight against the impulsive noise environment. In [4], the authors have analyzed the convergence and stability analysis of SAF based on LMS algorithm. A steady-state performance of SAF has been examined in [5].

In order to model the nonlinear system identification, the SAF is more attention for the practical use [6],[7]. The linear time-invariant model with the cubic spline function [8] can obtain the good performance working with the adaptive lookup table (LUT) [9] and the spline basis matrix on the adaptive control points coefficient vector.

Applications of SAF architecture have been applied in the infinite impulse response [10] and the system environment with impulsive noise [11]. A set-membership mechanism with the Wiener spline adaptive filtering and normalized least M-estimate algorithm have been obtained significantly the fast convergence in the environment of impulsive noise [11]. In [12], the authors have proposed the Hammerstein function with SAF based on LMS algorithm for improving the convergence rate. Further, a SAF based on the maximum correntropy criterion [13], [14] has been discussed that correntropy is robustness to non-Gaussian noise.

Least mean square (LMS) algorithm which is simple and low computation has been widely used [15]. Most researchers have modified accurately on LMS and NLMS algorithms [16] and [17], the variable step-size LMS [18], the sign mechanism with NLMS [2] and so on.

As stated in a steady-state of convergence analysis, a variable leaky mechanism has been depicted in use of tracking the systems. In [19], a variable leaky LMS algorithm based on the greedy heuristic algorithm has been leveraged to enhance with the high eigenvalue input. In [20], the authors have implemented the variable leaky LMS in the field programmable gate array implementation. The results have been shown that the algorithm can explore the various digital filter architecture.

Based on the variable leaky LMS algorithm which has been orchestrated against and attenuating the drifting [21]. In the field of adaptive signal processing, a variable leaky based on the orthogonal gradient adaptive algorithm with the minimized cost function has been applied for the wireless communications [22].

The novelty of this paper is to merge an adaptive step-size and a modified variable leaky method with least mean square algorithm for linear and nonlinear network part of spline adaptive filtering in term of fast convergence enhancement. The analysis of the convergence performance of the proposed algorithm is derived in forms of the properties and mean square error performance.

In this paper, we organize this paper as follows. Section 2 explains shortly in the structure of SAF. Next, Section 3 introduces the modified adaptive step-size mechanism and the modified variable leaky criterion on the minimization cost function based on the LMS algorithm. Section 4 describes the performance analysis of the proposed adaptive step-size and variable leaky LMS algorithm in terms of the properties and the mean square error performance. Further, the experiment results and discussion show in Section 5 and Section 6, respectively. Finally, Section 7 summarizes the proposed algorithm.

2. Spline Adaptive Filter

Spline adaptive filter (SAF) is namely a combination of linear and nonlinear structures shown in Fig. 1, where x_k is the input of SAF structure and y_k is the output of system.

The objective is that adaptive lookup table in the nonlinear structure generates an output of SAF y_k nearly to a desired sequence d_k as

where the error of system e_k should be small. Thus, the adaptive FIR filter brings an output φ_k in the linear structure, while the input signal is a sequence of x_k at the linear structure.

An adaptive FIR filter output φ_k is given by [3]

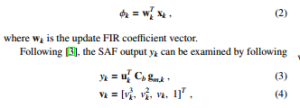
where g_mk is the coefficient of control point vector and C_b is a spline basis matrix.

The local parameter v_k and index m are usually indicated as [5]

where ∆x is the uniform space between two adjacent-coefficients of control points [6], P is the size of control point coefficient, and the floor operator b·c is applied.

By using the minimized objective function based on least mean square (LMS) [5], it becomes

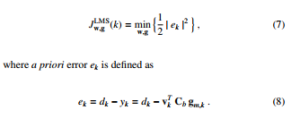
The update FIR coefficient vector w_k can compute by the gradient vector of (7) with respect to the coefficients w_k in terms of the recursion form as [3]

where µ_w is a step-size and ∇J_w^LMS(k) is the gradient vector for w_k.

Similarly, the update control points vector g_m,k can be expressed by the gradient vector of (7) with respect to the coefficients g_m,k [3]

where µ_g is a step-size and ∇J_g^LMS(k) is the gradient vector for g_m,k. Thus, the FIR weight vector w_k and the control points update coefficient vector g_m,k are the particularly simple forms as [5]

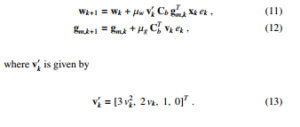
and the local parameter v_k is given in (5).

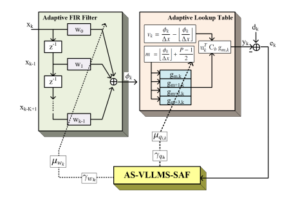
Figure 1: Linear-Nonlinear structure of proposed adaptive step-size variable leaky LMS algorithm for spline adaptive filter (AS-VLLMS-SAF).

3. Proposed Adaptive Step-size and Variable Leaky Least Mean Square based on Spline Adaptive Filter

Based on the least mean square (LMS) algorithm, the advantage of the leaky LMS algorithm is that it avoids the drift of weights

[23]. Meanwhile, the step-size parameter is an efficient approach to improve the convergence rate [16].

Following [1] and [11], the cost function using adaptive stepsize and variable leaky criterion for SAF based on least mean square (AS-VLLMS-SAF) algorithm can be minimized as

where γ_w and γ_g are the leaky paramters for the linear FIR coefficient vector w_k and the control points weight vector g_m,k, respectively. The a priori error of system e_k is given as

Considering the chain rule on the cost function in (14) with respect to (w.r.t) w_k, we get

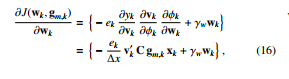
The gradient of cost function in (14) w.r.t g_m,k can be expressed by using the chain rule in the form of vector below

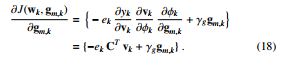
Hence, the proposed update linear FIR coefficient vector w_k of

AS-VLLMS-SAF algorithm is the stochastic adaptation formula as

where µ_wk is a adaptive step-size parameter at symbol k.

By substituting (16) into (19), the proposed update tap-weight vector w_k can be expressed as

where γ_wk is a variable leaky parameter for w_k. It is noticed that (1 − µ_wkγ_wk) is also defined as the leakage factor [23] for updated weight w_k in which its value is generally close to 1.

The adaptive control points coefficient vector g_m,k of AS-

VLLMS-SAF becomes

By substituting (18) into (21), the proposed control points vector

g_m,k is given as

where µ_g is a step-size parameter and γ_gk is a variable leaky parameter for g_m,k+1. It is noted that (1 − µ_gγ_gk) is also defined as the leakage factor [23] for updated weight g_m,k+1 in which its value is generally close to 1.

3.1. Modified Variable Leaky mechanism

Following [24], we introduce the modified variable leaky algorithm with the optimal leaky parameter for weights w_k and g_m,k in the recursion form as

where ρ_w, ρ_g and γ_w^opt, γ_g^opt are the adaptation rate and the optimal leaky parameters of weights w_k and g_m,k. We rewrite (20) as

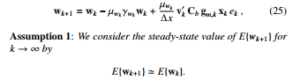
We determine the optimal leaky parameter for w_k by using this

assumption above in (25), we arrive at

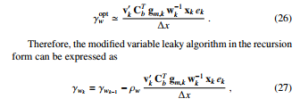
where ρ_w is an adaptation rate for w_k.

Consequently, the a posterior AS-VLLMS error [1] is rewritten as

Assumption 2: We consider the steady-state value of proposed algorithm is stable for k → ∞ by

                                          E{eVL-LMS_pk   } ‘ E{e_k}.

By using Assumption 2 in (28), the optimal leaky parameter can be defined as

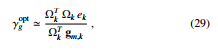
Table 1: Proposed Variable Leaky Least Mean Square based on Spline Adaptive Filtering with the adaptive step-size (AS-VLLMS-SAF) algorithm.

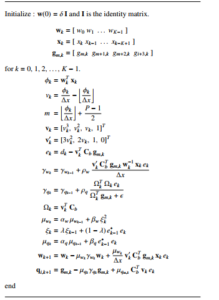
Therefore, the modified variable leaky algorithm can be expressed in the recursion method as

where ρ_g is an adaptation rate for g_m,k and  is a regularization parameter with a small constant.

3.2. Modified Adaptive Step-size Approach

According to the better convergence of proposed AS-VLLMS-SAF algorithm, the step-size parameter should be adapted recursively.

The behavior of convergence rate is which the algorithm starts converging, the value of step-size parameter should be large in order to boost up the learning rate of convergence. At closely to the steady-state, the step-size parameter might be decreased adequately to get the lower adjustment. This leads to adjust accordingly the step-size parameter.

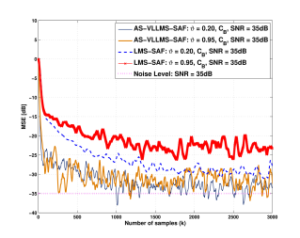
Figure 2: MSE of proposed AS-VLLMS-SAF and LMS-SAF [3] on the B-spline matrix C_B with the different ϑ = 0.20,0.95 and SNR = 35dB.

We assume that the step-size parameters µ_wk and µ_gk are regulated by squared estimated error. Hence, the proposed adaptive step-size µ_wk for weight w_k based on AS-VLLMS algorithm is in-

troduced for spline adaptive filtering as [4]

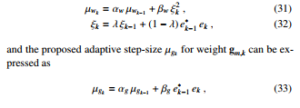
A summary of proposed variable leaky least mean square for spline adaptive filtering based on adaptive step-size algorithm (ASVLLMS) is depicted in Table 1.

4. Performance Analysis

In this section, we analyze the convergence performance of the proposed variable leaky LMS based on SAF. Compared to the LMSSAF algorithm, the proposed AS-VLLMS algorithm is presented by introducing an additional concept.

Variable leaky algorithm is used in the iterative of weights w_k and g_m,k, respectively. So, the computational complexity of ASVLLMS-SAF is more complex than that of the LMS-SAF algorithm.

4.1. Properties of AS-VLLMS Algorithm

The properties of adaptive step-size and variable leaky LMS algorithm may be derived by examining the behaviour of E{w_k} and E{g_m,_k} of SAF.

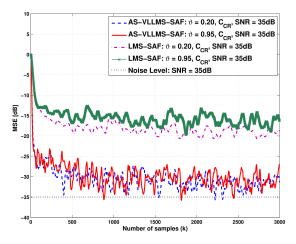
Figure 3: MSE of proposed AS-VLLMS-SAF and LMS-SAF [3] on the Catmul-Rom matrix C_CR with ϑ = 0.20,0.95 and SNR=35dB.

Taking expectation value and using the independence assumption [25], we then have

Thus, we take the expectation value and using the independence assumption [25], it becomes

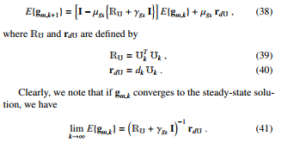
It is noticed that the leakage coefficient introduces a bias into the steady-state solution.

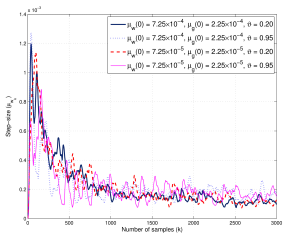
Figure 4: Learning curves of adaptive step-size µ_wk of coefficient vector w_k of proposed AS-VLLMS-SAF on the B-spline matrix C_B with α = 0.20,0.95 and SNR = 35dB.

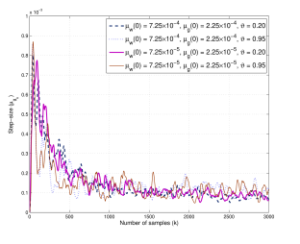
Figure 5: Learning curves of adaptive step-size µ_gk of coefficient vector g_m,_k of proposed AS-VLLMS-SAF on the B-spline matrix C_B with α = 0.20,0.95 and SNR = 35dB.

4.2. The Leaky Adjustment

In this section, the leaky adjustment is investigated in form of the a posterior error compared with a priori error in the spline adaptive filtering. We determine the a posteriori LMS error as [1]

where f_k is described in (37).

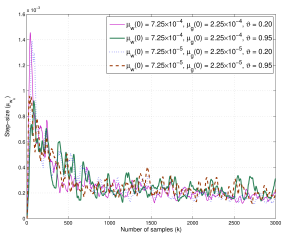
Figure 6: Learning curves of adaptive step-size µ_wk of coefficient vector w_k of proposed AS-VLLMS-SAF on the Catmul-Rom matrix C_CR with α = 0.20,0.95 and SNR = 35dB.

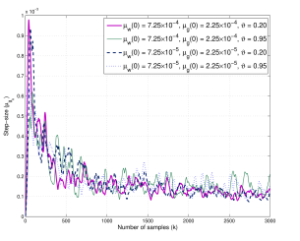
Figure 7: Learning curves of adaptive step-size µ_gk of coefficient vector g_m,_k of proposed AS-VLLMS-SAF on the Catmul-Rom spline matrix C_CR with α = 0.20,0.95 and SNR = 35dB.

Correspondingly, we examine the a posteriori variable leaky least mean square (VL-LMS) error as

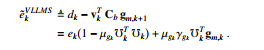
It is noticed that the leaky adjustment will be achieve based on a greedy heuristic algorithm with each iteration, which can get the appropriate leaky value, if |e˜^VLLMS_k | < |e˜_k^LMS |. That means the proposed VL-LMS algorithm would allow to get the efficient LMS algorithm. Otherwise, the leak parameter should be diminished.

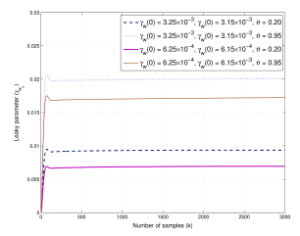
Figure 8: Learning curves of variable leaky γ_wk of coefficient vector w_k of proposed AS-VLLMS-SAF on C_B with ϑ = 0.20,0.95 and SNR = 35dB.

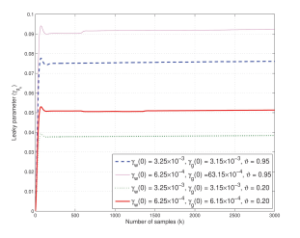
Figure 9: Learning curves of variable leaky γ_gk of coefficient vector g_m,_k of proposed AS-VLLMS-SAF on C_B with α = 0.20,0.95 and SNR = 35dB.

4.3. Mean Square Error Performance

We investigate the mean square error (MSE) performance of the proposed AS-VLLMS-SAF algorithm at the steady-state. Assumption 3: We assume that the a priori and a posteriori optimal errors are identical, we have

E eopt,g .

Assumption 4: We consider the convergence condition for k → ∞, that is of

E{_g^opt} → 0 , as k → ∞

E{gm,k} → goptm,k , as k → ∞

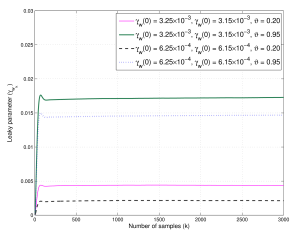
Figure 10: Learning curves of variable leaky γ_wk of coefficient vector w_k of proposed AS-VLLMS-SAF on C_CR with ϑ = 0.20,0.95 and SNR = 35dB.

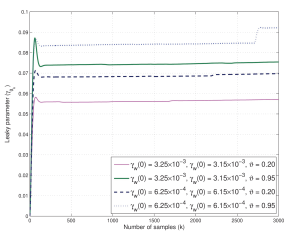
Figure 11: Learning curves of variable leaky γ_wk of coefficient vector w_k of proposed AS-VLLMS-SAF on C_CR with α = 0.20,0.95 and SNR = 35dB.

Following [12], we decompose the MSE under these assumptions above as follows.

4.4. Experimental conditions on parameters setting

In this section, the theoretical experiments are simulated in system identification over the random process and under the Gaussian noise scenario. We evaluate the performance of proposed adaptive step-size variable leaky least mean square algorithm based on spline adaptive filter (AS-VLLMS-SAF) as compared to the conventional least mean square algorithm based on spline adaptive filter (LMS-SAF) [3].

The coloured input signal generates for all experiments over 100

Monte Carlo trials and 5,000 samples used that is generated by [2]

where ζ_k is a unitary variance type of zero mean white Gaussian noise, ϑ = [0,0.95] and an interval sampling ∆x is used at 0.2 [11].

An unknown Wiener system is composed by a linear component as [3]

The linear filter w₀ is initialzed as w₀ = [1, 0,…, 0] and δ = 0.001. Other parameters are fixed at the length of coefficient vector T = 5, a signal to noise ratio S NR = 35dB . The spline basis matrices are used as the B-spline matrix C_B and the CatmulRom spline matrix C_CR in [8] which are selected for simulation experiments as follows:

The fixed parameters of proposed AS-VLLMS-SAF algorithm are as follows: α = 0.20,0.95, α_w = 7.55 × 10⁻³, β_w = 2.75 × 10⁻³, α_g = 6.55 × 10⁻³, β_g = 1.85 × 10⁻³, λ = 0.97,  = 1 × 10⁻⁶ and ρ_w = 1.5 × 10⁻⁶, ρ_g = 1.125 × 10⁻⁶. And the initial parameters for proposed AS-VLLMS-SAF are γ_w(0) = 3.25 × 10⁻², γ_g(0) = 3.25 × 10⁻², µ_w = 7.75 × 10⁻⁴,µ_g = 2.25 × 10⁻⁴. Other fixed parameter of SAF-LMS [3] are as: µ_w = 0.05 and µ_g = 0.05.

Table 2: Summary of MSE of proposed AS-VLLMS-SAF with the initial parameters: µ_w(0) = 7.25×10⁻⁵, µ_g(0) = 2.25×10⁻⁵, γ_w(0) = 6.25×10⁻⁴, γ_g(0) = 6.15×10⁻⁴, of VL-LMS in [1] with γ_w(0) = 3.15 × 10⁻⁴, γ_g(0) = 3.15 × 10⁻⁴ and of LMS-SAF in [3] with µ_w = µ_g = 0.05 over 100 Monte Carlo trials and 5,000 samples used at

SNR = 35dB

Algorithm	ϑ in (47)	Spline matrix	MSE at steady-state condition
			MSE	dB
AS-VLLMS	ϑ = 0.20	CB	1.268 × 10−3	-28.969
		CCR	1.448 × 10−3	-28.392
	ϑ = 0.95	CB	1.768 × 10−3	-29.293
		CCR	2.342 × 10−3	-26.304
VL-LMS in[1]	ϑ = 0.20	CB	1.815 × 10−3	-27.409
		CCR	1.931 × 10−3	-27.144
	ϑ = 0.95	CB	2.175 × 10−3	-26.625
		CCR	2.592 × 10−3	-25.862
LMS in[3]	ϑ = 0.20	CB	3.303 × 10−3	-24.811
		CCR	1.352 × 10−2	-18.688
	ϑ = 0.95	CB	8.345 × 10−3	-20.786
		CCR	2.858 × 10−2	-15.439

5. Simulation Results

For the experiment results, the mean square error (MSE) is simulated at ϑ = 0.20,0.95. Fig. 2 and Fig. 3 show the MSE convergence curves of proposed AS-VLLMS-SAF compared with the original

LMS-SAF [5] based on the B-spline matrix (C_B) matrix and the

Catmul-Rom spline matrix (C_CR) with the parameters ϑ = 0.2,0.95 in (47) shown in dB and SNR=35dB, respectively. We notice that the curves of MSE of proposed AS-VLLMS-SAF based on both spline basis matrices outperform when comparable to that of the LMS-SAF algorithm.

Furthermore, Fig. 4 and Fig. 5 based on the B-spline matrix and Fig. 6 and Fig. 7 based on the Catmul-Rom spline matrix demonstrate the curves of learning rate of µ_wk of coefficient vector w_k and µ_gk of control points ^g_m,k for the proposed AS-VLLMS-SAF at ϑ = 0.20,0.95 and SNR=35dB, respectively. Their learning curves are depicted to converge to their equilibrium at the steady-state, even the initial of µ_wk and µ_gk are varied.

Finally, Fig. 8 and Fig. 9 based on the B-spline matrix and Fig. 10 and Fig. 11 based on the Catmul-Rom spline matrix present the curves of learning parameters of γ_wk of coefficient vector w_k and γ_gk of adaptive control points vector ^g_m,k for the proposed ASVLLMS-SAF at ϑ = 0.20,0.95 and SNR=35dB, respectively. It can seen clearly that their learning rates are shown to converge for the tracking ability at the steady-state with the different initial parameters.

Summary of MSE of proposed AS-VLLMS-SAF with the initial parameters as µ_w(0) = 7.25 × 10⁻⁵, µ_g(0) = 2.25 × 10⁻⁵, γ_w(0) = 6.25 × 10⁻⁴, γ_g(0) = 6.15 × 10⁻⁴ and of LMS-SAF in [3] with the fixed parameter as µ_w = µ_g = 0.05 over 100 Monte Carlo trials and 5,000 samples used at SNR = 35dB and ϑ = 0.20,0.95 is presented in Table. 2. Simulation results suggest that mean square error performance of proposed algorithm can be partially assessed using adaptive step-size with the variable leaky parameters indicating better than the conventional least mean square algorithm by

16.76% with the B-spline matrix.

6. Discussion

The comparison of MSE averaged over 100 trials are shown the robustness and superiority of proposed AS-VLLMS algorithm over the conventional LMS algorithm. We have plotted the learning curves of adaptive step-size µ_wk of coefficient vector w_k, µ_gk of control points g_m,k for the proposed AS-VLLMS algorithm and of variable leaky γ_wk of coefficient vector w_k and γ_gk of adaptive control points vector g_m,k after 5,000 iterations, which are seen that their learning curves converges to their equilibrium, even the initial values are assigned to be varied.

7. Conclusion

We have orchestrated an adaptive step-size and a variable leaky approach based on least mean square algorithm for spline adaptive filtering. The proposed AS-VLLMS-SAF algorithm has been explained how to derive using the variable leaky mechanism. We have designed an adaptive step-size algorithm with the methods of an energy of squared previous and present estimated error. We have designed a modified leaky algorithm with the methods of an optimal leaky parameter. Simulation experiments have shown that the proposed AS-VLLMS-SAF algorithm can perform well with the corresponding LMS-SAF algorithm.

In general, spline adaptive filtering structure is already fascinatingly applied in many applications such as signal processing for communications in nonlinear channel estimation and acoustic processing in bio-acoustic signal.

Conflict of Interest

The authors declare no conflict of interest.

1. A. Saengmuang, S. Sitjongsataporn, “Spline Adaptive Filtering based on Vari- able Leaky Least Mean Square Algorithm,” in Proc. IEEE International Elec- trical Engineering Congress (iEECON), Chiang Mai, Thailand, 2020.
2. C. Liu, Z. Zhang, X. Tang, “Sign Normalised Spline Adaptive Filtering Al- gorithms Against Impulsive Noise”, Signal Processing, 148, 234-240, 2018, doi:10.1016/j.sigpro.2018.02.022.
3. M. Scarpiniti, D. Comminiello, R. Parisi, A. Uncini, “Nonlinear spline adaptive filtering,” Signal Processing, 93(4), 772-783, 2013, doi:10.1016/j.sigpro.2012.09.021.
4. A. Saengmuang, S. Sitjongsataporn, “Convergence and Stability Analysis of Spline Adaptive Filtering based on Adaptive Averaging Step-size Normalized Least Mean Square Algorithm ”, International Journal of Intelligent Engineer- ing and Systems, 13(2), 267-277, 2020, doi:10.22266/ijies2020.0430.26.
5. M. Scarpiniti, D. Comminiello, G. Scarano, R. Parisi, A. Uncini, “Steady- State Performance of Spline Adaptive Filters”, IEEE Transactions on Signal Processing, 64(4), 816-828, 2015, doi:10.1109/TSP.2015.2493986.
6. M. Scarpiniti, D. Comminiello, R. Parisi, A. Uncini, “Novel cascade spline ar- chitectures for the identification of nonlinear systems,” IEEE Transactions on Circuits and Systems I: Regular Papers, 62(7), 1825-1835, 2015, doi: 10.1109/TCSI.2015.2423791.
7. M. Scarpiniti, D. Comminiello, R. Parisi, A. Uncini, “Hammerstein uniform cubic spline adaptive filtering : learning and convergence properties,” Signal Processing, 100, 112-123, 2014, doi:10.1016/j.sigpro.2014.01.019.
8. S. Guan, Z. Li, “Normalised Spline Adaptive Filtering Algorithm for Nonlin- ear System Identification,” Neural Processing Letter, 46(2), 595-607, 2017, doi:10.1007/s11063-017-9606-6.
9. S. Prongnuch, R.E. Valmoria, “Applied of Co-design in Reconfigurable System for Remote Image Noise Filtering via Ethernet Technology”, in Proc. Inter- national Science, Social Science, Engineering and Energy Conference, 92-98, 2013.
10. M. Scarpiniti, D. Commiiniello, R. Parisi, A. Uncini, “Nonlinear system identi- fication using IIR spline adatpive filers,” Signal Processing, 108, 30-35, 2015, doi:10.1016/j.sigpro.2014.08.045.
11. C. Liu, Z. Zhang, “Set-membership normalised least M-estimate spline adap- tive filtering algorithm in impulsive noise,” Electronics Letters, 54(6), 393-395, 2018, doi:10.1049/el.2017.4434.
12. S. Prongnuch, S. Sitjongsataporn, “Stability and Steady-State Performance of Hammerstein Spline Adaptive Filter Based on Stochastic Gradient Algorithm ”, International Journal of Intelligent Engineering and Systems, 13(3), 112-123, 2020, doi:10.22266/ijies2020.0630.11.
13. W. Wang, H. Zhao, X. Zeng, K. Dogancay, “Steady-State Performance Analysis of Nonlinear Spline Adaptive Filter Under Maximum Correntropy Criterion”, IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67(6), 1154-1158, 2020, doi: 10.1109/TCSII.2019.2929536.
14. W. Shi, Y. Li, Y. Wang, “Noise-Free Maximum Correntropy Crite- rion Algorithm in Non-Gaussian Environment”, IEEE Transactions on Circuits and Systems II: Express Briefs, 67(10), 2224-2228, 2020, doi:10.1109/TCSII.2019.2914511.
15. D. Bismor, M. Pawelczyk, “Stability Conditions for the Leaky LMS Algorithm based on Control Theory Analysis”, Archives of Acoustics, 41(4), 731–739, 2016, doi:10.1515/aoa-2016-0070.
16. S. Sitjongsataporn, W. Chimpat, “Adaptive Step-size Normalised Least Mean Square Algorithm for Spline Adaptive Filtering”, in 2019 IEEE International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), 544-547, 2019, doi:10.1109/ITC-CSCC.2019.8793383.
17. L. Deng, Y. M. Huang, Q. Chen, Y. He, X. Sui, “Collaborative Blind Equaliza- tion for Time-Varying OFDM”, IEEE Access, 8, 103073-103087, 2020, doi: 0.1109/ACCESS.2020.2999387.
18. K. Xiong, S. Wang, B. Chen, “Robust Normalized Least Mean Absolute Third Algorithm”, IEEE Access, 7, 10318-10330, 2019, doi:10.1109/ACCESS.2019.2891549.
19. M.Kamenetsky, B.Widrow, “A Variable Leaky LMS Adaptive Algorithm,” in 2004 IEEE Asilomar Conference on Signals, Systems and Compute (ASILO- MAR), 125-128, 2004, doi:10.1109/ACSSC.2004.1399103.
20. P. Kalkar, J.S.R.Alex, “Field Programmable Gate Array implemen- tation of a Variable Leaky Least Mean Square Adaptive Algorithm,” Asian Journal of Pharmaceutical and Clinical Research, 2017, doi:10.22159/ajpcr.2017.v10s1.19566.
21. T.R.Gwadabe, M.S.Salman, H.Abuhilal, “A Modified Leaky-LMS Algorithm,” International Journal of Computer and Electrical Engineering, 6(3), 222-225, 2014, doi:10.1109/4234.1001664.
22. S. Sitjongsataporn, P. Nurarak, “Low Complexity Variable Leaky Normalised Orthogonal Gradient Adaptive Algorithm”, in 2017 IEEE International Con- ference on Advanced Information Networking and Applications Workshops (WAINA), 1-4, 2017, doi:10.1109/WAINA.2017.110.
23. H. Kaur, K. Kaur, R. Mehra, “Adaptive Filter For Audio Signal Enhancement Using Leaky and non leaky algorithms,” International Journal of Electrical and Electronic Engineering and Telecommunications, 3(2), 114-122, 2014.
24. S. Sitjongsataporn, “Modified adaptive forgetting-factor recursive least squares-based frequency-domain equalisation,” in 2013 IEEE International Electrical Engineering Congress (iEECON), 1-4, 2013.
25. M. H. Hayes, Statistical Digital Signal Processing and Modeling, John Wiley&Sons, 1996.

(Click Here)

(Click Here)