1. Introduction

In machining processes, milling processes are ones of the most common machining methods. Especial, the application of CNC technology with high precision and high machinability, milling processes have been used popularly to machine the surfaces with high precision and high productivity. Therefore, more and more studies on the application of milling method have been performed. These studies were performed to improve the quality of machining quality, reduce cutting heat, reduce cutting forces, reduce vibrations, increasing the material removal rate, etc. in milling processes. In application of machines such as for thermal power generation system, marine propulsion elements, mines and quarries, wind’s kinetic energy system, automation, etc. the spiral bevel gears are the most important components of power transmission system [1, 2]

In the manufacturing of spiral bevel gears, many different methods were applied to cut the gear teeth of spiral bevel gears. In which, most of the machining of spiral bevel gears were conducted by the specialized machines. Some of machining systems for manufacturing of the spiral bevel gears consist of the Klingelnberg’s Palliod system [3], Klingelnberg’s and Oerlikon’s Cyclo Palliod systems [4], and the Gleason’s gearing [5] Several studies were conducted to machining the spiral bevel gears using five-axis CNC milling machines [6-8]

In machining processes, cutting forces, vibrations, material removal rate (MRR) are the most important factors. Cutting forces, vibrations, and MRR influence on the machining quality and machining productivity. So, many studies were performed to predict the cutting forces, vibrations, and MRR, and to determine the influence of cutting parameters on the cutting forces, vibrations, MRR. In milling processes, cutting forces can be modeled by theoretical method for ball end mill [9] or flat-end mill [10] and by experimental method [11] The vibrations also can be modeled by theoretical methods [12, 13] and experimental method [14] Normally, the MRR is calculated based on the relationship of cutting parameters such as cutting time, feed rate, cutting velocity, etc.

In the manufacturing of spiral bevel gears using five-axis milling processes, many research directions were performed to improve the quality and productivity of machining processes. Using universal multitasking machines or five-axis milling centers, a large sized spiral bevel gears were manufacture. The different machining strategies, toolpath patterns, and parameters were conducted for both roughing and finishing operations. The machining time, tool wear, and gear surface were analyzed to determine which are the best strategies and parameters for large modulus gear manufacturing on universal machines. Cutting forces, vibrations, and MRR have not been mentioned in this study [6].

A unity transformation model (UTM) was proposed to machine the spiral bevel gears and hypoid gears. This model can be applied in machining process of Gleason spiral bevel gears and hypoid gears, including generation machining and formation machining for wheel or pinion on a universal five-axis machining center. However, this study only focused on the generation of NC program. So, the machining quality and machining productivity have not been mentioned [15].

By combined with the general five-axis NC machine tool, the general expressions of trajectory for five-axis NC machining for the circle bevel gears were proposed. The results of cutter positions and states were verified by 3D modeling. And then, the final tool trajectory was applied in experimental processes. In the milling process of this kind of gear, the cutting forces, vibrations, and MRR have also not been mentioned in this study [16] Besides, several studies were performed using four or five-axis CNC machines to analysis, plan, and manufacture the bevel gears to reduce the cost and time and to improvement of the machining quality in machining processes [15-17].

Figure 1: Spiral bevel gear before using in experimental

2. Material and Experimental Method

2.1. Material

In this study, 40X steel was used to perform the experiment. The equivalent signs of this steel are described in Table 1 according several standard. The chemical compositions of 40X steel are listed in Table 2. The properties of the 40X were the listed in Table 3. The geometry of workpiece (a gear was rough machined) is described in Figure 1.

40Х steel is a structural alloy steel intended for use in heavy-duty components. Products made from this steel conform to DSTU 7806 and GOST 4543 standards. 40X structural alloy steel is used in heavy-duty components (shafts, axles, gear shafts, plungers, bars, crank and cam shafts, rings, spindles, drift pins, battens, cogs, bolts, half-shafts, bushings, screws etc.). 40X chromic steel is also used in forged, cold- and hot-stamped components, and the steel product is used in pipe, tank and other production.

Table 1: Equivalent symbol of 40X steel of according several Standard

1	US	5135, 5140, 5140H, 5140RH, G51350, G51400, H51350, H51400
2	Japan	SCr435, SCr435H, SCr440, SCr440H
3	EU	37Cr4, 37Cr4KD, 41Cr4, 41Cr4KD, 41CrS4
4	China	35Cr, 38CrA, 40Cr, 40CrA, 40CrH, 45Cr, 45CrH, ML38CrA, ML40Cr
5	Sweden	2245
6	Poland	38HA, 40H
7	Romania	40Cr10, 40Cr10q
8	Czech Republic	14140
9	Australia	5132H, 5140
10	South Korea	SCr435, SCr435H, SCr440, SCr440H

Table 2: Chemical composition of 40X steel

Element	С	Si	Mn	NI	Cr	Cu	P	S	Fe
%	0.36-0.44	0.17-0.37	0.5-0.8	≤0.3	0.8-1.1	≤0.3	≤0.035	≤0.035	Balance

Table 3: Properties of 40X steel

Youngs module (GPa)	Density (kg/m3)	Yield stress (GPa)	Brinell hardness (MPa)
214	7820	78.5	179
Specific heat capacity 50/100°C (J/kg°K)	Average CTE 20-300°C (µm/m°K)	Thermal conductivity Ambient temperature (W/m°K)	Electrical resistivity Ambient temperature (µΩm)
466	11.9	46	0.210 – 0.285

2.2. Experimental Machine, Tool, and Measurement systems

A five-axis vertical machining center (DMU 50 – 5 Axis Milling) was used to perform the experiments as shown in Figure 1. A ball-end mill cutter (HSLB-2030) was used to finish milling the Spiral Bevel Gear with number of flutes of 2, helix angle of 30⁰, rake angle of 5⁰, and the diameter of 6 mm. In this study, the cutting forces were measured using a cutting force measurement system including a dynamometer (Kistler type 9139AA: force ranges: (-3 KN÷3 KN), a data processing box, and a PC with DynoWare software. Vibration measurement system including the acceleration sensor (type 4525-B-001), the data processing box, and the PLUSE software was used to measure the system vibration acceleration. The detail of measurement system was illustrated in Figure 2. The machining time of each gear teeth was determines based on the time machining from the control system of five-axis CNC machine. And then, the productivity was calculated by (1).

Figure 2: Experimental machine and measurement system

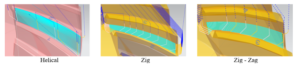
Figure 3: The toolpath strategy in five-axis milling process

where T is the finish machining time of one gear teeth.

2.3. Experimental design

In this research, four factors that were used as the input parameters were spindle speed, feed rate, tool path strategy, and maximum scallop height, and their levels were expressed in Table 4. The toolpath strategies in five-axis milling process were described in Figure 3, and the scallop height in five-axis milling process was calculated by (2), (3), and presented in Figure 4 [18] In the experimental layout plan, with four factors and three levels, the most suitable Taguchi orthogonal array (L₂₇) was selected to design the experimental matrix as listed in Table 5.

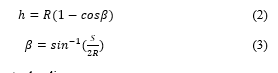
where     R is the tool radius.

          S is the step over (radial depth of cut).

Table 4: The factors and their levels

Parameter	Unit	Coded sign	Levels
			1	2	3
Spindle speed (S)	rpm	A	5000	8000	11000
Feed rate (F)	mm/min	B	400	520	640
Strategy		C	Helical	Zig	Zig – Zig
Maximum Scallop Height (µm)	µm	D	1	3	5

3. Experimental Results and Discussion

3.1. Evaluation of the Cutting Force

ANOVA for Cutting Force Amplitude

The experimental results were listed in Table 5. The measured results of cutting force were listed in column 10 of this Table. Analysis results of variance of cutting force were listed in Table 6 and the main effect of cutting parameters, toolpath strategy, and the maximum scallop height on F was described in Figure 5. The ANOVA results that were used to evaluate the effect of input parameters on the output parameters with 95% confidence level and 5% significance level. The analysis results in Table 6 and Fig 3 showed that: During five-axis finish milling process of the spiral bevel gear, the parameter that has most influence on F was the spindle speed (37.51 %). The parameter that has the second influence degree on F was the feed rate (22.97 %). The parameter that has the third influence degree on F was the maximum scallop height (16.45 %). The toolpath strategy has negligible influence on the F (less than 1 %).

In addition, the influence of each input parameter on F was shown in Figure 5, the results from this figure showed that the spindle speed, feed rate, and maximum scallop height were the parameters that have significant effect on F And the influence degree of toolpath strategy on the F was quite small.

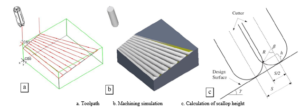
Figure 4: The calculation of scallop height in five-axis milling process

Table 5: Taguchi L27 experimental matrix and results No. A B C D S (rpm) f (mm/min) Strategy Scallop Height (µm) F (N) a (m/s2) Productivity (tooth/min) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) 1 1 1 1 1 5000 400 Helical 1 63.388 7.081 0.235 2 1 1 2 2 5000 400 Zig 3 81.056 9.119 0.291 3 1 1 3 3 5000 400 Zig-Zag 5 167.432 10.495 0.566 4 1 2 1 2 5000 520 Helical 3 202.366 10.566 0.531 5 1 2 2 3 5000 520 Zig 5 171.882 9.072 0.472 6 1 2 3 1 5000 520 Zig-Zag 1 129.055 9.433 0.323 7 1 3 1 3 5000 640 Helical 5 219.478 10.513 0.667 8 1 3 2 1 5000 640 Zig 1 81.921 8.906 0.243 9 1 3 3 2 5000 640 Zig-Zag 3 134.358 11.486 0.690 10 2 1 1 1 8000 400 Helical 1 88.621 9.637 0.240 11 2 1 2 2 8000 400 Zig 3 115.231 10.735 0.290 12 2 1 3 3 8000 400 Zig-Zag 5 196.270 12.710 0.566 13 2 2 1 2 8000 520 Helical 3 191.313 10.935 0.455 14 2 2 2 3 8000 520 Zig 5 177.027 12.154 0.472 15 2 2 3 1 8000 520 Zig-Zag 1 232.821 11.496 0.280 16 2 3 1 3 8000 640 Helical 5 264.235 13.993 0.789 17 2 3 2 1 8000 640 Zig 1 211.871 10.841 0.243 18 2 3 3 2 8000 640 Zig-Zag 3 285.355 14.711 0.690 19 3 1 1 1 11000 400 Helical 1 163.627 7.188 0.240 20 3 1 2 2 11000 400 Zig 3 214.324 7.798 0.291 21 3 1 3 3 11000 400 Zig-Zag 5 243.956 10.046 0.566 22 3 2 1 2 11000 520 Helical 3 260.916 10.738 0.536 23 3 2 2 3 11000 520 Zig 5 237.999 10.120 0.472 24 3 2 3 1 11000 520 Zig-Zag 1 190.603 9.656 0.323 25 3 3 1 3 11000 640 Helical 5 320.031 12.794 0.789 26 3 3 2 1 11000 640 Zig 1 236.119 9.300 0.242 27 3 3 3 2 11000 640 Zig-Zag 3 289.907 10.939 0.690

Table 6: ANOVA results for cutting force

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	P-Value
Model	13	105562	86.72%	105562	8120.2	6.53	0.001
Linear	4	94142	77.34%	80109	20027.2	16.10	0.000
A	1	45657	37.51%	45657	45657.0	36.71	0.000
B	1	27956	22.97%	27956	27955.9	22.48	0.000
C	1	510	0.42%	138	137.9	0.11	0.744
D	1	20019	16.45%	5516	5515.9	4.44	0.055
Square	4	7934	6.52%	8405	2101.2	1.69	0.212
A*A	1	254	0.21%	254	253.8	0.20	0.659
B*B	1	823	0.68%	823	822.8	0.66	0.431
C*C	1	6422	5.28%	5239	5239.5	4.21	0.061
D*D	1	435	0.36%	1317	1317.5	1.06	0.322
2-Way Interaction	5	3487	2.86%	3487	697.4	0.56	0.728
A*B	1	838	0.69%	838	837.8	0.67	0.427
A*C	1	98	0.08%	98	97.9	0.08	0.783
A*D	1	442	0.36%	442	441.5	0.36	0.561
B*C	1	2074	1.70%	1329	1329.1	1.07	0.320
B*D	1	36	0.03%	36	35.6	0.03	0.868
Error	13	16166	13.28%	16166	1243.6
Total	26	121729	100.00%

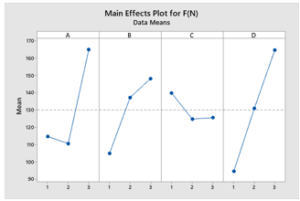
Figure 5: Main Effects Plot for Cutting Force

3.2. Regression of Cutting Force Amplitude Model

The measured data were used to model the cutting force amplitude. The regression model of cutting force amplitude is described by (4). The analysis results showed that the most suitable regression model for cutting force amplitude was a quadratic polynomial function of the spindle speed, feed rate, tool path strategy, and maximum scallop height. The regression model of cutting force amplitude was analyzed and built with high determination coefficients R² (86.72 %).

Cutting Force Regression Equation in coded variables

3.3. Verification of Cutting Force Amplitude Model

The cutting force amplitude model was successfully verified by comparison of predicted and measured results of cutting force amplitude as described in Figure 6.  The compared results from this figure showed that the predicted cutting force amplitude was quite close to the measured cutting force amplitude. It can be concluded that the quadratic regression model can be used to model the cutting force amplitude in in the finish milling process of the spiral bevel gear. The average difference between predicted and measured of cutting force amplitude is about 11.863 %.

3.4. Evaluation of the Vibration Acceleration

• ANOVA for Vibration Acceleration Amplitude

The measured results of cutting force were listed in column 11 of Table 5. Analysis results of variance of vibration acceleration were listed in Table 7 and the main effect of cutting parameters, toolpath strategy, and the maximum scallop height on the vibration acceleration was described in Figure 7. In five-axis finish milling process of the spiral bevel gear, the parameter that has most influence on the vibration acceleration was the feed rate (22.48 %). The parameter that has the second influence degree on the vibration acceleration was the maximum scallop height (21.73 %). The parameter that has the third influence degree on the vibration acceleration was the toolpath strategy (3.65 %). The spindle speed has negligible influence on the vibration acceleration (less than 1 %).

In addition, the influence of each input parameter on vibration acceleration was shown in Figure 7, the results from this figure showed that the feed rate and maximum scallop height were the parameters that have significant effect on the vibration acceleration. And the influences degree of spindle speed and toolpath strategy on the vibration acceleration were quite small.

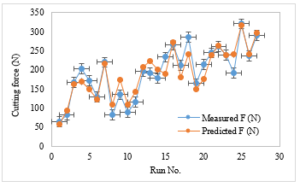
Figure 6: Comparison of predicted and measured cutting force

Table 7: ANOVA results for vibration acceleration

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	P-Value
Model	13	80.5415	93.46%	80.5415	6.1955	14.29	0.000
Linear	4	41.4468	48.09%	30.5043	7.6261	17.59	0.000
A	1	0.2023	0.23%	0.2023	0.2023	0.47	0.507
B	1	19.3716	22.48%	19.3716	19.3716	44.67	0.000
C	1	3.1463	3.65%	2.0195	2.0195	4.66	0.050
D	1	18.7266	21.73%	6.4265	6.4265	14.82	0.002
Square	4	36.0108	41.79%	35.3239	8.8310	20.36	0.000
A*A	1	28.4142	32.97%	28.4142	28.4142	65.52	0.000
B*B	1	0.0000	0.00%	0.0000	0.0000	0.00	0.992
C*C	1	6.2205	7.22%	4.1697	4.1697	9.62	0.008
D*D	1	1.3761	1.60%	1.9240	1.9240	4.44	0.055
2-Way Interaction	5	3.0839	3.58%	3.0839	0.6168	1.42	0.280
A*B	1	1.1963	1.39%	1.1963	1.1963	2.76	0.121
A*C	1	0.9248	1.07%	0.9248	0.9248	2.13	0.168
A*D	1	0.3875	0.45%	0.3875	0.3875	0.89	0.362
B*C	1	0.5197	0.60%	0.5510	0.5510	1.27	0.280
B*D	1	0.0557	0.06%	0.0557	0.0557	0.13	0.726
Error	13	5.6373	6.54%	5.6373	0.4336
Total	26	86.1788	100.00%

3.5. Regression of Vibration Acceleration Amplitude Model

The measured data of vibration acceleration were used to model the vibration acceleration amplitude. The regression model of vibration acceleration amplitude is described by (5). The analysis results showed that the most suitable regression model for vibration acceleration amplitude was also a quadratic polynomial function of the spindle speed, feed rate, tool path strategy, and maximum scallop height. The regression model of vibration acceleration amplitude was analyzed and built with high determination coefficients R² (93.46 %).

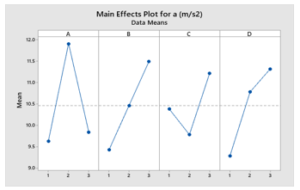
Figure 7: Main Effects Plot for vibration acceleration (a)

Vibration Acceleration Regression Equation in coded variables

3.6. Verification of Vibration Acceleration Amplitude Model

The vibration acceleration amplitude model was also successfully verified by comparison of predicted and measured results of vibration acceleration amplitude as described in Figure 8.  The compared results from this figure showed that the predicted vibration acceleration amplitude was quite close to the that one of measured value. It can be also concluded that the quadratic regression model can be used to model the vibration acceleration amplitude in in the finish milling process of the spiral bevel gear. The average difference between predicted and measured of vibration acceleration amplitude is about 3.371 %.

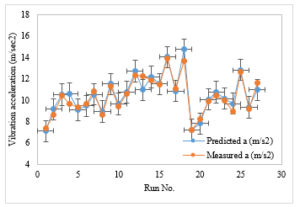
Figure 8: Comparison of predicted and measured vibration acceleration

3.7. Evaluation of the Machining Productivity

• ANOVA for Machining Productivity

The measured results of cutting force were listed in column 12 of Table 5. Analysis results of variance of machining productivity were listed in Table 8 and the main effect of cutting parameters, toolpath strategy, and the maximum scallop height on the machining productivity was described in Figure 9. In five-axis finish milling process of the spiral bevel gear, the parameter that has the most influence on the machining productivity was the maximum scallop height (54.90 %). The parameter that has the second influence degree on the machining productivity was the feed rate (18.92 %). The spindle speed and toolpath strategy have negligible influence on machining productivity (less than 1 %). The influence of each input parameter on the machining productivity was shown in Figure 9, the results from this figure showed that the feed rate and maximum scallop height were the parameters that have significant effect on the machining productivity. And the influence degree of spindle speed and toolpath strategy on the machining productivity were quite small.

Table 8: ANOVA results for productivity

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	P-Value
Model	13	0.895721	98.85%	0.895721	0.068902	85.97	0.000
Linear	4	0.672323	74.20%	0.483583	0.120896	150.84	0.000
A	1	0.000957	0.11%	0.000957	0.000957	1.19	0.294
B	1	0.171417	18.92%	0.171417	0.171417	213.88	0.000
C	1	0.002461	0.27%	0.002616	0.002616	3.26	0.094
D	1	0.497488	54.90%	0.275714	0.275714	344.01	0.000
Square	4	0.215948	23.83%	0.163925	0.040981	51.13	0.000
A*A	1	0.000251	0.03%	0.000251	0.000251	0.31	0.586
B*B	1	0.006666	0.74%	0.006666	0.006666	8.32	0.013
C*C	1	0.182564	20.15%	0.128643	0.128643	160.51	0.000
D*D	1	0.026468	2.92%	0.014949	0.014949	18.65	0.001
2-Way Interaction	5	0.007450	0.82%	0.007450	0.001490	1.86	0.170
A*B	1	0.001143	0.13%	0.001143	0.001143	1.43	0.254
A*C	1	0.001458	0.16%	0.001458	0.001458	1.82	0.200
A*D	1	0.001182	0.13%	0.001182	0.001182	1.47	0.246
B*C	1	0.003151	0.35%	0.001388	0.001388	1.73	0.211
B*D	1	0.000516	0.06%	0.000516	0.000516	0.64	0.437
Error	13	0.010419	1.15%	0.010419	0.000801
Total	26	0.906140	100.00%

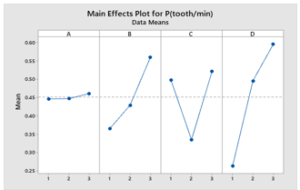
Figure 9: Main Effects Plot for productivity (P)

3.8. Regression of Machining Productivity Model

The measured data of machining productivity were used to model the machining productivity. The regression model of machining productivity is described by (6). The analysis results showed that the most suitable regression model for the machining productivity was also a quadratic polynomial function of the spindle speed, feed rate, tool path strategy, and maximum scallop height. The regression model of machining productivity was analyzed and built with very high determination coefficients R² (99.85 %).

Productivity Regression Equation in coded variables

3.9. Verification of Machining Productivity Model

The machining productivity model was also successfully verified by comparison of predicted and measured results of machining productivity as described in Figure 10. The compared results from this figure showed that the predicted machining productivity was quite close to the that one of measured value. It can be also concluded that the quadratic regression model can be used to model the machining productivity in in the finish milling process of the spiral bevel gear. The average difference between predicted and measured of machining productivity is about 2.867 %.

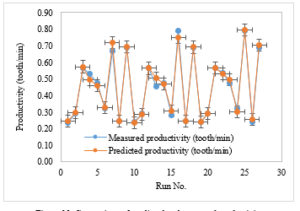
Figure 10: Comparison of predicted and measured productivity

4. Conclusion

In this study, the Taguchi method and ANOVA that were successfully applied to determine the influence of  the spindle speed, feed rate, tool path strategy, and maximum scallop height on cutting forces, vibrations, productivity in the finish milling process of the spiral bevel gear. From the achieved results, the conclusions of this study were drawn as follows:

During the finish milling process of the spiral bevel gear with a ball-end mill cutter (HSLB-2030), the parameter that has most influence on the cutting force amplitude was the spindle speed (37.51 %). The parameter that has the second influence degree on the cutting force amplitude was the feed rate (22.97 %). The parameter that has the third influence degree on the cutting force was the maximum scallop height (16.45 %). The toolpath strategy has negligible influence on the cutting force (less than 1 %)

The feed rate was the most influence factor on the vibration acceleration (22.48 %). The parameter that has the second influence degree on the vibration acceleration was the maximum scallop height (21.73 %). The parameter that has the third influence degree on the vibration acceleration was the toolpath strategy (3.65 %). The spindle speed has negligible influence on the vibration acceleration (less than 1 %).

The parameter that has the most influence on the machining productivity was the maximum scallop height (54.90 %). The parameter that has the second influence degree on the machining productivity was the feed rate (18.92 %). The spindle speed and toolpath strategy have negligible influence on machining productivity (less than 1 %).

Quadratic regression that was determined as the most suitable regression of cutting force amplitude and vibration acceleration amplitude, and productivity in the finish milling process of the spiral bevel gear with the determination coefficients (R²) 86.72 % for cutting force amplitude, 93.46 % for vibration acceleration amplitude, and 99.85 % for machining productivity. These regression models were successfully verified by comparison of predicted and experimental results of cutting force amplitude and vibration acceleration amplitude, and productivity.

Taguchi method, ANOVA, and these regression models in this study can be applied to improve the quality of the machining process by reducing the cutting force components, vibration components, and improve the productivity of machining process. There are the research directions in the next issues of this study.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors thank for the support of Hanoi University of Industry (HaUI) during the implementation of this study.

1. G. Xu, D. Hua, W. Dai, and X. Zhang, “Design and performance analysis of a coal bed gas drainage machine based on incomplete non-circular gears,” Energies, 10(12), 1933, 2017, doi: https://doi.org/10.3390/en10121933.
2. Z. Qin, Y. Luo, K. Li, H. Peng, “Optimal design of a novel hybrid Electric powertrain for tracked vehicles,” Energies, 10(12), 2141, 2017, doi:https://doi.org/10.3390/en10122141.
3. H. J. Watson, Modern gear production, Elsevier, 2013.
4. G. Lechner, Klingelnberg spiral bevel gears, W. Krumme Springer, Berlin, 1968.
5. H. J. Stadtfeld, Gleason Bevel Gear Technology: The Science of Gear Engineering and Modern Manufacturing Methods for Angular Transmissions, Gleason Works, 2014.
6. Á. Álvarez, A. Calleja, N. Ortega, L. N. De Lacalle, “Five-axis milling of large spiral bevel gears: toolpath definition, finishing, and shape errors,” Metals, 8(5), 353, 2018, doi:https://doi.org/10.3390/met8050353.
7. T. Xiang , J. Yi, W. Li, “Five-Axis Numerical Control Machining of the Tooth Flank of a Logarithmic Spiral Bevel Gear Pinion,” Transactions of FAMENA, 42(1), 73-84, 2018, doi: https://doi.org/10.21278/TOF.42107.
8. I. Tsiafis, P. Mamouri, S. Kompogiannis, “Design and manufacturing of spiral bevel gears using CNC milling machines,” InIOP Conference Series: Materials Science and Engineering, 393(1), 0120662018, 2018.
9. Y. C. Kao, N. T. Nguyen, M. S. Chen, S. C. Huang, “A combination method of the theory and experiment in determination of cutting force coefficients in ball-end mill processes,” Journal of Computational Design and Engineering, 2(4), 233-47, 2015, doi:https://doi.org/10.1016/j.jcde.2015.06.005.
10. Y. C. Kao, N. T. Nguyen, M. S. Chen, S. T. Su, “A prediction method of cutting force coefficients with helix angle of flat-end cutter and its application in a virtual three-axis milling simulation system,” The International Journal of Advanced Manufacturing Technology, 77(9-12), 1793-809, 2015, doi: https://doi.org/10.1007/s00170-014-6550-8.
11. T. D. Hoang, N. T. Nguyen, D. Q. Tran, V. T. Nguyen, “Cutting Forces and Surface Roughness in Face-Milling of SKD61 Hard Steel,” Strojniski Vestnik/Journal of Mechanical Engineering, 65(6), 375-385, 2019, doi: https://doi.org/10.5545/sv-jme.2019.6057.
12. N. T. Nguyen, Y. C. Kao, H. T. Dung, “A Prediction Method of Dynamic Cutting Forces and Machine-Tool Vibrations When Milling by Using Ball-End Mill Cutter,” In International Conference on Engineering Research and Applications, 47-54. Springer, Cham, 2019, doi:https://doi.org/10.1007/978-3-030-37497-6_5.
13. K. Weinert, P. Kersting, T. Surmann, D. Biermann, “Modeling regenerative workpiece vibrations in five-axis milling,” Production Engineering, 2(3), 255, 2008, doi:https://doi.org/10.1007/s11740-008-0113-5.
14. P. S. Sivasakthivel, V. Velmurugan, R. Sudhakaran, “Prediction of vibration amplitude from machining parameters by response surface methodology in end milling,” The International Journal of Advanced Manufacturing Technology, 53(5-8), 453-61, 2011, doi:https://doi.org/10.1007/s00170-010-2872-3.
15. T. Wang, Y. Xing, L. Zhao, Q. Li, “NC machining of spiral bevel gear and hypoid gear based on unity transformation model,” Transactions of Tianjin University, 17(4), 264-9, 2011, doi:https://doi.org/10.1007/s12209-011-1641-1.
16. B. Wang, M. Fan, X. Sun, J. Li, A. Xu, G. Li, J. Yang, “Cutter position calculation of machining equal base circle bevel gears with a pot-shaped milling cutter,” The International Journal of Advanced Manufacturing Technology, 87(9-12), 2625-37, 2016, doi:https://doi.org/10.1007/s00170-016-8657-6.
17. J. Tang, X. Yang, “Research on manufacturing method of planing for spur face-gear with 4-axis CNC planer,” The International Journal of Advanced Manufacturing Technology, 82(5-8), 847-858, 2016, doi:https://doi.org/10.1007/s00170-015-7417-3.
18. K. H, Product manufacturing and cost estimating using CAD/CAE: the computer-aided engineering design series, Academic Press, 2013.

(Click Here)

(Click Here)