1. Introduction

     The waste of plastic products continues to increase due to increased use in recent years. Among these materials we find PVC which covers all sectors of economic activity  [1–5]. It’s the second position after polyethylene. The PVC tonnages recycled under Vinyl Plus between 1 January and 31 December 2016 by the initiatives of the EuPC Sector Groups, Sector Associations and Recovinyl  [6] are growing, in particular for window profiles, flexible PVC and cables, which involve industrial and scientific research to study the actions of recycled PVC.

     The recycling of PVC is becoming a current necessity in the industry in order to upgrade it. However, this process requires the addition of fillers on the aged PVC to improve the mechanical characteristics. Before attempting this process based in the difference method consisting in proposing and validating a model from tests by evaluating the difference between the performances measured experimentally and the performances simulated numerically as shown in the figure 1.

     This method also makes it possible to check the expected performances by evaluating the difference between a specification and the tests, and to predict the performances from the models, by evaluating the difference between the simulated performances and the performances expressed in the experimental specifications. In this context, an artificial aging model was carried out experimentally and numerically validated by the finite element modeling.

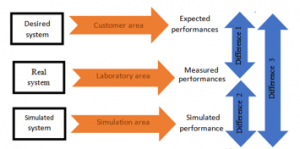
Figure 1: Engineering difference method [7]

     Currently, the recycling of PVC requires loading in order to ameliorate its mechanical characteristics. A variety of studies are focused on the bio loading of materials in view of the requirements in terms of sustainable development and the environment

     In this study and using three numerical models, finite elements, Mori-Tanaka and Double inclusion [8, 9]. We will predict the behavior of bio-loaded PVC after aging. The fillers used are coconut and cow horn fibers.

     The aim of the present study is to validate the aging model of PVC material experimentally and numerically, and to predict by a numerical modeling, the mechanical behavior of this material bio loaded.

2. Study of the PVC aging model

2.1. Description of the adopted aging model

2.1.1. Types of aging

     Two types of aging are adopted. The Rigid and flexible PVC samples as illustrated in figure 2.

Figure 2: Flexible and rigid PVC specimen [3]

     We took two configurations, accelerated artificial and under normal conditions aging at an average Moroccan temperature [3].

The figure 3 below shows the two types of aging

328. Aging by a constant temperature oven of 328.15 K
329. Aging by solar energy for 10h at average temperature T_mean= 300.15 K

Figure 3: aging configuration [3]

Table 1 illustrate that mean reference temperature is 300.15 K.

Table 1: Mean reference temperature in Morocco [3]

OUARZAZATE	Average temperature for 60 years	Maximum average temperature	Minimum average temperature	Record maximum temperature in 60 years	Record minimum temperature in 60 years	Average precipitation
unit	°K	°K	°K	°K	°K	°K
year	299.15	300.15	284.15	319.15	265.15	283.65
January	281.15	291.15	294.15	299.15	268.15	273.95
February	284.15	293.15	276.15	304.15	268.15	273.65
March	288.15	296.15	279.15	312.15	271.15	274.45
April	291.15	300.15	283.15	314.15	272.15	273.65
May	295.15	304.15	286.15	318.15	276.15	273.45
June	299.15	309.15	290.15	322.15	281.15	273.45
July	303.15	313.15	293.15	323.15	287.15	273.45
August	302.15	311.15	293.15	320.15	316.15	273.65
September	298.15	306.15	289.15	316.15	283.15	274.65
October	292.15	300.15	284.15	306.15	276.15	274.65
November	287.15	295.15	280.15	303.15	271.15	274.65
December	282.15	290.15	275.15	301.15	265.15	274.45

2.1.2. Results and discussion

     After a tensile test carried out by the EZ-20 tensile machine (figure 4) and a numerical analysis using the finite element method, which is known for its strong ability to predict the behavior of more complex materials [10–19], on the flexible and rigid PVC samples after and before aging, the results obtained from the test are grouped together in the figures 5 and 6 and table 2.

Figure 4: Tensile Testing machine EZ-20

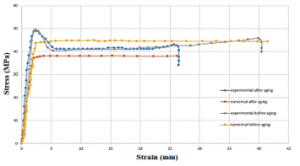
Figure 5: Tensile curves of rigid PVC before & after aging

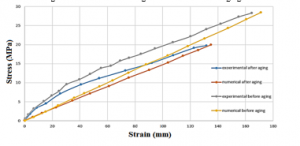
Figure 6: Tensile curves of flexible PVC before & after aging

Table 2: Experimental and numerical results

	Experimental Stress at break (MPa)	Numerical Stress at break (MPa)	Experimental Strain at break (mm)	Numerical Strain at break (mm)
Rigid PVC before aging	40	44	42	42
Rigid PVC after aging	34	37,5	26	26
Flexible PVC before aging	28	28	168	169
Flexible PVC after aging	20	20	135	135

      We note that the stiffness of rigid PVC has changed slightly after aging and this is due to the inclination of the slope towards the elastic region. Its deformation potential before breaking has also been reduced. The flexibility of the flexible PVC is decreased at the elongation stage and become more rigid, its elastic limit is decreased.      Results of the analysis obtained numerically reveals that the numerical finite element modeling supports the findings already reported experimentally and that it is able to predict the mechanical behavior of more complex materials. The deformation ability of rigid PVC after aging has decreased, the stress at break for flexible PVC has decreased and the rigidity has increased because the deformation after aging is much less than before this process.       In order to return these products to their reference characteristics after many recycling, we have tried to establish a reference model for potential recycling studies.       Experimental research and numerical modeling were carried out using the finite elements approach on flexible and rigid PVC before and after aging.      Heat and ultraviolet rays are the key requirements for modifying the mechanical and thermal parameters of PVC, because the sensitivity of rigid PVC to these two conditions for 15 days, and 7 days for flexible PVC has been able to modify its mechanical characteristics.

3. Numerical Study of the Bio Loaded PVC

3.1. Numerical Models

• Finite elements

This analysis is founded on the division of the bio composite by a good mesh and bringing together the sub-domains thereafter.

      We will use the quadratic elements due to their efficiency of computation and the simplicity of convergence.

• Mori-Tanaka

The mathematical model of this model is presented as follows:

ϵ(x)= ξ(I, ) : ϵ*, ∀ x ∈(I)                      (16)

 ξ(I, ) : Eshelby tensor

ϵ* : The deformation acting the Eshelby volume.

The strain concentration tensor: = I, , )            (17)

With:

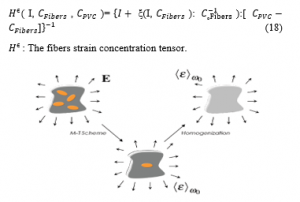
Figure 7: The Mori Tanaka model [8]

• Double Inclusion

The strain concentration tensor in Coconut and cow horn fibers to its contour on the PVC matrix is presented by the following equation.

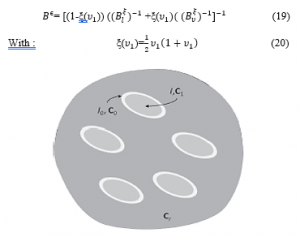
Figure 8: The Double inclusion model [9]

3.2. Bio loads

     The loads used are from animal and natural origin, having a light density and a lower cost unlike classical loads affecting the environment. We will be interested in two types of loads in order to know their effect on the performance of PVC materials after aging

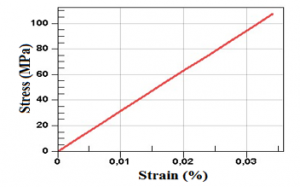
Figure 9: Tensile curve of the cow horns

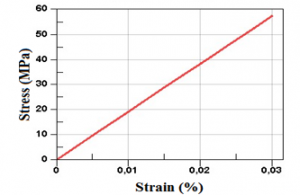
Figure 10: Tensile curve of the coconut

The two bio loads behave elastically with good values ​​of the stresses at break and Young modulus as presented in the table 3.

Table 3: Numerical properties of cow Horns fibers in MPa

	Stress at break	Young modulus
Horn fibers	106.92	3148.4
Coconut fibers	57	1920

3.3. Results and Discussion

     We studied in the previous chapter that the performances of PVC were modified after an accelerated aging which simulates reality. Before starting a first experimental recycling we will carry out a numerical modeling to predict what will happen.

The procedure consists in taking around10% of the two bio loads (cow horns and coconut), and adding it to PVC and comparing the results to see the improvements or degradations of the PVC material.

     The idea is to find the material that will improve the performance of PVC and then use it as a bio load to improve recyclability. In what follows, we will simply choose rigid PVC as an object of this study

3.3.1. Internal Structure of the Bio loaded PVC

     In this modeling, we choose a random distribution of coconuts and cow horns fibers in the PVC presented in figure 11 below

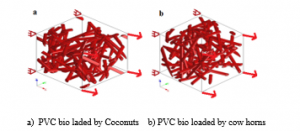
Figure 11: internal structure of bio loaded PVC

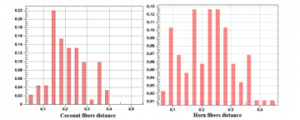
Figure 12: Ccoconut and horn fibers distance

The following table shows the statistical distance for the coconuts and cow horn fibers in PVC.

Table 4: coconuts and cow horn fibers distance

	Mean	Min	Max	Std dev
PVC bio loaded by Coconut	0.212	0.026	0.545	0.093
PVC bio loaded by Cow Horns	0.22	0.0538	0.455	0.0899

The meshes obtained by the numerical modeling of the coconut and cow horns are illustrated in Figure 13.

Figure 13: PVC bio loaded mesh

The following table shows the parameters of mesh used in the present modeling.

Table 5: parameters of mesh

	Elements	Nodes	Size	Min size
PVC bio loaded by Coconut	330731	507283	0.029181	0.0058362
PVC bio loaded by Cow Horns	1449438	2182774	0.029181	0.0058362

      We can deduce that the optimal percentage of the bio fillers in rigid PVC leading to better mechanical properties is 9.3Wt% for Coconut and 9.5 Wt% for Horn fibers.

Table 6: Number of fibers used and optimal content of bio loads

	Number of fibers	Content (Wt%)
PVC bio loaded by Coconut	31	9.3
PVC bio loaded by Cow Horns	32	9.5

We used two Rho and Gamma indicators for the two charging forms to check the consistency of the mesh, which are often used between 0 and 1 with better stability and convergence far from null.

     We note that for Gamma it is between 0.6 and 1, whereas Rho is between 0.4 and 0.8, so they are far from 0 which verifies the mesh quality. Figures 14 and 15 demonstrate how those two indicators are distributed

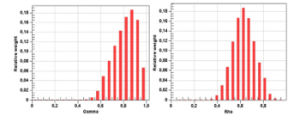
Figure 14: Gamma and Rho distribution of PVC bio loaded by Coconut

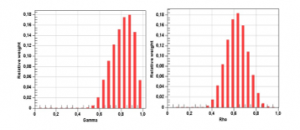
Figure 15: Gamma and Rho distribution of PVC bio loaded by Cow horns

Table 7 presents the average values ​​obtained for Gamma and Rho criterion

Table 7: Average values of Gamma and Rho criterion

	Gamma criterion	Rho criterion
PVC bio loaded by Coconut	0.813	0.632
PVC bio loaded by Cow Horns	0.81	0.626

3.3.2. Effect of Bio loading on Rigid PVC

The three numerical models, finite elements, Mori-Tanaka and double inclusion illustrated in figures 16, 17 and 18 presents almost the same results as summarized in the table 8 and 9.

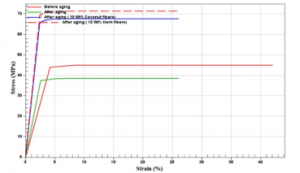
Figure 16: Tensile curve with the Finite element model

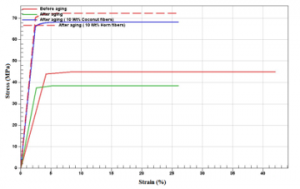
Figure 17: Tensile curves with the Mori-Tanaka model

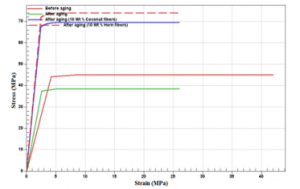
Figure 18: Tensile curves with the double inclusion model

Table 8: Numerical Stress at break in MPa obtained by different models for different content of Coconut fibers

Model	Content (Wt%)	Stress at break at
Mori-Tanaka	0	37.5
	10	68.521
Double inclusion	0	37.5
	10	69.799
Finite element	0	37.5
	9.3	68

Table 9: Numerical Stress at break in MPa obtained by different models for different content of Horn fibers

Model	Content (Wt%)	Stress at break at
Mori-Tanaka	0	37.5
	10	72.433
Double inclusion	0	37.5
	10	74.2
Finite element	0	37.5
	9.5	71.75

      The analysis of the results obtained numerically for the different bio composites after a first aging show that the stresses at breakage improve by adding the two types of bio-loads compared to pre and post aging as shown in figures 16, 17, 18 and the tables 8 and 9.     Horn fibers have given better mechanical properties than coconut fibers. These results are validated by the different numerical models used. The numerical results show that the optimal percentages of Cow horns and Coconut fibers are 10 Wt% obtained by Mori-Tanaka and Double inclusion models and 9.3 Wt% obtained by the Finite element method for Coconut and 9.5 Wt% for cow horns fibers.

4. Conclusion

     In this study, the mechanical behavior of flexible and rigid PVC pre and post aging was experimentally simulated and validated numerically. The submission of these PVCs to ultra violet rays and heat has caused the degradation of its performance. We then proceeded to bio loading rigid PVC after aging in order to compare its behavior with the pure state.The modeling of these homogenizations are made by three numerical models, the finite element, Mori-Tanaka and Double inclusion models which have shown a power to predict the behavior of the bio loaded PVC after aging. The fillers used are Coconut and Cow horn fibers, resulting in an improvement in the performance characteristics of PVC after aging for an optimum percentage of around 10 percent Wt.Cow horns fibers have given better mechanical properties than coconut fibers. These results are validated by the different numerical methods used.Hence the improvement of the mechanical properties of rigid PVC after aging using this natural bio loading by these two fibers friendly to the environment and presenting a lower cost and more lightness.In future works, we will opt for other numerical methods by simulating other natural bio loads and in different orientations of fibers in order to search for bio composites with better mechanical characteristics.

1. E.T. Abdullah, S.M. Hasan, A.N. Naje, “Optical properties of PVC-MWCNT nano composites,” 2013.
2. A.M. El Sayed, W.M. Morsi, “Dielectric relaxation and optical properties of polyvinyl chloride/lead monoxide nanocomposites,” Polymer Composites, 34(12), 2031–2039, 2013.
3. A. Lakhdar, M. Jammoukh, L. Zahiri, K. Mansouri, A. Moumen, B. Salhi, “Numerical and Experimental Study of the Behavior of PVC Material Subjected to Aging,” in 2020 1st International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), IEEE: 1–6, 2020.
4. W. V Titow, Stabilisers: general aspects, Springer: 255–333, 1984.
5. I. Janajreh, M. Alshrah, S. Zamzam, “Mechanical recycling of PVC plasticwaste streams from cable industry: A case study,” Sustainable Cities and Society, 18, 13–20, 2015.
6. C.D.E.S. Activités, L. De Vinylplus, “RAPPORT D ’ AVANCEMENT 2017,” 2017.
7. J.-L. Martinand, “La didactique des sciences,” Revue Française de Pédagogie, 91(1), 114–117, 1990.
8. A. Moumen, M. Jammoukh, L. Zahiri, K. Mansouri, “Study Of The Optimal Micromechanical Behavior Of A Polymer Reinforced By Snail Shell Particles Using The Mori-Tanaka Numerical Model,” in 2020 IEEE International conference of Moroccan Geomatics (Morgeo), 1–6, 2020, doi:10.1109/Morgeo49228.2020.9121908.
9. S. Nemat, M. Hori, Micromechanics: overall properties of heterogeneous materials, 1993.
10. A. Moumen, M. Jammoukh, L. Zahiri, K. Mansouri, “Numerical modeling of the thermo mechanical behavior of a polymer reinforced by horn fibers,” International Journal of Advanced Trends in Computer Science and Engineering, 9(4), 6541–6548, 2020, doi:10.30534/ijatcse/2020/342942020.
11. P. Marimuthu, C. Kumar, “Finite element modelling to predict machining induced residual stresses in the end milling of hard to machine Ti6Al4V alloy,” Periodicals of Engineering and Natural Sciences, 7(1), 1–11, 2019.
12. Ö.Y. Bozkurt, İ.C. Dai, Ö. Özbek, “The finite element analysis and geometry improvements of some structural parts of a diesel forklift truck,” Periodicals of Engineering and Natural Sciences, 5(2), 2017.
13. S. Komurcu, A. Gedikli, “Numerical modelling of the in-plane loaded homogenized masonry walls,” Periodicals of Engineering and Natural Sciences, 5(3), 2017.
14. J.J. Lee, E. Piersanti, K.-A. Mardal, M.E. Rognes, “A mixed finite element method for nearly incompressible multiple-network poroelasticity,” SIAM Journal on Scientific Computing, 41(2), A722–A747, 2019.
15. M. Ghalandari, S. Bornassi, S. Shamshirband, A. Mosavi, K.W. Chau, “Investigation of submerged structures’ flexibility on sloshing frequency using a boundary element method and finite element analysis,” Engineering Applications of Computational Fluid Mechanics, 13(1), 519–528, 2019.
16. S.-F. Yin, S.-L. Xue, B. Li, X.-Q. Feng, “Bio–chemo–mechanical modeling of growing biological tissues: Finite element method,” International Journal of Non-Linear Mechanics, 108, 46–54, 2019.
17. Y. Hong, Y. Yan, Z. Tian, F. Guo, J. Ye, “Mechanical behavior analysis of 3D braided composite joint via experiment and multiscale finite element method,” Composite Structures, 208, 200–212, 2019.
18. J. Naveen, M. Jawaid, A. Vasanthanathan, M. Chandrasekar, Finite element analysis of natural fiber-reinforced polymer composites, Elsevier: 153–170, 2019.
19. P. SPITERI, “Variational Approach for The Finite Element Method,” AF503 V1, 2012.
20. O.C. Vincent, M.E. Cyril, K.C. Okolie, D.A. Obodoh, “Finite Element Modeling for Wind Response of Aluminum Wall Cladding in Tall Building.”
21. V.D. Quoc, Q.N. Duc, “A perturbation finite element approach for correcting inaccuracies on thin shell models with the magnetic field formulation,” Advances in Science, Technology and Engineering Systems, 5(3), 166–170, 2020, doi:10.25046/aj050322.

(Click Here)

(Click Here)