1. Introduction

Over the last years, Methods of experimental studies applied to the musical field have improved considerably. Only think of an ever-increasing amount of music sites that stream. There are nearly as many options to catalog and label music recordings as there are websites today. What features may be used to execute these processes though? What elements of the song will be taken into consideration when deciding descriptors used and What is the essence of music composing?

There is currently no method or rationale for an artificial arrangement for oriental music in a composer’s style and manner. In comparison, numerous analyses have been established in the sense of occidental music.

Musical composition is an art based on the learning baggage that the composer learns implicitly by listening to a varied set of musical styles, we suppose that in the human being there are natural algorithms that allow in a very intelligent way to analyze, calculate and measure the stored data on a natural learning basis in effort to allow new creations and innovations, and we suppose that is the case of composer who produces new musical phrases.

Based on this idea that our work will reposition itself. The oriental music artificial by appealing to the ideas and thoughts of the great composers of history such as Mohammed ABDELWAHAB, Farid el ATTRACHE and others.

We present here a profound model of the algorithmic composition of the monophonic oriental melodies centered on a description from musical scores in alphabet form controlled by a number of compositional rules allowing for the production of words to constitute musical pieces. We extend the previous model to two distinct tasks: quantifying attributes and writing derivative words, which constitutes a song. The remainder of the paper is structured as follows: In section 2, we discuss the prior works as state-of-the-art on the collection of artificial music composition. Section 3 is devoted to our method modeling. The algorithm in question is developed in section 4. Section 5 is dedicated to Test and validate results. Finally, in section 6, we conclude this article and propose future work related to it.

2. State of the Art

The first studies of mathematical description for compositional music are related according to the literature to (Pierre Barbaud) [1]. From 1957 on, this style of music often referred to like electronic music or automated composition, brought the technical fascination that the Illiac String Quartet Suite created by both the author Lejaren Hiller and also the theorist Leonard M Isaacson, a work produced at the University of Illinois using the Illiac IV (Illinois Accumulator) computer [2]. Many plays consequently in display throughout the day. Use of Markov chains and stochastic processes by combining different theoretical properties that lead to composition [3]-[5]. According to [6], Single process systems will not appear to be successful, a network which is writing songs with harmonic attachment and other models of music composition has been presented in [7]-[11]. In the Blues style [12] we find an approach that helps producing monophonic songs of chord progression. Another idea is outlined in a device that produces F0 contour dynamically whenever a partition is provided out of an automated learning frame. This is expressed as a mathematical black box forming a contour of F0 with required characteristics like naturalness & expressiveness [13]. Using the well-established uniform distance from compression as a reference feature, which genetic algorithms can use to produce music automatically in a known style [14]. Neural networks in the thinking process might be helpful [15]-[20]. Neural networks in the thought process could help with more specifics [21]-[25]. A model considers melody and rhythm in tandem when modeling the relation among these two features, this method allows for the creation of fascinating full melodies or suggests alternative a series have broken harmony in accordance with the features of the splitting itself [26]. The classification of the oriental notes was suggested in [27] for identification by a system for modeling a musical sound by collecting a set of harmonic features representing the greatest knowledge found in this sound. Another method of audio classification was described in [28] enhancing the extraction of features using of constant transformation model, including initial musical context-related to audio features where notes occur. The simulation of a lute’s sounds is discussed in [29]. Another model that considers notes as abstract functions, we find in [30], an eastern note and a quarter-tone scale pattern. In [31], an automated composition process of eastern music, which allows the generation of derived terms, based on the original features of a selected composer. In [32], the studies highlighted functionalities of SVM on a common songs database of 409 sounds of 16 groups, a comparison of SVM-based distinction Guo was established with other traditional methods, while proposing a new audio recovery criterion, called Boundary Deviation (DFB). [33] work on automated singer identification by distinguishing instrumental and singing sounds using audio information such as timbre parameters, pitch level, mel frequency cepstral coefficients (MFCC), linear predictive coefficients (LPC) and Indian video songs (IVS) audio signal loudness. In [34], an examination of the influence of texture choice on the identification of automated music genres and a novel K-Means-based texture filter aimed at distinguishing different sound textures in each album. The results indicate that the capture of texture heterogeneity within songs is necessary in order to improve the classifier accuracy and also reveal that the K-Means texture selection is capable of achieving substantial improvements over all the baseline using fewer textures per track than that of the other texture selectors examined and that the use of multiple texture representation makes for more possibilities. In [35] authors suggest a new paradigm for the classification of songs, integrating a Bidirectional Recurrent Neural Network dependent attention system. It also incorporates two focus-based models (serial focus and parallel attention). Compared to sequential attention, the parallel focus becomes more robust and the studies yield better results. In [36] an algorithm that illustrates a hierarchical structure from a series of discrete signs by replacing the repeated sentences with a grammatical method generating the sentence. In [37] a study of language identification in the field of artificial intelligence. In [38] a vertical partitioning model based on the Decision Tree mechanism for rhythmic music.

3. Modeling

To grasp the composer’s logic composition of opera, symphony or something similar of Arabic musical art, it seems impossible to research a musical score as a whole, although our concept is to research the form and logic of which each word of the partition was composed, recognizing that there are N bars in the piece (play). measures are taken as words and word series forms a musical phrase. Original terms contain some amount of specific information that could be used in artificial compositions as input features. with more precision, our concept is based on the study of the word belonging to a musical piece, the word can contain relevant information forming a thought of the composer that we can decipher using the descriptors, this will allow us to reuse these parameters in order to artificially compose music while respecting the laws applied to the original word

3.1. Originality of Arabic Music

Students learn repertoire and technical methods through oral practice conveyed by a teacher. He evolves after some mastery of those components and places himself in the improvisation game and in the art of making music. He builds on the background of the components conveyed to him as well combine them so according to his desires, or even from that he creates variations that enrich a common repertoire. That oral tradition stays one of the most important elements of the understanding and pedagogy of Eastern music. Hence it is essential to have clear control of rhythmic and melodic structures to compose and analyze Eastern music. Students study melodic parts and never present them precisely as originally recorded. Professional Arabic musicians, like Indian professional musicians and American Jazz musicians, add musical innovations or improvisations to established pieces. Improvisations may be pretty long, converting 10-minute song into one-hour presentations, and often have nothing in common with the initial model. Carries different understanding of what constitutes a specific artist (in the last century, the older aesthetic frame lived side by side with a new aesthetic of modernization and creativity, leading to new combinations and fusions). One could sum up the traditional aesthetics as follows: A professional musician is required to memorize a vast repertoire of tunes, musical words, ornamental techniques, etc., while rarely playing the same song the same manner. Individuality and originality are important-but it can only be appreciated to the degree that it generates and expands hereditary awareness.

3.2. The Alphabet

We consider in our method two alphabets, one rhythmic alphabet, and one symbolic alphabet.

3.2.1 The Symbolic Alphabets

There are seven basic notes (C, D, E, F, G, A, B, S) in both Western and Arabic music plus (S) silence, which is known as a tone. But the peculiarity of the Oriental world comes from the fact that a quarter-tone is present, a note can be assigned to one of five states instead of one of three as in occidental music.

Figure 1:  Notes states

Name of notes in traditional Arab vocabulary:

Table 1: Arabic Note Name

Name of Common Arabic Notes	Name of Occidental Notes
ELYAKAH	G (low)
ELTIK YAKAH	G+
ELQARAR ELHISAR	G#/ Ab
ELQARAR ELTIK HISAR	G#+/ Ab-
ELOUCHAÏRAN	A
ELQARAR ELNIM ADJAM	A+
ELQARAR ELADJAM	Bb
ELIRAQ	Bb+
ELQAOUACHT	B
ELTIK ELQAOUACHT	B+
ELRAST	C
ELNIM ELZIRKOULAH	C+
ELZIRKOULAH	C#/Db
ELTIK ELZIRKOULAH	C#+/Db-
ELDOUKAH	D
ELNIM ELKOURDI	Eb-/D+
ELKOURDI	Eb
ELSIKAH	Eb+
ELBOUZALIK	E
ELTIK ELBOUZALIK	E+/F-
ELDJAHARKAH	F
ELNIM ELHEDJAZ	F+/Gb-
ELHEDJAZ	F#/Gb
ELTIK ELHEDJAZ	G-/F#+
ELNAOUA	G (medium)

Bearing in mind the infinity of tones, we inferred infinity of musical notes. Human ear hears frequencies varying between 20 Hz (weakest frequency) to 20,000 Hz (maximum frequency), music culture artists defined this principle in a representation of musical keys.

Figure 2:  Note range

For this post, for each note, we’ll find five states and seven different pitches.

Symbolic Alphabet Matrix:

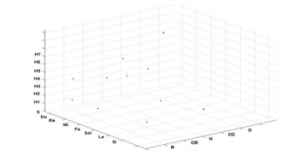
Figure 3: Matrix of the symbolic alphabet

3.2.2 Ranges Representation

A scale represents a subset of the alphabet consisting of seven notes of its derivatives plus the (S) silence. We may identify each spectrum at a 49-symbol height representing the terms and their heights. Finally, we have a number of symbols equal to 50.

Maqam:

Improvisation is not a free-for-all of Arabic literature. It must express a specific musical mode (known as maqam), that further means even more than playing on a given scale; so every maqam has a large vocabulary of idiomatic harmonic phrases as well as ornaments which the performer must perfect. Therefore, modulations are required (mood and scale changes), and melodies are required to be opened and closed, for some improvisation in a specific maqam.

Maqam is the term applied to the Eastern music scales, that title means the set of tonal intervals of the seven fundamental notes (as well as five notes in the sense of Eastern pentatonic scales). Scales are named by a note which even the sound was interrupted. oriental Maqam is different from the occidental ones as they are composed of a quarter of a tone while they are still smooth and sharp.

Example of Maqam RAST:

Figure 4: RAST Maqam

In Arabic, Maqam Rast is the title of a maqam (musical mode) and associated music systems. Rast is a Persian term that signifies “true” or “correct.” Rast is known as the fundamental maqam in both Iranian and Eastern music, in the very same manner as major scale in occidental music, but in detail, it is unique from the major scale (the big scale is actually kind of like Ajam Maqam). Rast includes a third half flat with a seventh-scale half flat degree.

Tone Interval of Main Maqam:

This table contains our own work to define the interval of oriental maqam.

Table 2: The Interval of Maqam

Rast Genre	Tone Interval of Maqam
Rast	1 – 3/4 – 3/4 – 1 – 1 – 3/4 – 3/4
Kirdane	3/2 – 1/4 – 3/4 – 1 – 1 – 3/4 – 3/4
Sazkar	3/2 – 1/4 – 3/4 – 1 – 1 – 3/4 – 3/4
Suznak	1 – 3/4 – 3/4 – 1 – 1/2 – 3/2 – 1/2
Nairuz	1 – 3/4 – 3/4 – 1 – 3/4 – 3/4 – 1
Yakah	1 – 3/4 – 3/4 – 1 – 3/4 – 3/4 – 1
Dalanshine	1 – 3/4 – 3/4 – 1 – 1 – 3/4 – 3/4
Suzdalara	1 – 3/4 – 3/4 – 1 – 1 – 1/2 – 1
Mahur	1 – 3/4 – 3/4 – 1 – 1 – 1 – 1/2
Bayati Genre
Bayati	3/4 – 3/4 – 1 – 1 – 2/1 – 1 – 1
Bayati Shuri	3/4 – 3/4 – 1 – 1/2 – 3/2 – 1/2 – 1
Husayni	3/4 – 3/4 – 1 -1 – 3/4 – 3/4 – 1
Muhayyar	3/4 – 3/4 – 1 – 1 – 1/2 – 1 – 1
Nikriz Genre
Nikriz	1 – 2/1 – 1,5 – 2/1 – 1 – 2/1 – 1
Nawa Athar	1 – 2/1 – 1,5 – 2/1 – 2/1 – 1,5 – 1/2
Athar Kurd	1/2 – 1 – 3/2 – 1/2 – 1/2 – 3/2 – 1/2
Nahawand Genre
Nahawand	1 – (1/2) / 1 – 1-1 – (1/2) / 1 – 1,5 – 2/1
Farahfaza	1 – 1/2 – 1 – 1 – 1/2 – 3/2 – 1/2
Nahawand Murassa	1 – 1/2 – 1 – 1/2 – 3/2 – 1/2 – 1
Ushaq Masri	1 – 1/2 – 1 – 1 – 3/4 – 3/4 – 1
Hijaz Genre
Hijaz	1/2 – 1,5 – 1/2 – 1-2 – 1/2 – 1 – 1
Hijazkar	1/2 – 3/2 – 1/2 – 1 – 1/2 – 3/2 – 1/2
Shadd Araban	1/2 – 3/2 – 1/2 – 1 – 1/2 – 3/2 – 1/2
Shahnaz	1/2 – 3/2 – 1/2 – 1 – 1/2 – 3/2 – 1/2
Suzidil	1/2 – 3/2 – 1/2 – 1 – 1/2 – 3/2 – 1/2
Zanjaran	1/2 – 1 – 1/2 – 1 – 3/2 – 1/2 – 1
Kurd Genre
Kurd	2/1 – 1 – 1 – 1 – 2/1 – 1 – 1
Hijazkar Kurd	1/2 – 1 – 1 – 1 – 1/2 – 1 – 1
Sikah Genre
Sikah	3/4 – 1 – 1 – 4/3 – 4/3 – 1 – 3/4
Houzam	3/4 – 1 – 2/1 – 1,5 – 1/2 – 1 – 3/4
Rahat al-Arwah	3/4 – 1 – 2/1 – 1,5 – 1/2 – 1 – 3/4
Iraq	3/4 – 1 – 3/4 – 3/4 – 1 – 1 – 3/4
Awj Iraq	3/4 – 1 – 1/2 – 3/2 – 1/2 – 3/2 – 1/4
Bastanikar	3/4 – 1 – 3/4 – 3/4 – 1/2 – 3/2 – 1/2
Mustaar	5/4 – 1/2 – 1 – 1/2 – 1 – 1 – 3/4
Ajam Genre
Ajam	1 – 1 – 2 – 1 – 1 – 1 – 1/2
Ajam Ouchayrane	1 – 1 – 1/2 – 1 – 1 – 1 – 1/2
Shaouq Afza	1 – 1 – 1/2 – 1 – 1/2 – 3/2 – 1/2
Independents Maqam
Maqam Jiharkah	1 – 1 – 1/2 – 1 – 1 – 3/4 – 3/4
Maqam Lami	1/2 – 1 – 1 – 1/2 – 1 – 1 – 1
Maqam Saba	3/4 –  3/4 – 2/1 – 1,5 – 2/1 – 1 – 1
Maqam Saba Zamzam	1/2 – 1 – 1/2 – 3/2 – 1/2 – 1 – 1/2
Maqam Sikah Baladi	3/4 – 1 – 3/4 – 1/2 – 1/2 – 3/4 – 1

The scale reduces the number of available alphabets; also, every scale does have its own alphabet specified by the tonal intervals by considering the silence S also as a note into account.

Standard range: A{s, q1; q2; q3; …; q49} pentatonic range: A{s, q1; q2; q3; …; q35}.

3.2.3 The Rhythmic Alphabet

A musical note’s shape-or number-defines its duration, and it shapes the musical rhythm by integrating the various durations. There are many types of note and specific silences or figures: Round, White, Black, Eighth, Sixteenth, Sixteenth, Triple Eighth, Quadruple Eighth, dotted notes, etc.

Example:

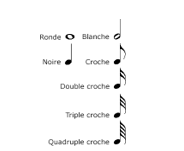
Figure 5:  Rhythmic alphabet

Every note pattern’s rhythm has always been worth twice as much as that which follows. We should find, in our analysis, the following set of durations (1/16, 3/32, 7/64, 1/48.1/48.1/48, 1/8, 3/16, 7/32, 1/24.1/24.1/24, 1/4, 3/8, 7/16, 1/12.1/12.1/12, 1/2, 3/4, 7/8, 1/6.1/6.1/6, 1, 3/2, 7/4, 1/3.1/3.1/3, 2, 3, 7/2, 2/3.2/3.2/3, 4, 6, 7, 4/3.4/3.4/3)

Every musical word is a mixture of symbols belongs to a symbolic alphabet and also has a length belongs to a rhythmic alphabet; the construction of musical words refers to the concatenation of a number of symbolic alphabets aligned to their rhythmic alphabet.

4. Proposed Algorithms

We suggest two algorithms: the first feeds a research base with calculated descriptors and second produces measurements involving derived terms that, while taking into account the grammar of western music, follow the same constraints as the original words in the study base.

4.1. Learning Steps

We will present a learning algorithm in this section, based on descriptors we described before. Those descriptors constitute the necessary details about a score’s musical metric. 11 information’s piece of fundamental for extracting from the initial term while respecting laws of Eastern musical grammar, condition of distance among the notes shall be regulated by scale, note and, note figures.

The measure in the first sense is a segmentation of the interval between musical discourse. In other words, measure is the separation of a musical piece into equal parts of the same duration. Vertical bars on the staff show this section named measuring bars. This is determined by a certain number of periods-times being units for period calculation. Furthermore, the metric should be used as a broader unit of measurement that requires multiple periods in this respect.

Figure 6:  The Measure

A bar includes two kinds of information, essential information describing the form of the music (rhythm, harmony, polyphony), and details of expression called nuances. In Western music, nuance is a symbol indicating the relative strength of note, a phrase, or a whole passage of a musical composition. During their performance, the nuances permit the musician to reproduce the dynamics of the work.

Figure 7:  The Nuances

In comparison, the use of variations is almost absent in Arabic music. The peculiarity of oriental music lies with the fact that, in an ensemble, each musician will perform the same song but with different nuances. For this reason, nuances are excluded from this work.

Figure 8: The Absence of Nuances

4.1.1 Proposed Learning Algorithm

The proposed algorithm consisting of browsing a piece of music from an entered score, determining the descriptors, and then feeding a chronologically ordered learning base. This will allow us to have a database containing calculated features preventing initial words, the parameters stored in different tables constitute the thoughts of the composers but it is presented in a mathematical way including for each musical piece: the composer, the chosen scale, the chosen rhythm, the number of notes in a word, the sum of the intervals detected, the largest interval between two consecutive notes, and the smallest interval between two consecutive notes, the greatest duration of a note referring to the word concerned, the smallest duration of a note belonging to the word in question, the greatest pitch of note pertaining to the word and the smallest pitch of a note which belongs to that word and the pitch of the first note referring to the word concerned.

Figure 9:  The Learning Algorithm

4.1.1.1 Representation of Descriptors

We identified eleven descriptors:

• Nnote: Notes numbers.
• Gnote: Maqam (indicated on armor, taken on consideration alterations the first and the last note of partition).
• Snote: Sum of tonal intervals among notes (depending on Maqam).
• Gd: Largest tonal interval among two notes (in terms of the Maqam).
• Pd: Smallest tonal interval among two notes (in terms of the Maqam).
• R: Rhythm
• Dnote: Longest note duration (in terms of the Maqam).
• Pnote: Shortest note duration (in terms of Rhythm)
• Hnote: First note pitch of the term.
• Gh: Highest height of the word.
• Ph: Lowest height of the word.

4.1.1.2 Browse an Entered Score

The algorithm beginning checks the score’s first/last notes to determine the scale’s main note then checks the rhythm (R) and starts measuring each note’s length consecutively and as per the specified time unit. When sum of durations of note achieves the rhythm, the system Sees the previous sequence as a term, and then goes on to next one.

R = Rhythm

I = duration note for I = 0 to I = R → I=in + in+1

When terminal segmentation is complete, the system moves to descriptor estimating.

4.1.1.3 Calculation of the descriptors of each word:

The Algorithm for each segmented term:

1. Calculate the Nnote number.
2. checks the presence on the basis of the main note previously mentioned of the seven deferential notes constituting the Maqam, and measures distances (tonal interval) among them to conclude the Maqam
3. Calculates for each term, sum of the intervals tones among notes.
4. For each sentence, the system calculates the larger Gd, and between two sentences, the smallest tonal interval Pd.
5. For each term the system determines, largest duration Dnote and smallest one Pnote.

4.1.1.4 Power supply for the learning base

The algorithm takes each word to be a sequence (Gh, Ph, Note, Pnote, Hnote, Gnote, R, Dnote Snote, Pd, Gd). Feeding takes place on a learning base, which comprises the structure as follow:

1. Symbolic terms matrix table of heights.
2. Rhythmic alphabet table.
3. Ranges table.
4. Table of composers.
5. Pieces table
6. Descriptors and words table

4.2. Composition

The proposed model aims to create derivative words automatically in terms of the music descriptors contained in the database. First, the method starts by splitting the rhythmic word from symbolic word and by milking each one in a particular way. A collection of rules for calculating distance and filtering is implemented to create derived terms, then the system proceeds to a concatenation operation at the end, the entire process is rebooted N times to produce a similar musical song in the chosen composer’s style of composition. It is sort of a continuation of the composer’s thinking.

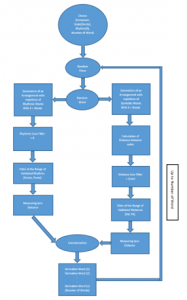
Figure 10:  The Composition Algorithm

Option of (composer, scale, rhythm): In effort to create derived words, three essential elements (composer, scale, rhythm) should be filling at the beginning.   the selection of Maqam will decide the rules applied to both the measure and the rhythm and will determine the size of measures.

RANDOM Piece: Randomly the algorithm selects a piece from among many pieces selected by a filter (composer, scale, rhythm).

RANDOM Measurement: Randomly the algorithm selects a measurement then retrieves its descriptors from multiple measurements of same piece.

4.2.1 The Symbolic Word

 Generation repetition arrangement: All combinations are generated by the algorithm: n^k with k = Gnote scale note and specified by [Gh and Ph].

Calculation of distances between notes: Each of the 2 successive notes represents a distance, and the algorithm measures each distance by the scale concerned.

Filter on sum of distances = Score: If the distances between notes have been determined, the algorithm calculates the sum of all distances that constitute the term. All terms including Snote (word-derived) ! = Snote (original word) are excluded.

Filter of the range of validated distances [Gd, Pd]: The algorithm holds the terms [Gd, Pd] valued by distances.

Filtering by Measuring the Jaro Distance: In effort to choose words which is much less similar than the initial symbolic word, all words produced honoring all conditions and rules must be placed in competition.

The Jaro Similarity simj of two given strings

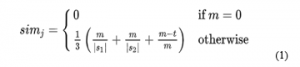
where:

• |Si| is the length of sting Si;
• m is the number of matching characters
• t is half the number of transpositions

Two characters from S1 and S2 become considered matching even if they are similar and not further than the:

4.2.2 Rhythmic word

Generation of an arrangement with repetition: The method generates all different variations in rhythm as the same method as symbolic terms: n^k with k = Nnote.

 Rhythm sum filter = R: The algorithm calculates sum of all distances which make up the term. All terms including R (word derivative)! = R (original word) are excluded.

Filter of the range of validated rhythms [Dnote, Pnote]: The system preserves terms whose letters respect [Dnote, Pnote].

Filtering by Measuring the Jaro Distance: All the words produced that comply with all laws and conditions should be placed in competition to prioritize terms that are less similar to the initial rhythmic word

Concatenation of Symbolic word and Rhythmic word:

Concatenation: The system randomly selects a derived word from the list of preserved terms and derived rhythmic term from the list of preserved rhythmic terms and combines the two.

The system reboots many times up to the No words.

5. Process Implementation

In this section, we are interested in generating a musical score by respecting laws and rules defined before. We have chosen to compose music by appealing to the thoughts of Mohammed ABDELWAHAB and this through his musical words that he composed before. all the musical libraries of different composing artists are considered intellectual heritage. in our algorithm, we try to create derived words from initial words.

Generation of pieces:

1. four words: Composer = Mohammed ABDELWAHAB; Maqam = Nahawand ; R = 4/4.
2. six words: Composer = Mohammed ABDELWAHAB; Maqam = Bayati ; R = 4/4.
3. Two words: Composer = Mohammed ABDELWAHAB; Maqam = Nahawand; R = 4/4.

5.1. Table of original words randomly selected from the learning base

Table 3: Original Words Randomly Selected from the Learning Bases

Composers	R	Maqam	Songs	Initial words
Mohammed abdelwahab	C	ELNAHAWAND	Al Fan	2do(2)1sib(2)1sol(2)
			Elfantazy	3/2mib(2)1/2re(2)3/4mib(2)1/4 re(2)3/4mib(2)1/4re(2)
			Elfan	1/2sib(2)1/2do(2)1/2re(2)1/2mi b(2)2fa(2)
			Elfan	3/2mib(3)1/2re(3)1st(3)1/4re(3)1/4re(3)1/4mib(3)1/4fa(3)1/4s ol(2)
			Limta Zaman	1sol(2)2sol(2)2sol(2)1fa(3)
			Elfantazy	1/2re(2)1/2mib(2)1/2fa(2)1/2fa (2)1/2sol(1)3/4mib(2)1/4re(2)1/ 2do(2)1/2re(2)
			Limta Zaman	1sol(2)1/2lab(2)1/2sib(2)1lab(2)1sol(2)
		ELBAYATI	Elfantazy	3/2sol(1)1/2fa(2)3/2lab(1)1/2so l(1)
			Ya mousafir Wahdak	1/2sol(2)1/2do(2)1/2sib(2)1/2la db(2)1sol(2)1st(2)
			Manaa Sali	1sib(2)1ladb(2)1/2sib(2)1/2sib( 2)1/2do(2)1/2sib(2)1/2ladb(2)
			Ya mousafir Wahdak	1/2re(2)1/2mib(2)1/2re(2)1/2re (2)1/2do(2)1/2sib(2)1/2do(2)1/ 2do(2)1/2sib(2)1/2ladb(2)
			Manaa Salie	1s(0)1do(2)1sib(2)1do(2)
			Manaa Salie	3/2re(2)1/2do(2)1sib(2)1ladb(2)
			Ya mousafir wahdak	1sol(2)1ladb(2)1sib(2)1do(2)
		ELNAHAWAND	Elfantazy	1/4lab(1)1/4sol(1)1/2fa(2)1/4fa (2)1/4fa(2)1/2mib(2)1/4fa(2)1/ 4fa(2)1/4mib(2)1/2re(2)1/4mib (2)1/2do(2)
			Alfan	2sib(2)1lab(2)3/4sol(2)1/4lab(2)

5.2. Table of Calculated Descriptors

Table 4: Calculated Descriptors

	Calculated Descriptors
Initial Words	Nnote	Snote	Gd	Pd	Dnote	Pnote	Hnote	Gh	Ph
2do(2)1sib(2)1sol(2)	3	2,5	1,5	1	2	1	2	2	2
3/2mib(2)1/2re(2)3/4mib(2)1/4re(2)3/4mib(2)1/4re(2)	6	2,5	0,5	0,5	1,5	0,25	2	2	2
1/2sib(2)1/2do(2)1/2re(2)1/2mib(2)2fa(2)	5	3,5	1	0,5	2	0,5	2	2	2
3/2mib(3)1/2re(3)1re(3)1/4re(3)1/4mib(3)1/4fa(3)1/4sol(2)	7	3	1	0	1,5	0,25	3	3	2
1sol(2)2sol(2)1fa(3)	3	1	1	0	2	1	2	3	2
1/2re(2)1/2mib(2)1/2fa(2)1/2sol(1)3/4mib(2)1/4re(2)1/2do(2)1/2re(2)	8	7	2	0,5	1,5	0,25	2	2	1
1sol(2)1/2lab(2)1/2sib(2)1lab(2)1sol(2)	5	3	1	0,5	1	0,5	2	2	2
3/2sol(1)1/2fa(2)3/2lab(1)1/2sol(1)	4	3	1,5	0,5	1,5	0,5	1	2	1
1/2sol(2)1/2do(2)1/2sib(2)1/2ladb(2)1sol(2)1re(2)	6	8,5	3,5	0,75	1	0,5	2	2	2
2sib(2)1lab(2)3/4sol(2)1/4lab(2)	4	2	1	0,5	2	0,25	2	2	2
3/2mib(2)1/2re(2)3/4mib(2)1/4re(2)3/4mib(2)1/4re(2)	6	2,5	0,5	0,5	1,5	0,25	2	2	2
1sib(2)1ladb(2)1/2sib(2)1/2do(2)1/2sib(2)1/2ladb(2)	6	4,25	1	0,75	1	0,5	2	2	2
1/2re(2)1/2mib(2)1/2re(2)1/2do(2)1/2sib(2)1/2do(2)1/2sib(2)1/2ladb(2)	8	5,75	1	0,5	0,5	0,5	2	2	2
1s(0)1do(2)1sib(2)1do(2)	4	2	1	1	1	1	2	2	2
3/2re(2)1/2do(2)1sib(2)1ladb(2)	4	2,75	1	0,75	1,5	0,5	2	2	2
1/4lab(1)1/4sol(1)1/2fa(2)1/4sol(1)1/4fa(2)1/2mib(2)1/4fa(2)1/4mib(2)1/2re(2)1/4mib(2)1/4re(2)1/2do(2)	12	9	1	0,5	0,5	0,25	1	2	1
1sol(2)1ladb(2)1sib(2)1do(2)	4	2,5	1	0,75	1	1	2	2	2

5.3. Generation of an Arrangement with Repetition of Symbolic Words with k=Nnote

Table 5: Generation of arrangement with repetition of symbolic words with k=Note

Generation of 3375 symbolic term with n = 15, k=3, Gh=3 and Ph=2
DO2,DO2,	DO2,RE	DO2,FA	DO2,LAB2,L
DO2,DO2	2,SOL3	2,RE3	AB2,LAB2
DO2,DO2,	DO2,RE	DO2,FA	DO2,LAB2,S
DO2,RE2	2,LAB3	2,MIB3	IB2
DO2,DO2,	DO2,RE	DO2,FA	DO2,LAB2,D
DO2,MIB2	2,SIB3	2,FA3	O3
DO2,DO2,	DO2,MI	DO2,FA	DO2,LAB2,R
DO2,FA2	B2,DO2	2,SOL3	E3
DO2,DO2,	DO2,MI	DO2,FA	DO2,LAB2,MI
DO2,SOL2	B2,RE2	2,LAB3	……………

5.4. Example of Symbolic Derived Words Meeting the Conditions for the Original Word 1sol(2)2sol(2)1fa(3)

Table 6: Example of Symbolic Derived word

	W1	W2	W3
Word1	RE2	DO2	S
Word2	RE2	DO2	DO2
Word3	RE2	RE2	DO2
Word4	RE2	MIB2	RE2

All features generated respect the rule: Distance Sum Filter = Score; Filter of the Range of Validated Distances [Gd, Pd], and the Measuring of Jaro Distance to choose the derived word with the least similarity to the original word.

In the end, operation of RANDAM is executed to choose a single word among the words respecting all the conditions and this to reduce the probability of falling on the same word the next iteration.

5.5. Generation of an arrangement of rhythmic words with k=Nnote

Table 7: Generation of Arrangement of Rhythmic Words with K=Nnote

Generation of 125 rhythmic term with n = 5, k =3, Dnote=2 and Pnote=1
1;1;1,5	1;2;1,5	1,5;1;1,5	1,75;1,75;1,5
1;1;1,75	1;2;1,75	1,5;1;1,75	1,75;1,75;1,75
1;1;1	1;2;1	1,5;1;1	1,75;1,75;1
1;1;2	1;2;2	1,5;1;2	1,75;1,75;2
1;1,5;1	1,5;1;1	1,5;2;1	1,75;1;1
1;1,5;1,5	1,5;1;1,5	1,5;2;1,5	1,75;1;1,5
1;1,5;1,75	1,5;1;1,75	1,5;2;1,75	1,75;1;1,75
1;1,5;1	1,5;1;1	1,5;2;1	1,75;1;1
1;1,5;2	1,5;1;2	1,5;2;2	1,75;1;2
1;1,75;1	1,5;1,5;1	1,75;1;1	1,75;2;1
1;1,75;1,5	1,5;1,5;1,5	1,75;1;1,5	1,75;2;1,5
1;1,75;1,75	1,5;1,5;1,75	1,75;1;1,75	1,75;2;1,75
1;1,75;1	1,5;1,5;1	1,75;1;1	1,75;2;1
1;1,75;2	1,5;1,5;2	1,75;1;2	1,75;2;2
1;1;1	1,5;1,75;1	1,75;1,5;1	1;1;1
1;1;1,5	1,5;1,75;1,5	1,75;1,5;1,5	1;1;1,5
1;1;1,75	1,5;1,75;1,75	1,75;1,5;1,75	1;1;1,75
1;1;1	1,5;1,75;1	1,75;1,5;1	1;1;1
1;1;2	1,5;1,75;2	1,75;1,5;2	1;1;2
1;2;1	1,5;1;1	1,75;1,75;1	…………

5.6. Example of rhythmic derived words meeting the conditions for the original word 1sol(2)2sol(2)1fa(3)

Table 8: Example of Symbolic Derived Words

Filtering with R = 4
W1	W2	W3
1	1	2
1	3/2	3/2
1	2	1
3/2	1	3/2
3/2	3/2	1
2	1	1

5.7.  Filtering with Jaro Distance

Table 9: Filtering Based on Jaro Distance

Filtering With Jaro Distance
W1	W2	W3
1	1	2
1	3/2	3/2
1	2	1
3/2	1	3/2
3/2	3/2	1
2	1	1

5.8. Concatenation of Symbolic Word and Derived Word

The last operation consists of concatenating respectively the derived symbolic words with the derived rhythmic words.

Table 10: Example of Concatenated Word

Concatenated Word
3/2	1	3/2
RE2	MIB2	RE2
3/2RE(2)	1MIB(2)	3/2RE(2)

5.9. Partition generated

Figure 11:  Automatic Generated Music

6. Conclusion and Future Works

The proposed algorithm permitted us to produce musical words that constitute parts from the descriptors we described, each word generated through its own alphabet according to the laws relating to this term by crossing a collection of filters that held only the correct words. We have been attempting to address the theory of the composition of known Arabic music composers. The result obtained and demonstrated in an artificially and automatically generated and written piece of music, shows that the machine can be an artist and we can guarantee the continuity of the composer’s thoughts, On the other hand, this area of artificial composition of oriental music still needs to be developed, we suggest the incorporation of the principle of alterations identified by the existence in a word of a foreign text, The meaning of an immediate change of scale, taking into account the relations between the terms and the introduction of the patterns of the ranges according to their definition, taking into account the unique changes in each range.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The H2020 Project SybSPEED, N 777720, supports this work.

1. P. Barbaud, R. Philippe, “L’ordinateur et la musique,” Communication & Langages, 3(1), 17–25, 1969, doi:10.3406/colan.1969.3744.
2. C.A. Wamser, C.C. Wamser, “Lejaren A. Hiller, Jr.: A Memorial Tribute to a Chemist-Composer,” Journal of Chemical Education, 73(7), 601, 1996, doi:10.1021/ed073p601.
3. C. Ames, “The Markov Process as a Compositional Model: A Survey and Tutorial,” Leonardo, 22(2), 175–187, 1989, doi:10.2307/1575226.
4. K. Jones, “Compositional Applications of Stochastic Processes,” 1981, doi:10.2307/3679879.
5. D.P. Kingma, J. Ba, “Adam: A Method for Stochastic Optimization,” ArXiv:1412.6980 [Cs], 2017.
6. G. Papadopoulos, G. Wiggins. “Ai methods for algorithmic composition: A survey, a critical view and future prospects,” In AISB Symposium on Musical Creativity, pages 110-117, Edinburgh, UK, 1999, doi.org/10.1080/17513472.2012.738554.
7. J.D. Fernandez, F. Vico, “AI Methods in Algorithmic Composition: A Comprehensive Survey,” Journal of Artificial Intelligence Research, 48, 513–582, 2013, doi:10.1613/jair.3908.
8. P.M. Todd, “A Connectionist Approach to Algorithmic Composition,” Computer Music Journal, 13(4), 27–43, 1989, doi:10.2307/3679551.
9. K.M. Kitani, H. Koike, ImprovGenerator: Online Grammatical Induction for On-the-Fly Improvisation Accompaniment, Proceedings of the International Conference on New Interfaces for Musical Expression, 469–472, 2010, doi:10.5281/zenodo.1177827.
10. P. Worth, S. Stepney, “Growing Music: Musical Interpretations of L-Systems,” in: Rothlauf, F., Branke, J., Cagnoni, S., Corne, D. W., Drechsler, R., Jin, Y., Machado, P., Marchiori, E., Romero, J., Smith, G. D., and Squillero, G., eds., in Applications of Evolutionary Computing, Springer, Berlin, Heidelberg: 545–550, 2005, doi:10.1007/978-3-540-32003-6_56.
11. M.C. Mozer, “Neural Network Music Composition by Prediction: Exploring the Benefits of Psychoacoustic Constraints and Multi-scale Processing,” Connection Science, 6(2–3), 247–280, 1994, doi:10.1080/09540099408915726.
12. D. Eck, J. Schmidhuber, “Finding temporal structure in music: blues improvisation with LSTM recurrent networks,” in Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing, 747–756, 2002, doi:10.1109/NNSP.2002.1030094.
13. J. Franklin, “Computational models for learning pitch and duration using lstm recurrent neural networks”. In Proceedings of the Eighth International Conference on Music Perception and Cognition (ICMPC8), Adelaide, Australia. Causal Productions, 2004. doi: 10.1007/978-3-319-55750-2.
14. M. Alfonseca, M. Cebrián, A. Ortega, “Evolving computer-generated music by means of the normalized compression distance,” in Proceedings of the 5th WSEAS international conference on Simulation, modelling and optimization, World Scientific and Engineering Academy and Society (WSEAS), Stevens Point, Wisconsin, USA: 343–348, 2005.
15. S. Hochreiter, “The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 06(02), 107–116, 1998, doi:10.1142/S0218488598000094.
16. F.A. Gers, J. Schmidhuber, F. Cummins, “Learning to Forget: Continual Prediction with LSTM,” Neural Computation, 12(10), 2451–2471, 2000, doi:10.1162/089976600300015015.
17. A. Graves, A. Mohamed, G. Hinton, “Speech recognition with deep recurrent neural networks,” in 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 6645–6649, 2013, doi:10.1109/ICASSP.2013.6638947.
18. J. Chung, C. Gulcehre, K. Cho, Y. Bengio, “Empirical evaluation of gated recurrent neural networks on sequence modeling,” NIPS 2014 Workshop on Deep Learning, December 2014, 2014.
19. K. Cho, B. van Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, Y. Bengio, “Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation,” in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Association for Computational Linguistics, Doha, Qatar: 1724–1734, 2014, doi:10.3115/v1/D14-1179.
20. R. Jozefowicz, W. Zaremba, I. Sutskever, “An empirical exploration of recurrent network architectures,” in Proceedings of the 32nd International Conference on International Conference on Machine Learning – Volume 37, JMLR.org, Lille, France: 2342–2350, 2015.
21. Y. LeCun, Y. Bengio, G. Hinton, “Deep learning,” Nature, 521(7553), 436–444, 2015, doi:10.1038/nature14539.
22. J. Schmidhuber, “Deep Learning in Neural Networks: An Overview,” Neural Networks, 61, 85–117, 2015, doi:10.1016/j.neunet.2014.09.003.
23. I. Sutskever, O. Vinyals, Q.V. Le, “Sequence to sequence learning with neural networks,” in Proceedings of the 27th International Conference on Neural Information Processing Systems – Volume 2, MIT Press, Cambridge, MA, USA: 3104–3112, 2014.
24. A. Graves, “Generating Sequences With Recurrent Neural Networks,” ArXiv:1308.0850 [Cs], 2014.
25. T.J. Sejnowski, “The unreasonable effectiveness of deep learning in artificial intelligence,” Proceedings of the National Academy of Sciences, 2020, doi:10.1073/pnas.1907373117.
26. F. Colombo, S.P. Muscinelli, A. Seeholzer, J. Brea, W. Gerstner, “Algorithmic Composition of Melodies with Deep Recurrent Neural Networks,” ArXiv:1606.07251 [Cs, Stat], 2016, doi:10.13140/RG.2.1.2436.5683.
27. L. Bahatti, M. Zazoui, O. Bouattane, A. Rebbani, “Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform,” Journal of Signal and Information Processing, 04(01), 51, 2013, doi:10.4236/jsip.2013.41006.
28. L. Bahatti, O. Bouattane, M. Zazoui1, A. Rebbani, Fast Algorithm for In situ transcription of musical signals: Case of lute music, ResearchGate, 2020.
29. L. Bahatti, A. Rebbani, O. Bouattane, M. Zazoui, “Sinusoidal features extraction: Application to the analysis and synthesis of a musical signal,” in 2013 8th International Conference on Intelligent Systems: Theories and Applications (SITA), 1–6, 2013, doi:10.1109/SITA.2013.6560805.
30. B. Marzouki, Application of Arithmetic and Cyclic Groups to Music, First International conference on mathematics and applications. Department of Mathematics and Informatics Faculty of Sciences Oujda, 2013.
31. M. Zhar, O. Bouattane, L. Bahatti, “New Algorithm For The Development Of A Musical Words Descriptor For The Artificial Synthesis Of Oriental Music,” in 2020 1st International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), 1–8, 2020, doi:10.1109/IRASET48871.2020.9092157.
32. Y. Zhu, Z. Ming, Q. Huang, “SVM-Based Audio Classification for Content- Based Multimedia Retrieval,” in: Sebe, N., Liu, Y., Zhuang, Y., and Huang, T. S., eds., in Multimedia Content Analysis and Mining, Springer, Berlin, Heidelberg: 474–482, 2007, doi:10.1007/978-3-540-73417-8_56.
33. T. Ratanpara, N. Patel, “Singer identification using perceptual features and cepstral coefficients of an audio signal from Indian video songs,” EURASIP Journal on Audio, Speech, and Music Processing, 2015(1), 16, 2015, doi:10.1186/s13636-015-0062-9.
34. J.H. Foleis, T.F. Tavares, “Texture selection for automatic music genre classification,” Applied Soft Computing, 89, 106127, 2020, doi:10.1016/j.asoc.2020.106127.
35. Y. Yu, S. Luo, S. Liu, H. Qiao, Y. Liu, L. Feng, “Deep attention based music genre classification,” Neurocomputing, 372, 84–91, 2020, doi:10.1016/j.neucom.2019.09.054.
36. C.G. Nevill-Manning, I.H. Witten, “Identifying Hierarchical Structure in Sequences: A linear-time algorithm,” Journal of Artificial Intelligence Research, 7, 67–82, 1997, doi:10.1613/jair.374.
37. E.M. Gold, “Language identification in the limit,” Information and Control, 10(5), 447–474, 1967, doi:10.1016/S0019-9958(67)91165-5.
38. S. Guggari, V. Kadappa, V. Umadevi, A. Abraham, “Music rhythm tree based partitioning approach to decision tree classifier,” Journal of King Saud University – Computer and Information Sciences, 2020, doi:10.1016/j.jksuci.2020.03.015.

(Click Here)

(Click Here)