1. Introduction

To solve the one-degree equations is the first learning situation where the students are asked to develop proper mathematical reasoning. In fact, their previous activities were almost of an algebraic computation nature, while resolving one-degree equations requires abstraction after modeling a real context into a mathematical problem. A survey on a sample of 1000 students how learners are disappointed while solving certain equations: they no longer know where to start, or what to find [1]. For example, to check that x=3 value is a solution to the equation “17+2x=9x-4“:

• Only 35% of students think to substitute the value x=3 in the equation;
• More than 50% try first to solve the equation and secondly to check that the solution found is effective;

• 20% fail to give any answer,

The main difficulties in solving equations are: what are we looking for? How to find it and where to start? To overcome these difficulties, we propose didactic remediation, in the form of an educational game, whose main goal is to accompany the student in developing his strategic techniques and mathematical reasoning.

The bad representation of the use letters in mathematics is identified as a didactic obstruction while solving equations [2-5]. The second goal of our didactic balance is to help the students well understand the different roles that letters may help in mathematics.

The remainder of our paper is organized as follows. In a section, we will approach the theoretical framework of some concepts like the didactic obstruction, the one-degree equations, the literal arithmetic, the educational games. The section devoted to the educational game we propose is divided in two parts. In the first one, we will show how our didactic balance was designed in order to respect the norms and standards of educational games. In the second part, we propose a simulation of the game. Finally, we conclude by some interpretations and research perspectives.

2. Literature review

2.1. Motivation and novelty

Our interest in the one-degree equations is part of a general reflection on the teaching of algebra in middle school and more specifically on the role that algebraic equations can play to help middle school students in developing their algebraic reasoning. Indeed, the false apparent simplicity of the algebraic chapters in middle school and the symbolic way this chapter is proposed to justify the enormous difficulties encountered by middle school students in algebra [6, 7]. This challenges us to innovate the teaching techniques and tools in this mathematical area more precisely [8-11].

The originality of our game is to provide children with pedagogically-appropriate ideation scaffolding, as it incorporated one-degree equations resolution best strategies. Its novelty is to be open to the incorporation of newly invented methods, provided the new additions fit with its existing system components. We guided the children through a series of steps targeted at enabling them to model a real context into a one-degree equation and then resolve the equation. These steps are described next. Moreover, the game combines two major techniques used in serious games:

• Competition: when the learner tries to maintain the equilibrium of the balance while adding coins;
• Strategy: when the learner tries to maintain the equilibrium of the balance while distributing the city with buildings of the same floors.

2.2. The didactic obstruction

Historically, this terminology was the first one to be introduced [12] while analyzing some experiences in the physical sciences. The didactic obstruction was defined [12] as an obstacle between the concept studied and the learner’s desire to learn. It is considered as an important and being interested “piece of knowledge” that unexpectedly became erroneous or unusual, or simply unsuitable [13]. They are seen as false representations of the learning task induced by previous learning, which hinders new ones [14]. They are obstinate to appear inside a given context by producing false answers. Three types are distinguished according to their origin [15]:

• The onto-genetic obstruction is related to the biological learner’s development;
• The epistemological obstruction is related to the historical development of the concept studied;
• The didactic obstruction is related to the teaching process itself.

The traversal nature of these obstacles and their resistance to prompt the educational community to propose different remediation strategies.

      For example, a certain flexibility is proposed that allows students to put in their own ideas and a rigidity that guarantees. The concept will not be losing insight to be constructed [16]. The first identify the origin of the didactic obstruction by analyzing the student answers and secondly to propose some alternative teaching activities that allow the students to overcome the identified obstruction [17].

2.3. One-degree equations

The one-degree equations

                                         a.x + b  =  c.x + d                                   (1)

are the first taught ones by learners are those of the first degree. We distinguish different solving methods:

• The substitution method, very suitable for the reduced equations of the form

                                         e.x   =  f                                            (2)

consists to try many numerical values until obtaining a solution. Using such methods opens up the learner on some classical mathematical reasoning, like true or false, the absurd or the cases distinction [18].

• The overlap method, which is an extended form of the substitution method, consists of replacing the unknown by an entire algebraic expression. For example, to solve the equation “2(x-2)=2“, we expect that the student considers the expression “x-2” as an unknown, to deduce by substitution that “x-2=1“, before concluding that “x = 3” is a solution. Looks at this method, a preparation of the student to recurrence and variables changes reasoning [19, 20].
• The formal method: consists to identify first the operations that have been applied in the equation (1) to the unknown, then recognize secondly the reciprocal operations, then finally apply a common operator to the two members of the equation in order to transform it into another reduced equation (2) that can be resolved by a substitution approach. For example, to solve the equation “3x+6=12“, the student is asked to structure his strategy as follows:

Table 1: Example of operations and their opposite ones in

the substitution method

Operations applied to the unknown	Reverse operations to find the solution
Operation 1: the unknown is multiplied by 3. Result 1= 3.x
Operation 2: we add 6 to Result 1. Result 2= 3x+6	Opposite operation 2: we subtract 6 from the second member Opposite result 2 = 6
	Opposite operation 1:  we divide the opposite result 2 by 3. Solution = 3

2.4. Literal arithmetic

This terminology was the first to be introduced and was defined [21] as any arithmetic operations on arbitrary quantities. it was rather seen as an a formal game involving writing [22]. It was pointed as the main origin of difficulties by many researches [23, 24, 25] that the students found in mathematics, especially in the algebra part. The results of the survey show us the non-mastery of the status of the letter when solving a mathematical problem in literal calculus. In a sample of 300 students, only one person correctly answered the following question: Which is the greater number n or w, if 7+n+22=109 and 7+w+22=109. For many others, w was greater than n, because it’s lexicographic rank [11].

In fact, the students are generally confused about the role and nature that the letter can play in the literal arithmetic, since the rules change completely compared to those known in the numerical calculus [26]. For example, the equation “4(2x+3)=2(4x+2)+6” means implicitly that the relation is true for any real numbers. This is never specified and therefore not necessarily obvious for the student. Here, the letter plays the role of a variable, which can take any value. While, in the example, “2x + 3 = 4“, the student is rather asked to find a value of x verifying the equality. This is not specified here either.

2.5. The educational games

In educational games were interested and have been pointed out how by many researches [27, 28, 29], they differ from the standard one by their contexts and objectives. However, their common point is that in both the player has to put up a strategy while dealing with a critical situation (for example, freeing prisoners in ordinary games or solving a one-degree equation in educational ones). One may ask why educational games (as a distraction tool) deal with mathematics (as a rigorous discipline). The answer is that in both, the player-learner is asked to resolve a problem, by taking initiatives, making choices, making decisions, anticipating solutions. In short, by putting up a logical and rigorous reasoning. In addition, the educational games help the player-learner to overcome his didactic and cognitive difficulties. Indeed, in the case of a failure situation in a classroom, the students prefer to make no additional effort. While the educational games lead the students to relax, to try again and again, to make mistakes. This is essential for the teaching-learning process [16]. We are recalled the social contribution of educational games, “a child who plays is a child who socializes”[30]. Indeed, in educational games, both adversaries and partners should respect the rules, if not this is synonymous with exclusion. This is a kind of socialization.

Furthermore, the official instructions in many educational systems recognize the educational value of the educational games by reaffirming their contribution in the teaching-learning process. We cite for example, the French official instructions which state that the educational games “lead to a multiplicity of sensory, motor, emotional, intellectual experiences … It can be the starting point for many didactic situations proposed by the teacher… “.

3. The balance game

3.1. The theoretical approach

 In subsection 2.3, we have discussed how the students fall into the situation, which was pointed out, in a failure one, their role is abandoned as learners [31, 32]. Since they think that in terms of didactic contract, it is the teacher’s role to note, correct, and validate. In an educational game, the student-learner in a failure situation never gives up; motivated by surpassing himself he tries again and again.

Their difficulties have been pointed also in the literal arithmetic, as the main obstacle to resolve equations. In the educational game, we propose instead of considering the letter as an obstacle, it will be rather considered as an objective following the “objective-obstacle” approach [33]. The resolution method that has been adopted while implementing our game is the formal one.

On the other hand, students have a private and proper knowledge validation which is not generally get-at-able to the teacher [34]. In our balance game, the student can perform his computation capacities, his reflection, his reasoning … In a failure situation, the game does not resolve the equation, but encourages the student to detect his error, to correct it, to formulate a new answer and then to validate it.

3.2. A simulation

 Let us recall that the educational games are generally designed in several levels (or stages, or rounds,…) which generally correspond to the unity and signifies a progression, which symbolizes an achievement of a knowledge component for the student and an evaluation tool for the teacher. Our game is organized in four stages:

Figure 1: The starting point when the student choose his profile

Round 0: The Modeling step.

At this stage, the game asks the student to model a real situation, drawn from his daily life, in the form of a one-degree equation. He can click on the “Beginner” button which leads to a reduced equation of the form

                                                  a.x = b                                             (3)

Or on the “Initiated” button which leads to that of the form :

                                              a.x + b  =  c                                        (4)

While the “Advanced” button leads to equations of the form (1). We are thus in the approach to adapt the learning to the student profile [35-37].

Once done, the game proposes to the student an enigma and asks him to model it in a one-degree equation. He can change it or even change his profile at any time of the game.

Figure 2: The starting point when the student choose his profile

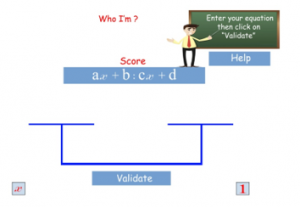
Figure 3:When the student is asked to enter the equation

Round 1: The Modeling step.

      At this stage of the game, the student is asked to enter the one-degree equation he got after modeling the enigma proposed in the last level. The game does not propose the classic keyboard method to enter the equation but rather to drop coins in the both sides of the balance. Each side of the balance itself is divided in two areas: an area for the unknown where coins of the form «x» can be dropped and an area for the constants where he can drag that of the form «1». As in a building game, the balance is introduced here as an area with four buildings, where each one contains a given number of top and bottom floors. Dragging a coin somewhere, means adding a top or a bottom floor.

• Building A : the left panel of the left side of the balance;
• Building B : the right panel of the left side of the balance;
• Building C : the left panel of the right side of the balance;
• Building D : the right panel of the right side of the balance.
• 
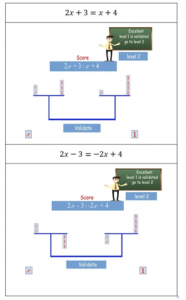
• Figure 4: Example of the right way to enter equations

Table 2: Example of help tutorial

left side of the balance		right side of the balance
Building A	Building B	Building C	Building D
Drop “a” times the coin «x» above when is positive and below when is negative.	Drop “b” times the coin «1» above when is positive and below when is negative.	Drop “c” times the coin «x» above when is positive and below when is negative.	Drop “d” times the coin «1» above when is positive and below when is negative.

A screen displays the equation obtained after each coin addition, thereby, the student feels himself in a game situation, like in a football match for example. Once the score displays the equation that has been modeled before, the game felicitates the student and invites him to press the “Validate” button. A “Help” button is incorporated in each phase of the game in any case for more technical instructions.

Round 2: The reduction step.

      The task here is to reduce the inputted equation (1), into an equivalent one of the form (2). In a classroom blackboard, the student should apply the same additions and subtraction simultaneously on both members of the equation. In the screen game, he should drag-drop the same numbers of coins simultaneously in both sides and panels of the balance. While doing, he should respect these following strict rules of the algebraic and literal computations:

• Adding the same expression to each member of the equation should be done by adding the same number of coins in top appropriate panel and side of the balance;
• Subtracting the same expression to each member of the equation should be done by adding the same number of coins in the bottom appropriate panel and side of the balance.

      If something was done wrong during the student manipulations, then an error message invites him to restore the broken equilibrium.

Table 3: The steps to follow while reducing the equation

	blackboard manipulations	game manipulations
Initial equation First manipulation Second manipulation Third manipulation Reduced form	6x-4=3x+2 6x-4+4=3x+2+4 6x=3x+6 6x-3x=3x+6-3x 3x=6	comment 0 comment 1 comment 2 comment 3 comment 4

• Comment 0: this manipulation was already done in level 1 when he enters the equation (1) he got after modeling the enigma of the level 0;
• Comment 1: he should add 5 coins of the form «1» in the right top panel of each side of the balance. If not well done, he got this “teacher” instruction: “the number of tops and bottom floors in your building B should be the same”;
• Comment 2: normally, in such a blackboard classroom situation the student should erase the expression -5+5 by himself. In the game a “delete” button is incorporated: when pressed, a window is opened and proposes to the student to enter a number (in our situation, he should enter the number 5). Then, he is asked to press once in the top floors and again in top floors of the right building (here in the building B). We consider that a middle-school student has no problem in the addition, thus the operation 10+5=15 is automatically done by the game by adding automatically floors up or down the building when coins are added in a panel;
• Comment 3: he should add 3 coins of the form «x» in the left bottom panel of each side of the balance. If not well done, he got this “teacher” instruction: the number of tops and bottom floors in your building C should be the same. He should once again simplify the erase the expression “3x-3x” by using the “delete” button;
• Comment 4: finally, the player-learner gets his reduced equation and is felicitated and invited to go to the next level.

Round 3: The resolution step.

      At this stage where the equation is reduced to the form (2), the building A contains “e” floors, the building D contains “f” floors, while the other ones are empty. Then, the game asks the student to redistribute the “f” floors of the building D, in many “f” floors sub-buildings. Once well done, the next game instruction is a window that invites the student to enter the value of “x“, which is the number of the sub-buildings in panel D.

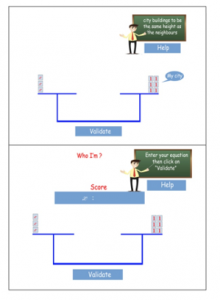
Figure 5: The final resolution step

The case when “e” and “f” are both positive, is an elementary case which will not pose great problems to the student. Otherwise, the game proposes an “Inverse” button which interprets the multiplication of one equation member by -1. Its effect in the game is inverse bottom floors to tops floors.

• If “e” or else “f” is negative, then the player should push the “Inverse” button and then click on the right panel. Then the game stores this information and will multiply by -1 the value of “x” entered by the student when asked.
• If both “e” and “f” is negative, then the player repeats the inverse manipulation twice. The game will store this information and will not change the value of “x” entered by the student when asked.

Figure 6: Simulation of the equation 3x=-6

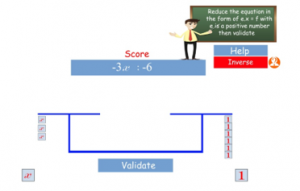
Figure 7: Simulation of the equation

4. Discussion

As early mentioned in this paper, our main goal is to help middle-school students to develop their rigor, logic, and mathematical reasoning while playing to solve one-degree equations. In its current state, the paper presents only the theoretical philosophy, the technical design, and a virtual simulation of the game. The future work on progress is to develop the “game”, to experiment on a sample of middle-school students to know how they transpose their “gaming” skills to performance of solving equations on the blackboard. Thus, our discussion will be theoretical to argue that our didactic balance is beyond being an educational game maybe also a real and alternative teaching-learning activity.

Firstly, our game is an a-didactic situation (as shown by in Table 3), which is a teaching activity where the decisions were made by the learner based on his proper knowledge, without the teacher intervention [15].

We know also that in each learning situation, the students need to adjust their actions according to their own knowledge.  Any teaching situation should offer flexibility doses which enable the learner to confront the persistent of his knowledge [16]. Our game fits into the same approach as he takes care to ensure this freedom area by limiting the teacher (illustrated by an interactive photo) interventions to only the cases of false technical manipulations.

Table 4: Example of steps to follow while  reducing the equation

a-didactic situation moment	the associated game moment
Decentralization	When the game proposes an enigma.
Action	The moment preferred by the players, here when they drag and drop coins.
Formulation	When they decide to validate a manipulation.
Validation	When the click on a button validation.
Institutionalization	When the game felicitate the student and invite him to go to the next level.

      Our game also deals with [38], who suggests assisting the student in any cognitive transition as must give up its initial system of action and adopting another different system of action. By proposing coins for both variables and numbers, the transition from numbers to letters should be smoothly easy.

      On the other hands, resolving equations in mathematics involves two types of skills:

• the ability to model a real problem into a mathematical problem;
• the ability to establish a strategy to solve the underlying mathematical problem.

      Our didactic balance agrees with [39] who deplores the fact that handbooks focus on the solving methods more than on the modeling philosophy and who suggest that both of these skills should be learned simultaneously.

      As mentioned early in this paper (to resolve one-degree equations), we adopt the formal method. In [40], the author pointed out the possible negative effect of this method: the student finds himself in an out of context situation, when sometimes he loses the sense of what he was looking for. The game we propose is mindful to avoid this possible confusion, since as in a movie, the main goal (to find « x ») accompanies the student, during all the stages and levels of the game.

      Finally, we can conclude that our educational game takes care to respect all these requirements: to contextualize the learning, to give the learner-player a free margin to make his proper initiatives and decisions, to allow the learner to overcome his didactic and cognitive obstructions, to accompany the student in a situation of failure.

5. Further work

      The authors are aware to evaluate the game in practice by operating factual information and discussing its educational advantages. Indeed, the game conception is in progress and real simulations will be done by a sample of students. The data collected will be presented in a future work.

1. J. VLASSIS and I. DEMONTY, La résolution des équations du premier degré à une inconnue, Cahiers du Service de Pédagogie Expérimentale de Université de Liège, 2000.
2. A. Cortés and N. Kavafian, “Les principes qui guident la pensée dans la résolution des équations” Petit x, no. 51, 47-73, 1999.
3. F. Chalancon, S. Coppé and N. Pascal, “Les vérifications dans les équations, inéquations et en calcul littéral” Petit x, no 59, 2002.
4. G. Combier, J. C. Guillaume and A. Pressiat, Les débuts de l’algèbre au collège: au pied de la lettre!, Institut National de Recherche Pédagogique, 1996.
5. J. Vlassis and I. Demonty, La résolution des équations du premier degré à une inconnue, Cahiers du Service de Pédagogie Expérimentale de Université de Liège, 2000.
6. J. P. Drouhard, J. L. Dorier, L. Coulange and A. Robert, Enseignement de l’algèbre élémentaire: bilan et perspectives, La Pensée Sauvage, 2012.
7. G. Gattegno, The Common Sense of Teaching Mathematics, Educational Solutions World, 2010.
8. T.L. Kurz and I. Batarelo, “Using anchored instruction to evaluate mathematical growth and understanding” Journal of Educational Technology Systems, 33(4), 421- 436, 2005. https://doi.org/10.2190/78JG-57N4-0702-XH25
9. Y. Li and E.A.Sillver, “Can younger students succeed where older students fail? An examination of third graders solutions of a division-with-reminder (DWR) problem” Journal of Mathematical Behavior, 19(2), 233-246, 2000. https://doi.org/10.1016/S0732-3123(00)00046-8
10. J. Sharp and B. Adams, “Children’s construction of knowledge for fraction division after solving realistic problems” The Journal of Educational Research, 95(6),333-347, 2002.https://doi.org/10.1080/00220670209596608
11. S. Wagner and C. Kieran, An agenda for research on the learning and teaching of algebra, Research issues in the learning and teaching of algebra, Routledge,220-237, 2018.
12. G. Bachelard, La formation de l’esprit scientifique Contribution à une psychanalyse de la connaissance objective, Libraire Philosophique J. VRIN, Paris, 1938.
13. J. Piaget, L’épistémologie génétique, Presses Universitaires de France, Paris, 1970.
14. G. Brousseau, “Les obstacles épistémologiques et les problèmes en mathématiques” Recherches en Didactiques des Mathématiques, 4(2), 164-198, 1983.
15. G. Brousseau, ” Obstacles épistémologiques, conflits socio-cognitifs et ingénierie didactique” in Actes du colloque international Obstacles épistémologiques, conflits socio-cognitifs et ingénierie didactique, Montréal, Canada, 1986.
16. J. P. Astolfi, L’erreur, un outil pour enseigner, ESF éditeur, Paris, 1997.
17. R. Berthelot and M. H. Salin, “L’enseignement des angles aux élèves de 10 à 13 ans: Identification d’un obstacle didactique” Revue des sciences de l’éducation, 22(2), 417-442, 1996. https://doi.org/10.7202/031887ar
18. J. Vlassis, “The balance model: Hindrance or support for the solving of linear equations with one unknown” Educational Studies in Mathematics, 49(3), 341-359, 2002. https://doi.org/10.1023/A:1020229023965
19. J. Vlassis, Sens et symboles en mathématiques: étude de l’utilisation du signe” moins” dans les réductions polynomiales et la résolution d’équations du premier degré à une inconnue, Peter Lang, 2010.
20. A. H. Schoenfeld, Mathematical problem solving, Elsevier, 2014.
21. O. Terquem, Manuel d’algèbre, ou Exposition élémentaire des principes de cette science, à l’usage des personnes privées des secours d’un maître, Paris, RORET, 1834.
22. Y. Chevallard,”Le passage de l’arithmétique à l’algébrique dans l’enseignement des mathématiques au collège, Deuxième partie : Perspectives curriculaires : la notion de modélisation” Petit x, no 19, 43-72, 1989.
23. D. Celik, G. Gunes, “Different Grade Students Use and Interpretation of Literal Symbols” Educational Sciences: Theory and Practice, 13(2), 1168-1175, 2013.
24. K. P. Christou and S. Vosniadou, ” What kinds of numbers do students assign to literal symbols? Aspects of the transition from arithmetic to algebra” Mathematical Thinking and Learning, 14(1), 1-27, 2012. https://doi.org/10.1080/10986065.2012.625074
25. M. Zeljić, “Modelling the relationships between quantities: Meaning in literal expressions” EURASIA Journal of Mathematics, Science and Technology Education, 11(2), 431-442, 2015. https://doi.org/10.12973/eurasia.2015.1362a
26. D. Guerrier, M. Le Berre, C. Pontille and J. Reynaud-Fleury, Le statut logique des énoncés dans la classe de mathématiques. Éléments d’analyse pour les enseignants, IREM de Lyon, 2000.
27. N. Pelay, “Jeu et apprentissages mathématiques: élaboration du concept de contrat didactique et ludique en contexte d’animation scientifique,” Doctoral dissertation, Université Claude Bernard-Lyon I, 2011.
28. L. Sauvé and D. Kaufman, Jeux et simulations éducatifs: Études de cas et leçons apprises, Presses de l’Université du Québec, 2010.
29. T. M. Connolly, E. A. Boyle, E. MacArthur, T. Hainey and J. M. Boyle, “A systematic literature review of empirical evidence on computer games and serious games” Computers & education, 59(2), 661-686, 2012. https://doi.org/10.1016/j.compedu.2012.03.004
30. S. De Freitas, “Are games effective learning tools? A review of educational games” Journal of Educational Technology & Society, 21(2), 74-84, 2018. http://www.jstor.org/stable/26388380
31. Y. Chevallard, Sur l’analyse didactique. Deux études sur les notions de contrat et de situation, IREM d’Aix Marseille, 1988.
32. G. Brousseau, “Fondements et méthodes de la didactique des mathématiques” Recherches en didactique des mathématiques, 7(2), 1986.
33. J. L. Martinand, Connaître et transformer la matière, Peter Lang, 1986.
34. I. Shor, When students have power: Negotiating authority in a critical pedagogy, University of Chicago Press, 2014.
35. S. Connac, La personnalisation des apprentissages: agir face à l’hétérogénéité, à l’école et au collège, ESF Sciences Humaines, 2018.
36. A. Feyfant, Individualisation et différenciation des apprentissages, Dossier d’actualité de la VST, no 40, 2008.
37. M. Romero, Jeux numériques et apprentissages, Editions JFD, 2016.
38. H. Squalli, “La généralisation algébrique comme abstraction d’invariants essentiels” in 2015 Actes du congrès Espace Mathématique Francophone (EMF), Alger, 2015.
39. J. Colomb, Combier Georges, Guillaume Jean-Claude, Pressiat André, Calcul littéral : Savoir des élèves de collège, Institut National de Recherche pédagogique, 1995.
40. L. Not, Les pédagogies de la connaissance, Toulouse : Sciences de l’Homme, Privat, 1988.

(Click Here)

(Click Here)