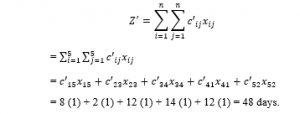1. Introduction

The significant factor in the investigation of the profitability of a creation framework is the human viewpoint. The practicality of some laborers and their abilities cause the sketchy executing time and cost for the creation attempts [1]. In genuine cases, the effectiveness of the laborers shifts from an assignment to another, with the goal that the best specialist for an undertaking isn’t really the best for another errand. Subsequently, appointing the best specialist to each assignment can altogether improve the profitability of the framework [2].

The task issue is the particular type of transportation issue. This is especially significant in the hypothesis of dynamic. The soonest utilization of a direct whole number programming issue is the task issue [1]. Other techniques have been introduced for task issues and different articles have been distributed regarding the matter [3]. See [4], [5], and Taha [6] for the historical backdrop of these strategies [7].

      An imperative number of systems has been so far introduced for task issue in which the Hungarian approach is dynamically valuable technique among them [8]. This iterative technique depends on add or take away a steady to each component of a line or section of the cost network, in a minimization demonstrate and make somewhere in the range of zeros in the given cost framework and afterward attempt to locate a total task as far as zeros. By a total task for a cost framework n × n, we mean a task plan containing precisely n doled out autonomous zeros, one in each line and one in every section. The key idea of the task issue is to locate the ideal designation of certain assets to an equivalent number of interest focuses. A task plan is ideal if enhances the absolute expense or expenditure of doing all the occupations [7].

Indeed, [13] demonstrated that the summed up task issue is a NP-complete combinatorial advancement and the current accurate techniques are viable just for specific occurrences where there are no extra limitations. In examination with this exploration, the commitment of the introduced research is to propose a strategy for taking care of task issues which is different from the past strategies.

2. Methodology

 The task issues are one specific instance of direct programming issues by and large. In business and industry, the board frequently faces issues identified with the ideal task of different profitable sources or diverse proficiency level faculty for various assignments. The Hungarian Method is one of a couple of available dealing with systems for task issues. This strategy was initially developed by an acclaimed mathematician from Hungarian known as D. Konig in 1916 [14].

The utilization of the Hungarian strategy, the quantity of sources allocated must match precisely the quantity of undertakings to be finished. Moreover, every source have to relegated distinctly for one assignment. Along these lines, the task issue will incorporate some n sources that have n assignments. There is n! potential tasks in an issue because of coordinated blending. This issue can be clarified effectively by the rectangular network structure, in which the lines demonstrate the sources and segments indicating the undertaking or reason [14].

In the transportation model, the creators decide the  dissemination which will limit the all-out expense of transport and meet the limit of the source ( ) just as the goal demand ( ). The task model might be thought of as an uncommon type of the transportation model. In this model, the ith asset or jth goal is one by the essential idea, so the ideal estimation of the    choice variable must be just zero or one [15].

The overall type of the numerical transportation model condition, as follows:

Subject to:

 = , for i = 1,2, …, m

 = , for j = 1,2, …, n

where .

The model is disentangled in the task model with the goal that the  value is one so does    for the ideal estimation of the  choice variable, it must be zero or one. Along these lines, the overall type of the efficient model of task as follows:

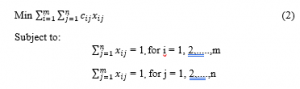
Subject to:

 = 1_, for i = 1, 2,…..,m

 = 1_, for j = 1, 2,….,n

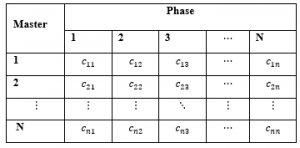
For details in the assignment matrix displyed in Table 1.

where  = 0 or 1, and

= the assignment from ith master to jth phase

= the cost unit from ith master to jth phase

Table 1: The Initial Assignment Matrix Form

The educational plan as per Lewis and Miel in [16] is a lot of objectives about individuals’ chances to be taught by others and with all the fixings (all transporters of data, procedures, methods, and qualities) in a specific reality setting. Anderson and Bowman, referred to by Akangbou, characterize arranging as a procedure of setting up a lot of choices for future activity. Along these lines, educational plan arranging is worried about setting up a progression of choices about the subject and topic that the educator will show future students [16]. For this situation, the educational program plan must experience certain stages. As per Lewy referred to in [16] is preparation obviously schedule that basically portrays the topic; production of showing materials; and implementation of the educational program in the framework.

There are five phases of activities engaged with the educational program arranging and improvement process, in particular objective setting, specialized activity (Technology), application stage, usage, and assessment [17].

• Objective Determination

This capacity includes the assurance of general instructive objectives and particulars of the fundamental goals. The universally useful of instruction is political intrigue. Shared objectives are normally communicated in expansive terms with the goal that the objective gets the accord of most social orders. The broadly useful fills in as a reason for dynamic on school daily ought to be composed and what ought to be educated in school, however in itself it doesn’t establish or legitimately decide the useful subtleties of school life [17]. Choices on educational program targets are impacted by three fundamental elements, incorporate students, society, and topic (disciplines) [16,18].

• Technology (Selecting and organizing learning experience)

When overall instruction objective has been resolved, proficient organizers start to make an interpretation of it into explicit educational plan exercises. Choices are made on the targets of explicit subjects, content, instructing learning, educational program groups will build up the primary rendition of learning content that will be utilized in the homeroom. At this stage incorporate composing writings, getting ready practicum materials, understudy courses of action, movement plans, etc [19].

• Application

The application stage alludes to preliminaries and modifications in which instructive projects will be tried exactly before they are affirmed for huge scope use. As a rule, little consideration is paid to joining or enhancing proficient intelligence with exact proof. For preliminary work of materials [17]. Numerous educational plans have fizzled in the past because of an absence of educational program testing before usage. A significant number of them are affirmed dependent on emotional decisions of instructive specialists [19].

• Implementation

Execution alludes to the open utilization of the educational plan all through the educational system. This will require a few changes in the training framework. A portion of the exercises are the arrangement of instructing and learning and in-administration preparing for school chiefs, instructors, and school administrators [17, 16].

• Evaluation

The procedure of assessment as per Tyler, is the way toward deciding the degree to which the reason for instruction is being acknowledged by educational program and instructing programs. At the end of the day, the mission statement isn’t just the premise of choice and sorting out the learning experience however the norm on which the program is based. In this way, Tyler expresses that assessment is a procedure where one’s desires coordinate the underlying desires as social goals with results. Such educational plan arranging ideas have a characteristic and exceptionally regular intrigue, particularly when advanced with models of modern and framework the executives, apparently a savvy and down to earth approach to survey the achievement of a business as per Tyler in [18].

3. Results and Discussion

The Ones Assignment Method depends on making somewhere in the range of ones in the task network and afterward attempt to locate a total task regarding ones. A task plan containing precisely m appointed free ones, one in each line and one in every segment [7]. The Matrix Ones Assignment decide punishments, partition least or most extreme point in each line and section [8].

This method utilizes one of the determinant properties of n×n lattice to get the ideal arrangement of the task issue. The ideal arrangement of the task issue in condition (2) doesn’t change if the line or section of the cost network is partitioned or increased by a steady. This can be demonstrated as follows:

If every cell form ith row and jth column divided by p_i and q_j, the new cost element be .  Thus, we obtain the new objective function.

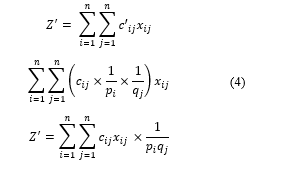
where:

 = the new cost element

= the assignment from ith master to jth phase

= the cost or time unit from ith master to jth phase

 =  ith master capacity

 = jth capacity demand

with . Thus, obtain

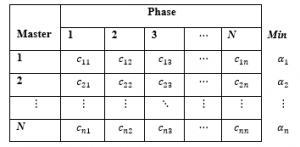
This shows the minimization of the target work produces a similar arrangement by limiting . For additional subtleties introduced by the lattice in Table 2 [2].

Table 2: The Cost Matrix Form

The algorithm are as follows [7]:

Step 1.

In a minimization (expansion) case, locate the base (greatest) component of each line in the task lattice (state   ) and compose it on the right-hand side of the network. For additional subtleties, introduced in Table 3.

Table 3:  Minimum (Maximum) Cost Of Each Row

At that point separate every component of the ith line of the network by . These activities make in any event one in each column. For additional subtleties, introduced in Table 4

Table 4: The Divide by Maximum (Minimum) Cell in Row

Master	Phase
	1	2	3		N
1	c11/ 1	n12/ 1	c13/ 1		c1n/ 1
2	c21/ 2	n22/ 2	c23/ 2		c2n/ 2
N	cn1/ n	nn2/ n	cn3/ n		cnn/ n
	β1	β2	β3		βn

As far as ones for every line and section do task, in any case go to stage 2.

Step 2.

Locate the base (most extreme) component of every section in the task network (say β_j), and compose it underneath jth segment. At that point separate every component of jth segment of the framework by β_j.

These tasks make at any rate one in every section. Make task as far as ones. On the off chance that no attainable task can be accomplished from step (1) and (2) at that point go to stage 3.

Step 3.

Draw the base number of lines to cover all the value of ones of the grid. On the off chance that the quantity of drawn lines not as much as n, at that point the total task is unimaginable, while in the event that the quantity of lines is actually equivalent to n, at that point the total task is gotten.

Step 4.

On the off chance that a total task program is unimaginable in sync 3, at that point select the littlest (biggest) component (state dij) out of those which don’t lie on any of the lines in the above lattice. At that point isolate by dij every component of the revealed lines or segments, which dij lies on it. This activity makes some new ones to this line or segment.

On the off chance that still a total ideal task isn’t accomplished in this new lattice, at that point use stage 4 and 3 iteratively. By rehashing a similar methodology the ideal task will be gotten. At the point when the ideal task has been accomplishing either step (3) or step (4) at that point utilize the need rule, which is to choose the littlest expense in arrangement for the minimization issue and the best benefit for the augmentation issue of all lattice components put away to one side of the network in sync (1), that is _i.

In this research, the authors explore the new application of the ones assignment algorithm in the field of higher education services, in order to gain optimal time results in solving the curriculum development.

4. Illustrative Example

Think about the accompanying task issue. Allocate the five occupations to the three machines to limit the all out expense. The information is then reproduced for issues in an educational program advancement advisor organization with 5 specialists and 5 phases of educational program arranging and improvement process. More explanation is introduced in Table 5.

Table 5: The Solution Time of Curriculum Planning and Development

Master	Phase
	G	T	A	I	E
ERS	24	16	14	30	8
DJ	14	18	2	28	20
IS	18	12	24	12	14
CS	14	12	28	12	20
DIE	18	12	24	20	12

Phase: G (Goal Determination stage), T (Technology stage), A (Application stage), I (Implementation stage), and E (Evaluation stage)

Step 1.

 Locate the base component of each column in the task lattice (state _i) and compose it on the right-hand side of the network, as follows:

Table 6: The Minimum Time on Every Row

Master	Phase
	G	T	A	I	E
ERS	24	16	14	30	8
DJ	14	18	2	28	20
IS	18	12	24	12	14
CS	14	12	28	12	20
DIE	18	12	24	20	12

At that point separate every component of the ith line of the lattice by _i. These activities make ones for each column, and the lattice diminishes to the accompanying framework.

Table 7: The Divide by The Minimum Time In Every Row

Master	Phase
	G	T	A	I	E
ERS	24/8	16/8	14/8	30/8	8/8
DJ	14/2	18/2	2/2	28/2	20/2
IS	18/12	12/12	24/12	12/12	14/12
CS	14/12	12/12	28/12	12/12	20/12
DIE	18/12	12/12	24/12	20/12	12/12

The operation result displayed in Table 8.

Table 8: The Solution Of Divide By The Minimum Time In Every Row

Master	Phase
	G	T	A	I	E
ERS	3	2	14/8	30/8	1
DJ	7	9	1	14	10
IS	18/12	1	2	1	14/12
CS	14/12	1	28/12	1	20/12
DIE	18/12	1	2	20/12	1

Step 2.

Presently locate the base component of every section in the task lattice (state β_j), and compose it beneath that segment. The operation result is displayed in Table 9.

Table 9: The Minimum Time in Every Column

Master	Phase
	G	T	A	I	E
ERS	3	2	14/8	30/8	1
DJ	7	9	1	14	10
IS	18/12	1	2	1	14/12
CS	14/12	1	28/12	1	20/12
DIE	18/12	1	2	20/12	1

At that point partition every component of the jth segment of the framework by β_j as follows:

Table 10: The Divide By The Minimum Time In Every Column

Master	Phase
	G	T	A	I	E
ERS		2/1	14/8		1/1
DJ		9/1	1/1	14/1	10/1
IS		1/1	2/1	1/1
CS		1/1		1/1
DIE		1/1	2		1/1

The solution represented in Table 11.

Table 11: The Solution Of Divide By The Minimum Time In Every Column

Master	Phase
	G	T	A	I	E
ERS	36/14	2	14/18	30/8	1
DJ	6	9	1	14	10
IS	18/14	1	2	1	14/12
CS	1	1	28/12	1	20/12
DIE	18/14	1	2	20/12	1

Thus, we obtain the new objective function as stated in the Equation (4).

Step 3.

Draw a line that passes all the bits 1 to the cross portion. The base number of lines needed to experience all the ones of the network is 5. For more detail presented in Table 12.

Table 12: Lines That Cover All 1 Values in Cell

Master	Phase
	G	T	A	I	E
ERS	36/14	2	14/18	30/8	1
DJ	6	9	1	14	10
IS	18/14	1	2	1	14/12
CS	1	1	28/12	1	20/12
DIE	18/14	1	2	20/12	1

The task can be finished in light of the fact that the quantity of lines approaches n (request framework). Select the littlest worth speaking to just one line and one segment utilizing the need rules from Table 13.

Table 13: The Minimum Time in Row and Column

Master	Phase
	G	T	A	I	E
ERS	36/14	2	14/18	30/8	1
DJ	6	9	1	14	10
IS	18/14	1	2	1	14/12
CS	1	1	28/12	1	20/12
DIE	18/14	1	2	20/12	1

Select beginning from the littlest incentive in each line or segment that is Row 2 with esteem 2 in segment 3, line 1 with esteem 8 in section 5, line 3 with esteem 12 in segment 4 (Value 12 on line 3 is double, that is in segment 2 and segment 4, the chose estimation of 12 in segment 4 of the explanation in segment 2 will be spoken to by the worth 12 in line 5), line 5 with esteem 12 in segment 2 (Value 12 in line 5 is double, that is in segment 2 and segment 5, the chose esteem 12 in segment 2 of the explanation in segment 5 has been spoken to by the worth 8 in line 1), and the last line 4 with esteem 14 in segment 1 (The littlest worth in line 4 is the worth 12 in segment 2 and 4. Notwithstanding, segment 2 has been spoken to by an estimation of 12 in line 5 and section 4 has been spoken to by an estimation of 12 in line 3 with the goal that it is chosen to speak to push 4 that is esteem 14 in segment 1). The outcomes are introduced in Table 14.

Table 14: The Final Assignment Result

Master	Phase
	G	T	A	I	E
ERS	24	16	14	30	8
DJ	14	18	2	28	20
IS	18	12	24	12	14
CS	14	12	28	12	20
DIE	18	12	24	20	12

  : The minimum time for one expert to one operation process

The results in details are as follows:

Table 15: The Time Minimum Result

Master	Phase	Duration (days)
ERS	Application stage	8
DJ	Evaluation stage	2
IS	Implementation stage	12
CS	The technological stage	14
DIE	The goal-setting stage	12

In this manner, the base chance to embrace educational program arranging and advancement in a science educational plan improvement counseling firm is

5. Conclusions

In this paper, another and basic technique was presented for taking care of task issues. The new strategy depends on making some ones in the task grid, and discover a task as far as the ones. The need assumes a significant job in this strategy. To improve a task issue, indicate the one in the column that has the biggest component for the amplification issue and the littlest component for the minimization issue on the correct side. After applying this method to the problem of curriculum development, the research results obtained the minimum time to complete curriculum development stages is 48 days. As respects the explaining technique proposed for the task issue in the writing, creating amplify target capacity could be a smart thought for future investigates.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors expressed gratitude to the UIN Sunan Gunung Djati Bandung Rector and his staff for their support to this research.

1. E. R. Wulan et al, “Determine the Optimal Solution for Linear Programming with Interval Coefficients”, in 2018 IOP Conf. Ser.: Mater. Sci. Eng. 288 012061, 2018. https://doi.org/10.1088/1757-899X/288/1/012061
2. L.E. Idris, and Sukamto, “Modifikasi Metode Hungarian Untuk Menyelesaikan Masalah Penugasan”, 2013. available at: http://repository.unri.ac.id [accessed December 5, 2017]
3. E. R. Wulan, D. Jamaluddin, A. H. Hermawan and T. Ratnasih, “The Application of Assignment Problem Optimal Solution Using Ones Assignment Method in The Curriculum Developer Team,” 2019 IEEE 5th International Conference on Wireless and Telematics (ICWT), Yogyakarta, Indonesia, 1-6, 2019. doi: 10.1109/ICWT47785.2019.8978255
4. M.S. Bazarra, J.J. Jarvis, and Sherali, H.D.” Linear programming and network flows”, 2005
5. B.S. Goel, “Operations Research”, Fifth Ed., 2405-2416, 1982.
6. H.A. Taha, “Operations Research, an introduction”, 8th Ed, 2007.
7. H. Basirzadeh, “Ones Assignment Method for Solving Assignment Problems”, Applied Mathematical Sciences, 6(47), 2345 – 2355, 2012.
8. E.R. Wulan et al, “The comparative analysis of Hungarian assessment, matrix ones assignment and alternate mansi method in solving assignment problem”, in J. Phys.: Conf. Ser. 1402 077090, 2019. https://doi.org/10.1088/1742-6596/1402/7/077090
9. G.T. Ross, R. M. Soland, “A Branch and Bound Algorithm for the Generalized Assignment Problem.” Mathematical programming, 8 (1): 91–103, 1975.
10. D. Klingman, J. Stutz, “Computational Testing on an Integer Generalized Network Code.” 45th Joint National Meeting of the Operations Research Society and the Institute of Management Sciences, Boston, MA, April 1974.
11. D. Maio, A., and C. Roveda, “An All Zero-one Algorithm for a Certain Class of Transportation Problems.” Operations Research, 19 (6): 1406–1418, 1971.
12. S.E. Moussavi, M. Mahdjoub, O. Grunder, “Productivity improvement through a sequencing generalised assignment in an assembly line system”, International Journal of Production Research, 55(24), 7509-7523, 2017. DOI: 10.1080/00207543.2017.1378828
13. P.C. Chu, J.E. Beasley, “A Genetic Algorithm for the Generalised Assignment Problem.” Computers & Operations Research, 24 (1): 17–23, 1997.
14. P. Subagyo, “Dasar-dasar Operations Research”. Yogyakarta: BPFE, 1983.
15. Siswanto, “Operations Research”,Yogyakarta: Erlangga, 2007.
16. S.D. Akangbou, “Planning the junior secondary school curriculum”. In Pai Obanya (edited). Curriculum In Theory and practice. Ibadan: Educational Research and study group, 1984.
17. R.S. Longe, “Planning for a Responsive curriculum”. In Pai Obanya edited. Curriculum, in theory and in practice Ibadan: Educational Research and study group, 1984.
18. G.A. Badmus, “Curriculum development and changes in mathematics education in Nigeria”. A paper presented during the mathematics education Summit at National Mathematical Centre, Abuja, February, 2012.
19. A.B. Festus, K.M. Seraphina, “Curriculum Planning and Development in Mathematics from the Formative Stages”, Journal of Education and Practice, ISSN 2222-1735 (Paper) ISSN 2222-288X (Online), 6(2), 62 -66., 2015.

(Click Here)

(Click Here)