1. Introduction

This paper is an extension of work originally presented at the IEEE 10th International Conference on Awareness Science and Technology [1]. In that work, we found that a chaos neural network (CNN) is able to generate pseudo-random numbers (PRNs) at high speed, 49% faster than that produced with the Advanced Encryption Standard (AES) [2], [3], and it can be easily implemented even for embedded devices.

Generally, electronic devices embedded in vehicles to control vehicle systems are called electronic control units (ECUs). A modern vehicle is usually equipped with more than 70 ECUs [4]. To share information and control the subsystems, those ECUs are connected together with network protocols, such as a Controller Area Network (CAN), Local Interconnect Network (LIN), Media Oriented Systems Transport (MOST), or FlexRay.

The CAN is a broadcast serial communications bus that is widely introduced because of its fault tolerance. The CAN identifier (ID) (see Sec. 2 and Fig. 1) is used for prioritizing messages on the bus and avoids collisions by design. However, security issues were ignored during designing since people took it for granted that a vehicle would be a closed system [5], [6]. Unfortunately, messages are broadcast on the CAN bus, and external devices, such as onboard diagnostics readers, are able to access the CAN bus in modern vehicles.

A pseudo-random number generation (PRNG) is crucial to a stream cipher in information security field. We have reported various PRNG methods [7]–[11] and the property of PRNs from a CNN [9] has been confirmed [10] by National Institute of Standards and Technology (NIST) Special Publication 800-22 [12]. An ultra-long period PRNs that has reached 10²²⁴³² [11] can be generated with the chaotic time series from the CNNs. The chaotic time series is hard to predict because it is sensitive to tiny change of the initial status.

In this paper, we propose a fast stream cipher based on a CNN to protect CAN messages by encrypting them. The remainder of this paper is organized as follows: Section 2 introduces CAN and security issues and surveys some related work. Section 3 describes our CNN and discusses some of its characteristics. Section 4 presents the CNN stream cipher, including sharing of the symmetric key and the procedure for encryption and decryption of the stream cipher. A performance evaluation of the proposed CNN stream cipher is given in Section 5. Finally, Section 6 concludes this paper.

2. Related Work

A CAN is a serial communications bus defined by the International Organization for Standardization (ISO) and originally developed for the automotive industry to replace the complex wiring harness with a two-wire bus [13]. Balanced differential signaling reduces noise coupling and enables high noise immunity in the CAN bus.

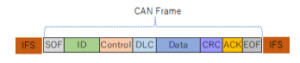
Figure 1: Structure of the CAN data frame

The CAN communication protocol is a carrier-sense multiple access protocol with collision detection and arbitration on message priority. A CAN message contains a unique ID field that represents the priority and function of the message. The CAN protocol supports four different message types: overload, error, remote, and data frame. The CAN data frame begins with a start-of-frame (SOF) bit and is followed by the ID, a control field (6 bits), 4-bit data length code (DLC), 0-64 bits of data, a cyclic redundancy check (CRC) sequence (15 bits), a 2-bit acknowledgment (ACK), and a 7-bit end of frame (EOF) sequence that marks the end of the frame. Between CAN frames, a 7-bit inter-frame space (IFS) is required by the CAN controller to provide time for moving a received frame to a message buffer area (see Fig. 1).

The CAN was subsequently adopted as ISO standards. ISO

11519 (low-speed CAN) is for applications up to 125 kbps with a standard 11-bit ID, while ISO 11898 (high-speed CAN) provides for signaling rates from 125 kbps to 1 Mbps. Furthermore, high-speed CAN supports two data frame formats, where the standard frame consists of an 11-bit ID, while the extended format contains a 29-bit ID.

Unfortunately, security issues were ignored during designing because people took it for granted that CANs would be a closed system in automobiles [5], [6]. Security issues with CANs relate mainly to authentication and encryption at the present time.

Authentication: To identify whether an ECU is authorized, several authentication proposals based on message authentication codes (MACs) have been released. Key sharing is a matter of grave concern. CANAuth [14] implements a backward-compatible message authentication protocol on the CAN bus. One or more pre-shared

128-bit MAC keys are to be available on each CANAuth node. CANAuth assumes that the keys are intended to be stored in tamperproof storage that cannot be queried by anything but the node itself. LiBrA-CAN [15] splits authentication keys between groups of multiple nodes, rather than achieving authentication independently for each node.

Encryption: A CAN frame is broadcast over the bus. In modern vehicles, external devices, such as on-board diagnostics readers, are able to access the CAN bus, making it is easy to intercept a CAN message. Cryptographic approaches based on the AES have been proposed to guard against such interception. The problem is the computation load of the AES, which might have an undue influence on the response of the ECU. Wolf and Gendrullis [16] and the

EVITA Project [17], [18] implemented a hardware security module

(HSM) to accelerate the AES measures. However, even if a HSM is used, the cryptographic measure requires 60 clock cycles (at 100 MHz) for the encryption of one AES block [18]. This is insufficient for dealing with the real-time response required of an ECU. Also, the additional hardware increases the cost of the ECU.

In this study, we focused on the encryption issues in CANs. We propose a fast stream cipher based on a CNN that does not need the additional HSM hardware.

3. Chaos Neural Network

As a chaos generator the CNN consisted of 4 neurons in a discrete time system (see Fig. 2).

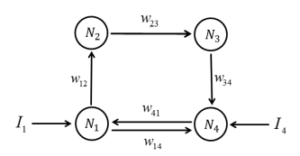
Figure 2: CNN consisting of four artificial neurons

An output from the jth neuron at time t + 1 is defined as:

                                             x_j(t + 1) = f[u_j(t)]                                        (1)

Here, An activation-function f (see Fig. 3) is an asymmetric piecewise-linear function (APLF).

For the jth neuron, the total value of inputs at time t is defined as :

n

X

                                        u_j(t) =          w_ijx_i(t) + I_j                                                      (2)

i=1

I_j is an external input of the jth neuron. x_i(t) is an input from the ith neuron at time t, and w_ij is a synaptic. Generally, the start value of x_i is set as 0, and the synaptic weights are set as follows: w₁₂ = −12.60001, w₁₄ = 4.511, w₂₃ = 5.951, w₃₄ = −4.7004 and w₄₁ = −7.345007. The synaptic weights adjust the input values from other neurons. If extreme synaptic weights were set, the output range of neurons would be limited [19]. The external inputs I₁ and I₄ share a common value (I₁ = I₄), and I₂ and I₃ are set as 0 (I₂ = I₃ = 0). Thus, a different CNN would be obtained if a different value for I₁ and I₄ were set.

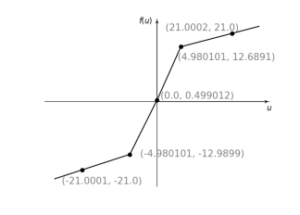
Figure 3: An activation-function f (APLF)

An activation-function APLF can avoid a periodic window corresponding to a non-chaotic periodic orbit. The activation-function APLF composed of linear functions by connecting five points. Those points can be changed as independent parameters. In a cipher system, the points of APLF can be selected as secret keys [9], [10],

[20].

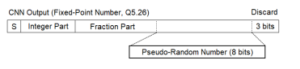
Figure 4: The extraction method of a PRN from a CNN output

Generally, discrete time system of the CNN is implemented with floating-point arithmetic [9]. But many embedded devices do not support 64-bit floating-point arithmetic. In this paper, the CNN is computed by 32-bit fixed-point arithmetic (Q5.26) and it allows overflow and underflow of variables. Comparing to 32-bit floating-point arithmetic, the fractional part of Q5.26 has enough long bit length. PRNs are extracted by the method presented in Figure 4. With regard to the CNN output, the lowest 3 bits of the fraction are discarded [8] and the lower 8 bits of the fraction are extracted as a PRN. Those PRNs from the CNN are applied to the proposed stream cipher .

3.1. Chaotic Orbit

A chaotic orbit is hard to predict because it is sensitive to tiny changes of the initial status. Here, Figure 5 shows time series from a CNN (Q5.26). Corresponding to all external inputs, output time series in the diagram present no bifurcation pattern but chaotic characteristics. It suggests that all external inputs can be used for chaos generation. In fact, the CNN generates the same time series on the ARM CPU and X86 CPU when the same parameters are set. Therefore the CNN is portable between different machines. Moreover, the Lyapunov exponents λ are computed per time series. The maximum Lyapunov exponents is about 2.5 and all of value is λ > 0. The Kolmogorov-Sinai entropy [21] is also computed by use of Lyapunov exponents, it is about 4.2. Those results demonstrate that the time series from the CNN has chaotic orbit and a high degree of randomness.

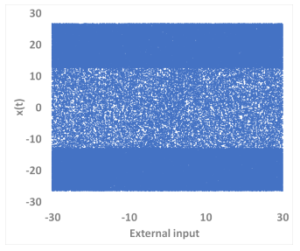
Figure 5: The input-output characteristics of time series from a CNN

3.2. Randomness

Randomness of the PRNs that were extracted from the CNN was confirmed by NIST Special Publication 800-22 statistical test suite [12]. Since NIST test has a couple of trouble (asymptotic approximation, etc.) even the test suite is updated [22], [23], NIST test method presented in the literature [24] was adopted.

We performed the NIST test for 1,000 times. And 10⁶ × 1,000 bits of PRNs were generated by the method shown in Fig. 4 for per test. NIST test results are presented in Table 1. The failure ratio for the proportion is under 1%, and the failure ratio for the P-values that check for uniformity of distribution is less than 0.1%. All of those results suggest that all of tests passed these criteria, and the tested PRNs from the CNN have good statistical properties.

4. CNN Stream Cipher

The proposed stream cipher has two phases: an ID-based encryption (IBE) phase and a stream phase (see Fig. 6). Each phase uses different CAN IDs; that is, the CAN ID associates a CAN frame with a specific phase. In the advance IBE phase, the symmetric key is shared with IBE [25], [26] among authorized ECUs. Subsequently, an authorized ECU sends encrypted data frames to other authorized ECUs and those ECUs can decrypt data using the symmetric key in the stream phase.

Table 1: NIST SP800-22 statistical test results

FR^a BF^a CS^a RU^a LR^a RK^a FF^a NT^a

Proportion	0.3	0.2	0.3		0.5		0.4		0.4		0.9		0.2
P-value	0.0	0.0	0.0		0.0		0.1		0.0		0.1		0.0
	OTa	UNa	AEa		REa		RVa		SEa		LCa
Proportion	0.3	0.7		0.2		0.4		0.2		0.2		0.1
P-value	0.0	0.0		0.0		0.0		0.0		0.0		0.1

FR: Frequency, BF: Block Frequency, CS: Cumulative Sums, RU: Runs, LR: Longest Run, RK: Rank, FF: FFT, NT: Non-overlapping Template, OT: Overlapping Template, UN: Universal, AE: Approximate Entropy, RE: Random Excursions, RV: Random Excursions Variant, SE: Serial, LC: Linear Complexity

^a Numbers are average ratio of failed tests (%).

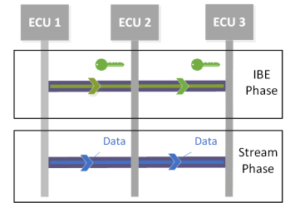
Figure 6: Overview of CNN stream cipher

4.1. IBE phase

It is an important step for the stream cipher to create, manage, and share the symmetric key. A public key infrastructure is used in the Internet to ensure secure communication generally. With this infrastructure, an on-line certificate authority (CA) is necessary, and the cost for issuing digital certificates may become prohibitive [27].

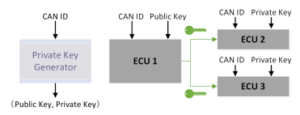
Figure 7: IBE phase

In the proposed stream cipher, we use IBE [26] to create, manage, and share the symmetric key. Fig. 7 shows how the symmetric key is shared among authorized ECUs. The private key generator (PKG) can be offline and does not need to use digital certificates instead of a CA. The PKG initially defines which CAN IDs are used in the IBE phase. For each valid CAN ID, the PKG outputs a public and private key pair that is issued to authorized ECUs. Thus, an ECU can use the public key to encrypt the symmetric key that is used in the stream phase and send it over the CAN bus. When an ECU receives a CAN frame, it checks the CAN ID to confirm the phase and decrypts the data in the CAN frame to obtain the symmetric key in the IBE phase.

4.2. Stream phase

In the stream phase, authorized ECUs use the symmetric key that was obtained during the IBE phase to encrypt and decrypt CAN frames (see Fig. 8). The CNN implemented in authorized ECUs generates a stream of pseudo-random bits: R₁, R₂, R₃, …, R_i with the symmetric key. This stream is XORed with a stream of bits, D₁, D₂, D₃, …, D_i, which are from the data in a CAN frame, to produce the stream of cipher text bits. Then each cipher text character is given by C_i = D_i ⊕ R_i, which is loaded into a CAN frame and translated with the CAN bus. The procedure of decryption is almost the same: when an authorized ECU has received a CAN data frame, the CNN in the ECU generates the same stream of pseudo-random bits R_i and the original data is obtained by D_i = C_i ⊕ R_i.

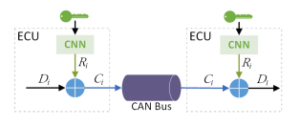
Figure 8: Stream phase

5. Evaluation

It is most important to ensure the safety of the vehicle and its passengers. Therefore, the embedded software of the ECU must run quickly to deal with the constraints of a real-time response. This section describes the performance evaluation of the CNN stream cipher with two embedded CAN boards (listed as Board A and B in Table 2) that were provided by P&A Technologies Inc. These CPUs have a different architecture, where Board A was implemented with a SH2A CPU, while Board B used an ARM CPU. Those boards are connected by a length of about 80cm twisted pair cable with D-sub connector.

Table 2: Specifications of experimental CAN boards

Component	Board A	Board B
CPU	R5S72630P200FP	SAMA5D27C-D1G
	SH2A-FPU core	ARM Cortex-A5
	(196 MHz)	(492 MHz)
RAM	SDR SDRAM	DDR2-SDRAM
	(64 MHz)	(120 MHz)
CAN Controller	Built-in CPU	FPGA IP

5.1. Experimental setup

In our experiments, we tested only the high-speed CAN whose bit rate is typically 500 Kbps, up to 1 Mbps. In fact, another CAN standard specifies low-speed CAN (see Sec. 2) at transmission rates above 40 Kbps up to 125 Kbps. It is more difficult to deal with realtime constraints at the high-speed CAN bit rate. Thus, we assumed that our stream cipher would work well at the low-speed CAN bit rate if it successfully ran with the high-speed CAN.

The PKG can be performed offline. Thus, we assume that Boards

A and B are two authorized ECUs and they have already gained the symmetric key. Then we implemented the CNN on Boards A and B. According to the symmetric key, the same stream of pseudo-random numbers was generated in both boards and used to encrypt the data part of a CAN frame in one board and decrypt it in the other board.

5.2. Experimental Results

One thousand CAN message frames were sent between Boards A and B to confirm the validity of the CNN stream cipher and measure the encryption and decryption time. We tested with 500-Kbps and 1-Mbps bit rates. The CAN bus was loaded with over 60% higher-priority traffic.

Table 3: Results of performance testing with CAN boards

	average time
Board A	44 µs
Board B	4 µs

We confirmed the CAN log data of Boards A and B, which showed that each board encrypted and decrypted CAN data frames successfully. With Board A, the procedure for encryption or decryption was performed within 44 µs on average. With Board B, the procedure only took 4 µs on average (see Table 3). The results suggest that the performance of the CNN stream cipher is adequate for real-time requirements of an ECU without additional HSM hardware.

6. Conclusions

In this paper, we have proposed and evaluated a fast stream cipher based on a CNN to provide security for the ECUs on a CAN bus. We have shown that the CNN is chaotic and have strong randomness, and that PRNs with a high degree of randomness can be generated from a CNN. In the proposed stream cipher, IBE is used to create, manage, and share the symmetric key. The PKG can be performed offline and does not need to use digital certificates. The stream cipher was evaluated with embedded CAN boards. The performance test results suggested that our method is efficient for software embedded in an ECU and has no need for a HSM to accelerate the encryption process.

As future work, we will design a new activation-function APLF to extend randomness of the CNN and improve the performance of the stream cipher based on the CNN.

1. Z. Liu, T. Murakami, S. Kawamura, H. Yoshida, “Parallel Implementation of Chaos Neural Networks for an Embedded GPU,” in 2019 IEEE 10th Interna- tional Conference on Awareness Science and Technology (iCAST), 1–6, IEEE, 2019, doi:10.1109/ICAwST.2019.8923383.
2. NIST FIPS PUB, “197, Advanced Encryption Standard (AES),” Federal information processing standards publication, 197(441), 0311, 2001, doi: 10.6028/NIST.FIPS.197.
3. J. Daemen, V. Rijmen, Rijndael/AES, 520–524, Springer US, 2005, doi: 10.1007/0-387-23483-7 358.
4. A. Albert, et al., “Comparison of event-triggered and time-triggered concepts with regard to distributed control systems,” Embedded world, 2004, 235–252, 2004.
5. P. Carsten, T. R. Andel, M. Yampolskiy, J. T. McDonald, S. Russ, “A system to recognize intruders in controller area network (CAN),” in 3rd International Symposium for ICS & SCADA Cyber Security Research 2015 (ICS-CSR 2015) 3, 111–114, 2015, doi:10.14236/ewic/ICS2015.15.
6. R. Buttigieg, M. Farrugia, C. Meli, “Security issues in controller area networks in automobiles,” in 2017 18th International Conference on Sciences and Tech- niques of Automatic Control and Computer Engineering (STA), 93–98, IEEE, 2017, doi:10.1109/STA.2017.8314877.
7. H. Yoshida, Y. Nihei, T. Nakanishi, “Comparative study on structurally differ- ent chaos neural network,” in Proceedings of Papers, International Symposium on Information Theory and its Applications, ISITA 2004, 1046–1050, 2004.
8. S. Kawamura, H. Yoshida, M. Miura, M. Abe, “Implementation of Uniform Pseudo Random Number Generator and Application to Stream Cipher based on Chaos Neural Network,” in The International Conference on Fundamentals of Electronics, Communications and Computer Sciences, 2002, 4–9, 2002.
9. H. Yoshida, T. Murakami, Z. Liu, “High-speed and highly secure pseudo- random number generator based on chaos neural network,” New Trends on System Science and Engineering: Proceedings of ICSSE, 276, 224–237, 2015, doi:10.3233/978-1-61499-522-7-224.
10. H. Yoshida, T. Murakami, T. Inao, S. Kawamura, “Origin of Randomness on Chaos Neural Network,” Trends in Applied Knowledge-Based Systems and Data Science, 9799, 587–598, 2016, doi:10.1007/978-3-319-42007-3 51.
11. H. Yoshida, Y. Akatsuka, T. Murakami, “Implementation of High-Performance Pseudo-Random Number Generator by Choas Neural Networks using Fix-Point Arithmetic with Perturbation,” in Proceedings of Papers, The 2018 Interna- tional Symposium on Nonlinear Theory and Its Applications, NOLTA2018, 46–49, 2018.
12. A. Rukhin, J. Soto, J. Nechvatal, M. Smid, E. Barker, editors, A statistical test suite for random and pseudorandom number generators for cryptographic applications, NIST Special Publication 800-22, 2001.
13. S. C. HPL, “Introduction to the controller area network (CAN),” Appl. Rep. SLOA101, 1–17, 2002.
14. A. Van Herrewege, D. Singelee, I. Verbauwhede, “CANAuth – a simple, back- ward compatible broadcast authentication protocol for CAN bus,” in ECRYPT Workshop on Lightweight Cryptography, volume 2011, 2011.
15. B. Groza, S. Murvay, A. Van Herrewege, I. Verbauwhede, “LiBrA-CAN: a lightweight broadcast authentication protocol for controller area networks,” in International Conference on Cryptology and Network Security, 185–200, Springer, 2012, doi:10.1007/978-3-642-35404-5 15.
16. M. Wolf, T. Gendrullis, “Design, implementation, and evaluation of a ve- hicular hardware security module,” in International Conference on Infor- mation Security and Cryptology, 302–318, Springer, 2011, doi:10.1007/ 978-3-642-31912-9 20.
17. O. Henniger, A. Ruddle, H. Seudie´, B. Weyl, M. Wolf, T. Wollinger, “Securing vehicular on-board IT systems: The evita project,” in VDI/VW Automotive
    nference, 41, 2009.
18. H. Schweppe, Y. Roudier, B. Weyl, L. Apvrille, D. Scheuermann, “Car2x communication: securing the last meter-a cost-effective approach for ensur- ing trust in car2x applications using in-vehicle symmetric cryptography,” in 2011 IEEE Vehicular Technology Conference (VTC Fall), 1–5, IEEE, 2011, doi:10.1109/VETECF.2011.6093081.
19. H. Yoshida, H. Fukuchi, T. Murakami, “Implementation of High-Speed Pseudo- Random-Number Generator with Chaotic and Random Neural Networks,” in Proceedings of the 53rd Hawaii International Conference on System Sciences, 2020, doi:10.24251/HICSS.2020.786.
20. H. Yoshida, T. Murakami, Japan patent JP5504501B, 2014.
21. T. S. Parker, L. O. Chua, “Chaos: A tutorial for engineers,” Proceedings of the IEEE, 75(8), 982–1008, 1987, doi:10.1109/PROC.1987.13845.
22. K. Hamano, T. Kaneko, “Correction of overlapping template matching test included in NIST randomness test suite,” IEICE transactions on fundamentals of electronics, communications and computer sciences, 90(9), 1788–1792, 2007, doi:10.1093/ietfec/e90-a.9.1788.
23. H. Okutomi, K. Nakamura, “A study on rational judgement method of random- ness property using NIST randomness test (NIST SP. 800-22),” IEICE Trans. A, 93(1), 11–22, 2010.
24. H. Yoshida, T. Murakami, S. Kawamura, “Study on testing for randomness of pseudo-random number sequence with NIST SP800-22 rev. 1a,” Technical report, IEICE Technical Report, 2012.
25. A. Shamir, “Identity-based cryptosystems and signature schemes,” in Workshop on the theory and application of cryptographic techniques, 47–53, Springer, 1984, doi:10.1007/3-540-39568-7 5.
26. D. Boneh, M. Franklin, “Identity-based encryption from the Weil pairing,” in Annual international cryptology conference, 213–229, Springer, 2001, doi: 10.1007/3-540-44647-8 13.
27. A. Nash, W. Duane, C. Joseph, PKI: Implementing and Managing E-security, McGraw-Hill, Inc., 2001.

(Click Here)

(Click Here)