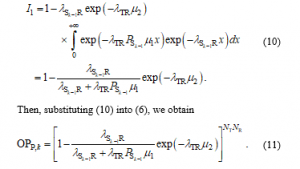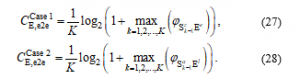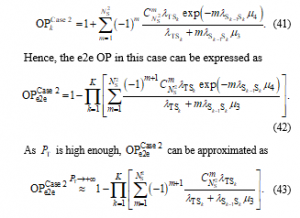1. Introduction

MIMO (Multiple Input Multiple Output) [1, 2] and diversity relaying [3-4] are efficient techniques used for wireless communication systems operating on interference, path-loss, fading, noise environment. In MIMO, transmitters and receivers are equipped with multiple antennas, and use transmit and receive diversity techniques to enhance data rate, channel capacity, diversity order as well as to reduce outage probability (OP), error rates. Efficient combiners such as SC (Selection Combining) [5, 6], EGC (Equal-Gain Combining) [7], MRC (Maximal Ratio Combining) [8] are commonly used by the receivers to enhance reliability of the data decoding. The best combiner is MRC, but its implementation is too difficult, while the SC combiner is simplest. Indeed, using SC, the receivers only use the receive antenna which provides the highest signal-to-interference plus noise ratio (SINR) to decode the received signals. In transmit diversity techniques, transmit antenna selection (TAS) [9, 10] and maximal ratio transmission (MRT) [11] are often used. In TAS, the transmitters select one of their antennas to send data to the receivers.  To obtain the highest SINR, TAS requires feedback channel state information (CSI) from the receivers for selecting the best transmit antenna. Unlike TAS, the receivers employing MRT use all the antennas to transmit data. The implementation of MRT is hence more difficult than that of TAS, but it obtains higher performance. To further enhance the system performances for wireless communication systems, combination between the transmit diversity and receiver diversity techniques, such as TAS/SC [12], TAS/MRC [12], MRT/SC [13], MRT/MRC [14], were proposed.

Relaying techniques can be efficiently used when the distance between a source and a destination is enough far or a source node cannot directly communicate with a destination node. In these techniques, intermediate nodes or relay nodes are employed to help the source-destination data transmission [3-4, 15-16]. Depends on the signal processing methods, the relays are categorized into two main groups: DF (decode and forward) [15-16] and AF (amplify and forward) [17-18]. The DF relays first decode the received data, encode it again, before sending the encoded signal to the destination. On the contrary, the AF relays only forward the amplified signals to the destination without performing the decoding. Hence, the AF technique is simpler than the DF one, but DF outperforms AF because the noises can be removed at the DF relays. Until now, published works concerned with performance evaluation of the relaying scenarios have mainly focused on dual-hop networks, e.g. [3-4, 15-18]. In [19-20], the authors considered multi-hop relaying models, where the source data are relayed to the destination over multi-hop or multi-relay. Reference [19] evaluated end-to-end (e2e) symbol error rate of the multi-hop AF relaying protocol. In [20], the multi-hop DF relaying protocol was proposed and analyzed. To enhance the e2e system performances for the multi-hop relaying networks over fading environments, various diversity relaying methods were proposed.  References [20, 21] introduced path-selection strategies to exploit spatial diversity. The authors in [22, 23] studied the e2e OP of multi-hop MIMO relaying protocols where the TAS/MRC technique was used to obtain diversity gain at each hop.

In wireless communication systems, security is a critical issue because the transmitted data can be easily overheard by eavesdroppers. Recently, physical-layer security (PLS) [24, 25] has gained much attention as a promising solution to guarantee secure communication. PLS can be simply implemented in practice because the security can be attained, relying on physical channel information such as link distances and channel quality. Indeed, the data transmission can be considered to be secure if the data channel is better than the eavesdropping one. The secrecy performances of the PLS systems can be evaluated via secrecy capacity defined as difference of channel capacity obtained on the data and eavesdropping links. References [26-29] proposed the transmit and receive diversity techniques to enhance secrecy performances for the MIMO systems. In [30-31], secure communication relaying protocols operating over fading channels were proposed and analyzed. Conventionally, the source and relays cooperate together to confuse the eavesdropper, i.e., they randomly generate code-books as transmitting the data [31]. Reference [32] analyzed the e2e secrecy performance of the multi-hop DF relaying protocol over Nakagami-m fading channels with imperfect transceiver hardware. Unlike [26-32], performance metrics of the PLS systems considered in [33, 34] are OP of the data transmission and intercept probability (IP) of the eavesdroppers. As shown in [33, 34], trade-off between IP and OP was investigated.

Due to rapid increasing of wireless devices, J. Mitola proposed cognitive radio (CR) [35] to solve spectrum scarcity issue. In CR, primary users can share their licensed bands to secondary users provided that the primary QoS is guaranteed. To realize this, the secondary users have to adjust their transmit power appropriately so that co-channel interference at the primary receivers must be below a given threshold [36, 37]. Recently, PLS in CR [38, 39] has been much attention of researchers. Reference [40] investigated trade-off between IP and OP of the secure communication in the secondary network operating over Rician fading channels. Moreover, in [40], the TAS/SC technique is used for the primary data transmission. The authors in [41] proposed a cooperative routing approach to enhance the e2e secrecy performances for the underlay CR networks, as compared with a conventional multi-hop relaying method.  In [42], the TAS/SC technique is used at each hop in the secondary network to obtain better secrecy performance in presence of hardware imperfection. In [43], a best-path selection strategy was proposed for secrecy performance enhancement of cluster-based CR networks using cooperative jamming technique.

This paper investigates the e2e IP and OP performance of the multi-hop MIMO relaying protocol in the underlay CR network with presence of a secondary multi-antenna eavesdropper. In the proposed scheme, the TAS/SC technique is used by both the primary and secondary networks.  More particularly, the secondary source and relays must reduce their transmit power to guarantee that OP at the primary receiver is always below a required threshold. Under the joint impact of the limited transmit power and co-channel interference, the secondary transmitters use TAS/SC at each hop to improve the reliability of the data transmission. Also in the secondary network, the eavesdropper with the SC combiner attempts to illegally decode the transmitted data over multiple hops. Moreover, we consider two cases where the interference from the primary transmitter on the secondary nodes is known or not. From two these cases, we propose different TAS/SC techniques for the secondary network. Different with [40, 43] in which the wireless devices only have single antenna; all the nodes in our proposed protocol have multiple antennas, and employ TAS/SC to attain higher diversity order. While references [41-44] derived the secrecy performance by using secrecy capacity, this paper investigates the trade-off between IP and OP. Moreover, references [42, 43] do not consider the presence of the primary transmitter, as well as ignore the impact of the co-channel interference from the primary network.

In the following, we summarize the main contribution of this paper as

• We propose TAS/SC-based multi-hop MIMO relaying protocols in PLS underlay CR networks. Moreover, under impact of the co-channel interference, we consider two efficient TAS/SC techniques applied for the secondary network, depending on channel state information (CSI) between the secondary nodes and the primary transmitter is known or not.
• From an exact closed-form formula of the outage performance of the primary network, we derive expressions of the transmit power for the secondary transmitters including source and relays.
• Exact closed-form expressions of the e2e OP and IP over Rayleigh fading channel are derived, and are validated by Monte-Carlo simulations.

This paper is organized into sections as follows. Section 2 describes system model and operation principle of the proposed model. Section 3 measures the system performances in terms of IP and OP. Both simulation results and analytical results are presented in Section 4. Finally, conclusions are provided in Section 5.

2. System Model

In Fig. 1, the primary transmitter (T) and the primary receiver (R) are equipped  and  antennas, respectively, and they use TAS/SC to communicate with each other. Considering the secondary network; the source node  wants to sends its data to the destination  via  intermediate relays named , , …, . Assume that all of the nodes  have antennas, and the  data transmission is accomplished via  orthogonal time slots. In addition, at the  hop,  sends the data to  by performing TAS/SC. Also in the secondary network, an -antenna eavesdropper (E) attempts to overhear the data transmitted at each hop.

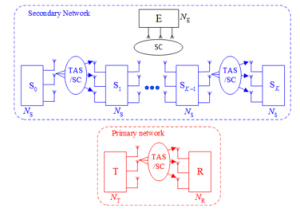
Figure 1: System model of the proposed TAS/SC-based multi-hop relaying protocol in the underlay CR networks.

We denote  as channel gain of the  Rayleigh fading channel, and hence the channel gain is an exponential random variable (RV). Similar to [3], parameter of  is  where is X-Y distance, and  is path-loss exponent. More particularly, distribution functions of  are given as follows:

where   and are CDF (cumulative distribution function) and PDF (probability density function) of RV U, respectively.

Next, we consider the primary and secondary data transmission at the  time slot, in which  and T at the same time send their data to  and R, respectively.  Assume that  uses the transmit antenna, T uses the the antenna,  uses the receive antenna and R uses the receive antenna, where  , , , . Due to the cross co-channel interference between two networks, the instantaneous SINR obtained at  and R can be formulated by (2) and (3), respectively as

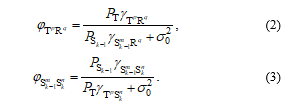
Now, we introduce notations used in (2)-(3).  is transmit power of each antenna of T.  is variance of Gaussian noises at R, and it is also variance at all the receivers.  is transmit power of .  is channel gain between the antenna of X and the antenna of Y, where  and .

Considering the transmission; the TAS/SC technique is used to obtain the maximum SINR between T and R, as

where and are the optimal transmit-receive pair, , .

Comment 1: To realize the strategy given in (4), the T and R nodes have to know the interference component  which can be obtained by requesting the cooperation from .

2.1. OP of Primary Network

From (4), the instantaneous channel capacity of the T-R link is given as

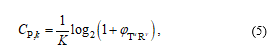
where the fraction 1/K implies that the data transmission in the secondary network is realized in K orthogonal time slots.

Next, OP of the primary network is defined as the probability that is below a positive value denoted by . Then, combining (2), (4) and (5), we can formulate OP at R as

 Substituting CDF  and PDF obtained in (1) into (8); which yields

2.2. Transmit Power of Secondary Transmitters

At first, the primary QoS is defined as , where  is a predefined threshold. By solving , an exact closed-form expression of can be given as

Comment 2: The transmit power of the secondary transmitters is calculated by the primary network as in (12), and then sent to the node. Next, it is worth noting that means the primary network does not obtain the required QoS, i.e., . Finally, equation (13) shows that as   is high enough, the primary QoS is always satisfied, and the transmit power  becomes a linear function of  .

2.3. TAS/SC methods

In this section, two practical TAS/SC techniques are considered. The TAS/SC technique is proposed in [12], in which the transmitter and receiver select an optimal transmit-receive antennas to maximize the instantaneous SINR of the data link. However, with presence of the co-channel interference, the TAS/SC technique in [12] may not be optimal any more. This motivates us to reconsider the TAS/SC technique in the interference environment.

Case 1: Co-channel interference from  is known

In this case, we assume that the co-channel interference can be perfectly estimated by the secondary nodes. Hence, similar to (4), the TAS/SC technique can be set up by  and  as

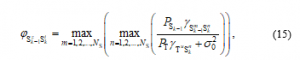
where and are the selected transmit-receive antenna pair at  and , respectively, .

For a fair comparison, assume that the interference from the primary network is also known by E. With the SC combiner, the SINR obtained at E can be given as

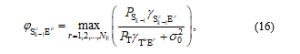
where is the selected antennas at E for decoding the source data, and .

Case 2: Co-channel interference from  is unknown

It is worth noting that in practice the primary network does not need to cooperate with the secondary network (but the secondary network must cooperate with the primary network). Hence, the secondary nodes may not obtain perfectly the information about the co-channel interference caused by PT. In this case, the TAS/SC technique should be performed, only relying on CSIs of the data links, i.e.

where and are the chosen antennas at  and , respectively, .

We can observe that the TAS/SC technique in (17) is only sub-optimal because the  and  nodes have not perfect information of the channel gain .

Hence, the SINR obtained at in this case can be given as

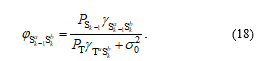
Also, it is assumed that E has no information of the co-channel interference links, and hence the best antenna selected by E is given as

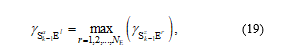
where is the selected antennas at E for decoding the source data. Then, we can formulate the SINR obtained at E as

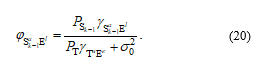
At high transmit power , i.e. , , from (13), equations (15), (16), (18) and (20) can be approximated respectively as

Comment 3: As observed from (21)-(24), at high  values, the obtained SINRs do not depend on  .

2.4. E2e Channel Capacity of Data and Eavesdropping Links

Due to usage of the DF relaying technique, the e2e channel capacity of the link in the first and second cases can be respectively given as (see [19, 29])

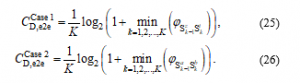
 Considering the channel capacity obtained at the eavesdropper. Because of the random code-book generation at each hop, the channel capacity at E in Case 1 and Case 2 can be formulated, respectively as

3. Evaluation of E2e OP and IP

At first, the e2e OP and IP are respectively defined as in [36]:

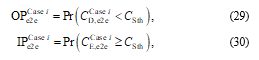
where   is a pre-determined threshold,

3.1. E2e OP

In this sub-section, we exactly and asymptotically evaluate the e2e OP in two cases considered in Sub-section 2.3. At first, combining (25), (26) and (29), we can obtain (31) as

Similar to the derivation steps in (8)-(10); substituting CDF  and PDF obtained in (1) into (33), after some manipulation, we can obtain (35) as follows:

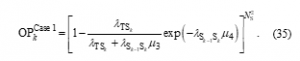
Substituting (35) into (31), an exact closed-form formula of the e2e OP in the first case can be written as

At high  values, by using the approximate expression of  in (21), with the same derivation method,  can be approximated as follows:

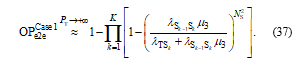
Case 2: Co-channel interference from  is unknown

Substituting (18) into , we can obtain (38) as

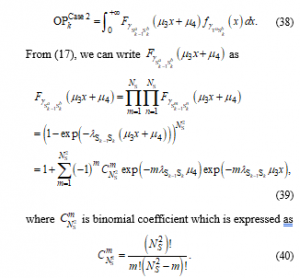
Substituting (39) and PDF into (38), after some manipulation, we obtain

3.2. E2e IP

Combining (27), (28) and (30), which yields

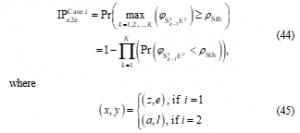
With the same derivation methods of    and , we can calculate , and then  and  can be respectively written as in (46) and (47):

4. Simulation Results

Section 4 verifies the formulas obtained in Section 3 by Monte-Carlo simulations realized by MATLAB. Assume that the nodes T, R, , and E are located at ( , ),  ( , ), , and ( , ), respectively. In all the simulations, the system parameters are set as follows:   , and the by , .

4.1. OP of Primary Network and Transmit Power of Secondary Transmitters

Figure 2 presents OP of the primary network as a function of   in dB when the number of hops (K) is 2, and the positions of T and R are ( , ) and  ( , ), respectively. It is worth noting that OP at T in two time slots is same, and hence the OP value in Fig. 2 is OP in both time slots. We can see that when , OP at T is higher than  when , and when , OP at T is higher than  when . This means than the primary network can obtain the required QoS with lower transmit power  by equipping more antennas at T and R. It is shown in this figure that the OP value converges to  at high  value due to the data transmission of the secondary networks.  Finally, we can observe from Fig. 2 that the simulation results verify the theoretical ones.

Figure 2: OP of the primary network as a function of (dB) when , , , , .

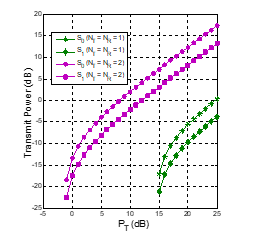
Figure 3: Transmit power of the secondary transmitters as a function of (dB) when , , , , .

Figure 3 illustrates the transmit power of   and  as a function of   in dB. We note that the system parameters in Fig. 3 are same with those in Fig. 2. As shown in Fig. 3, the secondary transmitters    and  can use the licensed bands when  is high enough, i.e., when  then , and when  then . Because the OP performance of the primary network is better when the T and R nodes are equipped with more antennas, the secondary network has more opportunity to access the licensed bands. Finally, we can see that the transmit power of  is higher than that of  because the distance is higher than the one.

4.2. OP and IP of Secondary Network

In this sub-section, we present the e2e OP and IP of the proposed protocol in two cases considered in Section 3. In all of the presented figures, we fix the number of antennas at T and R by 2 ( ), and the positions of T and R at ( , ) and  ( , ), respectively.

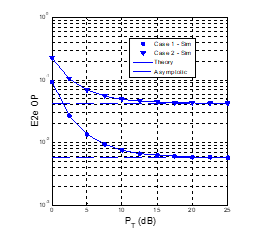
Figure 4: E2e OP as a function of (dB) when , , , , .

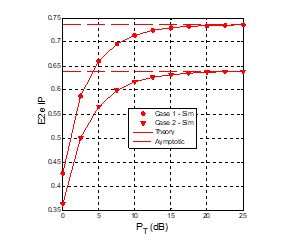
Figure 5: E2e IP as a function of (dB) when , , , , .

Figures 4 and 5 present OP and IP as a function of   in dB when the number of hops (K) equals to 3. As we can see, the OP and IP values at high  region do not depend on , as proved in Section 3. This also means that with the impact of the co-channel interference from the primary network, the secondary network cannot obtain diversity order, i.e., there exists the error floor in the OP performance. As shown in Fig. 4, the e2e OP in Case 1 is much lower than that in Case 2. However, Figure 5 presents that the e2e IP in Case 1 is higher than that in Case 2. From Figs. 4 and 5, it is clearly presented the trade-off between OP and IP. Particularly, if the transmit power  is higher, the e2e OP is lower but the e2e IP is higher. Also, if the TAS/SC technique in Case 1 is used, the OP performance is better, but the IP performance is worse. Finally, it is also illustrated that the simulation results verify the derived formulas of the e2e OP and IP in Section 3.

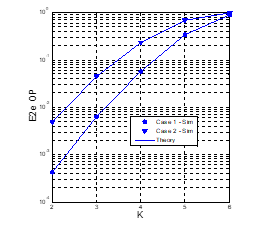
Figure 6: E2e OP as a function of  when , , , , (dB).

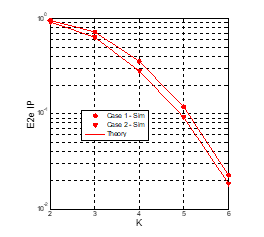
Figure 7: E2e IP as a function of  when , , , , (dB).

In Figs. 6-7, the e2e OP and IP is presented as a function of the number of hops (K) with (dB). As presented, the OP values increase with the increasing of the number of hops, but the IP values decrease. Similar to Figs. 4-5, the OP and IP values in Case 1 are lower and higher than those in Case 2. Again, it is shown that there exists the trade-off between the e2e OP and IP performance, and the value of K should be carefully designed. For example, if the required OP of the secondary network is 0.1, then the optimal number of hops used in Case 1 and 2 (to obtain minimum value of IP) is 4 and 3, respectively.

5. Conclusion

This paper proposed the TAS/SC based multi-hop relaying protocol in the PLS underlay CR networks. The practical applications of the proposed protocol are listed as: i) enhancing the spectrum usage efficiency with underlay CR approach; ii) enhancing the performance of the primary and secondary networks with the TAS/SC techniques; iii) two practical TAS/SC techniques are applied for the secondary network; iv) all the derived expressions are in closed-form, which can be easily used for evaluating and optimizing the systems. Moreover, the results showed the trade-off between the IP and OP at the secondary network, and the bad effect of the co-channel interference from the primary network. Finally, the important parameters such as the number of hops and the transmit power of the primary transmitter should be carefully designed.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.04-2017.317.

1. L. Liu, R. Chen, S. Geirhofer, K. Sayana, Z. Shi, Y. Zhou, “Downlink MIMO in LTE-advanced: SU-MIMO vs. MU-MIMO” IEEE Commun. Mag., 50(2), 140–147, 2012. https://doi.org/10.1109/MCOM.2012.6146493
2. Y. Kim, H. Ji, J. Lee, Y.-H. Nam, B. Loong Ng, I. Tzanidis, Y. Li, “Full Dimension MIMO (FD-MIMO): The Next Evolution of MIMO in LTE Systems” IEEE Wireless Commun., 21(3), 92-100, 2014. https://doi.org/10.1109/MWC.2014.6845053
3. J. N. Laneman, D. N. Tse, G. W. Wornell, “Cooperative Diversity in Wireless Networks: Efficient Protocols and Outage Behavior” IEEE Trans. Inform. Theory, 50(12), 3062–3080, 2004. https://doi.org/10.1109/TIT.2004.838089
4. M. A. Beserra de Melo, D. Benevides da Costa, “An Efficient Relay–Destination Selection Scheme for Multiuser Multirelay Downlink Cooperative Networks” IEEE Trans. Veh. Techn., 61(5), 2354 – 2360, 2012. https://doi.org/ 10.1109/TVT.2012.2192488
5. M. D. Selvaraj, Ranjan K. Mallik , “Performance of Full CSI Selection Combining for Cooperative Diversity Systems” IEEE Trans. Commun., 60(9), 2482 – 2488, 2012. https://doi.org/10.1109/TCOMM.2012.071212.110101
6. O. S. Badarneh, D. B. da Costa, M. Benjillali and M. Alouini, “Selection Combining Over Double $\alpha$-$\mu$ Fading Channels,” IEEE Trans. Veh. Techn., 69(3), 3444-3448, 2020. https://doi.org/10.1109/TVT.2020.2969224
7. Y. Song, S.D. Blostein, J. Cheng, “Exact Outage Probability for Equal Gain Combining with Cochannel Interference in Rayleigh Fading” IEEE Trans. Wireless Commun., 2(5), 865-870, 2003. https://doi.org/10.1109/TWC.2003.816796
8. X.W. Cui, Q.T. Zhang, Z.M. Feng, “Outage Probability for Maximal Ratio Combining of Arbitrarily Correlated Faded Signals Corrupted by Multiple Rayleigh Interferers” IEEE Trans. Veh. Techn., 55(1), 383- 386, 2006. https://doi.org/10.1109/TVT.2005.861186
9. S. Kim, M. Shin, C. Lee, “Transmit Antenna Selection Scheme for Iterative Receivers in MIMO Systems” IEEE Sig. Proces. Lett., 14(12), 916 – 919, 2007. https://doi.org/10.1109/LSP.2007.906230
10. S. Kim, “Transmit Antenna Selection for Precoding-Aided Spatial Modulation,” IEEE Access, 8, 40723-40731, 2020. https://doi.org/10.1109/ACCESS.2020.2976732
11. M. K. Arti, M. R. Bhatnagar, “Maximal Ratio Transmission in AF MIMO Relay Systems Over Nakagami-m Fading Channels,” IEEE Trans. Veh. Techn., 64(5), 1895-1903, 2015. https://doi.org/10.1109/TVT.2014.2334631
12. D. T. Hung, T. T. Duy, T. T. Phuong, D. Q. Trinh, T. Hanh, “Performance Comparison between Fountain Codes-Based Secure MIMO Protocols With and Without using Non-Orthogonal Multiple Access” Entropy, 21(10), 928, 2019. https://doi.org/10.3390/e21100982
13. A. F. Coskun, O. Kucur, “Performance Analysis of Maximal-Ratio Transmission/Receive Antenna Selection in Nakagami-m Fading Channels With Channel Estimation Errors and Feedback Delay” IEEE Trans. Veh. Techn., 61(3), 1099-1108, 2012. https://doi.org/10.1109/TVT.2012.2183650
14. V. C. Papamichael, P. Karadimas, “Performance Evaluation of Actual Multielement Antenna Systems Under Transmit Antenna Selection/Maximal Ratio Combining,” IEEE Antennas Wireless Propag. Lett., 10, 690 – 692, 2011. https://doi.org/10.1109/LAWP.2011.2161662
15. T. T. Duy, Trung Q. Duong, D.B. da Costa, V.N.Q. Bao, M. Elkashlan, “Proactive Relay Selection with Joint Impact of Hardware Impairment and Co-channel Interference” IEEE Trans. Commun., 63(5), 1594-1606, 2015. https://doi.org/10.1109/TCOMM.2015.2396517
16. P. N. Son, T. T. Duy, “A New Approach for Two-Way Relaying Networks: Improving Performance by Successive Interference Cancellation, Digital Network Coding and Opportunistic Relay Selection” Wireless Netw., 26(2), 1315-1329, 2020. https://doi.org/10.1007/s11276-019-02186-1
17. E. Bjornson, M. Matthaiou, M. Debbah, “A New Look at Dual-Hop Relaying: Performance Limits with Hardware Impairments,” IEEE Trans. Commun., 61(11), 4512-4525, 2013. https://doi.org/10.1109/TCOMM.2013.100913.130282
18. J. Ma, C. Huang, S. Cui, Q. Li, “Energy Efficiency of Amplify-and-Forward Full-Duplex Relay Channels,” IEEE Wireless Commun. Lett., 8(5), 1365 – 1368, 2019. https://doi.org/10.1109/LWC.2019.2918290
19. G. Farhadi, N. C. Beaulieu, “A General Framework for Symbol Error Probability Analysis of Wireless Systems and Its Application in Amplify-and-Forward Multihop Relaying” IEEE Trans. Veh. Techn., 59(3), 1505 – 1511, 2010. https://doi.org/10.1109/TVT.2009.2037642
20. M. R. Bhatnagar, “Performance Analysis of a Path Selection Scheme in Multi-Hop Decode-and-Forward Protocol” IEEE Commun. Lett., 16(12), 1980 – 1983, 2012. https://doi.org/10.1109/TVT.2009.2037642
21. T. D. Hieu, T. T. Duy, B.-S. Kim, “Performance Enhancement for Multi-hop Harvest-to-Transmit WSNs With Path-Selection Methods in Presence of Eavesdroppers and Hardware Noises” IEEE Sensors Journal, 18(12), 5173 – 5186, 2018. https://doi.org/10.1109/JSEN.2018.2829145
22. I. H. Lee, D. Kim, “Outage Probability of Multi-Hop MIMO Relaying With Transmit Antenna Selection and Ideal Relay Gain Over Rayleigh Fading Channels” IEEE Trans. Commun., 57(2), 357 – 360, 2009. https://doi.org/10.1109/TCOMM.2009.02.070058
23. A. A. AbdelNabi, F. S. Al-Qahtani, M. Shaqfeh, S. S. Ikki, H. M. Alnuweiri, “Performance Analysis of MIMO Multi-Hop System With TAS/MRC in Poisson Field of Interferers,” IEEE Trans. Commun., 64(2), 525-540, 2016. https://doi.org/10.1109/TCOMM.2015.2496291
24. A. D. Wyner, “The Wire-tap Channel” Bell System Technical Journal, 54(8), 1355 – 1387, 1975. https://doi.org/10.1002/j.1538-7305.1975.tb02040.x
25. I. Csiszar, J. Korner, “Broadcast Channels with Confidential Messages” IEEE Trans. Inform. Theory, 24(3), 339 – 348, 1978. https://doi.org/10.1109/TIT.1978.1055892
26. N. S. Ferdinand, D. B. da Costa, A. L. F. de Almeida, M. Latva-aho, “Physical Layer Secrecy Performance of TAS Wiretap Channels with Correlated Main and Eavesdropper Channels” IEEE Wireless Commun. Lett., 3(1), 86-89, 2014. https://doi.org/10.1109/WCL.2013.112313.130733
27. J. Xiong, Y. Tang, D. Ma, P. Xiao, K. Wong, “Secrecy Performance Analysis for TAS-MRC System With Imperfect Feedback” IEEE Trans. Inf. Forensics Security, 10(8), 1617-1629, 2015. https://doi.org/10.1109/TIFS.2015.2421358
28. J. Si, Z. Li, J. Cheng, C. Zhong, “Asymptotic Secrecy Outage Performance for TAS/MRC Over Correlated Nakagami-m Fading Channels,” IEEE Trans. Commun., 67(11), 7700-7714, 2019. https://doi.org/10.1109/TCOMM.2019.2935444
29. D. Tran, H. Tran, D. Ha, G. Kaddoum, “Secure Transmit Antenna Selection Protocol for MIMO NOMA Networks Over Nakagami-m Channels,” IEEE Systems Journal, 14(1), 253-264, 2020. https://doi.org/10.1109/JSYST.2019.2900090
30. I. Krikidis, “Opportunistic Relay Selection For Cooperative Networks With Secrecy Constraints” IET Commun., 4(15), 1787 – 1791, 2010. https://doi.org/ 10.1049/iet-com.2009.0634
31. J. Mo, M. Tao, Y. Liu, “Relay Placement for Physical Layer Security: A Secure Connection Perspective,” IEEE Commun. Lett., 16(6), 878–881, 2012. https://doi.org/10.1109/LCOMM.2012.042312.120582
32. P. T. Tin, D. T. Hung, T. T. Duy, M. Voznak, “Analysis of Probability of Non-zero Secrecy Capacity for Multi-hop Networks in Presence of Hardware Impairments over Nakagami-m Fading Channels” RadioEngineering, 25(4), 774-782, 2016. http://dx.doi.org/10.13164/re.2016.0774
33. Y. Zou, B. Champagne, W. P. Zhu, L. Hanzo, “Relay-Selection Improves the Security-Reliability Trade-off in Cognitive Radio Systems,” IEEE Trans. Commun., 63(1), 215 – 228, 2015. http://dx.doi.org/10.1109/TCOMM.2014.2377239
34. G. Zhang, Y. Gao, H. Luo, S. Wang, M. Guo and N. Sha, “Security Performance Analysis for Best Relay Selection in Energy-Harvesting Cooperative Communication Networks,” IEEE Access, vol. 8, pp. 26-2020, http://dx.doi.org/10.1109/ACCESS.2019.2960819
35. J. Mitola, G. Q. Maguire, “Cognitive Radio: Making Software Radios More Personal” IEEE Pers. Commun., 6(4), 13-18, 1999. http://dx.doi.org/10.1109/98.788210
36. Y. Guo, G. Kang, N. Zhang, W. Zhou, P. Zhang, “Outage Performance of Relay-Assisted Cognitive-Radio System Under Spectrum-Sharing Constraints” Electronics Lett., 46(2), 1-2, 2010. http://dx.doi.org/10.1049/el.2010.2159
37. K. Tourki, K. A. Qaraqe, M.-S. Alouini, “Outage Analysis for Underlay Cognitive Networks Using Incremental Regenerative Relaying” IEEE Trans. Veh. Techn., 62(2), 721-734, 2013. http://dx.doi.org/ 10.1109/TVT.2012.2222947
38. Y. Liu, L. Wang, T. D. Tran, M. Elkashlan, T. Q. Duong, “Relay Selection for Security Enhancement in Cognitive Relay Networks” IEEE Wireless Commun. Lett., 4(1): 46-49, 2015. http://dx.doi.org/10.1109/LWC.2014.2365808
39. M. Elkashlan, L. Wang, T. Q Duong, G. K. Karagiannidis, A. Nallanathan, “On the Security of Cognitive Radio Networks” IEEE Trans. Veh. Techn., 64(8), 3790 – 3795, 2015. http://dx.doi.org/10.1109/TVT.2014.2358624
40. P. M. Nam, T. T. Duy, P. V. Ca, “End-to-end Security-Reliability Analysis of Multi-hop Cognitive Relaying Protocol with TAS/SC-based Primary Communication, Total Interference Constraint and Asymmetric Fading Channels” International Journal of Communication Systems, 32(2), 1-16, 2019. http://dx.doi.org/10.1002/DAC.3854
41. H. D. Hung, T. T. Duy, M. Voznak, “”Secrecy Outage Performance of Multi-hop LEACH Networks Using Power Beacon Aided Cooperative Jamming With Jammer Selection Methods,” AEU International Journal of Electronics and Communications, 124, 1-24, 2020. https://doi.org/10.1016/j.aeue.2020.153357
42. P. T. Tin, D. T. Hung, N. N. Tan, T. T. Duy, M. Voznak, “Secrecy Performance Enhancement for Underlay Cognitive Radio Networks Employing Cooperative Multi-hop Transmission With and Without Presence of Hardware Impairments” Entropy, 21(2), 217, 2019. https://doi.org/10.3390/e21020217
43. P. T. Tin, P. M. Nam, T. T. Duy, T. T. Phuong, M. Voznak, “Secrecy Performance of TAS/SC-based Multi-hop Harvest-to-Transmit Cognitive WSNs under Joint Constraint of Interference and Hardware Imperfection” Sensors, 19(5), 1160, 2019. https://doi.org/10.3390/s19051160
44. P. M. Nam, P. V. Ca, T. T. Duy, Khoa N. Le, “Secrecy Performance Enhancement Using Path Selection Over Cluster-Based Cognitive Radio Networks” in 5th EAI International Conference on Industrial Networks and Intelligent Systems, HoChiMinh city, Vietnam, 2019. https://doi.org/10.1007/978-3-030-30149-1_6

(Click Here)

(Click Here)