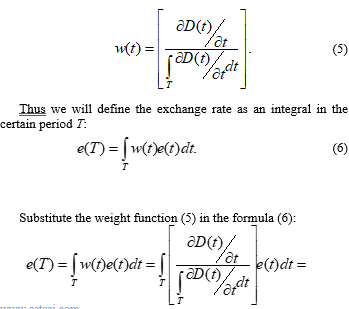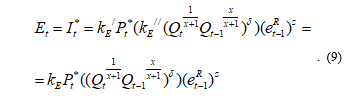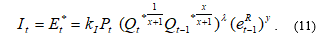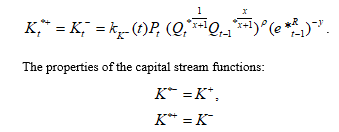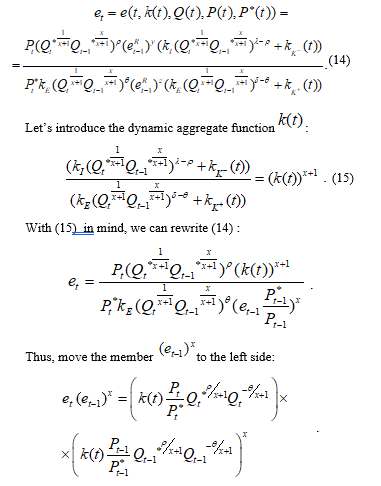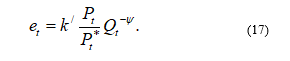1. Introduction

This paper is an extension of work originally presented in  Twelfth International Conference “Management of large-scale system development” (MLSD’2019) [1].

The theory of exchange rate determination is one of the most important components of modern economic theory. Mathematical  models of the medium-term dynamics of the exchange rates are widely presented in the works of classics in [2]-[7], and the monetarist school pay considerable attention to modeling the medium-term and the long-term dynamics of exchange rates. The same can be said about   DSGE-models   in [8].

Medium-term modeling of the exchange rates including the Russian ruble, based on the IFEER-concept (International Flows Equilibrium Exchange Rate concept), was carried out by [9]. This  concept is based on mathematical modeling of the foreign trade operations and the capital flows as the most important macroeconomic fundamental determinants of the exchange rate movements. Several studies (for example, in [10])  consider sources of exchange rate fluctuations in other cases.

Against this background, only a few studies are devoted to the short-term exchange rate dynamics. And first of all, it is necessary to note here the works explained in [11-13].

Mathematical modeling of short-term dynamics will reveal the mechanisms of explosive changes in the exchange rate in crisis periods.

This study will build a new model of the short-term exchange rate dynamics. First of all, we will be interested in the reasons for the deviation from the medium-term equilibrium, and these aspects will be formalized mathematically. But in any case, the basis for mathematical modeling will be the fundamental economic factors that affect the dynamics of the exchange rate. Thus we will use the author’s IFEER-concept and develop it.

2. Conceptual Framework of Exchange Rate Modelling

In the basic version, discrete flows are considered in the previous author’s works [9]. For exchange rates that have market pricing, in a certain period we defined in the i-th market transaction:

 – the nominal exchange rate,

 – the volume of the market transaction in the foreign currency,

 – the volume of the market transaction in the national currency.

From  a financial point of view these variables are linked as follows:

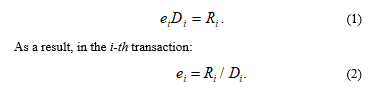However, in this study due to the short-term modeling period author will also apply a differential approach.

Let’s define R(t) as a streaming continuously differentiated function of funds in the national currency in the foreign exchange market. Accordingly, D(t) is a streaming continuously differentiated function of funds in the foreign currency and  e(t) is the nominal bilateral exchange rate at time t.

By analogy with (1) in the differential form at t:

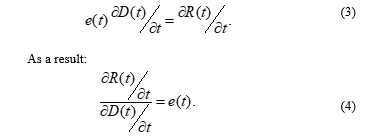By analogy with the previously used discrete IFEER-concept [9] we introduce the weight function w(t) for the exchange rate. In the discrete version, the weight function w(i) showed the contribution of the particular i-th transaction, depending on the volume in the foreign currency:

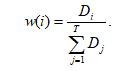In the integral version, the weight function w(t) is also based on the volume of funds in the foreign currency in a certain period T:

Substitute the weight function (5) in the formula (6):

Let’s use properties (3) and (4) and take the denominator beyond the integral:

Now we can disaggregate the streaming functions according to the balance of payments accounts:

Here funds with the upper index CA belong to the current balance, funds with the upper index K belong to the capital flows balance.

This formula is the main intermediate result of the IFEER-concept, allowing us to identify foreign trade operations and capital flows as  the main factors of the exchange rate movements.

Let’s denote:

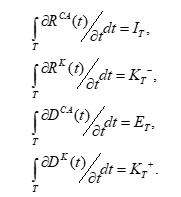From an economic point of view, E_T is the volume of funds as the supply of the foreign currency from export operations, I_T is the demand in the national currency for the foreign currency from import operations.  is the capital outflow as the demand in the national currency for the foreign currency and  is the capital inflow as the supply of the foreign currency.

At this conceptual level, the exchange rate dependence has a dynamic form by T:

However, for the two involved parties, the nominal exchange rate is determined symmetrically because the country’s export is another country’s import and the capital outflow is the inflow for the other side.  Here the asterisk shows the financial and economic variables of the opposite counterparty in this two-country world:

It should be noted that the dependence (7) is natural from the economic point of view,  since,  for example,  the increase in demand for imports and an increase in capital outflow leads to an increase in the exchange rate:

The upper sign “-” or “+” here and further on this factor shows that the function respectively strictly decreases or increases.

In terms of partial derivatives, for example:

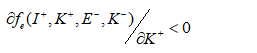3. TheTwo-Country Model: TheLevel of theCurrent Account Balance

We will build a two-period model of the exchange rate in periods t and t-1. Since we are going to use point estimates, we will replace the large Т as a period index with the small t for convenience.

Under these conditions formula (7) will take a more decent look, which has already been used by us:

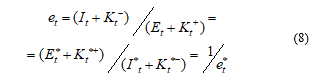      One of the most important components of the foreign currency inflow to the domestic market is export revenue. However, its level in the period t is determined by decisions of national exporters in the previous period t-1:

here:  is a constant,

 – the aggregate foreign price level,

  – the total domestic real output,

 – the indicator of the international competitive advantages.

The exports of one side in this two-country world are imports of the other side.

 The dependence (9) indicates that only the part of export revenue comes to the domestic currency market. In general, the volume of exports is determined by the part of the total domestic real output  in the foreign prices .

Here intertemporal averaging of the total real output  is used for modeling. Note, that . In this case, the income at t is given more weight than the income at t-1. The method of intertemporal averaging of should not have a significant impact  since it is the least volatile factor.

One of the most important factors of the model is the indicator of the international competitive advantages. This is the real bilateral exchange rate in the previous period t-1:

 Thus, in formula (9) we take into account the possible different degrees of the export functions responses to changes in the indicator of the international competitive advantages and the total domestic real output. For these purposes, we use various adjustable parameters in degrees: . Their relationships will be shown later.

Functional dependence (9) at the same time also has a natural functional character from the economic point of view with respect to the system of the main determinants of the exchange rate:

In accordance with the previous modeling, the demand for the foreign currency from imports is determined completely symmetrically for the other side:

Here:   k_I is a constant,

   – the total foreign real output.

For the purposes of simulation, it is necessary to impose the restrictions: , x=z-y.

      The properties of the stream functions of the current balance operations:

E*=I, I*=E.

Here it is important to note, that the dependencies (10) and (11) we define for the medium-term environment. But we can assume that these dependencies retain their mathematical factor structure even for the short-term modeling. This is due to the economic inertia of exports and imports in the world economy.

4. TheTwo-Country Model: the Level of the Capital Flows

Of course, the capital flows are one of the most important factors of the exchange rates dynamics. And the developed author’s IFEER-concept allows us to conduct mathematical modeling taking into account the capital flows.

We need to accept the hypotheses about mathematical forms of the basic capital flows dependencies. The capital inflow dependence is an increasing function by the aggregate foreign prices, the indicator of international competitive advantages, and the total domestic real output.

In this context, it is important to note that these functions must be modified for short-term exchange rate modeling in relation to the previously discussed functions in the author’s work [9]. Here the constants k becomes functions by time. For the functional dependence of the capital outflow, for example, it is an increasing function in a crisis period. This shows a short-term increase in capital outflow compared to the medium-term equilibrium dynamics.

For the capital outflow, thus, the dependence must satisfy the following condition:

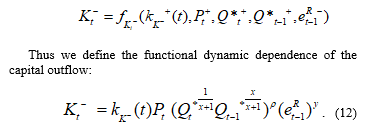The  capital outflow is a part of the domestic product produced in foreign prices.

In the short-term period in the currency market the crisis phenomena lead to a sharp increase in the capital outflow. Mathematically this is expressed in the strict increase function  by t in the dynamic formula (12):

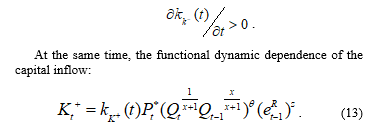Perfectly symmetrical, in the domestic currency market the crisis phenomena leads to a significant reduction of the capital inflows:  a strict decrease of the function by t in the formula (13):

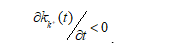Here  we use the hypotheses about the type of the functions k_К(t), that are not constants for the capital flows in the short-term period.  This distinguishes this model from the previously developed author’s models.

In accordance with the methodology of modeling dependencies are interrelated:

Let’s substitute the functional dependencies (9)-(13) into the basic formula (8):

Let’s  make a temporary separation of the modeling variables and re-define and  for convenience:

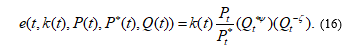5. Assessment of Short-Term Dynamic Effects

The main result of mathematical modeling is the new nonlinear multi-factor functional dependence of the exchange rate. Here, it should be emphasized that the dynamic functional dependence (16) differs from the previous medium-term dependencies by the type of the dynamic function .

Economically, this function in the short-term period is responsible for explosive changes in the exchange rate dynamics. So, this is the main fundamental difference between this model and the previous author‘s models [9], etc. In those works, these functions are constants in the medium-term in various modifications.

There is significant stability of  in the dynamic functional dependence (15) in comparison with other fundamental factors in the short-term period. So, a strict decrease of the internal function  and a strict increase of the internal function  guarantees us a strict increase of the aggregate function  in a crisis period: . Mathematically this reflects the reasons for the deviation from the medium-term equilibrium.

Direct economic assessment of the short term impact of the function is quite difficult. But we will try to do it using the example of the Russian ruble.

Let’s use the main result of the author‘s work [9]. The medium-term dynamic functional dependence of the exchange rate of the Russian ruble against the US dollar is:

here:  is a constant,

– an estimated parameter.

For  research and verification of this model we used the Russian CPI (Consumer Price Index)  as the model variable P (Federal service of state statistics of Russia), the index of the real Russian GDP as the model variable Q, the prices of blend crude oil as the model variable P* (Intercontinental Exchange, US dollars per brent-mix barrel, Bloomberg information  agency, Bloomberg Terminal).

For  our research the most appropriate  is the crisis period 2013 – 2015. This period is associated with the currency crisis and the significant depreciation of the Russian ruble.

The  ruble/dollar exchange rate (USD/RUR)  is the main rate on the Russian foreign exchange market.  The value of the ruble exchange rate in relation to other world currencies is determined through the cross-rate system.

Thus, as the starting point of the research period, December 2013 was selected. At that time, both the international environment and the domestic macroeconomic situation were stable. The exchange rate of the ruble at that moment was 32,73 USD/RUR according to the Central Bank of Russia.

This study suggests using the least squares method with normalization of the exchange rate values. Since the exchange rate changes quite seriously during crisis periods, it is more important to use relative indicators of changes.

Thus, in accordance with numerical simulation, the solution of the parametric minimization problem

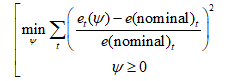is . Here e(nominal) is the nominal exchange rate USD/RUR, according to the Bank of Russia monthly calculations at the end of each period.

       In Figure 1 (monthly data, author’s calculations) we present the dynamics of the exchange rate of the Russian ruble against the US dollar in accordance with the nominal exchange rate e(nominal) and the result dynamic functional dependence of this research e(Theor) (17).

Figure 1: The calculated and nominal exchange rates of the Russian ruble  to the US dollar (USD/RUR, monthly data, 2013 – 2015).

The average of absolute normalized deviations of the calculated and nominal exchange rates was 3%, and the average of normalized deviations was 0,3%. As a result, this allows us to conclude that the model quality is high.

This research has shown a high correlation between the exchange rate of the ruble, the inflation, the Russian balance of payments, and other fundamental variables (for example, we can also recommend a work [14]).

Using the methodology, presented in this paper, and the author’s work [15] (in Russian) it can be shown, that short-term dynamic functional dependence of the exchange rate of the Russian ruble against the US dollar is:

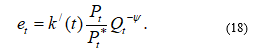Here, the system of main fundamental economic factors of the exchange rate dynamics in relation to the dependencies (16) and (17) is saved.

In Figure 2 (Moscow Exchange, executions ТОМ) in the period 2013 – 2015solid line represents the medium-term dynamics of the exchange rate of the Russian ruble against the US dollar. We schematically overlaid data from the author’s work [9] and Figure 1. Based on the presented data, we can estimate the cumulative contribution of the function to changes in the ruble exchange rate during crisis periods in the short-term in the amount of 20-25%. The contribution to the crisis period in 2015-2016 can also be estimated at the same amount approximately.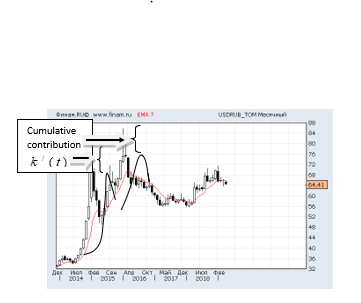Figure 2: USD/RUR quotes

(Moscow Exchange,  monthly data, executions ТОМ, Japanese candlesticks, 2013 – 2018, Information agency *FINAM*)

1. Conclusion

In this study, the new model of short-term exchange rate dynamics was constructed. First of all, we were interested in the reasons for the deviation from the medium-term equilibrium.

The author used the  IFEER-concept as a base and developed it. In this study due to the short-term modeling period, the differential approach was applied. The result was an integrated version of the exchange rate dynamics model. The functional dependencies of the export-import operations and the capital flows were mathematically formalized.

The main result of mathematical modeling is the nonlinear multi-factor dynamic functional dependence of the exchange rate that differs from the previous medium-term functional dependencies by the type of the internal dynamic function. Economically, this function in the short-term period is responsible for explosive changes in the exchange rate dynamics. But in any case, the basis for mathematical modeling was the system of the fundamental economic factors that affect the dynamics of the exchange rate.

The most important limitation of mathematical modeling is the significant difficulty in directly economic assessment of the internal functions  and  that determine short-term capital flows in crisis periods.

But the influence of crisis events on the model in the short term is studied on the Russian financial market at a previous time by assessment of the short-term impact of the function . The  conducted research allowed us to analyze and evaluate the quantitative impact of the short-term effects of the dynamics of the exchange rate of the Russian ruble against the US dollar. The estimated indicators allow us to conclude that the Bank of Russia needs to pursue a more active interventionist policy to maintain the stability of the national currency.

 At the same time, such economic assessments are individual and specific for each currency and each crisis period.

The developed IFEER-concept allows us to model the exchange rate dynamics in other economic conditions. First of all, this concerns the future research of the long-term dynamics of the main world currencies and the Russian ruble.

Conflict of Interest

The author declares no conflict of interest.

1. A. Kuzmin, “Modeling of Short-Term Exchange Rates Dynamics” in Twelfth International Conference “Management of large-scale system development” (MLSD 2019), Publisher: IEEE, 2019, https://doi.org/10.1109/MLSD.2019.8911067
2. R.A. Mundell, “Capital Mobility and Stabilization Under Fixed and Flexible Exchange Rates” Canadian Journal of Economics and Political Science, November, 475-485, 1963. https://doi.org/10.2307/139336
3. A.C. Stockman, “A Theory of Exchange Rate Determination” Journal of Political Economy, August, 88, 673-698, 1980. https://doi.org/10.1086/260897
4. P.B. Clark, R. MacDonald, Exchange Rates and Economic Fundamentals: A Methodological Comparison of BEERs and FEERs, IMF Working Paper 98/67, Washington: International Monetary Fund, March, 1998.
5. P.B. Clark, R. MacDonald, Filtering the BEER a permanent and transitory decomposition, IMF Working Paper 00/144, Washington: International Monetary Fund, 2000.
6. M. Mussa, “The Theory of Exchange Rate Determination” in Exchange Rate Theory and Practice, J.E.O. Bilson, R.C. Marston (eds.), Chicago: University of Chicago Press, NBER, 13-78, 1984.
7. L. Killian, “Exchange Rates and Monetary Fundamentals: What Do We Learn from Long-Horizon Regressions?” Journal of Applied Econometrics, 14( 5), 491-510, 1999. https://doi.org/10.1002/(SICI)1099-1255(199909/10)14:5<491::AID-JAE527>3.0.CO;2-D
8. M. Obstfeld, K. Rogoff, “Exchange Rate Dynamics Redux” Journal of Political Economy, 103 (3), 624-660, 1995. https://doi.org/10.3386/w4693
9. A. Kuzmin, “Exchange Rate of the Ruble Modeling” Advances in Systems Science and Applications, 19(4), 87-93, 2019. https://doi.org/10.25728/assa.2019.19.4.830
10. I. Chowdhury, “Sources of Exchange Rate fluctuation: empirical evidence from six emerging market countries” Applied Financial Economics, 14(1), 697-705, 2004. https://doi.org/10.1080/0960310042000243538
11. R. Dornbush, “Capital Mobility, Flexible Exchange Rate and Macroeconomic Equilibrium” in Recent Developments in International Monetary Economics, E. Claasen, P. Salin (eds.), North-Holland, 261-278, 1976.
12. R. Dornbush, “ Expectations and Exchange Rates Dynamics” Journal of Political Economy, 84, December, 1161-1176, 1976. https://doi.org/10.1086/260506
13. R. Dornbusch, “Equilibrium and Disequilibrium Exchange Rates” Zeitschrift fur Wirtschafts- und Socialwissenschaften, Berlin, 102(6), 573-599, 1982. https://doi.org/10.3386/w0983
14. L. Strizhkova, “The relationship between inflation, exchange rate and parameters of economic policy (on an example of Russia)” Bulletin of the Institute of Economics of the Russian Academy of Sciences, 5, 156-176, 2017. (Article in Russian with an abstract in English)
15. A. Kuzmin, “Modeling short-term dynamics of the ruble exchange rate” Money and credit, 8, 59-65, 2015. (Article in Russian with an abstract in English)

Citations by Dimensions

Citations by PlumX

Google Scholar

Crossref Citations

1. Li Weiguo, Chen Yanhong, Yang Libing, Yang Liyan, "Integration and Innovation of a Micro-Topic-Pedagogy Teaching Model under the New Engineering Education Paradigm", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 4, pp. 32–40, 2025. doi: 10.25046/aj100404
2. Chukwuemeka Alexander. Osueke, Obiageli Josphine Ugonabo, Tafon Williams Sivla, Akor John Yakubu, Eucheria Chidinma Okoro, "The First Study on Ionospheric Peak Variability over Equatorial Africa (COSMIC-2)", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 4, pp. 14–19, 2025. doi: 10.25046/aj100402
3. Maikel Leon, "Generative Artificial Intelligence and Prompt Engineering: A Comprehensive Guide to Models, Methods, and Best Practices", Advances in Science, Technology and Engineering Systems Journal, vol. 10, no. 2, pp. 01–11, 2025. doi: 10.25046/aj100201
4. Brandon Wetzel, Haiping Xu, "Deploying Trusted and Immutable Predictive Models on a Public Blockchain Network", Advances in Science, Technology and Engineering Systems Journal, vol. 9, no. 3, pp. 72–83, 2024. doi: 10.25046/aj090307
5. John Tsiligaridis, "Tree-Based Ensemble Models, Algorithms and Performance Measures for Classification", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 6, pp. 19–25, 2023. doi: 10.25046/aj080603
6. Mauricio Flores-Nicolás, Magally Martínez-Reyes, Felipe de Jesús Matías-Torres, "The Graded Multidisciplinary Model: Fostering Instructional Design for Activity Development in STEM/STEAM Education", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 5, pp. 55–61, 2023. doi: 10.25046/aj080506
7. Yangshichi, Hayoung Oh, HyunJong Kim, "The Influence Analysis of Internet Finance on China’s Banking Industry Development", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 250–261, 2023. doi: 10.25046/aj080328
8. Hermagasantos Zein, Ahmad Deni Mulyadi, Achmad Mudawari, "Minimum Static VAR Compensation Capacity for Bad Voltage Drop Buses in Power Systems", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 212–217, 2023. doi: 10.25046/aj080324
9. Mohammadali Hayerikhiyavi, Aleksandar Dimitrovski, "Three-phase Continuously Variable Series Reactor – Realistic Modeling and Analysis", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 202–211, 2023. doi: 10.25046/aj080323
10. Evgeniy Kostyrin, Evgeniy Sokolov, "Social Financial Technologies for the Development of Enterprises and the Russian Economy", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 3, pp. 118–135, 2023. doi: 10.25046/aj080314
11. Zhanna Dedovets, Mikhail Rodionov, Anna Novichkova, "A Model for Teaching Mathematics to Gifted Students Based on an Effective Combination of Various Approaches for their Preparation", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 1, pp. 138–148, 2023. doi: 10.25046/aj080117
12. Ossama Embarak, "Multi-Layered Machine Learning Model For Mining Learners Academic Performance", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 850–861, 2021. doi: 10.25046/aj060194
13. Richard Romero Izurieta, Segundo Moisés Toapanta Toapanta, Luis Jhony Caucha Morales, María Mercedes Baño Hifóng, Eriannys Zharayth Gómez Díaz, Oscar Marcelo Zambrano Vizuete, Luis Enrique Mafla Gallegos, José Antonio Orizaga Trejo, "Prototype to Identify the Capacity in Cybersecurity Management for a Public Organization", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 1, pp. 108–115, 2023. doi: 10.25046/aj080113
14. Sathyabama Kaliyapillai, Saruladha Krishnamurthy, Thiagarajan Murugasamy, "An Ensemble of Voting- based Deep Learning Models with Regularization Functions for Sleep Stage Classification", Advances in Science, Technology and Engineering Systems Journal, vol. 8, no. 1, pp. 84–94, 2023. doi: 10.25046/aj080110
15. Mikhail Lavrentiev, Andrey Marchuk, Konstantin Oblaukhov, Mikhail Shadrin, "Natural Tsunami Wave Amplitude Reduction by Straits – Seto Inland Sea", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 161–166, 2022. doi: 10.25046/aj070616
16. Fabrizio Striani, Chiara Colucci, Angelo Corallo, Roberto Paiano, Claudio Pascarelli, "Process Mining in Healthcare: A Systematic Literature Review and A Case Study", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 151–160, 2022. doi: 10.25046/aj070615
17. Segundo Moisés Toapanta Toapanta, Rodrigo Humberto Del Pozo Durango, Luis Enrique Mafla Gallegos, Eriannys Zharayth Gómez Díaz, Yngrid Josefina Melo Quintana, Joan Noheli Miranda Jimenez, Ma. Roció Maciel Arellano, José Antonio Orizaga Trejo, "Prototype to Mitigate the Risks, Vulnerabilities and Threats of Information to Ensure Data Integrity", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 139–150, 2022. doi: 10.25046/aj070614
18. Angela Pearce, "The Perceptions of Students and Teachers When using ICTs for Educational Practices Matter: A Systematic Review", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 6, pp. 1–12, 2022. doi: 10.25046/aj070601
19. Ferdinand Friedrich, Christoph Ament, "Model Order Reduction and Distribution for Efficient State Estimation in Sensor and Actuator Networks", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 146–156, 2022. doi: 10.25046/aj070516
20. Jabrane Slimani, Abdeslam Kadrani, Imad EL Harraki, El hadj Ezzahid, "Long-term Bottom-up Modeling of Renewable Energy Development in Morocco", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 129–145, 2022. doi: 10.25046/aj070515
21. Javier Calle, Itziar Sagastiberri, Mikel Aramburu, Santiago Cerezo, Jorge García, "Automatic Counting Passenger System using Online Visual Appearance Multi-Object Tracking", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 113–128, 2022. doi: 10.25046/aj070514
22. Bouassale Nasr-Eddine, Sallaou Mohamed, Aittaleb Abdelmajid, Benaissa Elfahim, "DEM models Calibration and Application to Simulate the Phosphate Ore Clogging", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 5, pp. 79–90, 2022. doi: 10.25046/aj070511
23. Kelebaone Tsamaase, Japhet Sakala, Kagiso Motshidisi, Edward Rakgati, Ishmael Zibani, Edwin Matlotse, "Performance Adjustment Factor for Fixed Solar PV Module", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 98–104, 2022. doi: 10.25046/aj070413
24. Zhumakhan Nazir, Temirlan Zarymkanov, Jurn-Guy Park, "A Machine Learning Model Selection Considering Tradeoffs between Accuracy and Interpretability", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 4, pp. 72–78, 2022. doi: 10.25046/aj070410
25. Lu Xiong, Spendylove Duncan-Williams, "Generalized Linear Model for Predicting the Credit Card Default Payment Risk", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 3, pp. 51–61, 2022. doi: 10.25046/aj070306
26. Haruka Motohashi, Hayato Ohwada, "Interpretable Rules Using Inductive Logic Programming Explaining Machine Learning Models: Case Study of Subclinical Mastitis Detection for Dairy Cows", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 2, pp. 143–148, 2022. doi: 10.25046/aj070214
27. Nils Finke, Ralf Möller, "On the Construction of Symmetries and Retaining Lifted Representations in Dynamic Probabilistic Relational Models", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 2, pp. 73–93, 2022. doi: 10.25046/aj070207
28. Rachida Hassani, Younès El Bouzekri El Idrissi, "IT Project Management Models in an Era of Digital Transformation: A Study by Practice", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 2, pp. 53–62, 2022. doi: 10.25046/aj070205
29. Alexander Núñez, Fernando Solares, Alejandro Crisanto, "Estimation of Non-homogeneous Thermal Conductivity using Fourier Heat Equation Considering Uncertainty and Error Propagation", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 1, pp. 90–99, 2022. doi: 10.25046/aj070109
30. Nganyang Paul Bayendang, Mohamed Tariq Khan, Vipin Balyan, "Thermoelectric Generators (TEGs) and Thermoelectric Coolers (TECs) Modeling and Optimal Operation Points Investigation", Advances in Science, Technology and Engineering Systems Journal, vol. 7, no. 1, pp. 60–78, 2022. doi: 10.25046/aj070107
31. Lucie Böhmová, Antonín Pavlíček, "Innovations in Recruitment—Social Media", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 6, pp. 88–97, 2021. doi: 10.25046/aj060613
32. Toshiki Watanabe, Hiroyuki Kameda, "Designing a Model of Consciousness Based on the Findings of Jungian Psychology", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 356–361, 2021. doi: 10.25046/aj060540
33. Ibnu Daqiqil Id, Masanobu Abe, Sunao Hara, "Acoustic Scene Classifier Based on Gaussian Mixture Model in the Concept Drift Situation", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 167–176, 2021. doi: 10.25046/aj060519
34. Rim Mrani Alaoui, Abderrahim El-Amrani, Ismail Boumhidi, "Model Reduction H? Finite Frequency of Takagi-Sugeno Fuzzy Systems", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 5, pp. 53–58, 2021. doi: 10.25046/aj060507
35. Olena Nosovets, Vitalii Babenko, Ilya Davydovych, Olena Petrunina, Olga Averianova, Le Dai Zyonh, "Personalized Clinical Treatment Selection Using Genetic Algorithm and Analytic Hierarchy Process", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 406–413, 2021. doi: 10.25046/aj060446
36. Zhiyuan Chen, Howe Seng Goh, Kai Ling Sin, Kelly Lim, Nicole Ka Hei Chung, Xin Yu Liew, "Automated Agriculture Commodity Price Prediction System with Machine Learning Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 376–384, 2021. doi: 10.25046/aj060442
37. Ahmed R. Sadik, Christian Goerick, "Multi-Robot System Architecture Design in SysML and BPMN", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 176–183, 2021. doi: 10.25046/aj060421
38. Montaño-Arango Oscar, Ortega-Reyes Antonio Oswaldo, Corona-Armenta José Ramón, Rivera-Gómez Héctor, Martínez-Muñoz Enrique, Robles-Acosta Carlos, "Multidisciplinary Systemic Methodology, for the Development of Middle-sized Cities. Case: Metropolitan Zone of Pachuca, Mexico", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 80–90, 2021. doi: 10.25046/aj060410
39. Kwun-Ping Lai, Jackie Chun-Sing Ho, Wai Lam, "Exploiting Domain-Aware Aspect Similarity for Multi-Source Cross-Domain Sentiment Classification", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 4, pp. 01–12, 2021. doi: 10.25046/aj060401
40. Mark Gourary, Sergey Rusakov, "Technique to Simulate an Oscillator Ensemble Represented by the Kuramoto Model", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 3, pp. 311–318, 2021. doi: 10.25046/aj060335
41. Svetlana Segarceanu, George Suciu, Inge Gavăt, "Environmental Acoustics Modelling Techniques for Forest Monitoring", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 3, pp. 15–26, 2021. doi: 10.25046/aj060303
42. Marlene Ofelia Sanchez-Escobar, Julieta Noguez, Jose Martin Molina-Espinosa, Rafael Lozano-Espinosa, "Supporting the Management of Predictive Analytics Projects in a Decision-Making Center using Process Mining", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 1084–1090, 2021. doi: 10.25046/aj0602123
43. Mamudu Hamidu, Jerry John Kponyo, "Closed Loop Capacitive Accelerometer Model using Simple Regression Test for Linearity", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 1038–1045, 2021. doi: 10.25046/aj0602118
44. Natalia Yevtushenko, Nataliia Kuzminska, Tetiana Kovalova, "Dependence of the Knowledge Structure of the Company Employees on a Set of the Competencies", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 699–708, 2021. doi: 10.25046/aj060281
45. Antoni Wibowo, Inten Yasmina, Antoni Wibowo, "Food Price Prediction Using Time Series Linear Ridge Regression with The Best Damping Factor", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 694–698, 2021. doi: 10.25046/aj060280
46. Marion Olubunmi Adebiyi, Oludayo Olufolorunsho Olugbara, "Homology Modeling of CYP6Z3 Protein of Anopheles Mosquito", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 580–585, 2021. doi: 10.25046/aj060266
47. Pritesh Shah, Ravi Sekhar, Iswanto Iswanto, Margi Shah, "Complex Order PI\(^{a+jb}\)D\(^{c+jd}\) Controller Design for a Fractional Order DC Motor System", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 541–551, 2021. doi: 10.25046/aj060261
48. Abdulla M. Alsharhan, "Survey of Agent-Based Simulations for Modelling COVID-19 Pandemic", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 439–447, 2021. doi: 10.25046/aj060250
49. Amany Khalil, Osama Tolba, Sherif Ezzeldin, "Design Optimization of Open Office Building Form for Thermal Energy Performance using Genetic Algorithm", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 254–261, 2021. doi: 10.25046/aj060228
50. Amine Mounaam, Ridouane Oulhiq, Ahmed Souissi, Mohamed Salouhi, Khalid Benjelloun, Ahmed Bichri, "A Model-Driven Digital Twin Framework Development for Sulfur Dioxide Conversion Units Simulation", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 122–131, 2021. doi: 10.25046/aj060215
51. Yousra Karim, Abdelghani Cherkaoui, "Fuzzy Analytical Hierarchy Process and Fuzzy Comprehensive Evaluation Method Applied to Assess and Improve Human and Organizational Factors Maturity in Mining Industry", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 2, pp. 75–84, 2021. doi: 10.25046/aj060210
52. Futra Zamsyah Md Fadzil, Alireza Mousavi, Morad Danishvar, "Event Modeller Data Analytic for Harmonic Failures", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1343–1359, 2021. doi: 10.25046/aj0601154
53. Naeem Ahmed Haq Nawaz, Musab Bassam Al-Zghoul, Hamid Raza Malik, Omar Radhi Aqeel Al-Zabi, Bilal Radi Ageel Al-Zabi, "Wireless Sensor Networks Simulation Model to Compute Verification Time in Terms of Groups for Massive Crowd", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1229–1240, 2021. doi: 10.25046/aj0601140
54. Thinh Dang Cong, Toi Le Thanh, Phuc Ton That Bao, Trang Hoang, "A Novel Approach to Design a Process Design Kit Digital for CMOS 180nm Technology", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1191–1198, 2021. doi: 10.25046/aj0601135
55. Laurent Nana, François Monin, Sophie Gire, "Formal Proof of Properties of a Syntax-Oriented Editor of Robotic Missions Plans", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1049–1057, 2021. doi: 10.25046/aj0601116
56. Shahrinaz Ismail, Faes Tumin, "Simulating Get-Understand-Share-Connect Model using Process Mining", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1040–1048, 2021. doi: 10.25046/aj0601115
57. Syeda Nadiah Fatima Nahri, Shengzhi Du, Barend Jacobus van Wyk, "Active Disturbance Rejection Control Design for a Haptic Machine Interface Platform", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 898–911, 2021. doi: 10.25046/aj060199
58. Sana Elhidaoui, Khalid Benhida, Said Elfezazi, Yassine Azougagh, Abdellatif Benabdelhafid, "Model of Fish Cannery Supply Chain Integrating Environmental Constraints (AHP and TOPSIS)", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 798–809, 2021. doi: 10.25046/aj060189
59. Abdulla M. Alsharhan, "Simulating COVID-19 Trajectory in the UAE and the Impact of Possible Intervention Scenarios", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 791–797, 2021. doi: 10.25046/aj060188
60. Deddy Kurniawan, Ditdit Nugeraha Utama, "Decision Support Model using FIM Sugeno for Assessing the Academic Performance", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 605–611, 2021. doi: 10.25046/aj060165
61. Arman Mirmanov, Aidar Alimbayev, Sanat Baiguanysh, Nabi Nabiev, Askar Sharipov, Azamat Kokcholokov, Diego Caratelli, "Development of an IoT Platform for Stress-Free Monitoring of Cattle Productivity in Precision Animal Husbandry", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 501–508, 2021. doi: 10.25046/aj060155
62. Mochammad Haldi Widianto, "Analysis of Pharmaceutical Company Websites using Innovation Diffusion Theory and Technology Acceptance Model", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 464–471, 2021. doi: 10.25046/aj060150
63. Eugeny Smirnov, Svetlana Dvoryatkina, Sergey Shcherbatykh, "Technological Stages of Schwartz Cylinder’s Computer and Mathematics Design using Intelligent System Support", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 447–456, 2021. doi: 10.25046/aj060148
64. Lixin Wang, Jianhua Yang, Sean Gill, Xiaohua Xu, "Data Aggregation, Gathering and Gossiping in Duty-Cycled Multihop Wireless Sensor Networks subject to Physical Interference", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 369–377, 2021. doi: 10.25046/aj060142
65. Najat Messaoudi, Jaafar Khalid Naciri, Bahloul Bensassi, "Mathematical Modelling of Output Responses and Performance Variations of an Education System due to Changes in Input Parameters", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 327–335, 2021. doi: 10.25046/aj060137
66. Eva Rolia, Dwita Sutjiningsih, Yasman, Titin Siswantining, "Modeling Watershed Health Assessment for Five Watersheds in Lampung Province, Indonesia", Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 99–111, 2021. doi: 10.25046/aj060111
67. Murtada Khalafallah Elbashir, Saleh N. Almuayqil, "Time-to-Event Analysis for Recovery from Coronavirus Disease (COVID-19): A Case Study on Wuhan and Elsewhere in China from Jan 1 to Feb 11, 2020", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1609–1617, 2020. doi: 10.25046/aj0506192
68. Hakimjon Zaynidinov, Sayfiddin Bakhromov, Bunyod Azimov, Sarvar Makhmudjanov, "Comparative Analysis Spline Methods in Digital Processing of Signals", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1499–1510, 2020. doi: 10.25046/aj0506180
69. Abubakar Umar, Zhanqun Shi, Lin Zheng, Alhadi Khlil, Zulfiqar Ibrahim Bibi Farouk, "Parameter Estimation for Industrial Robot Manipulators Using an Improved Particle Swarm Optimization Algorithm with Gaussian Mutation and Archived Elite Learning", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1436–1457, 2020. doi: 10.25046/aj0506174
70. Nicolò Speciale, Rossella Brunetti, Massimo Rudan, "Solution of the Semiconductor-Device Equations by the Numerov Process", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1414–1421, 2020. doi: 10.25046/aj0506171
71. Marcin Kuropatwi´nski, Leonard Sikorski, "Empirical Probability Distributions with Unknown Number of Components", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1293–1305, 2020. doi: 10.25046/aj0506154
72. Aaron Don M. Africa, Emmanuel T. Trinidad, Lawrence Materum, "Projection of Wireless Multipath Clusters Using Multi-Dimensional Visualization Techniques", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1064–1070, 2020. doi: 10.25046/aj0506129
73. Aarthi Ramachandran, Amudha Joseph, Shunmuga Velayutham, "Feature Gate Computational Top-Down Model for Target Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 1001–1006, 2020. doi: 10.25046/aj0506120
74. Gehad Ali Alsayed, Zahraa Ismail, Sameh O. Abdellatif, "Investigating the Optical Behavior of Single/Multi-Dimensional Photonic Crystal Structures for Photovoltaic Applications", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 951–958, 2020. doi: 10.25046/aj0506113
75. Ismail Ktata, Naoufel Kharroubi, "A Model-Driven Approach for Reconfigurable Systems Development", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 801–810, 2020. doi: 10.25046/aj050695
76. Luisella Balbis, "Optimal Irrigation Strategy using Economic Model Predictive Control", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 781–787, 2020. doi: 10.25046/aj050693
77. Yohei Yamauchi, Mitsuyuki Saito, "Adaptive Identification Method of Vehicle Model for Autonomous Driving Robust to Environmental Disturbances", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 710–717, 2020. doi: 10.25046/aj050685
78. Khalid Chennoufi, Mohammed Ferfra, "Fast and Efficient Maximum Power Point Tracking Controller for Photovoltaic Modules", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 606–612, 2020. doi: 10.25046/aj050674
79. Jojo Blanza, Lawrence Materum, "Interface for Visualization of Wireless Propagation Multipath Clustering Outcomes", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 544–549, 2020. doi: 10.25046/aj050665
80. Jojo Blanza, Lawrence Materum, "Variation Between DDC and SCAMSMA for Clustering of Wireless MultipathWaves in Indoor and Semi-Urban Channel Scenarios", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 538–543, 2020. doi: 10.25046/aj050664
81. Alexander Raikov, "Accelerating Decision-Making in Transport Emergency with Artificial Intelligence", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 520–530, 2020. doi: 10.25046/aj050662
82. Mokhlis Salah-eddine, Said Sadki, Bahloul Bensassi, "Microcontroller Based Data Acquisition and System Identification of a DC Servo Motor Using ARX, ARMAX, OE, and BJ Models", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 507–513, 2020. doi: 10.25046/aj050660
83. Robert Antonio Romero-Flores, "An Economic Theory Perspective for the Fight Against Poverty in the Peruvian Andes", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 497–506, 2020. doi: 10.25046/aj050659
84. Gede Putra Kusuma, Jonathan, Andreas Pangestu Lim, "Emotion Recognition on FER-2013 Face Images Using Fine-Tuned VGG-16", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 315–322, 2020. doi: 10.25046/aj050638
85. Ravi Sekhar, Tejinder Paul Singh, Pritesh Shah, "Complex Order PI\(^{\alpha + j\beta} \)D\(^{\gamma+j\theta}\) Design for Surface Roughness Control in Machining CNT Al-Mg Hybrid Composites", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 299–306, 2020. doi: 10.25046/aj050636
86. Eugen Harinda, Hadi Larijani, Ryan M. Gibson, "Trace-Driven Simulation of LoRaWAN Air Channel Propagation in an Urban Scenario", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 211–220, 2020. doi: 10.25046/aj050625
87. Sergiy Kostrikov, Rostyslav Pudlo, Dmytro Bubnov, Vladimir Vasiliev, Yury Fedyay, "Automated Extraction of Heavyweight and Lightweight Models of Urban Features from LiDAR Point Clouds by Specialized Web-Software", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 72–95, 2020. doi: 10.25046/aj050609
88. Fadhillah Moulita Andiani, Faizal Abid, Hendri, Abba Suganda Girsang, "Business Intelligence for Generating Comprehensive Report in Electronic Completion and Handover", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 6, pp. 45–51, 2020. doi: 10.25046/aj050606
89. Redha Touati, Max Mignotte, Mohamed Dahmane, "A Circular Invariant Convolution Model-Based Mapping for Multimodal Change Detection", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1288–1298, 2020. doi: 10.25046/aj0505155
90. Nhu-Tung Nguyen, Dung Hoang Tien, Do Duc Trung, "Development of the Surface Roughness Model in the Grinding Processes", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 1184–1188, 2020. doi: 10.25046/aj0505143
91. Emad Kareem Mutar, "Matrix-based Minimal Cut Method and Applications to System Reliability", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 991–996, 2020. doi: 10.25046/aj0505121
92. Gcobisile Matafeni, Ritesh Ajoodha, "Using Big Data Analytics to Predict Learner Attrition based on First Year Marks at a South African University", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 920–926, 2020. doi: 10.25046/aj0505112
93. Gene Patrick Rible, Nicolette Ann Arriola, Manuel Ramos Jr., "Modeling and Implementation of Quadcopter Autonomous Flight Based on Alternative Methods to Determine Propeller Parameters", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 727–741, 2020. doi: 10.25046/aj050589
94. Abdelghani Lakhdar, Aziz Moumen, Laidi Zahiri, Mustapha Jammoukh, Khalifa Mansouri, "Experimental and Numerical Study of the Mechanical Behavior of Bio-Loaded PVC Subjected to Aging", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 607–612, 2020. doi: 10.25046/aj050574
95. Kerin Augustin, Natasia, Ditdit Nugeraha Utama, "Butterfly Life Cycle Algorithm for Measuring Company’s Growth Performance Based on BSC and SWOT Perspectives", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 554–558, 2020. doi: 10.25046/aj050568
96. Józef Pawelec, "The Newtonian Model of the Smolensk Catastrophe", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 550–553, 2020. doi: 10.25046/aj050567
97. Abdi Sukmono, Arief Laila Nugraha, Arsyad Nur Ariwahid, Nida Shabrina, "Growth Models and Age Estimation of Rice using Multitemporal Vegetation Index on Landsat 8 Imagery", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 506–511, 2020. doi: 10.25046/aj050563
98. Nghia Duong-Trung, Nga Quynh Thi Tang, Xuan Son Ha, "Interpretation of Machine Learning Models for Medical Diagnosis", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 469–477, 2020. doi: 10.25046/aj050558
99. Vikas Anand Vatul, Arputha Aravinth, Narayanan K, Gulshan Sharma, Tomonobu Senjyu, "A Novel Demand Side Management by Minimizing Cost Deviation", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 262–268, 2020. doi: 10.25046/aj050532
100. Mimi Mohaffyza Mohamad, Alias Masek, Jailani Md Yunos, Maizam Alias, Nor Hidayah Hamdan, Andika Bagus Nur Rahma Putra, "Assessing Heutagogical Elements in Learning of Engineering Education: Instrument Validation", Advances in Science, Technology and Engineering Systems Journal, vol. 5, no. 5, pp. 245–252, 2020. doi: 10.25046/aj050530