1. Introduction

On the other hand, several simulations have been conducted which makes the frequency bands more and more crowded.

Game theory represents a decision-making mathematical tool ^{in the United States and showed that 60 % of the frequency} that attracts much attention, when it comes to networks for re- bands are not used [1]. Several solutions have been recomsource sharing, congestion control, transmission-rate adapta- ^{mended by the Federal Communications Commission (FCC)} tion, etc. This theory was originally and exclusively proposed ^{in order to enhance the usage of the spectrum. Opportunistic} for economics before being applied to many other topics, such ^{Spectrum Access (OSA) in CR, represents one of the pro}as: financial, regulation, military, political science and also ^{posed solutions, where users are categorized into two groups} biology. The main objective for using the game theory is to ^{namely: Licensed users (Primary Users: PUs) who have the} study and analyze cooperative or competitive situations for ^{right to access the frequency bands at any time, and unli}rational players in order to find an equilibrium among them. censed users (Secondary Users: SUs) that can access the freWhen, players reach the equilibrium point, then none of them ^{quency bands in an opportunistic manner. Usually, SUs can} can gain more by changing its action. coexist with PUs in the same frequency bands as far as they dont cause any harmful interference to these latter. Indeed, ^{Game theory is widely applied in Cognitive Radio (CR)} SUs are able to access the frequency bands currently unused in order to enhance the spectrum efficiency of the licensed by PUs. SUs in OSA have many challenges in order to reduce frequency bands. Indeed, according to many recent studies, the interference with PUs:

the frequency bands are not well used. On the one hand, the

demands on high data rate applications and wireless devices • Spectrum Sensing: A SU should sense the frequency have experienced unprecedented advancement since 1990s bands and identify the available spectrum holes before

making any decision. The main challenge is to gather an accurate information about the status of the spectrum (free or busy) in order to access only the unused channels without causing any harmful interference to PUs. Due to hardware constraints, delay and high energy consummation, a SU may be able to sense a portion of the frequency bands (e.g. one channel at each time slot) and decides whether the selected channel is free to transmit.

• Spectrum Decision: At each time slot, a SU should decide which channel to access based on past success or failure decisions. As a result, a SU can gather some information about the availability and quality of channels and build a database of the spectrum access environment. This database is used in order to make a good decision and enhance the future actions of the SU.
• Spectrum Sharing: In order to share the available spectrum among SUs, two main models exist: Cooperative or competitive access. In the cooperative behaviors, the users need to exchange information with each other in order to maximize their opportunities and thus decrease the interference among themselves. Despite the latter benefits of the cooperative access, each user should be informed about others decisions before making any action which may increase the complexity of the secondary network. While, in the competitive access, each SU makes an action based on its local observation. However, this lack of information exchange can increase the number of collisions among users. To solve this issue, a specific policy is required to learn the vacancy probabilities of available channels and decrease the number of collisions among users.

APL	All-Powerful Learning
CR	Cognitive Radio
DMC	Dynamic Musical Chairs
EXP3	Exponential weights for Exploration and Exploitation
FCC	Federal Communications Commission
MAB	Multi-Armed Bandit
MEGA	Multi-user e-greedy collision Avoiding
OSA	Opportunistic Spectrum Access
PU	Primary User
QoS	Quality of Service
SU	Secondary User
SLK	Selective Learning of the kth largest expected rewards
TS	Thompson Sampling
UCB	Upper Confidence Bound

Table 1: List of acronyms

• Finally, in the Spectrum Mobility, a SU should evacuate the selected channel when a PU reappears. Moreover, a SU may badly identify its dedicated channel and then access a channel that does not correspond to its prior rank^[1]. Therefore, the user should evacuate its current channel when he identifies its targeted channel.

This paper is an extension of our original work presented in [2] with a novel policy called All-Powerful Learning (APL) is proposed in order to maximize the opportunities of SUs, share the available spectrum among them, and limit the interference among PUs and SUs. Instead of only considering the availability, this paper takes into account a quality information metric, where the priority users should access only best channels with the highest availability and quality.

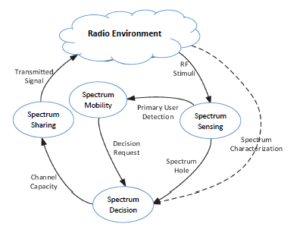
Figure 1: Cognitive cycle as introduced in [3].

2. Multi-Armed Bandit Problem

Multi-Armed Bandit (MAB) model represents one of the famous models, in game theory, that is adopted to enhance the efficiency of the licensed frequency bands. Moreover, MAB problem represents a simple case of the Reinforcement Learning (RL).

In the RL, the agent should enhance his behavior from the feedback (e.g. reward). Indeed, the RL may allow an agent to adapt to his environment by finding a suitable action to reach the best reward. The agent can maximize his reward without any prior information about his environment. However, by memorizing the states of an environment or the actions he took, the agent can make a better decision in the future. The reward feedback, also called reinforcement signal, has an important role to help an agent to learn from its environment. The RL is widely used in several domains: Robotics, Aircraft control, self- driving cars, Business strategy planning, etc. It was first developed for a single agent who should find an optimal policy that maximizes his expected reward knowing that the optimal policy depends on the environment. Unlike the case of a single agent, for multiple agents, the optimal policy depends not only on the environment but also on the policies selected by other agents. Moreover, when multiple agents apply the same policy their approaches in such systems often fail because each agent tries individually to reach a desired result. In other words, it is impossible for all agents in a certain system to maximize simultaneously their personal reward, although find an equilibrium for the system representing a point of interest. Subsequently, it is important to find a policy for each agent in order to guarantee the convergence to an equilibrium state in which no agent can gain more when modifying its own action. In RL, Exploitation-Exploration dilemma represents an attractive problem. In order to maximize his performance (exploitation), the agent should gather some information about his environment (exploration). This is known as the Exploration-Exploitation dilemma in the reinforcement learning. If the agent spends a lot of time on the exploration phase, then he cannot maximize his reward. Similarly, when the agent focuses on the exploitation phase by exploiting his current information, then he may miss the best action that leads to the highest reward. Thus, the agent needs to balance the tradeoff between Exploration and Exploitation in order to obtain an appropriate result.

Due to its generic nature, the MAB model is widely adopted in many fields, such as: wireless channel access, jamming communication or object tracking. In such model, an agent can play a single arm at each time trying to maximize its long-term reward. To reach its goal, the agent needs to find the best arm in terms of expected reward. At each time slot, the agent can choose the current best arm (exploitation) or play other arms trying to obtain a robust estimation of their reward (exploration). Generally, an optimal policy, used by the agent, should balance between the exploitation and the exploration phases while pulling the arms.

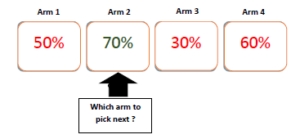
Figure 2: Several Arms with different expected reward. After a finite period of time the agent has a perception about the reward obtained from each arm.

Like most RL frameworks, the agent starts the game without any priori knowledge about the expected reward of the arms. The main goal of the agent is to find the arm with the highest expected reward. Here, we should define two classes of arms:

Optimal arm: This arm has the highest expected reward and is represented by the arm 2 in Fig. 2. The agent tries to reach this arm in order to maximize his expected reward.

Suboptimal arms:               Include all other arms considered as non-optimal. Efficient MAB algorithms should be able to limit playing with suboptimal arms.

To solve the MAB problem, several algorithms have been proposed, such as: Thompson Sampling [4], Upper Confidence Bound (UCB) [5], e-greedy [6], Exponential weights for Exploration and Exploitation (EXP3) [7], etc. The performance of a given MAB algorithm is usually measured by a regret that represents the gap between the reward obtained in the ideal scenario, where the user know the expected reward of each arm and often pulls the best one, and that obtained using a given MAB algorithm.

It is worth mentioning that these algorithms have been suggested for a single SU in the context of OSA where the SU is considered as an agent and the channels become equivalent to the different arms. Then, it is assumed that each channel is associated with a distinct availability probability and the SU should estimate this latter after a finite number of time slots. In this work, we first start to formulate the classical OSA as a MAB problem, in which, we consider a single Secondary User (SU) that needs to access opportunistically the frequency band. Later on, we will consider more realistic conditions that deal with the OSA (e.g. multiple users, Quality of Service, collision among users, dynamic access).

2.1     Thompson Sampling

Thompson Sampling (TS), a randomized algorithm with a bayesian spirit, represents one of the earliest algorithms proposed to tackle the MAB problem. In TS, each arm has assigned an index B_i(t, T_i(t)) that contains information based on the past success and failure observations. After a finite number of time slots, the index B_i(t, T_i(t)) will be very close to the mean reward of each arm. By selecting the arm with the highest index at each time slot, the agent often selects the best arm with the highest reward. This index achieves a trade-off between the exploration and the exploitation phases and can be defined as follows:

where W_i(t, T_i(t)) and Z_i(t, T_i(t)) represent respectively the success and failure access; a and b are constant numbers.

Despite its excellent performance that can exceed the stateof-the-art MAB algorithms [8, 9, 10], TS is widely ignored in the literature. This ignorance is due to the fact that this algorithm is proposed with a lack of proof and a slight mathematical background unlike other MAB algorithms, such as: UCB or e-greedy. Recently, TS has attracted more attention and is being used in several fields [11, 12, 13]. Recent studies have found a theoretical upper bound for its convergence to the best choice [14, 15, 16].

2.2    Upper Confidence Bound

Upper Confidence Bound (UCB) represents one of the famous MAB algorithms firstly proposed in [5]. Like TS, the index B_i(t, T_i(t)) of UCB contains two phases, the exploration and the exploitation phases, in order to estimate the vacancy probabilities of channels and then access the best one. In the literature, several variants of UCB have been proposed to enhance the performance of the classical UCB, such as: UCB1, UCB2, UCB-tuned, Bayes-UCB, KL-UCB [8, 17, 18, 19]. UCB1 [17] represents the simplest version that balances between the complexity and the optimality.

Algorithm 1: Thompson Sampling Algorithm

Input: C, n,

• C: number of channels,
• n: total number of slots,
• Parameters: S_i(t), T_i(t),W_i(t, T_i(t)), Z_i(t, T_i(t)),
• S_i(t): the state of the selected channel, equals one if the channel is free and 0 otherwise,
• T_i(t): number of times the i^th channel is sensed by SU,
• W_i(t, T_i(t)): the success access of the i^th channel,
• Z_i(t, T_i(t)): the failure access of the i^th channel,

Output: B_i(t, T_i(t)),

• B_i(t, T_i(t)): the index assigned for the i^th channel,
• foreach t = 1 to n do 10 a_t = arg max_i B_i(t, T_i(t)),
• Observe the State S_i(t),
• W_i(t, T_i(t)) = ∑ⁿ_t=0 S_i(t)1_at=i,
• % 1_at=_i: equal 1 if the user selects the i^th channel and

0 otherwise, 14 Z_i(t, T_i(t)) = T_i(t) − W_i(t, T_i(t)),

15           Bi(t, Ti(t)) = Wi(t,Ti(Wt))+i(t,TZii((tt))+,Ti(ta))+a+b

Algorithm 2: UCB1 Algorithm

Input: α, C, n,

• α: exploration-exploitation factor,
• C: number of channels,
• n: total number of slots,

4 Parameters: T_i(t), X_i(T_i(t)), A_i(t, T_i(t)),

5 T_i(t): number of times the i^th channel is sensed up to t, 6 X_i(T_i(t)): the exploitation contribution of i^th channel,

7 A_i(t, T_i(t)): the exploration contribution of i^th channel,

Output: B_i(t, T_i(t)),

8 B_i(t, T_i(t)): the index assigned for i^th channel,

For this reason, UCB1 is the widely adopted version scheme in the context of CR to help a SU make an optimal decision [20, 21, 22, 23, 24, 25]. In UCB1, the index B_i(t, T_i(t)) essentially comprises two important factors: X_i(T_i(t)) and A_i(t, T_i(t))) that represent respectively the exploitation (or the expected reward) and the exploration phases:

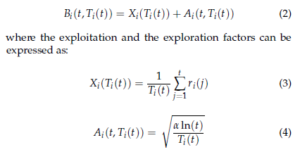
The factor A_i(t, T_i(t)) has an important role in learning the availability probabilities of channels by pushing the algorithm to examine the state of all available channels. Thus, after a finite time t, X_i(T_i(t)) of the i^th channel will approximately equal to its availability probability µ_i.

In [17], the authors found an upper bound of the sum of regret (i.e. the loss of reward by selecting the worst channels) for a single agent and C arms. It has shown that the upper bound of the regret achieves a logarithmic asymptotic behavior, which means that after a finite number of time slots, the agent will be able to identify the best arm and always select it.

2.3 e-greedy

One of the simplest MAB algorithms to tackle the MAB problem is referred to e-greedy that was firstly proposed in [6]. A recent version of this algorithm is proposed in [17] in order to achieve a better performance compared to several previous versions (see algorithm 1). Like several MAB algorithms, e-greedy contains two phases completely separated: exploration and exploitation. During the exploration phase, the user chooses a random channel in order to learn the vacancy probability of channels.

While in the exploitation phase, the user usually selects the channel with the highest expected reward X_i(T_i(t)). The authors of [17] have also investigated the analytical convergence of the e-greedy and proved that the regret (i.e. the loss of reward by selection the worst channel) achieves a logarithmic asymptotic behavior.

3. Problem Formulation

In the previous section, we introduced the well-known MAB algorithms that help a MAB agent makes a good decision. In this section, we present the classical OSA for a single SU in order to formulate it as a MAB problem. However, MAB algorithms can represent an optimal solution for the classical OSA, as it can be seen in section 5. On the other hand, we consider more developed scenarios compared to the classical OSA such as multiple SUs, decreasing the collisions among users and also estimating the quality of the available channels. We first present the OSA for multiple SUs in the next section and, hereinafter, we propose the new APL policy to manage a secondary network.

Algorithm 3: e-greedy Algorithm

Input: C, H, n,

• C: number of channels,
• H: exploration constant,
• n: total number of slots,

4 Parameters: T_i(t),

• T_i(t): number of times the channel is sensed up to time t,
• χ: a uniform random variable in [0,1],

Output: X_i(T_i(t)),

• X_i(T_i(t)): the expected reward that depends on T_i(t),

8 foreach t = 1 to n do

3.1     Single User Case

Let us consider a SU accesses C channels, each of which associated with a vacancy probability µ_i ∈ [0, 1]. Let the vacancy probabilities be ordered by their availability probabilities, µ₁ > µ₂ > … > µ_C, which are initially unknown for the secondary user. A most important objective of the SU is to estimate the vacancy probabilities of channels after a finite time in order to access the best channel that has µ₁ as vacancy probability. At each time slot, the user can select one channel and transmit its data if available; otherwise, it should wait the next slot to sense another channel. Let the state of the i^th channel at slot t be referred to S_i(t): S_i(t) equals 1 if the i^th channel is free and 0 otherwise. Hereinafter, we consider that the obtained reward from the i^th channel r_i(t), at slot t is equal to its state: r_i(t) = S_i(t). Let T_i(t) represent the number of times to access the i^th channel up to the slot t. The user should be rational by adopting a given policy in order to quickly identify the best channel. A policy selected by the SU may not be considered as optimal in term of the accuracy of the channels’ vacancy estimation or the convergence speed towards the best channel. Finally, let us introduce the regret that rerepsents the gap between the reward obtained in an ideal scenario and that can be obtained using a given policy as follows:

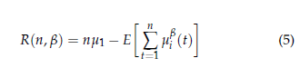
where n represents the total number of time slots and µ_i^β(t) stands for the vacancy probability of the selected channel at slot t under the policy β, and E(.) is the mathematical expectation.

3.2     Multi-User Case

In this section, we consider U SUs trying to learn the vacancy probabilities of the C channels and then access only the U best ones (C > U). When several SUs existing in the spectrum, their main challenge is to learn collectively or separately the vacant probability of channels as much as possible in order to access the best ones. Therefore, a policy selected by users should estimate the vacancy of channels as much as possible, and should also be able to decrease the collisions number among users. Therefore, let us define the regret for multiple users that takes into account both the convergence speed to the U best channels and the collision number among users as follows:

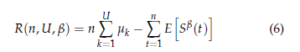
where µ_k stands for the vacancy probability of the k^th best channel; S^β(t) represents the global reward obtained by all users at time t using the policy β and is defined as follows:

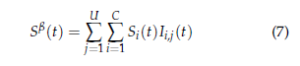
where S_i(t) represents the state of the i^th channel at time t: S_i(t) = 1 if the i^th channel is available and 0 otherwise; I_i,j(t) indicates that no collisions have appeared in the i^th channel by the j^th user at slot t: I_i,j(t) = 1 if the j^th user is the sole occupant of the channel i and 0 otherwise. Finally, the regret that takes into consideration the channels’ occupancy and the collisions number among users can be expressed by:

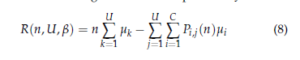
where P_i,j represents the expectation of times that the j^th user is the only occupant of the i^th channel up to n, and the mean of reward can be given by:

1 n µ_i ≈ ∑ S_i(t) n t=1

4. Multi-Priority Access

In the existing models of OSA where several SUs exist in the network, the main challenge is to learn collectively (via a cooperative learning) or separately (via a competitive learning) the available channels while decreasing the number of collisions with each other. In our work, we focus on the competitive priority access, where the k^th user should selfishly estimate the vacancy probabilities of channels in order to access the k^th best one. Our proposed policy for the priority access takes into account the dynamic access where the priority users can enter/leave the network at any time. To the best of our knowledge, only the priority or the random access are considered without the dynamic access in several proposed MAB policies [24, 25, 26, 27] (a simple example for the priority dynamic access is shown in Fig. 3).

To formulate the OSA as a MAB problem, recent works extend the simple case of MAB (i.e. the case of a single agent) to consider several agents [20, 25, 26, 28, 29]. In our work, we are interested in the OSA for multiple priority access in which SUs should access the spectrum according to their ranks. Moreover, decreasing the number of collisions among SUs represents a point of interest to enhance the global performance of the secondary network. In general, when two SUs access the same channel to transmit, their data cannot be correctly received because of the interference between them. When a collision occurs among users, several proposals can be found in the literature in order to enhance their behavior in the next slots. We present below two well-known collision models in the literature that are widely used in OSA:

• ALOHA-like model: If a collision occurs between two or more users, then none of them receives a reward, despite the selected channels is free. This model may ensure the fairness among users, and no collision avoidance mechanism is used.
• Reward sharing model: If two or more users select the same channel at the same time, the colliding users share the obtained reward from the selected channel (each of them receives the same reward).

The above models can affect the methodologies used to collect the reward from the target channel while the learning phase is not affected. In our work, we consider the most widely used, ALOHA-like.

Based on the ALOHA-like, the works of [2, 20, 21, 25, 26, 27, 28, 30] proposed semi-distributed and distributed algorithms in which users cannot exchange information with each other. Liu and Zhao in [28], proposed Time-Division Fair Share (TDFS) policy and showed that the proposed algorithm may achieve an asymptotic logarithmic behavior. In such algorithm, the users access the channels with different offsets. TDFS also ensures the fairness among users; while in our work we are interested in the priority access where users access the channels based on their prior rank. In [28], TDFS policy was been used to extend UCB1 algorithm to consider multiple users. Beside TDFS, the authors of [20] proposed Random Rank policy, based on UCB1, to manage the secondary network. Random Rank represents a distributed policy (i.e. no-information exchange among users) in which the user achieves a different throughput.

The authors of [24] proposed the Selective Learning of the k^th largest expected rewards (SLK) policy, based on UCB1, that represents an efficient policy for the priority access. However, SLK allows only a fixed number of users to access the available channels. So that, the dynamic access under SLK cannot be considered since this latter restricts the access. Similarly to SLK, the authors of [25] proposed the kth − MAB for the priority access which is based on UCB1 and e-greedy. In kth − MAB, the time is slotted and each slot is divided into multi sub-slots depending on the users priority ranks. For instance, the slot of SU_U is divided into U sub-slots in order to find the U^th best channel and transmit data via this channel. Therefore, the main limitation of this policy remains in the dissatisfaction of transmission time of high ranked users.

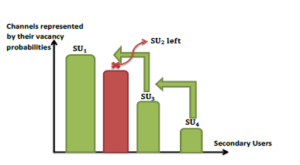
Figure 3: Priority access after a user left its dedicated channel

For the random access, several learning policies can be found in the literature, where the SU selects randomly its channel. The authors of [26] proposed the Musical Chairs policy as well the Dynamic Musical Chairs (DMC) policy for a dynamic access. In both policies, the SU selects a random channel up to time T₀ in order to estimate the vacancy of channels and the number of users, U, in the network. After T₀, the SU chooses a random channel between {1, …,U}. The main drawback of the Musical Chairs and DMC is that the users should known the total number of transmission time slots as well as the number of available channels. Moreover, in DMC a restrict access is considered, where the users cannot leave the network during the time T₀. To find the U-best channels, the authors of [27] proposed the Multi-user e-greedy collision Avoiding (MEGA) algorithm based on the e-greedy algorithm proposed in [17]. However, their algorithm suffers the same drawbacks of the Musical Chairs and the Dynamic Musical Chairs and it does not consider the priority access. In order to solve all these limitations, we propose in section (4.1) a novel policy called APL for the priority dynamic access.

4.1     APL for the Priority Access

In this section, we propose a new policy for the priority access. This policy enables a secondary user to learn the vacant probabilities of channels and ensures the convergence to his dedicated channel. Moreover, it can be used with all learning MAB algorithms such as: Thompson Sampling (TS), Upper Confidence Bound (UCB), AUCB, e-UCB, e-greedy, etc. We should highlight that our proposed policy does not require prior knowledge about the channels as in the case for other policies, such as: Musical Chair [26], SLK [24], k-th MAB [25], MEGA [27], etc. Indeed, existing policies to manage a secondary network suffer from one or more of the following disadvantages:

1. The number of users should be fixed and known to all users.
2. SUs should have a prior information about the number of channels.
3. Expected transmission time should be known.
4. The dynamic access is not suggested. To recall, in a dynamic access, the users can at any given time enter or leave the network.
5. Some algorithms consider a restricted dynamic access, where a SU can’t leave the network during the learning or the exploration phases.
6. The vacant probabilities of channels should be static; otherwise, users cannot adapt to their environment.
7. The priority access is seldomly suggested in the literature, while the random access represents the most used model.

Unlike SLK and k-th MAB, our proposed policy for the priority access, called All-Powerful Learning algorithm (APL), doesn’t suffer from the above mentioned drawbacks. As a matter of fact, SLK and k-th MAB policies suffer from the 1^st, 2^nd and 4^th mentioned drawbacks.

In a classical priority access, each channel has assigned an index B_i(t) and the highest priority user SU₁ should sense and access the channel with the highest index B_i(t) at each time slot. Indeed, the best channel, after a finite number of time slots, will have the highest index B_i(t).

As the second priority user SU₂ should avoid the first best channel and try to access the second best one. To reach his goal, SU₂ should sense the first and second best channels at each time slot in order to estimate their vacant probabilities and then access the second best channel if available. In this case, the complexity of the hardware is increased, and we conclude that a classical priority access represents a costly and impractical method to settle down each user to his dedicated channel. In the case of APL, at each time slot, the user senses a channel and transmits his data if the channel is available (see algorithm 4). In our policy, each SU_k has a prior rank, k ∈{1, …,U}, and his target is to access the k-th best channel. The major problem of the competitive priority access is that each user should selfishly estimate the vacant probabilities of the available channels. Our policy can intelligently solve this issue by making each user generate a rank around his prior rank to get information about the channels availability. For instance, if the rank generated by the k-th user equals 3 (considering that k > 3), then he should access the channel that has the third index, i.e. B₃(t). In this case, SU_k can examinate the states of the k best channels and his target is the k-th best one.

Algorithm 4: APL for the priority dynamic access

Input: k, ξ_k(t), r_i(t),

• k: indicates the k − th user or k − th best channel,
• ξ_k(t): indicates a presence of collision for the k − th user at instant t,
• r_i(t): indicates the state of the i − th channel at instant t, r_i(t) = 1 if the channel is free and 0 otherwise,

4 Initialization

However, if the rank created by SU_k is different than k, then he selects a channel with one the following probabilities:

{µ₁, µ₂, …, µ_k−1} and he may collide with a priority user, i.e. SU₁, SU₂, …, SU_k−1. Therefore, SU_k should avoid regenerating his rank at each time slot; otherwise, a large number of collisions may occur among users and transmitted data can be lost. So, after each collision, SU_k should regenerate his rank from the set {1, …, k}. Thus, after a finite number of slots, each user settles down to his dedicated channel. It remains to investigate the analytical convergence of APL to verify its performance in a real radio environment.

4.2     Quality of Service

As mentioned before, UCB represents one of the popular MAB algorithms that is widely suggested in the literature, where several variants have been proposed. In [23], we proposed a new variant of UCB called the Quality of Service UCB1 (QoS-UCB1) for a single SU, where this latter is able to learn channels’ vacancy and quality. To consider multiple SUs, this version of UCB is extended using the Random Rank policy proposed in [20] to manage a secondary network. It has been shown that the Random Rank policy with the QoS-UCB1 represents an optimal solution to allow users to learn separately channels’ vacancy and quality. However, in this paper, we evaluate the performance of our APL policy with QoS-UCB1 for the priority access.

Supposing that each channel has a binary quality represented by q_i(t) at slot t: q_i(t) = 1 if the channel has a good quality and 0 otherwise. Then, the expected quality collected from the channel i up to time n is given by:

where the parameter γ stands for the weight of the quality factor; M_i(t, T_i(t)) = G_max(t) − G_i(T_i(t)) being the difference between the maximum expected quality over channels at time t, i.e. G_max(t), and the one collected from channel i up to time slot t, i.e. G_i(T_i(t)). However, when the i^th channel has a good quality G_i(T_i(t)) as well as a good availability X_i(T_i(t)) at time t. The quality factor Q_i(t, T_i(t)) decreases while X_i(T_i(t)) increases. Subsequently, by selecting the maximum of its index B_i^Q(t, T_i(t)), the user has a large chance to access the i^th channel with a high quality and availability.

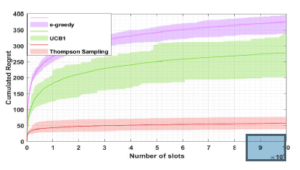
Figure 4: Evaluate the performance of TS, UCB1 and e-greedy in OSA

5. Simulations and Results

In our simulations, we consider three main scenarios: In the first one, a SU tries to learn the vacancy of channels using the MAB algorithms: TS, UCB1 and e-greedy in order to access the best one with the highest vacancy probability. We also compare the performance of these MAB algorithms to show which one can offer more opportunities for the SU. In a second scenario, we considered 4 SUs trying to learn the vacancy of channels with a low number of collisions. In this scenario, we show that, based on our policy APL, users reach their dedicated channel faster than several existing policies. In the last scenario, using APL with the QoS-UCB1, users should learn both vacancy and quality of channels and then converge towards channels that have a good vacancy and quality.

In our algorithm, two factors can affect the convergence: α or H while the convergence of UCB1 and e-greedy are affected by α and H respectively. We consider the value of α and H for which UCB1 and e-greedy achieve their best performance. According to [17], the best value of H _d (i.e. c = 0.1 is a constant number, K = 9 and d = min_i(µ₁ −µ_i) = 0.1) and α are 90 and 2 respectively in order to ensure a balance between the exploration and exploitation phases.

Let us initially consider a SU trying to access 9 channels associated with the following vacancy probabilities:

Γ = [0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1]

Fig. 4 compares the regret of the SU using the three MAB algorithms: TS, UCB1 and e-greedy over 1000 Monte Carlo runs. The simulation outcomes are presented with a shaded region enveloping the average regret. As we can see, the regrets of the 3 MAB algorithms have a logarithmic asymptotic behavior with respect to the number of slots, while TS produces a lower regret for all simulations. That means that the SU can quickly reaches the best channel that offers more opportunities for the user compared to other channels. In the second scenario of our simulation, we evaluate the performance of APL and its ability to make each user selects his dedicated channel after a finite number of time slots. We evaluate the performance of APL compared to the existing learning policies such as Musical Chair and SLK.

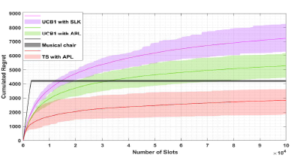
Figure 5: TS, UCB1 with APL compared to SLK and Musical Chairs

To make this comparison, we use two main performance indexes: the regret related to the access of worst channels and the percentage of times to access best channels by each user. A collision may occur when two or more users try to access the same channel. We adopt in our simulations the ALOHA model, widely used one in OSA, in which none of the collided users receives a reward. After each collision, and based on our policy APL, the collided users should regenerate their rank. First, we consider a static setting of users, then we investigate the dynamic access in which the priority users can enter or leave the network.

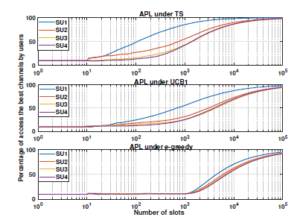
Figure 6: The percentage of times where each SU_k selects its optimal channel using the proposed approach

In Fig. 5, we compare the regret of APL to SLK and Musical Chair. APL and SLK take into consideration the priority access while Musical Chair is proposed for the random access. Despite the regret of APL and SLK has a logarithmic asymptotic behavior, the regret of Musical Chair has two parts:

• A linear part at the beginning, during the learning period, due to the large number of collisions resulting from the random selection.
• A constant part in which the users exploit the U best channels.

As we can see from Fig. 5, APL using TS outperforms Musical Chair and SLK by achieving the lower regret.

Fig. 6 shows the percentage of times that the k-th user accesses his ded- icated channel based on our policy APL up to n, P_k(n). This latter is given by:

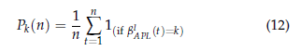
where β^l_APL(t) represents the channel selected at time t under APL using the learning algorithm l, such as: TS, UCB1 or egreedy. As we can see, based on our policy APL, the users are able to converge to their targeted channels: SU₁ converges to the best channel µ₁, followed by SU₂ , SU₃ and SU₄ to the channels µ₂ , µ₃ and µ₄ respectively. In addition, we can observe a fast converges of APL using TS compared to TS.

This figure clearly shows that, based on APL, the users converge to their dedicated channels: the first priority user SU₁ converges towards the best channel µ₁ = 0.9, followed by SU₂, SU₃ and SU₄ towards channels µ₂ = 0.8, µ₃ = 0.7 and µ₄ = 0.6 respectively. In addition, we can see that the users quickly reach their dedicated channels using TS and a slow one under UCB1 and e-greedy.

Fig. 7 compares the regret of APL and DMC for the dynamic access where the dotted line indicates the entering and leaving of users on the network. Figures (6a) and (6b) represent respectively the cumulative and average regrets of APL, where at each entering or leaving of users, a significant increase in the regret is observed. It is worth mentioning that, in the dynamic scenario and based on APL, the user can change its current channel for two reasons:

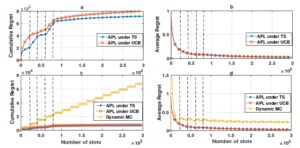
Figure 7: APL and DMC for dynamic access

1. When a collision occurs, SU_k should generate a random rank from the set {1, …, k}.
2. When a PU reappears in the network and accesses the current channel used by SU_k, the index of this channel decreases, and it may be overwhelmed by another channel that has a low index.

To the best of our knowledge, two policies exist in the literature that consider the dynamic access but without considering priority access: DMC [26] and MEGA [27]. The authors of [26] show that the DMC achieves better performance compared to MEGA policy. In Figures (6c) and (6d), we can see that the performance of APL outperforms the one of DMC and achieves a lower regret. However, after the dynamic access interval, our algorithm achieves a logarithmic regret although the regret of DMC keeps growing with time. Thus, the access under DMC algorithm is realized in epochs, where each one is composed of a learning phase with enough rounds of random exploration to learn the U best channels and the number of users under the dynamic access. The length of an epoch and the learning phase are T₁ and T₀ respectively. These two parameters depend on the number of channels C and the total number of slots n.

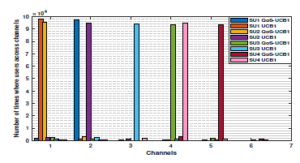
Figure 8: Access channels by priority users using APL

Let us start with the last scenario in which users are able to learn both channels’ vacancy and quality using our APL policy where the empirical mean of the quality collected from channels as follows: G = [0.7 0.9 0.2 0.8 0.8 0.7 0.7 0.8 0.8]. Thus, the global mean reward that takes into consideration both quality and vacancy µ_Q is given by: µ_Q = [0.63 0.72 0.14 0.48 0.4 0.28 0.21 0.16 0.08].After estimating the channels’ availability and quality (i.e. µ_Q) and based on our APL policy with QoS-UCB1, the first priority user SU₁ should converge towards the channel that has the highest global mean, i.e. channel 2, while the target of SU₂, SU₃ and SU₄ should be respectively channels 1, 4 and 5. On the other hand, in the case of APL with UCB1, the target of the priority users SU₁, SU₂, SU₃, and SU₄ should be respectively the channels 1, 2, 3 and 4. This result can be confirmed in Fig. 8, where the priority users access their dedicated channels using APL with QoS-UCB1 or UCB1. Fig. 9 displays the achievable regret of APL with QoS-UCB1 and UCB1 in the multi-user case. Despite the fact that the two curves have a logarithmic asymptotic behavior, we notice an improvement regret of APL with QoS-UCB1 compared to UCB1.

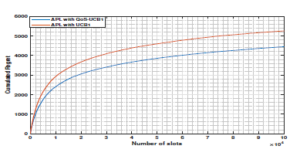
Figure 9: The regret of APL with QoS-UCB1 and UCB1

6. Conclusion

This paper deals with the Opportunistic Spectrum Access (OSA) problem in the context of Cognitive Radio (CR) for a single or multiple Secondary Users (SUs). Recently, several Multi-Armed Bandit (MAB) algorithms have been suggested to help a single SU make a good decision. To tackle the problem of OSA with several SUs, we proposed a novel policy for the priority access called All-Powerful Learning (APL) that allows several SUs to learn separately the channels’ vacancy without any cooperation or a prior knowledge about the available channels. Moreover, APL considers the priority dynamic access while only the priority or the dynamic access are separately considered in several recent works, such as Selective Learning of the k^th largest expected rewards (SLK), Musical

Chairs, Multi-user e-greedy collision Avoiding (MEGA) and kth − MAB. In our work, the Quality of Service (QoS) have been also investigated where SU is able to learn both quality and availability of channels and then make an optimal decision with respect to its prior rank. Like most important works in OSA, this work focuses on the Independent Identical Distributed (IID) model in which the state of each channel is supposed to be drawn from an IID process. In future work, we will consider the Markov process as a dynamic memory model to describe the state of available channels, although it is a more complex process compared to IID.

1. M. Marcus, C. Burtle, B. Franca, A. Lahjouji, N. McNeil, “Federal Com- munications Commission (FCC): Spectrum Policy Task Force,” in ET Docket no. 02-135, November 2002.
2. M. Almasri, A. Mansour, C. Moy, A. Assoum, C. Osswald, D. Lejeune, “All-Powerful Learning Algorithm for the Priority Access in Cognitive Network,” in EUSIPCO, A Corua, Spain, September 2019.
3. S. Haykin, “Brain-Empowered Wireless Communications,” IEEE Jour- nal on Selected Areas in Commun.
4. W. Thompson, “On the likelihood that one unknown probability ex- ceeds another in view of the evidence of two samples,” Biometrika, 25(3), 285–294, 1933.
5. T. Lai, H. Robbins, “Asymptotically efficient adaptive allocation rules,” Advances in Applied Mathematics, 6(1), 4–22, 1985.
6. C. Watkins, Learning from delayed rewards, Ph.D. thesis, University of Cambridge, 1989.
7. P. Auer, N. Cesa-Bianchi, Y. Freund, R. E. Schapire, “The nonstochastic multiarmed bandit problem,” SIAM journal on computing, 32(1), 48–77, 2002.
8. G. Burtini, J. Loeppky, R. Lawrence, “A survey of online experi- ment design with the stochastic multi-armed bandit,” arXiv preprint arXiv:1510.00757, 2015.
9. S. Scott, “A modern Bayesian look at the multi-armed bandit,” Applied Stochastic Models in Business and Industry, 26(6), 639–658, 2010.
10. O. Chapelle, L. Li, “An empirical evaluation of thompson sampling,” in Advances in neural information processing systems, Granada, Spain, December 2011.
11. S. Guha, K. Munagala, “Stochastic regret minimization via Thompson sampling,” in Conference on Learning Theory, 317–338, 2014.
12. T. Koca´k, M. Valko, R. Munos, S. Agrawal, “Spectral thompson sam- pling,” in Twenty-Eighth AAAI Conference on Artificial Intelligence, 2014.
13. I. Osband, D. Russo, B. V. Roy, “(More) efficient reinforcement learning via posterior sampling,” in Advances in Neural Information Processing Systems, 3003–3011, 2013.
14. S. Agrawal, N. Goyal, “Analysis of thompson sampling for the multi- armed bandit problem,” in conf. on Learning Theory, Edinburgh, Scot- land, June 2012.
15. E. Kaufmann, N. Korda, R. Munos, “Thompson sampling: An asymptot- ically optimal finite-time analysis,” in International conf. on Algorithmic Learning Theory, Lyon, France, October 2012.
16. S. Agrawal, N. Goyal, “Further optimal regret bounds for thompson sampling,” in Artificial intelligence and statistics, Scottsdale, USA, April 2013.
17. P. Auer, N. Cesa-Bianchi, P. Fischer, “Finite-time Analysis of the Multi- armed Bandit Problem,” Machine Learning, 47(2), 235–256, 2002.
18. E. Kaufmann, O. Cappe´, A. Garivier, “On Bayesian upper confidence bounds for bandit problems,” in Artificial intelligence and statistics, La Palma, Canary Islands, April 2012.
19. O. Maillard, R. Munos, G. Stoltz, “A finite-time analysis of multi-armed bandits problems with kullback-leibler divergences,” in Annual conf. On Learning Theory, Budapest, Hungary, July 2011.
20. A. Anandkumar, N. Michael, A. Tang, A. Swami, “Distributed Algo- rithms for Learning and Cognitive Medium Access with Logarithmic Regret,” IEEE Journal on Sel. Areas in Com., 29(4), 731–745, 2011.
21. M. Almasri, A. Mansour, C. Moy, A. Assoum, C. Osswald, D.Lejeune, “Distributed Algorithm to Learn OSA Channels Availability and En- hance the Transmission Rate of Secondary Users,” in ISCIT, HoChiMinh, Vietnam, September 2019.
22. M. Almasri, A. Mansour, C. Moy, A. Assoum, C. Osswald, D. Lejeune, “Distributed algorithm under cooperative or competitive priority users in cognitive networks,” EURASIP Journal on Wireless Communications and Networking, 2020(1), 1–31, 2020.
23. N. Modi, P. Mary, C. Moy, “QoS driven Channel Selection Algorithm for Cognitive Radio Network: Multi-User Multi-armed Bandit Approach,” IEEE Trans. on Cog. Com. & Networking, 3(1), 1–6, 2017.
24. Y. Gai, B. Krishnamachari, “Decentralized Online Learning Algorithms for Opportunistic Spectrum Access,” in GLOBECOM, Texas, USA, De- cember 2011.
25. N. Torabi, K. Rostamzadeh, V. C. Leung, “Rank-optimal channel selec- tion strategy in cognitive networks,” in GLOBECOM, California, USA, December 2012.
26. J. Rosenski, O. Shamir, L. Szlak, “Multi-player bandits-a musical chairs approach,” in ICML, New York, USA, June 2016.
27. O. Avner, S. Mannor, “Concurrent bandit and cognitive radio networks,” in European Conf. on Machine Learning and Principles and Practice of Knowledge Discovery in Databases, Nancy, France, September 2014.
28. K. Liu, Q. Zhao, B. Krishnamachari, “Decentralized multi-armed bandit with imperfect observations,” in 2010 48th Annual Allerton Conference on Communication, Control, and Computing, Monticello, USA, October 2010.
29. Y. Gai, B. Krishnamachari, “Decentralized Online Learning Algorithms for Opportunistic Spectrum Access,” in GLOBECOM, Texas, USA, De- cember 2011.
30. M. Almasri, A. Mansour, C. Moy, A. Assoum, C. Osswald, D. Lejeune, “Distributed Algorithm under Cooperative or Competitive Users with Priority Access in Cognitive Networks,” EURASIP journal on wireless communications and networking, (Accepted).

(Click Here)

(Click Here)