1. Introduction

Modern industrial systems are affected usually by various event of faults such as, loss of actuator effectiveness, failures or offsets of actuators/sensors, deviations of output measurement, etc. Indeed, the presence of fault causes an unacceptable performances of design controllers, thus deteriorating the overall system execution, and so leading to wrong dangerous situations.

Thus, it is important to encourage the development of research on fault tolerant control (FTC), which is divided on two types. The first one, the so-called passive FTC, is focused on to conceive a robust controller against disturbances and uncertainties. A key limitation is that the system stability cant be guaranteed in the presence of faults.

Nevertheless, based on online fault estimation (FE), such as the size and the shape, active FTC can develop robust controller such that the fault effects are eliminated and the system stability is achieved. In the literature, several research results on the FTC techniques are documented, see for example [1–9], and the references therein.

In industrial processes, most of systems are described by nonlinear mathematical models. Takagi-Sugeno (TS) fuzzy systems [10] provide a powerful tool to approximate nonlinear characteristics. T-S fuzzy systems are nonlinear models represented by a set of local linear models. By fuzzy blending of linear representations with appropriate membership functions, the overall fuzzy model of the system is achieved, which greatly simplifies the analysis and control for complex nonlinear systems. Therefore, excellent results in FE and FTC problems of T-S fuzzy systems are developed in [11–17]. In [18], a FTC is designed for TS fuzzy systems subject to actuator faults. However, this result must verify the rank condition, which is really hard to fulfill for many practical systems. In [19], the problem of FE and FTC for a T-S fuzzy systems with uncertainties and actuator faults is investigated without the requirement of rank condition. It deals only with constant faults, however, the faults are time-varying in many real systems. In [20], a sliding mode observer (SMO) is designed to estimate sensor fault for nonlinear stochastic systems for FTC. However, the actuator fault is not considered. In [21], a FTC is developed for T-S fuzzy systems affected by actuator faults. Since in many practical systems, actuator and sensor faults may occur at the same time and uncertainties may exist. It is desirable to consider actuator and sensor faults under one unified framework. For example, in [22], a SMO-based FE and FTC is designed for a class of nonlinear systems subject to actuator and sensor faults. A major disadvantage of this approach is the appearance of chattering mode. In [23], FE and FTC problems are studied to simultaneously estimate sensor and actuator faults using two observers and filter. However, this method is more expensive since it requires a high additional computation cost. In [24], a robust adaptive observer is developed to simultaneously estimate state and both sensor and actuator faults for nonlinear systems despite the presence of disturbances. A FTC law is applied to stabilize the closed-loop system and compensate the fault effects. However, sufficient conditions of observer and controller gains are formulated in an unified optimization problem and computed by solving a set of LMIs only in single step. Unfortunately, these results need the knowledge of the upper bounds of faults. If the information of fault is unknown, the SMO cannot be obtained.

The aim of this work is to address fault estimation and fault tolerant control problems for T-S fuzzy systems subject to simultaneously actuator faults, sensor faults and uncertainties. First, a novel robust adaptive SMO is proposed to estimate the states and both actuator and sensor faults using equivalent output error injection approach. Then, based on online fault information a static outputfeedback fault-tolerant control (SOFFTC) is designed to compensate the fault effects and stabilize the closed-loop system. All the design conditions are formulated in an optimization problem under LMIs constraints. Finally, the simulation result of an inverted pendulum with cart system is given to prove the effectiveness of the proposed method.

The main contributions of the present work are the following:

1. A novel fuzzy adaptive SMO is designed for the estimation of states and faults in a T-S fuzzy systems affected by simultaneously actuator faults, sensor faults and uncertainties. Robustness against uncertainties is analyzed using the H_∞ technique to reduce its effect.
2. Most existing SMO design methods such as those reported in [22–24] assume that the value of the upper bounds of actuator faults ρ_a and sensor faults ρ_s is known. If the information of fault is unknown or exceeds the admissible value, these methods cannot be feasible. To overcome this problem, a new adaptive law is constructed to estimate the upper bounds online.
3. The problem of both actuator and sensor FE under one unified framework for T-S fuzzy systems is investigated. Whereas, many researchers have considered only sensor faults [25–27] or actuator faults [28,29].
4. Basedon the FE, a SOFFTC is designed to effectively accommodate the influence of fault and ensure the stability of the resulting closed-loop system. The proposed method is easily be implemented in practice and is much simpler than dynamic output feedback fault tolerant controller.
5. Sufficient conditions of the observer and controller are formulated in an optimization problem under LMIs constraints which can be designed separately.

The rest of this paper is organized as follows: Section 2 presents the problem formulation and preliminaries. The design of the observer and the analysis of the stability of the error dynamics are given in Section 3. FE is studied in Section 4. Section 5 gives the SOFFTC scheme. Finally, simulation example in Section 6 validates the efficiency of the proposed algorithm.

2. Problem Formulation and Preliminaries

Consider a TS fuzzy model with actuator faults, sensor faults and uncertainties. The ith rule of the T-S fuzzy model is of the following form:

Plant Rule i: If ξ₁(t) is µ_1,i and … ξ_g(t) is µ_g,i, Then

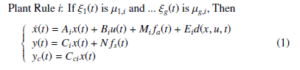
where x(t) ∈ Rⁿ represents the state vector; u(t) ∈ R^m is the input; y(t) ∈ R^p is the output; y_c(t) ∈ R^p1 is the controlled output; A_i, B_i, M_i, E_i, C_i, N and C_ci are real known constant matrices with appropriate dimensions; f_a(t) : R⁺ → R^q and f_s(t) : R⁺ → R^h represent additive actuator fault and sensor fault vector, respectively; d(x,u,t) ∈ R^l models the uncertainties, which is assumed to belong to L₂ [0, ∞); the pairs (A_i,C_i) are observable, and the pairs (A_i, B_i) are controllable; ξ_j(j = 1,…,g) are the premise variables, and µ_j,i(j = 1,…,g;i = 1,…,k) are fuzzy sets; g and k are the number of premise variables and IF-THEN rules, respectively. The fuzzy model is given by:

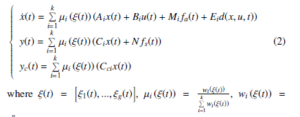
• θ_ij µ_j(t) and here θ_ij(.) stands for the order of the membership

function of θ_ij. It is assumed that

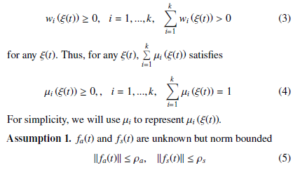
where ρ_a and ρ_s are unknown positive scalars.

Assumption 2 [30]. The actuator fault distribution matrices M_i in (2) satisfy:

Lemma 3 [33]. Under Assumption 2, there exists coordinate trans where A_11,i ∈ Rq×q, A_22,i ∈ R(n−q)×(n−q), B_1,i ∈ Rq×m, M_1,i ∈ Rq×q, E_1,i ∈ Rq×l, N₂ ∈ R(p−q)×h, C_11,i ∈ Rq×q and C_22,i ∈ R(p−q)×(p−q) is invertible, i = 1,…,k.

Through coordinate transformations, the system (2) is converted into the following two subsystems:

where S ₁₁,_i ∈ R^(p−q)×p and S ₂₂,_i ∈ R^q×p. The variable z₁(t) can be obtained by:

Lemma 4 [33]. The pair (A_0,i,C_0,i) is observable, if the pair (A_22,i,C_22,i) is detectable, i = 1,…,k. Then, there exists matrices L_i,

h     i having the special structure L_i =     L_1,i                 0              , such that A_22,i+L_iC_22,i is stable, i = 1,…,k.

Let   the          transformation     of            coordinates           h(t)          = ^h h^T1 (t)               h^T₂ (t) ^iT = T_L,_iz₀(t) with

Therefore, T-S fuzzy subsystems (12) and (13) can be rewritten respectively as:

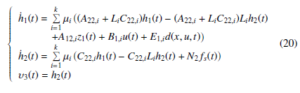
For system (19), we construct the following adaptive SMO:

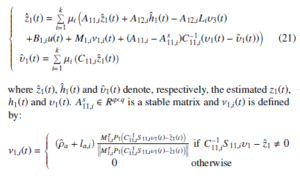
where zˆ₁(t), hˆ₁(t) and υˆ₁(t) denote, respectively, the estimated z₁(t), h₁(t) and _,i ∈ R^q×q is a stable matrix and ν_1,i(t) is defined

where P₁ ∈ R^q×q > 0 is the Lyapunov matrix for A₁₁^s _,i, ρˆ_a is adaptive parameter to estimate the unknown parameter ρ_a, and the scalar ρˆ_a is introduced using an update law with constant σ₁ > 0.

For system (20), we design the following adaptive SMO:

where P₀₂ ∈ R^{(p−q)×(p−q)} > 0, ρˆ_s is adaptive parameter to estimate the unknown parameter ρ_s, and the scalar ρˆ_s is introduced using an update law ρ˙ˆs = σ2    N2T P02 (υ3(t) − υˆ3(t))    (24) with constant σ₂ > 0.

Let us define e₁(t) = z₁(t) − zˆ₁(t), e₂(t) = h₁(t) − hˆ₁(t) and e₃(t) = h₂(t) − hˆ₂(t), then the error dynamic system as follows:

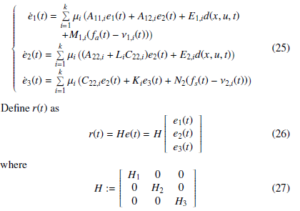
with H1 ∈ Rq×q, H2 ∈ R(n−q)×(n−q) and H3 ∈ R(p−q)×(p−q). The adaptive SMO design method under H_∞ performance to be addressed in this work is

• The observer error dynamics system (25) with d(x,u,t) = 0 is asymptotically stable, namely, there is no uncertainty;
• For a given γ₁ > 0. The following H_∞ performance is satisfied:

for all T > 0 and d(x,u,t) ∈ L₂ ^h 0             ^∞  under zero initial conditions.

3.1     Stability analysis

Theorem 1. Consider T-S fuzzy system (2) under Assumptions 13. The observer error dynamics system (25) is asymptotically stable and satisfy (28) with attenuation level γ₁ > 0, if there exist matrices P₁ > 0, P₀₁ > 0, P₀₂ > 0, X_i, Y_i, i = 1,…,k, such that:

Minimize γ₁ subject to

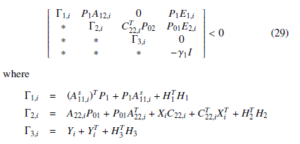
If the optimization problem is solved, then we can obtain the following observer gains

Proof. Let the following Lyapunov functional candidate:

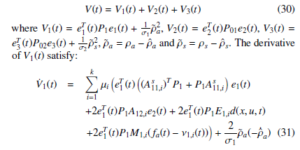
Using the definition of ν_1,i(t) and the bound of f_a(t), we have e^T₁ (t)P₁M_1,i(fa(t) − ν₁,_i(t)) + σ 1₁ ρ˜_a(−ρˆ˙_a)

When d(x,u,t) = 0, we have

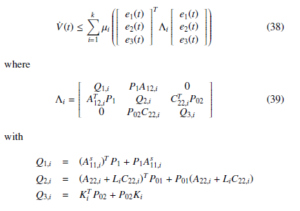
If Λ_i < 0, then V˙ (t) < 0, which implies that e → 0 as t → ∞.

Therefore, the error dynamics system is asymptotically stable.

When d(x,u,t) , 0, we define

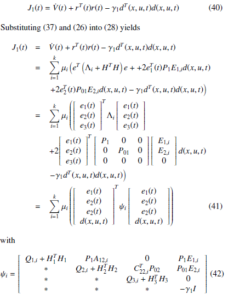
The previous inequalities are nonlinear because of P₀₁L_i and P₀₂K_i. This problem can be solved using the variable change X_i = P₀₁L_i and Y_i = P₀₂K_i. Applying the Schur complement, we can obtain the LMI form (29). So if J₁(t) < 0, the error dynamics system (25) is stable satisfying the H_∞ performance (28). .

3.2     Sliding motion analysis

For system (25), Let

Theorem 2. Consider system (2) satisfying Assumptions 13. The system error dynamics (25) can be driven to the sliding surface S in finite time and remain on it if the LMI (29) is solvable and the gains

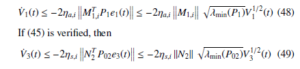
Then the reachability condition [34] is verified.

4. Fault Estimation

From Theorem 2, an ideal sliding mode take place on S and e˙₁(t) = e₁(t) = 0. Consequently, the error dynamics of e₁(t) becomes:

where ν_1eq(t) denotes the equivalent term [34] replaced by:

where β1 =    M1−1A12   maxσmax(H−1) and β2 =    M1−1E1   max. Thus for a small      γ₁β₁ + β₂, f_a(t) can be estimated as:

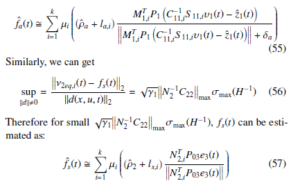
5. Fault Tolerant Controller Design

Define corrected output as:

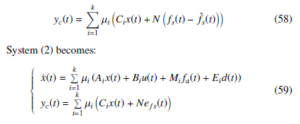
where e_fs(t) = f_s(t) − ^fˆ_s(t).

A SOFFTC law [35] is designed as follows:

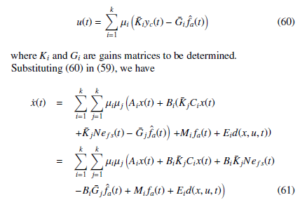
The gain G_i is designed so that B_iG_i = M_i where B⁺_i is the pseudo inverse of B_i [36]. It follows that

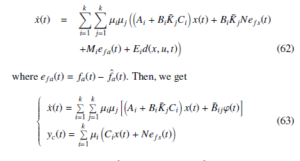
^h e^Tf s(t) e^T_fa(t) d^T(x,u,t) ⁱ . The control purpose in this paper for the closed-loop fuzzy system (63) is to design a SOFFTC (60) such that

• The closed-loop fuzzy system (63) with (ϕ(t) = 0) is asymptotically stable .
• For a given scalar γ₂ > 0, the following H_∞ performance is satisfied:

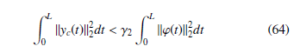
for all L > 0 and ϕ(t) ∈ L₂ [0, ∞) under zero initial conditions.

Theorem 3. The closed-loop system (63) is asymptotically stable and satisfy the H_∞ performance index (64), if there exist matrix P¯_x > 0, matrices R, S¯ _i and scalar  > 0, such that:

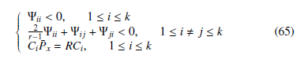
where

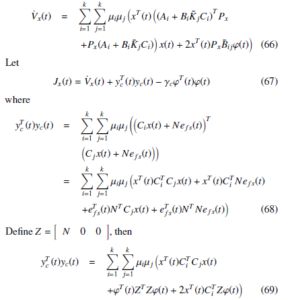
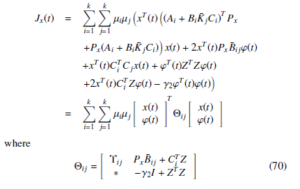
with Υij = (Ai + BiK¯ jCi)T Px + Px(Ai + BiK¯ jCi) + CiTCj. Thus, J_x(t) < 0, if

where Υ¯ _ij = (A_i + B_iK¯ _jC_i)^T P_x + P_x(A_i + B_iK¯ _jC_i). Premultiplying and postmultiplying by Π = diagnP⁻_x¹, P⁻_x¹, I, I, I^o

Notice that the matrix inequality Ω_ij < 0 is a Bilinear Matrix Inequalities (BMIs). Denoting C_iP¯_x = RC_i and K¯ _jR = S¯ _j, so that

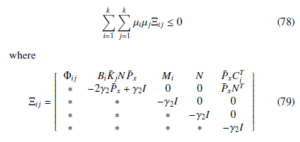
with

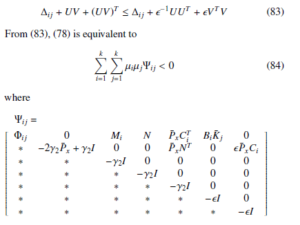
If (84) is verified, we have J_x(t) < 0, which can guarantee the closed-loop system is asymptotically stable.

6. Simulation Example

In this example, The inverted pendulum with cart system [37] is considered:

where x₁(t) and x₂(t) are the angular position and velocity, respectively; x₃(t) and x₄(t) are the cart position and velocity, respectively; m is the pendulum mass, M is the cart mass, g is the gravity constant, and a = 1/(m + M) . The values of the parameters used in this simulation are m = 0.2kg, M = 0.8kg, l = 0.5m, and L = 2m .

Then, we get the TS fuzzy system with the following fuzzy rules:

Rule1: If x₁(t) is about 0, Then

( x˙(t) = A₁x(t) + B₁(u(t) + f_a(t)) + E₁d(t) y(t) = C₁x(t) + N f_s(t)

Rule1: If x₁(t) is about ± , Then

we set d(x,u,t) = − f_c + m l x₂² (t) sin(x₁ (t)) where f_c = ρ sign(x₄ (t)) with ρ = 0.05 . The membership functions for rules 1 and 2 are chosen based on the method of sector nonlinearity [38] as follows:

By Choosing H₁ = 1, H₂ = I₃ and H₃ = I₂, we can solve the optimization problem of Theorem 1 using Matlab LMI Toolbox and we obtain γ₁ = 0.3614, A₁₁^s _,1 = −3.2457, A₁₁^s _,2 = −3.2457,

Solving the optimization problem in Theorem 3 results the following controller gain matrices for a minimum attenuation level γ₂ = 1.6128:

                  K¯₁ = ^h −2.7838     −6.8067      −11.1030 ⁱ

                   K¯₂ = ^h −2.1520     −7.5055      −11.8265 ⁱ

We simulate the closed-loop system be choosing σ₁ = 10, σ₂ = 15, δ₁ = 0.01, δ₂ = 0.02, l_a,1 = l_a,2 = 10 and l_s,1 = l_s,2 = 12, initial conditions x₁₀ = π/20, x₂₀ = 0, x₃₀ = 2 and x₄₀ = 0. f_a(t) and f_s(t) are assumed that, respectively

The simulation results of this example are given in Figures 1-5. Figures 1 and 2 show that the proposed adaptive SMO can estimate the actuator and sensor faults simultaneously despite the presence of uncertainties.

Actuator fault estimation

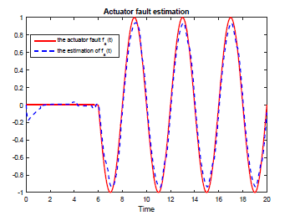
Figure 1: The actuator fault f_a(t) and its estimation.

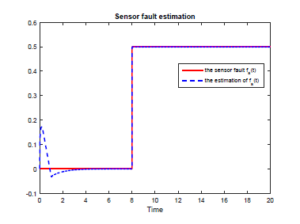
Figure 2: The sensor fault f_s(t) and its estimation.

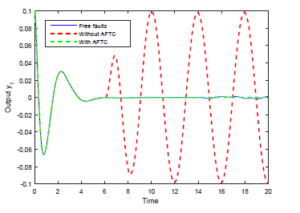
Figure 3: Output y₁(t) under the static output feedback FTC.

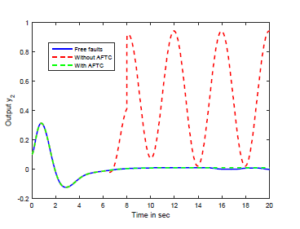
Figure 4: Output y₂(t) under the static output feedback FTC.

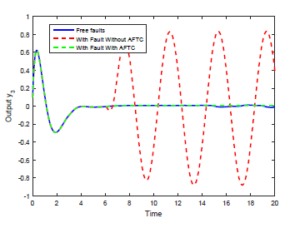
Figure 5: Output y₃(t) under the static output feedback FTC.

Simulation results for the systems outputs response are illustrated in Figures 3-5. It is clear to see that the outputs without SOFFTC do not converge to the outputs of the fault-free model (i.e. without any fault). However, the outputs’s trajectories of the system 7 with SOFFTC reach the outputs of nominal model.

Conclusion

In this paper, we have considered the problems of FE and FTC for T-S fuzzy systems with uncertainties, actuator and sensor faults, simultaneously. Using the H_∞ optimization technique, an adaptive fuzzy sliding mode observer has been firstly designed to estimate the system state, actuator and sensor faults, simultaneously. Secondly, using the information of online fault estimates, a novel SOFFTC has been developed to compensate the faults and stabilize the closedloop system. Thus, sufficient condition for the existence of the proposed ASMO and SOFFTC has been formulated in terms of LMIs. Finally, a simulation example was used to show the effectiveness of the proposed methods.

1. S. Ding, “Integrated design of feedback controllers and fault detectors” Annual Reviews in Control, 33(3), 124–135, 2009. https://doi.org/10.1016/j.arcontrol.2009.08.003
2. R. Isermann, Fault-Diagnosis Applications : Model-Based Bondition Mon- itoring : Actuators, Drives, Machinery, Plants, Sensors, and Fault- Tolerant Systems, Springer Science and Business Media, 2011.
3. H. Alwi, C. Edwards, C. Tan, Fault Detection and Fault-Tolerant Control Using Sliding Modes, Springer Science and Business Media, 2011.
4. S. Dhahri, A. Sellami, F. Ben Hmida, “Robust H∞ sliding mode observer design for fault estimation in a class of uncertain nonlinear systems with LMI opti- mization approach” International Journal of Control, Automation and Systems, 10(5), 1032-1041, 2012. https://doi.org/10.1007/s12555-012-0521-3
5. M. S. Shaker, R. J. Patton, “Active fault tolerant control for nonlin- ear systems with simultaneous actuator and sensor faults” International Journal of Control Automation and Systems, 11 (6), 1149–1161, 2013. https://doi.org/10.1007/s12555-013-0227-1
6. Z. Gao, C. Cecati, S. Ding, “A survey of fault diagnosis and fault tolerant techniques-part i : fault diagnosis with model-based and signal-based ap- proaches” IEEE Transactions on Industrial Electronics, 62 (6), 3757-3767, 2015. https://doi.org/10.1109/TIE.2015.2417501
7. J. Wang, “H fault-tolerant controller design for networked control systems with time-varying actuator faults” International Journal of Innovative Comput- ing, Information and control, 11(4), 1471-1481, 2015.
8. H. Azmi, M. J. Khosrowjerdi, “Robust adaptive fault tolerant control for a class of lipschitz nonlinear systems with actuator failure and distur- bances” Journal of Systems and Control Engineering, 230(1), 13-22, 2015. https://doi.org/10.1177/0959651815606628
9. Y. Tian, F. Zhu, “Fault estimation and observer based fault-tolerant controller in finite frequency domain” Transactions of the Institute of Measurement and Control, 40(5), 1659–1668, 2017. https://doi.org/10.1177/0142331216688617
10. T. Takagi, M. Sugeno, “Fuzzy identification of systems and its applications to modeling and control” IEEE Transactions on Systems, Man and Cybernetics, 15(1), 116-132, 1985. https://doi.org/10.1109/TSMC.1985.6313399
11. K. Zhang, B. Jiang, P. Shi, “Fault estimation observer design for discrete time TakagiSugeno fuzzy systems based on piecewise Lya- punov functions” IEEE Trans. Fuzzy Syst, 20(1), 192200, 2012. https://doi.org/10.1109/TFUZZ.2011.2168961
12. Q. Jia, W. Chen, Y. Jin, Y. Zhang, H. Li, “A New Strategy for Fault Estimation in TakagiSugeno Fuzzy Systems via a Fuzzy Learn- ing Observer” in Proceeding of the 11th World Congress on Intelligent Control and Automation (WCICA), Shenyang, China, 3228-3233, 2014. https://doi.org/10.1109/WCICA.2014.7053248
13. C. Sun, F. Wang, X.Q. He, “Robust fault estimation for a class of TS fuzzy singular systems with time-varying delay via improved delay partitioning approach” J. Control Sci. Eng., 2016, 2016. https://doi.org/10.1155/2016 1.
14. D. Ding, X. Du, X. Xie, M. Li, “Fault estimation filter design for discretetime TakagiSugeno fuzzy systems” IET Control Theory Appl., 10(18), 2456-2465, 2016. https://doi.org/10.1049/iet-cta.2016.0318
15. F. You, S. Cheng, K. Tian, X. Zhang, “Robust fault estimation based on learning observer for TakagiSugeno fuzzy systems with interval timevary- ing delay” Int. J. Adapt. Control Signal Process., 34(1), 92–109, 2020. https://doi.org/10.1002/acs.3070
16. S. Liu, X. Li, H. Wang, J. Yan, “Adaptive fault estimation for T-S fuzzy systems with unmeasurable premise variables” Advances in Difference Equations 2018, 105(2018), 2018. https://doi.org/10.1186/s13662-018-1571-5
17. Z. Gao, X. Shi, S.X. Ding, “Fuzzy state/disturbance observer de- sign for TS fuzzy systems with application to sensor fault esti- mation” IEEE Transactions on Cybernetics, 38(3), 875–880, 2018. https://doi.org/10.1109/TSMCB.2008.917185
18. Q. K. Shen, B. Jiang, V. Cocquempot, “Fault tolerant control for TS fuzzy systems with application to nearspace hypersonic vehicle with actuator faults” IEEE Trans. Fuzzy Syst., 20(4), 652665, 2012. https://doi.org/10.1109/TFUZZ.2011.2181181
19. X. H. Li, F. L. Zhu, A. Chakrabarty, “Nonfragile fault tolerant fuzzy observer- based controller design for nonlinear systems” IEEE Trans. Fuzzy Syst., 24(6), 16791689, 2016. https://doi.org/10.1109/TFUZZ.2016.2540070
20. M. Liu, X. B Cao, and P. Shi, “Fault Estimation and Tolerant Control Fuzzy Stochastic Systems” IEEE Trans. Fuzzy Syst., 21(2), 221229, 2013.
21. A. Navarbaf, M. J. Khosrowjerdi, “Fault-tolerant controller design with fault estimation capability for a class of nonlinear systems using generalized Takagi- Sugeno fuzzy model” Transactions of the Institute of Measurement and Control, 41(15), 42184229, 2019. https://doi.org/10.1177/0142331219853687
22. M. Liu, X. Cao, P. Shi, “Fuzzy-model-based fault-tolerant design for nonlinear stochastic systems against simultaneous sensor and actuator faults” IEEE Trans. Fuzzy Syst., 21(5), 789799, 2013. https://doi.org/10.1109/TFUZZ.2012.2224872
23. M. Sami, R. J. Patton, “Active fault tolerant control for nonlinear systems with simultaneous actuator and sensor faults” Int. J. Control Autom. Syst., 11(6), 11491161, 2013. https://doi.org/10.1007/s12555-013-0227-1
24. S. Makni, M. Bouattour, A.E. Hajjaji, M. Chaabane, “Robust fault toler- ant control based on adaptive observer for Takagi-Sugeno fuzzy systems with sensor and actuator faults: Application to single-link manipulator” Transactions of the Institute of Measurement and Control, 2020, 2020. doi.org/10.1177/0142331220909996.
25. P. Aboutalebi, A. Abbaspour, P. Forouzannezhad, A. Sargolzaei, “A novel sensor fault detection in an unmanned quadrotor based on adaptive neural observer” Journal of Intelligent and Robotic Systems, 90, 473484, 2018. https://doi.org/10.1007/s10846-017-0690-7
26. H. Li, Y. Gao, P. Shi, H. K. Lam, “Observer-based fault detection for nonlinear systems with sensor fault and limited communication capac- ity” IEEE Transactions on Automatic Control, 61(9), 27452751, 2016. https://doi.org/10.1109/TAC.2015.2503566
27. A. Valibeygi, A. Toudeshki, K. Vijayaraghavan, “ Observer based sensor fault estimation in nonlinear systems” Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 230(8), 759777, 2016. https://doi.org/10.1177/0959651816654070
28. M. Buciakowski, M. Witczak M, V. Puig, et al., “A bounded-error ap- proach to simultaneous state and actuator fault estimation for a class of nonlinear systems” Journal of Process Control, 52, 1425, 2017. https://doi.org/10.1016/j.jprocont.2017.01.002
29. M. Bataghva, M. Hashemi, “Adaptive sliding mode synchronisation for fractional-order non-linear systems in the presence of time-varying actuator faults” IET Control Theory Appl., 12(3), 37783, 2018. https://doi.org/10.1049/iet-cta.2017.0458
30. H. Schulte, E. Gauterin, “Fault-tolerant control of wind turbines with hydrostatic transmission using TakagiSugeno and sliding mode techniques” Annual Reviews in Control, 40, 8292, 2015. https://doi.org/10.1016/j.arcontrol.2015.08.003
31. H. Moodi, M. Farrokhi, “On observer-based controller design for sugeno sys- tems with unmeasurable premise variables” ISA Transactions, 53(2), 305316, 2014. https://doi.org/10.1016/j.isatra.2013.12.004
32. T. Dang, W. Wang, L. Luoh, C. Sun, “Adaptive observer design for the uncer- tain takagisugeno fuzzy system with output disturbance” IET Control Theory Applications, 6(10), 13511366, 2011. https://doi.org/10.1049/iet-cta.2011.0022
33. M. Corless, J. Tu, “State and input estimation for a class of uncertain systems” Automatica, 34(6), 757764, 1998. https://doi.org/10.1016/S0005- 1098(98)00013-2
34. V.I. Utkin, Sliding modes in control optimization, Springer, Berlin, 1992.
35. K. Tanaka, H. Wang, Fuzzy control systems design and analysis: a linear matrix inequality approach, Wiley, New York, USA, 2001.
36. Z. Gao, P. J. Antsaklis, “Stability of the pseudo inverse method for reconfigurable control systems” Int. J. of Control, 53, 717–729, 1991. https://doi.org/10.1080/00207179108953643
37. K. Ogata, Modern control engineering, 3rd ed. Englewood Cliffs, NJ: Prentice- Hall, 1997.
38. M. C. M. Teixeira, S. H. Zak, “Stabilizing controller design for uncertain nonlinear systems using fuzzy models” IEEE Transaction on Fuzzy Systems, 7(2), 133–142, 1999. https://doi.org/10.1109

(Click Here)

(Click Here)