1. Introduction

In industry and transportation, the resistance furnace is a very commonly device. Its temperature control has the characteristics of the one-direction temperature rise, large inertia, time delay and time-varying parameters. In the temperature control system, it is difficult to establish accurate models and determine parameters by mathematical methods, especially when it is disturbed.

The traditional control methods based on the exact object mathematical model, such as feedback control, PID control [1-3] can meet the system performance requirements, and has the advantage of eliminating the steady-state error, but its performance depends on the tuning of the parameters.

Fuzzy logic controller (FLC) has the advantage of inaccurate object model, rapidity and small overshoot, but the control process will have steady-state error. The research works [4-7] used only fuzzy logic for controlling temperature of the resistance furnace and achieved limited results. The quality of the temperature fuzzy logic control system depends on expert experiment and FLC’s parameters These works only stopped at the computer simulation, did not solve the effects of disturbance.

The research works [8-16] were combined the advantages of the PID controller with fuzzy logic to design the intelligent controller for the resistance furnace. However, all most of them are still stopped in simulation on computer, but have not given the hardware control board with the intelligent control algorithm on microprocessor.

The research work [17] introduced the fuzzy PID based on genetic algorithm for the resistance furnace. This work [17] indicated that the temperature control system dynamic quality and stable precision is improved, but has not been conducted experimentally on physical equipment and has not assessed the impact of disturbance.

      This paper presents a novel fuzzy-PID controller combined with PSO algorithm to control temperature of the resistance furnace with disturbance: from theory to practical experiments. The fuzzy-PID is designed based on the combination of PID control and fuzzy logic control, in which the basic parameters of PID are calculated by fuzzy logic control, and the parameters of fuzzy-PID are determined by multiplying the basic parameters of PID with the scaling weights. These multiplied scaling weights of the fuzzy-PID controller are calculated based on PSO algorithm, so that the dynamic response of the control system is better and the steady-state error is eliminated. The part 2 of the paper presents the resistance furnace identification, determining the PID basic parameters. In part 3, a new PSO-based fuzzy-PID controller is given, here PSO algorithm is used to optimized the scaling weights of the fuzzy-PID controller. And then the simulation model of the resistance furnace temperature control system is built on Matlab in part 4 in order to verify the feasibility of the proposed PSO-based fuzzy-PID controller. Then, the design of the temperature control board using PIC16f microcontroller with PSO-based fuzzy-PID algorithms is introduced in part 5. Finally, part 6 is conclusions. The simulation and experimental results show that the proposed PSO-based fuzzy-PID controller improve the resistance furnace temperature control system quality.

2. The resistance furnace mathematical model by identification method

The resistance furnace, the studied object in this paper, has dimensions L375xW255xH345mm. The furnace uses resistance wire, powered by 220VAC/50Hz, maximum power of 1000W, maximum temperature of 100^oC. In this system, a 2-wire K-type thermocouple sensor with the setting temperature range 0-100^oC corresponding to the electrical signal 0-5VDC is adopted. Controlling the AC power supply capacity for the thermistor wire changes the furnace temperature here, the authors use the TRIAC BTA10-800B 10A 600V [18].

For resistance furnace identification, the control board here only plays the role of opening 100% the TRIAC to supply 220VAC power to the resistance wire. When the TRIAC was active with 100% capacity of the resistance furnace, at the time of measurement the authors realized that the furnace temperature was not changed immediately, it took a certain amount of time to convert electricity into heat energy, heat transfer in the furnace – delay time of the furnace. The temperature in the furnace will gradually increase to the maximum value, corresponding to the maximum power of the furnace.

Figure 1. The resistance furnace identification process

Based on this experimental method, the resistance furnace mathematical model can be identified. The identification process was carried out at the ambient temperature about 27.8^oC. The measured steady temperature was about 91.4^oC. The time to reach the steady output temperature of the furnace was about 30 minutes.

Table 1. The experimental temperature values of the furnace

No.	Time [minute]	Temperature [oC]	Note
1	1	27.8	ambient temperature
2	2	29.1
3	3	30.5
4	4	32.0
5	5	33.5
6	6	35.9
7	7	38.5
8	8	41.3
9	9	44.7
10	10	47.8
11	11	51.2
12	12	54.9
13	13	58.2
14	14	61.6
15	15	65.0
16	16	68.2
17	17	71.1
18	18	74.2
19	19	76.8
20	20	79.4
21	21	81.7
22	22	84.0
23	23	86.0
24	24	87.7
25	25	88.9
26	26	89.9
27	27	90.5
28	28	91.0
29	29	91.4
30	30	91.4

The measured temperature curve of the resistance furnace as shown in Fig.2.

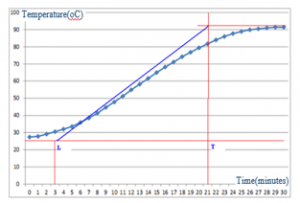
Figure 2. Measured furnace temperature curve

The measured furnace temperature curve has the S-shape, so the furnace mathematical model is describled as below [1]:

where L is the time delay, period time that the output signal does not respond immediately; K is the transfer coefficient, is the limit output value as t®∞; T is the inertial time.

Based on the furnace temperature characteristic curve, the authors draw the tangent line with the inflection point of this curve, the parameters of the furnace as follows:

3.  Design of PSO-based Fuzzy-PID controller

3.1.  Proposed PSO-based Fuzzy-PID controller

To improve the performance efficiency of the fuzzy-PID controller for the resistance furnace, this work proposed a novel control approach applying the PSO algorithm to tune the scaling weights of the fuzzy-PID controller. The structure diagram describing the incorporate between the fuzzy-PID controller and PSO algorithms is presented in Figure 3.

The fuzzy-PID controller is synthesized based on the structure of the PID with K_P, T_I and T_D parameters, determined according to the fuzzy logic calculated blocks P, I, D corresponding to defuzzied output values K_Pf or T_If or T_Df  and then multiply with the corresponding scaling weights, i.e. K_a, K_b, K_c, following formula as below:

The PSO algorithm is used to optimize three scaling weights, i.e. K_a ® K_a^*, K_b ® K_b^*, K_c® K_c^*. So that after applying the PSO algorithms, the parameters’ Fuzzy-PID is optimized as below:

For this proposed PSO-based fuzzy-PID controller, the parameters of the fuzzy-PID are continuously adjusted in a specified range. However, the scaling weights’ fuzzy-PID is optimized by PSO algorithm. Therefore, the furnace temperature control quality will be greatly improved

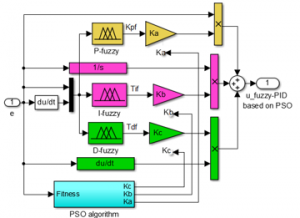
Figure 3. Structure diagram of a PSO-based Fuzzy-PID

3.2.  Design of the fuzzy logic calculated blocks

Each fuzzy logic calculated block has two inputs and one output: first input as temperature error (e=T_d^o-T^o), in which T_d^o– setpint temperature, T^o– measured temperature, and second input as temperature error derivation (de/dt), the output corresponding to P-fuzzy, I-fuzzy, D-fuzzy are the K_Pf, T_If, T_Df.

The P, I, D – fuzzy logic calculated blocks, corresponding to K_Pf, T_If, T_Df, are presented in Fig.4.

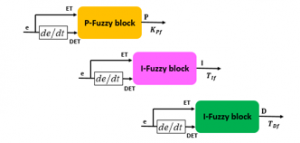
Figure 4. Structure diagram of the fuzzy calculated blocks

Two input fuzzy variables of each P-fuzzy, I-fuzzy, D-fuzzy are ET and DET, corresponding to e and de/dt. The output fuzzy variables of the P-fuzzy, I-fuzzy, D-fuzzy blocks are P, I, D, corresponding to parameters K_Pf, T_If, T_Df.

The physical value range of the input variables and the output variables are as follows: ETÎ[-20.0,20.0], DETÎ[-2.0,2.0], PÎ[0,20], IÎ[0,0.05], DÎ[0,2000]. For D-fuzzy calculated block,          ETÎ[-100.0,100.0], DETÎ[-10.0,10.0]

In these fuzzy blocks, membership functions are selected triangles, and setting the input variables by 5 fuzzy sets: ET= {HQ, HD, HI, HV, HL}; DET= {TA, TZ, TI, TV, TL}, and output variables are equal to 5 fuzzy sets, corresponding to the language variables P, I, D we have P= {VD, VG, VI, VV, VL}; I= {VD, VG, VI, VV, VL}; D= {VD, VG, VI, VV, VL}.

With the number of fuzzy sets of five inputs and two fuzzy inputs for each fuzzy calculated block K_Pf, T_If, T_Df,  so we have the total of 5 x 5 = 25 fuzzy rules for each fuzzy calculated block. Based on the resistance furnace specification and the principle of PID parameters adjustment, the authors built the fuzzy rules table for the fuzzy block of calculated K_Pf, T_If, T_Df,  as Table 2.

Table 2. Fuzzy rules of the P,I,D-fuzzy calculated blocks

P I D		ET
		HQ	HD	HI	HV	HL
DET	TA	VD	VD	VD	VD	VD
	TZ	VD	VG	VD	VD	VD
	TI	VD	VD	VI	VI	VV
	TV	VD	VD	VI	VV	VL
	TL	VD	VD	VV	VL	VL

These P-fuzzy, I-fuzzy, D-fuzzy calculated blocks in this study use Max-Min inferential law and defuzzification according to the centroid point method, the output clear values of the P-fuzzy, I-fuzzy, D-fuzzy calculated blocks, corresponding to K_Pf, T_If, T_Df,  are defined.

3.3.  Building the PSO algorithm

The particle swarm optimization is one of the best effective optimization techniques. Firstly, all particles are assigned initial position and velocity values. Based on optimal value of fitness function, new position and velocity of the particles are updated. There are two fitness value are required in the update process of particles, that are p_best (personal best) and g_best (global best). The p_best value is trace in every iteration of particles and g_best value is computed among the best solution in p_best value [19]. In the PSO algorithm, the velocity value and position values of particles are continuously updated by following formulas.

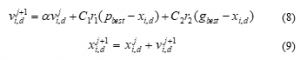
where – new updated velocity of i-particle in (j+1) iteration.  -the velocity of i-particle in j-iteration; – new updated position of i-particle in (j+1) iteration.  -last position of i-particle in j-iteration; C₁ and C₂ are the acceleration factors for updating the particle velocity; r₁ and r₂ are initially random positive values which should be less than one; a is the assigned inertial weight coefficient to maintain the particles last velocity while the accelerations factors drive the flow of particles towards optimum solutions.

It is easy to see that the particles position is mainly depended upon the update velocity, and this update velocity is handled by the acceleration factors and assigned inertial weight coefficient.  During the update process, the velocity and position of particles must satisfy the constraints, as shown below.

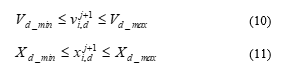
In this study, PSO algorithm is used to determine three the scaling weights of the Fuzzy-PID controller, i.e. K_a, K_b, K_c, And the fitness function can be selcted based on the combination of three goals, i.e. settling time – T_STL, quality index of integral of the absolute magnitude of the error – E_IAE, and peak overshoot – M_POT.

where are parameters to optimized. T denotes the simulation time. g₁, g₂, g₃ are the assigned weights, here g₁ = 1, g₂ =1, g₃ =0.5.

The search boundary for the scaling weights of the Fuzzy-PID controller is assigned as follows:

The PSO algorithm continuously varies the values of Fuzzy-PID controller parameters, following equation (6), until the objective function J is minimized to ?_min. The implementation of PSO algorithm involves the following steps:

Step 1. Initialize size of particles N=10, dimension search-space D=3 corresponding to K_a, K_b, K_c, maximum iteration M=30, inertial weight a=0.5, acceleration factors C₁=2, C₂=2,

Step2. Initialize two velocity and position values vectors, and then compute the initial fitness p_best values vector for each particle.

Step 3. Minimize g_best value from the p_best values vector, following the formulas (12), (13), (14).

Step 4. Update new velocity and position values into the velocity and position vectors of particles in step 3, following the formulas (8), (9).

Step 5. Compute the values of fitness p_best and then p_best for new update position if these fitness values are improved the replaced last values with these new values (less than the previous fitness values).

Step 6. Repeat the step 3, 4, 5 until the last iteration or the desired value of the fitness function is satisfied.

4. Simulating the furnace temperature control system using the proposed PSO-based Fuzzy-PID controller

4.1.  Modeling fuzzy-PID controller on Matlab

Based on Mamdani fuzzy method, the proposed fuzzy-PID in this study, was built on Matlab as show in Figure 5.

Figure 5. Modeling the new-type fuzzy-PID on Matlab

The triangle membership functions were selected. The fuzzy rules were built based on Table 2. The fuzzy inference mechanism was chosen Max-Min method and the defuzzification according to the centroid point method were adopted. The relational surface of the P-fuzzy, I-fuzzy, D-fuzzy blocks are described in Figure 6.

Figure 6. The relational surface of the P, I, D-fuzzy blocks

The simulation diagram of the heater temperature control system is built on Matlab, as shown Fig.7. We conducted the quality assessment of the control system with three designed controllers above: PID-ZN1, PID-CHR and new-type fuzzy-PID.

4.2.  Determining the optimal parameters of the fuzzy-PID by the PSO algorithm

The initial scaling weights of the Fuzzy-PID controller, i.e. K_a, K_b, K_c, in simulation are selected randomly based on the initial parameters of PID, following the formular (5), so as to improve the quality of the furnace temperature control system. Here, the initial values K_a, K_b, K_c are as follows K_a=10, K_b=0.02, K_c=5.5

When applying the proposed PSO algorithm in part 3.3 to determine optimal parameters of fuzzy-PID controller, at this point, the optiaml values K_a, K_b, K_c are as follows K_a=22.2, K_b=0.021, K_c=5.1

4.3.  Simulation results on Matlab

The simulation scenarios are carried out with 3 controllers: PID controller with the parameters determined by Ziegler-Nichols 1, denoted PID-ZN1; Fuzzy-PID controller with the unoptimized parameters, denoted FPID; and Fuzzy-PID controller with the optimal parameters, denoted PSO-FPID.

When there is not disturbance, the response of the system corresponding to three controllers as shown Figure 7.

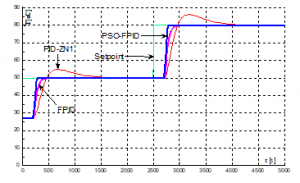
Figure 7. Response of the control system without disturbance

The overshoot of the control system with the proposed fuzzy-PID controller (FPID and PSO-FPID) is better than conventional PID controller (PID-ZN1). Specifically, when applying the PSO-based fuzzy-PID and the fuzzy-PID controller then the control system is not overshoot, meanwhile with PID-ZN1 controller then the control system is an overshoot of about 10%. The settling time of the system (included the time delay, 225 seconds) at the desired temperature value, T_d=50^oC, for the proposed PSO-based fuzzy-PID controller is so rapid, about 278 seconds, and for the proposed fuzzy-PID controller is about 401 seconds. The rising time of the system with the proposed fuzzy-PID controller is faster than PID controller. The steady-state error of the system with the proposed fuzzy-PID controller is almost eliminated.

Table 3. The system quality indexes without disturbance

Quality indexes	PID	Fuzzy-PID	PSO-based fuzzy-PID
Rising time (sec)	117.6	71.8	38.8
Settling time (sec)	1243.6	401.5	278.4
Overshoot (%)	<10	0	0
Steady-state error (%)	<1	~0	~0

Therefore, the two controllers proposed in this study (FPID, PSO-FPID) can bring improved quality of the furnace temperature control system.

When the sine disturbance impacts on the system: In fact, the operation environment is not ideal. The system operation is always affected by external disturbance, so that it makes to change the actual signals. Assume that the sine disturbance has the mixed frequency in range of 0.01-50Hz, and maximum amplitude of 50. At this time, the response of the furnace temperature control system corresponding to three controllers PID-ZN1, FPID, PSO-FPID, are shown in Figure 8.

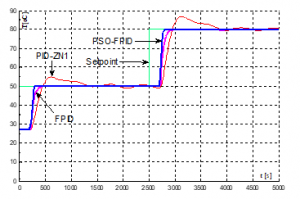
Figure 8. Response of the control system with sine disturbance

Figure 8 indicated the traditional PID controller (PID-ZN1) causes the system to oscillate around the set-point temperature value. This oscillated amplitude depends on the disturbance amplitude. Meanwhile, applying the proposed fuzzy-PID or PSO-based fuzzy-PID, the system quality is quite good, ensuring the system stability.

If the disturbance amplitude is so large, the furnace temperature control system may be unstable with the traditional PID controller, but still ensure stability of the system with the proposed PSO-based fuzzy-PID.

Table 4. The system quality indexes with disturbance

Quality indexes	PID	Fuzzy-PID	PSO-based fuzzy-PID
Rising time (sec)	110.5	65.5	36.4
Settling time (sec)	1255	380.1	265.1
Overshoot (%)	<15	<1	~0
Steady-state error (%)	-2 ÷ 2	-0.5 ÷ 0.5	~0
Oscillated response	Yes	Small	No

5. Design of the temperature control board

5.1.  Block diagram of temperature control board

In this section, the authors present the design of the PIC16F control board for controlling temperature of the resistance furnace. This temperature control board is designed by using PIC16F877A microcontroller [20], as shown in Figure 9.

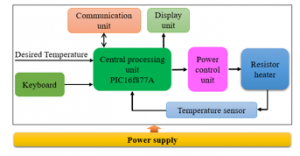
Figure 9. Block diagram of the temperature control board

The power supply block is responsible for supplying power to the entire system. The control object here is the resistance wire, wrapped around the copper pipe, causing the heat in the copper pipe to rise temperature in the furnace, it is controlled via the voltage signal of the power control unit. The temperature in the heater is measured by a temperature sensor. The display unit is responsible for displaying the actual temperature and set-point temperature. The keyboard is responsible for entering the set-point temperature. The central processing unit converts from analogue signal to digital values and performs the functions of fuzzification block, fuzzy-rules law table, defuzzification block and generating signals to command the power unit, thereby stabilizing the furnace temperature according to the set values. The power unit is responsible for controlling the AC power supplied to the resistance wire. The communication unit, using USB/RS232 port, is responsible for communicating between the board and the computer.

5.2.  Layout circuit of the temperature control board

The principle schematic circuit diagram of the temperature control board includes the schematic circuit diagram of the PIC16f central processing unit, the LCD display block, the power control unit, the USB/RS232 communication block and the AC/DC converter block. The detail schematic circuit of the temperature control board is presented in [18].

Based on the principle schematic circuit, the layout circuit diagram is given in Figure 10 and the realistic layout circuit of the control board as shown in Figure 11.

Figure 10. Layout circuit of the temperature control board

Figure 11. Realistic layout circuit of the control board

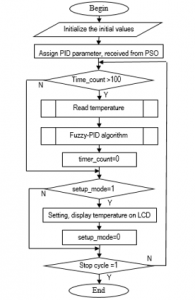
Figure 12. The main program flowchart for controlling the furnace temperature using PSO-based fuzzy-PID

5.3.  Temperature control algorithm on PIC16f chip

The furnace temperature control algorithm is installed on the PIC16f microprocessor as described in Fig.12.

The detail of algorithm flowcharts corresponding to each subprogram, are presented in Fig.13.

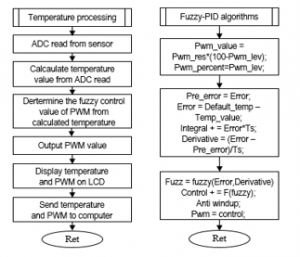
Figure 13. Algorithm flowchart of subprograms

5.4.  Experimental control for the heater in the laboratory

Experiment of the resistance furnace temperature control system, using PIC16F control board with the proposed PSO-based fuzzy-PID algorithm, is presented in Figure 1.

The monitoring control interface based on Visual C# is developed on the computer to obtain the actual temperature value of the resistance furnace. From this interface, the set-point temperature value and the parameters of the PSO-based fuzzy-PID controller also can be assigned remotely and easily.

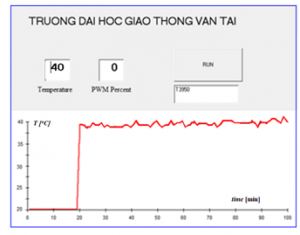
Figure 14. Real temperature response at setpoint 40^oC

At the beginning of the experiment, the control board with installed PSO-based fuzzy-PID algorithm, will create the 100% PWM output signal to supplying the suitable AC power values to the resistance wire, after the delay time, the temperature in the furnace changes from environmental temperature T₀=20^oC up to 39^oC, and then reduce PWM signal to maintain the actual temperature value at setpoint value of T_d=40^oC. When the furnace temperature exceeds 40^oC, the PIC16f microcontroller interrupts the PWM signal so that the temperature will reduce to the setpoint temperature value.

The experimental results in laboratory showed that the proposed PSO-based fuzzy-PID controller brings good control quality for the resistance furnace temperature control system. The proposed PSO-based fuzzy-PID controller with the optimal parameters usually gives better quality the proposed fuzzy-PID controller, because the parameters of the fuzzy-PID controller was not optimized. However, these two proposed controllers offer better quality than the traditional PID controller, especially when the disturbance impacts on the system.

6. Conclusion

This paper presented a novel control approach applying the PSO algorithm to tune the scaling weights coefficients of the fuzzy-PID controller which is combination of the advantage of the traditional PID control and fuzzy logic control. The fuzzy-PID controller is designed based on the typical fuzzy rules, and combined with the PID control, but the fuzzy-PID three scaling weights are tuned by the PSO algorithm. And then the simulation model of the resistance furnace temperature control system without/with disturbance using the proposed controller was built on Maltab. The simulation results have confirmed the effectiveness of the two proposed controllers for the resistance furnace temperature control system, i.e. fuzzy-PID controller and PSO-based fuzzy-PID controller. Then the proposed PSO-based fuzzy-PID algorithm was implemented on the temperature control board which made of PIC16f microprocessor. Experimental results showed that proposed PSO-based fuzzy-PID algorithm provided better control quality than the traditional PID algorithm. In addition, the proposed PSO-based fuzzy-PID controller is consider to be an efficient control strategy applying for a class of nonlinear and uncertain complicated control objects.

From this research, the future work focusing on optimization structure of fuzzy logic calculated blocks, and apply adaptive control to tuning online/adaptive parameters of the fuzzy-PID controller. The future work also continues to develop the temperature control board using PIC16f in order to complete the equipment, and put the equipment into the actual application to control the temperature of materials in industry and transportation.

Conflict of interest

The authors declare no conflict of interest.

1. Aidan O’Dwyer, Handbook of PI and PID Controller Tuning Rules, Imperial College Press, 2003.
2. Yu Feng Zhang, Ming Li and Jing Min Dai, PID Heating and Temperature Control Method Based On Dynamic Assignment, 5th International Conf. on Mechatronics, Materials, Chemistry and Computer Eng., 2017. https://doi.org/10.2991/icmmcce-17.2017.208
3. V.Kabila, Glan Devadhas, Comparative Analysis of PID and Fuzzy PID Controller Performance for Continuous Stirred Tank Heater, Indian Journal of Science and Technology, Volume 8, Issue 23, Pages: 1-9, 2015, https://doi.org/10.17485/ijst/2015/v8i23/85351
4. L.X. Wang, A course in Fuzzy Systems and Control, Prentice Hall International, Inc, 2002.
5. Z.R. Radakovica et al., Application of temperature fuzzy controller in an indirect resistance furnace, Applied Energy, Volume 73, Issue 2, 2002. https://doi.org/10.1016/S0306-2619(02)00077-6
6. Moh Syahrir Bin Ribuan, Development Of Fuzzy Logic: Temperature Controller Implementation – Microcontroller Based, University Teknikal Malaysia Melaka, 2009.
7. P. Singhala, D. N. Shah, B. Patel, Temperature Control using Fuzzy Logic, International Journal of Instrumentation and Control Systems, Vol.4, No.1, 2014, https://doi.org/10.5121/ijics.2014.4101
8. Nguyen Chi Ngon, Fuzzy PI controller: From design to application, Science magazine, Can Tho University, 2011.
9. Shi Dequan, et al., Application of Expert Fuzzy PID Method for Temperature Control of Heating Furnace, 2012 International Workshop on Information and Electronics Engineering, Procedia Engineering, Volume 29, 2012, https://doi.org/10.1016/j.proeng.2011.12.703
10. Sneha S Patole1, Shailendra K Mittal, Fuzzy PID Controller Design for Heating Control System, International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, Vol. 6, Issue 6, 2007, https://doi.org/10.15662/IJAREEIE.2017.0606140
11. Qingjie Yang, Guohou Li, Xusheng Kang, Application of fuzzy PID control in the heating system, 2008 Chinese Control and Decision Conference, 2008, https://doi.org/10.1109/CCDC.2008.4597814
12. Jiangjiang Wang, Dawei An, Chengzhi Lou, Application of Fuzzy-PID Controller in Heating Ventilating and Air-Conditioning System, 2006 International Conference on Mechatronics and Automation, June 2006, https://doi.org/10.1109/ICMA.2006.257656
13. L. D. Vijay Anand, Lakshmi Asok,, Design of Fuzzy PID with Expert Control for a Temperature Process, International Journal of Engineering Research & Technology, Volume 03, Issue 02, 2014.
14. Guofang G., Zhengzhong L., Design of Heating Furnace Temperature Control System Based on Fuzzy-PID Controller, Information Engineering and Applications. Lecture Notes in Electrical Engineering, Volume 154. Springer, https://doi.org/10.1007/978-1-4471-2386-6_196
15. Trinh Luong Mien, Design of Fuzzy-PI Decoupling Controller for the Temperature and Humidity Process in HVAC System, International journal of engineering research & technology, Vol. 05, Issue 01, January-2016. https://doi.org/10.17577/IJERTV5IS010473
16. Y.Zhang, et al., Application and Research of Fuzzy PID Control in Resistance Furnace Temperature Control System, IOP Conf. Series: Earth and Environmental Science, Vol.186, Issue 5, 2018. https://doi.org/10.1088/1755-1315/186/5/012051
17. Liu Jing Yan, The Fuzzy PID Control of Resistance Furnace Temperature System Based on Genetic Algorithm, Applied Mechanics and Materials Vol. 273, 2013, https://doi.org/10.4028/www.scientific.net/AMM.273.678
18. Trinh Luong Mien, Vo Van An, Lecture notes: Design of the temperature controller based on fuzzy logic using PIC16f microprocessor, University of transport and communications, 2018.
19. A.H. Al-Mter and S. Lu, A Particle Swarm Optimization Algorithm Based On Uniform Design, International Journal of Data Mining &
    Knowledge Management Process, Vol. 6, No. 2, 2016. https://doi.org/ 10.5121/ijdkp.2016.6203.
20. Microchip, PIC16F/LF1825/1829 Data Sheet DS41440A, Microchip Technology Inc., 2010.

(Click Here)

(Click Here)