1. Introduction

Parallel mechanisms have been researched and applied in many areas such as motion simulators, which simulate the experience of being in a car, plane, tank, and in a virtual reality environment or create motions to serve different goals. Parallel mechanisms have outstanding advantages compared to serial machines such as: high rigidity, high load bearing capacity, ability to change position and spiritual orientation, activation accuracy, high stability, high loading capability. The simulation model has 6-DOF [1] based on Stewart-Gough structure, this structure has good load capacity, however it needs to use 6 driving mechanisms leading to complex control.

For motion simulation model for devices such as cars, tanks moto bike…in fact we only need 4-DOF is enough. These car motion simulators consist rotating and translating along the vertical OZ axis, rotating around the OX axis and OY axis. In this research the authors focus on the hybrid mechanism including parallel and serial mechanism, which generate 4 motions (4-DOF) in the space. The control problem for 4-DOF car motion simulators is difficult because of many non-linear parameters. Currently, a number of control methods have been developed and applied to control problems for a defined model or a model with constant parameter uncertainty in [2-7]. However, the control problem for a driving practice model with indefinite parameters has always paid much attention to further improving the kinetic quality and dynamics of the driving platform [8]. Sliding mode controller is used in nonlinear systems. It is robust and efficient in maintaining stability for nonlinear dynamic systems. Later this method was more interested by scientists because of its stability and stability even when there is the impact of noise as well as changes of model parameters. However, the chattering phenomenon remains the main  disadvantage of this robust control. As solution to this problem,  a  PID  sliding  mode  approach  is  exposed  and  tested  in  this  paper. Sliding mode controller with type PID is used to eliminate the oscillation around the sliding surface when the amplitude of the slider control law changes greatly. The gain before the sign function in the sliding mode control law is calculated according to the Lyapunov stability criterion introduce in [9], [10] [11]. This gain, unless properly selected, is likely to cause oscillation. In this study, the authors  presented the 4-DOF car motion simulators with the serial and parallel mechanism, kinematics and dynamic equations. Base on dynamics equations authors focused on building intelligent control algorithms for the 4-DOF car motion simulators model. Specifically, the author will develop an SMC-type-PID and compared the results with the SMC-type-PID with GA Optimization with uncertain parameters.

2. Kinematics and dynamics model

In this section, the model of the 4-DOF car motion simulator shown in fig 1 would be constructed. The car motion simulators mechanism model with the global axis is chosen. The motion of the upper plate is due to the movement of three vertical linear actuator and the rotation of the revolute joint attached below the lower plate. The piston’s movement makes changes in vertical movement, rotate around the OX axis and OY axis of the mobile platform. The revolute joint rotates the moving parts around the OZ axis. Therefore, the car motion simulators has 4-DOF. The systems variables need to control to track the desired trajectory are the length of three robot’s legs and the rotation angle around the OZ axis of the revolute joint. Fig.1 illustrates the car motion simulator model with the movements that are translation along the OZ axis, rotation along the OZ, rotation along OX axis, and rotation along the OY axis and they are defined by , , , and .

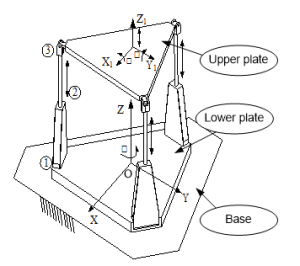
Figure 1: 3D model of the 4DOF car motion simulator

2.1.  Inverse Kinematics of 4-DOF car motion simulators

In this part author briefly present the kinematics of 4-DOF car motion simulator [12],  from the trajectory of the center point of upper plate we need to find the limb lengths  and the angle of rotation about OZ axis . The kinematic parameters are demonstrated in the vector diagram in Fig. 2 with  is the radius of an upper plate, is the radius of a lower plate, in this research assumption as .

The vector loop equation for each limb of 4-DOF car motion simulator [12], [13] can be written as:

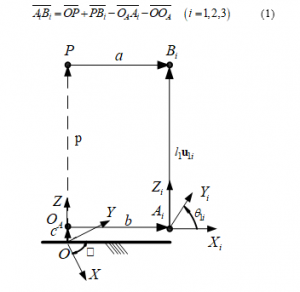
Figure 2: Vector diagram of the 4DOF car motion simulator

The positions of center of the lower plate and upper plate can be written as:

where and we obtain the vector .

2.2.  Dynamic Model of 4-DOF car motion simulators

In the section, the author using Euler-Lagrange to establish the dynamic model of the car motion simulator, the equation is described by [13],

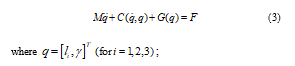
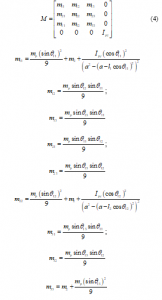
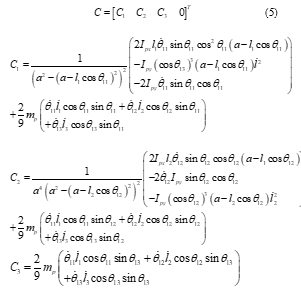
with , , and are the mass of the cover of pistons, the mass of pistons, the mass of motors and the mass of the upper plate, respectively.

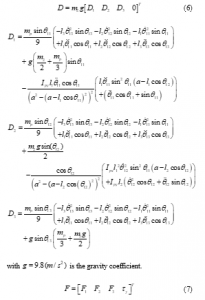
is defined as a control signal vector.

3. Design controller for 4dof car motion simulator

3.1.  Sliding mode controller with PID

The sliding mode control (SMC) is strongly requested due to its robustness against the disturbances. To ensure the convergence of the system to the wished state, a high level switching control is requested which generates the chattering phenomenon. In this way, a PID sliding surface with a saturation function will be proposed in this paper to solve this problem. Slide control law are designed based on the sliding function. In this case, the author has chosen the sliding function of the following form to eliminate the oscillation around the sliding surface when the amplitude of the slider control law changes greatly.

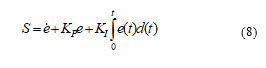
where are PID parameters

The trajectory deviation is defined by with is the desire trajectory of . The goal of the controller design is to control  following the desire trajectory  with the small . Select the sliding surface of controller as:

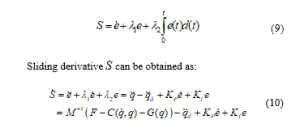
The control signal in SMC design consisting of equivalent control and switching control where the control action is corresponding with the sliding phase and reaching phase .The equivalent control is determined when s(t)=0, while the switch control is described when . With , equivalent control can be defined as:

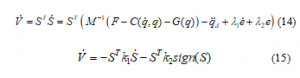
with control signal is calculated in eq.7 above, and ,  is selected as positive definite diagonal matrices, so we have the system of stability and lead to .

3.2.  Design of Sliding Mode Controller type PID with GA Optimization

In this controller, are the constant parameters existing in sliding surfaces and control laws determine the overall performance. Hence, it is necessary to find the optimal values of them using optimization algorithm. Genetic algorithm (GA) is one of the fundamental evolutionary stochastic optimization algorithms. It mimics the process of natural selection and uses biological evolution to develop a series of search space points toward an optimal solution.

The goal of SMC-type-PID is to achieve accuracy trajectory tracking for 4-DOF car motion simulators; that is, the smaller the trajectory errors are, the more effective the controller is. Those parameters to be optimized are relevant to trajectory error; hence the fitness function is defined as follows:

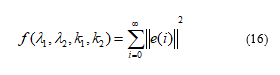
with the fitness function, those parameters can be found with the minimization of tracking errors by using the designed control law with the minimization of tracking errors. The flowchart of GA Optimization is shown in figure 3 and figure 4.

After 15 generations, we have the following results: ; ; and ; ;

3.3.  Numerical simulate and compare the results of two designed control algorithm.

The simulation parameters of 4-DOF car motion simulator are shown in Table 1. At the initial time, the position of the robot is denoted by   .

The control results of the proposed controller are evaluated through numerical simulation using Matlab/Simulink tool. Reference trajectory equations are described by a ternary function [13]:

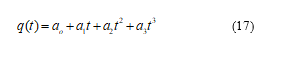
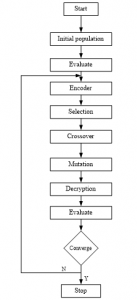
Figure 3: Genetic algorithm flowchart

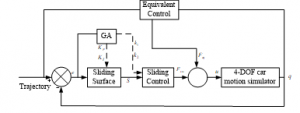
Figure 4: Flowchart of SMC-type-PD controller with a genetic algorithm optimisition

Table 1: 4-DOF Car Motion Simulator Specifications

Items	Value
Base radius	500 [mm]
Moving radius	500[mm]
Leg strust	300[mm]
c	50[mm]
mp	15(kg)
m1	0.5(kg)
m2	10(kg)
mdc	3(kg)
(SMC-PID)	14.79
(SMC-PID)	14.79
(SMC-PID)	15.1
(SMC-PID)	14.79

From the motion of the center point of upper plate we can calculate the length of legs  using inverse kinematic equation of 4-DOF car motion simulator, the length of each limb shown in figure 5.

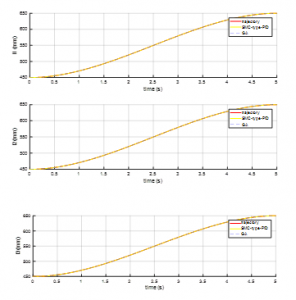
Figure 5: The trajectory responses of 3legs

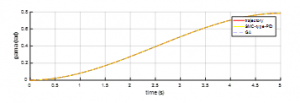
Figure 6: The trajectory responses of trajectory angle gama

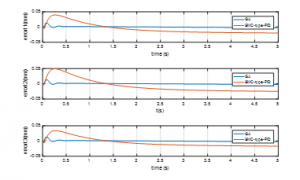
Figure 7: The trajectory error of the 3legs

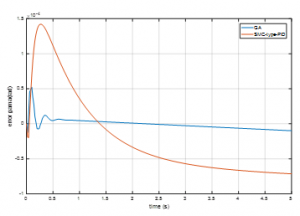
Figure 8: The tracking error of the angle trajectory

The simulation results show that the adaptive controller constructed by combining the SMC-type-PID with the GA optimization is able to ensure the stability for the car driving simulator system and the tracking error converge to zero rapidly. In general, the SMC-type-PID control with the GA Optimization is achieved accuracy trajectory tracking; that is, the smaller the trajectory errors are, the more effective the controller is.

4. Conclusions

This paper presented an adaptive control method for the 4DOF car motion simulator. The control method design is based on the sliding mode controller type PID structure combined with the sliding mode controller type PID with GA optimization for the system. In the simulation results we can see that the SMC-type-PID with the saturation functions give us good results, stability and accuracy of the process output and control evolution. The parameters selected by the genetic algorithm give good results and smaller errors. The stability of the system is proven by using Lyapunov theory, the simulation results show the proposed controller can be ensure the stability and tracking performance for the system. Through the simulation results, the author found that the sliding mode controller type PID with GA optimization gives better results because the deviation of the set value with the actual value is very small, approximately 0. Therefore, the sliding mode controller type PID with GA optimization can find the optimal values using optimization algorithm and it be recommended for nonlinear systems request for high accuracy as 4-DOF car motion simulators. Further and conduct experiments on real models in the near future.

Acknowledgment

This work is funded by VAST project under grant number VAST01.06/19-20.

1. J. Pearce, “Research and Development of a 6 Degrees of Freedom Electric Motion Platform,” Bachelor’s Thesis, 2016.
2. Y. Qiu, X. Liang, and Z. Dai, “Backstepping dynamic surface control for an anti-skid braking system,” Control Eng. Pract., vol. 42, pp. 140–152, 2015. https://doi.org/10.1016/j.conengprac.2015.05.013
3. G. Sun, D. Wang, X. Li, and Z. Peng, “A DSC approach to adaptive neural network tracking control for pure-feedback nonlinear systems,” Appl. Math. Comput., vol. 219, no. 11, pp. 6224–6235, 2013. https://doi.org/10.1016/j.amc.2012.12.034
4. T. Zhang, M. Xia, and Y. Yi, “Adaptive neural dynamic surface control of strict-feedback nonlinear systems with full state constraints and unmodeled dynamics,” Automatica, vol. 81, pp. 232–239, 2017. https://doi.org/10.1016/j.automatica.2017.03.033
5. S. Qi, D. Zhang, L. Guo, and L. Wu, “Adaptive Dynamic Surface Control of Nonlinear Switched Systems with Prescribed Performance,” J. Dyn. Control Syst., vol. 24, no. 2, pp. 269–286, 2018. https://doi.org/10.1007/s10883-017-9374-7
6. K. A. Semprun, L. Yan, W. A. Butt, and P. C. Y. Chen, “Dynamic surface control for a class of nonlinear feedback linearizable systems with actuator failures,” IEEE Trans. neural networks Learn. Syst., vol. 28, no. 9, pp. 2209–2214, 2016. https://doi.org/10.1109/TNNLS.2016.2572205
7. Y.-J. Liu, J. Li, S. Tong, and C. L. P. Chen, “Neural network control-based adaptive learning design for nonlinear systems with full-state constraints,” IEEE Trans. neural networks Learn. Syst., vol. 27, no. 7, pp. 1562–1571, 2016.https://doi.org/10.1109/TNNLS.2015.2508926
8. X. Ji, X. He, C. Lv, Y. Liu, and J. Wu, “A vehicle stability control strategy with adaptive neural network sliding mode theory based on system uncertainty approximation,” Veh. Syst. Dyn., vol. 56, no. 6, pp. 923–946, 2018. https://doi.org/10.1080/00423114.2017.1401100
9. M. Kim, B. Jung, B. Han, S. Lee, and Y. Kim, “Lyapunov-based impact time control guidance laws against stationary targets,” IEEE Trans. Aerosp. Electron. Syst., vol. 51, no. 2, pp. 1111–1122, 2015. https://doi.org/10.1109/TAES.2014.130717
10. A. Wolf et al., “Determining Lyapunov exponents from a time series,” vol. 16, no. 3, pp. 285–317, 2017. https://doi.org/10.1016/0167-2789(85)90011-9
11. S. K. Y. Nikravesh, Nonlinear systems stability analysis: Lyapunov-based approach. CRC Press, 2018.
12. Kiem Nguyen Tien, Duyen Ha Thi Kim, Tien Ngo Manh, Cuong Nguyen Manh, Ngoc Pham Van Bach, Hiep Do Quang. “Adaptive Dynamic Surface Control for Car Driving Simulator based on Artificial Neural Network” , 2019 International Conference on Mechatronics, Robotics and Systems Engineering (MoRSE), 2019 https://doi.org/10.1109/MoRSE48060.2019.8998749
13. L. W. Tsai, Robot Analysis: The Mechanics of Serial and Parallel Manipulators, Wiley, 1999.

(Click Here)

(Click Here)