1. Introduction

Soccer or the term synonym to Football has its evolution as a team sport way back more than 200 decades ago. It originated in Asia. Greeks, Romans, and parts of Central Americans also claim having initiated the sport Moosavian et al. in [1]. Eventually, it was the British who transformed and revolutionized the game of soccer into the game perceived and played today.

Any game requires a set of rules or guidelines which need to be institutionalized and British are the ones who will take this credit who regulated and imposed basic rules needed for the same, which included forbidding tumbling the opponents, to hold or touch the ball with hands when the game is at play Moosavian et al. in [1]. As the timeline increased there required more amendments in soccer and needed more rules which were to be implemented. One of them being penalty kick which was introduced way back in 1891 which penalized players any offense inside the D area. When a spot-kick or goal kick is taken in the penalty area, no other player other than the goalkeeper is allowed inside (shown in “Figure 1”).

The Federation International Football Association (FIFA) was registered as an official member of the International Football Association Board during the year 1913. To caution players for bad conduct on the field, referees were given the privilege of penalizing players at the game of play with caution cards. These cards were introduced during the 1970 World Cup finals which included a yellow card for caution and a red card for dangerous play. Recent changes included goalkeepers being banned from handling deliberate back passes towards the D Area, tackles from behind, and obstruction of the goalkeeper when a goal is being scored. These amendments did not bring down the viewership of the games but have helped gain more popularity and momentum over any other game. For instance, Cricket which started with Test format in its early stages came down to 50 over format then to 20 over and recently to 10 over format making it far more reachable to audiences throughout.

 Over 250 million players spanning over 200 countries and dependencies play soccer, which makes it the world’s most popular sport. As per the recent statistics on the top ten most popular sports in the world, with a fan following the base of almost 3.5 billion from every continent, the sport remains at the top with no other game coming close to it. And for the reasons above, soccer has its mainstay in most countries because of its cost-efficiency. Soccer just requires a ball, which will be tactically kept in procession by a team on the field which will be comprised of 11 players and their opponents in equal numbers. Another reason for soccer being such a popular game throughout the globe is that the rules have been very adaptive and simple to adhere to. Also, the rules have not been tampered or amended in terms of usage on a major basis, making the game more of a learning process than changing one.

The field area played in each game is 100 meters in length and 60 meters in width. As per the recent survey on the ground dimension of length and width, the conducive area of play depends on the minimum possibility of length and width for a full-fledged game. And hence every ground varies with the maximum amount of space available for a ground to be built keeping in mind the spectators to be seated while watching a game.

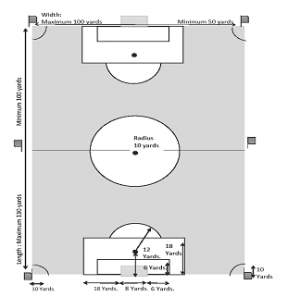
Figure 1: Soccer Field.

Soccer at school, College or, Club level has always generated interest only in a league format because 10 teams participating in the tournament. Each team tends to play each other minimum once or maximum twice as the 1st leg usually considered a home game and 2nd leg considered as away game. Teams usually have their home ground in their region of practice zone and only in a league format can we know the real quality of team performance. Such kinds of league games are played not only in Soccer but in other games such as Basketball, Hockey, Cricket, Kabaddi, and other competitive sport. These games have always drawn huge crowds from their respective home pitch audience and harness huge interest. These also involve a lot of sport management strategies.

1.1.  Role of Coach/ Manager

Coach or manager for any team plays a very important role and spearheads the main responsibility of how to handle a potential squad of players in all possible means for an entire season. Coach also has the mentorship and administrative role to guide and mold players and bring in their best in all the matches to be inducted into.  Soccer is taken in Club level matches; an elite team needs to play at different levels to attain mass recognition and importance in the said field. Fanfare has always surrounded the elite teams as they promise in building not only a team in terms of acquiring better and best players around the globe but keeps the money bank ticking for the club. Most of the time it is the fans that are responsible for any management based decision to rope in better coach or manager for the club in replacement of the other if the desired results are not met.

The yearly season is usually a time spanning from August of every year to June of consecutive year. Within which a winter break of 20 days will be applied in December. So when inking a deal with any club, a player needs to be available for the entire season and provide his optimal performance in every game of which the club represents at different levels. Elite clubs always gives the complete role of responsibility to coach/manager in acquiring the best possible players and strengthening the squad and see through the possibility of player availability for crucial matches. The squad acquired by a coach/manager cannot be changed at every point of time once the transfer season is complete. The transfer season usually happens before the season commences and each clubs coach/manager is liable to enable talks with other clubs in acquiring their desired players, if the other club obliges with the offer, well and good or else have to enhance their offer in terms of money to ink the deal. If in the worst case the squad selected by the coach/manager doesn’t fare well in the league matches can avail his winter window session transfers which usually happen in December.

Playing a balanced squad for any match in whatsoever circumstances has always been an important aspect and a prerequisite of any coach/manager yielding to a win (3 Points) preferably and on worst-case scenario a draw (1 Point). A win won’t be compromised at any cost and will be usually expected by the team owner and the main stakeholders that are committed and fans of the club who won’t hold on to a loss on a more frequent note. Due to various reasons, there might be situations wherein the coach takes dubious decisions while picking the squad and in this regard, might elevate players of his choice while discriminating against others even when the credentials of the players not selected are well above the ones selected.

2. Review of literature

Darren J. Paul and Geroge P. Nassis in their paper titled, Testing strength and power in soccer players: The application of conventional and traditional methods of assessment Darren et al. in [2], have measured various factors such as physical, tactical and psychological aspects measuring the influences of them in Soccer and emphasize the importance of strength and power as key factors assessed in a soccer club/team. The work revolves around selection factors such which are valid and reliable which makes a trustworthy analysis of implementing the system. Since the tests carried out in this process are having moderate to high levels in soccer players at several of either training or matches without compromising on the accuracy and minimized time delay. Hence the implementation phase of the paper provides monitoring of players at more specified intervals of time only in a specified season rather than specific time intervals. The major aspects taken from this paper finds a limited way as on how traditional or manual method might be a very moderate way of analyzing players evaluation factors as compared to various other parameters what SEPGSA can achieve and another main constraint is that the period of applicability is only confined to a particular season, rather than the complete history of a player once he has got into the professional level as discussed towards implementing SEPGSA method. Miguel Angel Perez Toledano, Francisco J. Rodriguez, Javier Garcia Rublo and Sergio Jose Ibanez in their work on Player’s Selection for Basketball teams through performance Index rating, using multiobjective evolutionary algorithms Miguel et al. in [3], discuss on the stochastic methods deployed based on evolutionary techniques towards the selection of players for a basketball team. Financial limitations, sports characteristics, and participation of teams in various levels of competitions hence making the process of player selection very complex since multiple variables are involved in subjectivity.

Bukhari et al. in [4], discuss the various characteristics which enhance the players who are recruited in a team. Parameters include the composition of body parameters, vision-based tests, psychomotor tests and various and anaerobic activities to make a good sports team. The process is discussed in the paper as very difficult and time- consuming for team coaches towards individual players to be recruited in a team. To measure such parameters there is a huge limitation since human judgment is more biased and error-prone hence making a huge limitation on the same. To overcome such kind of limitations the authors have gone with fuzzy logic in application towards the same.

Bastien Talgorn et al. in [5] their work on statistical project formulation for simulation-based design and Optimization. In which the direct search algorithm is compared to that of surrogate-based algorithms that are completely oriented towards models based on surrogate methods. The main problem discussed here is on the evaluation of black boxes which will be used for Optimization and is quintessential simulation-based function since black boxes have various challenges deployed such as noise, high computational cost, and other constraints. The article has its major contributions towards formalizing surrogate problems which specifically Dyna-tree models. A total of 8 formulations were proposed in this paper out of which 3 are constrained while rest are considered using statistical criterion. The major work involved here is to compare the performance using 20 benchmark problems in which the functions are constrained towards simulation aspects of aircraft design. This novel problem using statistical surrogates combining it with a derivative-free Optimization algorithm towards simulation Optimization where the statistical features and exploring better design space. The experiments conducted towards appropriate use of surrogate models could be better improvised with considering Optimization concepts involved for the same.

Sethuraman sankaran et al. in [6] their article on a method for stochastic constrained optimization using derivative-free surrogate pattern search and collocation. The major aim of this work is towards developing computational Optimization technique which can be practically experimented on stochastic problems to evaluate cost functions. Since the complexity of the problem is for large scale equations. Various types of such problems such as biological applications of Solid Mechanics where surrogate models have been used and in the current article derivative-free surrogate Framework which embeds the methods for robust designing. The major drawbacks for gradient-based are not feasible for problems that are more complex on physics which have constraints such as large scale simulation, noise, and gradient information.

Pooriya Beyaghi et al. in [7] their article on “Delaunay-based derivate-free optimization via global surrogates, Part I: linear constraints, where a new optimization algorithm based on a derivative-free method for more non-convex functions are bounded by linear constraints. The algorithm which is developed in this research paper is extended to Part II since the problems which can be more convex constraints derivative-free methods are well suited where derivative or approximation is available on an instant nature. Direct search methods are a class of algorithms in which derivative-free methods are well suited for problems where derivative or approximation is available in an instant nature. Direct search methods are a class of algorithms in which, derivative-free algorithms are classified. The Nelder-Mesh Simplex algorithm was used for numerical optimization. The adaptive direction search algorithm was another category of direct search methods and more modern methods such as Rosenbrock and Powell methods, Pattern search methods that are characterized by various parameter spaces. The direct search methods are a model of the actual function of summarizing the data points. The Kriging method was one of the popular surrogate functions used in global optimization schemes which will automate in building estimate and uncertainity involved in this estimation.

Charles Audet et al. in [8] their paper on Mesh-based Nelder-Mead algorithm for inequality constrained optimization discusses the lack of support that is involved in theoretical and practical convergence and the Nelder-Mead algorithm considered towards solving unconstrained optimization problems. The current work proposes a method to enhance the Nelder Mead algorithm towards replacing the worst point of a simplex method. The methodology is to use the search step of mesh adaptive direct search which is inspired by the Nelder-Mead algorithm. It doesn’t exhibit any limitations of convergence but overcomes this by using convergence analysis present in mesh adaptive direct search algorithm.

3. Need for Gravitational Search Algorithm for Soccer

When we consider a deterministic function f: Rn->R. This could be used over any domain of interest on the lower and upper bound of the variables. Parameters considered for the work involves more of dynamic and constantly evolving variables and hence various parameters towards selecting the type of Optimization technique which could be deployed for the current work. Comparison of bench-marking of the types of Optimization algorithms which is daunting and involves a high level of complexity first level of unbiased that could arise should be fair while evaluated. The number of Optimization algorithms and its implementation in various domains has evolved exponentially in relevance to the time taken. Comparative studies carried forward by researchers in various domains and Fields have been tested and experiment at different levels by carrying out experiments which have yielded result in an improved for the enhanced manner and considered as great help towards scrutinizing of algorithms based on Optimization for problems related to a specific domain of field and enhance the bench-marking of such technique in optimization-based algorithms.

There are various types or classes of Optimization algorithms that are distributed in network planning methods of which they are classified into two broader perspectives.

• Classical Optimization algorithms,
• Meta heuristic-based Optimization algorithms

In classical Optimization algorithm, there are a few which are listed below

• Transportation algorithm
• Branch and bound algorithm
• Mixed-integer programming
• Derivative free methods.

And in Meta heuristic-based, there are all the evolutionary algorithms which are sub-classified classified into,

• Trajectory based algorithm
• Population-based algorithm

The classical Optimization such as mixed-integer, branch and bound, derivative-free methods are summarized upon the lower and upper bounds on the problem variables which are of high importance. In a derivative-free Optimization technique which is applicable when the information of the derivative function is not available, not complete, not reliable or practically not feasible to obtain. When we consider a function derivative ‘d’ which contains noise or expensive to be evaluated practically confined to very few usages and differences, such type of problems is referred to as derivative-free Optimization. Another vision towards the derivative-free method is to that in the algorithm which involves derivatives of those particular functions other than the evaluating function‘d’. The problem that we consider has no such implications of uses of the derivative tree method since the function revolves more on data that is more certain unambiguous in many situations.

In the local search methods which are also one of the methods in classical Optimization, we see various methods of direct local search methods such as Hooke and Jeeves, Nelder-Mead Simplex algorithm, Mesh Adaptive direct search methods, Trust-region methods, Implicit filtering. The Global search methods which are also based on classical Optimization techniques based upon the construct and optimization of a function which underestimates their original one. Various algorithms such as Lipschitizian based partitioning, Branch-and-Bound method where it partitions the search space and will find the lower and upper bound values and the inferior 1 are eliminated. The branch and bound method will not be practically feasible to apply since it eliminates the inferior function which cannot be done in in the proposed work since we are concerned with not eliminating any player who is bought by a club or part of a college team, but it on how we could improvise the player in the best possible way. The surrogate management framework is a classical Global search Optimization method in which the accuracy of the surrogate model is done by stepwise search to produce optimal points. It evaluates the candidate function along with the surrogate model and does the measurement. The branch and fit method also deploy the concept of surrogate models and randomization which are combined. Optimizing the models based on the evaluation of other points versus candidate points is used. The above algorithms will not be suitable for our research work since we are experimenting with a dynamic set of parameters with constant self-reference to the methods and functions and peer references in the data set.

Simulated annealing is a metaheuristic trajectory-based method, each iteration the algorithm generates the latest trial, which is compared with the incumbent and is accepted with probability function. Simulated annealing was initially proposed for handling problems based on Optimization and has been experimented and results obtained for global optimum have been recorded. But the guaranteed solution is not sustained and a good solution cannot be obtained within a finite set of iteration. Simulated annealing is not practically feasible for the research work carried out.

We have used the population-based evolutionary technique of the Gravitational Search Algorithm (GSA) which has features such as non-deterministic function as what is required in player selection from the given data set. The GSA algorithm is agent-based as the direct methods which cannot be practically created to. The position of every agent is important towards the system state and hence can be directly co-related to every player position which affects the team. The Other important aspect in GSA is that the agent’s absolute fitness is directly dependent on system state as we can correlate the fitness of every player which is important towards the overall aspect of a club or a team. This aspect is not available at direct methods. An important and valuable aspect is that as compared to the direct method is completely inform the method as contradicting to direct methods that have very limited information. The rigorous solution of Agent dynamics which is feasible in GSA is not practically feasible in direct method and hence the selection of GSA towards initial simple population-based to completely normalize on what needs to obtain as result towards estimating the influential parameter.

4. Gravitational Search Algorithm (GSA)

4.1.  Introduction to GSA

Gravitational search algorithm (GSA) which is based on soft computing technique is exhilarated on a conceptual skeleton and more relevantly derived from nature and has its origins in gravitational kinematics Kelton et al. in [9].  The model is based on the motion of masses which moves under the influence of gravity Abhinav Sharma et al. in [10]. The preeminent concept of GSA is in the collection of objects which internally interact with each other because of various influences of objects under the Newtonian gravity and principles of motion Damodar Reddy et al. in [11]. Masses measure the performances of objects. When there are plenty of objects in a particular region the gravity, force, and masses of all these objects play an important role as the influence of the objects and by the law of attraction and forces a global movement of all objects toward other objects of heavier masses P.B. De Oliveria et al. in [12]. The position of every object corresponds to a solution to the problem. During iteration, the position of the objects is updated and the best value along with the corresponding object is stored P.B. De Oliveria et al. in [12]. As per the law of physics, heavier masses tend to move more calmly or laziliy a more calm or lazy way than the lighter ones Tongzaing et al. in [13]. After a specific number of iterations, the algorithm terminates before which the best fitness value transforms to global fitness value for estimating the influential parameter of players’ goal-scoring capabilities and the positions of each corresponding object yield a global solution. Rajendra Kumar et al. in [14].

Heuristics and optimization play a very important role in any of the research fields of work which needs to be done Mohammad Massoud et al. in [15]. It is required for enabling to infer new knowledge out of the existing ones Ehsanol et al. in [16]. Without heuristics, it would be hard to conclude that none could learn many things that are not possible. Optimization is an entity where the quality of any work just doesn’t depend on finishing it alone but in making the best and effective use of all the available resources Ehsanol et al. in [16]. Optimization completes the task but finishes the task quickly and accurately Tolba et al. in [17]. Hence concerning both heuristics and optimization, many algorithms are designed and developed using heuristics and optimization concepts and Gravitational Search Algorithm very much ascertains the fact of it. GSA because of its practical application as a nature-based algorithm has gained tremendous significance amidst the research and scientific community.

4.2.  Working of SPEGSA

SPEGSA, as the name suggests, is very much taken all its inspiration from Mother Nature as it is established on one of Newton’s laws of gravity and law of motion Xing et al. in [18]. Most of the optimization algorithms have a high usage of Animals or insects and their different techniques in optimization since they make use of the best of the resources when it comes to optimization. Whether it is Ant Colony Optimization, Particle Swarm Optimization, Whale optimization, and many others, have seen the same techniques in technology as it can reflect on a real-world problem to an optimized level Alli A et al. in [19]. SPEGSA has more than enough credibility in providing a very accurate, effectual, and powerful high-quality solution for any such optimization-based problems Gonzalez et al. in [20].

SPEGSA is categorized under a population-based method due to various objects involved. SPEGSA is made up of certain things termed as particles, which are primarily comprised of four major parameters. That is the position, inertial mass, active gravitational mass, and passive gravitational mass Kyuchang Kang et al. in [21]. One of the unique features of SPEGSA is that it is a memory-less algorithm that does not compromise on efficiency as compared with any other memory-based algorithms R. Priyadarshini et al. in [22]. Since SPEGSA is in its infancy stage, more studies will be based on it. There is a high potential of the algorithm to provide optimal solutions for various problems in any possible domain.

G, which is gravitational constant computed in iteration t, is computed as follows,

Where G₀ and α need to be loaded before search. Their values will be gradually decremented during the search Esmat et al. in [23]. T is the total number of iterations. The masses of every object will abide by the law of gravity as mentioned in the equation “(2)”.

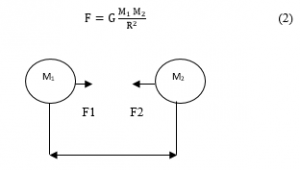
Figure 2: Force Acting between Mass M1 and M2.

Equation “(2)” represents Newton’s law of gravity, where, F is a magnitude of gravitational force acting upon various objects. G is gravitational constant. M₁and M₂ masses of first and second respectively objects Seyed et al. in [24]. R is the distance between two objects M₁ and M₂. Newton’s second law states that, when force F is applied to an object, the object moves with an acceleration ‘a’ depending on the applied force and the object mass ‘M’ as in the equation “(3)”.

Masses are of three kinds, Active gravitational mass M_a. Passive gravitational mass M_p, and Inertial mass M_i. The gravitational force F_ij that acts on mass i by mass j is defined by,

M_aj and M_pi are active and passive masses of objects j and i respectively.

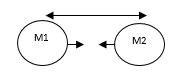
Figure 3: Gravitational Mass.

The acceleration of the object will be calculated as below.

Where M_ii is inertia mass of the particle. While searching the particles update their velocities and positions as below equations.

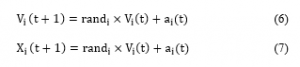
4.3.  Pseudocode for SPEGSA

Step 1: Initialize Player Gravitational constant G₀, a, ɛ along with iteration counter t.

Step 2: Randomly generate the initial population which consists of N particles, the position of each particle defined by, for i =1,2..n

Step 3: Iterate until termination criteria are satisfied.

Step 4: Evaluation of all particles in the population is done and the best, worst particles are assigned.

Step 5: Updating of player gravitational constant by

Step 6: The force applied when particle j acts upon particle I at a specific time (t) is calculated.

Step 7: Total force acting upon particle i at iteration t is calculated.

Step 8: Calculate the inertial mass.

Step 9: The acceleration of the particle ‘i’ is calculated.

Step 10: Computer the velocity and position of the particle ‘i’.

Step 11: Loop steps until termination criteria are satisfied.

Step 12: Optimal Solution attained in the process.

5. Proposed Methodology

5.1.  Experimental Setup

This study makes use of the SPEGSA model and proposes an efficient way of finalizing the players required to be fielded for a game in soccer. This takes into consideration various attributes as variables of players, Jersey Number (JN), Age, Goals Assisted (GA), Goals Scored (GS), and Goals Saved (GSV). The model helps the coaches and managers in helping them to select the best 11 players for the next game in a league based on various parameters. The data set is passed through different numbers of particles and iteration in variation so that the results obtained are varied and recorded.  The parameter selection for goal scoring forecasting in which four input parameters were used for estimating the players to be shortlisted and in forecasting which was for a period of one season, such as Jersey Number, Age, GS, GA, GSV since the forecasting and evaluating of current players have been made for the next possible match.

5.2.  Dataset

The dataset available for the current season for a particular team playing in ‘A’ division football tournament and the College football team is considered and the range of values for a particular attribute is given. The parameters which are used in the present study are:

1. GA (Range: 0 to 8), ii. GS (Range: 0 to 8), iii. GSV (Range: 0 to 9), JN(Range: 1 to 23).

In the training process, the Dataset is passed through different values of NOP (Number of Particles) to calculate the mass and variations in the number of iterations. As with GSA, the data set will result in different approximations of best mass, and hence calculating it further will estimate the amount of goal scored and the team to be selected. The dataset has been trained for the following values of NOP and iteration, NOP=70 and iteration=900, NOP=100 and iteration=1000, NOP=70, and iteration=700, for which the best mass values were recorded and evaluated further. The GSA model is proposed which takes effect into all the variables until the current season data is defined in the equation “(8)”.

Where D_a0, D_a1, D_a2, D_a3, D_a4, and D_a5 are various coefficients that will be evaluated using SPEGSA and F_t determines the fitness function to find the number goals to be scored by a player.

5.3.  Estimating of Coefficients by SPEGSA

The main purpose behind this implementation is to enhance upon the aforesaid coefficients based SPEGSA algorithm from the player’s record on historical grounds of Goals Scored data. The parameters in total used in this model show the effect of the above-mentioned variables.  The model parameter can be evaluated to reduce the error between the current goal scored by a player and the simulated goal-scoring estimation output using the fitness function f, for SPEGSA is defined in the equation “(9)”

Where n represents the experimental data set values.

5.4.  Metrics and Performance

Our main objective is to compare the actual goal scored by a player in addition to other attribute values such as Goal Saved and Goal Assisted which will influence the coach or the manager to take unbiased decisions on team selection for optimal performance. Hence the error between the actual goal scored and estimation of goal scored is forecasted using i) Mean Absolute Error (MAE) ii) Mean Absolute Percentage Error (MAPE) iii) Mean Square Error (MSE) which are defined as follows.

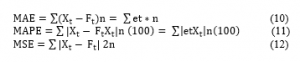
X_t is original data at period t, F_t is the estimation at period t, et is predicted forecast error at period t, while n is the number of observations.

6. Experimental Results

Estimation of goal scored by a player along with goal saved and assisted will optimize upon the best 14 players to be fielded at the time when maximum required and form the historical data of a player in the current season. These experimental evaluations of players might not only be pivotal for the manager or coach to select a player for the rest of the matches in the league but indeed will provide added information for selecting.

The particles in the problem space were assigned with the initial random values ranges between 0 and 1. Each particle will have its initial random position and velocity. Each particle will move place to place based on the amount of velocity and its position. The particle will have its own memory space to share their knowledge to reach the closest local best and hence reaches the global best. So, the minimizing function equation “(3)” reaches its global minima.

Table 1. Parameter Estimation Player Selection data model using SPEGSA

NOP/Iteration
	Da0	Da1	Da2
20/ 100	-0.5209	0.4979	0.0281
50/ 400	0.72929	-0.0724	0.02214
70/ 700	0.53006	0.15263	0.00455
70/ 900	0.34065	-0.6285	0.18529
100/ 1000	-0.0592	0.04748	0.25852

In SPEGSA Algorithm, every particle will have the following, its location, inertial mass, active gravitational mass, and passive gravitational mass. The SPEGSA parameters used in the Goal scoring model uses the number of mass as 70, initial position and velocity are random values between 0 and 1, gravitational constant (G) is 1.

Table 2. Parameter Estimation Player Selection data model using SPEGSA

NOP/Iteration
	Da3	Da4	Da5
20/ 100	1.5004	0.1972	0.5108
50/ 400	-0.7272	-0.6975	0.4576
70/ 700	0.03521	0.25772	0.3956
70/ 900	0.64474	1.07111	-0.1896
100/ 1000	0.19907	1.27980	-0.2068

Because of the random values generated at every point of execution have always got the best mass deterred from the previous one, which is required in this implementation. SPEGSA algorithm concept helps to explore and exploit the optimal values. The exploitation feature helps the particles in a particular region or environment to move towards another particle which has the heavier mass within the same. The values for G and M were calculated to update the position for each iteration until it reaches the optimal solution. The obtained results were tested using evaluation metrics, from different parameters that were available in our dataset such as, the actual goal scored, estimation from SPEGSA, and Fitness function.

The estimation of coefficients in “Table 1” and “Table 2” is for different values of NOP and Iterations respectively.

NOP=20 iteration=100

NOP=50 iteration=400.

NOP=70 iteration=700.

NOP=70 and iteration=900.

NOP=100 and iteration=1000.

Players for a club or team at the time of bidding. When a player is bought for 100 million pounds, what will be the impact of such players for the club to improve upon will be a rather difficult scenario when bidding of a player happens?  Hence the iterative method of multiple linear regressions using GSA was proposed to find the coefficient for Da0, Da1, Da2, Da3, Da4, and Da5 which is the current player record for the season.

Using these coefficients in the model equation “(4)”, the players selected on the number of goals scored is estimated for the known 23 data set of players, results once obtained were plotted in “Figure 4”, “Figure 5”, “Figure 6”, “Figure 7”, and “Figure 8”, respectively. The performances MAE, MAPE, MSE for the validated data of both the models were tabulated in “Table 1” and “Table 2”.

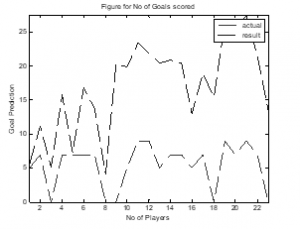
Figure 4: Goal Scored Estimation for NOP=20 and Iteration=100.

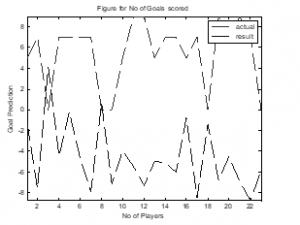
Figure 5: Goal Scored Estimation for NOP=50 and Iteration=400.

In “Figure 4”, the number of particles was considered as 20 and the iteration was 100 and it was observed that the i) Mean Absolute Error (MAE) was recorded with value 1.222073 ii) Mean Absolute Percentage Error (MAPE) was 22.30633 and iii) Mean Square Error (MSE) was 8.812746. As the NOP and iteration decreased considerably, the actual goal scored value for each player, and the estimated goal while plotted on the graph showed significant drift with relation to each other. And at any point in time, they had a resemblance to each other.

In “Figure 5”, the number of particles was considered as 50 and the iteration respectively was 100 and it was observed that, the i) Mean Absolute Error (MAE) was recorded with value 13.31048 ii) Mean Absolute Percentage Error (MAPE) was 175.0847 and iii) Mean Square Error (MSE)  was 218.3298. At this instance, the MAE, MAPE, and MSE experienced an exponential change in their values and it was conclusive that the actual and predicted results of goal scored had some instances of players matched but had a larger variance with each other.

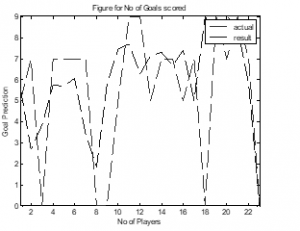
Figure 6: Goal Scored Estimation for NOP=70 and Iteration=700.

In “Figure 6”, the number of particles was considered as 70 and the iteration respectively was 700 and it was observed that, the i) Mean Absolute Error (MAE) was recorded with value -2.72485 ii) Mean Absolute Percentage Error (MAPE) was 30.82959 and iii) Mean Square Error (MSE)  was 9.821473. The actual goal scored value for each player and the estimated goal while plotted on the graph showed that for every player the results obtained for actual and estimated run parallel to each other and did not drift away at many points of time.

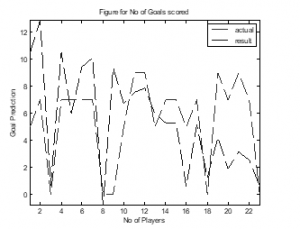
Figure 7: Goal Scored Estimation for NOP=70 and Iteration=900.

In “Figure 7”, the number of particles was considered as 70 and the iteration respectively was 900 and it was observed that the i) Mean Absolute Error (MAE) was recorded with value -0.03328 ii) Mean Absolute Percentage Error (MAPE) was 36.41223 and iii) Mean Square Error was (MSE)  14.08006. The actual goal scored value for each player and the estimated goal scored were significantly matching and hence the actual and predicted goal scored values were best for the set of values considered for NOP and number of iterations.

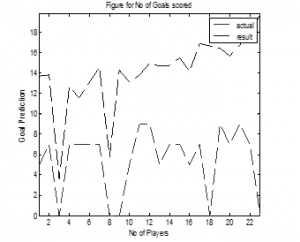
Figure 8: Goal Scored Estimation for NOP=100 and Iteration=1000.

In “Figure 8”, the number of particles was considered as 100 and the iteration respectively was 1000 and it was observed that, the i) Mean Absolute Error (MAE)was recorded with value -1.01699 ii) Mean Absolute Percentage Error (MAPE) was 13.69986 and iii) Mean Square Error (MSE) was 12.14193. The actual goal scored value for each player and the estimated goal while plotted on the graph showed that for every player there was a significant drift in terms of results.

In the above graphs plotted against various values of NOP and Iteration, we have varied with different values for the same to observe the kind of results obtained for MSE, MAE, and MAPE and have observed the approximations what the estimations predict. Observations from “Figure 5”, “Figure 6”, “Figure 7”, and “Figure 8” have estimations which are not close to the actual goal-scoring capability of every player in the team, and hence the lines in each of the graph are escalated above each other and run in parallel. But in “Figure 6” we observe that the lines in the graph intersect at regular intervals indicating a substantial coincidence in the estimation of goals scoring.

The proposed model helps to understand that even though a change in NOP and iterations yield us optimal results, even though in some instances the input parameters in the dataset have better accuracy. As shown in “Figure 6”, the goal scored in actual and estimated is accurate. The efficiency of SPEGSA is enhanced with sufficient parameters of soccer and GSA. The experimental analysis was made by varying the number of iterations and particles with the existing parameters yield better results with an accuracy of 90.18%. Hence the efficiency of the player predicting model performed well was evident from the results of GSA tabulated.

7. Conclusion and Future work

The GSA model was proposed to estimate the coefficients of goal prediction and player predicting model. Based on the models developed, trained, and validated, the estimated results which were observed can be improved and bettered in quite propositions. Hence the dataset can be trained with more statistical methods and Soft computing techniques such as Neural Networks and Backpropagation method.

Conflict of Interest

We know of no conflicts of interests associated with this publication, and there has been no significant financial support for this work.

1. N. Moosavian a and H. Moosavianb (2017). “Testing Soccer League Competition Algorithm in Comparison with Ten Popular Meta-heuristic Algorithms for Sizing Optimization of Truss Structures”, IJE TRANSACTIONS A: Basics Vol. 30, No. 7, pp 926-936.10.5829/idosi.ije.2017.30.07a.01
2.  Darren J Paul and George P Nassis (2015), “Testing Strength and Power in Soccer Players The Application of Conventional and Traditional Methods of Assessment”, Journal of Strength and Conditioning Research”, pp 1748-1758.
3.  Miguel Angel Pe´rez-Toledano1, Francisco J. Rodriguez, Javier Garci ´a-Rubio, Sergio Jose ´ Ibañez (2019), “Players’ selection for basketball teams, through Performance Index Rating, using multi-objective evolutionary algorithms”
4.  Muhammad Bukhari Burhanudin, Muhammad Syasman suhaimi, Muhammad Thaquif Isa, Umi Kalsom Yousuf, Mohd Nor Akmal Khalid (2018), “ Football Player Selection Using Fuzzy Logic”, pp 1-7.
5. Bastien Talgorn, Sebastian Le Digabel, Micheal Kokkalaras, “Statistical Surrogate Formulations for Simulation-based design optimization”, Vol 137, Issue 2, Journal of Mechanical Design”, 2015.
6.  S. Sankaran, Charles Audet, Alison L, “A method for stochastic constrained optimization using derivative-free surrogate pattern search and collection”, Vol 229, Issue 12, pp 4664-4682, 2010.
7. Pooriya Beghai, Daniel Caragieri, Thomas Bewley, “Delaunay-based derivative-free optimization via global surrogates, Part I: Linear constraints”, Journal of Global optimization, pp 1-52, Springier, 2015.
8. Charles Audet, Christophe Tribes, “Mesh-based Nelder-Mead algorithm for inequality constrained optimization”, Computational Optimization and Applications. Vol 71, Issue 2, pp 331-352, Springier, 2018.
9.  Kelton A.P Costa, Luis A.M. Pereira, Rodrigo Y.M, Nakamura, Clayton R. Pereira, Joaa.P.Papa, and Alexandre Xavier Falco, (2015). ”A nature inspired approach to speed up optimum path forecast clusterist”, Elsevier, Information Science, doi:10.1016/j.ins.2014.09.025
10.  Abhinav Sharma, Sanjay Mathur, and R. Gowri (2018). “Adaptive beamforming for linear antenna using Gravitational Search Algorithm”, Springer, AISC Vol 624, doi: 10.1007/978-981-10-5903-2_121
11.  Damodar Reddy Edla, Diwakar Tripathi1, Ramalingaswamy Cheruku1, and Venkatanareshbabu Kuppili1 (2017). “An Efficient Multi-layer Ensemble Framework with BPSOGSA-Based Feature Selection for Credit Scoring Data Analysis”, Springer Link, Arabian Journal for Science and Engineering, doi: 10.1007/s13369-017-2905-4
12.  P. B. de Moura Oliveira, Josenalde Oliveira, and José Boaventura Cunha (2018). “Trends in Gravitational Search Algorithm,” Springer International Publishing. doi: 10.1007/978-3-319-62410-5_33
13. Tongziang Wang, Xiangling Wei, Jianhua Fan, and Tao Liang (2018). “Adaptive Jammer Localization”, Elsevier, Vol 141, doi/10.1016/j.comnet.2018.05.002.
14. Rajendra Kumar Khndanga and Jitendriya Ku Satapathy (2015). “ A new hybrid GA- GSA algorithm for tuning damping controller parameters for a unified power flow controller”, International Journal of Electrical Power and International Journal of Electrical power and Energy systems, doi: 10.1016/j.ijepes.2015.07.016
15. Mohammad Massoud Javidi and Fatemeh Zarsifi Kermani (2017). “Utilizing the advantages of both global and local search strategies for finding a small subset of features in a two-stage method”, Springer Link, doi:10.1007/s10489-018-1159-5.
16. Ehsanol ah Assareh and Majtaba Biglari z (2015). ”A novel approach to capture the maximum power from variable speed wind turbines using PI controller, RBF neural network and GSA evolutionary algorithm”, Elseivier, Renewable and sustainable energy reviews, doi:10.1016/j.rser.2015.07.034
17.  Mohamed A. Tolba1,Ahmed A. Zaki Diab1,Vladimir N. Tulsky1, and Almoataz Y. Abdelaziz (2018). VLSI approach for optimal capacitors allocation in distribution networks based on hybrid PSOGSA optimization algorithm”, Springer link, doi: 10.1007/s00521-017-3327-7.
18. Bo Xing and Tshidlidzi Marwala (2018). “Introduction to intelligent search Algorithms”, Springer Link Smart Maintainance for Human Robot Interaction, SSDC, Val 129, pp 33-64.
19.  Alli A and D. Jhon Aravindhar (2017). ” A Comparative Study on Cash Management Models using Soft Computing Techniques”, International Journal of Applied Engineering Research ISSN 0973-4562 Volume 12.
20.  Beatriz Gonzalez, Fevrier Valdez, and Particia Melin (2017). “ A Gravitational Search Algorithm using Type – 2 Fuzzy logic for parameter adaption”, Springer linkg SCI, Vol 667, pp 127-138.
21.  Kyuchang Kang, Chang Seaok Bae, Henry Wing fung yeung and yuk ying chung (2018) “ Hybrid Gravitational Search Algorithm”, Elsevier Applied soft computing, Vol 66, pp 319-329.
22. R. Priyadarshini, M. R. Panda, and N. Dash (2017).” An Improvised Backpropagation Neural Network Model Based on Gravitational Search Algorithm for Multinomial Classification”, Springer Link, doi: 10.1007/978-981-10-6890-4_17.
23.  Esmat Rashedi, Elaheh Rashedi, and Hoosein Nezamabadi pour (2018). ”A Comprehensive Survey on Gravitational Search Algorithm”, Elsevier, Swarm and Evolutionary computation available online.
24.  Seyed Ali Mirjalli and Amir Gandomi (2017). “Chaotic gravitational constants for Gravitational Search Algorithm”, Elsevier, Vol 53, pp 407-419.

(Click Here)

(Click Here)