1. Introduction

This article is an extended version of a conference paper presented in 2019 at the International Conference on Control and Fault-Tolerant Systems [1].

Networked Control System (NCS) is a new generation of systems where the control loop is closed through a communication network. The defining feature of an NCS is that system states and control law exchange between the components of the system (sensors, actuators, and controllers) in the form of information packages via a wireless network. The use of wireless network diminishes system wiring, simplifies maintenance and diagnosis, and improves the system agility [2,3]. Nonetheless, the introduction of the wireless network to control the physical process brought some challenges, such as induced delay, and packet dropout, which harm the stability and reduce the system’s performances. The model of the NCS with data packet dropout and network induced delay has been treated in [4–6]. There are also other challenges of using the network as a mean to impart the information between the system components, like malicious intrusions, viruses, and cyber-attackers who always find a way to access the system network and make critical damages. Consequently, reinforcing system security attracts the attention of the specialists. Remarkable papers have studied the security of the network and the cyber-attacks [7].

This article addresses a particular cyber-attack, termed as replayattack, studied first in [8]. At our best knowledge, the trajectory tracking control (TTC) problem of NCS under a replay-attack based on an accurate mathematical model of the replay-attack is not fully investigated, and this will be the subject of this paper. In our previous work [1,9,10], we modeled the NCS under a replay-attack in three different ways. In [10], we used the Markovian jump linear system to model the replay-attack. In [1], we neglected the communication delay, and we assumed that the adversary attacks just the sensor reading, and in [9], we supposed that the adversary attacks the sensor reading and the actuator’s inputs simultaneously. This article involves a new contribution compared to the studies mentioned above. In this study we will give a new model of the NCS against a replay-attack, in which we take into account the effect of the delay that exists in the communication channel (sensor-controller).

This extended version deals with the TTC of a DC motor controlled through a wireless network and exposed to a replay-attack. The adversary seeks to destabilize the system by recording secretly the sensor reading and subsequently replayed it to the controller. To protect its anonymity on the network and stay undetectable for the most prolonged period, the adversary appears at different times (randomly), that sounds similar to the Stuxnet cyber-attack [11]. Moreover, we will take into account the packet dropout and the delay in the communication channel (sensor-controller). Nevertheless, the communication channel (controller-actuator) will be supposed perfect, that means 100% of packets have successfully arrived at the actuator from the controller without any delay.

The study will contain four fundamental parts. We will start by defining the structure of the global system. Then, we will give the model of the network. After that, we will provide our model of the replay-attack. Finally, by using the linear matrix inequalities (LMIs) formulation and the cone complementary linearization (CCL) approach we will calculate the controller gain which helps us to find the TTC gain.

2. Structure of the Global System

The structure of the NCS against a replay-attack is given in Figure1. The sensor measurement z(k_i), which has successfully arrived at the controller ( the switch S1 is closed ), will be first saved in a buffer. If a measurement z(k_i) is lost during the transmission ( the switch S1 is opened ), the controller will utilize the measurements that are already stocked in the buffer to calculate the new control law v(k_i). To avoid being detected by the classical detectors, the adversary will apply the attack at various times (randomly). The switch S2 models the replay-attack, if S2 is opened this means there is no attack in the buffer, whereas if S2 is closed this means there is an attack; this switching will harm the stability and the system’s performances, which will reflect negatively on the trajectory tracking.

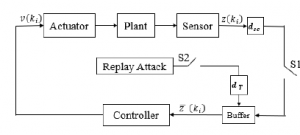
Figure 1: System architecture.

The plant of the system is defined as follows:

where z(k_i) ∈ Rⁿ is the system state and v(k_i) ∈ R^m is the control law. G ∈ R^n×n is the state matrix and H ∈ R^n×m is the input matrix. The state feedback controller is:

where F₁ is the controller gain, and z¯(k_i) ∈ Rⁿ is the controller input which will be defined in the next subsections.

2.1        Wireless network model

The iterative approach described in [12,13] was adjusted to give a model of the wireless network with the packet dropout and the communication delay d_sc in the channel (sensor-controller).

The Figure 2 shows the packets sent from the sensor to the controller. The green packets represent the received packets, whereas the red ones represent the dropouts packets. The notations k_i and k_i + m represent respectively the green packets and the red packets, where ,i ∈ Z and ,m ∈ N^∗.

At first, we will ignore the effect of the replay-attack and we will concentrate on the data packet dropout and the communication delay. Hence, the controller input can be written as:

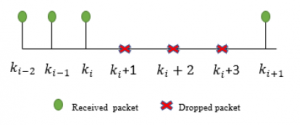
Figure 2: Received and lost packets [12].

As reported by Figure 2, the iterative approach can be defined as:

with N is the number of successive dropped packets.

2.2        Replay-attack model

We assume that an attacker has connected to the buffer can replace the received packet z(k_i) by the previous one z(k_i−dT ), with d_T is the replay-delay. For example, in the Figure 3 the third packet (102) was exposed to an attack with d_T=2T_e, so it was replaced by the first packet (100). The same for the packet (200) which was replaced by the packet (198).

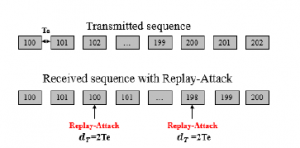
Figure 3: Replay-attack.

As reported by Figure 3, the system under a replay-delay can be defined as:

The overall system will switch between two subsystems. Subsystem 1 if S2 is ”off”, and subsystem 2 if S2 is ”on”. From (4) and (5) the global system becomes:

Therefore, the overall system can be equivalent to an asynchronous dynamical system expressed in (8), with

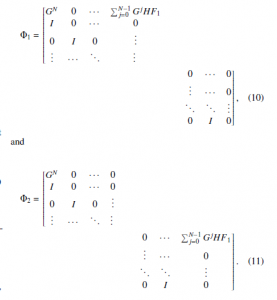
3.  Stability and Control Design

Lemma 1 [14] The asynchronous dynamical system z_k+1 = f_s(z_k), s = 1…N⁰, is exponential stable if there exists a Lyapunov function where β₁||z||² ≤ V(z) ≤ β₂||z||², β_1,2 > 0, and given positive scalars α_s satisfying:

Then, the system (8) is exponential stable.

Proof: applying (12) to (8), we have

Remark 1 It is clear that (18) is not linear because of the existence of P₁ and its inverse P⁻₁¹ in the same matrix. To fix this problem we will make a change of variable (P₂ = P⁻₁¹), and to guarantee the convergence of P₂ to P⁻₁¹, we will use the CCL approach [15]. The inequality matrices (18) becomes:

4.  Application

4.1        DC motor Model

A DC motor is a machine which converts direct current electrical power into mechanical power. The DC motor has vast applications in many fields including NCS. Owing to this importance, we chose the DC motor as an application system where we will apply our approach.

In this paragraph, the mathematical model of a DC motor will be studied.

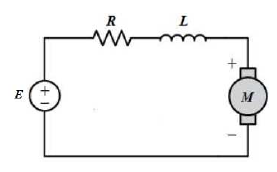
Figure 4: DC motor equivalent circuit model.

As shown in Figure 4, the system input is the voltage source

(E), while the system output is the rotational speed θ˙. The physical parameters of the DC motor are given in Table 1:

Table 1: Physical parameters of the Dc motor.

Symbol	Description	Value
J	Moment of inertia	0.02 Kg.m2
b	Motor viscous friction constant	0.2 N.m.s
Ke	Constant of emf	0.02V.s/rad
Kt	Motor torque constant	0.02N.m/A
R	Resistance	1.5 Ω
L	Inductance	0.5H

The motor torque and the back emf (e) are given in (23) and

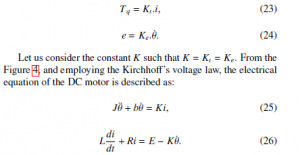
If we choose [θ,˙ i]^T as a state variables, the state space representation will be written as:

Replacing the parameters by their values, the state space representation becomes:

The command ”c2d” in Matlab is used to passe from the continuous-time to discrete-time, where the sampling time is T_e = 0.1s. The discrete-system can be written as follow:

Figure 5: DC motor control under network issues.

The Figure 5 shown the structure of the DC motor under wireless network issues. The initial condition is z(0) = [0 0]^T, v_i = 0, for i ≤ 0, the maximum number of the successive packets losses during the transmission is N=3 packets, the communication delay equals to 0.1s, and the replay-delay equals to 0.3s, that means d_sc = 1, and d_T=3. We will study three different situations. In the first situation, the event rate of the switch S2 equals 0.1, in the second situation, the event rate equals 0.5, in the third, the event rate equals 0.9.

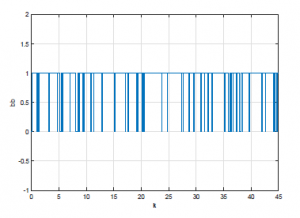
Figure 6: Event rate of S2 is 0.1.

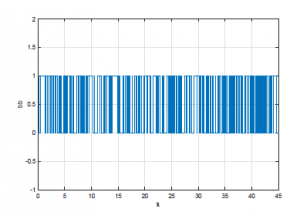
Figure 7: Event rate of S2 is 0.5.

Figure 8: Event rate of S2 is 0.9.

The figures (Figure 6, Figure 7, Figure 8) show the different event rate of the switch S2. 0.1, 0.5 and 0.9 respectively.

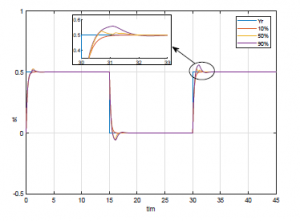
Figure 9: Trajectory tracking.

According to Theorem 1, the LMIs are feasible for α₁ = 0.1 and α₂ = 0.45. Solving the LMIs in Theorem 1 utilizing the Yalmip toolbox, we can find the controller gain and the trajectory tracking gain of the system as follow: F₁ = [0       0.0012] and F₂ = 20.9085.

From Figure 9, we can see that if the event rate of the switch S2 equals 0.1 (the percentage to have an attack is 10%) the output can tracks perfectly the trajectory Y_r, the same thing happens if the chance to have an attack rises to 50% or 90%. But, in these two cases an overshoot appears. However, the results stay acceptable, which reflects the potency of our approach.

5. Conclusion

This paper dealt with the TTC issue of a DC motor controlled through a wireless network. In this extended version, we took into account the packet dropout and the delay in the communication channel (sensor-controller). On the other hand, the communication channel (controller-actuator) was assumed perfect, that means all data have successfully transferred from the controller to the actuator without any delay. We also considered that the DC motor exposed to a replay-attack, where a cyber-adversary sought to destabilize the system and diminished its performances. A new mathematical model of the NCS under replay-attack was proposed. A sufficient condition for the stability of the resulting asynchronous dynamical system was given in the form of LMIs. The controller gain F₁ and the trajectory tracking gain F₂ were obtained by solving these LMIs employing the CCL approach. Finally, the simulation results proved the effectiveness of our approach. As a perspective of this study, our attention will be oriented towards studying the same problem with communication delay and packets losses in both communication channels.

1. R. El Abbadi and H. Jamouli, “Stabilization of cyber physical system with data packet dropout and replay attack via switching system approach,” in 2019 4th Conference on Control and Fault Tolerant Systems (SysTol). IEEE, 2019, pp. 325–329, doi: 10.1109/SYSTOL.2019.8864787.
2. T. C. Yang, “Networked control system: a brief survey,” IEE Proceedings- Control Theory and Applications, vol. 153, no. 4, pp. 403–412, 2006, doi: 10.1049/ip-cta:20050178.
3. J. P. Hespanha, P. Naghshtabrizi, and Y. Xu, “A survey of recent results in net- worked control systems,” Proceedings of the IEEE, vol. 95, no. 1, pp. 138–162, 2007, doi: 10.1109/JPROC.2006.887288.
4.  J. Xiong and J. Lam, “Stabilization of linear systems over networks with bounded packet loss,” Automatica, vol. 43, no. 1, pp. 80–87, 2007, doi: 10.1016/j.automatica.2006.07.017.
5.  L. Qiu, Q. Luo, S. Li, and B. Xu, “Modeling and output feedback con- trol of networked control systems with both time delays; and packet dropouts,” Mathematical Problems in Engineering, vol. 2013, 2013, doi: 10.1155/2013/609236.
6.  L. Qiu, Q. Luo, F. Gong, S. Li, and B. Xu, “Stability and stabilization of networked control systems with random time delays and packet dropouts,” Journal of the Franklin Institute, vol. 350, no. 7, pp. 1886–1907, 2013, doi: 10.1016/j.jfranklin.2013.05.013.
7.  J. M. R. Hernan, “Detection of attacks against cyber-physical industrial systems,” Ph.D. dissertation, 2017.
8. Y. Mo and B. Sinopoli, “Secure control against replay attacks,” in 2009 47th Annual Allerton Conference on Communication, Con- trol, and Computing (Allerton). IEEE, 2009, pp. 911–918, doi: 10.1109/ALLERTON.2009.5394956.
9. R. EL Abbadi and H. Jamouli, “Stabilization of a cyber physical system with network issues,” in 2019 8th International Conference on Systems and Control (ICSC). IEEE, 2019, pp. 508–512, doi: 10.1109/ICSC47195.2019.8950544.
10. R. El Abbadi and H. Jamouli, “Stabilization of cyber physical system ex- posed to a random replay attack modeled by markov chains,” in 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT). IEEE, 2019, pp. 528–533, doi: 10.1109/CoDIT.2019.8820311.
11.  P. Shakarian, J. Shakarian, and A. Ruef, “Attacking iranian nuclear facilities: Stuxnet,” Introduction to cyber-warfare: A multidisciplinary approach, pp. 223–239, 2013, doi: 10.1016/B978-0-12-407814-7.00013-0.
12.  A. Routh, S. Das, and I. Pan, “Stabilization based networked predictive con- troller design for switched plants,” in 2012 Third International Conference on Computing, Communication and Networking Technologies (ICCCNT’12). IEEE, 2012, pp. 1–6, doi: 10.1109/ICCCNT.2012.6396001.
13. M. Yu, L. Wang, T. Chu, and G. Xie, “Stabilization of networked control systems with data packet dropout and network delays via switching sys- tem approach,” in 2004 43rd IEEE Conference on Decision and Control (CDC)(IEEE Cat. No. 04CH37601), vol. 4. IEEE, 2004, pp. 3539–3544, doi: 10.1109/CDC.2004.1429261.
14.  A. Rabello and A. Bhaya, “Stability of asynchronous dynamical systems with rate constraints and applications,” IEE Proceedings-Control Theory and Ap- plications, vol. 150, no. 5, p. 546, 2003, doi: 10.1049/ip-cta:20030704.
15.  L. El Ghaoui, F. Oustry, and M. AitRami, “A cone complementarity lin- earization algorithm for static output-feedback and related problems,” IEEE transactions on automatic control, vol. 42, no. 8, pp. 1171–1176, 1997, doi: 10.1109/9.618250.

(Click Here)

(Click Here)