1. Introduction

As a substitute competitor for radio frequency (RF) communications, visible light communication (VLC) has lately brought significant attention of researchers, accompanied by the growing popularity of the emerging solid-state lighting like the laser diode (PD) and then light-emitting diode (LED) to realize the conventional illumination sources thanks to their extraordinary efficiency and massive bandwidth, exceptional security, inexpensive cost, independence from the spectral licensing problem, simple implementation into existing infrastructure [1,2]. In conventional VLC systems that convey information based on LEDs, because of the low hardware-cost and simplicity of implementation, the intensity-modulation (IM) with direct-detection (DD) designs are employed. Furthermore, the communications systems with optical multiple-input multiple-output (MIMO) techniques [3–6] can be engaged to obtain various data transmission rates [7]. Though, MIMO-VLC systems, which heavily depend on channel correlations, severely influence the achievable performance [8]. On the other hand, various modulation schemes have been proposed for MIMO-VLC, such as repetition code (RC), spatial modulation (SM), and spatial multiplexing (SMP) [9]. In RC the same signal is emitted simultaneously from all transmitters.

In SM, the conventional signal constellation diagram is extended to the spatial dimension, in which only one transmitter is activated at any symbol duration. In SMP, independent data streams are simultaneously emitted from all transmitters.

Recently, an appealing design named collaborative constellation

(CC) concerning MIMO-VLC systems with various numbers of PDs and LEDs was introduced [10]. To outlining the transmitted constellation of varied LED spaces, the Euclidean distances (EDs) were simultaneously maximized following the constrains in average transmit power. Later, to considerably enhanced the design of CC, the channel adaptive space CC (CASCC) was proposed in [11] by taking the channel influences on the system model into consideration. More particularly, in expressions including four primary points, CASCC design intended to a 2 × 2 MIMO systems and later prolonged to higher-order constellations. Noticeably, the idea about CASCC mentioned in [11] can accommodate to different channels among variations in positions of both LEDs and PDs.

In this study, we offer a practical algorithm to outline a multilayer CC (ECC) for MIMO-VLC system utilizing simultaneously the space-collaboration and channel-adaptation ideas [3]. Furthermore, the introduced approach attends to produce the constellations of each size based on particular primary points. Besides, with the help of the multilayer constellation scheme, the offered design can minimize the amount of constraint presented in optimization problems. More precisely, our offered design analyzes the distance of every pair of points; also, the form of the constellation in the PDs does not have to be distinct as in CASCC. Our proposed scheme considers the distance of any two constellation points and the shape of constellation in receiver space does not have to be a diamond shape. Hence, effectively design the adaptive collaborative constellation and achieve SNR gain in comparison with CASCC, both under perfect and imperfect CSI. Consequently, ECC efficiently produces the adaptive constellation and gains a notable SNR enhancement in comparing to CASCC including different designs.

2. Transmission model

In this study, the introduced principle of the ECC for MIMO-VLC systems, comparable to [10,11], have the numbers of LEDs and PDs are n = 2, respectively. Furthermore, we denote C that contains m = 2^r symbols as the constellation at the transmitting side, that is C = {x₁,…,x_m} with r bits as the transmission rate. Moreover, with x_α⁽¹⁾ denotes the signal value transmitted from 1th-LED while x_α⁽²⁾ denotes the signal value transmitted from 2th-LED, the overall transmitted signal x_α is represented as x. Since we have the number of constellation points in C should be a power of two, hence we at the beginning present detail procedure to design a constellation with several layers, so-called X. After the constellation X is initially formed, by picking a subset of constellation point in X, the constellation set C is optimally obtained. This is clear since the proposed constellation X with the number of layers is l, will have l(l + 1)/2 as the cardinality.

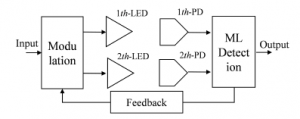
Figure 1: System model.

Following the constellation introduced in [10], a set of constellation points that contained in a number of g layers is first described . It can bee seen that, in the g-th layer of constellation (g=1, …,l), as shown in Fig.1 there areg points. Moreover, begin by the primary points x11 = (0,0)T , x21 = (x21(1), x21(2))T, and x22 = (x22(1), x22(2))T, the g layers constellation set can be obtained with x_αp = (x_α⁽¹_p⁾, x_α⁽²_p⁾)^T denotes the p-th constellation point in the α−th layer of the pro-

posed constellation set, and x_α⁽¹_p⁾, x_α⁽²_p⁾ denote the signal values that can be transmitted simultaneously by both 1th-LED and 2th-LED, respectively. Moreover, the at the transmitter side, the constellation set X will be expressed by

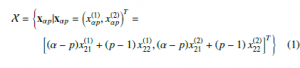
with 1 ≤ p ≤ α,1 ≤ α ≤ l.

The line-of-sight (LOS) VLC systems, which comprise two LEDs and two PDs is analyzed in this study. Moreover, the received signal y at the receiver, with x = x⁽¹⁾, x^(2)T are the conveyed signals and the i-th LED signal is denoted as x⁽ⁱ⁾, similar to, [11], can be rewritten as

Besides, we assume that n is the n_t ×1 additive white Gaussian noise with zero mean and σ² is the variance. Moreover, the assumption that the LEDs’ sufficient knowledge about the channel matrix H of size 2 × 2 through feedback channel is acceptable. Also, the channel element h_ji between the j-th PD and the i-th LED is described by [1] 

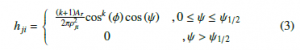
where the angle-of-emergence with the LED axes and the angleof-incidence with its normal axes can be denoted as φ and ψ, respectively. Also, the receiving area of the PDs can be generally expressed by A_y. ψ_1/2 indicates the field-of-view semi angle of the PDs. The distance from the j-th PD to the p-th LED is denoted as ρ_ji. The Lambertian order k will be described by k = _ln(cos^−ln2_Φ1/2₎ with the half-power semi angle of the LEDs is Φ_1/2.

On the other hand, with y⁽_α¹_p⁾,y⁽_α²_p⁾ denoting signals received by PD₁ and PD₂, the received symbol at both PDs y_αp can be expressed as follows

where the corresponding transmitted constellation x_αp ∈ X, X =

[x₁₁,x₂₁,x₂₂,x₃₁,x₃₂,x₃₃,…,x_l1,x_l2,…x_ll] and the channel matrix H of size 2 × 2. Therefore, the constellation in the PDs will be expressed as Y = y₁₁,y₂₁,y₂₂,y₃₁,y₃₂,y₃₃,…,y_l1,y_l2,…y_ll. Additionally, we have |Y| = |X| with Y = HX. Any symbol belong to X, as previously remarked in [11], will be exclusively assigned to Y. As a result, Y is

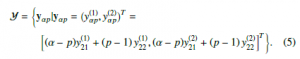
With a l layers-constellation set, the cardinality of it is calculated as l(l + 1)/2. Furthermore, there is the need to bound the number of layers l by using the constrain that l(l + 1)/2 ≥ M with a M = 2^y points constellation C. Therefore, we arrive at the condition that l  . Besides, to maintain a r bits constellation C from the primary constellation-points x₁₁,x₂₁,x₂₂, following steps are performed to obtain the full constellation:

Input: matrix {x₁₁,x₂₁,x₂₂} where x₁₁ = (0,0)^T, size of constellation.

Output: the optimal constellation set C

• Compute g
• Assign X = {x₁₁,x₂₁,x₂₂}
• form the full l(l + 1)/2 symbols – For α = 3 to l
• For p = 1 to α
• End
• End

Choose the set C from the set X to be the optimal constellation set.

• For xα_p ∈ X
• Choose M = 2^y constellation symbols that are nearest from (0,0) to make the set C.
• End
• With the power level requirement, normalize the set C.
• Output the set C as the final optimal constellation set.

3. Proposed design

In this section, the set of primary constellation points is adequately decided to maximize the minimum Euclidean distance between any two constellations on the receiver side. The optimization problem which can be manipulated to create a l layers constellation X that enhance the distance between each pair of points from the obtained constellation under the total average transmitting power P_max. More specifically, the optimization problem purpose is to determine optimal primary points x₁₁,x₂₁,x₂₂. Also, at the receiver, the constellation is Y = HX. Then, the resultant primary points will then be used to acquire l layers constellation. Moreover, we set µ = α − β; γ = p − q with the assumption that α ≥ β ≥ 1 without any loss of generality. We also define in this study the minimum Euclidean distance d_Y among any two constellation points y_αp,y_βq. In here, y_αp,y_βq are the elements of a particular Y.Consequently, the primary points x₁₁,x₂₁,x₂₂, based on the aforementioned criterion, would be optimally designed. From equation (5), The Euclidean distance among any two points, y_αp,y_βq ∈ Y will be expressed as

Still, to determine the global solutions of P−2 is challenging because P−2 is a non-convex optimization problem. Accordingly, the convex relaxation strategy can be engaged in order to approximate

P−2. More specifically, by linearizing u^Tv_(µ−γ)γu in u_k, the relaxed optimization problem can be presented as

P−3 :       max p

s.t.:             2u^T_k v₍µ₋γ₎γu − u^T_k v₍µ₋γ₎γu_k ≥ p;(µ − γ,γ) ∈ Φ

PX ≤ Pmax

Furthermore, because P−3 surely is a convex optimization problem, the optimization package helpful in solving convex optimization problems can be engaged to solve (P3). Besides, the initial primary constellation points are assumed as x₁₁ = (0,0)^T ,x₂₁ = (0.1,0.1)^T ,x₂₂ = (0.2,0.2)^T. Moreover, to efficiently overcome and lessen the complexity cost of solving the design optimization problem, we try to reduce the total number of constraints by defining the set Φ as Φ = (0,1);(1,0);(a, −b)|1 ≤ a,b. Moreover, to calculate the greatest common divisor between a and b, we denote a function as gcd(a,b). With the M”obius function µ(k), the cardinality of the constrain set is |Φ| = 2 + ^Pl_k−₌1₁ µ(k)jl−k1k2.

4. Generalized Constellation Design for MIMO-VLC systems

Because of the restrictions of this study, the constellations designing problem is chiefly centered on 2 × 2 MIMO VLC systems. This limitation was mentioned in [10,11] because of the mathematical complexity and large volume of numerical contents. Therefore, we shortly illustrate the idea in designing the ECC for larger numbers of LEDs and PDs. Perceive that optimization can be acquired, and the equivalent design rule would be achieved without any problem. Nevertheless, the main restriction in getting the optimal points for a larger numbers of LEDs and PDs rests in huge complexities of the optimization-problem solving when high quantities of variables and constraints are examined.

Consequently, in here a MIMO-VLC system with transmitter constellation C of M = 2^r symbols is considered and can be de noted as C = [a₁,…,a_M] where a_i = a_i ,a_i ,…,a_i ∈ C is a signal vector that can be conveyed through multiple LEDs. With n_t transmitters, we define a multidimensional layered constellation that each N_i-th-dimension (N_i-D) layer comprises all (N_i − 1)-D layers; for example, with n_t = n_r = 2, an 1D-layer can belong to a line, as in Fig.1; with n_t = n_r = 3, a 2D-layer consists of all 1D-layers that lie in it, and every 1D-layers is a line that can be similarly constructed as in n_t = n_r = 2; and so on the proposed constellation for any n_t = n_r can be built by generating all constellation-points belong to (n_t−1)D-layers. Similar to the 2×2 case, a constellation-point can be

represented as xα1α2…αnt = xα(11)α2…αnt , xα(21)α2…αnt ,…xα(n1tα)2…αnt Twhere the signal transmitted by the p-th LED will be rewritten as

where the primary points of the constellation here are x_11…1 = x,…, x222…2 and 1 ≤ αnt ≤ αnt−1 ≤ … ≤ α₂ ≤ α₁ ≤ L. Moreover, there will be l!/n_t! points in the constellation. Then, with any transmitted constellation x_{α1α2…αnt} ∈ X,

X = x₁₁₁…₁,x₂₁₁…₁,…,x_ntn_tn_t…_nt , we define the corresponding received constellation Y at the n_r PDs by vector y_{α1α2…αnt} using equation (4) and |Y| = |X|. It is observed that the constellation when n_t = n_r = 2 can be consider as a particular case. Even though not detailedly considered in this article, the constellation C o higher dimensions will be produced from a collection of primary points {x₂₁₁…₁,x₂₂₁…₁,…,x₂₂₂…₂} by a generalization of the algorithm in previous section. Following that, the optimization problem of the constellation forming can be readily determined in an equivalent way similar to P−0. The method of simplifying and solving the optimization problem is conceivable by orderly extending the method outlined in this article without any mathematical challenge. Nonetheless, this article focuses on the 2 × 2 VLC-MIMO scheme as earlier studies [10,11] and the expansion to the system with a higher numbers of PDs and LEDs will be presented in later study.

5. Simulation results

In this sector, the performances of the proposed ECC are presented in comparison with various conventional constellation design techniques in MIMO-VLC. Moreover, the CC and also the CASCC designs are utilized in systems with two LEDs and two PDs. Furthermore, A_r = 1cm², Φ_1/2 = 60^o, and ψ_1/2 = 60^o. Besides, the full transmitting power value is the same between the constellations to ensure between the compared schemes the fairness. As mentioned in [10,11], SNR value can be determined with the normalized channel matrix H and x. We generate a channel realization that is the channel matrix.

5.1        BER Performance With Perfect CSI

Initially, the BER performances of CC, ECC, and CASCC are shown in Fig. 2 for a low bit rate and in Fig. 3 for a high bit rate. More particularly, in the simulations, we fixed the values of the transmission rate r to 4, 8, 10, and 12 bits. It is perceived that when related to different designs such as CC and CASCC, ECC presents more beneficial BER performances. An SNR gain of around 2dB in relation to CASCC can be achieved in ECC. Nonetheless, ECC and CASCC produce remarkable performance gains through employing the spatial source. Besides, by considering the influence of channel coefficients in the optimization problem, the offered ECC and CASCC exceptionally relieve the association among LEDs. Moreover, ECC seeks to lessen the influence of channel correlation by further efficiently enhancing the Euclidean distances among symbols in the constellation under the equivalent power constraint in corresponding with CASCC. Hence, the offered ECC in overall can obtain more excellent performance for MIMO-VLC in comparison among different constellations.

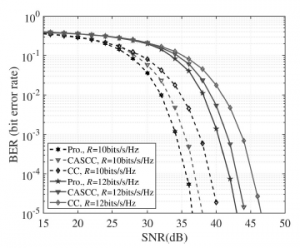
Figure 2: BER performances comparison where r = 4, 8 bits.

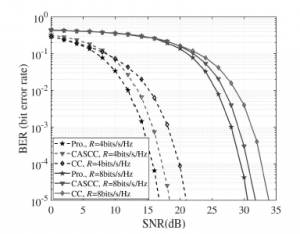
Figure 3: BER performances comparison where r = 10, 12 bits.

5.2        BER Performance With Imperfect CSI

Meanwhile, the channels in VLC for any particular transmitter and receiver fixed positions or specifications are deemed deterministic. In fact, the hypothesis of ideal CSI at the transmitter side is generally not vigorously practical for the indoor VLC environment [12]. To favorably obtain the conveyed symbol with a necessary degree of certainty, the information of each channel coefficient at received PDs would be of significant concern. Consequently, to assess and produce insights on the impairment of incomplete CSI on MIMOVLC system performance by the introduced ECC, in this section, suitable methods to imitate the channel estimating imperfection required to be carried out. Without the loss of generalization, the channel matrix evaluated at the receiver can be expressed as

where H is the estimated version of H with the estimation error values expressed in a matrix  of dimensions n_r × n_t. The channel estimation error  which is independent of H and elements follow N 0,σ2 .

In later simulations, we illustrate the situation at r=4 bits in channel H₂. To set the overall impact of the estimating error on the deploying of systems, the power of the estimating error σ² was set to 0.05 value for every SNR values, i.e., approximating 6.25% of the channel gain power. Particularly with ECC and CASCC that take the incomplete CSI to the design approach. Furthermore, regard that the estimation error will likewise worsen the performance of the MIMO-VLC system that engages all modulation as discussed designs such as CC, ECC, and CASCC; because ML detector is employed. Fig.4 presents the performance comparison of ECC with different designs under profoundly CSI error where σ² = 0.05.

It is clear that because of the ineffective utilization of energy that causes such small Euclidean distances in constellation-points, the performances of conventional schemes become worse. Consequently, while channel estimation errors are significant, both of them operate inadequately. In contrast, ECC notwithstanding outperforms various schemes.

Moreover, since the inadequate CSI can directly influence the design approach of both ECC and CASCC, we can easily obtain a thorough glimpse of those two designs in some incomplete CSI conditions in Fig.4. According to Fig.4, ECC can obtain at least 2dB of SNR gain in comparison with CASCC in moderate to great CSI imperfection. It is also deserving of noticing that the performance of both designs quickly deteriorates when CSI error rising.

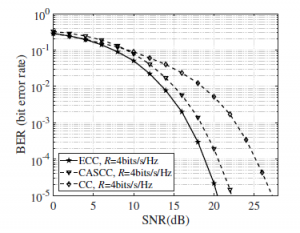
Figure 4: BER comparisons at r = 4 bits for incomplete CSI where σ² = 0.05.

6. Conclusion

In this study, a designing procedure concerning a constellation, particularly ECC, was offered for MIMO-VLC schemes. More specifically, the proposed scheme effectively exploits the layered structure of collaborative constellation and overcomes the aforementioned drawbacks of CASCC. By using simulations validation, the introduced method can give constellation, which achieves better BER results in comparison with several well-known constellation designs for VLC systems.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This work was supported by the Research Program through the National Research Foundation of Korea (NRF-2019R1A2C1005920).

1.  A. Jovicic, J. Li, T. Richardson, “Visible light communication: Opportunities, challenges and the path to market”, IEEE Commun. Mag., 51(12), 26-32, Dec. 2013. https://doi.org/10/gfxf7x
2.  S. Dimitrov, H. Haas, Principles of LED Light Communications, en. Cambridge University Press, Mar. 2015. ISBN:978–1–107–04942–0
3.  M. L. Tran, S. Kim, “Novel bit mapping for generalized spatial modulation in VLC systems”, IEEE Photonics Technol. Lett., 31(15) 1257-1260, Aug. 2019. https://doi.org/10/gf4gp4
4.  M. Le Tran, S. Kim, T. Ketseoglou, E. Ayanoglu, “LED Selection and MAP Detection for Generalized LED Index Modulation”, IEEE Photonics Technol.
   Lett., 12(8), 1254-1260, Aug. 2018. https://doi.org/10/gfr979
5. M. Simon, V. Vilnrotter, “Alamouti-type space-time coding for freespace opti- cal communication with direct detection”, IEEE Trans. Wirel. Commun., 4(1), 35-39, Jan. 2005. https://doi.org/10/d6hvvk
6. M. L. Tran, S. Kim, “Joint power allocation and orientation for uniform illu- minance in indoor visible light communication”, Opt. Express, OE, 27(20), 28575-28587, Sep. 2019. https://doi.org/10.1364/OE.27.028575
7.  L. An, H. Shen, J. Wang, Y. Zeng, R. Ran, “Energy Eciency Optimization for MIMO Visible Light Communication Systems”, IEEE Wirel. Commun.
   Lett.,12(10) 1322-1325, 2019. https://doi.org/10.1109/LWC.2019.2958802
8.  Q. Wang, Z. Wang, L. Dai, “Multiuser MIMO-OFDM for Visible Light Communications”, IEEE Photonics J., 7(6), 1-11, Dec. 2015. https://doi.org/10/gfxdm6
9.  M. L. Tran, S. Kim, “Layered adaptive collaborative constellation for MIMO visible light communication”, IEEE Access, 6, 74895-74907, 2018. https://doi.org/10.1109/access.2018.2883346
10. Yi-Jun Zhu, Wang-Feng Liang, Jian-Kang Zhang, Yan-Yu Zhang, “Space- collaborative constellation designs for MIMO indoor visible light commu- nications”, IEEE Photonics Technol Lett, 27(15), 1667-1670, Aug. 2015. https://doi.org/10/gfxdpb
11.  K. Xu, H.-Y. Yu, Y.-J. Zhu, H.-B. Cai, “Channel-adaptive space-collaborative constellation design for MIMO VLC with fast maximum likelihood detection”,
    IEEE Access, 5, 842-852, Jan. 2017. https://doi.org/10/gfxdj9
12. C. Zhang, H. Du, Z. Wu, “Robust Signal Recovery for MIMO VLC System with Incomplete Channel”, IEEE Commun. Lett., 16(8), 3327–3331, Jan. 2019. https://doi.org/10.1109 957115

(Click Here)

(Click Here)