1. Introduction

For satisfying the demand of advanced communications in terms of high data rates, relatively low costs and high-quality services, it is necessary to constantly improve the performance of wireless communication systems [1, 2]. However, protective intervals such as cyclic prefix or zero padding intervals are inserted to block transmission systems because of inter-symbol interference (ISI), which results in a decline in spectral efficiencies, especially in multipleinput multiple-output (MIMO) ISI channels having a long impulse response [3, 4]. In order to overcome the decrease of spectral efficiency and enhance the system performance, which attract lots of attention from the worldwide researchers. For example, redundancies are used instead of protector intervals throughout the signal processing to remove the ISI as in [5]-[9]. Moreover, various approaches based on the precoding scheme or the hybrid of precoding and equalization schemes of MIMO ISI channels were proposed [10]-[17].

In many approaches, it is assumed that channel status information (CSI) is able to be obtained perfectly. However, in practical scenarios, the perfect CSI is difficult to achieve in MIMO ISI systems because of the imperfection of channel estimation, feedback delay and finite rate channel quantization. Therefore, the research on a negative influences of imperfect CSI in MIMO ISI systems is necessary. A number of researches in this field developing precoders or connecting precoder and equalizer schemes with respect to the CSI at transmitters, receivers or transceivers have been published. There are many surveys expressed to analyze the performance of the MIMO system with imperfect CSI as follows.

Firstly, several surveys with the negative influences of imperfect CSI at transmitters were proposed and analyzed in [18]-[22]. To give a clear example, a MIMO system with joint decoding technique evaluated transmission rates which are affected by imperfect CSI [18]. Multi-user MIMO filterbank multicarrier systems employing the Zero Forcing technique are affected by imperfect CSI as demonstrated in [19]. The obtainable transmission rate of multipath channel systems with decoding technique was described in [20]. Analysis and investigation of MIMO systems occupying TomlinsonHarashima precoding are mentioned in [21, 22].

Next, there have been also some papers studied the negative influences of imperfect CSI at the receiver [23]-[27]. For instance, the achievable transmission rate was evaluated in [23] by assumption of knowing the transmitted training symbols. The impact of CSI and feedback quantization error bring to MIMO systems in term of adaptive modulation was investigated in [24]. The effect of CSI to a capacity of MIMO systems was studied in [25]-[27].

Finally, an investigation about the combination of linear precoding and decoding to minimize the total mean-square error of MIMO systems was shown in [28, 29] when there is the imperfect CSI at transceivers. Furthermore, the negative influences of the imperfect CSI on a resource allocation of base stations by using several techniques such as transmit antennas selection, power allocation and beamforming was considered in [30]-[32].

In this work, we focus on combination of both precoding and equalization schemes, which employ redundancies for MIMO ISI systems. The proposed scheme, shared redundancies for both transmitters and receivers are used to perform a combination design of precoder and equalizer. In the next part, an investigation of the negative influence of imperfect CSI on the performance of these systems will be performed. Herein, the length of protective intervals generally defines redundancies as in [8].

The contribution of the research is summarized as follows.

• The proposed joint scheme of precoding and equalization schemes with shared redundancy is mathematical analyzed in both perfect and imperfect CSI.
• The conventional methods, such as training zero and leading zero, are investigated to compare with the proposed scheme.
• The impact of imperfect CSI on the system performance is discussed based on bit error rate and channel capacity.
• The proposed scheme is evaluated based on different parameters, such as the accuracy of channel estimation, the order of the finite impulse response and the transmission block size.

The order of other parts in this paper are as follows: In Section 2, the system model with imperfect CSI is introduced, while both precoding and equalization techniques are combined for the MIMO ISI systems, and then the combination of them are demonstrated. The negative influences of imperfect CSI on the performance of system is analyzed in Section 3. Simulation results and conclusions are shown in Section 4 and Section 5, respectively. Notations in this paper are used as follows: sets of complex numbers are represented by symbol C, while (·)^H denotes the conjugate transpose, (·)^T is the transpose and boldface font is used for vector and matrix.

2. System Model

In this work, joint scheme of precoding and equalization for MIMO ISI channels of block transmission system models is proposed as illustrated in Fig.1. M_T and M_R denote the transmitting and receiving antennas, The channel model of this system is assumed to be frequency selective fading. Moreover, the finite impulse response (FIR) of channel has an order of D, in which the channel impulse response (CIR) is expressed by matrices H¯ [0],H¯ [1],…,H¯ [D], herein, H¯ [d] ∈ C^MT×MR,(d = 0,…, D).

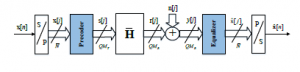
Figure 1: Hybrid scheme of precoder and equalizer in MIMO ISI systems

The system model of the MIMO ISI channel with joint scheme of precoder and equalizer in Figure 1 is expressed as follows. At the transmitter, a single input stream x[n] is transferred to a serialto-parallel converter, and then converted into a block of vectors x[j] with a block size of N¯ × 1. Then, the vector x[j] is sent to the precoder. The precoder performs signal processing procedure so as to perform symbol vector generation x[j] with the dimension of QM_T × 1 from input vector s[j]. Afterwards, the vector s[j] is divided into Q vectors, each of which has the size of M_T × 1, and converted by the parallel-to-serial converter, then transmitted over the MIMO ISI channel. At the output side, the received symbol vector y[j] has two parts because of the affection of noise, including an information vector r[j] and a noise sample vector n[j] that is considered as an additive white Gaussian noise sample vector, and n[j] v CN(0,1).

The signal processing procedure is employed conversely at the receiver. QM_R × 1 symbol vector y[j] is formed by the Q received vectors in the serial-to-parallel converter. Subsequently, the symbol vector y[j] is sent to the equalizer in order to regenerate the original symbol vector xˆ[i] with the dimension of N¯ × 1. Finally, the parallel-to-serial converter reforms the output symbol stream xˆ[n] from the symbol vector xˆ[i].

Based on the operation and signal processing of system mentioned above, the terms defined as x[j], s[j], y[j], xˆ[i], r[j] and n[j] according to the input symbol stream x[n] and the sampled vector of received signal xˆ[n], can be mathematically shown in the (1) – (6) equations, respectively.

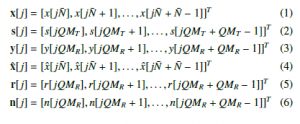
3. Performance Analysis

3.1        Joint Scheme of Precoder and Equalizer

In this section, the proposed joint scheme of precoder and equalizer based on MIMO ISI channels is explained. In addition, the channel model is assumed to be narrow-band, therefore the Saleh-Valenzuela model [33] can be adopted. In the case of Q ≥ D, the symbol xˆ[j] is expressed following the ideas in [6]

where n[j] ∈ CQMR×1; F ∈ CQMT×N¯ and G ∈ CN¯×QMR are respectively the precoding and the equalization matrices, and expressed by following equations

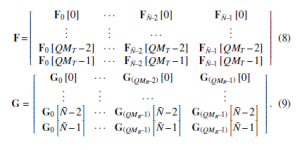
Additionally, H¯ ₀ and H¯ ₁ are utilized to give a definition of the Toeplitz matrices whose uniform dimension is QM_R × QM_T, and

The effect of ISI on the MIMO ISI system model shown in

Fig. 1 is the second component on the right side of the equation

(7), (GH₁Fs[i − 1]). With an assumption of QM_T = M¯ + DM_T, (N¯ ≤ M¯ ), two conditional methods (one is named by the trailing zero (TrZero) and the other one is the leading zero (LeZero) [6]) can be used to cancel the ISI.

Actually, although the performance of both TrZero and LeZero technical schemes is almost similar, the TrZero scheme is solely considered. For the TrZero technical scheme, the equalization matrix keeps the same (G_TrZero = G), whereas the precoding matrix changes the last DM_T rows to be zero. The precoding matrix has

Subsequently, the optimal criteria is utilized to design the F_TrZero precoder and the G_TrZero equalizer jointly to improve the system performance. Thus, when GH¯ ₁Fx[j − 1] is disappeared, it means that the ISI is not completely existent, the equation (7) becomes as follows xˆ[j] = GTrZeroHF¯ TrZerox[j] + GTrZeron[j]. (14) where the H¯ matrix comprises (Q − D)M_T first columns of the H¯ ₀

GTrZero = RxxFTrZeroH H¯ H(Rnn + HF¯ TrZeroRxxFTrZeroH H¯ H)−1, (17) where U and V are unitary matrices obtained from the eigenvalue decompositions (EVD) algorithm, and Φ is a diagonal matrix, whose main diagonal elements Λ matrix can be obtained from a water-

filling algorithm,

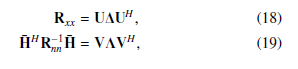
where R_xx and R_nn are the covariance matrices of the input signal and noise, respectively.

Obviously, the signal to interference noise ratios (SINRs) among the decoupled flat sub-channels are not similar because of the unequal eigenvalues obtained from (19). Hence, the sub-channel with low SINR significantly influences the performance of the system, it means that those sub-channels should be discarded to enhance the system BER [17]. In addition, when the protective interval or the redundancy is utilized, the ISI interference can be cancelled in the frequency selective channel, however the addition of the protective interval or the redundancy lets channel energy be lost.

For solving the above issue, the ideas expressed in [6, 9] were combined and both precoder and equalizer technique schemes relied on the unweighted MMSE criterion [10] was proposed. This proposal aimed to share redundancies to both the transmitter and the receiver. Especially, instead of setting the last DM_T rows of the F precoding matrix, only last KM¯ _T = ^{j DM}₂ ^{T k} rows are set to zero, while the first (D − K¯)M_R columns of the G equalization matrix are also set to zero at the receiver. Herein, the transmitter and the receiver obtain the shared protective interval, it means that the first (D−K¯)M_R rows of the H¯ ₀ channel matrix and the last KM¯ _T columns of H¯ ₀ channel matrix are removed by the G equalization matrix and the F precoding matrix, respectively. Consequently, the loss in H¯ ₀ channel matrix is able to reduced by the proposed design. In the other words, the partial channel energy loss can be reduced. Basing on the above analysis, in our method, the precoder and equalizer are designed as follows (20) and (21).

The unweighted MMSE criterion will be used to design the Fˆ precoder and the Gˆ equalizer [15]. weak eigenmodes are dropped, so they do not affect the BER of system. The transmit power is redistributed for the remaining eigenvalues. Consequently, power distribution to the higher eigenvalues is larger than that of the MIMO ISI channel.

When the ISI cancellation is complete, the equation (7) can be expressed as follows

herein, the noise sample block with the length of (Q − D + K¯)M_R is denoted as n⁰[j].

3.2        In the Case of Imperfect CSI

Factually, the perfect CSI cannot be produced at both the transmitter and the receiver. In this work, we assume that the perfect CSI exists at the transmitter, which means that its feedback is immediate and error-free, whereas the receiver has the imperfect CSI. Herein, the accurate channel matrix and the inaccurate channel matrix with a complex Gaussian distribution are denoted as Hˆ and Hˆ _e, respectively, in which Hˆ _e ∈ CN(0,1). Thus, the illustration of the channel matrix is as follows [34, 35]

The sizes of these matrices are Q − D + K¯ M_R ^× Q − K¯ M_T, and the accuracy of channel estimation is illustrated by ξ, where 0 ≤ ξ ≤ 1. Therefore, the equation (24) is rewritten as

The F˜ and G˜ matrices of the precoder and the equalizer are designed under the imperfect CSI at the receiver, and optimized in accordance with the unweighted MMSE criterion [15]. Therefore, the mathematical description is expressed as min:cG˜ ,F˜ = E   W1/2e   2,

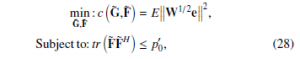
where e = x[j]−(G˜ H˜ Fx˜ [j]+Gn˜ ⁰[j]), the weight matrix W = I and the transmit power is constrained to p⁰₀. The expectation (E) relates to the distribution of x and n.

where the error covariance matrix is denoted the ReG˜ ,F˜ and defined as ReG˜ ,F˜ := E ee^H. Using the expression for e and the above assumption, we have

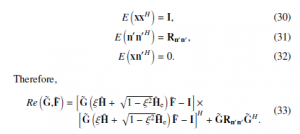
For solving the optimization problem in (28), the method of Lagrange duality and the Karush-Kuhn-Tucker (KKT) conditions are utilized, where η is the Lagrange multiplier.

Applying the derivatives of Lη,G˜ ,F˜ with respect to F˜ and G˜ as in [36] and substitute (35) into (36) and (37). As a result, the F˜ and G˜ matrices can be calculated as follows

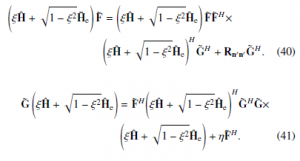
where F˜, G˜ are designed by the unweighted MMSE criterion. Consequently, the optimal F˜, G˜ matrices are derived as follows

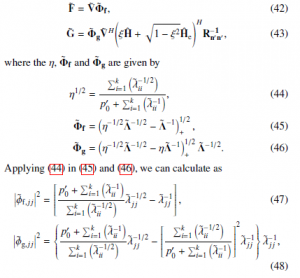
where the main diagonal element of Λ˜ is denoted by λ˜ _jj. Moreover, the Λ˜ and V˜ are matrices obtained from the EVD algorithm

4. Simulation Results

To evaluate the performance of the proposed scheme under the condition of imperfect CSI at the receiver, the system model is assumed to have four transmit antennas and four receive antennas. The system performance is evaluated according to the channel estimation accuracy ξ, the order of FIR D and transmit block size Q. The Saleh-Valenzuela indoor channel model is used to generate the CIR as in [33] and the 4-QAM modulation is applied. Additionally, the overall transmit power is standardized through transmit antennas (p⁰₀=1), and the system performance of the proposed scheme is simulated and calculated according to the Monte Carlo simulation.

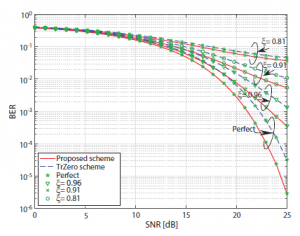
Figure 2: BER performance of the proposed scheme is compared with the TrZero scheme when D = 12 and Q = 26

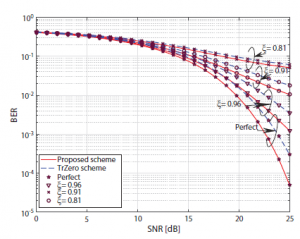
Figure 3: BER performance of the proposed scheme is compared with the TrZero scheme when D = 12 and Q = 30

On the other hand, the BER performance of the proposed and the TrZero schemes is compared in the different situations of the order of FIR and the transmission block dimension as illustrated in Figures 2, 3 and 4, respectively. In general, the BER of the TrZero scheme is significantly higher than that of the proposed one at all considered ξ values, such as ξ = 0.81, 0.91 and 0.96, and 1 (the perfect CSI). Furthermore, it is obvious that the accuracy of channel estimation proportionally affects the BER of the system, which means that the BER and the accuracy of channel estimation increase simultaneously, especially for the high SNR range. This is because of the fact that the residual interference due to imperfect CSI increases when the SNR increases. Consequently, the SINR of every sub-channel extremely decreases compared to the SNR of the perfect one.

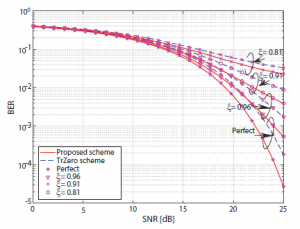
Figure 4: BER performance of the proposed scheme is compared with the TrZero scheme when D = 10 and Q = 26

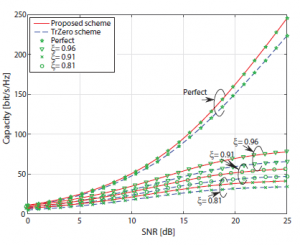
Figure 5: Comparison of system capacity in the proposed and TrZero schemes when D = 12 and Q = 26

As shown in Figures 2 and 3, the BER of the system is deteriorated when the Q increases, or the D decreases (Figures 2 and 4). It can be explained that the increase of Q makes the number of sub-channels increases while the shared redundancy is fixed. Thus, the channel energy for every sub-channel decreases. In contrast, when the D decreases, the shared redundancy decreases while the number of sub-channels is fixed, it leads the decrease in the channel energy for every sub-channel.

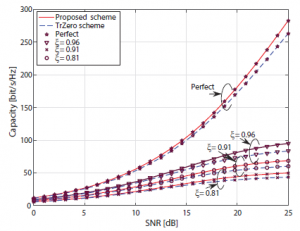
Figure 6: Comparison of system capacity in the proposed and TrZero schemes when D = 12 and Q = 26

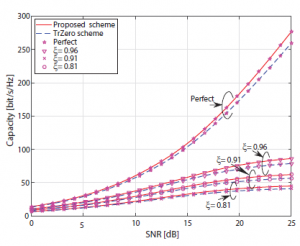
Figure 7: Comparison of system capacity in the proposed and TrZero schemes when D = 10 and Q = 26

Finally, the capacity of the proposed scheme is slightly higher than that of the TrZero scheme in all analyzed scenarios as in Figures 5, 6 and 7. Moreover, compared to the capacity of system with perfect CSI, the capacity of system with imperfect CSI is decreased dramatically. It is the same for both the TrZero and the proposed technical schemes. For more detail, at the 25 dB of SNR in Figure 5, when the accuracy of channel estimation ξ drops from 0.96 to 0.91, the system capacity witnesses a decrease from 80 to 55 bit/s/Hz.

Furthermore, the capacity of system under the imperfect CSI condition at the receiver increases due to the increase of the transmission block size. On the other hand, the capacity of system decreases once the order of FIR increases in both schemes. The reason is that when the transmission block dimension increases and/or the FIR order decreases, the SINR of every sub-channel decreases, however the number of sub-channels in MIMO ISI channels is increased. As a result, the capacity of the MIMO ISI system under the imperfect CSI condition increases.

5. Conclusion

In this paper, the combination scheme of precoder and equalizer relied on the unweighted MMSE criterion for the imperfect CSI of MIMO ISI channels has been developed. The proposed scheme lets the loss of channel energy decrease and eliminates some subchannels with extremely small eigenvalue in order to improve the system performance. The proposed scheme is evaluated by Monte Carlo simulation, and the simulation result shows that the proposed scheme under limited transmit power can achieve the higher system performance comparing to the conventional scheme in the considered scenarios even when the CSI is imperfect. However, the performance of the MIMO ISI system using redundancies is significantly affected by the CSI factor. Furthermore, the relationship between the performance of the system and several parameters, such as the accuracy of channel estimation, the transmission block size and the FIR order, are also discussed. The result in this research can help us to structure a practical MIMO ISI system which is close to the actual situation. The investigation of the impact of imperfect CSI on the advanced future communication system, such as massive MIMO or MIMO filterbank multicarrier systems, with combining designs of precoder and equalizer is left to future works.

1.  R. Vannithamby and S. Talwar, New Physicallayer Waveforms for 5G. Wiley, 2017. [Online]. Available: https://ieeexplore.ieee.org/document/8043580
2.  F. Corno, L. De Russis, and J. Pablo Senz, “On the advanced services that 5g may provide to iot applications,” in 2018 IEEE 5G World Forum (5GWF), pp. 528–531, July 2018.
3.  B. Kwon, S. Kim, S. Lee, Scattered Reference Symbol-Based Channel Es- timation and Equalization for FBMC-QAM Systems. IEEE Transactions on Communications, vol. 65, no. 8, pp. 3522 – 3537, 2017.
4. J. Wang, Q. Yu ; Z. Li, C. Bi, ”Distributed Space Time Block Transmission and QRD Based Diversity Detector in Asynchronous Cooperative Communications Systems,” IEEE Transactions on Vehicular Technology, vol. 67, no. 6, pp. 5111–5125, 2018.
5.  C. Dong, J. Lin, K. Niu, Z. He, and Z. Bie, “Block-iterative decision feedback equalizer with noise prediction for single-carrier MIMO transmission,” IEEE Transactions on Vehicular Technology, vol. 61, no. 8, pp. 3772–3776, 2012.
6.  A. Scaglione, G. B. Giannakis, and S. Barbarossa, “Redundant filterbank pre- coders and equalizers. i. unification and optimal designs,” IEEE Transactions on Signal Processing, vol. 47, no. 7, pp. 1988–2006, 1999.
7.  M.-W. Kwan and C.-W. Kok, “MMSE equalizer for MIMO-ISI channel with shorten guard period,” IEEE transactions on signal processing, vol. 55, no. 1, pp. 389–395, 2007.
8.  W. A. Martins and P. S. R. Diniz, “Block-based transceivers with minimum redundancy,” IEEE Transactions on Signal Processing, vol. 58, no. 3, pp.
   1321–1333, 2010.
9.  Y.-P. Lin and S.-M. Phoong, “Minimum redundancy for ISI free FIR filterbank transceivers,” IEEE Transactions on Signal Processing, vol. 50, no. 4, pp. 842–853, 2002.
10.  B. Q. Doanh, P. T. Hiep, T. C. Hieu et al., “A combining design of precoder and equalizer based on shared redundancy to improve performance of ISI MIMO systems,” Wireless Networks, pp. 1–10, 2019
11.  Y. Zhai, J. Tong, and J. Xi, “Precoder design for MIMO visible light com- munications with decision-feedback receivers,” IEEE Photonics Technology Letters, 2019.
12.  Y. Cheng, L. G. Baltar, M. Haardt, and J. A. Nossek, “Precoder and equalizer design for multi-user MIMO FBMC/)QAM with highly frequency selective channels,” in Acoustics, Speech and Signal Processing (ICASSP), 2015 IEEE International Conference on. IEEE, pp. 2429–2433, 2015.
13.  F. Rottenberg, X. Mestre, and J. Louveaux, “Optimal zero forcing precoder and decoder design for multi-user mimo FBMC under strong channel selectivity.” in ICASSP, pp. 3541–3545, 2016.
14.  F. Rottenberg, X. Mestre, F. Horlin, and J. Louveaux, “Single-tap precoders and decoders for multiuser MIMO FBMC-OQAM under strong channel fre- quency selectivity,” IEEE transactions on signal processing, vol. 65, no. 3, pp. 587–600, 2017.
15. H. Sampath, P. Stoica, and A. Paulraj, “Generalized linear precoder and de- coder design for MIMO channels using the weighted MMSE criterion,” IEEE Transactions on Communications, vol. 49, no. 12, pp. 2198–2206, 2001.
16.  H. Yang, C. Chen, W.-D. Zhong, and A. Alphones, “Joint precoder and equal- izer design for multi-user multi-cell mimo vlc systems,” IEEE Transactions on Vehicular Technology, vol. 67, no. 12, pp. 11 354–11 364, 2018.
17.  A. Scaglione, P. Stoica, S. Barbarossa, G. B. Giannakis, and H. Sampath, “Opti- mal designs for space-time linear precoders and decoders,” IEEE Transactions on Signal Processing, vol. 50, no. 5, pp. 1051–1064, 2002.
18.  N. Lee, O. Simeone, and J. Kang, “The effect of imperfect channel knowledge on a MIMO system with interference,” IEEE Transactions on Communications, vol. 60, no. 8, pp. 2221–2229, August 2012.
19.  D. Le Ruyet, R. Zakaria, and B. O¨ zbek, “On precoding MIMO-FBMC with imperfect channel state information at the transmitter,” in 2014 11th Interna- tional Symposium on Wireless Communications Systems (ISWCS). IEEE, pp. 808–812, 2014.
20. I. Dvorakova, A. Malyutin, and Y. Nechaev, “MMSE precoder for multipath channels with imperfectly known state information,” in 2015 38th International Conference on Telecommunications and Signal Processing (TSP), pp. 195–199, July 2015.
21. M. Huang, S. Zhou, and J. Wang, “Analysis of TomlinsonHarashima precoding in multiuser mimo systems with imperfect channel state information,” IEEE Transactions on Vehicular Technology, vol. 57, no. 5, pp. 2856–2867, Sep. 2008.
22. H. K. Bizaki and A. Falahati, “Tomlinson-Harashima precoding with imperfect channel state information,” IET Communications, vol. 2, no. 1, pp. 151–158, January 2008.
23.  J. Baltersee, G. Fock, and H. Meyr, “Achievable rate of MIMO channels with data-aided channel estimation and perfect interleaving,” IEEE Journal on Selected Areas in Communications, vol. 19, no. 12, pp. 2358–2368, Dec 2001.
24.  A. Maaref and S. A ̈ıssa, “Combined adaptive modulation and truncated arq for packet data transmission in mimo systems,” in Global Telecommunications Conference, 2004. GLOBECOM’04. IEEE, vol. 6. IEEE, pp. 3818–3822, 2004.
25.  B. Hassibi and B. M. Hochwald, “How much training is needed in multiple- antenna wireless links?” IEEE Transactions on Information Theory, vol. 49, no. 4, pp. 951–963, April 2003.
26.  A. Goldsmith, “Capacity and power allocation for fading mimo channels with channel estimation error,” IEEE Transactions on Information Theory, vol. 52, no. 5, pp. 2203–2214, May 2006.
27.  B. Q. Doanh, P. T. Hiep, and T. C. Hieu, “Impact of imperfect CSI on capacity of ISI MIMO systems based on joint precoding and equalization designs,” in 2019 19th International Symposium on Communications and Information Technologies (ISCIT). IEEE, pp. 334–338, 2019.
28.  M. Ding and S. D. Blostein, “MIMO minimum total MSE transceiver design with imperfect csi at both ends,” IEEE Transactions on Signal Processing, vol. 57, no. 3, pp. 1141–1150, March 2009.
29.  B. S. Thian, S. Zhou, and A. Goldsmith, “Transceiver design for MIMO sys- tems with imperfect csi at transmitter and receiver,” in 2011 IEEE International Conference on Communications (ICC), pp. 1–6, June 2011.
30.  Z. Chang, Z. Wang, X. Guo, Z. Han, and T. Ristaniemi, “Energy-efficient re- source allocation for wireless powered massive MIMO system with imperfect CSI,” IEEE Transactions on Green Communications and Networking, vol. 1, no. 2, pp. 121–130, June 2017.
31.  P. Aquilina and T. Ratnarajah, “Linear interference alignment in full-duplex MIMO networks with imperfect CSI,” IEEE Transactions on Communications, vol. 65, no. 12, pp. 5226–5243, Dec 2017.
32.  J. Cui, Z. Ding, and P. Fan, “Outage probability constrained MIMO-NOMA designs under imperfect CSI,” IEEE Transactions on Wireless Communications, vol. 17, no. 12, pp. 8239–8255, Dec 2018.
33.  A. A. Saleh and R. Valenzuela, “A statistical model for indoor multipath propa- gation,” IEEE Journal on selected areas in communications, vol. 5, no. 2, pp. 128–137, 1987.
34.  S. Serbetli and A. Yener, “MMSE transmitter design for correlated MIMO sys- tems with imperfect channel estimates: power allocation trade-offs,” IEEE Transactions on Wireless Communications, vol. 5, no. 8, pp. 2295–2304, Aug 2006.
35.  L. Musavian, M. R. Nakhai, M. Dohler, and A. H. Aghvami, “Effect of channel uncertainty on the mutual information of mimo fading channels,” IEEE Trans- actions on Vehicular Technology, vol. 56, no. 5, pp. 2798–2806, Sep. 2007.
36.  H. Lu¨tkepohl, “Handbook of matrices. wiley,” New York, 1996.

(Click Here)

(Click Here)